Scroll to:
Analysis of the stress-strain state of a radially inhomogeneous transversely isotropic sphere with a fixed side surface
https://doi.org/10.23947/2687-1653-2022-22-1-14-23
Abstract
Introduction. The paper considers an axisymmetric problem of elasticity theory for a radially inhomogeneous transversally isotopic nonclosed sphere containing none of the 0 and 𝜋 poles. It is believed that the elastic moduli are linear functions of the radius of the sphere. It is assumed that the side surface of the sphere is fixed, and arbitrary stresses are given on the conic sections, leaving the sphere in equilibrium. The work objective is an asymptotic analysis of the problem of elasticity theory for a radially inhomogeneous transversally isotropic sphere of small thickness, and a study of a three-dimensional stress-strain state based on this analysis.
Materials and Methods. The three-dimensional stress-strain state is investigated on the basis of the equations of elasticity theory by the method of homogeneous solutions and asymptotic analysis.
Research Results. After the homogeneous boundary conditions set on the side surfaces of the sphere are met, a characteristic equation is obtained, and its roots are classified with respect to a small parameter characterizing the thickness of the sphere. The corresponding asymptotic solutions depending on the roots of the characteristic equation are constructed. It is shown that the solutions corresponding to a countable set of roots have the character of a boundary layer localized in conic slices. The branching of the roots generates new solutions that are characteristic only for a transversally isotropic radially inhomogeneous sphere. A weakly damping boundary layer solution appears, which can penetrate deep away from the conical sections and change the picture of the stress-strain state.
Discussion and Conclusions. Based on the solutions constructed, it is possible to determine the applicability areas of existing applied theories and propose a new more refined applied theory for a radially inhomogeneous transversally isotropic spherical shell.
Keywords
For citations:
Akhmedov N.K., Yusubova S.M. Analysis of the stress-strain state of a radially inhomogeneous transversely isotropic sphere with a fixed side surface. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):14-23. https://doi.org/10.23947/2687-1653-2022-22-1-14-23
Introduction. One of the properties of materials affecting the stress-strain state of elastic bodies is their heterogeneity. Investigating the stress-strain state of inhomogeneous bodies based on three-dimensional equations of elasticity theory is associated with significant mathematical difficulties.
A number of studies are devoted to the investigation of three-dimensional problems of elasticity theory for the sphere.
In [1], based on the equations of elasticity theory for the sphere, a general solution satisfying the boundary conditions on the contour in the sense of Saint-Venant was obtained, the stress-strain state of the sphere was analyzed. In [2], based on the equations of elasticity theory for a thick isotropic sphere, homogeneous solutions depending on the roots of the transcendental equation are constructed. In [3], on the basis of solving three-dimensional problems of elasticity theory for a sphere of small thickness, the accuracy of existing applied theories is studied, and a method for constructing refined applied theories is given. A three-dimensional asymptotic theory of a transversally isotropic spherical shell of small thickness is presented in [4]. An analysis of the three-dimensional stress-strain state of a threelayer sphere with a soft filler is described in [5]. In [6], the torsion problem is studied by the method of homogeneous solutions for a radially inhomogeneous transversally isotropic sphere of small thickness, when the elastic characteristics are changed by linear, quadratic and inversely quadratic laws along the radius. In [7], the torsion problem for a radially layered sphere with an arbitrary number of alternating hard and soft layers is studied. The existence of weakly damping boundary-layer solutions and a possible violation of the Saint-Venant principle in its classical formulation are shown. An applied theory of torsion of a radially layered sphere is constructed, which adequately takes into account the emerging features. In [8], the problem of elasticity theory for a radially inhomogeneous hollow ball is investigated using the finite element method and spline collocation. In [8], using the finite element method and spline collocation, the problem of elasticity theory for a radially inhomogeneous hollow ball is studied. The results obtained by finite element methods and spline collocation are compared. The axisymmetric problem of the theory of elasticity for a radially inhomogeneous transversally isotropic sphere of small thickness is studied by the method of asymptotic integration of the equations of the theory of elasticity in [9]. Inhomogeneous and homogeneous solutions are constructed. The nature of the stress-strain state is established. In [10], an axisymmetric problem of elasticity theory for a sphere of small thickness with variable elasticity moduli is considered by the method of homogeneous solutions. Asymptotic formulas for displacements and stresses are obtained, which provides calculating the three-dimensional stress-strain state of a radially inhomogeneous sphere.
Materials and Methods. Deformation is considered within the framework of the linear theory of elasticity of a nonclosed sphere, whose material is transversely isotropic and inhomogeneous along the radial coordinate. The thickness of the hollow sphere is assumed to be small compared to the radius and size along the arc coordinate. Boundary conditions are considered that provide solving the problem in an axisymmetric formulation. We assume that the sphere does not contain any of the poles 0 and 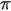 . In the spherical coordinate system, the area occupied by the sphere will be denoted by
. In the spherical coordinate system, the area occupied by the sphere will be denoted by 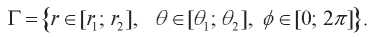
The linear dependence of the elastic properties of the material along the radius is considered:
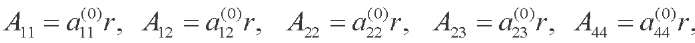 (1)
(1)
where 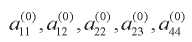 — some constants.
— some constants.
The system of equilibrium equations in the absence of body forces in a spherical coordinate system r, 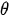 ,
, 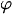 has the form [11]:
has the form [11]:
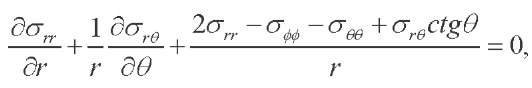 (2)
(2)
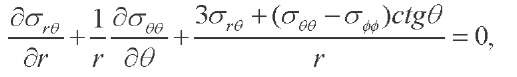 (3)
(3)
where
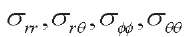 — stress tensor components, which are expressed in terms of displacement vector components
— stress tensor components, which are expressed in terms of displacement vector components 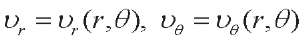 as follows [4]:
as follows [4]:
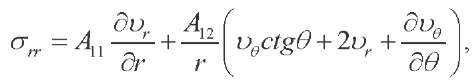 (5)
(5)
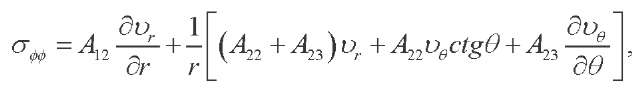 (6)
(6)
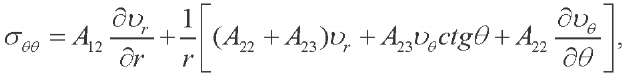 (7)
(7)
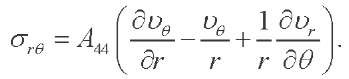 (8)
(8)
Substituting (5)–(8) into (2)–(3), taking into account (1), we obtain the equations of equilibrium in displacements.
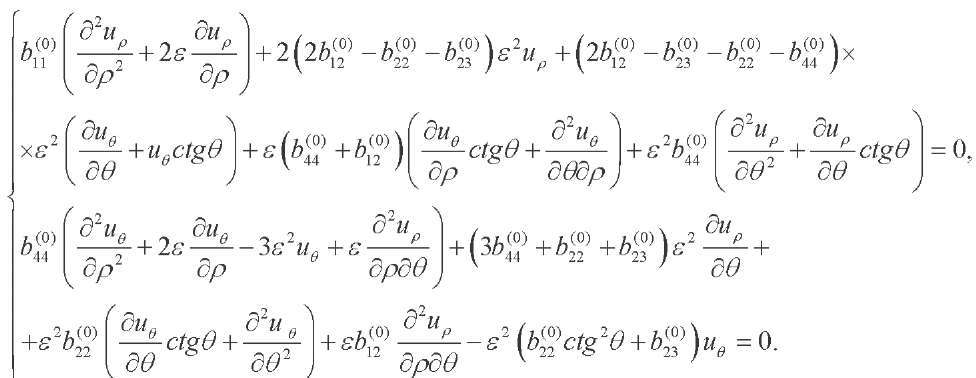 (9, 10)
(9, 10)
Here, 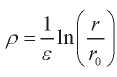 — new dimensionless variable;
— new dimensionless variable; 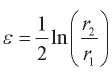 — a small parameter characterizing the thickness of the sphere;
— a small parameter characterizing the thickness of the sphere; 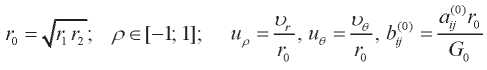 — dimensionless quantities; G0 — some parameter having the dimension of the elasticity modulus.
— dimensionless quantities; G0 — some parameter having the dimension of the elasticity modulus.
We assume that the lateral part of the sphere boundary is fixed, i.e.,
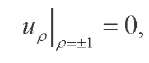 (11)
(11)
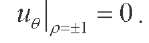 (12)
(12)
We assume that at the ends of the sphere (on the conical sections), the stresses are specified
 (13)
(13)
Here, 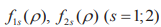 — sufficiently smooth functions that satisfy the equilibrium conditions.
— sufficiently smooth functions that satisfy the equilibrium conditions.
Solutions (9), (10) are sought in the form [3][4]:
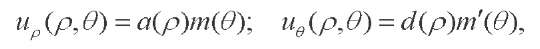 (14)
(14)
Where function m(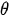 ) satisfies the Legendre equation:
) satisfies the Legendre equation:
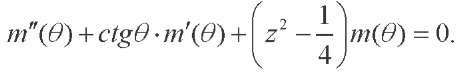 (15)
(15)
After substituting (14) into (9), (10), (11), (12), taking into account (15), we obtain:
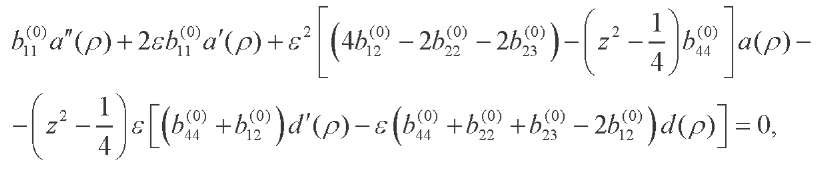 (16)
(16)
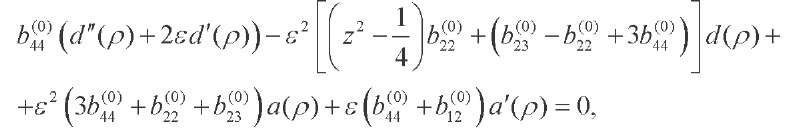 (17)
(17)
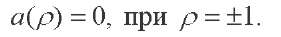 (18)
(18)
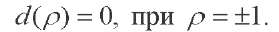 (19)
(19)
The solution to system (16), (17) has the form:
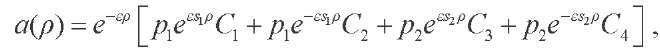 (20)
(20)
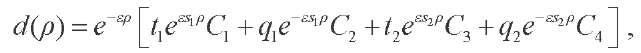 (21)
(21)
where 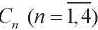 — arbitrary constants,
— arbitrary constants,
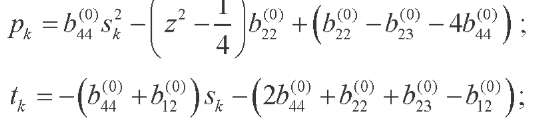
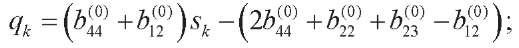
sk — equation roots
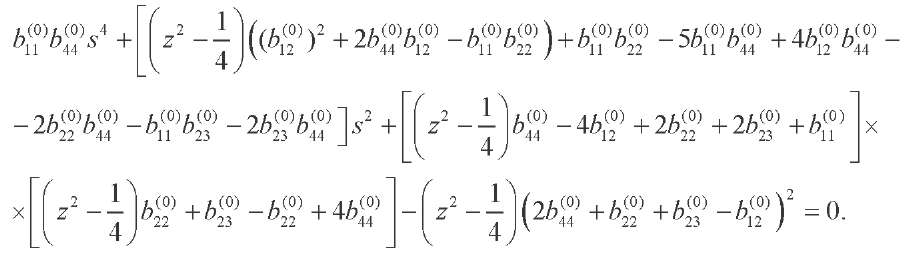 (22)
(22)
The system of linear algebraic equations with respect to C1,C2, C3,C4, is obtained through satisfying the homogeneous boundary conditions (18), (19). The zero equality of the determinant of this system is a condition for the existence of nonzero solutions and leads to a characteristic equation with respect to spectral parameter
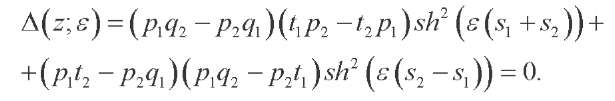 (23)
(23)
Equation (23) has countable set of roots zk. The general solution to the problem is obtained by summing over the roots of equation (23)
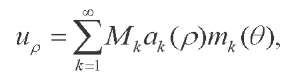 (24)
(24)
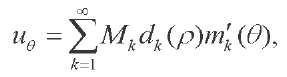 (25)
(25)
where
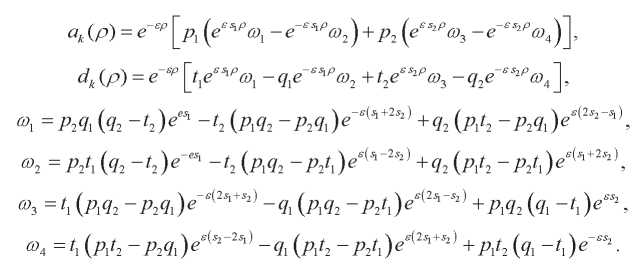
The set of roots of equation (23) at 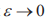 consists of countable sets of roots
consists of countable sets of roots
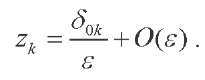 (26)
(26)
For  0k, we have:
0k, we have:
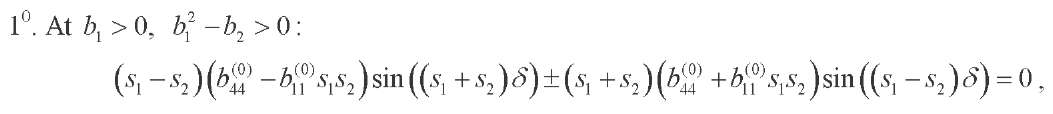 (27)
(27)
where
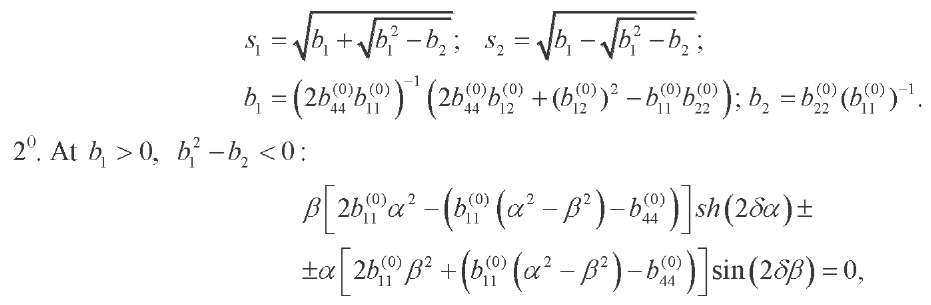 (28)
(28)
where
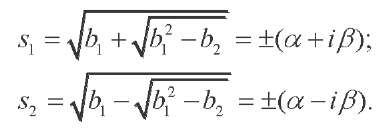
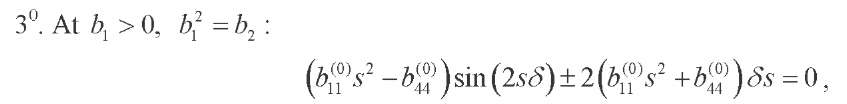 (29)
(29)
where
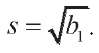
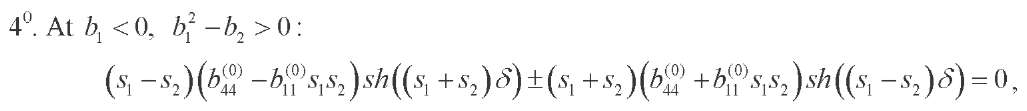 (30)
(30)
where
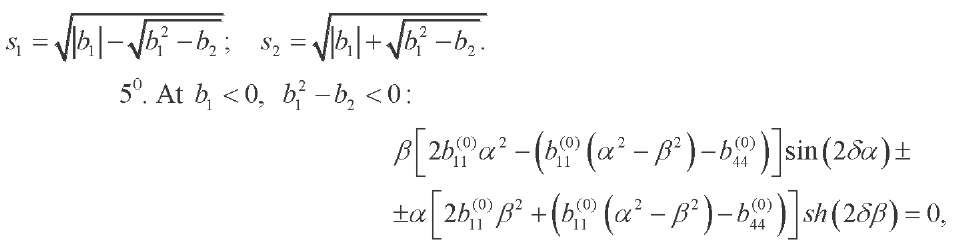 (31)
(31)
where
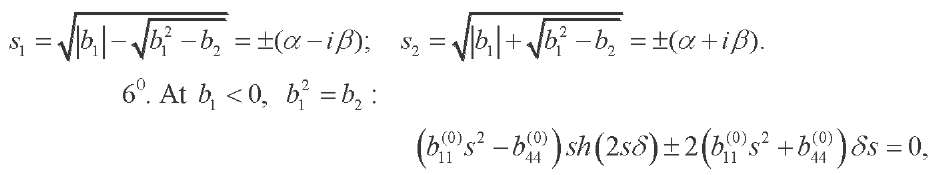 (32)
(32)
where
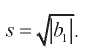
Equation (27)–(32) has a countable set of solutions.
Let us present an asymptotic construction of solutions corresponding to different groups of roots of the characteristic equation (23). Substituting (26) into (24), (25) and expanding the resulting expressions in powers 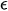 , we have:
, we have:
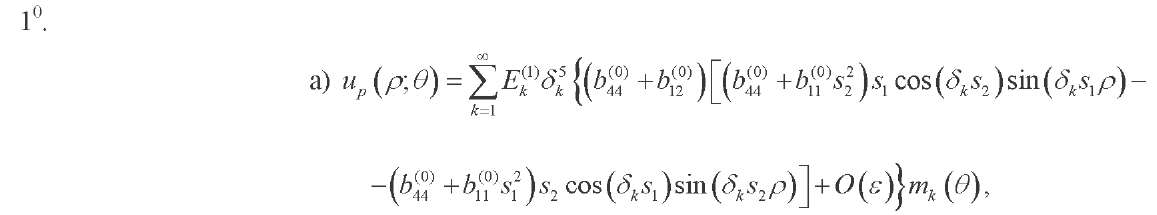 (33)
(33)
![]() (34)
(34)
where 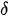 0k are the solutions to equation
0k are the solutions to equation
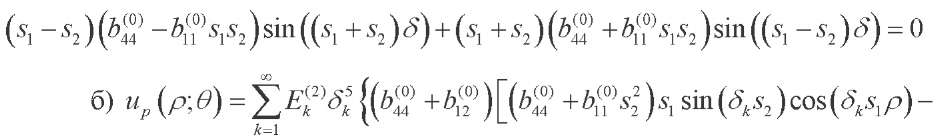 (35)
(35)
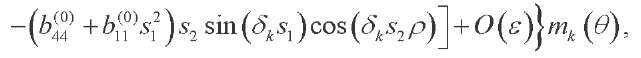 (36)
(36)
![]() (37)
(37)
where 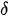 0k are the solutions to equation
0k are the solutions to equation
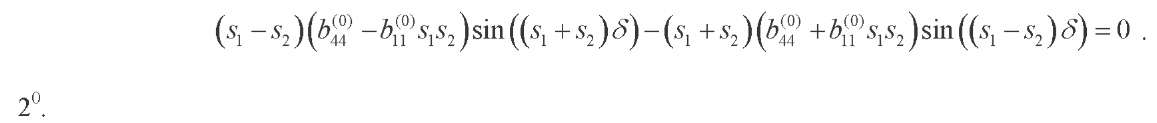
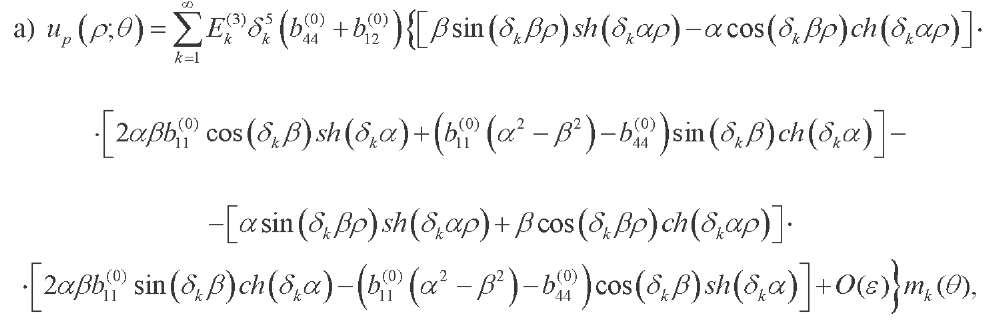 (38, 39)
(38, 39)
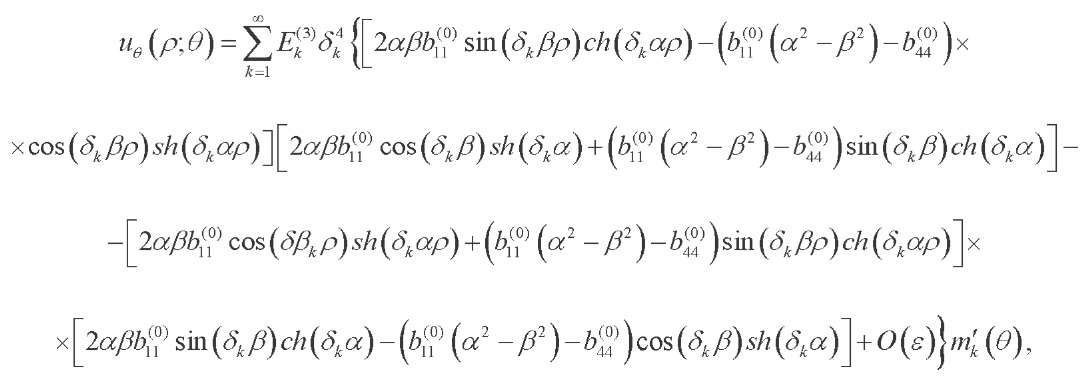 (40)
(40)
where 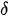 0k are the solutions to equation
0k are the solutions to equation
![]() (41)
(41)
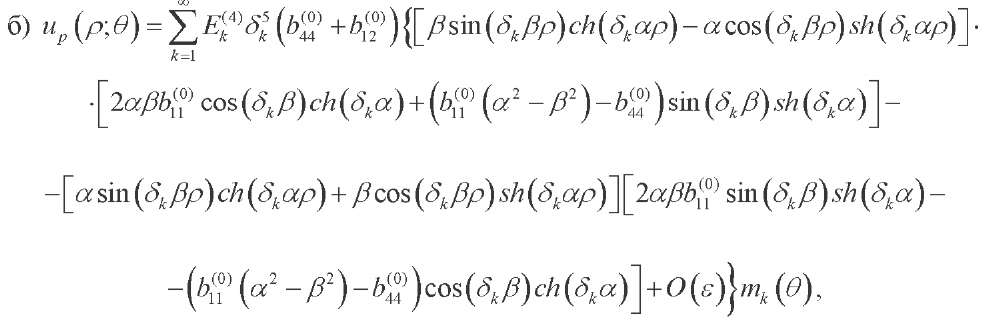 (42)
(42)
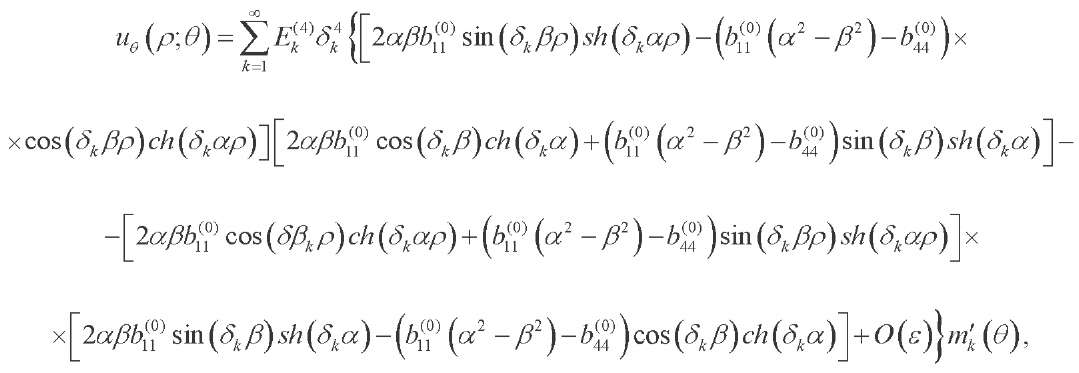 (43)
(43)
where 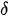 0k are the solutions to equation
0k are the solutions to equation
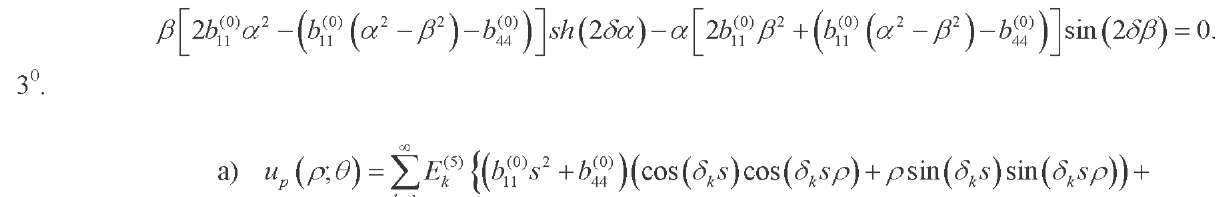
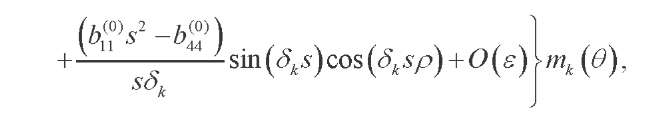 (44, 45)
(44, 45)
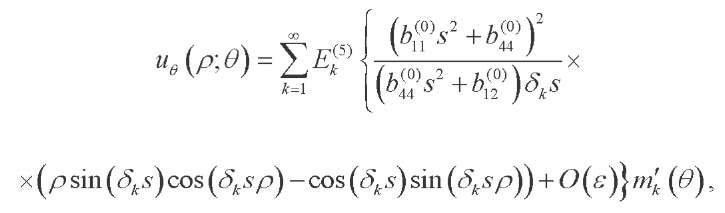 (46)
(46)
where 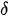 0k are the solutions to equation
0k are the solutions to equation
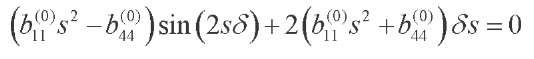 (47)
(47)
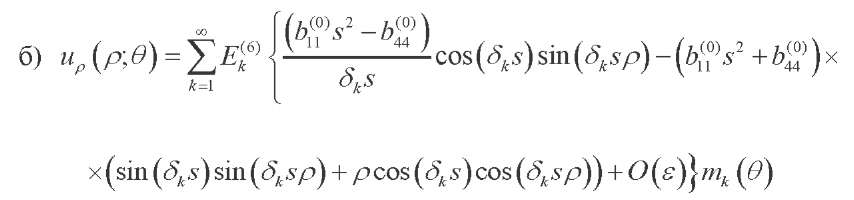 (48)
(48)
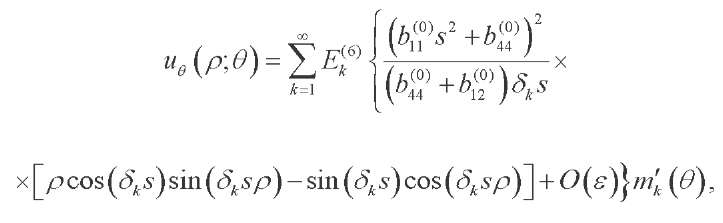 (49)
(49)
where 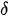 0k are the solutions to equation
0k are the solutions to equation
 (50, 51)
(50, 51)
We represent displacements in the form:
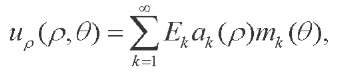 (52)
(52)
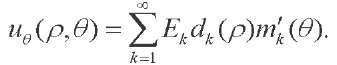 (53)
(53)
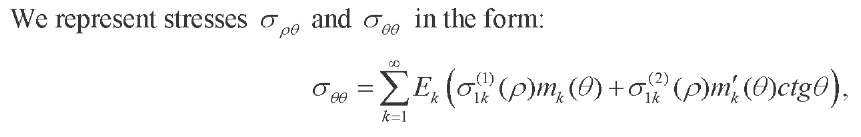 (54)
(54)
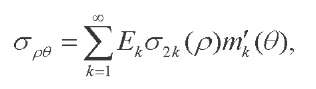 (55)
(55)
here,
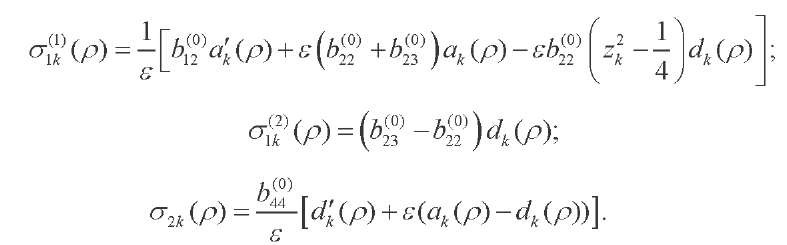
The character of solutions (33)–(50) depends essentially on the type of roots 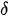 0k . The first boundary-layer terms of these solutions correspond to the Saint-Venant edge effect [4]. In the case of imaginary roots
0k . The first boundary-layer terms of these solutions correspond to the Saint-Venant edge effect [4]. In the case of imaginary roots 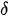 0k, these boundary layers have weak damping. Thus, the stress-strain state is far enough away from the ends and significantly depends on them. That is, in this case, the transversely isotropic properties of the inhomogeneous material significantly, in comparison to the isotropic material of the sphere, change the pattern of the stress-strain state. At the same time, for real or complex
0k, these boundary layers have weak damping. Thus, the stress-strain state is far enough away from the ends and significantly depends on them. That is, in this case, the transversely isotropic properties of the inhomogeneous material significantly, in comparison to the isotropic material of the sphere, change the pattern of the stress-strain state. At the same time, for real or complex 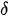 0k , the pattern of the stress-strain state of an inhomogeneous sphere for such materials qualitatively coincides, differing in the decay rate of the above-described Saint-Venant boundary layer solutions of an inhomogeneous plate.
0k , the pattern of the stress-strain state of an inhomogeneous sphere for such materials qualitatively coincides, differing in the decay rate of the above-described Saint-Venant boundary layer solutions of an inhomogeneous plate.
From (51), it turns out that when moving away from the conic sections 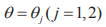 , solutions (33)–(50) decrease exponentially.
, solutions (33)–(50) decrease exponentially.
Since the constructed solutions satisfy the equilibrium equation and boundary conditions on the side surface, the Lagrange variational principle takes the following form [4][11]:
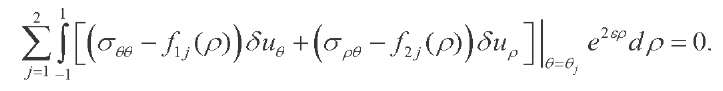 (56)
(56)
Substituting (52)–(55) into (56) and taking 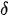 Ek as independent variations, we obtain an infinite system of linear algebraic equations
Ek as independent variations, we obtain an infinite system of linear algebraic equations
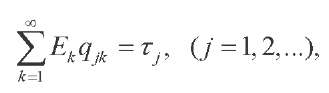 (57)
(57)
Here,
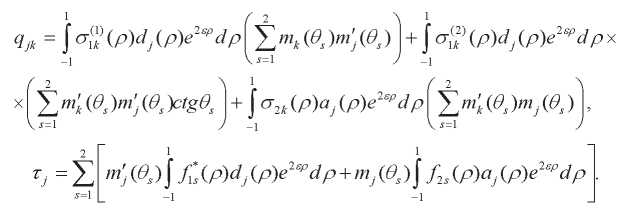
System (57) is always solvable under physically meaningful conditions imposed on the right side (57). The solvability and convergence of the reduction method for (57) is proved in [12].
Using the smallness of parameter 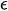 , it is possible to construct asymptotic solutions of system (57).
, it is possible to construct asymptotic solutions of system (57).
Research Results. The structure of the stress-strain state of a radially inhomogeneous transversally isotropic sphere of small thickness is analyzed under kinematic conditions on the side surface. It is shown that, in the case of fixing the side surface, the character of the solution is determined by the boundary layers. It is found that the asymptotic decomposition of the stress state starts with a solution describing the Saint-Venant edge effect in the theory of transversally isotropic inhomogeneous plates. In the case of transversal isotropy of the radially inhomogeneous material of the sphere, some boundary layer solutions decay very weakly, they can penetrate deep far from the conic sections and change the pattern of the stress-strain state. Asymptotic relations for displacements and stresses are derived, which provide calculating the three-dimensional stress-strain state of a radially inhomogeneous transversally isotropic sphere of small thickness with any predetermined accuracy. It is shown that the root branching generates a countable set of new solutions for a transversely isotropic radially inhomogeneous sphere.
Discussion and Conclusions. An asymptotic analysis of the stress-strain state of inhomogeneous shells, based on three-dimensional equations of elasticity theory, makes it possible to establish the limits of application of approximate theories. The identified behavior pattern of the solution far from the ends for different boundary conditions on the side surfaces can become the basis for creating refined applied theories for calculating the deformation of a radially inhomogeneous transversally isotropic spherical shell of small thickness. One of the applications of the asymptotic analysis performed can be the calculation of shells with thin coatings, in which, in this case, a radial inhomogeneity arises [13][14].
References
1. Галеркин, Б. Г. Равновесие упругой сферической оболочки / Б. Г. Галеркин // Прикладная математика и механика. — 1942. — Т. 6, № 6. — С. 487–496.
2. Лурье, А. И. Равновесие упругой симметрично нагруженной сферической оболочки / А. И. Лурье // Прикладная математика и механика. — 1942. — Т. 7, № 6. — С. 393–404.
3. Виленская, Т. В. Асимптотическое поведение решения задачи теории упругости для сферической оболочки малой толщины / Т. В. Виленская, И. И. Ворович // Прикладная математика и механика. — 1966. Т. 30, № 2. — С. 278–295.
4. Mekhtiyev, M. F. Asymptotic analysis of spatial problems in elasticity. — Springer, 2019. — Vol. 99. — P. 241. https://doi.org/10.1007/978-981-13-3062-9
5. Боев, Н. В. Пространственное напряженно-деформированное состояние трехслойной сферической оболочки / Н. В. Боев, Ю. А. Устинов // Изв. АН СССР. Механика твердого тела. — 1985. — № 3. — С. 136–143.
6. Ахмедов, Н. К. Асимптотическое поведение решения задачи кручения радиально-неоднородного трансверсально-изотропной сферической оболочки / Н. К. Ахмедов, Т. Б. Мамедова // Вестник Донского государственного технического университета. — 2011. — № 4. — С. 455–461.
7. Ахмедов, Н. К. Анализ структуры пограничного слоя в задаче кручения слоистой сферической оболочки / Н. К. Ахмедов, Ю. А. Устинов // Прикладная математика и механика. — 2009. — Т. 73, № 3. С. 416–426.
8. Grigorenko, A. Ya. Analysis of the axisymmetric stress-strain state of a continuously inhomogeneous hollow sphere / A. Ya. Grigorenko, N. P. Yaremchenko, S. N. Yaremchenko // International Applied Mechanics. 2018. — Vol. 54. — P. 577–583. https://doi.org/10.1007/s10778-018-0911-1
9. Akhmedov, N. K. Asymptotic analysis of three-dimensional problem of elasticity theory for radially inhomogeneous transversally-isotropic thin hollow spheres / N. K. Akhmedov, A.H. Sofiyev // Thin-Walled Structures. — 2019. —Vol. 139. — P. 232–241. https://doi.org/10.1016/j.tws.2019.03.022
10. Akhmedov, N. K. Asymptotic behavior of the solution of an axisymmetric problem of elasticity theory for a sphere with variable elasticity modules / N. K. Akhmedov, N. S. Gasanova // Mathematics and Mechanics of Solids. — 2020. — Vol. 25. — P. 2231–2251. https://doi.org/10.1177/1081286520932363
11. Лурье, А. И. Теория упругости / А. И. Лурье. — Москва : Наука, 1970. — 939 с.
12. Устинов, Ю. А. Математическая теория поперечно-неоднородных плит / Ю. А. Устинов. — Ростовна Дону : ЦВВР, 2006. — 257 с.
13. Tolokonnikov, L.A. Diffraction of cylindrical sound waves by an elastic sphere with an inhomogeneous coating / L.A. Tolokonnikov // Journal of Applied Mathematics and Mechanics. — 2015. — Vol. 79. — P. 467–474. https://doi.org/10.1016/j.jappmathmech.2016.03.008
14. Kiani, M. Radially inhomogeneous spherical structures; analysis of EM scattering using Taylor’s series method and their potential applications / M. Kiani, A. Abdolali, M. Safari // AEU – International Journal of Electronics and Communications. — 2017. — Vol. 80. — P. 199–209.
About the Authors
N. K. AkhmedovAzerbaijan
Natiq K. Akhmedov
Baku
S. M. Yusubova
Azerbaijan
Sevinj M. Yusubova
Baku
Review
For citations:
Akhmedov N.K., Yusubova S.M. Analysis of the stress-strain state of a radially inhomogeneous transversely isotropic sphere with a fixed side surface. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):14-23. https://doi.org/10.23947/2687-1653-2022-22-1-14-23













































