Анализ напряженно-деформированного состояния радиально-неоднородной трансверсально-изотропной сферы с закрепленной боковой поверхностью

Введение. Одним из свойств материалов, влияющих на напряженно-деформированное состояние упругих тел, является их неоднородность. Изучение напряженно-деформированного состояния неоднородных тел на основе трехмерных уравнений теории упругости связано со значительными математическими трудностями.

Исследованию трехмерных задач теории упругости для сферы посвящен ряд исследований.

В работе [1] на основе уравнений теории упругости для сферы получено общее решение, удовлетворяющее граничным условиям на контуре в смысле Сен-Венана, проведен анализ напряженнодеформированного состояния сферы. В [2] на основе уравнений теории упругости для толстой изотропной сферы построены однородные решения, зависящие от корней трансцендентного уравнения. В [3] на основе решения трехмерных задач теории упругости для сферы малой толщины изучена точность существующих прикладных теорий и дан метод построения уточненных прикладных теорий. В [4] изложена трехмерная асимптотическая теория трансверсально-изотропной сферической оболочки малой толщины. В [5] приведен анализ трехмерного напряженно-деформированного состояния трехслойной сферы с мягким заполнителем. В [6] методом однородных решений изучена задача кручения для радиально-неоднородной трансверсальноизотропной сферы малой толщины, когда упругие характеристики меняются линейным, квадратичным и обратно квадратичным законами по радиусу. В [7] изучена задача кручения для радиально-слоистой сферы с произвольным числом чередующихся жестких и мягких слоев. Показано существование слабозатухающих погранслойных решений и возможное нарушение принципа Сен-Венана в его классической формулировке. Построена прикладная теория кручения радиально-слоистой сферы, адекватно учитывающая возникающие особенности. В [8] с помощью метода конечных элементов и сплайн-коллокации исследована задача теории упругости для радиально неоднородного полого шара. Проведено сравнение результатов, полученных методами конечных элементов и сплайн-коллокации. В [9] методом асимптотического интегрирования уравнений теории упругости изучена осесимметричная задача теории упругости для радиально-неоднородной трансверсально-изотропной сферы малой толщины. Построены неоднородные и однородные решения.

Установлен характер напряженно-деформированного состояния. В [10] методом однородных решений рассмотрена осесимметричная задача теории упругости для сферы малой толщины с переменными модулями упругости. Получены асимптотические формулы для перемещений и напряжений, позволяющие рассчитать трехмерное напряженно-деформированное состояние радиально-неоднородной сферы.

Материалы и методы. Рассматривается деформация в рамках линейной теории упругости незамкнутой сферы, материал которой является неоднородным по радиальной координате и трансверсальноизотропным. Толщина полой сферы предполагается малой, по сравнению с радиусом и размером по дуговой координате. Рассматриваются граничные условия, позволяющие решать задачу в осесимметричной постановке.

Предполагаем, что сфера не содержит ни один из полюсов 0 и 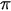. В сферической системе координат область, занятую сферой, обозначим через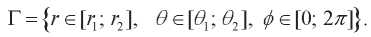

Рассматривается линейная зависимость упругих свойств материала по радиусу:

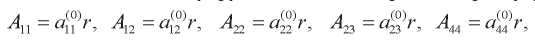(1)

где, 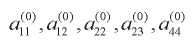— некоторые постоянные величины. 

Система уравнений равновесия при отсутствии массовых сил в сферической системе координат r, 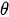,  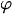 имеет вид [11]:

Здесь 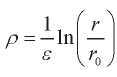— новый безразмерный переменный; 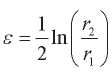—  малый параметр, характеризирующий толщину сферы; 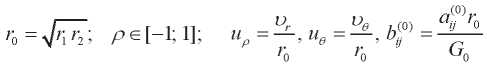— безразмерные величины; G₀ — некоторый параметр, имеющий размерность модуля упругости.

Предполагаем, что боковая часть границы сферы закреплена, т.е.

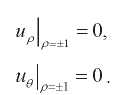(11, 12)

Считаем, что на торцах сферы (на конических срезах) заданы напряжения

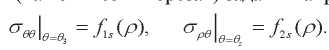(13)

Здесь 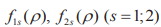; — достаточно гладкие функции, удовлетворяющие условиям равновесия.

Решения (9), (10) ищем в виде [3][4]:

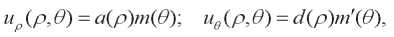(14)

где функция m(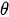) удовлетворяет уравнению Лежандра:

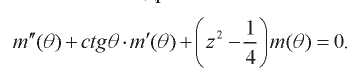(15)

После подстановки (14) в (9), (10), (11), (12) с учетом (15) получаем:

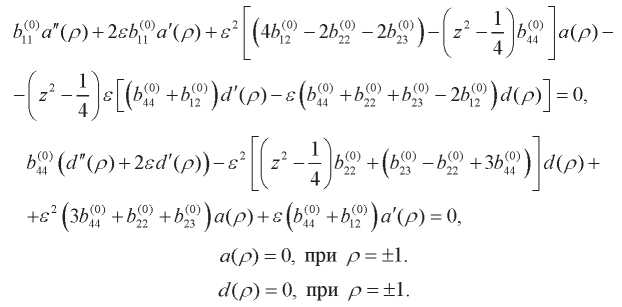(16-19)

Решение системы (16), (17) имеет вид:

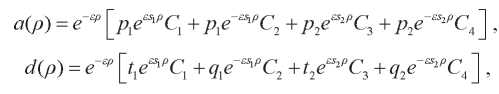(20, 21)

(22)

Система линейных алгебраических уравнений относительно 1234 C1, C2, C3, C4, получается путем удовлетворения однородным граничным условиям (18), (19). Равенство нулю определителя этой системы является условием существования ненулевых решений и приводит к характеристическому уравнению относительно спектрального параметра z :

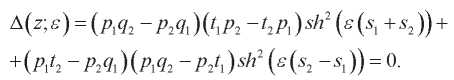(23)

Уравнение (23) имеет счетное множество корней z_k. Общее решение задачи получается путем суммирования по корням уравнения (23)

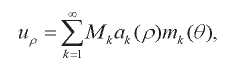(24)

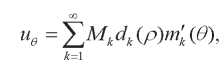(25)

где

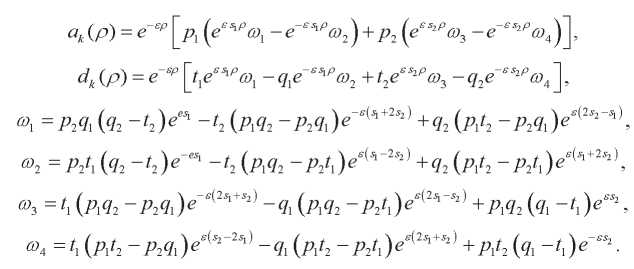
Множество корней уравнения (23) при 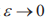состоит из счетных множеств корней

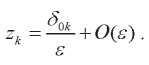(26)

Для 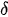_0k имеем:

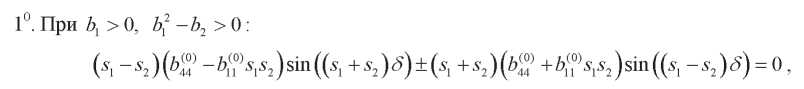(27)

где

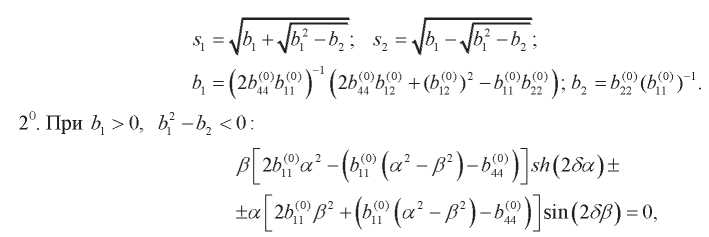(28)

где

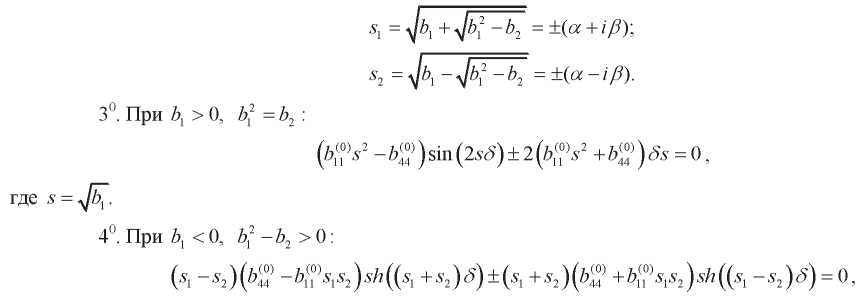(29,30)

где

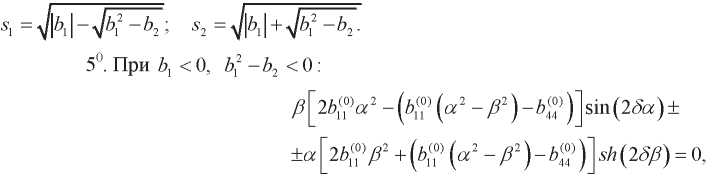(31)

где

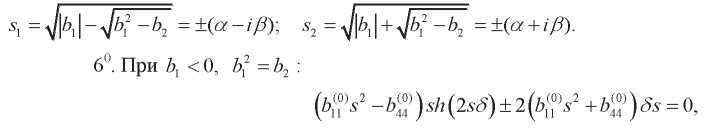(32)

где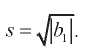 

Уравнение (27)–(32) имеет счетное множество решений.

Приведем асимптотическое построение решений, соответствующих различным группам корней характеристического уравнения (23). Подставляя (26) в (24), (25) и, раскладывая полученные выражения по степеням 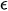, имеем: 1⁰.

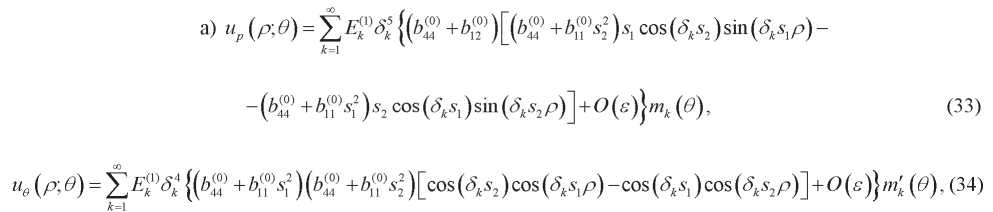
где 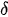_0k являются решениями уравнения

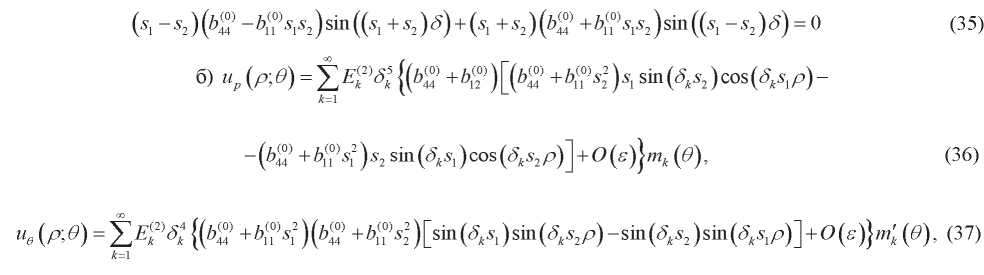
где 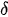_0k являются решениями уравнения

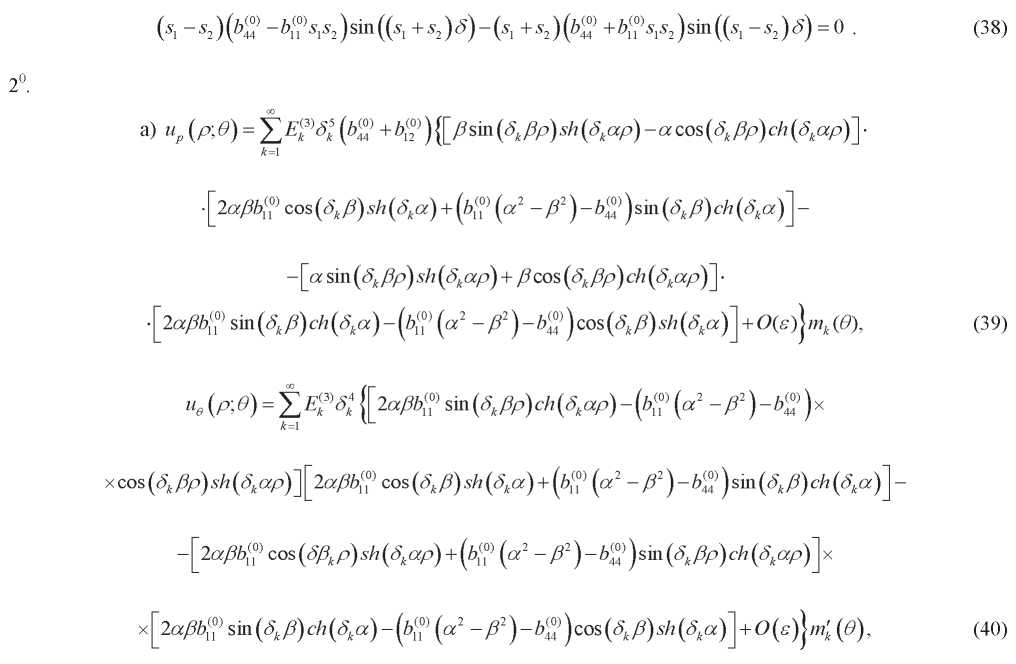
где 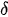_0k являются решениями уравнения

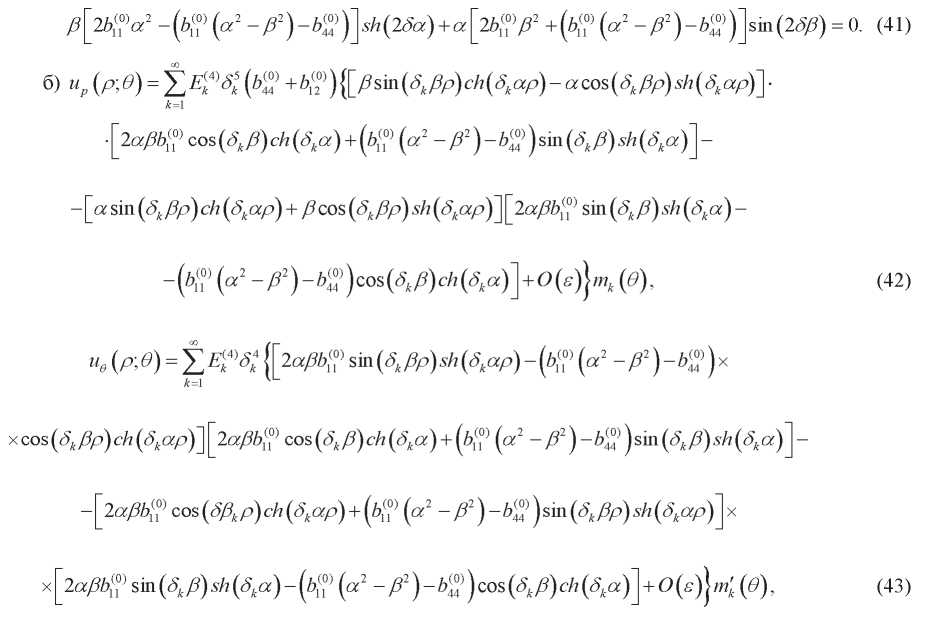
где 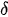_0k являются решениями уравнения

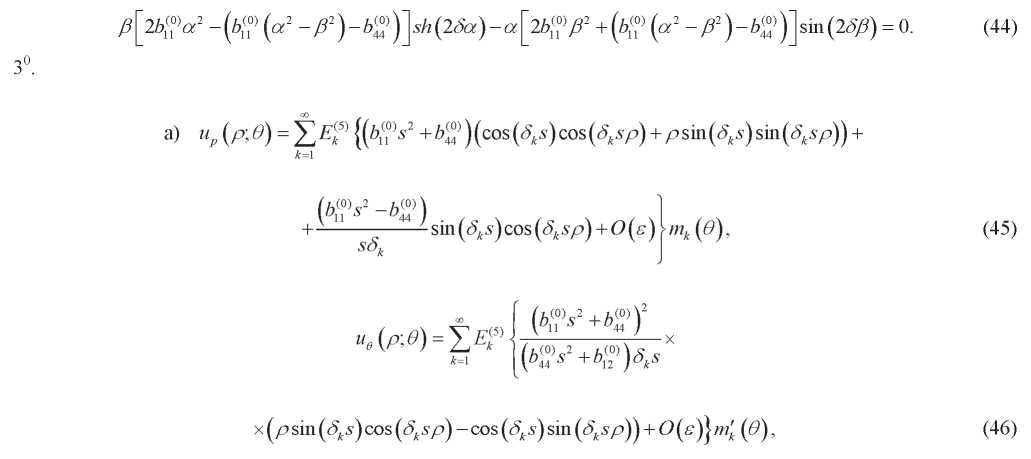
где 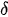_0k являются решениями уравнения

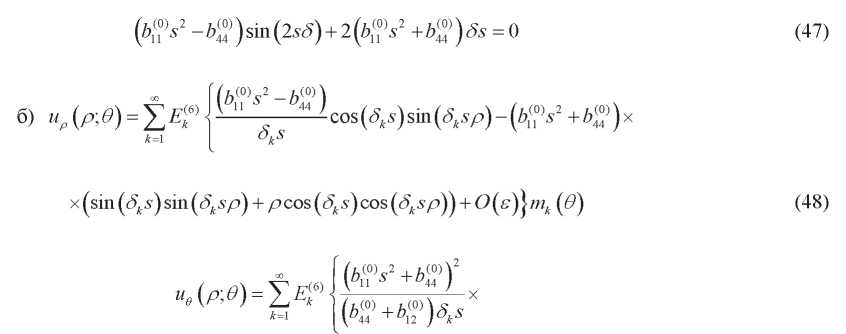
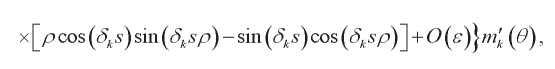(49)

где 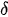_0k являются решениями уравнения

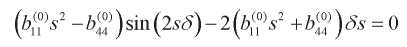
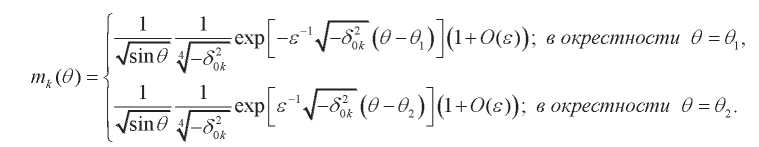(51)

Перемещения представим в виде:

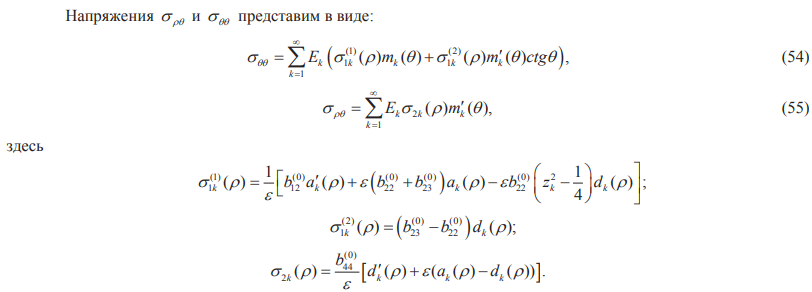
Характер решений (33)–(50) существенно зависит от типа корней 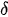_0k. Погранслойные первые члены этих решений соответствуют краевому эффекту Сен-Венана [4]. В случае мнимых корней 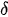_0k эти пограничные слои имеют слабое затухание. Таким образом, напряженно-деформированное состояние достаточно далеко от торцов существенно от них зависит. То есть в этом случае трансверсально-изотропные свойства неоднородного материала значительно, по сравнению изотропным материалом сферы, меняют картину напряженнодеформированного состояния. В то же время, при действительных или комплексных 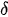_0k картина напряженнодеформированного состояния неоднородной сферы для таких материалов качественно совпадает, различаясь скоростью затухания вышеописанных погранслойных решений Сен-Венана неоднородной плиты.
Из (51) получается, что при удалении от конических сечений 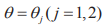решения (33)–(50) экспоненциально убывают.

Поскольку построенные решения удовлетворяют уравнению равновесия и граничным условиям на боковой поверхности, вариационный принцип Лагранжа принимает следующий вид [4][11]:

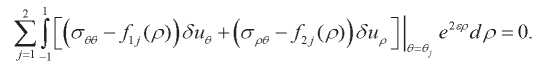(56)

Подставляя (52)–(55) в (56) и считая 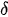E_k независимыми вариациями, получаем бесконечную систему линейных алгебраических уравнений

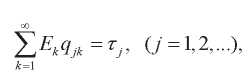(57)

здесь

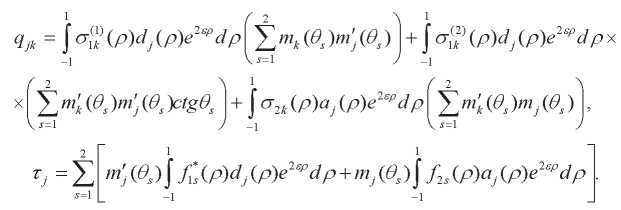
Система (57) всегда разрешима при физически осмысленных условиях, наложенных на правую часть (57). Разрешимость и сходимость метода редукции для (57) доказана в [12].

Используя малость параметра 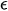, можно построить асимптотические решения системы (57).

Результаты исследований. Проведен анализ структуры напряженно-деформированного состояния радиально-неоднородной трансверсально- изотропной сферы малой толщины при кинематических условиях на боковой поверхности. Показано, что, в случае закрепления боковой поверхности, характер решения определяется погранслоями. Оказалось, что асимптотическое разложение напряженного состояния начинается с решения описывающего краевой эффект Сен-Венана в теории трансверсально-изотропных неоднородных плит. В случае трансверсальной изотропии радиально неоднородного материала сферы некоторые погранслойные решения затухают весьма слабо, могут проникать глубоко вдали от конических сечений и изменять картину напряженно-деформированного состояния. Выведены асимптотические соотношения для перемещений и напряжений, позволяющие рассчитать трехмерное напряженно-деформированное состояние радиальнонеоднородной трансверсально-изотропной сферы малой толщины с любой наперед заданной точностью. Показано, что разветвление корней порождает счетное множество новых решений для трансверсальноизотропной радиально-неоднородной сферы.

Обсуждение и заключения. Асимптотический анализ напряженно-деформированного состояния неоднородных оболочек, основанный на трехмерных уравнениях теории упругости, позволяет установить границы применения приближенных теорий. Выявленный характер поведения решения вдали от торцов для разных граничных условий на боковых поверхностях может стать основой для создания уточненных прикладных теорий расчета деформирования радиально-неоднородной трансверсально-изотропной сферической оболочки малой толщины. Одним из приложений проведенного асимптотического анализа может служить расчет оболочек с тонкими покрытиями, в которых возникает при этом радиальная неоднородность [13][14].