Перейти к:
Исследование системы автоматического управления стабилизации изображения бортовых оптико-электронных приборов наведения и слежения
https://doi.org/10.23947/2687-1653-2022-22-2-150-160
Аннотация
Введение. Движение носителя и внешние факторы (влияние атмосферы, температуры и давления) существенно ухудшают качество изображения смотрящих оптико-электронных систем (ОЭС) и точность позиционирования излучающих ОЭС. Рассматриваются проблемы повышения качества изображения и вероятность удержания изображения объекта наблюдения (ОН) на оптической оси следящей ОЭС.
Материалы и методы. Создание системы автоматического управления оптико-электронного прибора (САУ ОЭП) предполагает решение многокритериальной задачи оптимизации с учетом ряда противоречивых техникоэкономических (ТЭ) требований. Определение допустимых динамических погрешностей (ДДП) стабилизации изображения является ключевым вопросом в разработке бортовых оптико-электронных приборов (БОЭП). Уравнения Лагранжа II рода и смешанный метод Жильбера позволили получить математическую модель ОУ ОЭП. Затем выполнили декомпозицию двухсвязной САУ с нелинейными перекрестными связями в ОУ. Представлена функциональная схема модели формирования изображения БОЭП. Перечислены параметры матричного фотоприемника и требования, предъявляемые к динамической погрешности САУ ОЭП с учетом допустимой ФПМ ОЭП. Визуализированы функции передачи модуляции, линейного, гармонического и вибрационного сдвига изображения, соответствующие допустимым и достигнутым ДДП. В среде Mathcad созданы логарифмические частотные характеристики. Двухсвязная система управления ОЭП при заданных параметрах ОУ для рассматриваемого движения представлена как два независимых канала управления по азимуту и углу места.
Результаты исследования. Приведены процессы управления БОЭП в режимах стабилизации и слежения. Для исследования динамики пространственного управления БОЭП в соответствии с методикой САУ разработана компьютерная имитационная модель (КИМ) ЦСАУ ОЭП. Она реализована в среде Matlab и состоит из КИМ ОУ, приводов, пропорционально-интегрально-дифференцирующих (ПИД) регуляторов с учетом нелинейностей, центрального вычислительного устройства (ЦВУ), программного устройства наведения, КИМносителя, реализующего уравнения движения. Описаны гармонические колебания носителя. Определены погрешности слежения и стабилизации в режиме слежения при дополнительно введенном управляющем воздействии в виде постоянной скорости. Исследована динамика пространственного управления БОЭП. Визуализированы компьютерная имитационная модель цифровой системы автоматического управления оптико-электронным прибором, результаты моделирования ЦСАУ ОЭП без учета движения борта и процессы управления ОЭП с учетом движения.
Обсуждение и заключения. Для исследованных случаев рассчитана точность стабилизации. Установлено, что она в десятки раз превосходит заявленные ранее показатели, и это в десятки раз снижает требования к сходимости лазерного пучка и мощности излучения лазера при разработке оптического тракта рассматриваемого изделия. Предложенную КИМ можно использовать при разработке БОЭП. В этом случае применение представленной методики и КИМ поможет снизить трудозатраты и минимизировать ошибки.
Ключевые слова
Для цитирования:
Бурдинов К.А., Шашкина К.М., Шагхаей Э. Исследование системы автоматического управления стабилизации изображения бортовых оптико-электронных приборов наведения и слежения. Advanced Engineering Research (Rostov-on-Don). 2022;22(2):150-160. https://doi.org/10.23947/2687-1653-2022-22-2-150-160
For citation:
Burdinov K.A., Shashkina K.M., Shaghaei E. Investigation of ACS image stabilization of on-board optoelectronic guidance and tracking devices. Advanced Engineering Research (Rostov-on-Don). 2022;22(2):150-160. https://doi.org/10.23947/2687-1653-2022-22-2-150-160
Введение. При проектировании современных бортовых оптико-электронных приборов (ОЭП) и комплексов широко используются методы компьютерного моделирования оптико-электронных систем (ОЭС). Над этими задачами работали такие авторы, как Ю. Г. Якушенков, В. В. Тарасов, И. П. Торшина, В. П. Иванов, В. А. Балоев, В. А. Овсянников, В. Л. Филиппов. Компьютерное моделирование позволяет решать задачи рационального выбора структуры, параметров, элементной базы ОЭС, обеспечивающих требуемые показатели эффективности при заданных ограничениях без дорогостоящих натурных исследований и испытаний.
Движение носителя и внешние факторы (температура, давление) существенно ухудшают качество изображения для смотрящих ОЭС и точность позиционирования для излучающих ОЭС. Сокращается вероятность удержания изображения объекта наблюдения (ОН) на оптической оси следящей ОЭС. Для излучающих ОЭС снижается точность позиционирования и вероятность выполнения задач наблюдения. Для удержания изображения ОН в поле зрения или в секторе облучения необходимо захватить довольно большой телесный угол обзора. Значит, нужно увеличивать габариты оптических систем и мощностей силовой электроники. Чтобы этого избежать, применяют управляемые излучающие ОЭС. Указанные выше особенности ОЭП ограничивают разработки САУ ОЭП. Эту проблему рассматривали В. А. Стрежнев, В. М. Матросов, А. С. Земляков, Н. Н. Маливанов, Е. И. Сомов, А. И. Маликов, В. А. Кренев, А. И. Карпов, Д. А. Молин, А. В. Михалицын. При проектировании управляемых ОЭП, работающих в режимах наведения и слежения, установлен следующий факт: время наведения и точность стабилизации оптической оси, а также динамика подсистем ОЭП существенно влияют на качество изображения.
Таким образом, актуальна задача минимизации времени и увеличения точности наведения и удержания изображения ОН в поле зрения управляемого ОЭП. В этой связи необходимы:
- разработка математических моделей ОЭП как объектов управления;
- синтез алгоритмов управления;
- создание компьютерных имитационных моделей (КИМ);
- исследование систем управления, учитывающих динамику движения управляемого ОЭП;
- определение параметров, влияющих на динамические свойства и качество изображения.
Цель работы — улучшение точностных характеристик и повышение качества изображения ОЭП, работающих в режимах наведения, стабилизации и слежения, за счет рационального выбора их параметров при синтезе и моделировании.
Материалы и методы. Разработка САУ ОЭП начинается с решения многокритериальной задачи оптимизации, учитывающей противоречивые технико-экономические (ТЭ) требования. В развитие работы [1] предложена модифицированная методика проектирования САУ ОЭП. За критерий качества САУ примем совокупность динамических характеристик каналов управления, удовлетворяющих условиям:
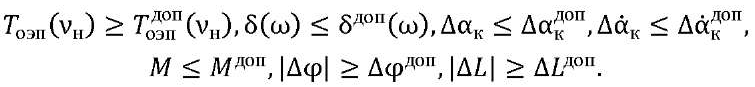 (1)
(1)
Здесь 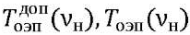 — допустимая и реализованная функция передачи модуляции (ФПМ) ОЭП на частоте Найквиста,
— допустимая и реализованная функция передачи модуляции (ФПМ) ОЭП на частоте Найквиста, 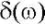 ;
; 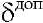 — амплитудная частотная характеристика перекрестных связей и ее допустимое значение декомпозиции;
— амплитудная частотная характеристика перекрестных связей и ее допустимое значение декомпозиции; 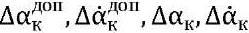 — допустимые и установившиеся значения динамических погрешностей САУ по углу и угловой скорости при действии возмущений в условиях, близких к реальной эксплуатации САУ; к = 1, 2, … — номер канала управления, обеспечивающего качество изображения; Мдоп = 1,05–1,25 — показатель колебательности,
— допустимые и установившиеся значения динамических погрешностей САУ по углу и угловой скорости при действии возмущений в условиях, близких к реальной эксплуатации САУ; к = 1, 2, … — номер канала управления, обеспечивающего качество изображения; Мдоп = 1,05–1,25 — показатель колебательности, 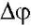 ; ΔL — запасы устойчивости по фазе и по амплитуде.
; ΔL — запасы устойчивости по фазе и по амплитуде.
Ключевой вопрос в разработке ОЭП — определение допустимых динамических погрешностей (ДДП) стабилизации изображения.
Схема формирования изображения бортового оптико-электронного прибора (БОЭП) представлена на рис. 1.
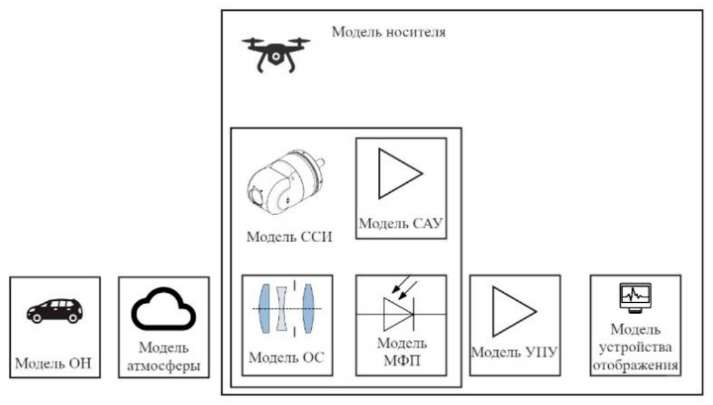
Рис. 1. Функциональная схема модели формирования изображения БОЭП: ОН — объект наблюдения; ОС — оптическая система; МФП — матричный фотоприемник; УПУ — усилительно-преобразовательное устройство; ССИ — система стабилизации изображения
ФПМ БОЭП должна удовлетворять условию, обеспечивающему допустимое качество изображения [2]:
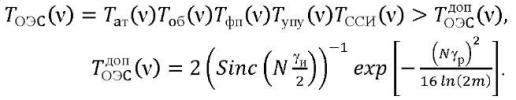 (2)
(2)
Здесь 𝑇ОЭC(ν) — ФПМ ОЭП; N — пространственная частота; 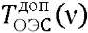 — допустимая ФПМ ОЭП; 𝑇aт(ν) — ФПМ атмосферы; 𝑇oб(ν) — ФПМ объектива; 𝑇фп(ν) — ФПМ фотоприемника; 𝑇упу(ν) — ФПМ преобразования оптической информации [1]; 𝑇ССИ(ν) — ФПМ сдвига изображения (динамической погрешности ССИ), зависящая от вида динамического смещения изображения: линейного (Л) — 𝑥(𝑡) = 𝑉𝑡, гармонического (Г) — 𝑥(𝑡)=𝑎0𝑠𝑖𝑛(𝑡), случайного (СЛ) и расфокусировки.
— допустимая ФПМ ОЭП; 𝑇aт(ν) — ФПМ атмосферы; 𝑇oб(ν) — ФПМ объектива; 𝑇фп(ν) — ФПМ фотоприемника; 𝑇упу(ν) — ФПМ преобразования оптической информации [1]; 𝑇ССИ(ν) — ФПМ сдвига изображения (динамической погрешности ССИ), зависящая от вида динамического смещения изображения: линейного (Л) — 𝑥(𝑡) = 𝑉𝑡, гармонического (Г) — 𝑥(𝑡)=𝑎0𝑠𝑖𝑛(𝑡), случайного (СЛ) и расфокусировки.
Допустимая ФПМ системы стабилизации изображения включает системы слежения, стабилизации, виброзащиты (СВ) и автоматической фокусировки (САФ) [3]:
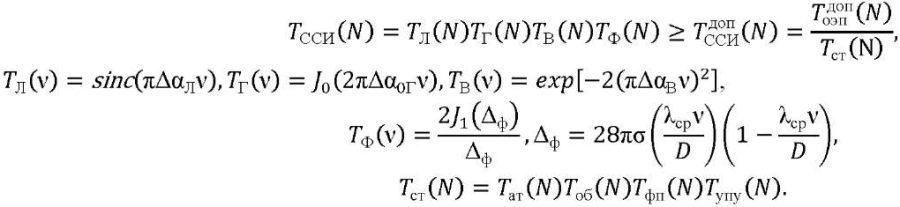 (3)
(3)
Здесь 𝑇Л(𝑁) — погрешность линейного смещения изображения; 𝑇Г(𝑁) — амплитуда погрешности синусоидального колебания; 𝑇В(𝑁) — среднее значение погрешности амплитуды вибраций; 𝐽0 — функция Бесселя первого рода нулевого порядка; 𝐽1(Δф) — функция Бесселя первого рода первого порядка; Δф — погрешность фокусировки (мм); σ — среднее значение волновой аберрации в долях длины волны; λср — средняя длина волны спектрального диапазона.
Будем исходить из условия, что каждая подсистема САУ должна вносить одинаковую долю изменения качества изображения ОЭП и 𝑇ст(𝑁) = сonst за время наблюдения. Тогда упростится определение допустимых ФПМ ССл, СВ, САФ (3):
 (4)
(4)
Разложим функции 𝑇Л(𝑁),𝑇Г(𝑁),𝑇В(𝑁),𝑇Ф(𝑁) (3) в ряд и получим выражения, определяющие ДДП:
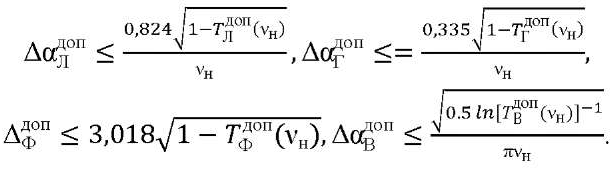 (5)
(5)
Здесь νн — частота Найквиста.
Предельная пространственная частота, которую должен разрешать ОЭП в процессе наблюдения, определятся критерием Джонсона:
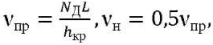 (6)
(6)
где νпр — угловая (штр/рад) предельная пространственная частота; 𝑁Д — число элементов разрешения (числа Джонсона); L — расстояние до ОН; hкр — критический размер ОН.
При разложении отбрасываются все члены ряда, кроме первых, поэтому полученные допуски следует уточнить путем градиентного спуска.
Представленные выше рассуждения позволили решить задачу определения точности стабилизации изображения бортовой оптико-электронной системы (БОЭС) для режимов слежения и стабилизации. Были разработаны методика и программа расчета ФПМ и допусков (патент RU20216603401).
Назовем требования, предъявляемые к динамической погрешности САУ ОЭП с учетом допустимой ФПМ ОЭП. Исходные данные для расчета:
- диаметр входного зрачка — 𝐷 = 90 мм,
- фокусное расстояние ОС — 𝑓`= 100 мм,
- длина волны — λ = 4 мкм,
- расстояние до объекта наблюдения — 𝐿 = 10 км,
- метеорологическая видимость — 𝑆𝑀 = 15 км,
- высота полета — 𝐻 = 5 км,
- количество элементов МФП — 256×256,
- частота кадров — 𝐹 = 400 Гц,
- вероятность правильного обнаружения — 𝑃обн = 0,8,
- вероятность ложной тревоги — 𝑃лт = 10−4,
- отношение сигнал/шум усилителя — оптимального фильтра — 𝑚 = 1,105,
- угловой размер объекта наблюдения — γ𝑠 = 5•10−5 рад,
- угловое расстояние между двумя соседними целями — γр = 3,34•10−3 рад.
Параметры МФП:
- 𝑑 = 0,25𝑎 — толщина фоточувствительного слоя,
- ε𝑛 = 4•10−5 — неэффективность переноса заряда,
- α𝑐 = 2 — число выборок на 1 элемент,
- 𝑘з = 0,6 — коэффициент заполнения,
- τ = 5,4•10−9 c — время считывания,
- τпр = 5•10−10 с — постоянная времени преобразователя.
На рис. 2 приведены ФПМ линейного, гармонического и вибрационного сдвига изображения, соответствующие допустимым и достигнутым ДДП САУ БОЭП.
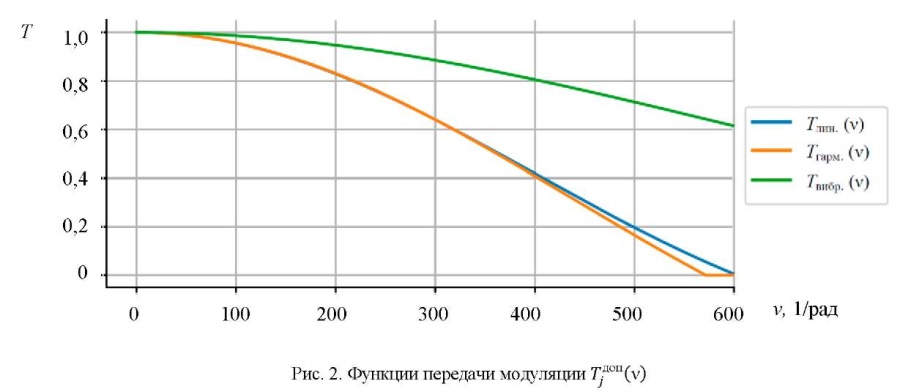
В соответствии с (3)–(5) и исходными данными для расчета вычислили: νпр = 600 рад–1 канала наблюдения БОЭП в инфракрасной области с вероятностью обнаружения Р = 0,8. Для ФПМ БОЭП и ДДП САУ: ΔαЛ = 3,5 угл. мин, ΔαГ = 3,1 угл. мин, ΔαВ = 3,0 угл. мин.
На основе уравнений Лагранжа II рода и смешанного метода Жильбера получили математическую модель ОУ ОЭП [4] наведения и слежения в виде трех информационных каналов, приводимых в движение электродвигателями типа ДБМ по осям Карданова подвеса. Представили ее в матричном виде2:
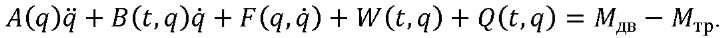 (7)
(7)
Здесь 𝑞 = (α β)𝑇, α, β — углы поворота ОУ по азимуту и углу места.
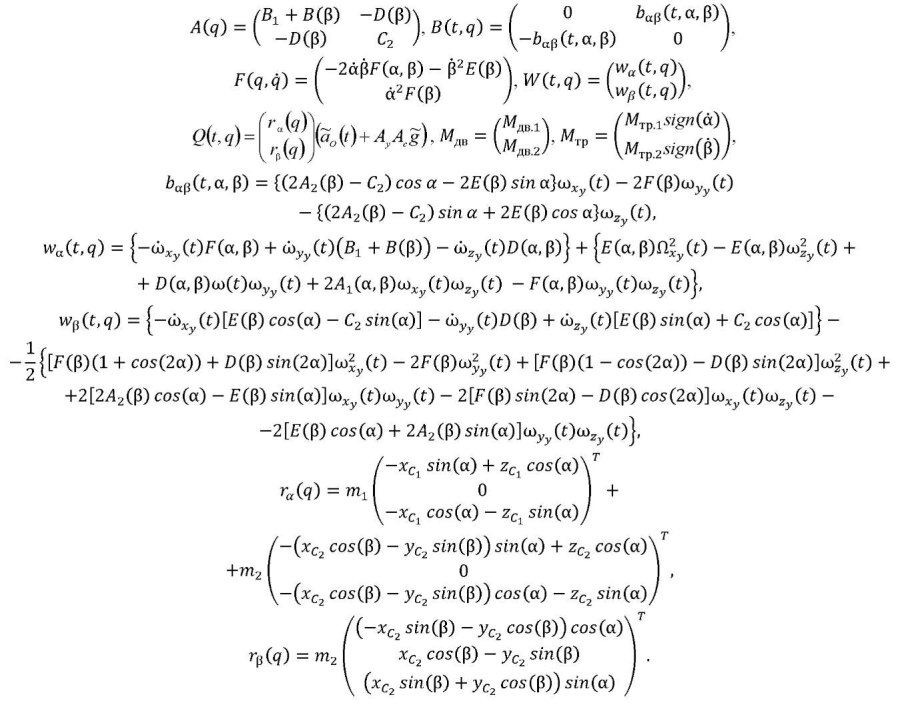
Следующий этап разработки — декомпозиция двухсвязной САУ [5] с нелинейными перекрестными связями в ОУ, каким и является исследуемый ОЭП. Линеаризованные уравнения движения относительно траектории имеют вид:
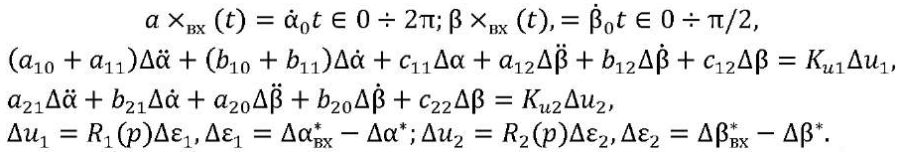 (8)
(8)
Построив переменные коэффициенты системы (8), определим их значения при t = tк* в «опасных» точках, в которых параметры значительно изменяются или меняют знаки в диапазоне углов 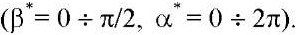
Тогда, сведя систему (8) (при t = tк*) к системе с постоянными параметрами и используя правило Крамера, выразим ее в форме передаточных функций (ПФ) в точках t = tк*:
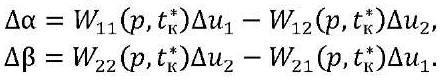 (9)
(9)
Полученные ПФ (9) с учетом (8) для каждого выбранного момента времени (t = tк*) можно представить в виде структурной схемы с прямыми перекрестными связями (ПС, рис. 3). Здесь и далее для простоты записи ПФ обозначим Wкij(р) = Wij(р,tк*).
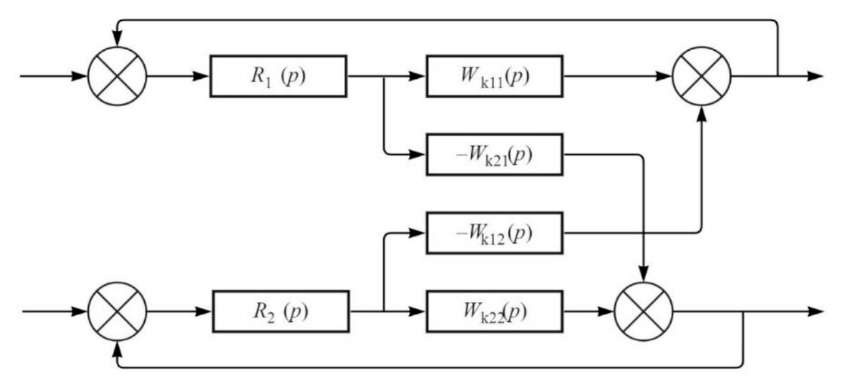
Рис. 3. Структурная схема двухсвязной САУ
Оценим ПС САУ по их частотным характеристикам (ЧХ). Для этого запишем ПФ разомкнутой системы с учетом 2-го замкнутого канала управления при Δβвх = 0 (рис. 4).
Рис. 4. Структурная схема САУ, разомкнутая по одному каналу управления
Построим годограф 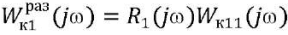 и трубки вокруг него с радиусами для каждого момента времени tк*:
и трубки вокруг него с радиусами для каждого момента времени tк*:
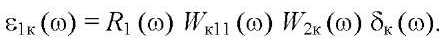 (10)
(10)
Учитывая (10) и критерий Найквиста, можно судить об устойчивости САУ (1), (2) и о влиянии ПС на ее устойчивость в диапазоне углов сканирования (3).
В результате для каждого (tк*-го) определим время ПС:
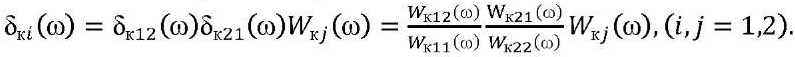 (11)
(11)
Рассмотрим ПС САУ, удовлетворяющие условиям декомпозиции.
Согласно (8), (11) по данным геометрии масс ОУ, для 11 выбранных точек по времени определили (tк* = 0; 0,89; 1,35; 1,58; 1,71; 2,3; 2,97; 3,8; 4,5; 4,75; 6,28 с). Построили aij(t), bij(t), cij(t). В среде Matcad создали логарифмические частотные характеристики (ЛАХ) 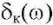 (k = 1,11) (рис. 5).
(k = 1,11) (рис. 5).
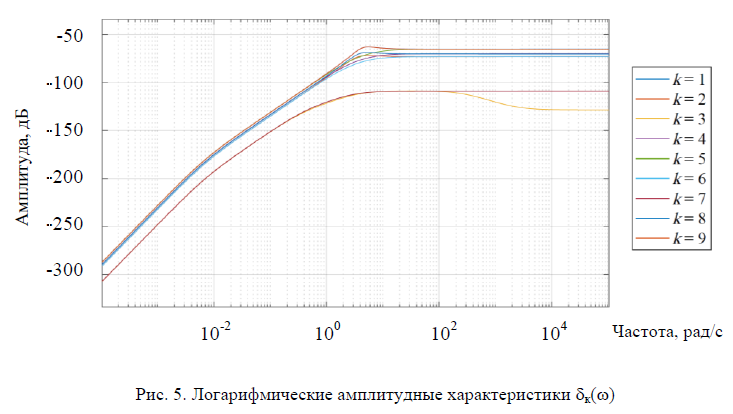
На рис. 5 видно, что все множество ЛАХ не превышает –50 дБ. Из анализа ЛАХ 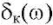 имеем представленные ниже результаты.
имеем представленные ниже результаты.
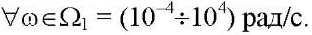
Определены:
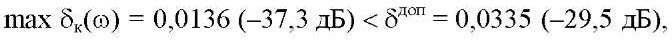
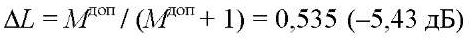
при М10 = М20 = 1,1; Мдоп = 1,15.
Таким образом, двухсвязную систему управления (8) ОЭП при заданных параметрах ОУ для рассматриваемого движения можно представить как два независимых канала управления по азимуту и углу места.
Результаты исследования. На рис. 6–7 показаны процессы управления БОЭП в режимах стабилизации и слежения. Масштаб графиков рассогласования увеличен в 600 раз. Графики программного управления и выходной величины визуально совпадают.
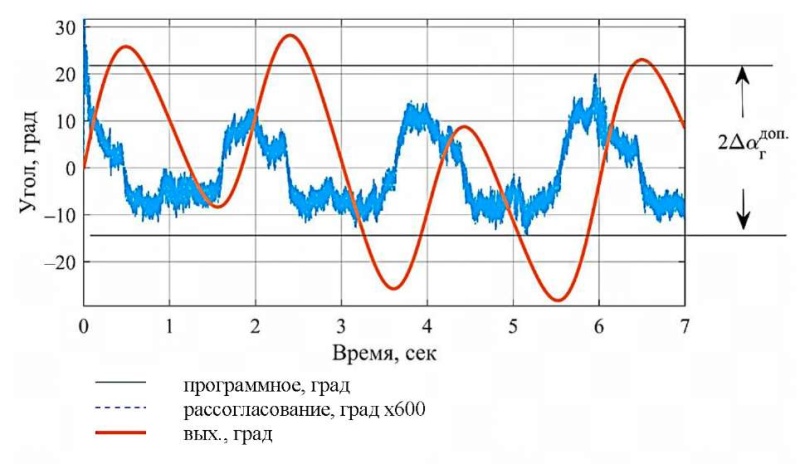
Рис. 6. Процессы стабилизации БОЭП по азимуту
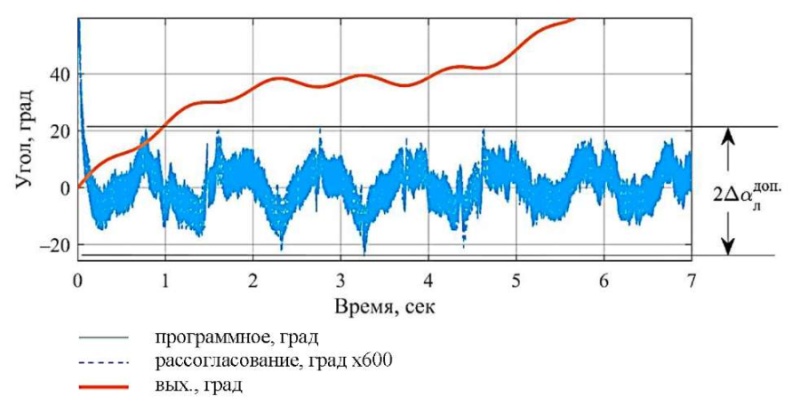
Рис. 7. Процессы слежения БОЭП по азимуту
Опишем гармонические колебания носителя: А1 = А2 = 20 (амплитуды), Т1 = Т2 = 1 с (периоды колебаний) и А1 = А2 = 120, Т1 = Т2 = 6,28 с. Укажем моменты нагрузки: Мдв1 = 2,2 Нм, Мдв1 = 0,3 Нм. При таких гармонических колебаниях и моментах нагрузки погрешность стабилизации оси визирования не превышает:
- по азимуту — 1,2 угл. мин,
- по углу места — 1,6 угл. мин.
В режиме слежения при дополнительно введенном управляющем воздействии в виде постоянной скорости 12град/с погрешность слежения и стабилизации не превышает 1,7 угл. мин по азимуту и 1,3 угл. мин по углу места.
Для исследования динамики пространственного управления БОЭП в соответствии с методикой САУ разработана КИМ цифровой системы автоматического управления (ЦСАУ) ОЭП конкретного назначения (рис. 8) [1].
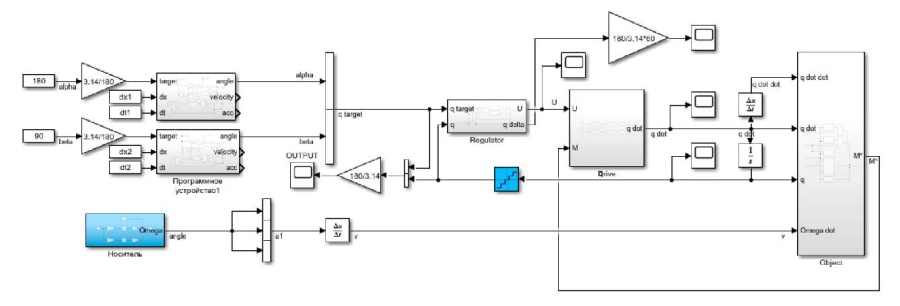
Рис 8. Компьютерная имитационная модель цифровой системы автоматического управления оптико-электронным прибором
Решение реализовано в среде Matlab Simulink. Его элементы:
- КИМ ОУ (Object), полученная согласно (7);
- КИМ приводов (Drive);
- КИМ ПИД-регуляторов (Regulator) с учетом нелинейностей и ЦВУ;
- КИМ программного устройства наведения;
- КИМ носителя, реализующего уравнения движения носителя.
На рис. 6 и 7 приведены результаты моделирования ЦСАУ ОЭП без учета движения борта. При этом:
- погрешность наведения не превышает по азимуту 18 угл. мин, по углу места — 10 угл. мин;
- погрешность слежения — 0,6 угл. мин по азимуту, 0,6 угл. мин по углу места;
- погрешность стабилизации — 0,45 угл. мин. по азимуту, 0,6 угл. мин по углу места.
На рис. 9 показаны процессы управления ОЭП с учетом его движения. Погрешность наведения по азимуту — 2 угл. мин, по углу места — 5 угл. мин. Погрешность слежения и стабилизации — 0,8 угл. мин по азимуту, 1,3 угл. мин по углу места.
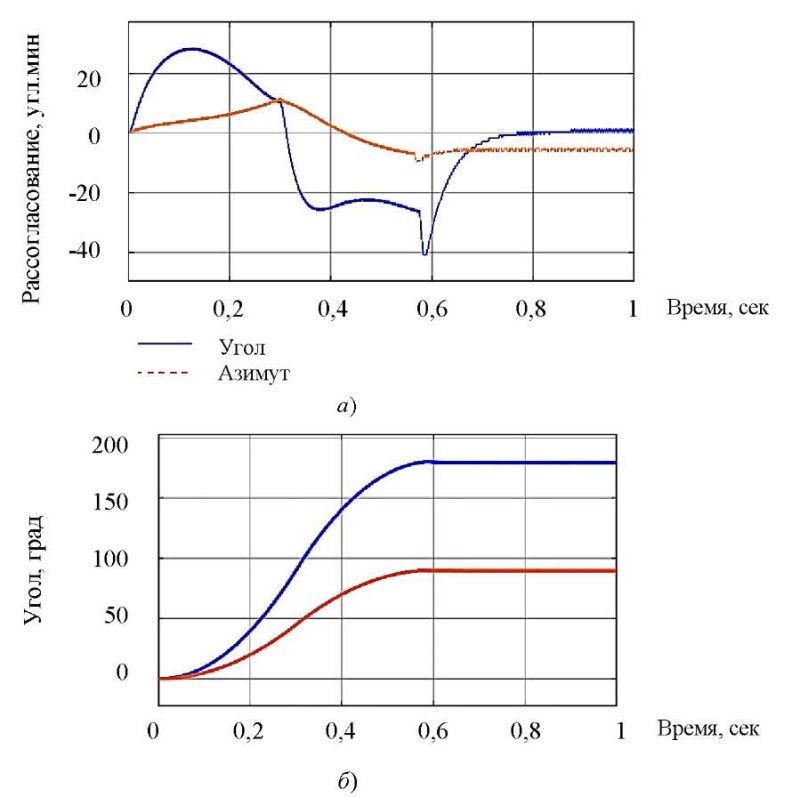
Рис. 9. Результаты моделирования системы в режиме наведения по двум каналам (градусы): а — рассогласование системы; б — графики переходных процессов. Во втором случае визуально совпадают график программного управления (alpha target, beta target) и выходной величины (alpha, beta)
Обсуждение и заключения. Полученные результаты представлены ниже.
- Предложена методика оценки допусков на точность стабилизации изображения БОЭП в условиях управляемых и температурных воздействий (патент RU2021660340). Представлены аналитические оценки ДДП стабилизации изображения по (4), (5) для режимов слежения и стабилизации на основе ФПМ ОЭП. Получены требования к САУ, обеспечивающие решение задачи обнаружения ОН в инфракрасной области.
- Назван критерий приемлемости декомпозиции, описана методика декомпозиции двухсвязной САУ ОЭП с применением компьютерных технологий. Для конструктивных параметров ОУ реального прибора определены требования, позволяющие синтезировать САУ ОЭП как два независимых канала управления.
- Предложены КИМ САУ ОЭП для исследования динамики изолированных каналов управления и пространственного управления. При этом учтены нелинейность и нестационарность ОУ конкретного назначения.
- Разработана механическая модель ОЭП, получены уравнения динамики пространственного движения (7) ОУ.
- Синтезированы параметры ПИД-регуляторов, обеспечивающие устойчивое наведение и стабилизацию ОЭП при всех заданных режимах. Добротность по скорости: 𝐾𝑣1=(3700 ÷ 4000)с−1, 𝐾𝑣2=(3000÷ 3300) с−1. Корректирующие звенья: 𝑇к11=𝑇к12=0,05с, 𝑇к21=𝑇к22=5×10−5 с. Это обеспечивает более точную работу системы планирования полета и построение траектории [6–8].
- Показано, что с помощью КИМ можно получить требуемые время и погрешность наведения, стабилизации и слежения. При этом скорость наведения — 0,6 с. Соответствующий показатель зарубежных аналогов — 1 c3.
- В [9] рассматривается система лазерного противодействия. Ее технические характеристики позволяют выполнять задачу при W = 1000 Вт/стерадиан и мощности лазера P = 3,1 Вт. В [10] показано, что необходима мощность излучения W = 2700 Вт/стерадиан при мощности лазера P = 200 мВт.
Рассчитаем требуемую точность стабилизации для каждого из представленных случаев по формуле
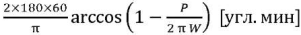
и сведем в табл. 1.
Таблица 1
Сравнение требуемой точности стабилизации

Таким образом, точность стабилизации предлагаемой системы в десятки раз превосходит требуемую в статьях [9][10]. И это в десятки раз снижает требования к сходимости лазерного пучка и мощности излучения лазера при разработке оптического тракта рассматриваемого изделия.
Список сокращений и условных обозначений
ОЭС — оптико-электронная система,
ОЭП — оптико-электронный прибор,
ОН — объект наблюдения,
КИМ — компьютерная имитационная модель,
САУ — система автоматического управления,
ФПМ — функция передачи модуляции,
ДДП — допустимая динамическая погрешность,
ССИ — система стабилизации изображения,
МФП — матричный фотоприемник.
1 Программа вычисления функции передачи модуляции оптико-электронного прибора, базирующегося на БПЛА : патент 2021660340 Рос. Федерация / К. А. Бурдинов ; Университет Иннополис. № 2021619174; заявл. 11.06.2021 ; опубл. 24.06.2021, Бюл. № 7, 1 с.
2 Математическая модель и синтез системы автоматического управления бортового оптико-электронного прибора / К. А. Бурдинов [и др.] // ХII Всерос. съезд по фундаментальным проблемам теоретической и прикладной механики : сб. тр. Уфа, 2019. С. 190–192.
3 Directed Infrared Countermeasure (DIRCM) / EMSOPEDIA // emsopedia.org : [сайт]. — URL: https://www.emsopedia.org/entries/directed-infrared-countermeasure-dircm/ (дата обращения: 01.05.2022).
Список литературы
1. Методика разработки и испытаний систем управления и виброзащиты бортовых оптико-электронных приборов / В. А. Балоев, К. А. Бурдинов, А. И. Карпов [и др.] // Оптический журнал. — 2021. — Т. 88, № 3. — С. 13–26 https://doi.org/10.17586/1023-5086-2021-88-03-24-36.
2. Молин, Д. А. Применение функции передачи модуляции для оценки допустимых характеристик оптикоэлектронных приборов / Д. А. Молин // Вестник Казанского государственного технического университета им. А. Н. Туполева. — 2011. — № 1. — С. 68–75.
3. Сокольский, М. Н. Допуски и качество оптического изображения / М. Н. Сокольский. — Ленинград : Машиностроение, 1989. — 220 с.
4. Балоев, В. А. Имитационное моделирование двухступенчатой системы управления сканирующим устройством бортового базирования / В. А. Балоев, А. И. Карпов, В. А. Кренев [и др.] // Оптический журнал. — 2017. — Т. 84, № 3. — С. 6–14.
5. Гаркушенко, В. И. Синтез многосвязной нестационарной системы управления при неполной информации / В. И. Гаркушенко // Вестник Казанского государственного технического университета им. А. Н. Туполева. — 2003. — № 3. — С. 47–49.
6. Bangura, M. Real-time model predictive control for quadrotors / M. Bangura, R. Mahony // IFAC Proceedings Volumes. — 2014. — Vol. 47. — Р. 11773–11780 https://doi.org/10.3182/20140824-6-ZA-1003.00203
7. Real-time long range trajectory replanning for MAVs in the presence of dynamic obstacles / Geesara Kulathunga, R. Fedorenko, S. Kopylov, A. Klimchik // URL: https://ieeexplore.ieee.org/document/9162605 (accessed: 13.06.2022) https://doi.org/10.1109/ACIRS49895.2020.9162605.
8. Optimization-Based Trajectory Tracking Approach for Multi-Rotor Aerial Vehicles in Unknown Environments / Geesara Prathap Kulathunga, Hany Hamed, D. Devitt, A. Klimchik // IEEE Robotics and Automation Letters. — 2022. — Vol. 7. — P. 4598–4605.
9. Development of a mid-infrared laser for study of infrared countermeasures techniques / H. H. P. Th. Bekman, J. C. van den Heuvel, F. J. M. van Putten, R. Schleijpen // URL: https://www.spiedigitallibrary.org/conferenceproceedings-of-spie/5615/0000/Development-of-a-mid-infrared-laser-for-study-of-infrared/10.1117/12.578214. short?SSO=1 (accessed: 13.06.2022) https://doi.org/10.1117/12.578214
10. Optical countermeasures against CLOS weapon systems / A. Toet, K. W. Benoist, J. N. J. van Lingen, R. H. M. A. Schleijpen // URL: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/8898/1/Opticalcountermeasures-against-CLOS-weapon-systems/10.1117/12.2028342.short (accessed: 13.06.2022) http://dx.doi.org/10.1117/12.2028342
Об авторах
К. А. БурдиновRussian Federation
Бурдинов Константин Алексеевич, старший инженер
г. Иннополис, ул. Университетская, д. 1
К. М. Шашкина
Russian Federation
Шашкина Ксения Михайловна, руководитель лаборатории беспилотных технологий
г. Иннополис, ул. Университетская, д. 1
Эхсан Шагхаей
Russian Federation
Эхсан Шагхаей, инженер
г. Иннополис, ул. Университетская, д. 1
Рецензия
Для цитирования:
Бурдинов К.А., Шашкина К.М., Шагхаей Э. Исследование системы автоматического управления стабилизации изображения бортовых оптико-электронных приборов наведения и слежения. Advanced Engineering Research (Rostov-on-Don). 2022;22(2):150-160. https://doi.org/10.23947/2687-1653-2022-22-2-150-160
For citation:
Burdinov K.A., Shashkina K.M., Shaghaei E. Investigation of ACS image stabilization of on-board optoelectronic guidance and tracking devices. Advanced Engineering Research (Rostov-on-Don). 2022;22(2):150-160. https://doi.org/10.23947/2687-1653-2022-22-2-150-160
JATS XML














































