Scroll to:
Selection and Identification of a Model of Elasto-Viscoplasticity of the Filled Fluorocomposite according to Free and Constrained Compression Tests
https://doi.org/10.23947/2687-1653-2022-22-3-180-192
Abstract
Introduction. Properties of filled composites based on polytetrafluoroethylene allow them to work at high contact pressures, reciprocating nature of shear loads, and in a wide temperature range. Due to this, they are used as antifriction layers of bearing parts with ball segment. To simulate the mechanical behavior of such materials under operating conditions, adequate constitutive equations of elasto-viscoplasticity and methods of their identification according to the data of basic experiments are needed.
Materials and Methods. The tensor-linear model of elasto-viscoplasticity should be identified according to the data of tests on free compression of samples. They were subjected to loading up to a maximum deformation of 10 %, allowed to remain, unloaded, and then, a similar loading cycle up to 160 MPa under constrained compression was carried out. The experiment with a composite based on polytetrafluoroethylene filled with 40 wt. % fine bronze, was conducted at room temperature. Tests for constrained compression were performed for two values of the strain rate, and for free compression – for three values of the strain rate in the range of 10-6 – 10-3 s-1. For the description, two models of elasto-viscoplasticity were considered, representing modifications of Swain and Kletschkowski’s models and corresponding to the connection of a viscoelastic or elastic nonlinear viscous element with a plastic or endochronic element. An integral operator with a Kohlrausch kernel was considered as a viscoelastic element.
Results. The results of the constrained compression tests made it possible to separate the elastic relationship of volumetric deformations and average stresses from the constitutive relations. The data of free compression cycles at different strain rates were used to determine the material constants of the model. For this purpose, an efficient search algorithm based on the simplex method of minimizing the discrepancy was implemented. Both models discovered the importance of the plastic component (independent of the deformation rate) for a qualitative description of the stress cycling that accompanied the cyclic deformation, as well as their dependence on the strain rate.
Discussion and Conclusions. Both models of elasto-viscoplasticity described correctly the behavior of the studied fluorocomposite under loading conditions close to the operating conditions of the antifriction layers of the bearing parts with ball segment. They can be considered as a basis for their further generalization, taking into account the dependence on temperature.
Keywords
For citations:
Petukhov D.S., Adamov A.A., Keller I.E. Selection and Identification of a Model of Elasto-Viscoplasticity of the Filled Fluorocomposite according to Free and Constrained Compression Tests. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):180-192. https://doi.org/10.23947/2687-1653-2022-22-3-180-192
Introduction. Properties of filled composites based on polytetrafluoroethylene (PTFE) allow them to work in a wide temperature range at high contact pressures and reciprocal sliding on the counterbody. Due to this, they are used as antifriction layers of bearing parts with a ball segment1, 2. PTFE as a base for antifriction polymer composites in a wide temperature range shows high stability of properties and exceptionally low coefficients of friction, sliding and rest. The introduction of fillers helps to significantly increase the wear resistance, stiffness and yield strength, as well as reduce the creep of the composite without marked increase in the friction coefficients. The rheological properties of the antifriction material should provide feasibility during the operation of the product in the temperature range from less than –50 to +50 °C:
- at calculated values of the compressive load of at least 60 MPa;
- at its peak values up to 150 MPa;
- at a normalized range of cyclic shear deformations.
The predictability of changes in the properties and thickness of the antifriction layer under its hinge mounting also matters.
During the operation of the materials under consideration, it is required to assess the performance of antifriction layers of the support parts with a ball segment, to predict the resource for the entire service life (up to 50 years). To do this, you need to construct and identify adequate constitutive equations of elasto-viscoplasticity according to the data of basic experiments. Models describing the rheological behavior of filled fluorocomposites are also important for calculating the operational properties of shaft seals and rods in high-power diesel engines3. To calculate the behavior of products under load during installation (for short periods of time), it is important that the models correctly describe the plastic (elastoplastic, viscoplastic) properties of the material. To calculate the behavior of products during operation (for long periods of time), it is required to adequately represent the phenomena of relaxation, creep, and cyclic creep (ratcheting).
Rheological models of filled fluorocomposites describing cycles of loading, holding, and unloading in wide ranges of time and strain rates are rarely found in the literature. We can specify only work [1] that meets all these requirements. It proposes a model corresponding to the parallel connection of endochronic and nonlinear viscous elements. This model describes all uniaxial tensile tests4 at room temperature. It is about:
- loading curves up to 0.08 strain with strain rates 10-4 –10-2 s-1;
- relaxation curves for 10 h with constant strain of 0.03–0.08;
- hysteresis loops in the load cycle up to 0.1 strain, short-term hold and unloading with subsequent hold.
A tensor geometrically nonlinear model is presented in [2]. It describes the behavior of filled fluorocomposites under various monotonic and cyclic loading histories in various stress states and at arbitrary temperatures. A viscoplastic rheological element in a series connection with a viscoelastic one is taken into account. On the whole, this model satisfactorily describes the curves corresponding to the experiments [1], but it is much more complicated and requires fourteen material constants. In [3], the model [4] is used to describe microindentation cycles of a filled fluorocomposite. The rheological block diagram is similar to [2], but it takes into account the relaxation time spectrum of the viscoelastic element. In [3], the model [4] is used to describe microindentation cycles of a filled fluorocomposite. The rheological block diagram is similar to [2], but it takes into account the relaxation time spectrum of the viscoelastic element.
The model [5] was designed to describe features of the elastoplastic behavior of solid polymers under cyclic uniaxial loading. The evolutionary equations for its internal variable, stresses and plastic deformations, had nonlinear cross-connections, therefore, the model did not correspond to any rheological structural scheme. The measure of internal time characteristic of the endochronic theory of plasticity was used. Twenty-one constants were required to identify the model.
The nonlinear one-dimensional Maxwell-type viscoelastic plasticity model [6–9] contains only two material functions. It describes incomplete recovery of deformations in the load-unloading cycle and cyclic creep (ratcheting) with asymmetric loading cycles. Nonlinear viscoelasticity models with fractional integro-differentiation operators are characterized by flexibility with a small number of material constants and functions [7]. It is necessary to investigate the applicability of such nonlinear models to describe the behavior of polymer materials in the loading and unloading cycle with holds [10–13]. Papers [14][15] are devoted to the identification of linear models of viscoelasticity based on the results of indentation tests. In [16][17], the dynamic mechanical analysis results are used for this purpose, but the significant nonlinearity of the materials studied in this work does not allow using this technique. Ratcheting of PTFE composites is experimentally investigated in [18][19], but there is no mathematical description of the results.
Paper [8] presents a method for identifying a model of isotropic elastoplastic behavior of filled composites based on PTFE and ultrahigh molecular weight polyethylene based on experimental data on free and constrained compression. Due to the peculiarities of the rheology of plastics [9], the methods [10] are applicable to them. This approach makes it possible to determine:
- the elastic volume compressibility function;
- the hardening function for shear elastoplastic properties within the framework of the theory of plastic flow.
Thus, the operating conditions of the products in question, the mechanical properties of polymer materials, and the presented literature analysis serve as the basis for further research.
Let us highlight the basic test for free compression of cylindrical samples of 20×20 mm. It consists of load cycles up to 0.1 deformation, a short-term hold of fifteen minutes, and unloading with a subsequent hold of fifteen minutes. In this way, data can be determined to describe elastic, plastic and viscous components of deformation, relaxation and reverse creep with residual deformations. A similar definition of hardness is provided by the standard6.
Loading is performed at three strain rates in the range of 10-6 –10-3 s-1. Besides, the samples are tested for constrained compression to a stress of 160 MPa at two strain rates from the same range. All tests are repeated for values from the operating temperature range of the polymer material. These data should be sufficient to identify a suitable model of elasto-viscoplastic compressible material with nonlinear elastic compressibility.
First of all, we are interested in the possibilities of describing experimental data at room temperature with the simplest elasto-viscoplasticity models of the type proposed in [1] and [4], which differ in structural schemes.
Materials and Methods. A composite based on PTFE PN 90 filled with 40 wt. % of fine bronze was chosen as the simulated material. Cylindrical samples with a diameter and height of 20 mm were made by pressing and sintering a mixture of powders. The following experiments were conducted to select and then identify the model:
- for constrained compression with a single nonzero component of the strain tensor;
- for free compression with a single nonzero component of the stress tensor.
In the first case, friction along the lateral boundary was excluded by lubrication, in the second — by a thin film of PTFE and grease.
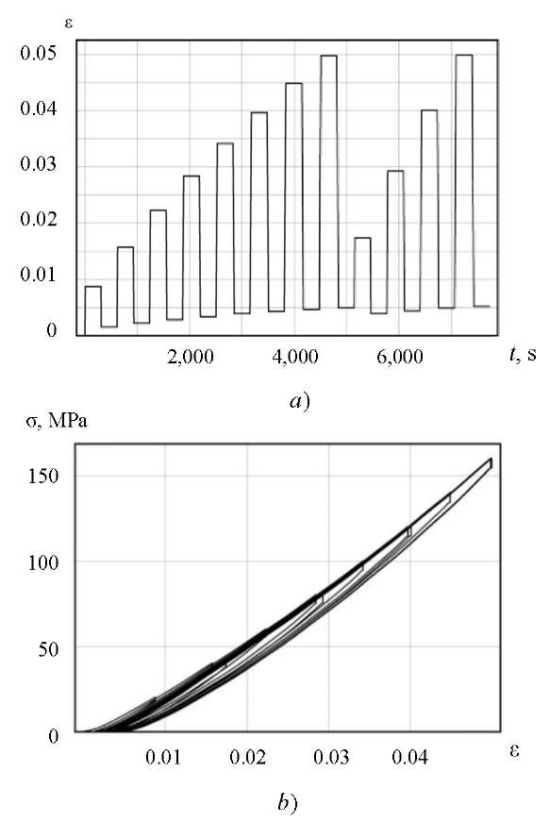
Fig. 1. Cyclic tight compression test: a — program; b — hysteresis curve
The experiments were aimed at identifying irreversible volumetric deformations and volume-elastic properties of the material. The first test was cyclic constrained compression with increasing amplitude (Fig. 1 а). It set the value of the deformation rate 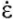 = 2.5 ×10-3 s-1 and the pause between unloading and loading for 300 s. During the first few cycles, a residual volume strain equal to approximately 5 ×10-3 accumulated (Fig. 1). It changed slightly when the sample was held in the unloaded state.
= 2.5 ×10-3 s-1 and the pause between unloading and loading for 300 s. During the first few cycles, a residual volume strain equal to approximately 5 ×10-3 accumulated (Fig. 1). It changed slightly when the sample was held in the unloaded state.
Further, compression tests were carried out up to 160 MPa with a significantly slower strain rate 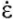 = 2.5 ×10-5 s-1 and subsequent unloading (Fig. 2 а):
= 2.5 ×10-5 s-1 and subsequent unloading (Fig. 2 а):
- of undeformed sample (1);
- of the same sample repeatedly (2);
- of the sample after the cyclic test shown in Figure 1 (3).
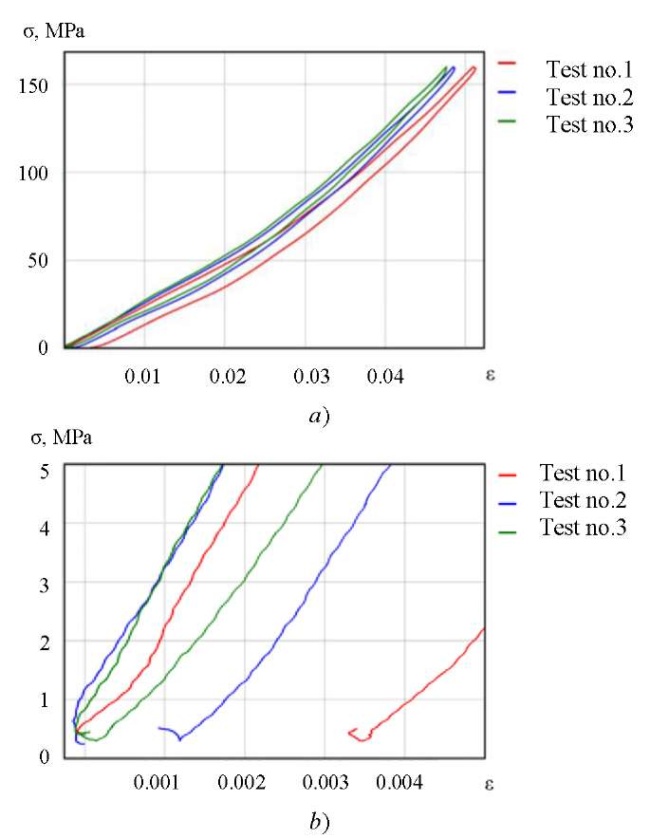
Fig. 2. Slow tight compression tests:
a — loading diagrams; b — initial and final sections of diagrams
Tests of the same sample were carried out in a day.
As can be seen in Figure 2 b, in the experiment with a new sample, the maximum residual strain of about 3.5 ×10-3 is observed. On repeated testing, it amounted to 1 ×10-3. In the third test, there is no residual strain. The properties of the material under cyclic constrained compression are accompanied by a transient irreversible process and are stabilized in several cycles.
The bulk properties were determined from the third test (Fig. 2 a), in which there are no residual strains. In this paper, bulk strains are assumed to be nonlinearly elastic. The data is described by a quadratic dependence:
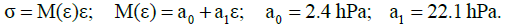 (1)
(1)
Here, σ, ε ― axial components of the Cauchy stress tensors and logarithmic strains; M ― constrained compression modulus, which is related to the bulk compression modulus K by the ratio:
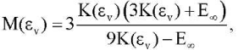 (2)
(2)
where E∞ ― equilibrium Young's modulus (independent of bulk strain); εv = εii, εj ― components of the logarithmic strain tensor.
Value E∞ = 690 МPа was obtained with the slope of the curve σ(ε) under uniaxial compression in the vicinity of 𝜎 = 1MPa and relaxation 8.65 %.
Using (1), (2) and 9.38 % correction for the compliance of the machine in the tight compression test, it is possible to obtain the desired dependence K(εv), which differs slightly (maximum by 0.03 %) from linear:
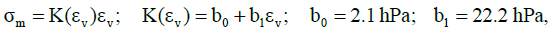 (3)
(3)
where 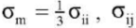 ― components of the Cauchy stress tensor.
― components of the Cauchy stress tensor.
Experiments to determine the relationship between average stress and volume strain were carried out on samples previously tested by constrained compression with irreversible volume strain. The same applies to the free compression experiments described below and required to determine the relationship of the deviatory parts of stress and strain tensors. As a result, the model reflected the properties of the compacted material. In production, processes associated with irreversible bulk strain occur under the crimping of a layer of antifriction polymer material during the assembly of the structure of the support part and do not affect the further behavior of the material.
Uniaxial compression tests were carried out to determine the relationships between the deviatory parts of stress and strain tensors. Figure 3 shows the results of experiments for three values of strain rates  = 4.63 × 10-6 s-1, 2.35 × 10-5 s-1, 2.27 × 10-3 s-1. Further, the data from these experiments will be interpreted in the framework of a one-dimensional model. When formulating a three-dimensional model, the elastic volume part can be excluded from these relations.
= 4.63 × 10-6 s-1, 2.35 × 10-5 s-1, 2.27 × 10-3 s-1. Further, the data from these experiments will be interpreted in the framework of a one-dimensional model. When formulating a three-dimensional model, the elastic volume part can be excluded from these relations.
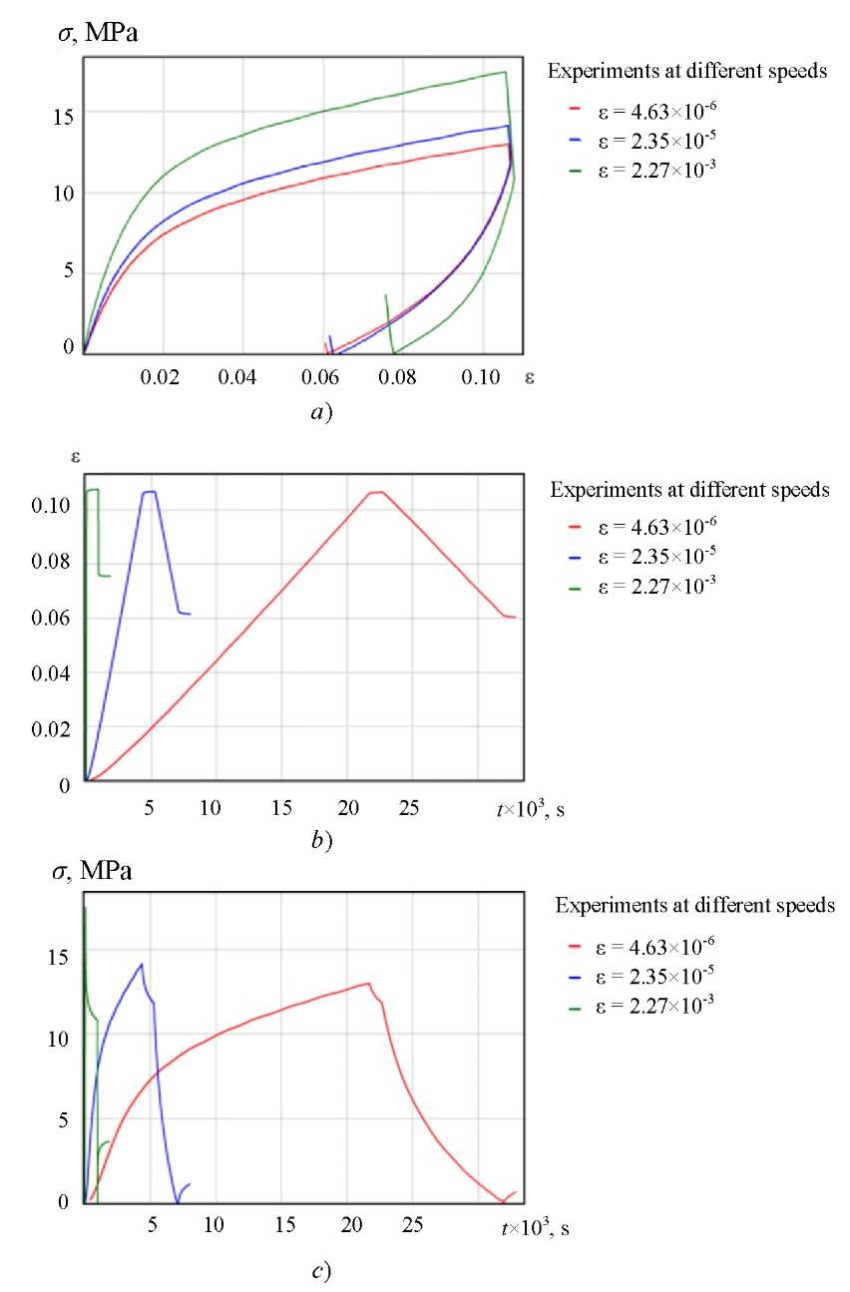
Fig. 3. Uniaxial compression experiment with three different speeds:
a — loading diagrams; b — deformation histories; c — stress histories
When choosing a suitable model, it turned out that the experimental data in Figure 3 were not described by the relations of a linear viscoelastic medium:
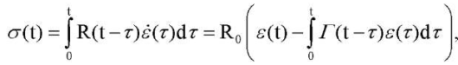 (4)
(4)
where σ(t), ε(t) ― stress and strain histories used to describe elastomers and polymers [10].
There have been attempts to use expressions for relaxation functions R(t) or relaxation rates Г(t) with a different number of parameters: the sum of exponents, the Robotnov fractional-exponential function7, the Koltunov kernel8, the kernel from the work of T. L. Smith9, the Kohlrausch kernel [10]:
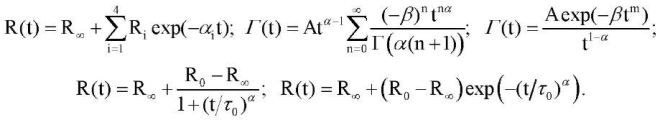 (5)
(5)
Here,
R∞, R0, Ri, α, β, τ0 ― material constants; Г ― gamma function, as well as monotonic approximation by cubic splines at eight points, whose coordinates served as parameters.
Models were considered, in which, in addition to viscous ones, plastic irreversible deformations were taken into account. Two basic models of this type were investigated.
Basic model 1 (Fig. 4 a) is a combination of models [4] and [10] and assumes a sequential connection of three elements.
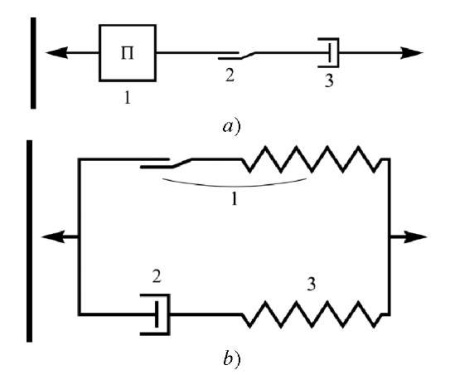
Fig. 4. Block diagrams of basic models: a — model 1; b — model 2
- Linear viscoelastic element with Kohlrausch kernel [10]:
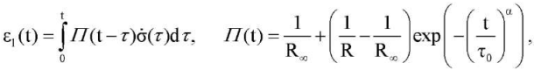 (6)
(6)
where R, R∞, τ0, α ― material constants, the first two have the physical meaning of instantaneous and equilibrium modules.
- Plastic element with linear hardening:
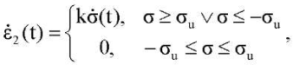 (7)
(7)
where σu, k ― material constants.
- Linear-viscous element:
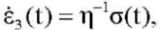 (8)
(8)
where η ― material constant.
The final expression for strains:
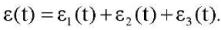 (9)
(9)
Model (6)–(9) is solved with respect to strains, therefore, it is convenient to have stress histories for its identification σ(t) (Fig. 3 c).
The block diagram of basic model 2 (Fig. 4 b), borrowed from [1], is a parallel connection of two elements.
- Endochronic plastic element with nonlinear elastic part:
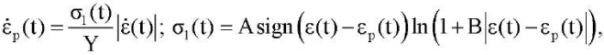 (10)
(10)
where εp ― an internal parameter that has the meaning of irreversible strain of the element, Y,A,B ― material constants.
- A pair of sequentially connected nonlinear-viscous (2) and linear-elastic (3) elements:
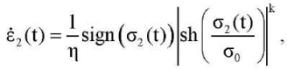 (11)
(11)
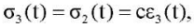 (12)
(12)
where sign — argument sign; η, σ0, k, с ― material constants.
The resulting expression for stresses:
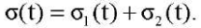 (13)
(13)
Model (10)–(13) is solved with respect to stresses, therefore, it is convenient to have strain histories for its identification ε(t) (Fig. 3 c). Expression σ1(t) in (13) is solved as the solution to a system of algebraic differential equations (10), and σ2(t) — as a system solution (11), (12) taking into account ε(t) = ε2(t) + ε3(t).
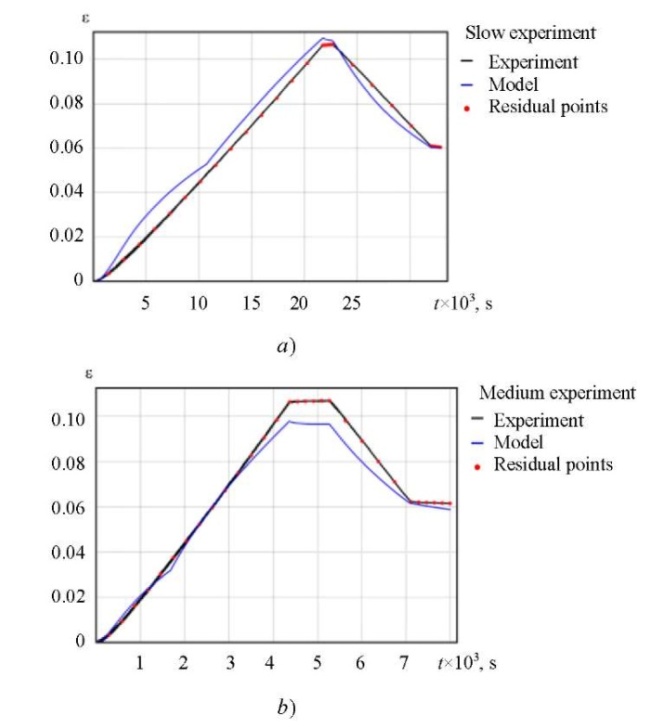
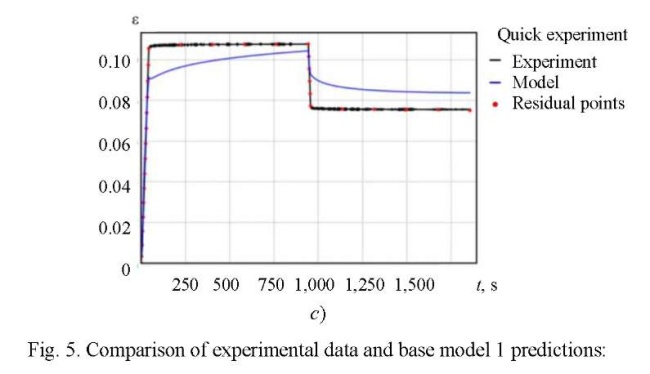
Research Results. Residual minimization between experimental strain histories (Fig. 3 b) and model predictions allowed us to find seven material constants of base model 1:
 (14)
(14)
The simplex method is used as a search procedure. Comparison of the calculated and experimental data is shown in Figure 5.
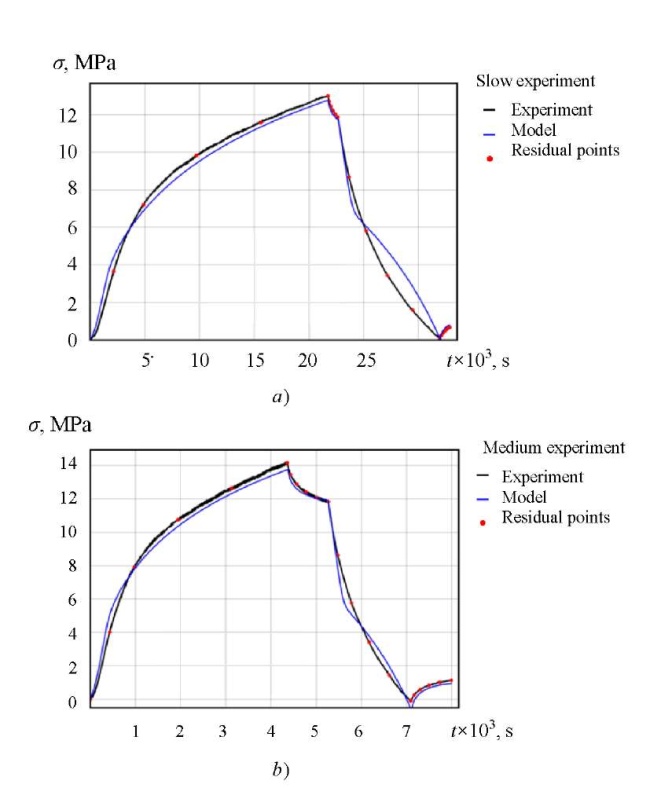
Residual minimization between the experimental stress histories (Fig. 3 b) and the model predictions allowed us to detect seven material constants of base model 2:
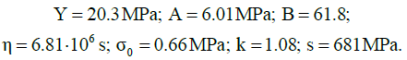 (15)
(15)
Here, strain histories were considered to be given (Fig. 3 b). Comparison of the calculated and experimental data is shown in Figure 6.
Discussion and Conclusions. The considered one-dimensional models were generalized to a spatial formulation that assumed isotropy of properties and immutability of the main axes of the strain tensor under loading. To do this, the Cauchy stress tensors and logarithmic deformations were decomposed into spherical and deviatoric parts:
The relationship between the ball parts σm and εv is given by expression (3). The relationship between the deviatoric parts s and e is given by the relations generalizing (6)–(9) or (10)–(13) depending on the selection of the base model. These expressions should be rewritten in terms of the histories of the deviatoric parts s(t) and e(t), excluding the ball part from uniaxial compression.
As a spatial generalization of the relations (7) for the plastic element of model 1, the plastic flow law associated with von Mises yield criterion, with isotropic linear strain hardening was considered. The connection of deviators will look like this:
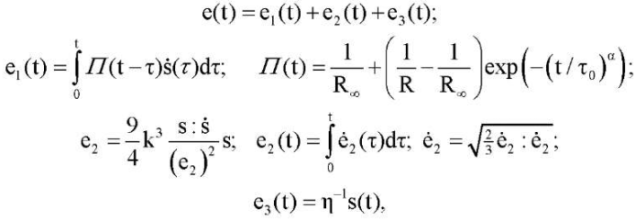
where colon means the operation of convolution of tensors A : B = AijBij given by the components in an orthonormal basis.
The relations of the endochronic plasticity theory (10) of model 2 are also generalized in the spirit of von Mises plasticity, which provides the following entry for deviators:
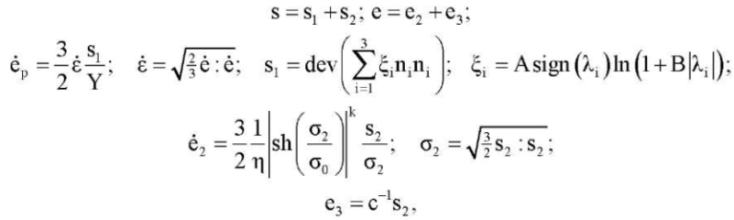
where “dev” means a tensor deviator, λi, ni — eigenvalues and eigenvectors of the tensor e – ep = λi ni ni .
It should be noted that the authors [1] used a model option with an endochronic parameter [14] equal to one. It seems appropriate to consider this parameter as a material constant, since its influence on the description of transients after changes of loading modes is known.
In the framework of this work, the experiments were carried out on constrained and free compression of a composite based on polytetrafluoroethylene filled with finely dispersed bronze with a mass fraction of 40 %. At the same time, loading, unloading and holding were carried out with different strain rates in the range of 10-6 –10-3 s-1. The experiments on constrained compression were carried out at pressures corresponding to the peak loads of the antifriction layer in hinges with a spherical segment. The inability of the standard linear viscoelastic model to describe test data for several strain rates was found. Two families of seven-constant models with plastic and nonlinear viscous structural elements that could describe the data of basic experiments were selected and identified. The model with an endochronic element showed great accuracy in describing the data at a high strain rate. The model with a plastic element can be improved if the nonlinearity in the viscous element and nonlinear strain hardening are taken into account, which will require an increase in the number of material constants. The data of these models were generalized to the spatial case for an isotropic material and strain histories with a constant orientation of the trihedron of the main axes.
1. EAD 050009-00-0301. Spherical and cylindrical bearing with special sliding material made of fluoropolymer. EOTA. Product regulation. URL: https://www.nlfnorm.cz/en/ehn/6189
2. Stanton JF, Roeder CW, Campbell TI. Appendix C: Friction and Wear of PTFE Sliding Surfaces. NCHRP Report 432: High-Load Multi-Rotational Bridge Bearings. Washington, DC: TRB; 1999. 413 p.
3. Hai Sui, Heiko Pohl, Achim Oppermann, et al. Material and Computational Analysis of PTFE Seals. SAE Paper Series. 1995:951055. URL: https://www.sae.org/publications/technical-papers/content/951055/?src=2001-01-1118
4. Material and Computational Analysis of PTFE Seals.
5. Material and Computational Analysis of PTFE Seals.
6. GOST 4670-2015 (ISO 2039-1:2001). Plastics. Determination of hardness. Ball indentation method. Interstate Council for Standardization, Metrology and Certification. Moscow: Standartinform; 2016. 10 p. (In Russ.)
7. Rabotnov YuN. Polzuchest' ehlementov konstruktsii. Moscow: Nauka; 1966. 752 p. (In Russ.)
8. Koltunov MA. Singulyarnye funktsii vliyaniya v analize relaksatsionnykh protsessov. Prochnost' i plastichnost'. Moscow: Nauka; 1971. P. 640–645. (In Russ).
9. Smith TL. Ehmpiricheskie uravneniya dlya vyazkouprugikh kharakteristik i vychisleniya relaksatsionnykh spektrov. Vyazkouprugaya relaksatsiya v polimerakh. Moscow: Mir; 1974. P. 44–56. (In Russ).
References
1. Kletschkowski, T. Endochronic Viscoplastic Material Models for Filled PTFE / T. Kletschkowski, U. Schomburg, A. Bertram // Mechanics of Materials. — 2002. — Vol. 34. — P. 795–808. https://doi.org/10.1016/S0167-6636(02)00197-7
2. Bergström, J. S. A Constitutive Model for Predicting the Large Deformation Thermomechanical Behavior of Fluoropolymers / J. S. Bergström, L. B. Hilbert Jr. // Mechanics of Materials. — 2005. — Vol. 37. — P. 899–913. https://doi.org/10.1016/j.mechmat.2004.09.002
3. Stan, F. Viscoelastic Characterization of Polytetrafluoroethylene (PTFE) Polymer by Sharp Indentation / F. Stan, A. V. Munteanu, C. Fetecau / AIP Conference Proceedings. — 2011. — Vol. 1315. — P. 221–226. https://doi.org/10.1063/1.3552445
4. Stan, F. Study of Stress Relaxation in Polytetrafluoroethylene Composites by Cylindrical Macroindentation / F. Stan, C. Fetecau // Composites Part B: Engineering. — 2013. — Vol. 47. — P. 298–307. 10.1016/j.compositesb.2012.11.008
5. Menčik, J. Determination of Viscoelastic-Plastic Material Parameters of Biomaterials by Instrumental Indentation / J. Menčik, Li Hong He, M. V. Swain // Journal of the Mechanical Behavior of Biomedical Materials. — 2009. — Vol. 2. — P. 318–325. https://doi.org/10.1016/j.jmbbm.2008.09.002
6. Drozdov, A. D. Cyclic Elastoplasticity of Solid Polymers / A. D. Drozdov, J. de C. Christiansen // Computational Materials Science. — 2008. — Vol. 42. — P. 27–35. https://doi.org/10.1016/j.commatsci.2007.06.002
7. Хохлов, А. В. Сравнительный анализ свойств кривых ползучести, порождаемых линейной и нелинейной теориями наследственности при ступенчатых нагружениях / А. В. Хохлов // Математическая физика и компьютерное моделирование. — 2018. — Т. 21, № 2. — С. 27–51. https://doi.org/10.15688/mpcm.jvolsu.2018.2.3
8. Хохлов, А. В. Индикаторы применимости и методики идентификации нелинейной модели типа Максвелла для реономных материалов по кривым ползучести при ступенчатых нагружениях / А. В. Хохлов // Вестник Московского государственного технического университета им. Н. Э. Баумана. Естественные науки. — 2018. — № 6 (81). — С. 92–112. http://dx.doi.org/10.18698/1812-3368-2018-6-92-112
9. Хохлов, А. В. Методики идентификации нелинейной модели типа Максвелла для реономных материалов по кривым обратной ползучести / А. В. Хохлов // Проблемы прочности и пластичности. — 2018. — Т. 80, № 2. — С. 238–254. https://doi.org/10.32326/1814-9146-2018-80-2-238-254
10. Огородников, Е. Н. Математические модели нелинейной вязкоупругости с операторами дробного интегродифференцирования / Е. Н. Огородников, В. П. Радченко, Л. Г. Унгарова // Вестник Пермского национального исследовательского политехнического университета. Механика. — 2018. — № 2. — С. 147–161. https://doi.org/10.15593/perm.mech/2018.2.13
11. Адамов, А. А. Экспериментальное обеспечение и идентификация модели изотропного тела с упругой объемной сжимаемостью дисперсно-наполненных композитов на основе фторопласта и сверхвысокомолекулярного полиэтилена / А. А. Адамов // Конструкции из композиционных материалов. — 2013. — № 2 (130). — С. 28–37. 12. Гольдман, А. Я. Объемное деформирование пластмасс / А. Я. Гольдман. — Ленинград: Машиностроение, 1984. — 232 с.
12. Адамов, А. А. Методы прикладной вязкоупругости / А. А. Адамов, В. П. Матвеенко, Н. А. Труфанов, И. Н. Шардаков. — Екатеринбург : УрО РАН, 2003. — 411 с.
13. Flat-Punch Indentation of Viscoelastic Material / L. Cheng, X. Xia, W. Yu [et al.] // Journal of Polymer Science. Part B: Polymer Physics. — 2000. — Vol. 38. — P. 10–22. 10.1002/(SICI)1099-0488(20000101)38:1<10::AID-POLB2>3.0.CO;2-6
14. Measurement of Creep Compliance of Solid Polymers by Nanoindentation / H. Lu, B. Wang, J. Ma [et al.] // Mechanics of Time-Dependent Materials. — 2003. — Vol. 7. — P. 189–207. https://doi.org/10.1023/B:MTDM.0000007217.07156.9b
15. Tóth, L. F. Thermal, Viscoelastic, Mechanical and Wear Behaviour of Nanoparticle Filled Polytetrafluoroethylene: A Comparison / L. F. Tóth, P. De Baets, G. Szebényi // Polymers. — 2020. — Vol. 12. — Р. 1940. https://doi.org/10.3390/polym12091940
16. Гавриленко, С. Л. Аттестация линейной вязкоупругой модели антифрикционного полимерного композита по результатам ускоренных испытаний на релаксацию / С. Л. Гавриленко, С. В. Шилько // Теоретическая и прикладная механика. — 2017. — № 32. — С. 155–158.
17. Конова, Е. М. Влияние природы наполнителя на физико-механические свойства радиационных модификаций композитов на основе политетрафторэтилена / Е. М. Конова, С. Г. Острер, С. А. Хатипов // Пластические массы. — 2011. — № 5. — С. 40–43.
18. Wenjuan Xu. Tensile Ratcheting Behaviors of Bronze Powder Filled Polytetrafluoroethylene / Wenjuan Xu, Hong Gao, LiLan Gao [et al.] // Frontiers of Chemical Science and Engineering. — 2013. — Vol. 7. — P. 103–109. https://doi.org/10.1007/s11705-013-1315-8
19. Kadashevich, Yu. Endochronic Model of Plasticity Generalizing Sanders's Theory / Yu. Kadashevich, S. Pomytkin // Scientific Letters of Rzeszow University of Technology. Mechanics. — 2014. — Vol. 31. — P. 539–547. https://doi.org/10.7862/RM.2014.57
About the Authors
D. S. PetukhovRussian Federation
1, Academika Koroleva St., Perm
A. A. Adamov
Russian Federation
1, Academika Koroleva St., Perm
I. E. Keller
Russian Federation
1, Academika Koroleva St., Perm
Review
For citations:
Petukhov D.S., Adamov A.A., Keller I.E. Selection and Identification of a Model of Elasto-Viscoplasticity of the Filled Fluorocomposite according to Free and Constrained Compression Tests. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):180-192. https://doi.org/10.23947/2687-1653-2022-22-3-180-192













































