Перейти к:
Выбор и идентификация модели упруговязкопластичности наполненного фторкомпозита по данным испытаний на свободное и стесненное сжатие
https://doi.org/10.23947/2687-1653-2022-22-3-180-192
Аннотация
Введение. Наполненные композиты на основе политетрафторэтилена обладают свойствами, позволяющими работать при высоких контактных давлениях, возвратно-поступательном характере сдвиговых нагрузок и в широком диапазоне температур. Благодаря этому их применяют в качестве антифрикционных слоев опорных частей с шаровым сегментом. Для моделирования механического поведения таких материалов в условиях эксплуатации нужны адекватные определяющие уравнения упруговязкопластичности и методы их идентификации по данным базовых экспериментов.
Материалы и методы. Тензорно-линейную модель упруговязкопластичности предлагается идентифицировать по данным экспериментов на свободное сжатие образцов. Их подвергают нагружению до максимальной деформации 10 %, выдерживают, разгружают и проводят аналогичный цикл нагружения до 160 МПа при стесненном сжатии. Эксперимент с композитом на основе политетрафторэтилена, наполненного 40 масс. % мелкодисперсной бронзы, проходил при комнатной температуре. Испытания на стесненное сжатие выполнялись для двух, на свободное сжатие – для трех значений скорости деформации в диапазоне 10-6 – 10-3 с-1. Для описания рассматривались две модели упруговязкопластичности, представляющие собой модификации моделей Свейна и Клечковски и соответствующие соединению вязкоупругого либо упругого нелинейновязкого элемента с пластическим или эндохронным элементом. В качестве вязкоупругого элемента рассматривался интегральный оператор с ядром Кольрауша.
Результаты исследования. Итоги испытаний по стесненному сжатию позволили отделить от определяющих соотношений упругую связь объемных деформаций и средних напряжений. Данные циклов свободного сжатия при различных скоростях деформации использовали для определения материальных констант модели. С этой целью реализован эффективный поисковый алгоритм на основе симплекс-метода минимизации невязки. Обе модели обнаружили важность пластической составляющей (не зависящей от скорости деформации) для качественного описания циклического изменения напряжений, сопровождающего циклическое изменение деформаций, а также их зависимость от скорости деформаций.
Обсуждение и заключения. Обе модели упруговязкопластичности корректно описывают поведение исследованного фторкомпозита в условиях нагружения, близких к условиям эксплуатации антифрикционных слоев опорных частей с шаровым сегментом, и могут рассматриваться в качестве основы для их дальнейшего обобщения с учетом зависимости от температуры.
Ключевые слова
Для цитирования:
Петухов Д.С., Адамов А.А., Келлер И.Э. Выбор и идентификация модели упруговязкопластичности наполненного фторкомпозита по данным испытаний на свободное и стесненное сжатие. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):180-192. https://doi.org/10.23947/2687-1653-2022-22-3-180-192
For citation:
Petukhov D.S., Adamov A.A., Keller I.E. Selection and Identification of a Model of Elasto-Viscoplasticity of the Filled Fluorocomposite according to Free and Constrained Compression Tests. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):180-192. https://doi.org/10.23947/2687-1653-2022-22-3-180-192
Введение. Наполненные композиты на основе политетрафторэтилена (ПТФЭ) обладают свойствами, позволяющими работать в широком диапазоне температур при высоких контактных давлениях и возвратно - поступательном скольжении по контртелу. Благодаря этому названные материалы применяют в качестве антифрикционных слоев опорных частей с шаровым сегментом для мостов1, 2. ПТФЭ как основа для антифрикционных полимерных композитов в широком диапазоне температур демонстрирует высокую стабильность свойств и исключительно низкие коэффициенты трения, скольжения и покоя. Введение наполнителей помогает без значительного увеличения коэффициентов трения существенно повысить износостойкость, жесткость и предел текучести, а также снизить ползучесть композита. Реологические свойства антифрикционного материала должны обеспечивать работоспособность в процессе эксплуатации изделия в диапазоне температур от менее ‒50 до +50 °С:
- при расчетных значениях сжимающей нагрузки не менее 60 МПа;
- при ее пиковых значениях до 150 МПа;
- при нормированном размахе циклических сдвиговых деформаций.
Имеет значение также предсказуемость изменения свойств и толщины антифрикционного слоя при его монтаже в шарнир.
При эксплуатации рассматриваемых материалов приходится оценивать работоспособность антифрикционных слоев опорных частей с шаровым сегментом, прогнозировать ресурс на весь срок службы (до 50 лет). Для этого необходимо строить и идентифицировать по данным базовых экспериментов адекватные определяющие уравнения упруговязкопластичности. Модели, описывающие реологическое поведение наполненных фторкомпозитов, также важны для расчетов эксплуатационных свойств уплотнений валов и штоков в мощных дизельных агрегатах3. Для расчета поведения изделий под нагрузкой при монтаже (на коротких отрезках времени) важно корректное описание моделями пластических (упругопластических, вязкопластических) свойств материала. Для расчета поведения изделий в процессе эксплуатации (на длинных отрезках времени) необходимо адекватное представление явлений релаксации, ползучести и циклической ползучести (рэтчетинга).
В литературе редко встречаются реологические модели наполненных фторкомпозитов, описывающие циклы нагрузки, выдержки и разгрузки в широких диапазонах времени и скоростей деформаций. Можно указать лишь работу [1], удовлетворяющую всем этим требованиям. В ней предложена модель, соответствующая параллельному соединению эндохронного и нелинейно-вязкого элементов. Данной моделью описаны все испытания4 одноосным растяжением при комнатной температуре. Речь идет о:
- кривых нагружениях до деформации 0,08 со скоростями деформации 10-4 –10-2 c-1;
- кривых релаксациях в течение 10 ч при постоянной деформации 0,03–0,08;
- петлях гистерезиса в цикле нагрузки до деформации 0,1, кратковременной выдержки и разгрузки с последующей выдержкой.
В [2] представлена тензорная геометрически нелинейная модель. Она описывает поведение наполненных фторкомпозитов при различных монотонных и циклических историях нагружения в различных напряженных состояниях и при произвольных температурах. Учитывается вязкопластический реологический элемент в последовательном соединении с вязкоупругим. Эта модель в целом удовлетворительно описывает кривые, соответствующие экспериментам [1], но она существенно сложнее и требует 14 материальных констант. В [3] для описания циклов микроиндентирования наполненного фторкомпозита используется модель [4]. Ее реологическая структурная схема схожа с [2], но учитывает спектр времен релаксации вязкоупругого элемента.
Модель [5] предназначена для описания особенностей упругопластического поведения твердых полимеров при циклическом одноосном нагружении. Эволюционные уравнения для ее внутренней переменной, напряжений и пластических деформаций имеют нелинейные перекрестные связи, поэтому модель не соответствует какой-либо реологической структурной схеме. Используется мера внутреннего времени, характерная для эндохронной теории пластичности. Для идентификации модели требуется 21 константа.
Нелинейная одномерная модель вязкоупругопластичности типа Максвелла [6–9] содержит всего две материальные функции. Она описывает неполное восстановление деформаций в цикле нагрузки-разгрузки и циклическую ползучесть (рэтчетинг) при несимметричных циклах нагружения. Для моделей нелинейной вязкоупругости с операторами дробного интегродифференцирования характерна гибкость при малом числе материальных констант и функций [7]. Необходимо исследовать применимость подобных нелинейных моделей для описания поведения полимерных материалов в цикле нагружения и разгрузки с выдержками [10–13]. Работы [14][15] посвящены идентификации линейных моделей вязкоупругости по результатам испытаний индентированием. В [16][17] для этой цели используются результаты динамического механического анализа, однако существенная нелинейность исследуемых в настоящей работе материалов не позволяет воспользоваться данной методикой. В [18][19] экспериментально исследуется рэтчетинг ПТФЭ композитов, но отсутствует математическое описание результатов.
В [8] представлена методика идентификации модели изотропного упругопластического поведения наполненных композитов на основе ПТФЭ и сверхвысокомолекулярного полиэтилена на основе экспериментальных данных по свободному и стесненному сжатию. Благодаря особенности реологии пластмасс [9] к ним применимы методы [10]. Такой подход позволяет определить:
- функцию упругой объемной сжимаемости;
- функцию упрочнения для сдвиговых упругопластических свойств в рамках теории пластического течения.
Итак, условия эксплуатации рассматриваемых изделий, механические свойства полимерных материалов и представленный анализ литературы служат основой для дальнейших изысканий. Выделим базовое испытание на свободное сжатие цилиндрических образцов 20×20 мм. Оно состоит из циклов нагрузки до деформации 0,1, кратковременной выдержки 15 мин. и разгрузки с последующей выдержкой 15 мин. Так можно определить данные для описания упругой, пластической и вязкой составляющих деформации, релаксации и обратной ползучести с остаточными деформациями. Аналогичное определение твердости предусмотрено стандартом6.
Нагружение выполняется при трех скоростях деформации в диапазоне 10-6 –10-3 c-1. Кроме того, образцы испытывают на стесненное сжатие до напряжения 160 МПа при двух скоростях деформации из этого же диапазона. Все испытания повторяются для значений из диапазона температур эксплуатации полимерного материала. Этих данных должно быть достаточно для идентификации подходящей модели упруговязкопластического сжимаемого материала с нелинейно-упругой сжимаемостью.
Интересуют, в первую очередь, возможности описания экспериментальных данных при комнатной температуре простейшими моделями упруговязкопластичности типа предложенных в [1] и [4], которые отличаются структурными схемами.
Материалы и методы. В качестве моделируемого материала выбрали композит на основе ПТФЭ ПН90, наполненного 40 масс. % мелкодисперсной бронзы. Цилиндрические образцы диаметром и высотой по 20 мм изготавливались прессованием и спеканием смеси порошков3. Для выбора и последующей идентификации модели провели эксперименты:
- на стесненное сжатие с единственной ненулевой компонентой тензора деформации;
- на свободное сжатие с единственной ненулевой компонентой тензора напряжений.
В первом случае трение по боковой границе исключалось смазкой, во втором — тонкой пленкой из ПТФЭ и смазкой.
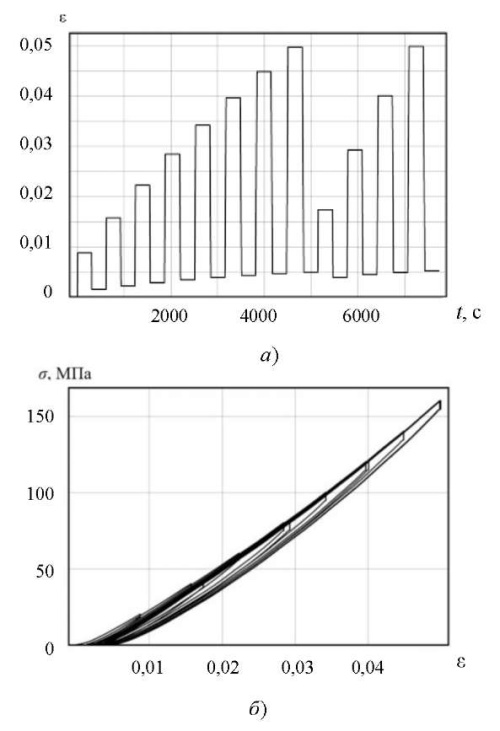
Рис. 1. Испытание на циклическое стесненное сжатие: а — программа; б — кривая гистерезиса
Цель экспериментов — выявление необратимых объемных деформаций и объемно-упругих свойств материала. Первым испытанием было циклическое стесненное сжатие с увеличивающейся амплитудой (рис. 1 а). В нем задавалась величина скорости деформации 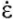 = 2,5 ×10-3 c-1 и паузы между разгрузками и нагрузками по 300 с. За несколько первых циклов накапливается остаточная объемная деформация, равная приблизительно 5 ×10-3 (рис. 1). Она слабо меняется при выдержке образца в разгруженном состоянии.
= 2,5 ×10-3 c-1 и паузы между разгрузками и нагрузками по 300 с. За несколько первых циклов накапливается остаточная объемная деформация, равная приблизительно 5 ×10-3 (рис. 1). Она слабо меняется при выдержке образца в разгруженном состоянии.
Далее провели испытания сжатием до 160 МПа со значительно более медленной скоростью деформации 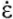 = 2,5 ×10-5 c-1 и последующей разгрузкой (рис. 2 а):
= 2,5 ×10-5 c-1 и последующей разгрузкой (рис. 2 а):
- недеформированного образца (1);
- того же образца повторно (2);
- образца после циклического испытания, приведенного на рис. 1 (3).
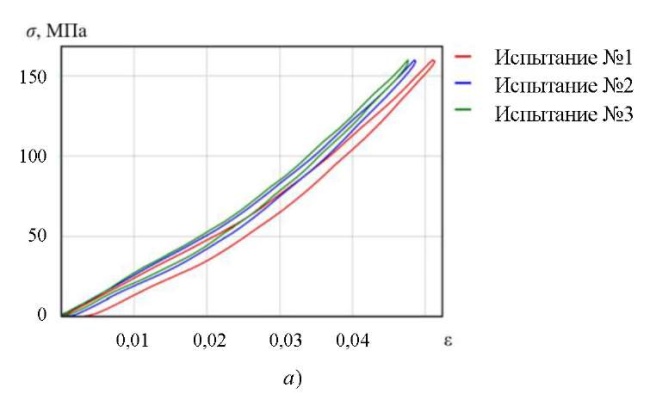
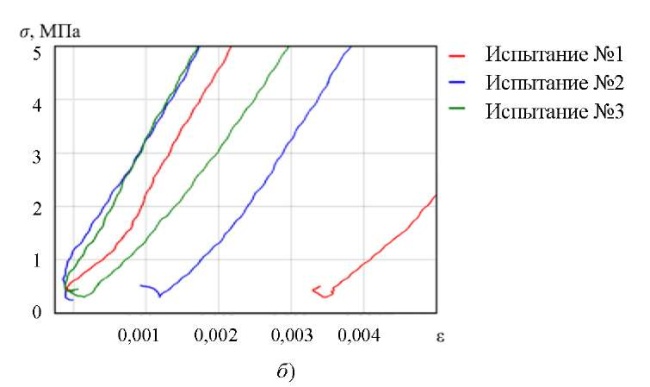
Рис. 2. Медленные испытания на стеснённое сжатие:
а — диаграммы нагружения; б — начальные и конечные участки диаграмм
Испытания одного и того же образца проводились через сутки.
Как видно на рис. 2 б, в опыте с новым образцом наблюдается максимальная остаточная деформация около 3,5 ×10-3. При повторном испытании она составила 1 ×10-3. В третьем испытании не наблюдается остаточной деформации. Свойства материала при циклическом стесненном сжатии сопровождаются переходным необратимым процессом и стабилизируются за несколько циклов.
Объемные свойства определялись из третьего испытания (рис. 2 а), в котором отсутствуют остаточные деформации. В настоящей работе объемные деформации полагаются нелинейно упругими. Данные описываются квадратичной зависимостью:
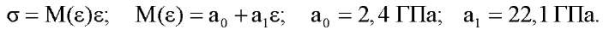 (1)
(1)
Здесь σ, ε ― осевые компоненты тензоров напряжений Коши и логарифмических деформаций; M― модуль стесненного сжатия, который связан с модулем объемного сжатия K соотношением:
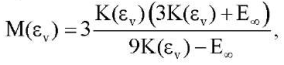 (2)
(2)
где E∞ ― равновесный модуль Юнга (не зависит от объемной деформации); 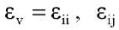 ― компоненты тензора логарифмических деформаций.
― компоненты тензора логарифмических деформаций.
Значение E∞ = 690 МПа получили с наклоном кривой σ(ε) при одноосном сжатии в окрестности σ - 1МПа и релаксации 8,65 %.
Используя (1), (2) и поправку 9,38 % на податливость машины в испытании на стесненное сжатие, можно получить искомую зависимость K(εv), которая слабо (максимум на 0,03 %) отличается от линейной:
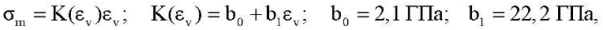 (3)
(3)
где 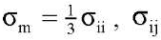 ― компоненты тензора напряжений Коши.
― компоненты тензора напряжений Коши.
Эксперименты для определения связи между средним напряжением и объемной деформацией проводятся на образцах, предварительно испытанных стесненным сжатием с необратимой объемной деформацией. То же касается и экспериментов на свободное сжатие, описанных ниже и необходимых для определения связи девиаторных частей тензоров напряжений и деформаций. В результате модель отражает свойства уплотненного материала. На производстве процессы, связанные с необратимой объемной деформацией, происходят во время опрессовки слоя антифрикционного полимерного материала при сборке конструкции опорной части и не влияют на дальнейшее поведение материала.
Испытания на одноосное сжатие проводили для определения соотношений между девиаторными частями тензоров напряжений и деформаций. На рис. 3 приводятся результаты опытов для трех значений скоростей деформаций 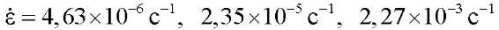 . Далее данные этих экспериментов будут интерпретироваться в рамках одномерной модели. При формулировке трехмерной модели из этих соотношений может быть исключена упругая объемная часть.
. Далее данные этих экспериментов будут интерпретироваться в рамках одномерной модели. При формулировке трехмерной модели из этих соотношений может быть исключена упругая объемная часть.

Рис. 3. Эксперимент на одноосное сжатие с тремя различными скоростями: а — диаграммы нагружения; б — истории деформаций; в — истории напряжений
При выборе подходящей модели оказалось, что экспериментальные данные, изображенные на рис. 3 не описываются соотношениями линейной вязкоупругой среды:
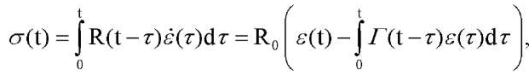 (4)
(4)
где σ(t), ε(t) ― истории напряжений и деформаций, применяемые для описания эластомеров и полимеров [10].
Были попытки использовать выражения для функций релаксации R(t) либо скорости релаксации Г(t) с различным числом параметров: сумма экспонент, дробно-экспоненциальная функция Работнова7, ядро Колтунова8, ядро из работы Т. Л. Смита9, ядро Кольрауша [10]:
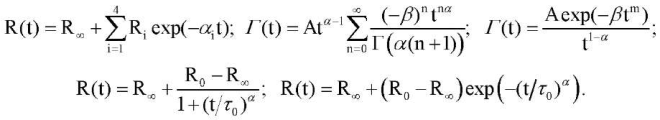 (5)
(5)
Здесь 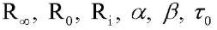 ― материальные константы; Г ― гамма-функция, а также монотонная аппроксимация кубическими сплайнами по восьми точкам, координаты которых служили параметрами.
― материальные константы; Г ― гамма-функция, а также монотонная аппроксимация кубическими сплайнами по восьми точкам, координаты которых служили параметрами.
Рассматривались модели, в которых кроме вязких учитываются пластические необратимые деформации. Исследовались две базовые модели такого типа.
Базовая модель 1 (рис. 4 а) представляет собой соединение моделей [4] и [10] и предполагает последовательное соединение трех элементов.
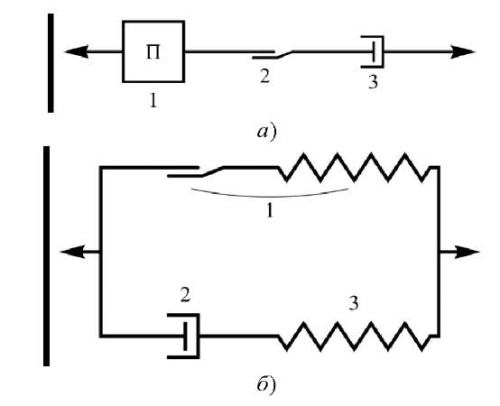
Рис. 4. Структурные схемы базовых моделей: а — модель 1; б — модель 2
- Линейный вязкоупругий элемент с ядром Кольрауша [10]:
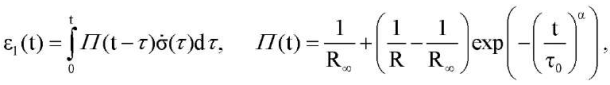 (6)
(6)
где 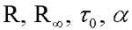 ― материальные константы, первые две имеют физический смысл мгновенного и равновесного модулей.
― материальные константы, первые две имеют физический смысл мгновенного и равновесного модулей.
- Пластический элемент с линейным упрочнением:
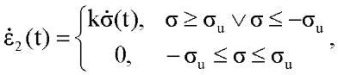 (7)
(7)
где σu, k ― материальные константы.
- Линейно-вязкий элемент:
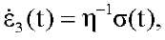 (8)
(8)
где η ― материальная константа.
Итоговое выражение для деформаций:
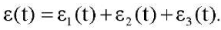 (9)
(9)
Модель (6)–(9) решается относительно деформаций, поэтому для ее идентификации удобно располагать историями напряжений σ(t) (рис. 3 в).
Структурная схема базовой модели 2 (рис. 4 б), заимствованной из [1], представляет собой параллельное соединение двух элементов.
- Эндохронный пластический элемент с нелинейной упругой частью:
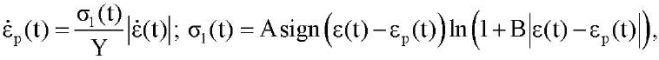 (10)
(10)
гд εp ― внутренний параметр, имеющий смысл необратимой деформации элемента ; Y, A, B ― материальные константы.
- Пара последовательно соединенных нелинейно-вязкого (2) и линейно-упругого (3) элементов:
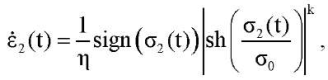 (11)
(11)
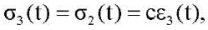 (12)
(12)
где sign — знак аргумента; 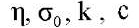 — материальные константы.
— материальные константы.
Результирующее выражение для напряжений:
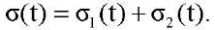 (13)
(13)
Модель (10)–(13) решается относительно напряжений, поэтому для ее идентификации удобно располагать историями деформаций ε(t) (рис. 3 в). Выражение σ1(t) в (13) вычисляется как решение системы алгебродифференциальных уравнений (10), а σ2(t) — как решение системы (11), (12) с учетом ε(t) = ε2(t) + ε3(t)
Результаты исследования. Минимизация невязки между экспериментальными историями деформаций (рис. 3 б) и предсказаниями модели позволила найти семь материальных констант базовой модели 1:
 (14)
(14)
В качестве поисковой процедуры использован симплекс-метод. Сравнение расчетных и экспериментальных данных приводится на рис. 5.
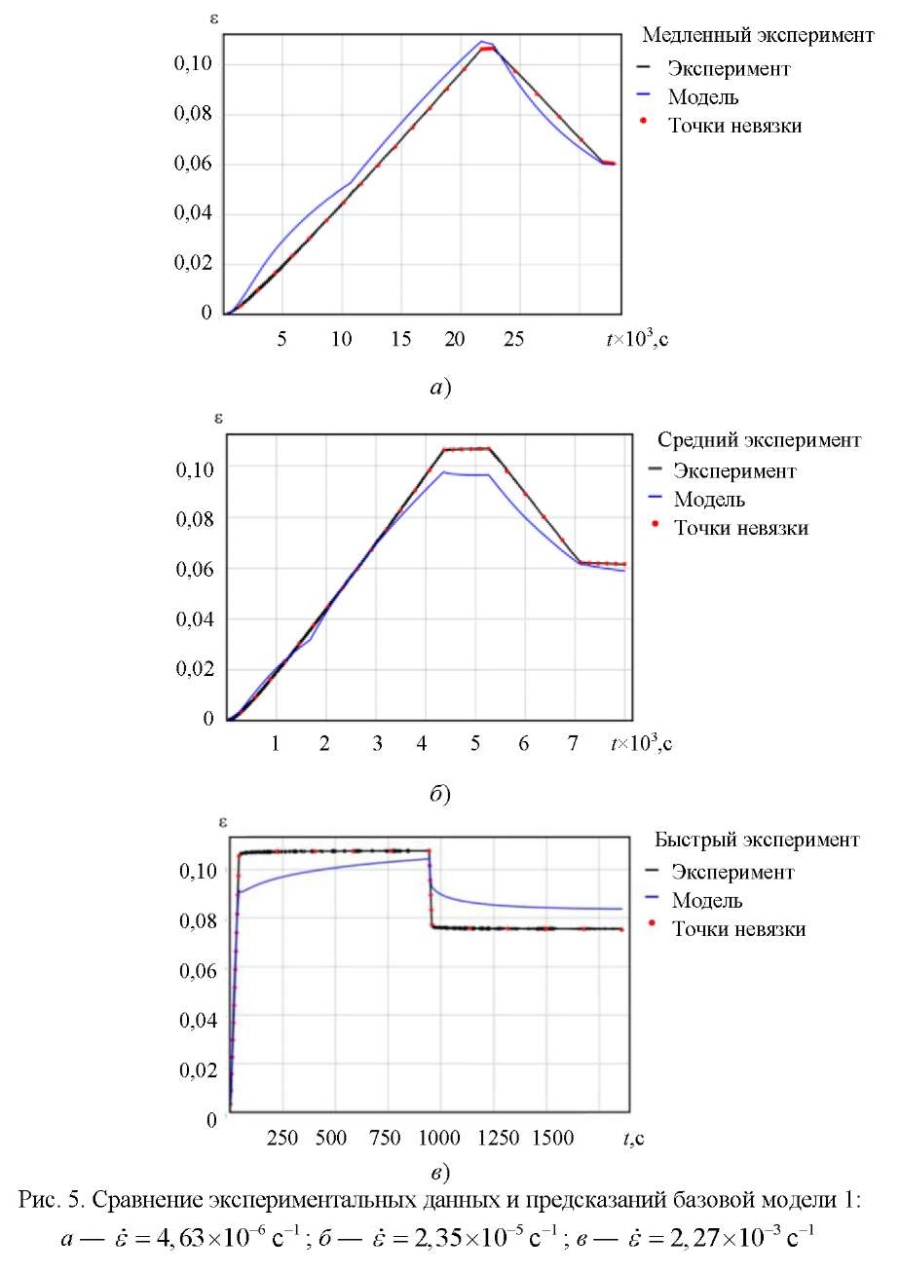
Минимизация невязки между экспериментальными историями напряжений (рис. 3 в) и предсказаниями модели позволила обнаружить семь материальных констант базовой модели 2:
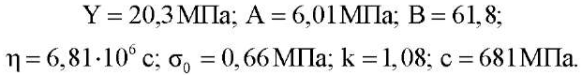 (15)
(15)
При этом считались заданными истории деформаций (рис. 3 б). Сравнение расчетных и экспериментальных данных приведено на рис. 6.

Обсуждение и заключения. Рассмотренные одномерные модели обобщаются на пространственную формулировку, которая предполагает изотропию свойств и неизменность главных осей тензора деформаций в процессе нагружения. Для этого тензоры напряжений Коши и логарифмических деформаций разлагаются на шаровую и девиаторную части:
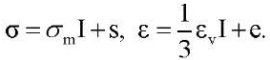
Связь между шаровыми частями σm и εv задается выражением (3). Связь между девиаторными частями s и e задается соотношениями, обобщающими (6)–(9) или (10)–(13) в зависимости от выбора базовой модели. Эти выражения следует переписать в терминах историй девиаторных частей s(t) и e(t), исключая из одноосного сжатия шаровую часть.
В качестве пространственного обобщения соотношений (7) для пластического элемента модели 1 рассматривается закон пластического течения, ассоциированный с критерием текучести Мизеса, с изотропным линейным деформационным упрочнением. Связь девиаторов будет выглядеть так:
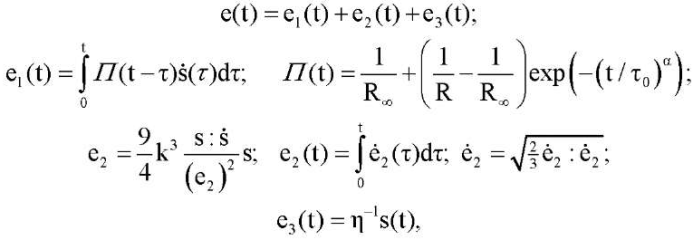
где двоеточие означает операцию свертки тензоров A : B = AijBij, заданных компонентами в ортонормированном базисе.
Соотношения эндохронной теории пластичности (10) модели 2 также обобщаются в духе пластичности Мизеса, что приводит к следующей записи для девиаторов:
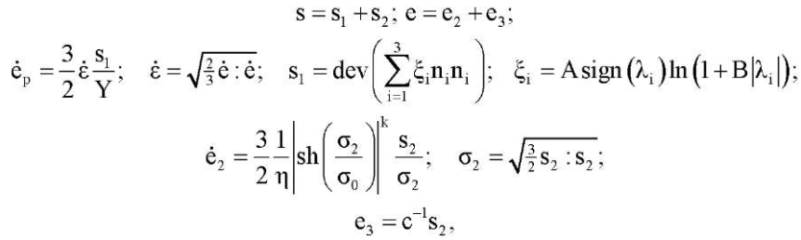
где dev означает девиатор тензора; λi, ni — собственные числа и собственные векторы тензора 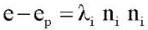 .
.
Следует заметить, что авторы [1] использовали вариант модели с параметром эндохронности [14], равным единице. Представляется целесообразным рассмотрение этого параметра в качестве материальной константы, поскольку известно его влияние на описание переходных процессов после смен режимов нагружения.
В рамках настоящей работы проводились опыты по стесненному и свободному сжатию композита на основе политетрафторэтилена, наполненного мелкодисперсной бронзой с массовой долей 40 %. При этом выполнялись нагрузки, разгрузки и выдержки с различными скоростями деформаций в диапазоне 10-6 –10-3 c-1. Эксперименты на стесненное сжатие проводились при давлениях, соответствующих пиковым нагрузкам антифрикционного слоя в шарнирах со сферическим сегментом. Обнаружена неспособность стандартной линейной вязкоупругой модели описывать данные испытаний для нескольких скоростей деформации. Выбраны и идентифицированы две семиконстантные модели с пластическими и нелинейными вязкими структурными элементами, которые могут описать данные базовых экспериментов. Модель с эндохронным элементом показала большую аккуратность описания данных при высокой скорости деформирования. Модель с пластическим элементом может быть усовершенствована, если учесть нелинейность в вязком элементе и нелинейное деформационное упрочнение, что потребует увеличения числа материальных констант. Данные моделей обобщены на пространственный случай для изотропного материала и историй деформирования с постоянной ориентацией трехгранника главных осей.
1. EAD 050009-00-0301 Spherical and cylindrical bearing with special sliding material made of fluoropolymer / EOTA // Product regulation : [сайт]. URL: https://www.nlfnorm.cz/en/ehn/6189
2. Stanton J. F., Roeder C. W., Campbell T. I. Appendix C: Friction and Wear of PTFE Sliding Surfaces // NCHRP Report 432: High-Load Multi-Rotational Bridge Bearings. Washington : TRB, 1999. 413 p.
3. Material and Computational Analysis of PTFE Seals / H. Sui [et al.] // SAE Paper Series : [сайт]. 1995, 951055. URL: https://www.sae.org/publications/technical-papers/content/951055/?src=2001-01-1118
4. То же.
5. То же.
6. ГОСТ 4670-2015 (ISO 2039-1:2001). Пластмассы. Определение твердости. Метод вдавливания шарика / Межгосударственный совет по стандартизации, метрологии и сертификации. М.: Стандартинформ, 2016. 10 с.
7. Работнов Ю. Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.
8. Колтунов М. А. Сингулярные функции влияния в анализе релаксационных процессов // Прочность и пластичность. М.: Наука. 1971. С. 640–645.
9. Смит Т. Л. Эмпирические уравнения для вязкоупругих характеристик и вычисления релаксационных спектров // Вязкоупругая релаксация в полимерах. М.: Мир, 1974. С. 44–56.
Список литературы
1. Kletschkowski, T. Endochronic Viscoplastic Material Models for Filled PTFE / T. Kletschkowski, U. Schomburg, A. Bertram // Mechanics of Materials. — 2002. — Vol. 34. — P. 795–808. https://doi.org/10.1016/S0167-6636(02)00197-7
2. Bergström, J. S. A Constitutive Model for Predicting the Large Deformation Thermomechanical Behavior of Fluoropolymers / J. S. Bergström, L. B. Hilbert Jr. // Mechanics of Materials. — 2005. — Vol. 37. — P. 899–913. https://doi.org/10.1016/j.mechmat.2004.09.002
3. Stan, F. Viscoelastic Characterization of Polytetrafluoroethylene (PTFE) Polymer by Sharp Indentation / F. Stan, A. V. Munteanu, C. Fetecau / AIP Conference Proceedings. — 2011. — Vol. 1315. — P. 221–226. https://doi.org/10.1063/1.3552445
4. Stan, F. Study of Stress Relaxation in Polytetrafluoroethylene Composites by Cylindrical Macroindentation / F. Stan, C. Fetecau // Composites Part B: Engineering. — 2013. — Vol. 47. — P. 298–307. 10.1016/j.compositesb.2012.11.008
5. Menčik, J. Determination of Viscoelastic-Plastic Material Parameters of Biomaterials by Instrumental Indentation / J. Menčik, Li Hong He, M. V. Swain // Journal of the Mechanical Behavior of Biomedical Materials. — 2009. — Vol. 2. — P. 318–325. https://doi.org/10.1016/j.jmbbm.2008.09.002
6. Drozdov, A. D. Cyclic Elastoplasticity of Solid Polymers / A. D. Drozdov, J. de C. Christiansen // Computational Materials Science. — 2008. — Vol. 42. — P. 27–35. https://doi.org/10.1016/j.commatsci.2007.06.002
7. Хохлов, А. В. Сравнительный анализ свойств кривых ползучести, порождаемых линейной и нелинейной теориями наследственности при ступенчатых нагружениях / А. В. Хохлов // Математическая физика и компьютерное моделирование. — 2018. — Т. 21, № 2. — С. 27–51. https://doi.org/10.15688/mpcm.jvolsu.2018.2.3
8. Хохлов, А. В. Индикаторы применимости и методики идентификации нелинейной модели типа Максвелла для реономных материалов по кривым ползучести при ступенчатых нагружениях / А. В. Хохлов // Вестник Московского государственного технического университета им. Н. Э. Баумана. Естественные науки. — 2018. — № 6 (81). — С. 92–112. http://dx.doi.org/10.18698/1812-3368-2018-6-92-112
9. Хохлов, А. В. Методики идентификации нелинейной модели типа Максвелла для реономных материалов по кривым обратной ползучести / А. В. Хохлов // Проблемы прочности и пластичности. — 2018. — Т. 80, № 2. — С. 238–254. https://doi.org/10.32326/1814-9146-2018-80-2-238-254
10. Огородников, Е. Н. Математические модели нелинейной вязкоупругости с операторами дробного интегродифференцирования / Е. Н. Огородников, В. П. Радченко, Л. Г. Унгарова // Вестник Пермского национального исследовательского политехнического университета. Механика. — 2018. — № 2. — С. 147–161. https://doi.org/10.15593/perm.mech/2018.2.13
11. Адамов, А. А. Экспериментальное обеспечение и идентификация модели изотропного тела с упругой объемной сжимаемостью дисперсно-наполненных композитов на основе фторопласта и сверхвысокомолекулярного полиэтилена / А. А. Адамов // Конструкции из композиционных материалов. — 2013. — № 2 (130). — С. 28–37. 12. Гольдман, А. Я. Объемное деформирование пластмасс / А. Я. Гольдман. — Ленинград: Машиностроение, 1984. — 232 с.
12. Адамов, А. А. Методы прикладной вязкоупругости / А. А. Адамов, В. П. Матвеенко, Н. А. Труфанов, И. Н. Шардаков. — Екатеринбург : УрО РАН, 2003. — 411 с.
13. Flat-Punch Indentation of Viscoelastic Material / L. Cheng, X. Xia, W. Yu [et al.] // Journal of Polymer Science. Part B: Polymer Physics. — 2000. — Vol. 38. — P. 10–22. 10.1002/(SICI)1099-0488(20000101)38:1<10::AID-POLB2>3.0.CO;2-6
14. Measurement of Creep Compliance of Solid Polymers by Nanoindentation / H. Lu, B. Wang, J. Ma [et al.] // Mechanics of Time-Dependent Materials. — 2003. — Vol. 7. — P. 189–207. https://doi.org/10.1023/B:MTDM.0000007217.07156.9b
15. Tóth, L. F. Thermal, Viscoelastic, Mechanical and Wear Behaviour of Nanoparticle Filled Polytetrafluoroethylene: A Comparison / L. F. Tóth, P. De Baets, G. Szebényi // Polymers. — 2020. — Vol. 12. — Р. 1940. https://doi.org/10.3390/polym12091940
16. Гавриленко, С. Л. Аттестация линейной вязкоупругой модели антифрикционного полимерного композита по результатам ускоренных испытаний на релаксацию / С. Л. Гавриленко, С. В. Шилько // Теоретическая и прикладная механика. — 2017. — № 32. — С. 155–158.
17. Конова, Е. М. Влияние природы наполнителя на физико-механические свойства радиационных модификаций композитов на основе политетрафторэтилена / Е. М. Конова, С. Г. Острер, С. А. Хатипов // Пластические массы. — 2011. — № 5. — С. 40–43.
18. Wenjuan Xu. Tensile Ratcheting Behaviors of Bronze Powder Filled Polytetrafluoroethylene / Wenjuan Xu, Hong Gao, LiLan Gao [et al.] // Frontiers of Chemical Science and Engineering. — 2013. — Vol. 7. — P. 103–109. https://doi.org/10.1007/s11705-013-1315-8
19. Kadashevich, Yu. Endochronic Model of Plasticity Generalizing Sanders's Theory / Yu. Kadashevich, S. Pomytkin // Scientific Letters of Rzeszow University of Technology. Mechanics. — 2014. — Vol. 31. — P. 539–547. https://doi.org/10.7862/RM.2014.57
Об авторах
Д. С. ПетуховРоссия
Петухов Дмитрий Сергеевич, ведущий инженер «Лаборатории нелинейной механики деформируемого твердого тела»
ResearcherID, ScopusID
614018, г. Пермь, ул. Академика Королева, 1
А. А. Адамов
Россия
Адамов Анатолий Арсангалеевич, ведущий научный сотрудник «Лаборатории нелинейной механики деформируемого твердого тела», доктор физико-математических наук
ScopusID
614018, г. Пермь, ул. Академика Королева, 1
И. Э. Келлер
Россия
Келлер Илья Эрнстович, заведующий «Лаборатории нелинейной механики деформируемого твердого тела»
ResearcherID, ScopusID
614018, г. Пермь, ул. Академика Королева, 1
Рецензия
Для цитирования:
Петухов Д.С., Адамов А.А., Келлер И.Э. Выбор и идентификация модели упруговязкопластичности наполненного фторкомпозита по данным испытаний на свободное и стесненное сжатие. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):180-192. https://doi.org/10.23947/2687-1653-2022-22-3-180-192
For citation:
Petukhov D.S., Adamov A.A., Keller I.E. Selection and Identification of a Model of Elasto-Viscoplasticity of the Filled Fluorocomposite according to Free and Constrained Compression Tests. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):180-192. https://doi.org/10.23947/2687-1653-2022-22-3-180-192













































