Scroll to:
Development of Properties Control Methods for Magnetorheological Medium to Regulate the Stiffness of Exoskeleton Variable-Length Link
https://doi.org/10.23947/2687-1653-2022-22-4-296-305
Abstract
Introduction. The article investigated one of the problems of creating exoskeletons — controlling the properties of magnetic rheological fluid in links of variable length with adjustable stiffness. Based on the research of domestic and foreign authors, the development and urgency of the topic was evaluated. The disadvantage of known exoskeleton models has been specified, i.e., the use of absolutely solid links, whose dynamics does not convey the dynamics of the human musculoskeletal system.
The scientific research aimed at the formation of a new direction in the development of exoskeletons that accurately simulate the biomechanics of movements.
Materials and Methods. Different states of structures of variable-length links with a magnetorheological fluid were studied. It has been noted that the links work on the principle of magnetic shock absorbers and consist of a piston rod, electromagnetic coils, and a housing filled with magnetorheological fluid. The ordering effect of an external magnetic field on the particles of a magnetorheological fluid was visualized and mathematically presented. The significance of such factors as time, charge density, magnetic field strength, as well as vectors of electric and magnetic induction, electric intensity and electric current density for this system was shown. The input parameter affecting the behavior of the magnetorheological fluid was determined. This was the magnetic field intensity. It was shown that the viscosity of the liquid varied depending on the shape of the magnetic particles (oblong or oblate ellipsoid).
Results. The dependences that were fundamental for solving the task were investigated and visualized. The magnetic field strength and the angle between the vector directed along a straight line connecting the centers of two micron particles, and the vector of the external magnetic field strength were taken as the basic parameters. It was shown how the magnetic moment, voltage and its antisymmetric part depended on them. It was established that to control the properties of a magnetorheological fluid, it was required to change: – the external magnetic field intensity; – the angle between the external magnetic field intensity and the orientation vector between the dipoles. Two values of force were compared: one – for a given link design, and the other — fixed when walking in the lower leg of a person. The consistency of these indicators was established.
Discussion and Conclusion. The scientific research results allowed us to present: – a method for controlling the properties of a magnetorheological fluid by an external magnetic field; – a variable-length link model with adjustable stiffness. The results obtained can be used in modeling multilink structures to create comfortable exoskeletons that interact synchronously with the human musculoskeletal system as a single human-machine system. The development is applicable to solving significant social and economic problems.
Keywords
For citations:
Blinov А.О., Borisov А.V., Konchina L.V., Novikova M.A., Chigarev A.V. Development of Properties Control Methods for Magnetorheological Medium to Regulate the Stiffness of Exoskeleton Variable-Length Link. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):296-305. https://doi.org/10.23947/2687-1653-2022-22-4-296-305
Introduction. Previously performed modeling allowed us to identify changes in the lengths of the links of the human musculoskeletal system, their sizes, movement speeds, as well as to determine the forces in the kinematic chain [1]. This made it possible to formulate requirements for the properties and modes of functioning of the exoskeleton link that repeats the basic biomechanical properties of the corresponding user link. The study aims at developing a model of a variable-length link with adjustable stiffness to create comfortable exoskeletons of a new generation that adequately reproduce the actions of the human musculoskeletal system. Exoskeletons are used in medical and rehabilitation centers to verticalize the position of the patient's body, in cosmonautics when creating spacesuits and rehabilitation suits.
Magnetic fields acting on a magnetorheological medium can be used to control models of links with adjustable stiffness. Exoskeletons with adjustable stiffness of variable length links will provide stable, safe, comfortable human locomotion. The implementation of drives for controlled configuration changes in such models is of practical value, which determines the urgency of the study.
From 2010 to 2020, the number of publications with the keyword “exoskeleton” in the database “Russian Science Citation Index” increased ten times (there were less than 50 and became more than 500). Since 2015, the number of patents for exoskeletons and their components has been growing, specialized software is being registered more often. Currently, there is no data on the links of variable-length exoskeletons with adjustable stiffness. Solutions with soft electric pumps and a pneumatic ring generator are mentioned, but they do not use magnetorheological fluids1. There is a description of an actuator with a magnetorheological fluid, whose viscosity changes under the influence of a magnetic field [2–4]2. It is proposed to use magnetorheological materials to create exoskeleton drives3. In [4–6], the use of magnetorheological fluid in the creation of an exoskeleton knee joint drive was studied. The torque in this joint has a damping effect when walking [7]. Magnetorheological drives were considered in [8–9]. An exoskeleton, whose links can be adjusted in length and stiffness, has not yet been developed.
Materials and Methods. It is assumed that the exoskeleton link will work on the principle of magnetic shock absorbers [10]. The link consists of a rod with piston АЕ, housing СВ, filled with a magnetorheological fluid, and electromagnetic coils (Fig. 1).
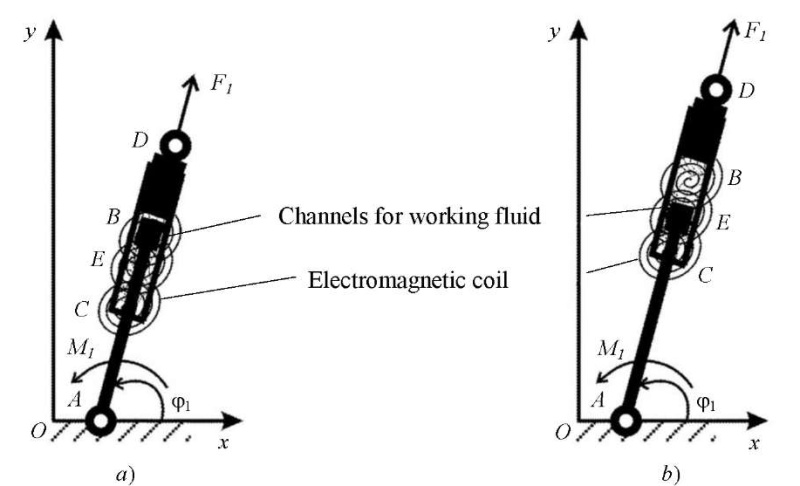
Fig. 1. Construction of a variable-length link with a magnetorheological fluid:
a — link in a compressed state in the phase of support on it;
b — link in a stretched state in the transfer phase (the authors' figure)
At points A and D, there are hinges that provide connection and relative rotation of the links in the exoskeleton. The magnetic field is created by an electromagnetic coil and acts on the magnetorheological fluid inside the link. The magnetic particles of the liquid are ordered under the electromagnetic-field effect, and the rheological properties change.
The properties of the magnetorheological fluid are due to polarization; therefore, magnetic particles line up along the lines of force (Fig. 2).
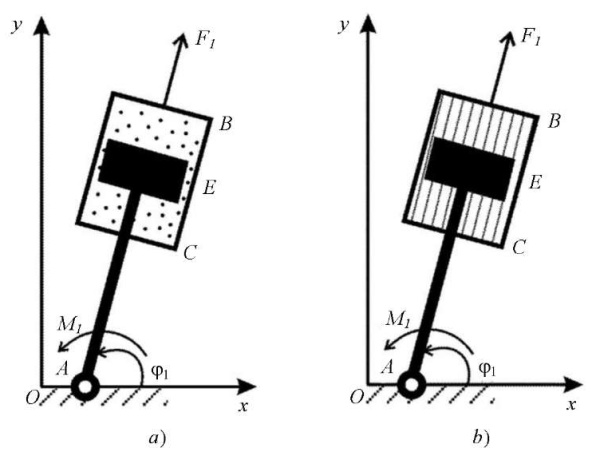
Fig. 2. Magnetorheological fluid particles in the cylindrical part of the link:
a — magnetic particles are randomly arranged without the application of an external magnetic field;
b — aligned chains of oriented magnetic particles along the lines of force under the action of an external magnetic field (the authors' figure)
Under the influence of an external electromagnetic field, polarization and magnetization occur in a magnetorheological fluid. For such fluid, Maxwell's equations have the form:
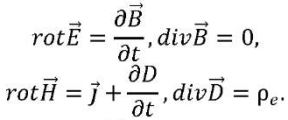 (1)
(1)
Here, D⃗ — electric induction vector; B⃗ — magnetic induction vector; t — time; E⃗ — electric intensity vector; H⃗ — magnetic field strength; ρ𝑒 — charge density; 𝑗 — electric current density vector.
The electric current density vector is related to the electric field strength:
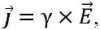 (2)
(2)
where γ — specific conductivity of the substance.
A magnetic particle in a magnetorheological fluid is a dipole, i.e., a system of two opposite charges equal in modulus Q, located at distance l from each other. The moment of a pair of forces acting from the side of the field on an elementary dipole is equal to
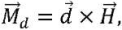 (3)
(3)
where d⃗ — elementary dipole moment.
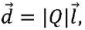 (4)
(4)
where 𝑙⃗ — dipole arm — vector drawn along the axis of the dipole from a negative charge to a positive one and equal to the distance between the charges 𝑙.
Magnetic induction vector 𝐵⃗ is related to magnetization vector M⃗ , which characterizes, from a macroscopic point of view, the ordered distribution in the body of magnetic dipoles:
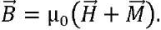 (5)
(5)
At low values of magnetization, it is directly proportional to the magnetic field strength:
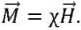 (6)
(6)
After the transformations:
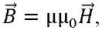 (7)
(7)
where χ = μ − 1— magnetic susceptibility of matter; μ0 = 1.26 ∙ 10−6 𝐻/𝑚 [11] — absolute magnetic permeability in vacuum; μ — relative magnetic permeability.
In [11–13], for the magnetic susceptibility of matter χ, the results of experimental studies of a kerosene-based magnetorheological fluid with different concentrations of magnetite particles in the range χ ∈ [ 1.04; 9.20] at a relative concentration φ ∈ [ 0.211; 1] are given.
Thus, the input parameter that determines the behavior of a magnetorheological fluid is the magnetic field strength H⃗ , which is generated by a coil wound on a variable-length link element. The field strength is a piecewise given step function. Magnetorheological fluids are magnetized in relatively small magnetic fields 𝐻 ∈ [ 100; 100,000] 𝐴/𝑚.
Let the magnetorheological fluid under the movement of the rod inside the link body (Fig. 2) realize a simple shear flow with velocity gradient γ̇, and the intensity of the external magnetic field H⃗ be directed at an angle Ψ to the gradient of the flow velocity. Suppose that magnetic particles have the shape of ellipsoids with the ratio of two semi-axes 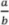 = 2 and 𝑏 = 𝑐.
= 2 and 𝑏 = 𝑐.
The intensity of the magnetorheological fluid can be estimated based on the results obtained in works [12–14]:
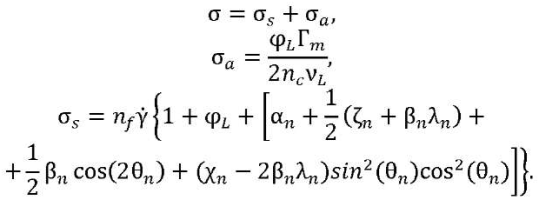 (8)
(8)
Here, σ𝑠 — symmetric stress component; σ𝑎 — antisymmetric stress component; φ𝐿 — volume fraction of micron particles equal to φ𝐿 = 0.0127; n — number of particles in the chain; 𝑛𝑐 — maximum number of particles in the chain; α𝑛, …, λ𝑛 — kinetic coefficients given in works [12][13]; Г𝑚 — magnetic moment tending to build a chain of particles along the field; ν𝐿 — volume of a micron particle; γ̇ — shear rate; 𝑛𝑓 — viscosity of magnetorheological fluid; θ — angle between the vector directed along a straight line connecting the centers of two micron particles and the vector of the external magnetic field strength.
As can be seen from formula (6), the stress tensor of a magnetorheological fluid in a magnetic field is asymmetric. The symmetrical part of the stress depends on the viscosity of the magnetorheological fluid. The direction and magnitude of the applied external magnetic field affect significantly the viscosity of the magnetorheological fluid. The viscosity coefficient may be less or greater than the initial value, depending on the direction of the applied field and the shape of the particles. This coefficient in the magnetic field varies for two reasons. The first reason is related to the retardation of particle rotation in the field, which causes an increase in the coefficient value. The second reason is the orienting influence of an external magnetic field on suspended particles. Depending on the direction of the field, the viscosity coefficient may decrease or increase. As an example, consider an external magnetic field that is applied along the direction of fluid flow. If its magnetic particles have the shape of oblong ellipsoids, then the viscosity decreases. If these are oblate ellipsoids, the viscosity increases.
Magnetic moment Г𝑚, which tends to build a chain of particles along the field, is calculated by the formula [12][13]:
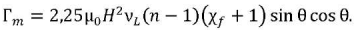 (9)
(9)
Here, ν𝐿 — micron particle volume; ν𝐿 = π𝑑𝐿3/6; 𝑑𝐿 — micron particle diameter; 𝑑𝐿 = 1 ∙ 10−6 m; θ — angle between the vector connecting the centers of two micron particles and the vector of the external magnetic field; χ𝑓 — magnetic susceptibility of the carrier ferrofluid (assume that it is constant and always equal to the initial value χ𝑓 = 3.05).
Research Results. We build a graph of the magnetic moment Г𝑚 from the magnetic field strength 𝐻 and angle θ.
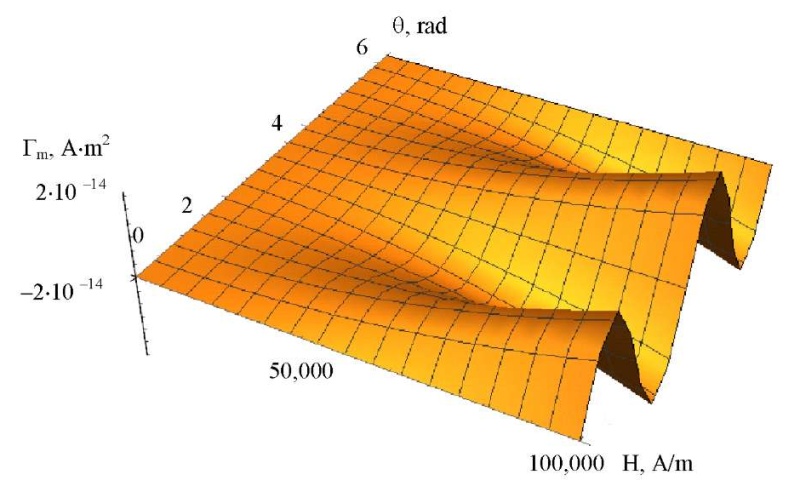
Fig. 3. Dependence of magnetic moment Г𝑚 on magnetic field strength 𝐻 and angle θ (the authors' figure)
According to Figure 3, it is possible to judge the behavior of magnetic moment Г𝑚 at different values of the magnetic field strength and the angles between the field and the dipoles, to estimate the antisymmetric part of voltage σ𝑎. Using formulas (8) and (9), we obtain:
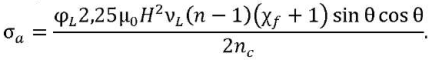 (10)
(10)
Taking into account works [12–14], as a result of solving the equation at 𝐻 = 105 A/m, we obtain 𝑛𝑐 ≈ 60. The viscosity of the magnetorheological fluid is assumed to be equal to 𝑛𝑓 = 1.36 Pa ∙ s [11].
The results of calculations of the antisymmetric part of the voltage are graphically presented in Figure 4.
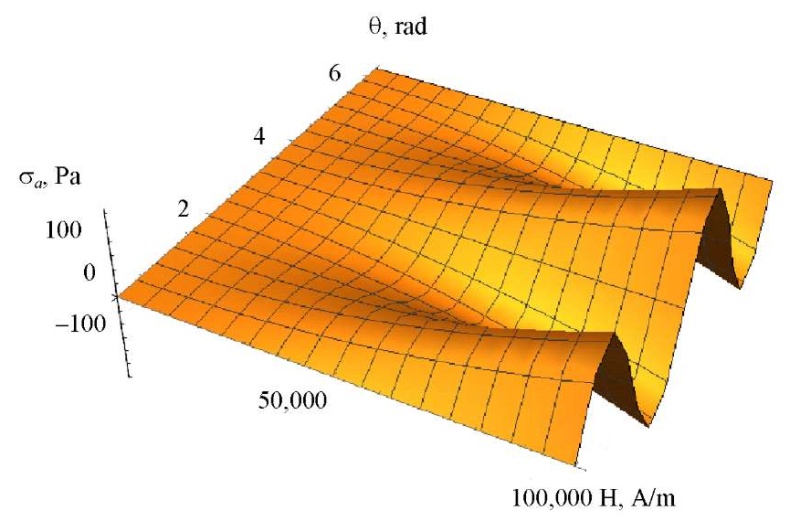
Fig. 4. Dependence of the antisymmetric part of stress σ𝑎 on magnetic field strength 𝐻 and angle θ (the authors' figure)
The graph shows that with an increase in the strength of the applied external magnetic field, the strength of the magnetorheological fluid monotonically grows taking into account angle θ. Dependence σ𝑎 on angle θ shows that the intensity of the magnetorheological fluid reaches:
- maximum values at angles that are multiples of
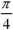 ;
; - zero values at angles that are multiples of
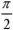 .
.
Consider the symmetric part of stress σ𝑠. In (8), there are kinetic coefficients for it. Let us calculate them using the expressions from [12][13], where they are shown in an analytical form. The number of particles in the chain is assumed to be equal to 𝑛 = 30 as the arithmetic mean, based on the estimate of the maximum number of particles. Let us determine qualitatively, in the first approximation, shear rate γ̇ between the outer layer of fluid near the wall of the link housing and the inner layer near the rod. At that, we will proceed from the requirements for the design of the exoskeleton link for the human lower leg model. In this case, we are talking about the maximum value of the rate of change in the length of a person's lower leg, with which the exoskeleton link should work synchronously. According to [15], the rate of change in the length of the lower leg is equal to 𝑙˙= 0.6 m/s−1. This does not contradict the results of other authors: γ̇ ∈ [ 0; 100] s−1. In the future, such an assessment will require clarification based on experiments, since no solutions or experimental results suitable for modeling exoskeletons or anthropomorphic robots have been found in the literature.
The results of calculations of the symmetric part of the stress are presented graphically in Figure 5.
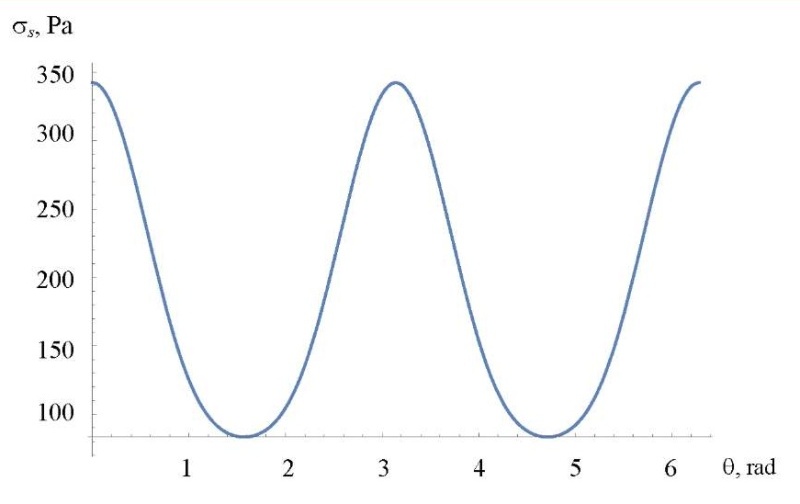
Fig. 5. Dependence of the symmetrical part of stress σ𝑠 on angle θ (the authors' figure)
The intensity of the magnetorheological fluid as the sum of the symmetric and antisymmetric parts is shown in Figure 6. Its cross-section at a fixed value of the magnetic field strength is shown in Figure 7.
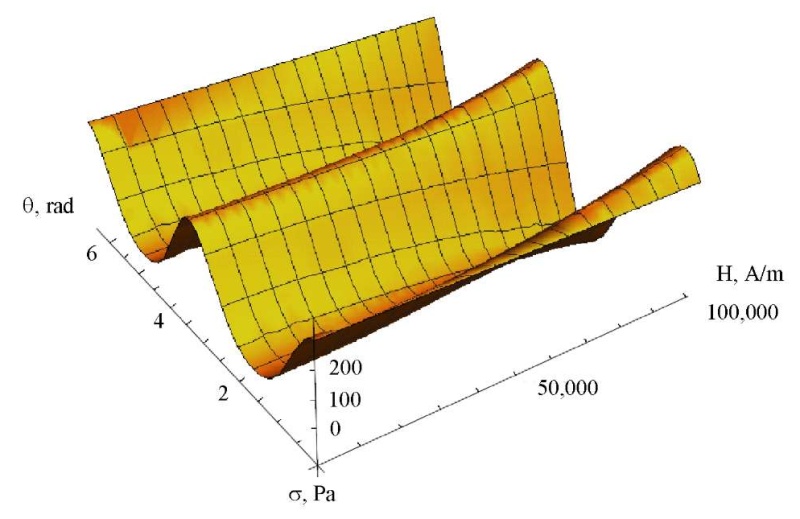
Fig. 6. Dependence of stress σ on magnetic field strength 𝐻 and angle θ (the authors' figure)
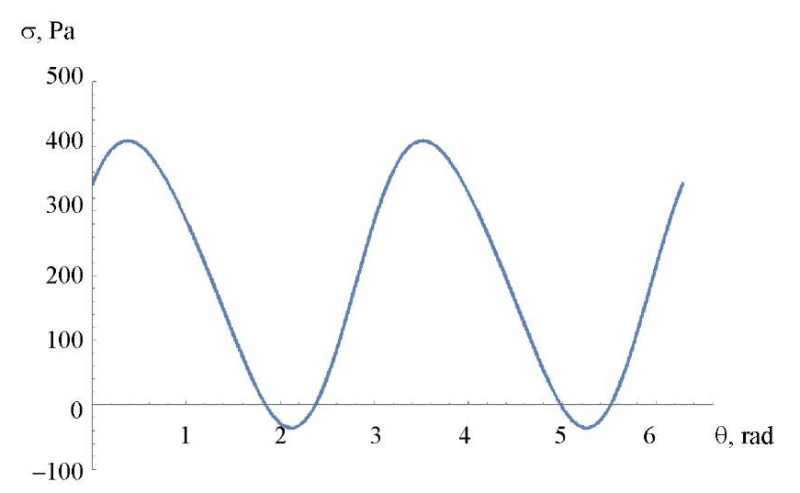
Fig 7. Dependence of stress σ on angle θ at fixed magnetic field strength value 𝐻 = 105 A/m (the authors' figure)
Maximum value σ𝑚𝑎𝑥 = 408.6 Pa is reached at θ = 0.37 rad. Thus, to control the properties of a magnetorheological fluid, it is required to change the angle between the intensity of the external magnetic field and the orientation vector between the dipoles. It is also necessary to change the intensity of the external magnetic field.
The inner diameter of the housing in which the rod is located is assumed to be equal to 𝐷 = 0.2 m. As the first approximation, assume that the calculated stresses are normal. Now, it is possible to determine the force with which the magnetorheological fluid acts in a variable-length link with adjustable stiffness:
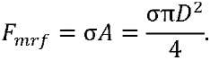 (11)
(11)
Figure 9 shows a graph constructed at a fixed value of the magnetic field strength 𝐻 for two control parameters: 𝐻 and angle θ (Fig. 8).
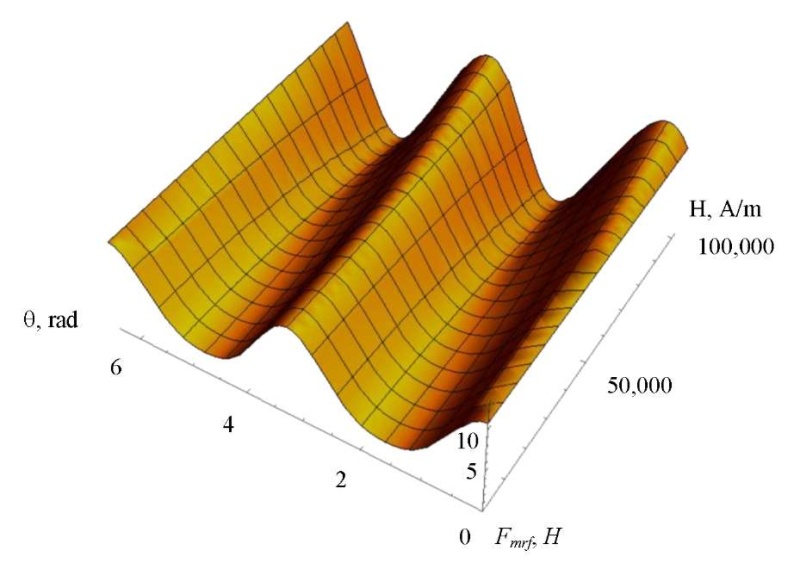
Fig. 8. Dependence of force 𝐹𝑚𝑟𝑓 on the magnetic field strength 𝐻 and angle θ (the authors' figure)
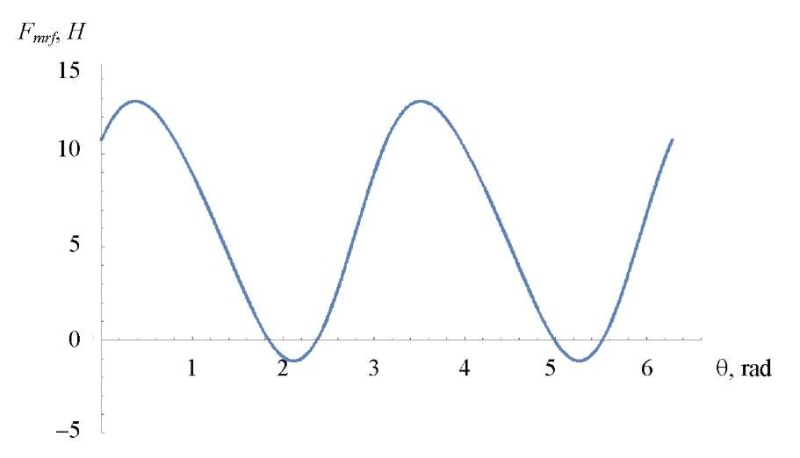
Fig. 9. Dependence of force 𝐹𝑚𝑟𝑓 on angle θ at fixed value of the magnetic field strength 𝐻 =105 A/m (the authors' figure)
Maximum value 𝐹𝑚𝑟𝑓𝑚𝑎𝑥 = 12.8 Н is reached at θ = 0.37 rad. This corresponds to the values at which, according to [14], the exoskeleton link functions. To further increase the force from the side of the magnetorheological fluid, it is required to increase the intensity of the external magnetic field.
Thus, in order for the particles to orient themselves along the field lines in the required way, you need to apply a magnetic field of the appropriate intensity and orientation.
Discussion and Conclusions. The research work results allow us to propose a method of controlling the effect of an external magnetic field on the properties of a magnetorheological fluid. For the first time, a model of a variable-length exoskeleton link with adjustable stiffness, which functions due to a magnetorheological medium, is proposed. The concept can be used to create:
- comfortable exoskeletons with links of variable length, hinges and connections;
- spacesuits and similar special equipment;
- transport systems in the form of anthropomorphic robots that provide convenient movement in rough terrain.
A widespread use of anthropomorphic robotic systems of a new generation (mechatronic modules synchronized with the movements of the human musculoskeletal system) will solve important social and economic problems:
- improve the quality of life of people with motor disabilities;
- contribute to the development of high technologies in various branches of the domestic industry.
1. Soft Robots Were Equipped with Electrophoretic Logic Circuits. planet-today.ru. URL: https://planet-today.ru/novosti/nauka/item/110728-myagkikh-robotov-osnastili-elektroflyuidnymi-logicheskimi-skhemami (accessed: 10.09.2022).
2. Psomopoulou E, et al. A Simple Controller for a Variable Stiffness Joint with Uncertain Dynamics and Prescribed Performance Guarantees. Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2012. Р. 5071–5076. https://doi.org/10.1109/IROS.2012.6385859
3. Jinzhou Chen, Wei-Hsin Liao. Design and Control of a Magnetorheological Actuator for Leg Exoskeleton. In: Proc. IEEE International Conference on Robotics and Biomimetics (ROBIO). 2007. P. 1388–1393. https://doi.org/10.1109/ROBIO.2007.4522367
References
1. Borisov, A. V. On Mathematical Modeling of the Dynamics of Multilink Systems and Exoskeletons / A. V. Borisov, I. E. Kaspirovich, R. G. Mukharlyamov // Journal of Computer and Systems Sciences International. — 2021. — Vol. 60. — P. 827–841. doi: 10.1134/S106423072104002X
2. Bougrinat, Y. Design and Development of a Lightweight Ankle Exoskeleton for Human Walking Augmentation / Y. Bougrinat, S. Achiche, M. Raison // Mechatronics. — 2019. — Vol. 64. — Art. 102297. doi: 10.1016/j.mechatronics.2019.102297
3. Jinzhou Chen. Design, Testing and Control of a Magnetorheological Actuator for Assistive Knee Braces / Jinzhou Chen, Wei-Hsin Liao // Smart Materials and Structures. — 2010. — Vol. 19. — Art. 035029. doi: 10.1088/0964-1726/19/3/035029
4. Carlson, J. Magnetorheological Fluid Actuators / J. Carlson // In book: Adaptronics and Smart Structures: Basics, Materials, Design, and Applications / Hartmut Janocha (ed.) — Saarbrücken : Springer, 1999. — P. 180–195.
5. Ahmadkhanlou, F. A Magnetorheological Fluid-Based Controllable Active Knee Brace / F. Ahmadkhanlou, J. L. Zite, G. N. Washington // Proceedings SPIE. — 2007. — Vol. 6527. — Art. 652700. doi: 10.1117/12.715902
6. Dollar, A. M. Lower Extremity Exoskeletons and Active Orthoses: Challenges and State-of-the-Art / A. M. Dollar, H. Herr // IEEE Transactions on robotics. — 2008. — Vol. 24. — Р. 144–158. doi: 10.1109/TRO.2008.915453
7. Design and Control of a Polycentric Knee Exoskeleton Using an Electro-Hydraulic Actuator / Taesik Lee, Dongyoung Lee, Buchun Song, Yoon Su Baek // Sensors. — 2020. — Vol. 20. — Р. 211. doi: 10.3390/s20010211
8. Laflamme, S. Online Learning Algorithm for Structural Control Using Magnetorheological Actuators / S. Laflamme. — Massachusetts: Institute of Technology, 2007. — 88 р. — URL: https://dspace.mit.edu/bitstream/handle/1721.1/39271/170931934-MIT.pdf?sequence=2
9. A Kinematic Model of a Humanoid Lower Limb Exoskeleton with Hydraulic Actuators / S. Glowinski, T. Krzyzynski, A. Bryndal, I. Maciejewski // Sensors. — 2020. — Vol. 20. — Р. 6116. doi: 10.3390/s20216116
10. Юсупбеков, Х. А. Активные подвески автомобиля с амортизаторами переменной жесткости / Х. А. Юсупбеков, М. М. Собиров, А. Р. Юлдашев // Наука, техника и образование. — 2020. — № 2 (66). — С. 18–27.
11. Lebedev, A. V. Viscosity of Magnetic Fluids Must Be Modified in Calculations of Dynamic Susceptibility / A. V. Lebedev // Journal of Magnetism and Magnetic Materials. — 2017. —Vol. 431. — P. 30–32. doi: 10.1016/j.jmmm.2016.09.110
12. Зубарев, А. Ю. К нелинейной реологии магнитных жидкостей / А. Ю. Зубарев, Л. Ю. Искакова, Д. Н. Чириков // Коллоидный журнал. — 2011. — Т. 73, № 3. — С. 320–333.
13. Зубарев, А. Ю. Магнитореологические свойства феррожидкостей c кластерными частицами / А. Ю. Зубарев, Д. Н. Чириков // Коллоидный журнал. — 2013. — Т. 75, № 5. — С. 567–576.
14. Applying the Models of Magneto-Rheological Substances in the Study of Exoskeleton Variable-Length Link with Adjustable Stiffness / A. Blinov, A. Borisov, L. Konchina, M. Novikova // Journal of Applied Informatics. — 2022. — Vol. 17. — Р. 133–142. doi: 10.37791/2687-0649-2022-17-2-133-142
15. Borisov, A. V. Mathematical Models of Exoskeleton. Dynamics, Strength, Control / A. V. Borisov, A. V. Chigarev. — Cham : Springer, 2022. — 232 р. doi: 10.1007/978-3-030-97733-7
About the Authors
А. О. BlinovRussian Federation
Аlexander О. Blinov
Smolensk Branch
1, Energeticheskii proezd
Smolensk
А. V. Borisov
Russian Federation
Аndrey V. Borisov
Smolensk Branch
1, Energeticheskii proezd
Smolensk
L. V. Konchina
Russian Federation
Larisa V. Konchina
Smolensk Branch
1, Energeticheskii proezd
Smolensk
M. A. Novikova
Russian Federation
Marina A. Novikova
Smolensk Branch
1, Energeticheskii proezd
Smolensk
A. V. Chigarev
Belarus
Anatoly V. Chigarev
4, Nezavisimosti Avenue
Minsk
Review
For citations:
Blinov А.О., Borisov А.V., Konchina L.V., Novikova M.A., Chigarev A.V. Development of Properties Control Methods for Magnetorheological Medium to Regulate the Stiffness of Exoskeleton Variable-Length Link. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):296-305. https://doi.org/10.23947/2687-1653-2022-22-4-296-305













































