Analysis of Stress-Strain State of a Cylinder with Variable Elasticity Moduli Based on Three-Dimensional Equations of Elasticity Theory

Introduction. Functionally graded materials are widely used in various constructions. Due to the dependence of mechanical properties on coordinates, it is possible to control the stress-strain state (SSS) of parts. An example of using such inhomogeneity is a cylinder whose mechanical properties depend on the radius. In this case, the cylinder may be of interest as a separate structure, or as being a division subring of a compound body, e.g., connecting two media with widely different properties. When calculating the SSS of a thin-walled cylinder, some applied theories can be used, an assessment of their adequacy. Especially in the case of inhomogeneous properties, it can be carried out using computer modeling or asymptotic analysis based on a three-dimensional formulation. The latter determines the relevance of this study.

A number of studies have been devoted to the investigation of the SSS of hollow cylindrical bodies within the framework of the linear theory of elasticity. In [1][2], the mechanical behavior of a radially inhomogeneous cylinder in a three-dimensional formulation was studied on the basis of the spline collocation method and the finite element method. In [3], the SSS of a cylinder whose properties depended on the radius loaded with uniform internal pressure was described. In [4], an analytical study was carried out for a functionally graded piezoelectric cylinder. In [5], an exact solution was constructed to a radially inhomogeneous hollow cylinder with exponential Young's modulus, with constant Poisson ratio and power Young's modulus. In [6][7], an analytical solution to the axisymmetric thermoelasticity problem for a continuous cylinder was obtained using the direct integration method when the coefficient of linear thermal expansion was an arbitrary function of the radius. In [8], a general asymptotic theory of a transversally isotropic homogeneous hollow cylinder was developed. New groups of solutions were obtained for a transversally isotropic homogeneous cylinder. The comparison of the constructed solutions to the solutions constructed using applied calculation methods was given. In [9][10], some boundary value problems of elasticity theory were studied for a functionally gradient isotropic and transversally isotropic (the plane of isotropy was perpendicular to the axis) cylinder, in the case when the elastic modules were arbitrary continuous functions of the radius of the cylinder. In [11], an analysis of the bending deformation problem for a radially inhomogeneous cylinder was carried out. The analysis of the above papers shows that not all types of boundary conditions on cylindrical surfaces have asymptotic representations of solutions.

In this article, on the basis of an asymptotic analysis of three-dimensional equations of elasticity theory, the features of the SSS of a thin-walled cylinder whose properties vary linearly along the radius were studied. In this case, the inner border was fixed in the axial direction and was free in the radial direction.

This goal was achieved using several steps: asymptotic integration of differential equations and the construction of homogeneous solutions; derivation of formulas for the components of the displacement vector and stress tensor; consideration of boundary conditions on the face surfaces.

Materials and Methods. Radially inhomogeneous hollow thin-walled cylinder is considered in a cylindrical coordinate system with the origin on its axis. The problem of its equilibrium, in the case of fixing cylindrical surfaces along the axis and zero normal stresses, is solved in an axisymmetric formulation under the action of stresses at its faces.

The boundary value problem consists of the equilibrium equations [8]:

, (1)

(2)

where — components of the stress tensor.

Defining relations [8]:

(3)

(4)

(5)

(6)

Here, — components of the displacement vector.

Lamé parameters vary linearly along the radius:

(7)

where — constants.

After substituting (3)–(7) into equations (1), (2), the dimensionless system of equations takes the form:

(8)

(9)

Here:

— new dimensionless coordinates;

— in the case of wall thinness, small parameter;

;

;

— some parameter having the dimension of stress.

Let us consider a problem in which homogeneous boundary conditions are set on the lateral surfaces of the cylinder:

(10)

(11)

Stresses are applied to the faces of the cylinder:

(12)

(13)

.

— dimensionless stresses.

Stress vector components satisfy the equilibrium conditions.

To construct homogeneous solutions, we seek the components of the displacement vector in the form:

(14)

Substituting representations (14) into the system (8)–(11), we obtain:

(15)

(16)

(17)

(18)

We investigate boundary value problems (15)–(18) at . To solve (15)–(18) at , we use the asymptotic method [9–13].

Nonzero solutions (15)–(18) correspond to the third iterative process, the components of the displacement vector are searched for in the form of expansions over a small parameter:

(19)

After substituting expansions (19) into equations (15)–(18) for terms of the first order, we have:

(20)

(21)

(22)

(23)

Following [13], the spectral problem (20)–(23) corresponds to a potential solution for the plate.

Thus, the solutions are presented in the form:

a) , (24)

. (25)

Here, is the solution to the equation:

(26)

The stresses corresponding to solutions (24), (25) have the form:

, (27)

, (28)

(29)

(30)

b) (31)

. (32)

Here, is the solution to the equation:

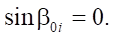(33)

The stresses corresponding to solutions (31), (32) have the form:

(34)

(35)

(36)

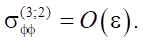(37)

The general solution (15)–(18) will be a superposition of solutions (24), (25), (31), (32):

(38)

(39)

Solutions (24), (25), (31), (32) have the character of a boundary layer. When moving away from the faces, solutions (24), (25), (31), (32) decrease exponentially.

To determine constants , we use Lagrange variational principle. The variational principle takes the form [8]:

(40)

Substituting (24–36) into (40), we have:

(41)

(42)

Here:

Constants are found from systems of linear algebraic equations (41), (42), analogous to which are studied in [13].

Research Results. In the article, in an axisymmetric formulation, the solution to the problem of linear elasticity theory for a functionally graded hollow thin-walled cylinder, whose properties vary in thickness according to a linear law, was considered. Homogeneous cross boundary conditions were set on the lateral surfaces of the cylinder, and a stress vector was set at the faces. The constructed homogeneous solutions satisfied boundary conditions on cylindrical surfaces. For their construction, an asymptotic approach based on the expansion by a small parameter characterizing the relative thickness of the cylinder was used. To account for inhomogeneous boundary conditions at the faces, systems of linear algebraic equations similar to those studied in the literature were obtained. It was shown that the constructed SSS solutions had a boundary-layer character, which corresponded to the edge effect similar to the theory of inhomogeneous plates, which bears the name of Saint-Venant.

Discussion and Conclusion. Usually, when studying the SSS of thin-walled structures, applied calculation methods are built that reduce the dimension of the problem. In this regard, the task of determining the range of geometric and mechanical parameters in which these methods give acceptable accuracy is critical. The solutions to three-dimensional equations constructed in the work on the basis of asymptotic analysis make it possible to assess the adequacy of such applied theories with a predetermined accuracy threshold. In addition, these solutions can find application in the evaluation of numerical solutions to problems for structures with functionally graded materials.