Scroll to:
Methods for Applying Matrices when Creating Models of Group Pursuit
https://doi.org/10.23947/2687-1653-2023-23-2-191-202
Abstract
Introduction. It is obvious that in the near future, the issues of equipping moving robotic systems with autonomous control elements will remain relevant. This requires the development of models of group pursuit. Note that optimization in pursuit tasks is reduced to the construction of optimal trajectories (shortest trajectories, trajectories with differential constraints, fuel consumption indicators). At the same time, the aspects of automated distribution by goals in group pursuit were not considered. To fill this gap, the presented piece of research has been carried out. Its result should be the construction of a model of automated distribution of pursuers by goals in group pursuit.
Materials and Methods. A matrix was formed to study the multiple goal group pursuit. The control parameters for the movement of the pursuers were modified according to the minimum curvature of the trajectory. The methods of pursuit and approach were considered in detail. The possibilities of modifying the method of parallel approach were shown. Matrix simulation was used to build a scheme of multiple goal group pursuit. The listed processes were illustrated by functions in the given coordinate systems and animation. Block diagrams of the phase coordinates of the pursuer at the next step, the time and distance of the pursuer reaching the goal were constructed as a base of functions. In some cases, the location of targets and pursuers was defined as points on the circle of Apollonius. The matrix was formed by samples corresponding to the distribution of pursuers by goals.
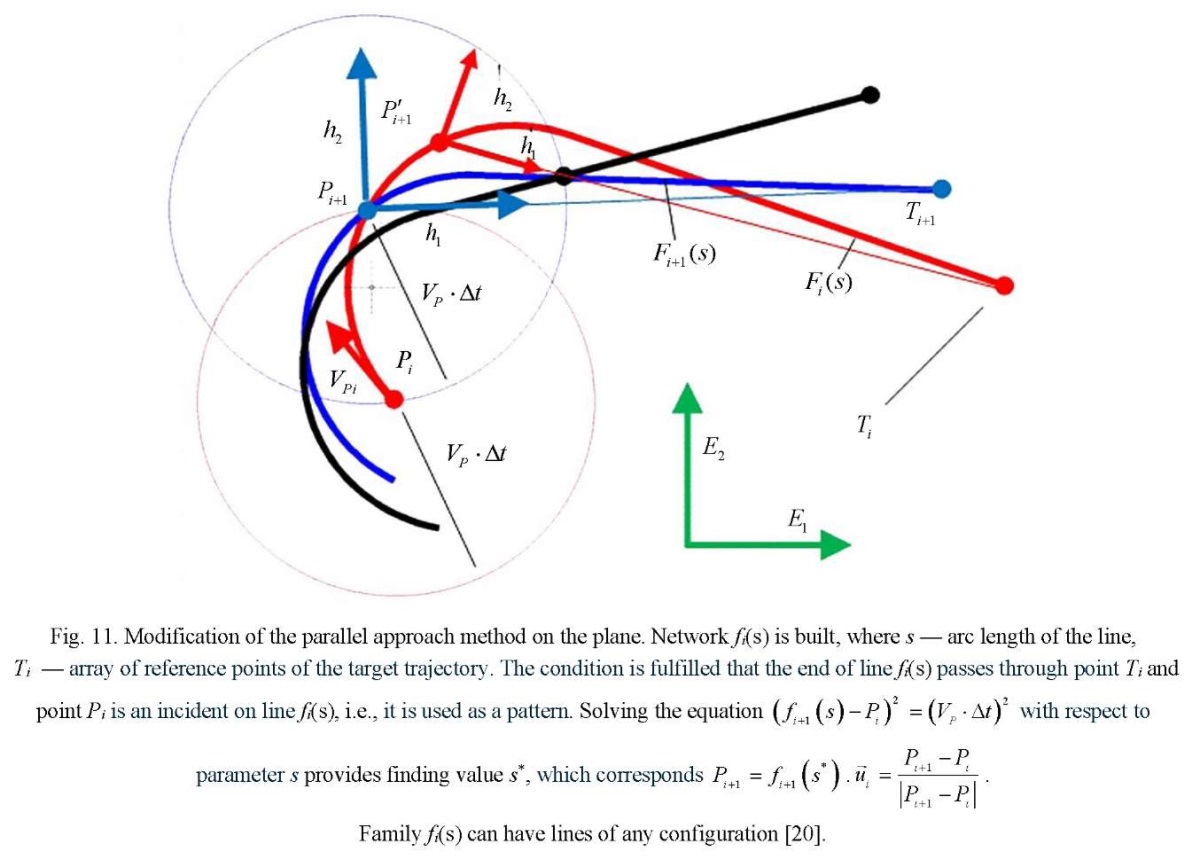
Results. Nine variants of the pursuit, parallel, proportional and three-point approach on the plane and in space were considered. The maximum value of the goal achievement time was calculated. There were cases when the speed vector of the pursuer was directed arbitrarily and to a point on the Apollonius circle. It was noted that the three-point approach method was convenient if the target was moving along a ballistic trajectory. To modify the method of parallel approach, a network of parallel lines was built on the plane. Here, the length of the arc of the line (which can be of any shape) and the array of reference points of the target trajectory were taken into account. An equation was compiled and solved with these elements. On an array of samples with corresponding time values, the minimum time was found, i.e., the optimal time for simultaneous group achievement of multiple goals was determined. For unified access to the library, the control vector was expressed through a one-parameter family of parallel planes. A library of calculations of control vectors was formed. An example of applying matrix simulation to group pursuit was shown. A scheme of group pursuit of multiple goals was presented. For two goals and three pursuers, six samples corresponding to the distribution of pursuers by goals were considered. The data was presented in the form of a matrix. Based on the research results, the computer program was created and registered – “Parallel Approach on Plane of Group of Pursuers with Simultaneous Achievement of the Goal”.
Discussions and Conclusion. The methods of using matrices in modeling group pursuit were investigated. The possibility of modifying the method of parallel approach was shown. Matrix simulation of group pursuit enabled to build its scheme for a set of purposes. The matrix of the distribution of pursuers by goals would be generated at each moment of time. Methods of forming matrices of the distribution of pursuers and targets are of interest in the design of virtual reality systems, for tasks with simulating the process of group pursuit, escape, evasion. The dynamic programming method opens up the possibility of automating the distribution with optimization according to the specified parameters under the formation of the matrix of the distribution of pursuers by goals.
Keywords
For citations:
Dubanov A.A. Methods for Applying Matrices when Creating Models of Group Pursuit. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):191-202. https://doi.org/10.23947/2687-1653-2023-23-2-191-202
Introduction. The pursuit algorithms are studied from the point of view of their classical and optimal implementation. Their role in differential pursuit games is investigated. The applied sphere of ready-made solutions is very wide, because the results of such scientific research are applicable in various information technologies and systems, in particular, in search engines. Undoubtedly, the issues of equipping moving robotic complexes with autonomous control elements will be of current concern for a long time, which also requires high-quality implementation of the algorithms under consideration.
In [1–4], the coordinated behavior of a group of pursuers and targets was investigated. For general theoretical and practical issues in the problems of persecution, works [5–9] were considered. The guidance of the pursuer to the target was analyzed considering the information provided in [10–13].
With all the theoretical and practical interest in this topic, optimization in pursuit problems was limited to the construction of optimal trajectories. Specifically, the shortest trajectories, trajectories with differential constraints, fuel consumption indicators were proposed. But the aspects of automated distribution by goals in group pursuit were not considered. To fill this gap, this scientific work was carried out. Its basic result was the construction of a model of automated distribution of pursuers by goals in group pursuit. The formation of a matrix of achieving goals by pursuers was shown. When assigning goals to the pursuers, all possible combinations of achieving goals were sorted out, and a combination of the minimum value of the criterion from the generated set with the maximum value was selected.
Optimization of the multiple goal group pursuit is a promising direction for the development of such a discipline as optimal motion control in tasks related to automated decision-making and autonomous management.
Materials and Methods. In the model of group pursuit described in the paper, targets move along predefined trajectories. However, this predestination does not matter in principle. The pursuers are distributed by the targets automatically, based on the minimax solution of the goal function. Then the control parameters of the pursuers' movement are modified. In this paper, this is the parameter of the minimum curvature of the trajectory. This approach allows for simultaneous achievement of goals.
Consider a group pursuit of a set of goals: N pursuers catch up with M goals. We form a matrix of the distribution of pursuers by goals:

Each cell Yij contains information about the phase coordinates of the i-th pursuer and the j-th target. Matrix Yij contains information about the method by which the i-th pursuer goes after the j-th goal.
The data stored in the cells of the matrix determines the access to the library of calculations of the control vectors of the pursuer.
In each cell of matrix Yij, the predicted time for the  -th pursuer to reach the j-th goal can be calculated: tij.
-th pursuer to reach the j-th goal can be calculated: tij.
Research Results
In each received sample  , it is required to find the maximum value of achievement times
, it is required to find the maximum value of achievement times  , e.g., from
, e.g., from  (Table 1).
(Table 1).
Table 1
Samples corresponding to the distribution of pursuers by goals
|
Pursuers |
Goals |
||||||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
||
|
1 |
× |
× |
× |
× |
× |
× |
|||||||
|
2 |
× |
× |
× |
× |
× |
× |
|||||||
|
3 |
× |
× |
× |
× |
× |
× |
|||||||
|
Samples |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|||||||
It is necessary to form matrices Yij, where i= 1…3, j=1…2 according to the possible samples
Ak,k = 1…6. Then, after the conversion, maximum value tk=Max{tij} is found. The calculation made it possible to establish that pursuer P1, demonstrated the greatest time of achievement, catching up with goal T1 from sample A2.
Thus, consider sample Ak. You can increase to the value of parameter tk, all values tij, depending on the velocity vectors of the pursuers and goals, as well as their permissible angular velocities. This determines maximum value tk.
Having received an array of samples {Ak} with corresponding time values {tij}, it is necessary to find minimum time tmin=Min{tk}. This is how the optimal time for simultaneous group achievement of multiple goals is determined.
Algorithms for calculating the next step of the pursuer and estimating the time when the pursuer reaches the goal. Figure 1 shows the algorithm of the function for calculating the next step and the speed vector of the pursuer.

Fig. 1. Flowchart for calculating phase coordinates of the pursuer in the next step
Figure 2 shows an algorithm for calculating the time and distance of the pursuer reaching the goal. Variable ε is the threshold value of the distance from the pursuer to the target, at which the goal is considered to have been achieved.

Fig. 2. Flowchart of the function for calculating the time and distance of reaching the goal by the pursuer
If the target moves along a predetermined trajectory, then the algorithm shown in Figure 2 can give an estimate of time tij for the -th pursuer to reach the j-th goal. In this case, the output parameter of the function can be the number of iterations of the pursuit process Nit. Number of iterations Nit — output parameter of the function for calculating the time and distance of reaching the goal by the pursuer.
If the goal replies to avoid achievement, you should evaluate the time differently. It is necessary to build predicted trajectories as composite segments of straight lines, arcs of circles, square and cubic parabolas and other known lines. This will make it possible not to solve boundary value problems in the calculation cycle.
Formation of a library of control vector calculations. The distribution matrix Yij, where i= 1…N, j=1…M pursuers by goals is built on each discrete time interval. In each cell of matrix Yij , information about the method of persecution is stored. It is based on the reference to the library of functions for calculating control vectors  (Fig. 3–11).
(Fig. 3–11).
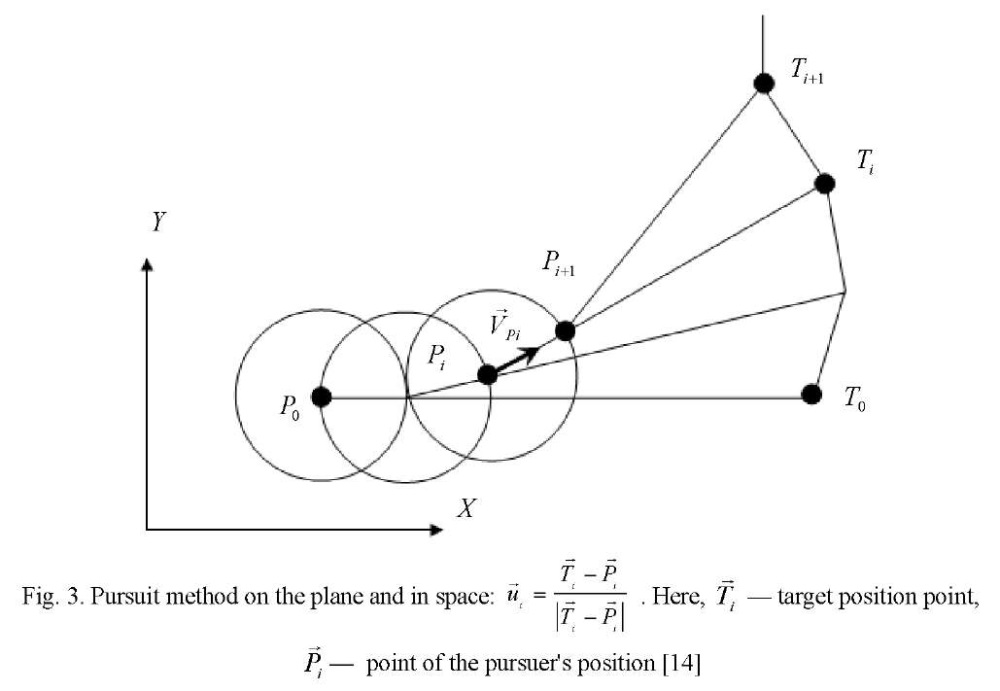
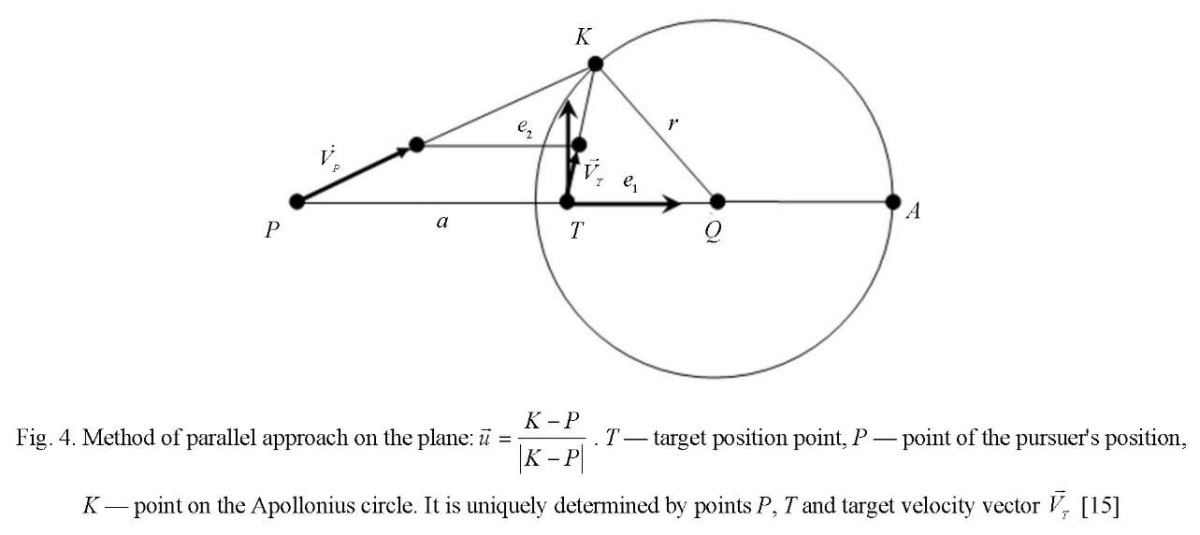
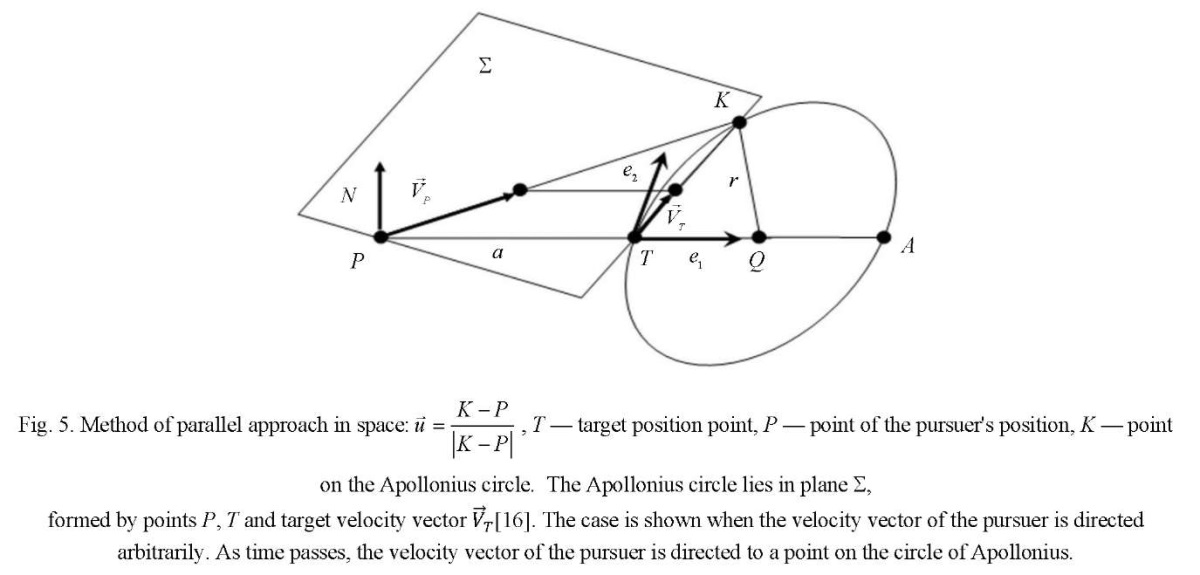
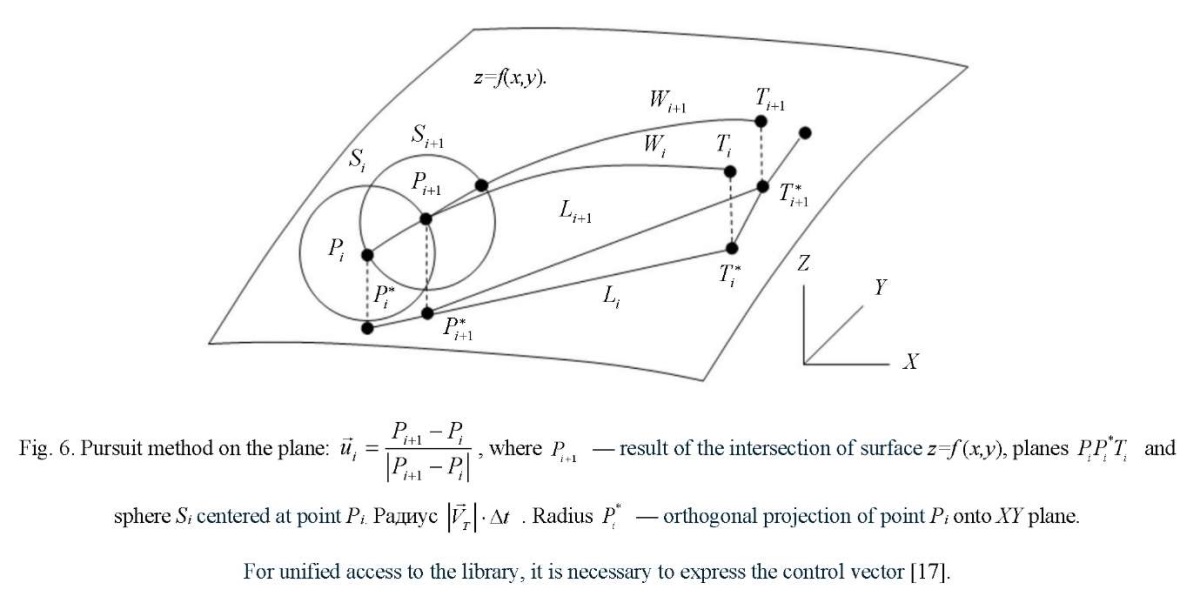
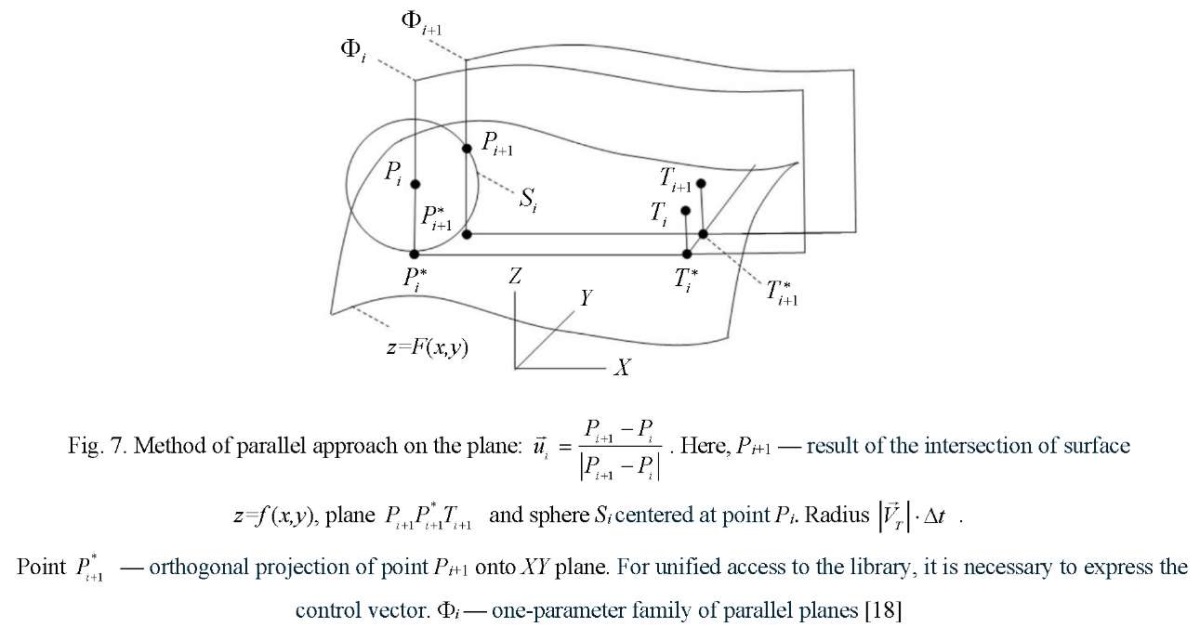
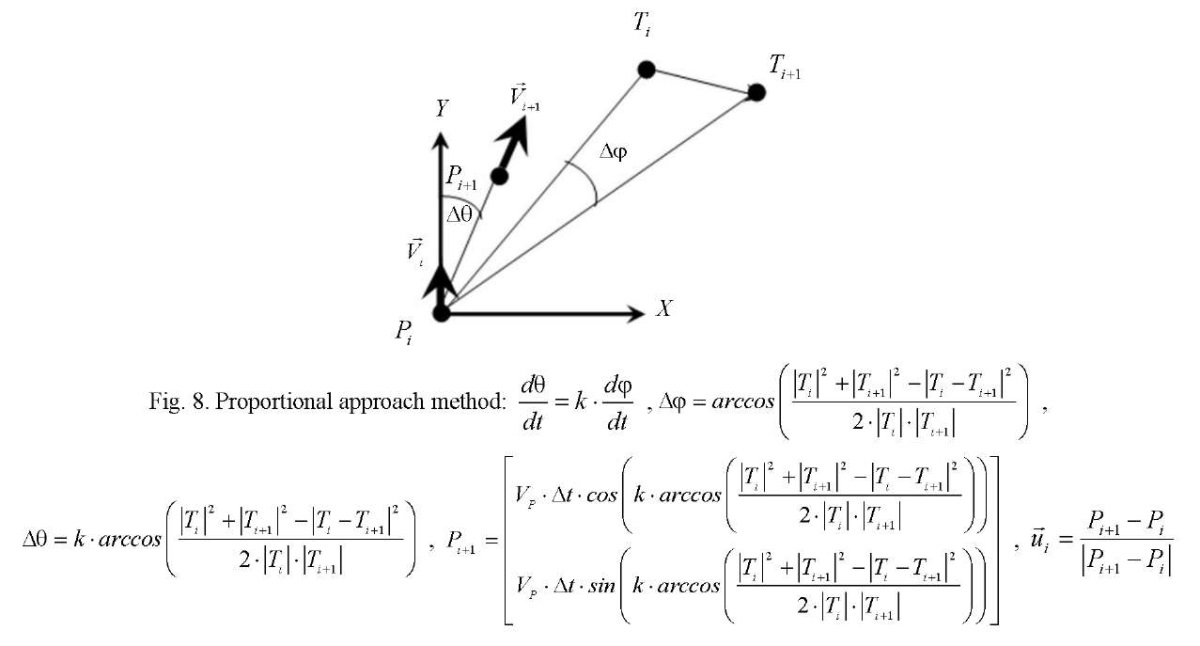
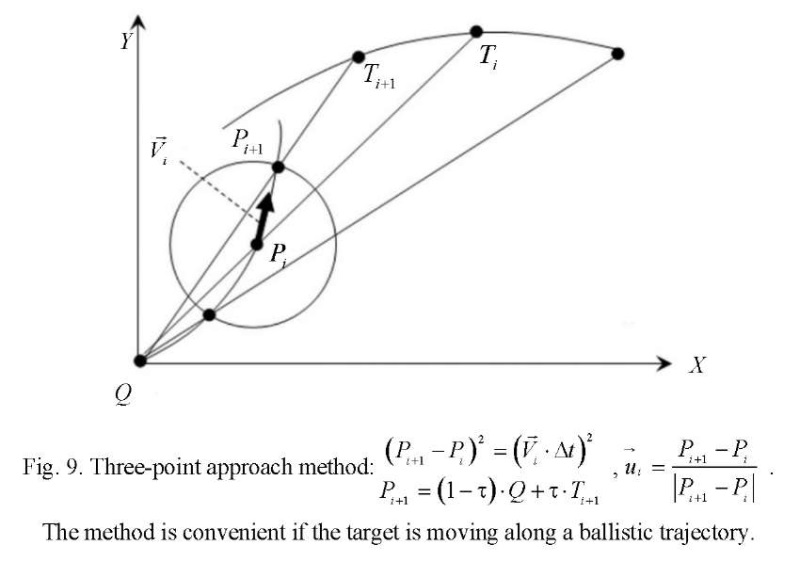
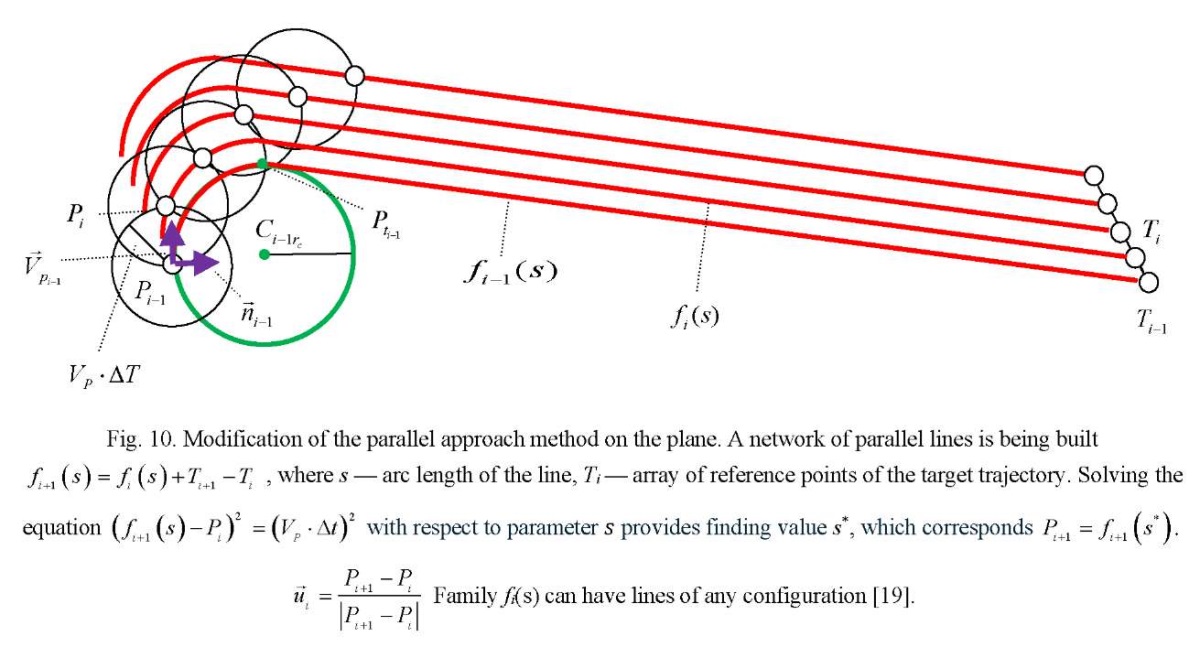
Thus, the library of calculations of control vectors contains methods of pursuit on the plane, in space, and on the surface. Parallel approach methods are calculated on the plane, in space, and on the surface. Proportional approximation methods are calculated on the plane and in space. Three-point methods are calculated on the plane and in space. Modified pursuit methods are calculated on the plane and in space, when the permissible curvature of the trajectories is used to control the pursuer. Modified methods of parallel approach are calculated on the plane and in space.
Modification of the methods of parallel approach and pursuit provide building a network of predicted trajectories that allow for various boundary conditions. This is illustrated in Figures 3-11. But not all methods of calculating control vectors are presented in them. It is assumed that this is an open, replenished library of functions.
Case of applying matrix modeling to group pursuit. Consider a case of group pursuit (Fig. 12).

Fig. 12. Scheme of multiple goal group pursuit
Here, all pursuers achieve the goal using a modified method of parallel approach, which corresponds to Figure 10. In the pursuit model in Figure 10, the curvature of the trajectory should not be greater than a certain value. Therefore, the initial radius of curvature of the trajectory increases for pursuers P2 and P3 as shown in Figure 12.
Sample Ak, has been formed, in which pursuer Pi catches up with Tj. Then there is a primary evaluation of the time of reaching tij. To estimate time tij, the following are calculated:
- length of the rectilinear section to the target,
- length of the arc of the mating circle of the permissible radius.
Then maximum value tk=Max{tij} is selected. An increase in time tij to tk occurs in this model due to an increase in radius of the mating circle from value ri to ri +dri. in pursuer Pi.
Figure 13 is supplemented with an animated image showing the process of multiple goal group pursuit [21].


Fig. 13. Schemes of group pursuit phases:
a — initial phase;
b — final phase
Based on the results of the study, a computer program, which implements an algorithm for group pursuit of several goals was created and registered [22]. This software solution is called “Parallel Approach on Plane of Group of Pursuers with Simultaneous Achievement of the Goal”.
Discussion and Conclusions. The methods of pursuit, parallel, proportional and three-point approach were described and visualized as functions on the plane, on the surface, and in space. In addition, the possibilities of modifying the method of parallel approach on the plane were shown. With the application of matrix modeling to group pursuit, a scheme of multiple goal group pursuit was built. The initial and final phases of this process were shown separately. The calculation of the achievement time made it possible to identify the pursuer who needed the most time to reach the goal from the sample under consideration.
Thus, it is assumed that the matrix of the distribution of pursuers by goals is generated at each moment of time. Goals and pursuers may disappear, new ones may appear. This matrix can also be used by the party representing the targets who evades prosecution. The results of the scientific research described in the article allow us to form the principles of automated distribution of pursuers by goals based on the selected target function. Algorithms for modifying the trajectories of pursuers to achieve goals simultaneously or according to a set schedule were proposed. The issues of forming a library of pursuit methods were also considered. The method of forming a matrix of the distribution of pursuers by goals can be in demand when designing virtual reality systems for game tasks in which the process of group pursuit, escape and evasion is simulated.
References
1. Rappoport IS. Strategii gruppovogo sblizheniya v metode razreshayushchikh funktsii dlya kvazilineinykh konfliktno-upravlyaemykh protsessov. Cybernetics and Systems Analysis. 2019;55(1):149–163. (In Russ.)
2. Bannikov AS. Some Non-Stationary Problems of Group Pursuit. Proceedings of the Institute of Mathematics and Computer Science of UdSU. 2013;1(41):3–46.
3. Khachumov MV. The Solution of the Problem of the Target Following by the Autonomous Aircraft. Artificial Intelligence and Decision Making. 2015;2:45–52.
4. Khachumov MV. Problems of Group Pursuit of a Target in a Perturbed Environment. Artificial Intelligence and Decision Making. 2016;2:46–54.
5. Abramyants TG, Maslov EP, Yahno VP. Evasion of Multiple Target in Three-Dimensional Space. Automation and Remote Control. 2008;5:3–14.
6. Samatov BT. O zadachakh gruppovogo presledovaniya pri integral'nykh ogranicheniyakh na upravleniya. Cybernetics and Systems Analysis. 2013;49(5):132–145. (In Russ.)
7. Chikrii AA. Game Dynamic Problems for Systems with Fractional Derivatives. In book: Altannar Chinchuluun, et al. (eds.) Pareto Optimality, Game Theory and Equilibria. New York, NY: Springer; 2008. Vol. 17. P. 349–387. https://doi.org/10.1007/978-0-387-77247-9_13
8. Borie RB, Tovey CA, Koenig S. Algorithms and Complexity Results for Pursuit-Evasion Problems. In: Proc. 21st Int. Joint Conf. on Artificial Intelligence (IJCAI). Pasadena, CA: Morgan Kaufmann Publishers Inc.; 2009. P. 59–66.
9. Sozinov PA, Gorevich BN. Kinematic Analysis of Proportional Navigation Methods as Applicable to Surface-to-Air Missile Guidance to a Ballistic Target. Vestnik Koncerna VKO “Almaz – Antey”. 2022;2:74–92.
10. Zarchan P. Tactical and Strategic Missile Guidance, 5th ed. Reston: American Institute of Aeronautics and Astronautics; 2006. 888 p.
11. Chikrii AA. Conflict-Controlled Processes. Dordrecht, Boston, London: Springer Science and Business Media; 2013. 424 p.
12. Chikrii AA, Chikrii GTs. Matrix Resolving Functions in Game Problems of Dynamics. Proceedings of the Steklov Institute of Mathematics. 2015;291(1):56–65. https://doi.org/10.1134/S0081543815090047
13. Chern F Chung, Tomonari Furukawa. A Reachability-Based Strategy for the Time-Optimal Control of Autonomous Pursuers. Engineering Optimization. 2008;40(1):67–93.
14. Dubanov AA. Model' metoda pogoni na ploskosti i v prostranstve. URL: https://youtu.be/PAu9Qg1dySM (accessed: 16.01.2023). (In Russ.)
15. Dubanov AA. Model' metoda parallel'nogo sblizheniya na ploskosti. URL: https://youtu.be/hGieKXNiuz8 (accessed: 16.01.2023). (In Russ.)
16. Dubanov AA. Model' parallel'nogo sblizheniya v prostranstve. URL: https://youtu.be/8nDUSi3ENB4 (accessed: 16.01.2023). (In Russ.)
17. Dubanov AA. Model' metoda pogoni na poverkhnosti. URL: https://youtu.be/sU724Db_VMk (accessed: 16.01.2023). (In Russ.)
18. Dubanov AA. Model' metoda parallel'nogo sblizheniya na poverkhnosti. URL: https://youtu.be/06qgINE4j8U (accessed: 16.01.2023). (In Russ.)
19. Dubanov AA. Modifikatsiya metoda parallel'nogo. URL: https://www.youtube.com/watch?v=qNXdykK21Z8 (accessed: 16.01.2023). (In Russ.)
20. Dubanov AA. Modifikatsiya metoda pogoni. URL: https://www.youtube.com/watch?v=UQ5bVKjVqZ4 (accessed: 16.01.2023). (In Russ.)
21. Dubanov AA. Rezul'taty modelirovaniya zadachi. URL: https://www.youtube.com/watch?v=NNJDJOJT34I (accessed: 9.07.2022). (In Russ.)
22. Dubanov AA, et al. Model' parallel'nogo sblizheniya na ploskosti gruppy presledovatelei s odnovremennym dostizheniem tseli. RF Certificate of State Registration of Computer Program No. 2021618920, 2021. (In Russ.)
About the Author
A. A. DubanovRussian Federation
Alexander A Dubanov, Cand.Sci. (Eng), Associate Professor of the Department of Geometry and Teaching Methodology
5, Ranzhurova St., Ulan-Ude, Republic of Buryatia, 670000, RF
Review
For citations:
Dubanov A.A. Methods for Applying Matrices when Creating Models of Group Pursuit. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):191-202. https://doi.org/10.23947/2687-1653-2023-23-2-191-202
JATS XML














































