Methods for Applying Matrices when Creating Models of Group Pursuit

Introduction. The pursuit algorithms are studied from the point of view of their classical and optimal implementation. Their role in differential pursuit games is investigated. The applied sphere of ready-made solutions is very wide, because the results of such scientific research are applicable in various information technologies and systems, in particular, in search engines. Undoubtedly, the issues of equipping moving robotic complexes with autonomous control elements will be of current concern for a long time, which also requires high-quality implementation of the algorithms under consideration.

In [1–4], the coordinated behavior of a group of pursuers and targets was investigated. For general theoretical and practical issues in the problems of persecution, works [5–9] were considered. The guidance of the pursuer to the target was analyzed considering the information provided in [10–13].

With all the theoretical and practical interest in this topic, optimization in pursuit problems was limited to the construction of optimal trajectories. Specifically, the shortest trajectories, trajectories with differential constraints, fuel consumption indicators were proposed. But the aspects of automated distribution by goals in group pursuit were not considered. To fill this gap, this scientific work was carried out. Its basic result was the construction of a model of automated distribution of pursuers by goals in group pursuit. The formation of a matrix of achieving goals by pursuers was shown. When assigning goals to the pursuers, all possible combinations of achieving goals were sorted out, and a combination of the minimum value of the criterion from the generated set with the maximum value was selected.

Optimization of the multiple goal group pursuit is a promising direction for the development of such a discipline as optimal motion control in tasks related to automated decision-making and autonomous management.

Materials and Methods. In the model of group pursuit described in the paper, targets move along predefined trajectories. However, this predestination does not matter in principle. The pursuers are distributed by the targets automatically, based on the minimax solution of the goal function. Then the control parameters of the pursuers' movement are modified. In this paper, this is the parameter of the minimum curvature of the trajectory. This approach allows for simultaneous achievement of goals.

Consider a group pursuit of a set of goals: N pursuers catch up with M goals. We form a matrix of the distribution of pursuers by goals:

Each cell Y_ij contains information about the phase coordinates of the i-th pursuer and the j-th target. Matrix Y_ij contains information about the method by which the i-th pursuer goes after the j-th goal.

The data stored in the cells of the matrix determines the access to the library of calculations of the control vectors of the pursuer.

In each cell of matrix Y_ij, the predicted time for the -th pursuer to reach the j-th goal can be calculated: t_ij.

Research Results

In each received sample , it is required to find the maximum value of achievement times , e.g., from (Table 1).

It is necessary to form matrices Y_ij, where i= 1…3, j=1…2 according to the possible samples
A_k,k = 1…6. Then, after the conversion, maximum value t_k=Max{t_ij} is found. The calculation made it possible to establish that pursuer P₁, demonstrated the greatest time of achievement, catching up with goal T₁ from sample A₂.

Thus, consider sample A_k. You can increase to the value of parameter t_k, all values t_ij, depending on the velocity vectors of the pursuers and goals, as well as their permissible angular velocities. This determines maximum value t_k.

Having received an array of samples {A_k} with corresponding time values {t_ij}, it is necessary to find minimum time t_min=Min{t_k}. This is how the optimal time for simultaneous group achievement of multiple goals is determined.

Algorithms for calculating the next step of the pursuer and estimating the time when the pursuer reaches the goal. Figure 1 shows the algorithm of the function for calculating the next step and the speed vector of the pursuer.

Figure 2 shows an algorithm for calculating the time and distance of the pursuer reaching the goal. Variable ε is the threshold value of the distance from the pursuer to the target, at which the goal is considered to have been achieved.

If the target moves along a predetermined trajectory, then the algorithm shown in Figure 2 can give an estimate of time t_ij for the -th pursuer to reach the j-th goal. In this case, the output parameter of the function can be the number of iterations of the pursuit process N_it. Number of iterations N_it — output parameter of the function for calculating the time and distance of reaching the goal by the pursuer.

If the goal replies to avoid achievement, you should evaluate the time differently. It is necessary to build predicted trajectories as composite segments of straight lines, arcs of circles, square and cubic parabolas and other known lines. This will make it possible not to solve boundary value problems in the calculation cycle.

Formation of a library of control vector calculations. The distribution matrix Y_ij, where i= 1…N, j=1…M pursuers by goals is built on each discrete time interval. In each cell of matrix Y_ij , information about the method of persecution is stored. It is based on the reference to the library of functions for calculating control vectors (Fig. 3–11).

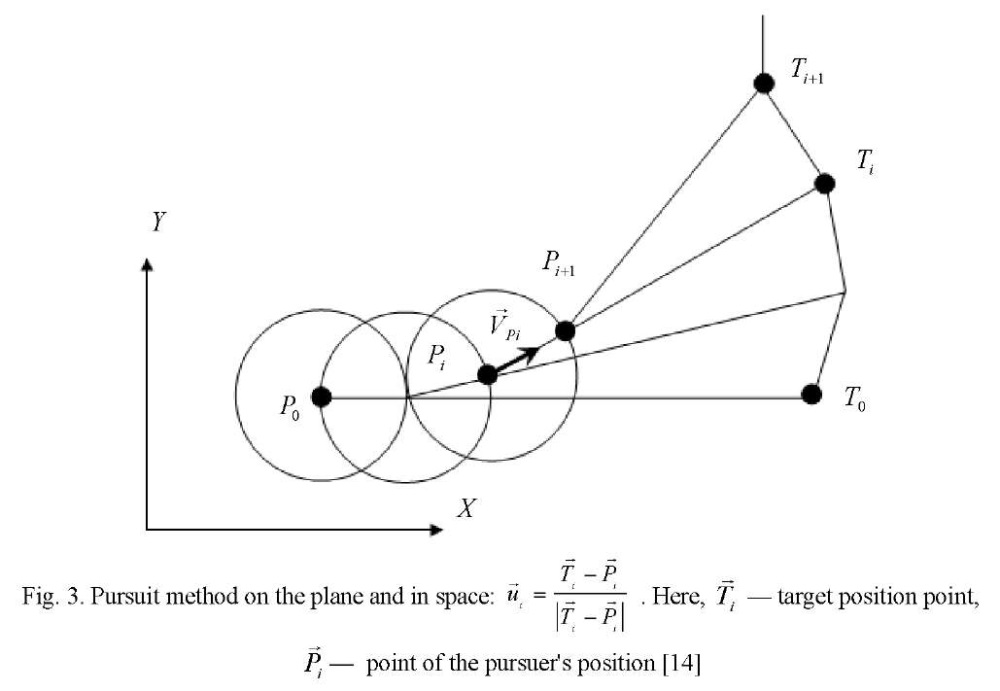
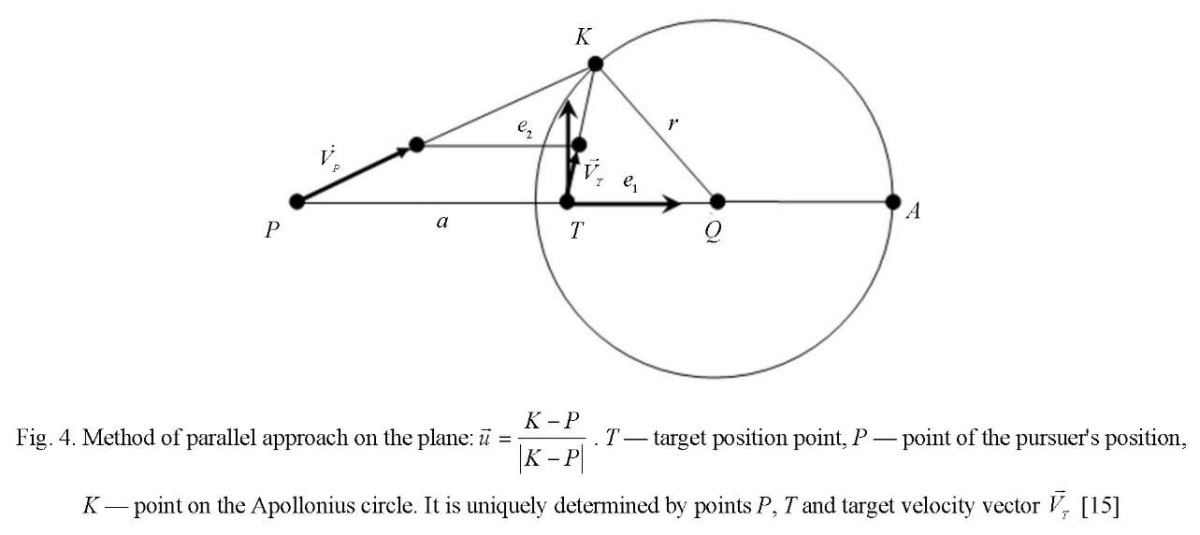
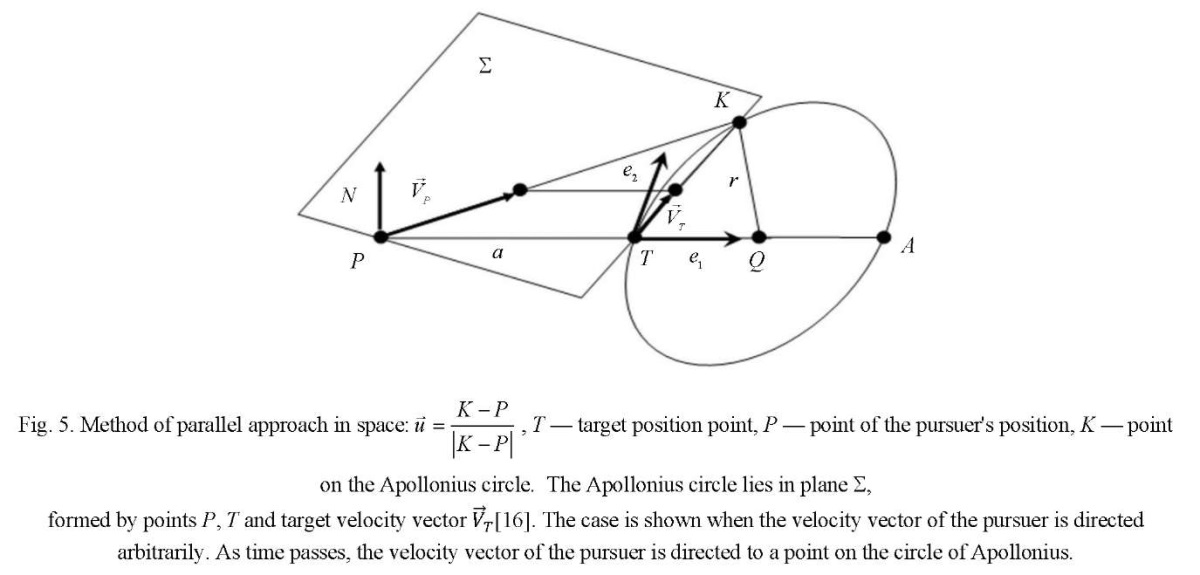
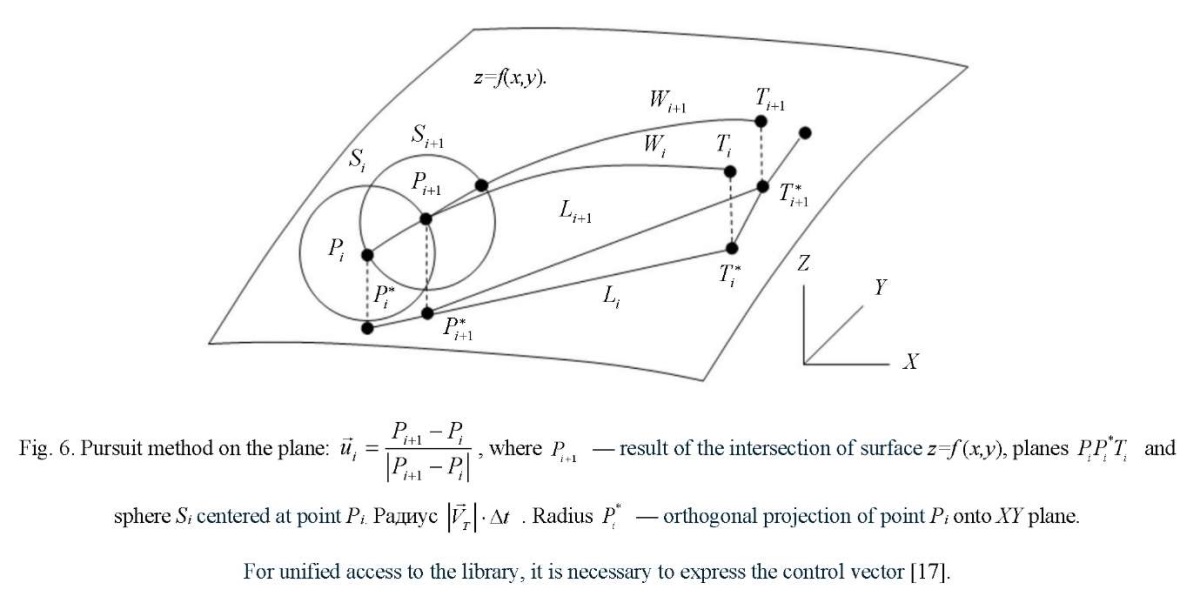
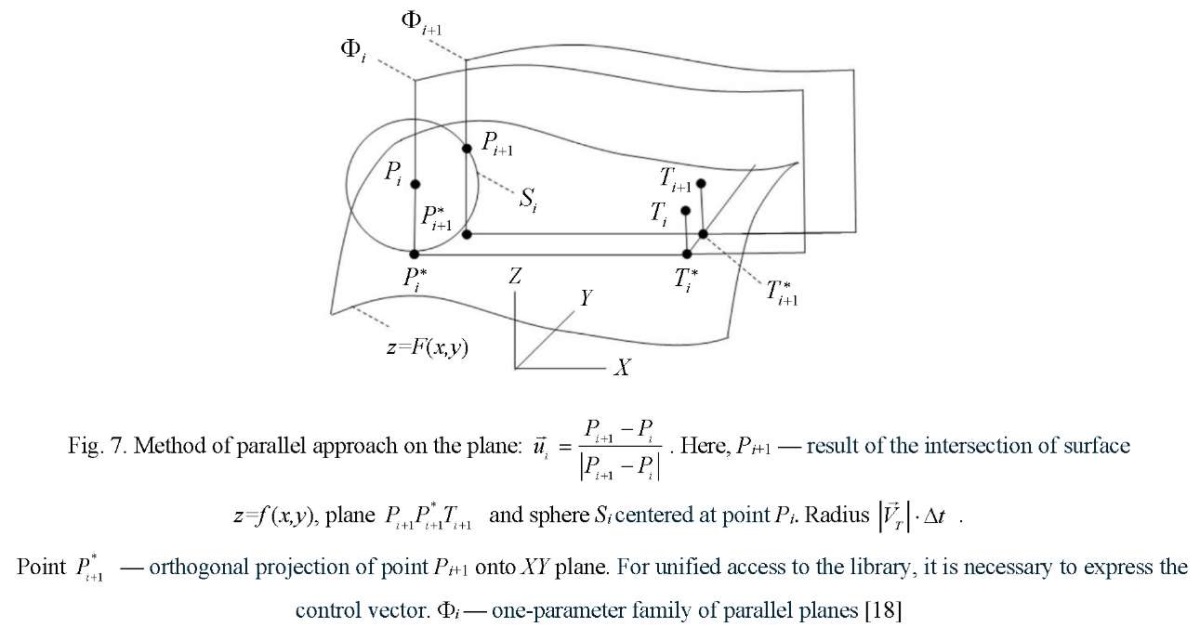
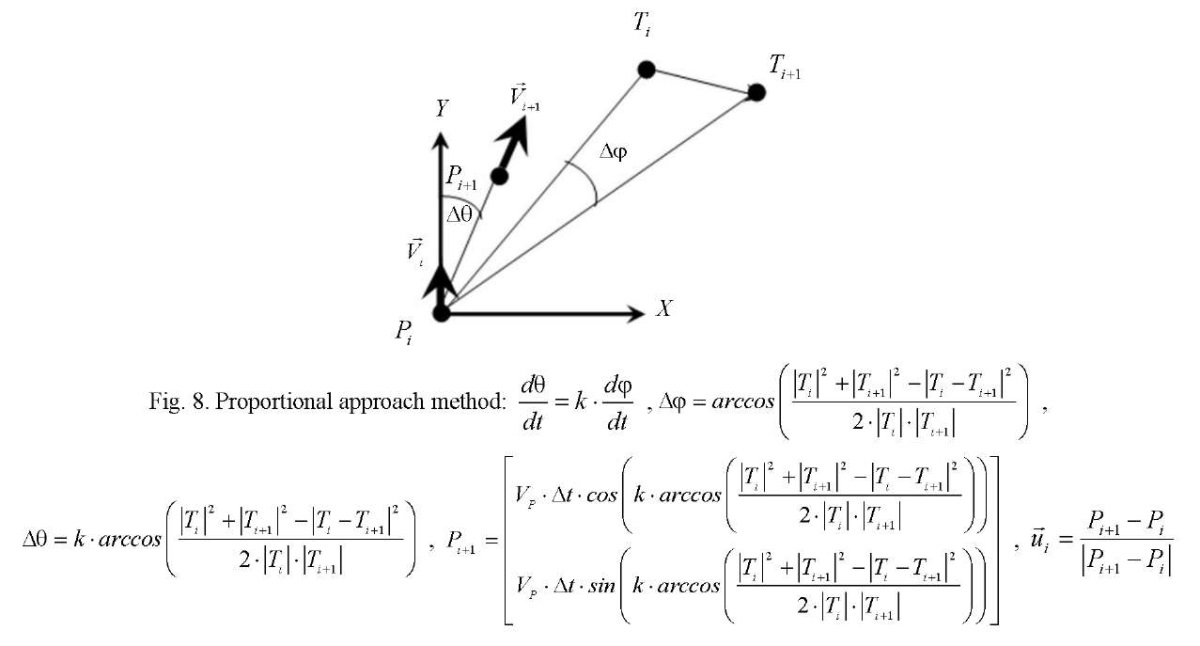
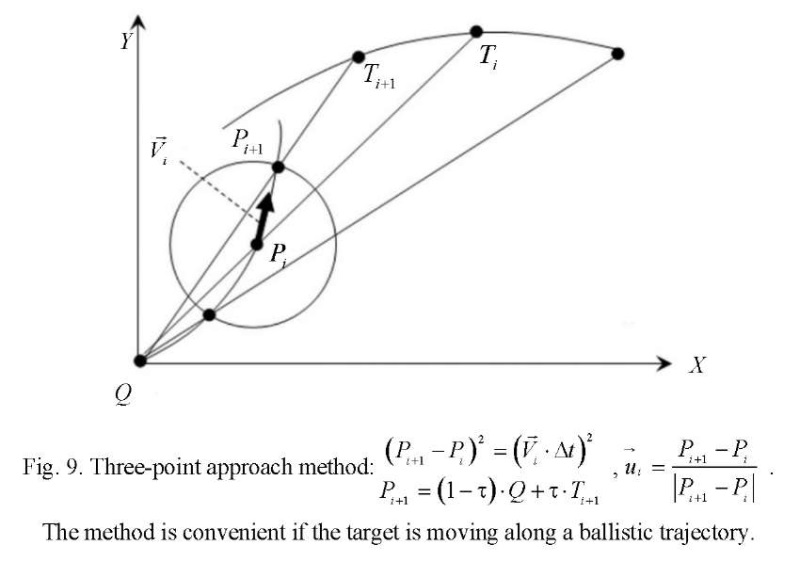
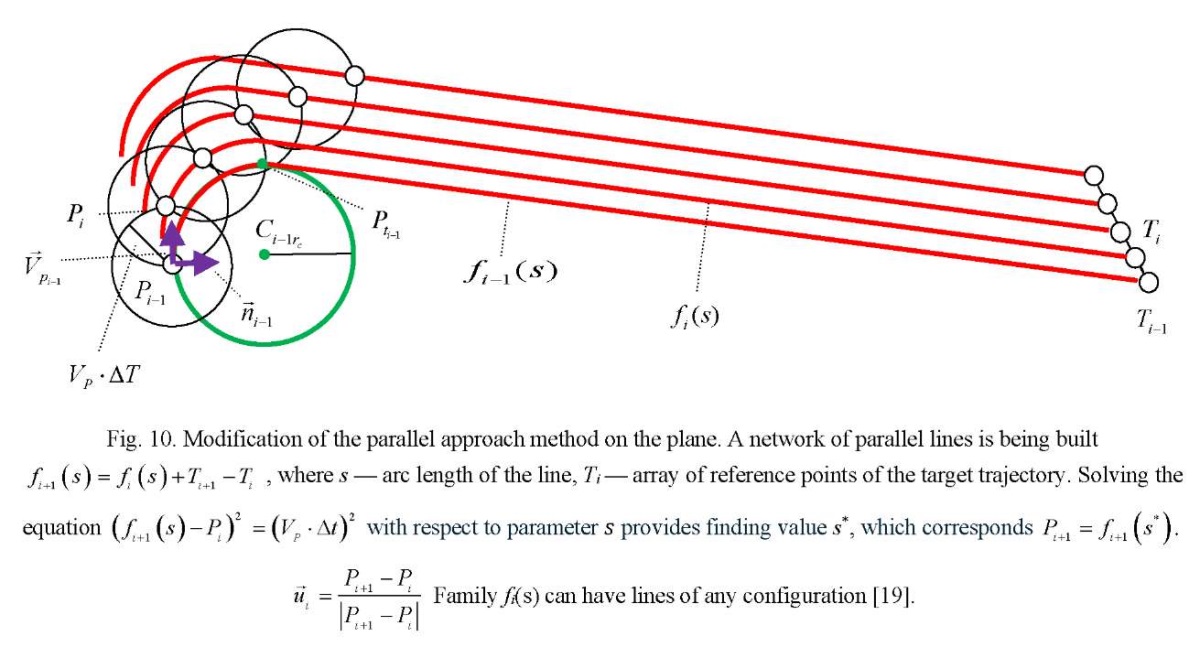
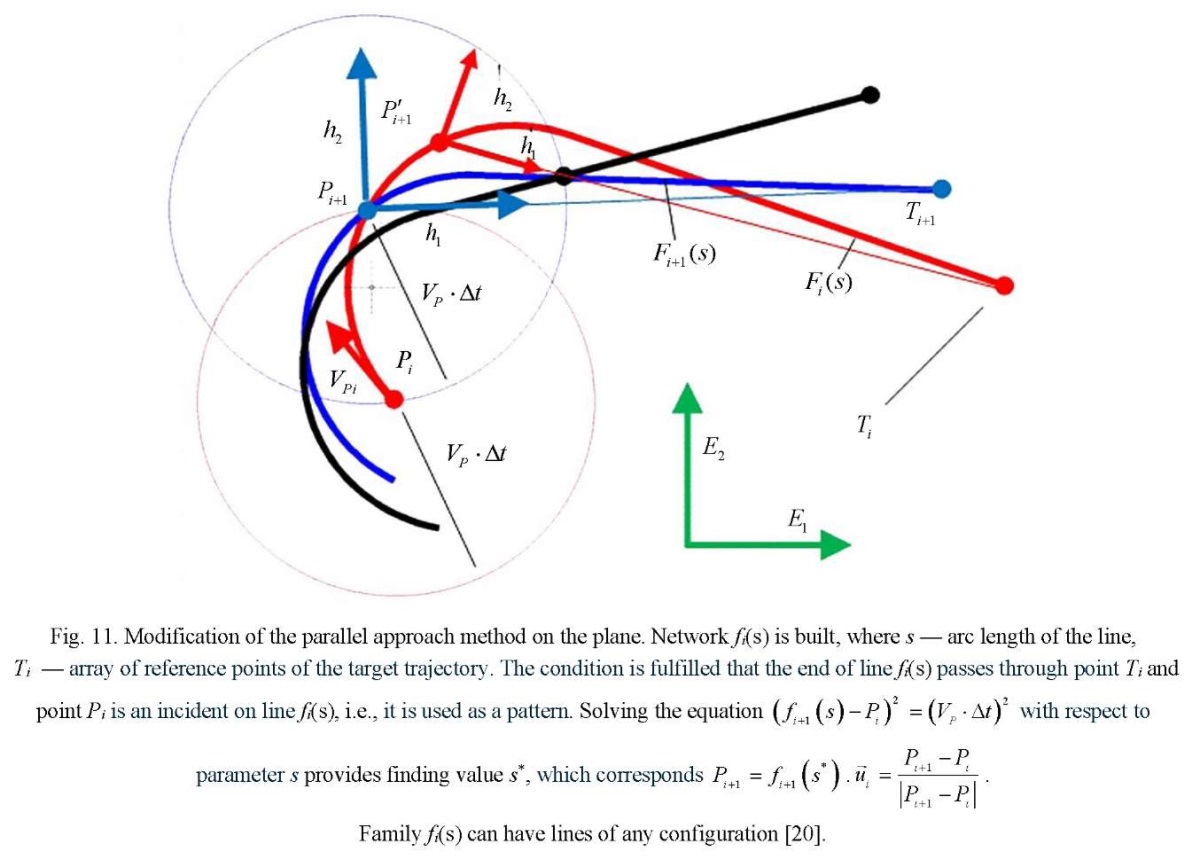
Thus, the library of calculations of control vectors contains methods of pursuit on the plane, in space, and on the surface. Parallel approach methods are calculated on the plane, in space, and on the surface. Proportional approximation methods are calculated on the plane and in space. Three-point methods are calculated on the plane and in space. Modified pursuit methods are calculated on the plane and in space, when the permissible curvature of the trajectories is used to control the pursuer. Modified methods of parallel approach are calculated on the plane and in space.

Modification of the methods of parallel approach and pursuit provide building a network of predicted trajectories that allow for various boundary conditions. This is illustrated in Figures 3-11. But not all methods of calculating control vectors are presented in them. It is assumed that this is an open, replenished library of functions.

Case of applying matrix modeling to group pursuit. Consider a case of group pursuit (Fig. 12).

Here, all pursuers achieve the goal using a modified method of parallel approach, which corresponds to Figure 10. In the pursuit model in Figure 10, the curvature of the trajectory should not be greater than a certain value. Therefore, the initial radius of curvature of the trajectory increases for pursuers P₂ and P₃ as shown in Figure 12.

Sample A_k, has been formed, in which pursuer P_i catches up with T_j. Then there is a primary evaluation of the time of reaching t_ij. To estimate time t_ij, the following are calculated:

• length of the rectilinear section to the target,
• length of the arc of the mating circle of the permissible radius.

Then maximum value t_k=Max{t_ij} is selected. An increase in time t_ij to t_k occurs in this model due to an increase in radius of the mating circle from value r_i to r_i +dr_i. in pursuer P_i.

Figure 13 is supplemented with an animated image showing the process of multiple goal group pursuit [21].

Based on the results of the study, a computer program, which implements an algorithm for group pursuit of several goals was created and registered [22]. This software solution is called “Parallel Approach on Plane of Group of Pursuers with Simultaneous Achievement of the Goal”.

Discussion and Conclusions. The methods of pursuit, parallel, proportional and three-point approach were described and visualized as functions on the plane, on the surface, and in space. In addition, the possibilities of modifying the method of parallel approach on the plane were shown. With the application of matrix modeling to group pursuit, a scheme of multiple goal group pursuit was built. The initial and final phases of this process were shown separately. The calculation of the achievement time made it possible to identify the pursuer who needed the most time to reach the goal from the sample under consideration.

Thus, it is assumed that the matrix of the distribution of pursuers by goals is generated at each moment of time. Goals and pursuers may disappear, new ones may appear. This matrix can also be used by the party representing the targets who evades prosecution. The results of the scientific research described in the article allow us to form the principles of automated distribution of pursuers by goals based on the selected target function. Algorithms for modifying the trajectories of pursuers to achieve goals simultaneously or according to a set schedule were proposed. The issues of forming a library of pursuit methods were also considered. The method of forming a matrix of the distribution of pursuers by goals can be in demand when designing virtual reality systems for game tasks in which the process of group pursuit, escape and evasion is simulated.