Перейти к:
Выпучивание прямоугольных пластин при нелинейной ползучести
https://doi.org/10.23947/2687-1653-2023-23-3-257-268
Аннотация
Введение. Задача анализа устойчивости пластин и оболочек в условиях ползучести актуальна для элементов конструкций из материалов, обладающих свойством старения, находящихся под действием длительных нагрузок, поскольку потеря устойчивости может происходить резко и задолго до исчерпания прочностного ресурса материала. Вопросы совместного учета геометрической нелинейности и ползучести в задачах выпучивания пластин в настоящее время остаются слабо изученными, существующие программные комплексы не позволяют выполнить такой расчёт. Целью настоящей работы выступает разработка алгоритма расчета на устойчивость прямоугольных пластинок с начальной погибью, испытывающих действие нагрузок в срединной плоскости с учетом геометрической нелинейности и ползучести.
Материалы и методы. При получении разрешающих уравнений в основу положены геометрические и статические уравнения теории гибких упругих пластин. Физические уравнения выводятся из предположения, что полные деформации равны сумме упругих деформаций и деформаций ползучести. Окончательно задача была сведена к системе из двух дифференциальных уравнений, в которых в качестве искомых функций выступают функция напряжений и прогиба. Решение полученной системы уравнений выполнялось численно с помощью метода конечных разностей в сочетании с методом последовательных приближений и методом Эйлера. В качестве граничных условий для функции напряжений используется рамная аналогия, как в случае плоской задачи теории упругости.
Результаты исследования. В рамках поставленной цели разработан алгоритм расчета и представлено решение задачи для пластины, сжимаемой в одном направлении равномерно распределенной нагрузкой. Исследован характер роста перемещений при различной величине нагрузки и начальной погиби. Установлено, что при достижении вертикальными перемещениями величин, соизмеримых с толщиной пластинки, скорость их роста начинает затухать даже при нагрузке больше длительной критической.
Обсуждение и заключение. Результаты анализа устойчивости с использованием разработанного алгоритма показывают, что рост прогиба пластины при рассмотренных граничных условиях ограничен, потеря устойчивости не наблюдается при любых значениях нагрузки, не превосходящих мгновенную критическую. Это говорит о возможности длительной безопасной эксплуатации таких конструкций при нагрузке менее мгновенной критической.
Ключевые слова
Для цитирования:
Языев С.Б., Чепурненко А.С. Выпучивание прямоугольных пластин при нелинейной ползучести. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):257-268. https://doi.org/10.23947/2687-1653-2023-23-3-257-268
For citation:
Yazyev S.B., Chepurnenko A.S. Buckling of Rectangular Plates under Nonlinear Creep. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):257-268. https://doi.org/10.23947/2687-1653-2023-23-3-257-268
Введение. Анализу устойчивости тонкостенных конструкций в виде пластин и оболочек уделяется большое внимание, поскольку такие конструкции широко используются в строительстве и других областях техники [1–3]. Одной из актуальных задач в области расчета пластин и оболочек является анализ их напряженно-деформированного состояния в условиях ползучести, что подтверждается значительным числом работ, опубликованных в последнее время по данной проблеме в отечественных и зарубежных источниках. Так, в работах [4–8] исследуются вопросы выпучивания при ползучести композитных тонкостенных конструкций. В статье [9] рассматривается задача устойчивости функционально-градиентных пластин с учетом зависимости свойств материала от температуры. В работе [10] в задаче выпучивания композитных пластин применены методы стохастического анализа. В статьях [11–17] изложены вопросы устойчивости вязкоупругих пластин и оболочек при воздействии динамической и следящей нагрузки, а в статье [18] рассматриваются пластины средней толщины с учетом зависимости свойств материала от времени. Возникающие при решении указанных задач математические трудности приводят к тому, что многие исследователи ограничиваются линейными законами вязкоупругого деформирования или рассматривают случай установившейся ползучести. Большие возможности в задачах расчета пластин и оболочек с учетом ползучести открывает метод конечных элементов. Однако в современные расчетные комплексы, такие как ANSYS, Abaqus, ЛИРА и др., заложен ограниченный набор реологических моделей, применимых для конкретных материалов в фиксированном диапазоне напряжений и температур. Существует необходимость в альтернативных методах расчета, подходящих для произвольных законов вязкоупругого деформирования, в том числе нелинейных.
Целью настоящей работы явилось построение системы разрешающих уравнений для задачи выпучивания пластин прямоугольной формы с нелинейными вязкоупругими свойствами при действии усилий в срединной плоскости, с учетом больших перемещений, а также алгоритма ее решения. Отметим, что проблема устойчивости элементов конструкций с учетом ползучести не может быть решена, как проблема чистой устойчивости. Ее решение требует наличия возмущений в виде начальных неправильностей. Обычно начальные несовершенства задаются в виде начальной погиби или эксцентриситетов приложения нагрузок.
Материалы и методы. Методику расчета рассмотрим на примере пластинки с начальной погибью w0(x,y), имеющей шарнирное опирание по контуру и сжимаемой в направлении оси x распределенной нагрузкой p [кН/м] (рис. 1).
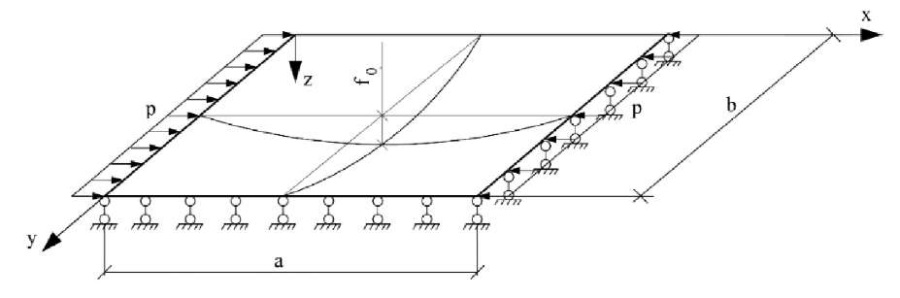
Рис. 1. Расчетная схема
В рассматриваемом случае при наличии ползучести, если сравнивать с теорией упругих гибких пластин, отличие будет проявляться только в форме физических уравнений. Полные деформации могут быть представлены в виде суммы деформаций срединной плоскости (переходящей в поверхность) и изгибных деформаций, которые вызваны изменением показателей кривизны срединной поверхности:
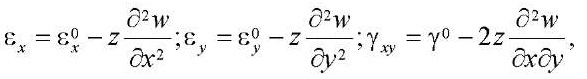 (1)
(1)
где
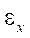 и
и 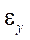 — полные линейные деформации;
— полные линейные деформации;
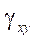 — полные угловые деформации;
— полные угловые деформации;
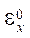 и
и 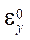 — линейные деформации срединной поверхности;
— линейные деформации срединной поверхности;
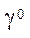 — угловые деформации срединной поверхности.
— угловые деформации срединной поверхности.
Для деформаций срединной поверхности может быть записано уравнение неразрывности деформаций [19]:
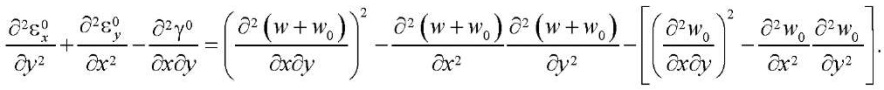 (2)
(2)
Для материалов с вязкоупругими свойствами полные деформации можно представить в виде:
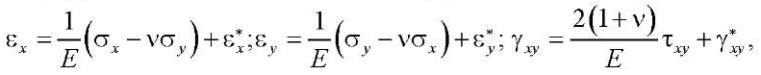 (3)
(3)
где
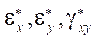 — деформации ползучести;
— деформации ползучести;
E — модуль упругости;
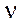 — коэффициент Пуассона;
— коэффициент Пуассона;
σx, σy, τxy — величины компонентов напряжений по соответствующим направлениям.
Выразив в (3) компоненты напряжений через деформации, запишем физические соотношения в обратной форме:
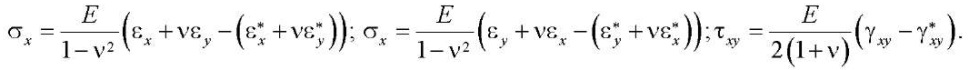 (4)
(4)
Связь внутренних силовых факторов с напряжениями определяется интегральными соотношениями:
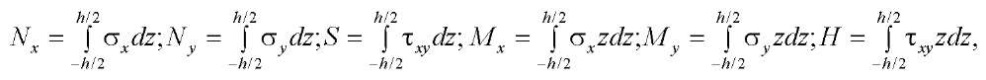 (5)
(5)
где
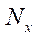 и
и 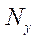 — погонные продольные силы;
— погонные продольные силы;
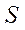 — погонные сдвигающие силы;
— погонные сдвигающие силы;
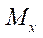 и
и 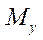 — погонные изгибающие моменты;
— погонные изгибающие моменты;
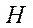 — погонные крутящие моменты;
— погонные крутящие моменты;
h — толщина пластинки.
Далее подставим (1) в (4), а также (4) в (5). В итоге получим:
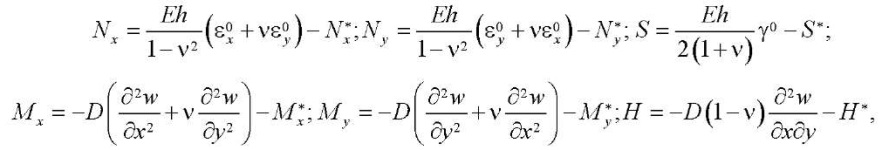 (6)
(6)
где
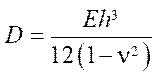 — цилиндрическая жесткость пластинки,
— цилиндрическая жесткость пластинки,
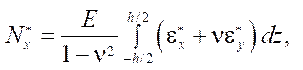
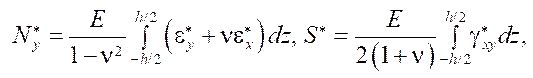
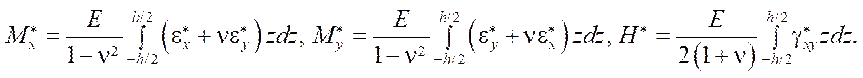
Величины 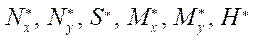 имеют размерность внутренних усилий и определяют вклад деформаций ползучести в перераспределение усилий.
имеют размерность внутренних усилий и определяют вклад деформаций ползучести в перераспределение усилий.
Статические уравнения теории гибких пластин имеют вид [19]:
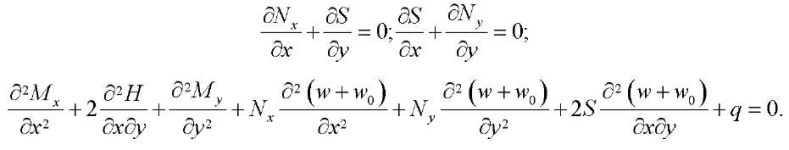 (7)
(7)
Здесь q — нормальная нагрузка по поверхности пластины, которая в данной задаче равна нулю.
Удовлетворить первым двум статическим уравнениям можно при помощи функции напряжений Эри, введенной по формулам:
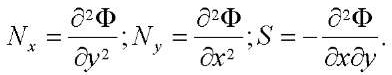 (8)
(8)
После подстановки последних трех равенств из (6) в последнее статическое уравнение в (7) и с учетом (8), получим первое разрешающее уравнение:
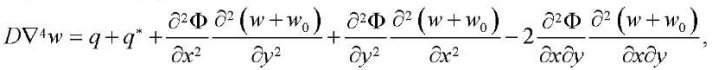 (9)
(9)
где
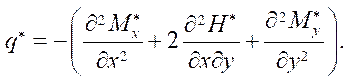
Чтобы получить второе разрешающее уравнение, необходимо выразить из (6) деформации срединной поверхности:
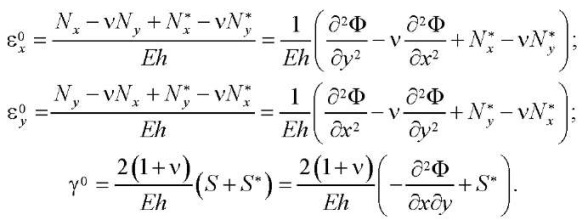 (10)
(10)
Подставив (10) в (2), получим:
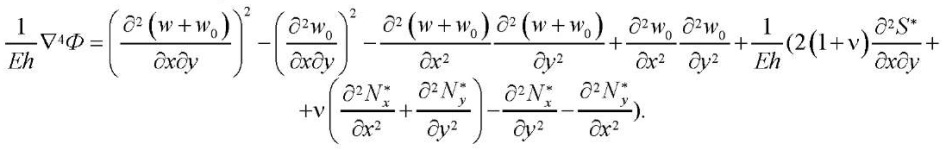 (11)
(11)
Таким образом, для рассматриваемой задачи получена система разрешающих уравнений из двух дифференциальных уравнений четвертого порядка (9) и (11). Уравнения (9) и (11) являются нелинейными. В полученных уравнениях величины 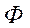 и w представляют собой функции координат x, y, а также времени t. В явном виде в данных уравнениях время отсутствует, зависимость от времени закладывается в деформации ползучести
и w представляют собой функции координат x, y, а также времени t. В явном виде в данных уравнениях время отсутствует, зависимость от времени закладывается в деформации ползучести 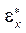 ,
, 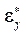 ,
, 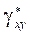 , которые учитываются введением интегральных величин
, которые учитываются введением интегральных величин 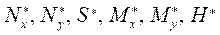 .
.
Для изображенной на рис. 1 расчетной схемы граничные условия записываются в виде:
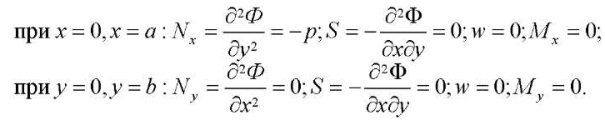 (12)
(12)
Уравнение (11) при малых перемещениях, в случае пластины из упругого материала, представляет бигармоническое уравнение, которое используется для решения плоской задачи теории упругости в напряжениях. Граничными условиями по функции напряжений для бигармонического уравнения может служить рамная аналогия. Контур пластины рассматривается как рама и функция напряжений на контуре будет равна в ней изгибающему моменту M, а ее производная по нормали к контуру — продольной силе N. Эпюры M и N в раме могут быть построены в одной из основных систем метода сил (ОСМС). Основная система, а также эпюры изгибающего момента и продольной силы в раме показаны на рис. 2.
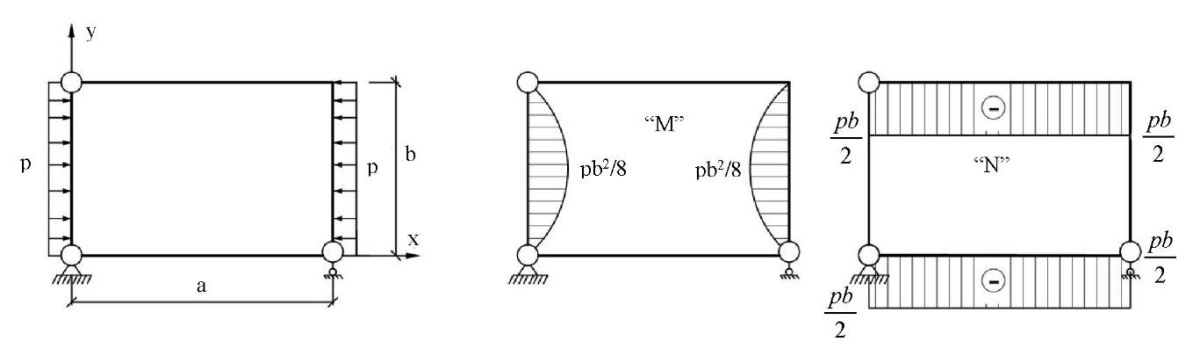
Рис. 2. ОСМС и эпюры изгибающих моментов и продольных сил
Если вертикальные перемещения не превышают четверть толщины пластинки, то можно принять усилия в срединной поверхности не зависящими от координат x и y
(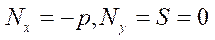 ) и использовать для расчетов линеаризованное уравнение:
) и использовать для расчетов линеаризованное уравнение:
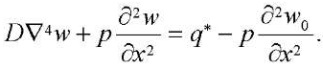 (13)
(13)
Аналитическое решение системы уравнений (9) и (11) связано с большими трудностями. Авторы предлагают решать данную систему численно. Используется метод конечных разностей (МКР) в комбинации с методом последовательных приближений. Для определения деформации ползучести во временной области применяется метод Эйлера. В качестве первого этапа выполняется решение для упругой пластинки. Нагрузка p прикладывается ступенчато с небольшим шагом. При начальных значениях нагрузки прогибы w1 вычисляются путем решения упрощенного уравнения (13). Затем выполняется подстановка вычисленных значений w1 в дифференциальное уравнение (11). Это позволяет определить функцию напряжений. Следующим шагом является решение дифференциального уравнения (9) с использованием известных величин функции Ф, что позволяет определить узловые величины прогибов 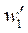 . После этого выполняется подстановка значений
. После этого выполняется подстановка значений 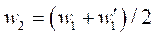 в уравнение (11). Повторение итерационного процесса на каждом шаге происходит до тех пор, пока относительное расхождение с нормами векторов узловых значений прогибов
в уравнение (11). Повторение итерационного процесса на каждом шаге происходит до тех пор, пока относительное расхождение с нормами векторов узловых значений прогибов 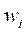 и
и 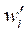 больше заданного значения (авторами оно принималось равным 0,1 %). Для второго шага по нагрузке начальным значением
больше заданного значения (авторами оно принималось равным 0,1 %). Для второго шага по нагрузке начальным значением 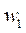 в каждом узле выступает конечный результат, полученный на первом шаге. Методика расчета во временной области с учетом ползучести аналогична. Интервал времени, на котором исследуется процесс, делится на шаги ∆t. В случае задания закона вязкоупругого деформирования в дифференциальной форме величины деформаций ползучести на шаге t + ∆t вычисляются на основе известной скорости их роста в момент времени t с использованием аппроксимации по Эйлеру:
в каждом узле выступает конечный результат, полученный на первом шаге. Методика расчета во временной области с учетом ползучести аналогична. Интервал времени, на котором исследуется процесс, делится на шаги ∆t. В случае задания закона вязкоупругого деформирования в дифференциальной форме величины деформаций ползучести на шаге t + ∆t вычисляются на основе известной скорости их роста в момент времени t с использованием аппроксимации по Эйлеру:
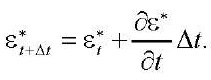 (14)
(14)
Блок-схема алгоритма расчета на ползучесть приведена на рис. 3.
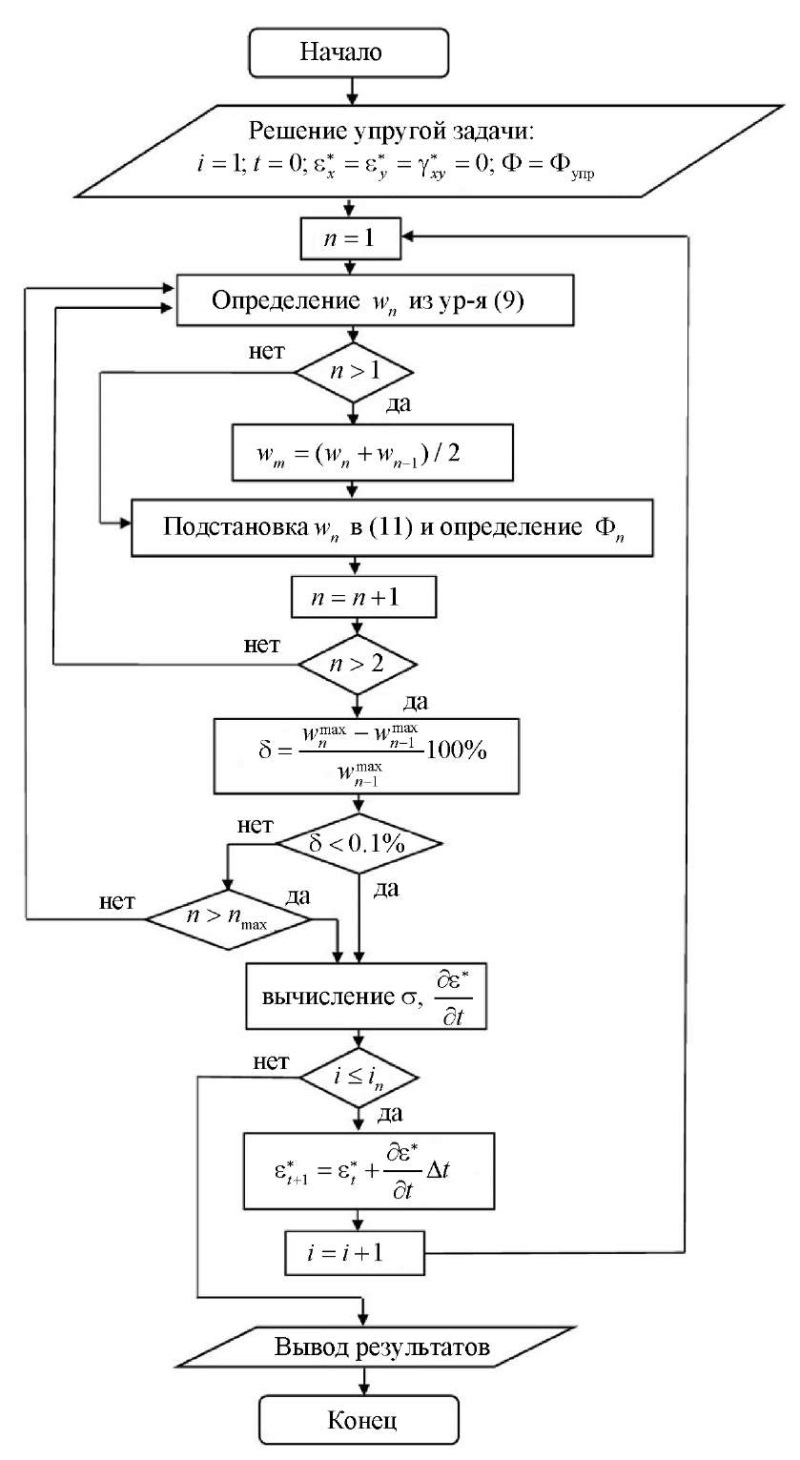
Рис. 3. Блок-схема алгоритма расчета на ползучесть
Отметим, что система уравнений (9) и (11) позволяет использовать схемы более высокого порядка точности, например, метод Рунге-Кутта четвертого порядка. При этом для достижения той же точности результатов можно задавать заметно большие шаги по времени. Однако при увеличении шага есть вероятность не уловить эффекты неустановившейся ползучести в начальные моменты времени. А при одинаковом шаге по времени метод Рунге-Кутта, по сравнению с методом Эйлера, требует выполнить в четыре раза больше операций.
Результаты исследования. Рассмотрена полимерная пластинка из поливинилхлорида размерами a = 2 м, b = 2 м, h = 1 см при E = 1480 МПа, ν = 0,3. В качестве закона, определяющего скорость роста деформаций ползучести, было принято нелинейное уравнение Максвелла-Гуревича:
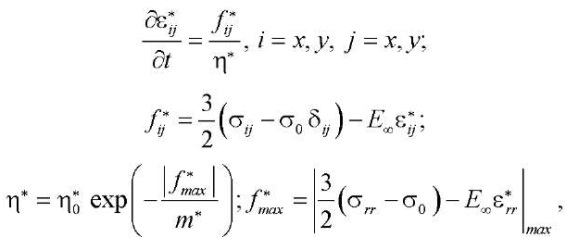 (15)
(15)
где
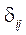 — символ Кронекера;
— символ Кронекера;
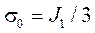 ,
, 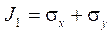 — первый инвариант тензора напряжений;
— первый инвариант тензора напряжений;
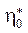 , E∞ и m — реологические параметры материала, называемые начальной релаксационной вязкостью, модулем высокоэластичности и модулем скорости.
, E∞ и m — реологические параметры материала, называемые начальной релаксационной вязкостью, модулем высокоэластичности и модулем скорости.
Индексами rr в формуле (15) обозначено направление главных напряжений.
Для ПВХ значения реологических параметров авторами были взяты из работы [20]: E∞ = 5,99∙103 МПа, m*=12,6 МПа, = 5,44·107 МПа·с. Форма начальной погиби w0(x,y) принималась в соответствии с первой формой потери устойчивости пластинки из упругого материала:
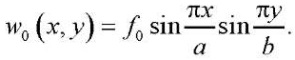 (16)
(16)
Для пластины из упругого материала без начальных несовершенств критическая нагрузка, в случае целого отношения сторон a/b, определяется по формуле [19]:
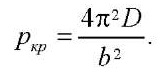 (17)
(17)
Для верификации разработанного алгоритма расчета первым этапом было выполнено решение тестовой упругой задачи и сравнение результатов с расчетом в конечно-элементном пакете ЛИРА-САПР (рис. 4). Величина стрелы начальной погиби f0 задавалась равной 0,15 мм. Размер сетки при использовании МКР составлял 20×20, количество шагов по нагрузке — 200. При расчете в ПК ЛИРА-САПР выполнялось разбиение пластинки треугольными конечными элементами с шагом триангуляции 0,1 м. Величина шага по нагрузке принималась такая же, как и при использовании МКР. Значение критической нагрузки для упругой пластинки, вычисленное по формуле (17), составило 1340 Н/м. В таблице 1 показано сравнение вертикальных перемещений в центре пластинки для различных значений нагрузки, полученных по авторской методике и при помощи метода конечных элементов (МКЭ). Прогибы, вычисленные с использованием двух альтернативных методов, достаточно близки, за исключением нагрузки 1330 Н/м. Отклонение при этой величине нагрузки можно объяснить тем, что при приближении к критической нагрузке перемещения устремляются в бесконечность.
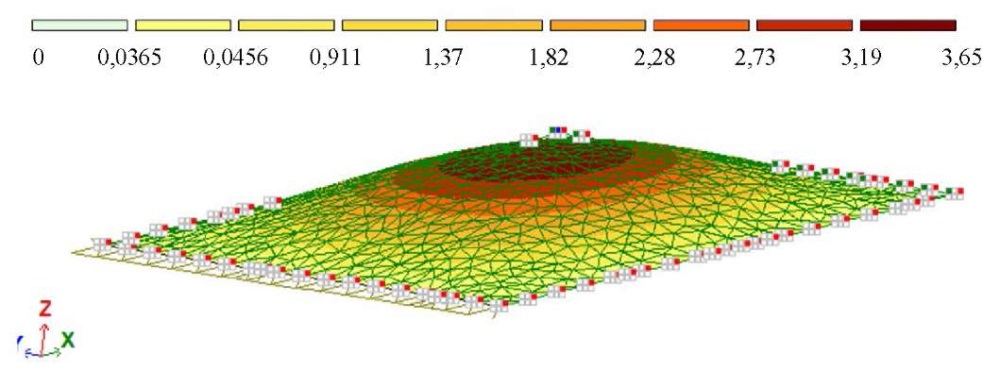
Рис. 4. Изополя вертикальных перемещений в ПК ЛИРА-САПР (p = 1330 Н/м):
нелинейное загружение 1, изополя перемещений по Z(G), единицы измерения — мм
Таблица 1
Сравнение результатов расчета по авторской методике и при помощи МКЭ
|
p, Н/м |
w∙103, мм
|
|
|
ЛИРА-САПР |
Aвторская методика |
|
|
133 |
16 |
16 |
|
266 |
37 |
37 |
|
399 |
63 |
63 |
|
532 |
98 |
99 |
|
665 |
146 |
148 |
|
798 |
218 |
221 |
|
931 |
336 |
342 |
|
1064 |
562 |
578 |
|
1197 |
1163 |
1229 |
|
1330 |
3646 |
4229 |
В статье [21] показана возможность перехода от решения упругой задачи расчета пластин к решению в конце процесса ползучести. Величину длительной критической нагрузки p∞ можно получить, заменив цилиндрическую жесткость D упругой пластинки на длительную цилиндрическую жесткость D∞, которая определяется по формуле:
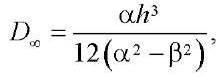 (18)
(18)
где
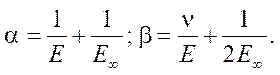
Для вязкоупругих стержней и круглых пластин было ранее установлено, что в случае p < p∞, рост перемещений во времени замедляется, и стрела прогиба приходит к конечному значению. Если p = p∞, прогибы растут с постоянной скоростью. При p > p∞ скорость роста прогибов возрастает.
Авторами также проведен анализ характера роста прогибов во времени для p < p∞, p = p∞ и p > p∞ для различных значений максимальной начальной погиби f0. Кривые изменения прогиба с течением времени в центре пластины при p = 0,9 p∞, p = p∞ и p = 1,1 p∞ приведены соответственно на рис. 5–7.
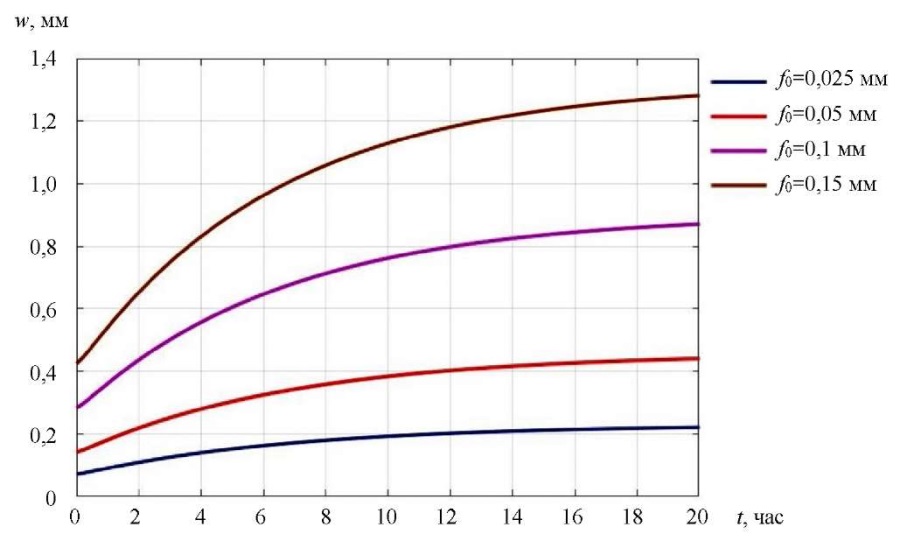
Рис. 5. Кривые изменения прогиба в центре пластины во времени при p = 0,9p∞
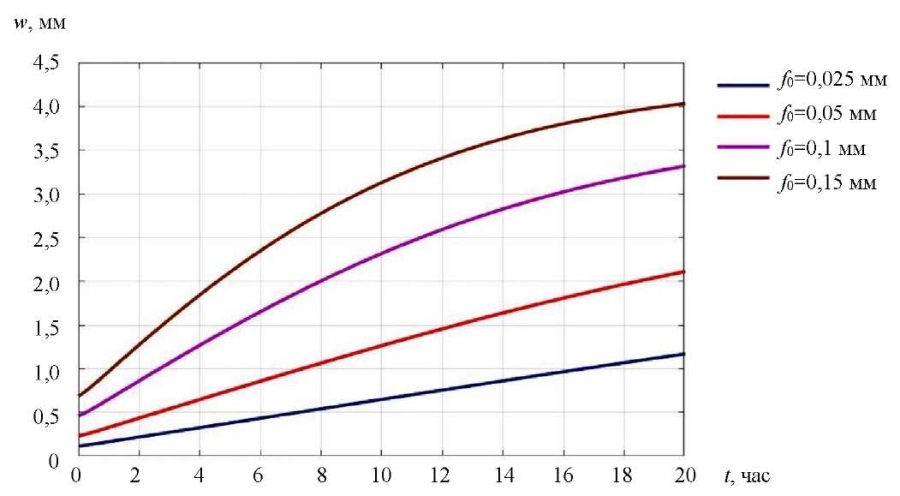
Рис. 6. Кривые изменения прогиба в центре пластины во времени при p = p∞
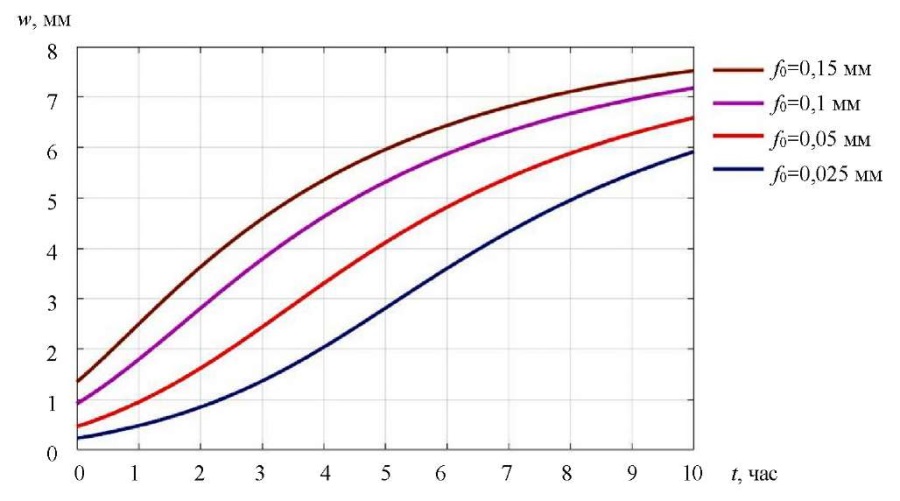
Рис. 7. Кривые изменения прогиба в центре пластины во времени при p = 1,1 p∞
Обсуждение и заключение. Из рис. 5 видно, что при p < p∞ стрела прогиба всегда приходит к конечному значению, независимо от значений начальных несовершенств. В то же время при p ≥ p∞ полученный в [21] характер роста прогибов имеет место только при малых перемещениях. При достижении прогибами значений, превышающих примерно четверть толщины пластины, скорость роста деформаций начинает убывать даже в случае нагрузок, превышающих длительную критическую. Следует также отметить полное отсутствие участка с возрастающей скоростью роста перемещений для пластин с большими начальными искривлениями. Объяснить выявленные эффекты можно перераспределением усилий 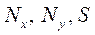 в срединной поверхности.
в срединной поверхности.
Резюмируя вышесказанное, можно сделать вывод, что вертикальные перемещения пластины, шарнирно опертой по контуру, при действии сжимающей нагрузки по одной оси, всегда приходят к конечному значению, если нагрузка не превышает мгновенную критическую. Иначе говоря, при рассмотренном закреплении и нагружении пластина в условиях ползучести находится в устойчивом равновесии.
Полученные уравнения и алгоритм вычислений позволяют рассчитывать пластинки из произвольных вязкоупругих материалов при любых вариантах закрепления. Закон связи между напряжениями и деформациями ползучести также может быть задан произвольно.
Список литературы
1. Yankovskii A.P. Refined Deformation Model for Metal-Composite Plates of Regular Layered Structure in Bending under Conditions of Steady-State Creep. Mechanics of Composite Materials. 2017;52(6):715–732. https://doi.org/10.1007/s11029-017-9622-7
2. Янковский А.П. Установившаяся ползучесть сложно армированных металлокомпозитных пластин, нагруженных в своей плоскости. Математическое моделирование. 2010;22(8);55–66. URL: https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mm&paperid=3007&option_lang=rus (дата обращения: 18.05.2023).
3. Хорошун Л.П., Бабич Д.В. Устойчивость прямоугольных пластин из слоистого композитного материала при длительной повреждаемости компонентов. Прикладная механика. 2010;46(12):67–75.
4. Zhongyu Lu, Guijun Xian, Khuram Rashid. Creep Behavior of Resin Matrix and Basalt Fiber Reinforced Polymer (BFRP) Plate at Elevated Temperatures. Journal of Composites Science. 2017;1(1):3. https://doi.org/10.3390/jcs1010003
5. Pawlus D. Stability of Three-Layered Annular Plate with Composite Facings. Applied Composite Materials. 2017;24(1):141–158. https://doi.org/10.1007/s10443-016-9518-z
6. Rouzegar J., Gholami M. Creep and Recovery of Viscoelastic Laminated Composite Plates. Composite Structures. 2017;181:256–272. https://doi.org/10.1016/j.compstruct.2017.08.094
7. Gräfe M., Dietsch P., Winter S. CLT under In-Plane Loads: Investigation on Stress Distribution and Creep. In: Proc. INTER International Network on Timber Engineering Research. Karlsruhe: Timber Scientific Publishing; 2018. P. 289–306. URL: https://mediatum.ub.tum.de/doc/1533836/document.pdf
8. Pawlus D. Dynamic Behaviour of Three-Layered Annular Plates with Viscoelastic Core under Lateral Loads. Journal of Theoretical and Applied Mechanics. 2015;53(4):775–788. https://doi.org/10.15632/jtam-pl.53.4.775
9. Sharma K., Kumar D. Elastoplastic Stability and Failure Analysis of FGM Plate with Temperature Dependent Material Properties under Thermomechanical Loading. Latin American Journal of Solids and Structures. 2017;14(7):1361–1386. https://doi.org/10.1590/1679-78253747
10. Kumar R.R., Mukhopadhyay T., Pandey K.M., Dey S. Stochastic Buckling Analysis of Sandwich Plates: The Importance of Higher Order Modes. International Journal of Mechanical Sciences. 2019;152:630–643. https://doi.org/10.1016/j.ijmecsci.2018.12.016
11. Kosheleva E. Dynamic Stability of a Viscoelastic Plate. MATEC Web of Conferences. 2017;117:00086. https://doi.org/10.1051/matecconf/201711700086
12. Abramovich H. Stability and Vibrations of Thin-Walled Composite Structures. Cambridge: Woodhead Publishing; 2017. 770 p.
13. Кирсанов М.Н. Выпучивание пластины из нелинейного реологического материала при переменном нагружении. Вестник Татарского государственного гуманитарно-педагогического университета. 2011;24:19–22. URL: https://cyberleninka.ru/article/n/vypuchivanie-plastiny-iz-nelineynogo-reologicheskogo-materiala-pri-peremennomnagruzhenii (дата обращения: 18.05.2023).
14. Абдикаримов Р.А., Жгутов В.М. Геометрически нелинейное математическое моделирование динамической устойчивости вязкоупругих пологих оболочек переменной толщины. Инженерно-строительный журнал. 2011;(6):12–22. https://cyberleninka.ru/article/n/geometricheski-nelineynoe-matematicheskoe-modelirovaniedinamicheskoy-ustoychivosti-vyazkouprugih-pologih-obolochek-peremennoy/viewer (дата обращения: 18.05.2023).
15. Абдикаримов Р.А., Худаяров Б.А. Динамическая устойчивость вязкоупругих гибких пластин переменной жесткости при осевом сжатии. Прикладная механика. 2014;50(4): 41–51.
16. Абдикаримов Р.А., Верлань А.Ф., Горошко И.О. Численное исследование динамической устойчивости вязкоупругих ортотропных прямоугольных пластин с переменной жесткостью. Моделювання та інформаційні технології. 2011;60:10–17.
17. Robinson M.T.A., Adali S. Nonconservative Stability of Viscoelastic Plates Subject to Triangularly Distributed Follower Loads. Journal of Theoretical and Applied Mechanics. 2017;55(3):1015–1027. https://doi.org/10.15632/jtampl.55.3.1015
18. Jafari N., Azhari M. Stability Analysis of Arbitrarily Shaped Moderately Thick Viscoelastic Plates Using Laplace– Carson Transformation and a Simple HP Cloud Method. Mechanics of Time-Dependent Materials. 2017;21(3):365–381. https://doi.org/10.1007/s11043-016-9334-8
19. Chepurnenko A.S., Yazyev B.M., Savchenko A.A. Calculation for the Circular Plate on Creep Considering Geometric Nnonlinearity. Procedia Engineering. 2016;150:1680–1685. https://doi.org/10.1016/j.proeng.2016.07.150
20. Chepurnenko A.S., Andreev V.I., Beskopylny A.N., Jazyev B.M. Determination of Rheological Parameters of Polyvinylchloride at Different Temperatures. MATEC Web of Conferences. 2016;67:06059. https://doi.org/10.1051/matecconf/20166706059
21. Андреев В.И., Языев Б.М., Чепурненко А.С. Осесимметричный изгиб круглой гибкой пластинки при ползучести. Вестник Московского государственного строительного университета. 2014;(5):16–24. URL: https://cyberleninka.ru/article/n/osesimmetrichnyy-izgib-krugloy-gibkoy-plastinki-pri-polzuchesti (дата обращения: 18.05.2023).
Об авторах
С. Б. ЯзыевRussian Federation
Сердар Батырович Языев, доктор технических наук, доцент, доцент кафедры строительной механики и теории сооружений
344003, г. Ростов-на-Дону, пл. Гагарина, 1
А. С. Чепурненко
Russian Federation
Антон Сергеевич Чепурненко, доктор технических наук, доцент, профессор кафедры строительной механики и теории сооружений
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Языев С.Б., Чепурненко А.С. Выпучивание прямоугольных пластин при нелинейной ползучести. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):257-268. https://doi.org/10.23947/2687-1653-2023-23-3-257-268
For citation:
Yazyev S.B., Chepurnenko A.S. Buckling of Rectangular Plates under Nonlinear Creep. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):257-268. https://doi.org/10.23947/2687-1653-2023-23-3-257-268
JATS XML














































