Перейти к:
Оптимизация геометрических характеристик циклоидальных профилей героторных гидромашин
https://doi.org/10.23947/2687-1653-2023-23-3-269-282
Аннотация
Введение. Производительность и надежность работы героторных гидромашин зависит от геометрических параметров профиля циклоидального зацепления. Существующие методики расчета и оптимизации параметров профиля громоздкие, многокритериальные, сложные для практического применения. Поэтому актуальной представляется проблема создания методики расчета параметров профиля рабочего органа героторной машины, пригодной для инженерных расчетов на этапе эскизного проектирования. В связи с этим целью данной работы являлась модернизация методики проектирования геометрии профилей торцевого сечения гипоциклоидальных зубчатых зацеплений, используемых в героторных гидравлических машинах, и анализ возможностей их оптимизации при предварительном проектировании. В ходе исследования была использована система компьютерной математики Mathcad, проведены численные эксперименты для изучения влияния геометрических параметров профилей на производительность и работоспособность героторной гидравлической машины. На основе полученных и проанализированных данных выработаны рекомендации по проектированию оптимальных профилей торцевого сечения героторных гидравлических машин.
Материалы и методы. Материалы включают в себя известные методики расчета параметров профиля, основанные на применении классических формул эквидистант гипоциклоид, используемых для очерчивания профилей зубьев рабочих органов героторных машин. Основной метод исследования — моделирование профиля героторной машины с помощью системы компьютерной математики Mathcad. Получены расчетные данные для выбранных диапазонов варьируемых параметров, обработанные методом регрессионного однофакторного анализа.
Результаты исследования. Разработан алгоритм анализа гладкости профилей зубьев. Определены два целевых параметра: площадь сечения торцевого профиля, влияющая на производительность, и наименьший приведенный радиус контакта, определяющий работоспособность рабочего органа. Предложена методика по расчету целевых параметров на ранней стадии проектирования. Получен ряд оптимальных значений параметров профиля по критериям производительности и работоспособности героторной машины. Построены зависимости, позволяющие установить оптимальные значения параметров профиля на стадии проектирования.
Обсуждение и заключение. Разработанная авторами методика дает возможность на этапе проектирования рабочего органа получить оценку производительности и работоспособности героторной гидромашины. Результаты исследований могут быть использованы в машиностроении при проектировании героторных гидромашин для улучшения их технико-эксплуатационных характеристик.
Ключевые слова
Для цитирования:
Киреев С.О., Лебедев А.Р., Корчагина М.В. Оптимизация геометрических характеристик циклоидальных профилей героторных гидромашин. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):269-282. https://doi.org/10.23947/2687-1653-2023-23-3-269-282
For citation:
Kireev S.O., Lebedev A.R., Korchagina M.V. Optimization of Geometric Characteristics of Cycloidal Profiles of Gerotor Hydraulic Machines. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):269-282. https://doi.org/10.23947/2687-1653-2023-23-3-269-282
Введение. Героторные гидравлические машины все чаще стали применяться в строительстве и при эксплуатации нефтяных и газовых скважин, причина — их конструктивно-эксплуатационные преимущества, основными из которых являются низкая неравномерность подачи для насосов или крутящего момента для двигателей, компактные габаритные размеры.
В научной литературе большое место занимают исследования, посвященные работе героторных гидромашин. Сильное влияние геометрических характеристик профиля ротора на производительность и надежность винтовых героторных гидромашин отмечают Д. и Ф. Балденко [1]. Основным узлом такой машины является многозаходный винтовой героторный механизм — цилиндрическая планетарная зубчатая передача внутреннего зацепления, состоящая из статора и ротора, с разницей в числах зубьев, равной единице. Профиль статора в торцовом сечении контактирует с профилем ротора, образуя замкнутые площадки. Авторы проанализировали также технологии изготовления зубчатых передач.
Р. Айер, В. Джатти исследовали эффективность применения математических моделей при конструировании винтовых насосов [2]. Они представили также результаты моделирования различных типоразмеров двухвинтовых насосов при перекачивании воды, смеси воды и воздуха. Суан-Фыонг Данг и Хонг-Сок Парк предложили процесс оптимизации CAD-модели с использованием результатов моделирования CAE и вычислений в Mathcad [3]. Другие авторы (А. Лебедев, С. Киреев, М. Корчагина, С. Власкин, А. Ефимов) в своих публикациях отметили эффективность проектирования разнообразных объектов и процессов на основе параметризации и последующей оптимизации конструкции по одному или нескольким целевым параметрам [4–6].
В совместной работе Ф.Д. Балденко и Яо Ян подчеркнули, что площадь живого сечения не зависит от относительного положения профилей ротора и статора и определяет производительность насоса, проанализировали влияние безразмерных геометрических параметров профиля на площадь живого сечения [7].
Лэй Чжэн, Сяодун Ву, Гоцин Хань, Хуачан Ли, Йи Цзо и Дэйк Чжоу разработали конечно-элементную модель рабочего органа винтового насоса с поверхностным приводом для нефтегазовой промышленности [8]. По результатам моделирования и экспериментальных проверок ими был сделан вывод, что зазоры в сопряжении и толщина статора являются двумя основными факторами, влияющими на оптимизируемый целевой параметр — объемную эффективность насоса.
Новые данные получены Х. Гамбоа, А. Оливет, С. Эспин при моделировании рабочего органа однозаходного винтового насоса [9]. Эти авторы определили существенную зависимость между площадью зазора проскальзывания и перепадом давления, связанным с механическими свойствами материала статора.
Яо Ян, Ф. Балденко исследовали влияние безразмерных коэффициентов торцового профиля героторной гидромашины на характеристики циклоидного зацепления, что позволяет проводить оптимизацию на основе геометрических и кинематических критериев [10]. И.А. Лягов, Ф.Д. Балденко, А.В. Лягов, В.У. Ямалиев, А.А. Лягова предложили методику выбора оптимальной конфигурации силовых секций при проектировании секционных забойных двигателей, отметив актуальность проблемы уменьшения габаритных параметров длины винтового насоса [11].
Ю.А. Коротаев, А.Н. Алпатов, А.В. Соболев и др. пришли к выводу, что наиболее эффективным является профилирование зацепления от исходного контура рейки, очерченного эквидистантой укороченной циклоиды [12]. В отношении профилей, полученных от эквидистанты обыкновенной гипоциклоиды, авторы указали на их основной недостаток: они строятся как специальные и не предусматривают натяг в зацеплении. Ю.А. Коротаев и Д.А. Голдобин обратили внимание на проблему, связанную с необходимостью повышения производительности винтовых насосов, и возникающие при этом недопустимые условия жесткости при производстве статоров и роторов [13].
А.Ф. Миникаев, В.А. Пронин, Д.В. Жигновская, Ю.Л. Кузнецов, Ф.Д. Балденко, А.Е. Ковалёнок разработали методику исследования напряженно-деформированного состояния статора при контактном взаимодействии с ротором винтового рабочего органа гидромашины с применением CAE-моделирования и утверждают, что классическая теория Герца о контактном взаимодействии не может быть применена для определения контактных напряжений в роторе и статоре из-за действия ряда особенностей: изменения кривизны соприкасающихся поверхностей ротора и статора, различной толщины эластичной обкладки по длине окружности корпуса, наличия предварительного натяга в паре, сложного планетарного движения ротора, сопровождающегося сочетанием трения качения и скольжения, смещения вектора радиальной силы относительно нормали в точке контакта.
Подводя итог обзору научных публикаций на тему проектирования героторной гидромашины, необходимо отметить, что большинство исследователей в данной области стремятся повысить эффективность работы этой машины, увеличивая площадь живого сечения и сокращая габаритные размеры рабочего органа. Достижение оптимальных результатов происходит за счет применения и варьирования коэффициентов внецентроидности, формы зуба, относительной скорости скольжения, смещения рейки и т. д. Методики расчета громоздкие, их сложно применять на практике. Торцевые профили строятся, как правило, на основе укороченных гипоциклоид, что приводит к возникновению проблемы с обеспечением кинематической точности движения, контактного взаимодействия ротора и статора. Некоторые авторы (Ю.А. Коротаев, А.Н. Алпатов, А.В. Соболев и др.) указали на невозможность создания натяга в случае применения обыкновенной гипоциклоиды, но натяг может быть создан за счет изменения эквидистантного расстояния профилей ротора и статора.
Материалы и методы. Для получения профилей ротора и статора в торцевом сечении рабочего органа героторной гидравлической машины зададимся следующим набором исходных параметров (рис. 1):
1) 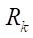 — контурный радиус профиля, определяющий диаметр окружности С1, описывающей профиль статора (мм). Фактически этот параметр задает радиальный габарит героторной машины, что особенно важно в нефтегазовой промышленности, когда проектируемый объект необходимо разместить, например, в стволе эксплуатационной колонны скважины;
— контурный радиус профиля, определяющий диаметр окружности С1, описывающей профиль статора (мм). Фактически этот параметр задает радиальный габарит героторной машины, что особенно важно в нефтегазовой промышленности, когда проектируемый объект необходимо разместить, например, в стволе эксплуатационной колонны скважины;
2) 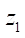 — число зубьев ротора;
— число зубьев ротора;
3) 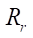 — радиус ролика, определяющий расстояние эквидистантной линии профилей ротора и статора относительно соответствующих гипоциклоид (мм);
— радиус ролика, определяющий расстояние эквидистантной линии профилей ротора и статора относительно соответствующих гипоциклоид (мм);
4) D — натяг в сопряжении ротора и статора (мм).
Напомним принцип образования профилей гипоциклоидального зацепления, который заключается в том, что внутри окружности 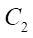 (основная окружность гипоциклоиды статора) перекатывается без скольжения окружность
(основная окружность гипоциклоиды статора) перекатывается без скольжения окружность 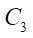 (основная окружность гипоциклоиды ротора). Центр окружности
(основная окружность гипоциклоиды ротора). Центр окружности 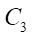 всегда находится на расстоянии e (эксцентриситет) относительно центра окружности
всегда находится на расстоянии e (эксцентриситет) относительно центра окружности 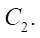
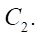
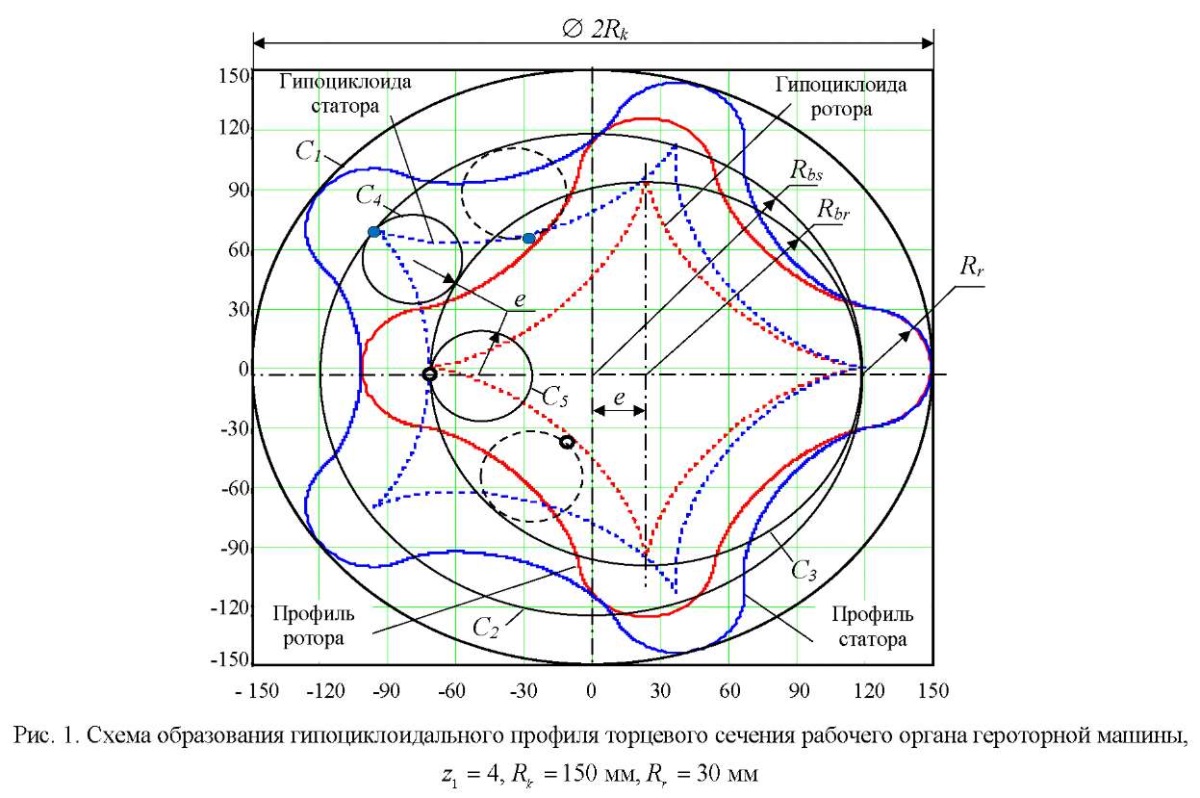
Внутри окружности 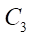 перекатывается без скольжения окружность
перекатывается без скольжения окружность 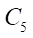 (производящая окружность гипоциклоиды ротора), одна точка которой образует гипоциклоиду ротора. Внутри окружности
(производящая окружность гипоциклоиды ротора), одна точка которой образует гипоциклоиду ротора. Внутри окружности 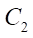 перекатывается без скольжения окружность
перекатывается без скольжения окружность 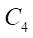 (производящая окружность гипоциклоиды статора), одна точка которой образует гипоциклоиду статора. Заметим, что радиусы окружностей
(производящая окружность гипоциклоиды статора), одна точка которой образует гипоциклоиду статора. Заметим, что радиусы окружностей 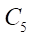 и
и 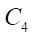 равны эксцентриситету е. Профили ротора и статора образуются как эквидистантные линии, отложенные на расстояние от соответствующих гипоциклоид.
равны эксцентриситету е. Профили ротора и статора образуются как эквидистантные линии, отложенные на расстояние от соответствующих гипоциклоид.
В такой постановке профили ротора и статора обеспечивают идеальный контакт при эксцентричном вращении ротора. При необходимости обеспечить натяг/зазор в соединении следует изменить эквидистантное расстояние для профиля ротора на величину D.
Перейдем к математическому описанию методики образования профилей торцевого сечения ротора и статора. Число зубьев статора равно
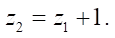 (1)
(1)
Радиус основной окружности гипоциклоиды статора 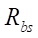 определим из условия (рис. 1):
определим из условия (рис. 1):
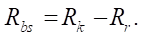 (2)
(2)
Определим эксцентриситет e передачи по условию равенства длины окружности 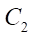 целому числу
целому числу 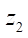 длин производящей окружности
длин производящей окружности 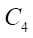 радиусом е:
радиусом е:
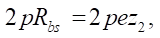
тогда
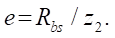 (3)
(3)
Заметим, что при 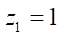 (механизм Муано) из условия размещения ротора в полости статора необходимо определять эксцентриситет и радиус ролика
(механизм Муано) из условия размещения ротора в полости статора необходимо определять эксцентриситет и радиус ролика 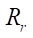 по другим формулам:
по другим формулам:
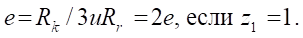 (4)
(4)
Радиус основной окружности гипоциклоиды ротора 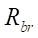 равен (рис. 1)
равен (рис. 1)
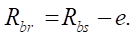 (5)
(5)
Введем функцию для определения радиуса основной окружности ротора или статора, выполняющую условия (2) и (5):
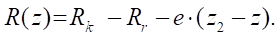 (6)
(6)
Параметрические формулы гипоциклоид ротора и статора в декартовой системе координат XOY:
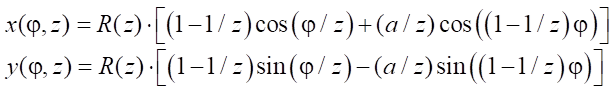 , (7)
, (7)
где z — число ветвей гипоциклоиды ротора
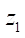 или статора
или статора 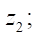 a — коэффициент укорочения гипоциклоиды. В случае обыкновенной гипоциклоиды в теории
a — коэффициент укорочения гипоциклоиды. В случае обыкновенной гипоциклоиды в теории 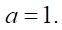 Однако в практических расчетах с применением систем компьютерной математики (Mathсad, MATHLAB) при
Однако в практических расчетах с применением систем компьютерной математики (Mathсad, MATHLAB) при 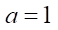 возникают сложности с вычислением эквидистантных профилей ротора и статора. Поэтому в модели мы допустили
возникают сложности с вычислением эквидистантных профилей ротора и статора. Поэтому в модели мы допустили 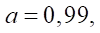 что для достижения наших целей вполне оправданно; j — угол поворота радиус-вектора, проведенного из начала координат до каждой точки гипоциклоиды. Если гипоциклоида должна быть построена по
что для достижения наших целей вполне оправданно; j — угол поворота радиус-вектора, проведенного из начала координат до каждой точки гипоциклоиды. Если гипоциклоида должна быть построена по 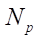 точкам, то
точкам, то
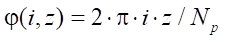 ,
, 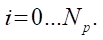 (8)
(8)
Профили ротора и статора определяются по известным формулам эквидистантной траектории относительно гипоциклоид ротора или статора на расстояние Rr c учетом натяга в сопряжении D
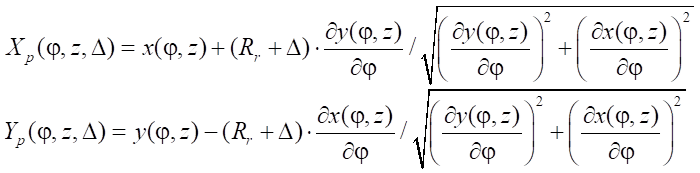 . (9)
. (9)
При работе передачи центр ротора движется по окружности радиусом e и поворачивается на угол α=0…2p. Все точки ротора при этом совершают дополнительный поворот на угол y, определяемый функцией
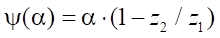 . (10)
. (10)
Модель вращения ротора описывается параметрическими функциями преобразования координат при перемещении и вращении объекта:
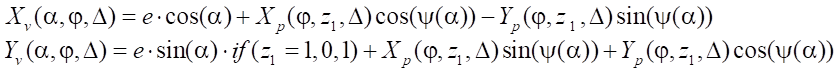 . (11)
. (11)
В выражении (11) применена условная функция, обнуляющая перемещение по оси Y в случае прямолинейного перемещения ротора в полости статора при 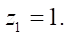
Опыт применения данной методики показал, что эквидистантные профили ротора и статора при увеличении эквидистантного расстояния или радиуса ролика 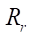 могут потерять гладкость. Это происходит в точках перехода от эквидистанты окружности в эквидистанту гипоциклоиды. На рис. 2 представлена проблема потери гладкости линии профиля статора в окрестности ±1 мм от точки перехода эквидистантных линий.
могут потерять гладкость. Это происходит в точках перехода от эквидистанты окружности в эквидистанту гипоциклоиды. На рис. 2 представлена проблема потери гладкости линии профиля статора в окрестности ±1 мм от точки перехода эквидистантных линий.
В математике известна формула критерия гладкости функции, заданной в параметрическом виде. Для профиля статора такая функция будет иметь вид:
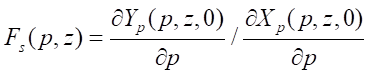 , (12)
, (12)
где 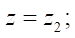 p — угол радиус-вектора точки профиля статора.
p — угол радиус-вектора точки профиля статора.
Необходимо отметить, что функция 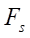 во всем диапазоне
во всем диапазоне 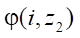 ведет себя нестабильно и найти какие-либо особенности ее поведения в интересующей нас точке перехода эквидистантных линий достаточно сложно. Поэтому поведение функции
ведет себя нестабильно и найти какие-либо особенности ее поведения в интересующей нас точке перехода эквидистантных линий достаточно сложно. Поэтому поведение функции 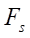 изучалось только в окрестности точки перехода при изменении углового параметра
изучалось только в окрестности точки перехода при изменении углового параметра
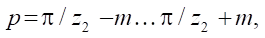 (13)
(13)
где m — угол отклонения от угла радиус-вектора точки перехода.
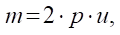 (14)
(14)
где u — часть углового сектора профиля статора для изучения гладкости в окрестности точки перехода. Величину u (для 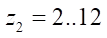 ) определяем по эмпирической формуле:
) определяем по эмпирической формуле:
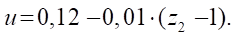 (15)
(15)
На рис. 2 можно заметить, что с увеличением радиуса ролика в окрестности точки перехода эквидистантных линий профиль статора из гладкого превращается в самопересекающийся. Поведение функции 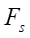 также изменяется, и при появлении эффекта самопересечения профиля возникает петля (рис. 2 в).
также изменяется, и при появлении эффекта самопересечения профиля возникает петля (рис. 2 в).
Этот эффект положен в основу предлагаемого авторами статьи алгоритма контроля гладкости профиля статора, приведенного на рис. 3. Следует отметить, что, судя по многочисленным замерам, если критерий гладкости статора выполняется, то гладкость профиля ротора проверять не требуется, так как он построен на гипоциклоиде с меньшим значением радиуса основной окружности.
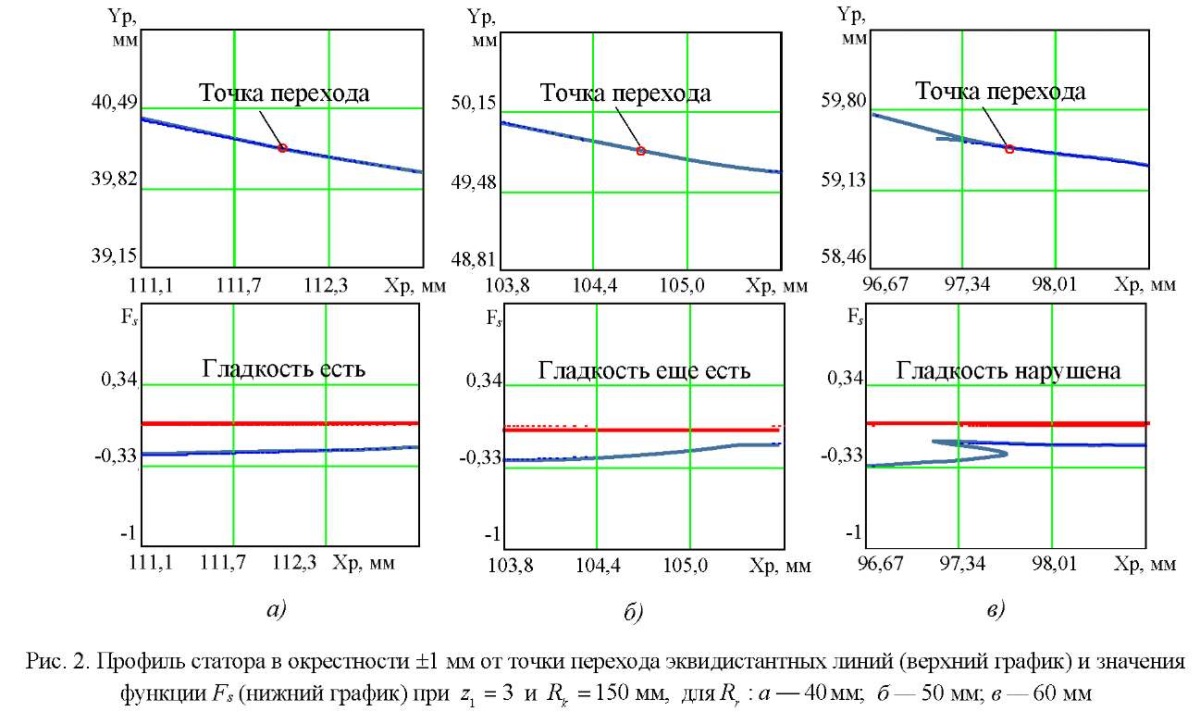
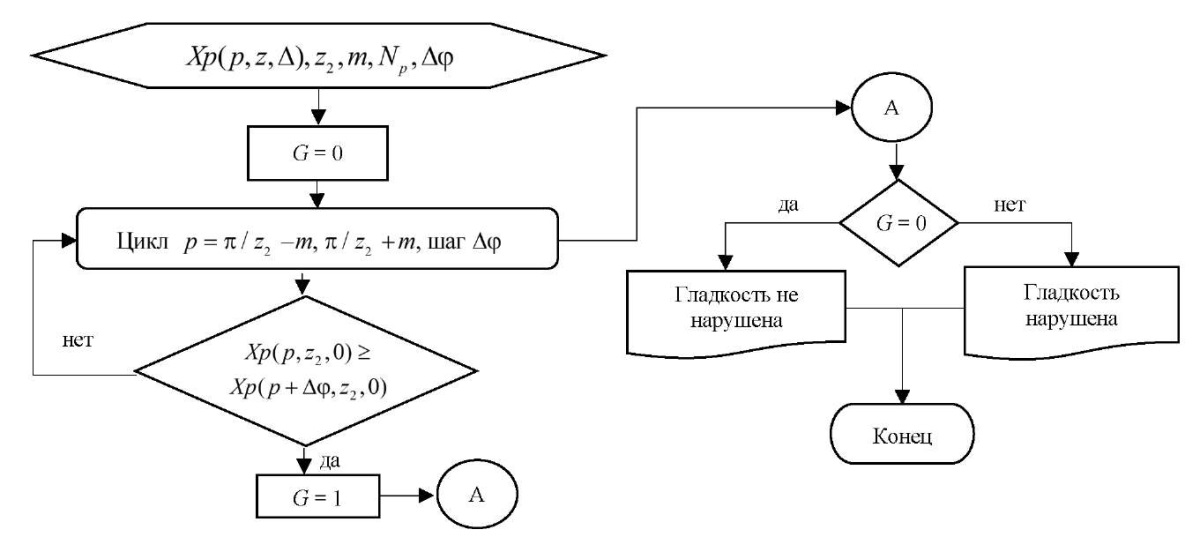
Рис. 3. Схема алгоритма контроля гладкости профиля статора
Контроль гладкости профиля статора должен проводиться всегда при проектировании геометрии торцевого сечения героторной машины. С целью изучения параметра максимального радиуса ролика 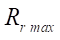 , ниже которого гладкость кривой не нарушается, авторы провели серию численных экспериментов, в которых задавались различными значениями контурного радиуса
, ниже которого гладкость кривой не нарушается, авторы провели серию численных экспериментов, в которых задавались различными значениями контурного радиуса 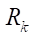 и числами зубьев ротора
и числами зубьев ротора 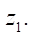
Первым целевым параметром данного исследования является площадь живого сечения рабочего органа S. Этот параметр входит в формулу подачи героторной машины и определяет ее производительность. С имеющимися параметрическими функциями, описывающими профили ротора и статора, задача по определению S сводится к вычислению разности площадей параметрических кривых статора 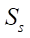 и ротора
и ротора 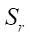 (9). Формула площади параметрической кривой известна из математики, и поэтому в методике авторов она выглядит так:
(9). Формула площади параметрической кривой известна из математики, и поэтому в методике авторов она выглядит так:
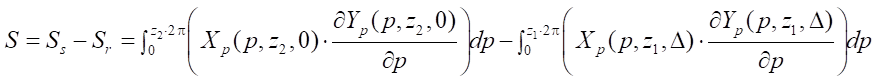 (16)
(16)
Вторым целевым параметром исследования является приведенный радиус 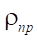 кривизны при контактном взаимодействии ротора и статора. Напомним, что согласно теории Герца, при контакте двух цилиндрических поверхностей рассчитывается приведенный радиус, который в формуле контактных напряжений находится в знаменателе. Следовательно, величина контактных напряжений наряду с физико-механическими параметрами материалов контактируемых поверхностей будет иметь наибольшую величину при наименьшем значении приведенного радиуса
кривизны при контактном взаимодействии ротора и статора. Напомним, что согласно теории Герца, при контакте двух цилиндрических поверхностей рассчитывается приведенный радиус, который в формуле контактных напряжений находится в знаменателе. Следовательно, величина контактных напряжений наряду с физико-механическими параметрами материалов контактируемых поверхностей будет иметь наибольшую величину при наименьшем значении приведенного радиуса 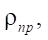 определяемого по формуле:
определяемого по формуле:
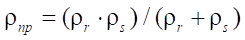 , (17)
, (17)
где 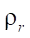 — радиус эквидистантной окружности ротора, равный параметру
— радиус эквидистантной окружности ротора, равный параметру 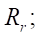
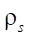 — радиус кривой профиля статора.
— радиус кривой профиля статора.
Заметим, если 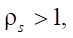 то числитель в формуле (17) всегда растет быстрее, чем знаменатель, следовательно, наименьшее значение
то числитель в формуле (17) всегда растет быстрее, чем знаменатель, следовательно, наименьшее значение 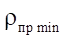 полностью определяется параметром наименьшего радиуса статора
полностью определяется параметром наименьшего радиуса статора 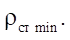
В торцевом сечении рабочего органа героторной машины при любом угле поворота ротора осуществляется непрерывный контакт его эквидистантной окружности со сложной кривой профиля статора. По результатам наблюдений за динамикой контактных взаимодействий можно сделать вывод, что наибольшие напряжения возникают в точках перехода эквидистанты гипоциклоиды в эквидистанту окружности профиля статора. Следовательно, наименьший радиус линии профиля статора 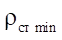 также будет находиться в зоне перехода эквидистантных линий и определится по известной из математики формуле:
также будет находиться в зоне перехода эквидистантных линий и определится по известной из математики формуле:
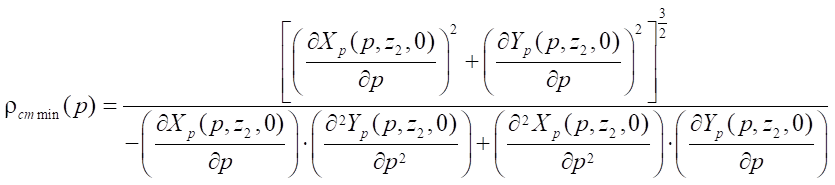 , (18)
, (18)
где 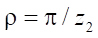 угловой параметр точки профиля статора в месте перехода эквидистантных линий. В случае потери гладкости линии статора параметр
угловой параметр точки профиля статора в месте перехода эквидистантных линий. В случае потери гладкости линии статора параметр 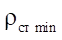 стремится к нулю.
стремится к нулю.
Описанная выше методика реализована в системе математических расчетов Mathcad. При выполнении расчетов коэффициент укорочения гипоциклоиды a=0,99,
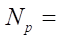 40 000.
40 000.
На первом этапе исследований планируется изучение максимального радиуса ролика 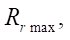 при котором критерий G гладкости линии профиля статора равен нулю. Изменяемые параметры — контурный радиус
при котором критерий G гладкости линии профиля статора равен нулю. Изменяемые параметры — контурный радиус 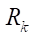 (100, 150, 200 мм) и число зубьев ротора
(100, 150, 200 мм) и число зубьев ротора 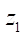 от 1 до 7). Расчеты проводятся при последовательном увеличении параметра
от 1 до 7). Расчеты проводятся при последовательном увеличении параметра 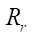 от 5 мм до срабатывания критерия гладкости G. Исследуемый параметр
от 5 мм до срабатывания критерия гладкости G. Исследуемый параметр 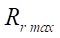 фиксируем с точностью до 1 мм.
фиксируем с точностью до 1 мм.
На втором этапе проводятся серии расчетов для изучения влияния радиуса ролика Rr (от 5 мм до 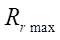 , числа зубьев ротора
, числа зубьев ротора 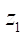 (от 2 до 7) и контурного радиуса
(от 2 до 7) и контурного радиуса 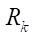 (100, 150, 200 мм) на площадь живого сечения S и минимальный приведенный радиус контакта
(100, 150, 200 мм) на площадь живого сечения S и минимальный приведенный радиус контакта 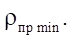
Описанная методика расчета геометрических параметров профиля торцевого сечения рабочего органа героторной машины может быть реализована в любой другой системе программирования или в системе компьютерной математики.
Результаты исследования. Данные численных опытов по определению параметра максимального радиуса ролика 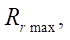 при котором гладкость линии профиля статора сохраняется, приведены в таблице 1.
при котором гладкость линии профиля статора сохраняется, приведены в таблице 1.
Таблица 1
Максимальный радиус ролика 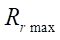 (мм)
(мм)
при различных контурных радиусах 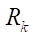 (мм)
(мм)
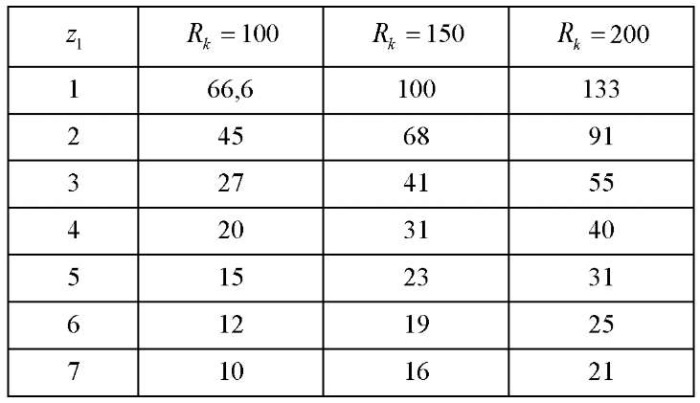
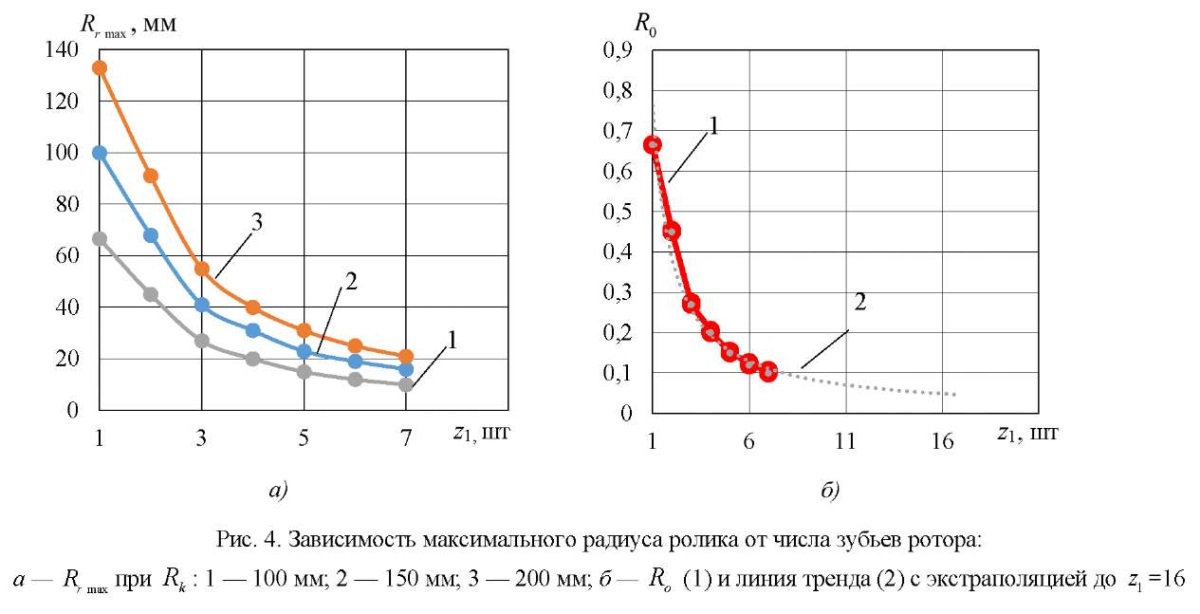
На основании данных таблицы 1 построены графики (рис. 4 а). Видно, что оцениваемый параметр 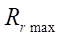 при увеличении контурного радиуса
при увеличении контурного радиуса 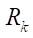 растет пропорционально. Введем в рассмотрение относительный параметр
растет пропорционально. Введем в рассмотрение относительный параметр 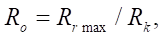 график которого представлен на рис. 4 б.
график которого представлен на рис. 4 б.
Эмпирическая формула, с помощью которой можно определить максимально допустимый радиус ролика 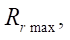 имеет вид:
имеет вид:
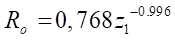 (19)
(19)
При 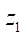 = 15,
= 15, 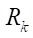 = 150 мм,
= 150 мм, 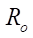 = 0,0517 мм,
= 0,0517 мм, 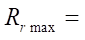 7,76 мм гладкость профиля достигается при Rr = 7,5 мм. При
7,76 мм гладкость профиля достигается при Rr = 7,5 мм. При 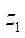 = 10,
= 10, 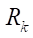 = 200 мм,
= 200 мм, 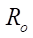 = 0,0775 мм,
= 0,0775 мм, 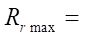 15,5 мм гладкость профиля достигается при Rr = 15,5 мм. Таким образом, можно сделать вывод об удовлетворительной точности эмпирической формулы (19) для предсказания максимально допустимого параметра Rr max.
15,5 мм гладкость профиля достигается при Rr = 15,5 мм. Таким образом, можно сделать вывод об удовлетворительной точности эмпирической формулы (19) для предсказания максимально допустимого параметра Rr max.
Следует отметить, что формула (19) получена при значениях коэффициента укорочения a = 0,99. Уменьшение а приводит к достижению гладкости профиля и при более значительном увеличении параметра 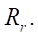 Однако при этом изменяется форма зуба циклоидального зацепления и нарушаются условия контактного взаимодействия ротора и статора, особенно в тех местах, где ротор должен касаться статора боковыми сторонами зубьев. Расчеты показывают, что при
Однако при этом изменяется форма зуба циклоидального зацепления и нарушаются условия контактного взаимодействия ротора и статора, особенно в тех местах, где ротор должен касаться статора боковыми сторонами зубьев. Расчеты показывают, что при 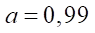 и
и 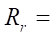 38 мм критерий гладкости находится на пределе выполнимости. Однако при
38 мм критерий гладкости находится на пределе выполнимости. Однако при 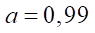 и
и 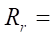 38 мм достигается хорошая гладкость профиля статора, но нарушается кинематический контакт деталей рабочего органа машины, восстановить который удается лишь специальным подбором значений параметров гипоциклоид ротора и статора. Поэтому исследование влияния коэффициента укорочения на параметр
38 мм достигается хорошая гладкость профиля статора, но нарушается кинематический контакт деталей рабочего органа машины, восстановить который удается лишь специальным подбором значений параметров гипоциклоид ротора и статора. Поэтому исследование влияния коэффициента укорочения на параметр 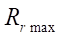 выведены за рамки данного исследования.
выведены за рамки данного исследования.
В таблице 2 представлены данные расчетов целевых параметров исследований для числа зубьев ротора 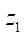 = 3 при различных значениях контурных радиусов. Полученные значения площади живого сечения S и минимального приведенного радиуса контакта
= 3 при различных значениях контурных радиусов. Полученные значения площади живого сечения S и минимального приведенного радиуса контакта 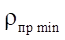 в последних двух колонках таблицы 2 приведены к безразмерному виду для удобства анализа.
в последних двух колонках таблицы 2 приведены к безразмерному виду для удобства анализа.
Таблица 2
Данные расчетов целевых параметров при z1=3
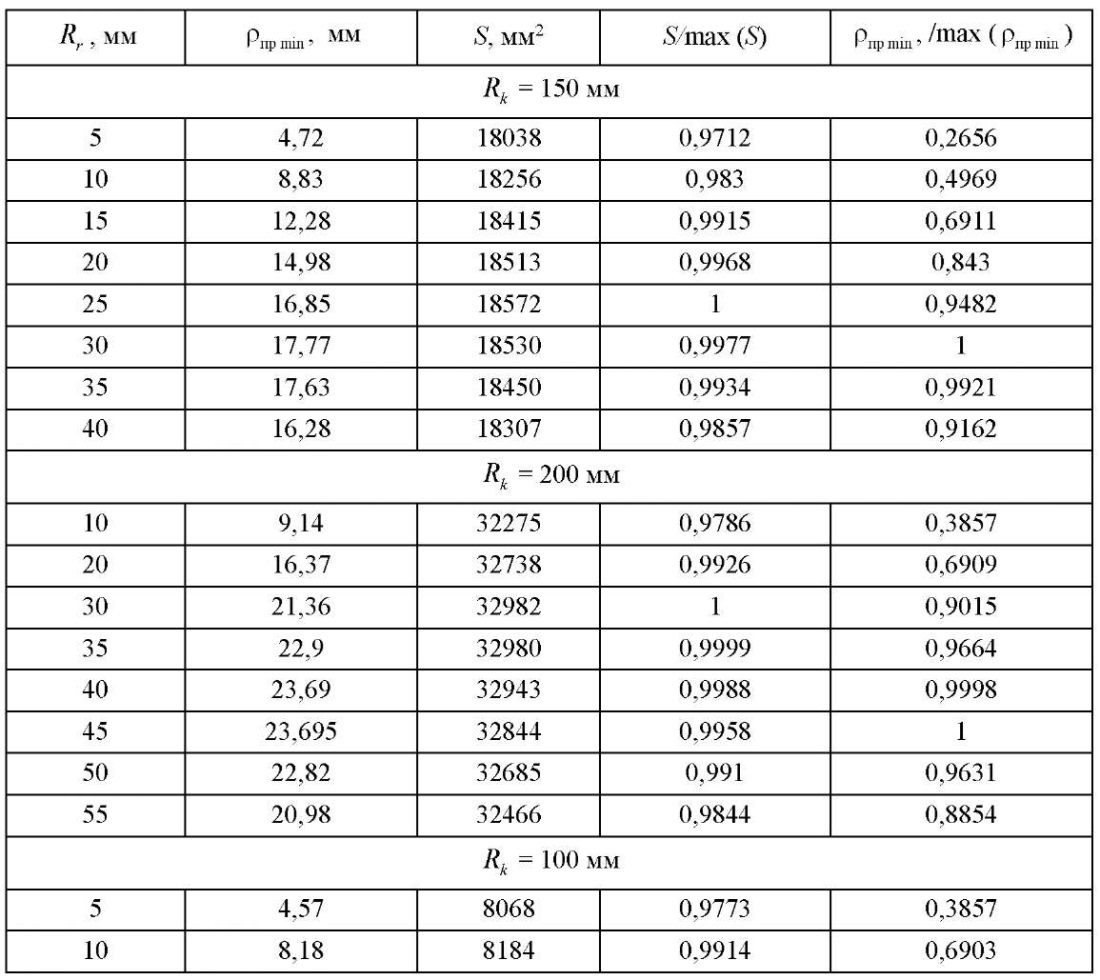
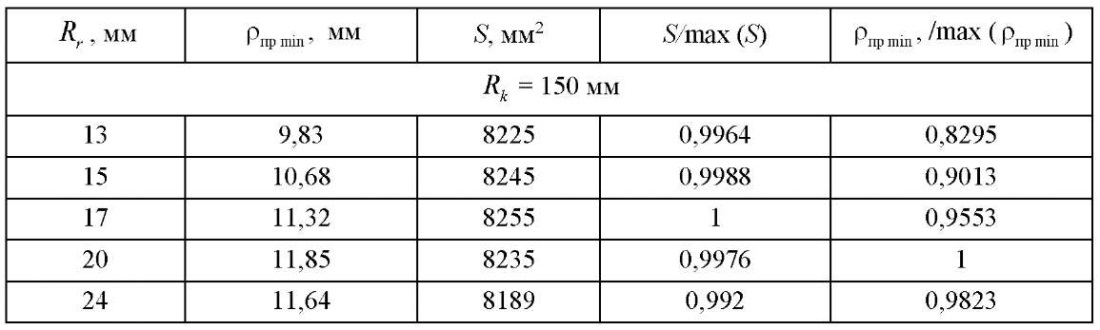
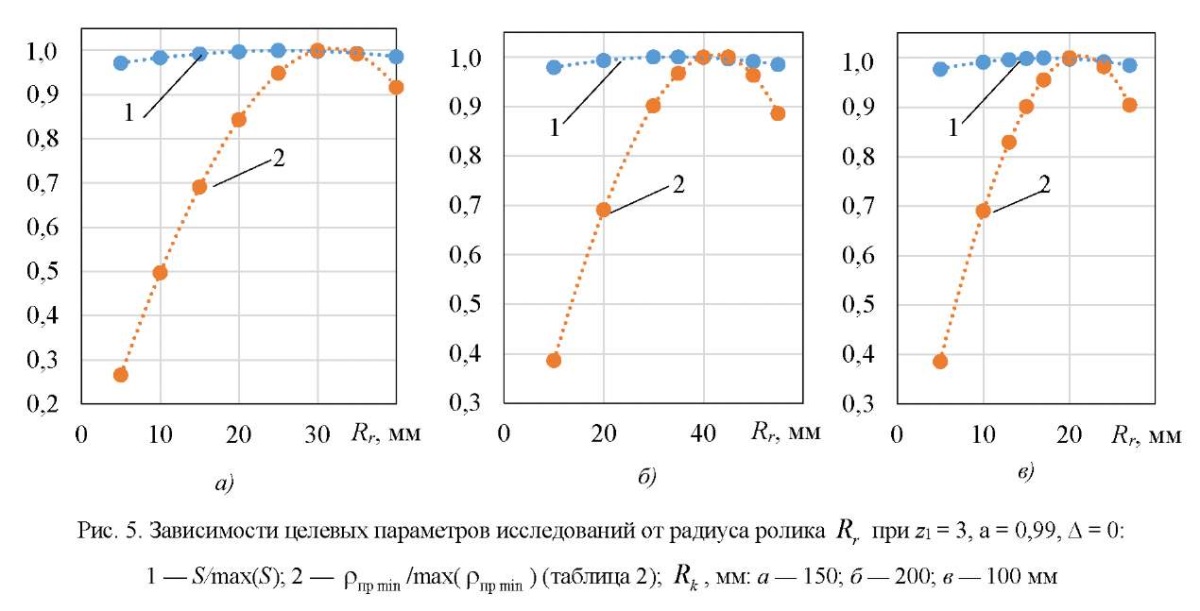
На рис. 5 представлены графики изменения целевых параметров исследований при 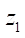 =3. На них нетрудно заметить, что при увеличении радиуса ролика
=3. На них нетрудно заметить, что при увеличении радиуса ролика 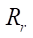 происходит незначительное изменение площади живого сечения S и достаточно сильное изменение приведенного радиуса контакта, максимальное значение которого приходится на достаточно узкий диапазон
происходит незначительное изменение площади живого сечения S и достаточно сильное изменение приведенного радиуса контакта, максимальное значение которого приходится на достаточно узкий диапазон 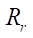 , что представляет для проектировщика наибольший интерес, так как при этом контактные напряжения будут минимальны. Расчеты для других значений
, что представляет для проектировщика наибольший интерес, так как при этом контактные напряжения будут минимальны. Расчеты для других значений 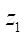 (от 2 до 7) показали примерно такую же качественную картину, как и на рис. 5.
(от 2 до 7) показали примерно такую же качественную картину, как и на рис. 5.
В таблице 3 представлены данные расчетов оптимальных радиусов роликов Rr opt для различных параметров 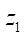 и
и 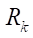 . В результате анализа выяснилось, что параметры Rr opt и
. В результате анализа выяснилось, что параметры Rr opt и 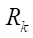 для одного
для одного 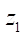 изменяются практически одинаково. Поэтому, если ввести параметр относительного оптимального радиуса ролика
изменяются практически одинаково. Поэтому, если ввести параметр относительного оптимального радиуса ролика
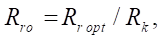 (20)
(20)
то с помощью однофакторной зависимости вида 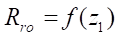 можно на предварительном этапе проектирования рабочего органа героторной машины определять оптимальный радиус ролика
можно на предварительном этапе проектирования рабочего органа героторной машины определять оптимальный радиус ролика 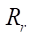 .
.
В результате аналогичных рассуждений для приведенных в таблице 3 параметров S и 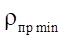 введены также безразмерные параметры относительного приведенного радиуса контакта
введены также безразмерные параметры относительного приведенного радиуса контакта 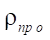 и относительной площади живого сечения
и относительной площади живого сечения 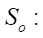
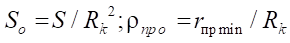 (21)
(21)
Новые относительные величины также представлены в таблице 3.
Таблица 3
Оптимальные радиусы 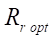
и относительные параметры зацепления
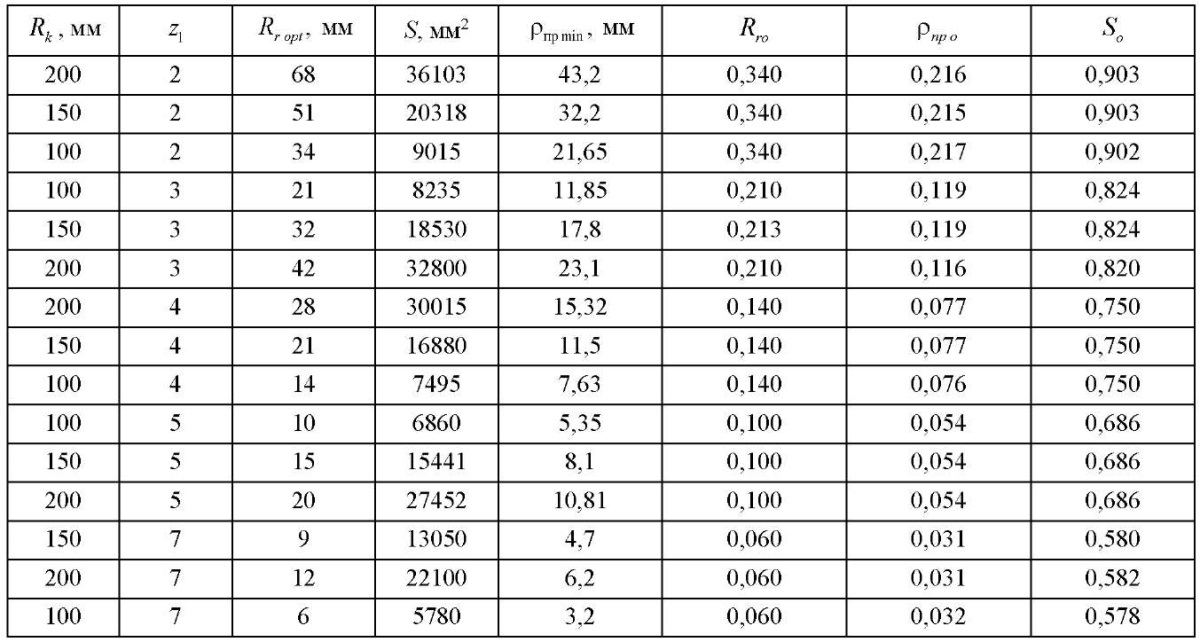
Следует отметить, что все вновь введенные относительные величины с высокой степенью достоверности подчиняются аппроксимирующим формулам, включающим один фактор — число зубьев ротора 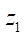 .
.
Формула относительного оптимального радиуса ролика 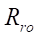 имеет вид:
имеет вид:
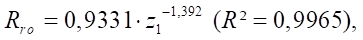 (22)
(22)
где 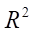 — величина достоверности аппроксимации.
— величина достоверности аппроксимации.
Формула относительного приведенного радиуса контакта 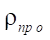 имеет вид:
имеет вид:
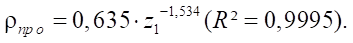 (23)
(23)
Формула относительной площади живого сечения So имеет вид:
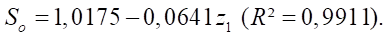 (24)
(24)
Рассмотрим пример применения полученных результатов при проектировании геометрии профиля торцевого сечения героторной машины. Зададимся следующим набором исходных данных: контурный радиус  120 мм, число зубьев ротора
120 мм, число зубьев ротора 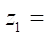 4, натяг в сопряжении D=0 мм (эмпирические формулы получены при нулевом натяге). Относительный оптимальный радиус ролика
4, натяг в сопряжении D=0 мм (эмпирические формулы получены при нулевом натяге). Относительный оптимальный радиус ролика 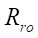 по формуле (22):
по формуле (22):
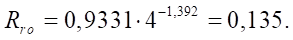
Абсолютное значение радиуса ролика 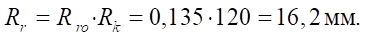
Относительный приведенный радиус контакта 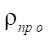 по формуле (23):
по формуле (23):
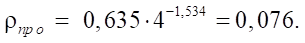
Абсолютное значение минимального приведенного радиуса контакта:
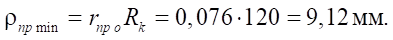
Относительная площадь живого сечения 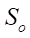 по формуле (24):
по формуле (24):
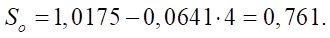
Абсолютное значение площади живого сечения:
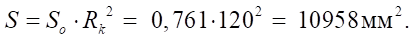
Расчеты по программе Mathcad дают следующие величины:
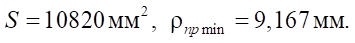
Как видно на этом примере, эмпирические формулы достаточно точно предсказывают основные параметры геометрии торцевого сечения героторной машины.
Обсуждение и заключение. Проведенное исследование направлено на решение задачи совершенствования рабочих органов героторных гидромашин и в достаточной степени соответствует работам отечественных и зарубежных авторов [10–15]. Основное отличие заключается в том, что при построении профилей ротора и статора использованы идеальные гипоциклоиды, обеспечивающие наибольшую кинематическую точность движения и контактного взаимодействия элементов зацепления. Известную проблему обеспечения натяга в сопряжении предлагается решить за счет разности параметров радиуса ролика, а для контроля гладкости профилей разработан специальный алгоритм [12]. Оптимальную геометрию профиля, как и в работе [10], предлагается определять на основе максимальной площади живого сечения рабочего органа героторной машины. Но при этом приведенный радиус контакта также должен иметь наибольшую величину, как залог наименьших контактных напряжений. В данном исследовании на основе большого числа расчетов по специально разработанной программе Mathcad в диапазоне чисел зубьев ротора 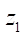 от 2 до 7 и контурного диаметра
от 2 до 7 и контурного диаметра 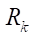 от 100 до 200 мм были определены оптимальные значения эквидистантного расстояния гипоциклоид, или радиусов роликов
от 100 до 200 мм были определены оптимальные значения эквидистантного расстояния гипоциклоид, или радиусов роликов 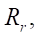 при которых достигается наилучшее сочетание приведенного радиуса контакта и площади живого сечения рабочего органа героторной машины. Выяснилось, что введение относительных величин радиуса ролика, площади живого сечения и приведенного радиуса контакта позволяет с помощью простых эмпирических зависимостей на раннем этапе проектирования получить абсолютные значения этих же величин для любого контурного радиуса в пределах установленных диапазонов.
при которых достигается наилучшее сочетание приведенного радиуса контакта и площади живого сечения рабочего органа героторной машины. Выяснилось, что введение относительных величин радиуса ролика, площади живого сечения и приведенного радиуса контакта позволяет с помощью простых эмпирических зависимостей на раннем этапе проектирования получить абсолютные значения этих же величин для любого контурного радиуса в пределах установленных диапазонов.
Разработанная методика дает возможность на этапе проектирования профилей ротора и статора оценить производительность и работоспособность героторной машины. В перспективе подобные изыскания могут быть проведены для эпициклоидных и смешанных зацеплений в героторных гидромашинах.
Результаты исследований могут быть использованы в машиностроении при проектировании героторных гидравлических машин для улучшения их технико-эксплуатационных характеристик.
Список литературы
1. Baldenko D.F., Baldenko F.D. Single-Screw Hydraulic Machines in the Oil and Gas Industry: Fields of Application and Development Prospects. Petroleum & Petrochemical Engineering Journal. 2019;3(5):000207. https://doi.org/10.23880/ppej-16000207
2. Ramakrishnan Balaji Iyer, Jatti V.K., Yeshpal Yadav, Anurag Verma, Jaimin Desai, Dewan C.P. Design Optimization of CAD Model Materials Today Proceedings 2017;4(8):7357−7364. https://doi.org/10.1016/j.matpr.2017.07.065
3. Hong-Seok Park, Xuan-Phuong Dang. Structural Optimization Based on CAD–CAE Integration and Metamodeling Techniques. Computer-Aided Design. 2010;42(10):889–902. https://doi.org/10.1016/j.cad.2010.06.003
4. Lebedev A., Kireev S., Korchagina M., Lubinec V. Improvement of Design of Device for Production of Cycloidal Pinion Gear. In book: M. Shamtsyan, M. Pasetti, A. Beskopylny (eds). Robotics, Machinery and Engineering Technology for Precision Agriculture. Smart Innovation, Systems and Technologies. Vol. 247. P. 223−236. Singapore: Springer; 2022. https://link.springer.com/chapter/10.1007/978-981-16-3844-2_24
5. Korchagina M., Lebedev A., Kireev S., Vlaskin S. Model of Hole Mandrel Process in Tubular Workpieces. In book: A. Guda (ed) Networked Control Systems for Connected and Automated Vehicles. Vol. 509. P. 1541−1550. Cham: Springer; 2022 . https://doi.org/10.1007/978-3-031-11058-0_156
6. Lebedev A., Kireev S., Korchagina M., Efimov A. Optimization of Structure Parameters of Semi-Trailer-Tank for Hydraulic Fracturing of Formation. In book: A. Guda (ed) Networked Control Systems for Connected and Automated Vehicles. Vol. 510. Cham: Springer; 2023. https://doi.org/10.1007/978-3-031-11051-1_178
7. Балденко Ф.Д., Яо Ян. Исследование площади камер рабочих органов одновинтовых гидравлических машин. Бурение и нефть. 2020;(6):24–29. https://burneft.ru/archive/issues/2020-06/24
8. Jie Chen, He Liu, Fengshan Wang, Guocheng Shi, Gang Cao, Hengan Wu. Numerical Prediction on Volumetric Efficiency of Progressive Cavity Pump with Fluid-Solid Interaction Model. Journal of Petroleum Science and Engineering. 2013;109:12–17. https://doi.org/10.1016/j.petrol.2013.08.019
9. Gamboa J., Olivet A., Espin S. New Approach for Modeling Progressive Cavity Pumps Performance. Journal of Petroleum Technology. 2003;56(5):51–53. https://doi.org/10.2118/84137-MS
10. Yang Yao, Baldenko F. Optimization of Cycloidal Gearing Geometric Parameters of Positive Displacement Motors. Equipment and Technologies for Oil and Gas Complex. 2021;(6):22−26. https://doi.org/10.33285/1999-6934-2021-6(126)-22-26
11. Lyagov I., Baldenko F., Lyagov A., Yamaliev V., Lyagova A. Methodology for Calculating Technical Efficiency of Power Sections in Small-Sized Screw Downhole Motors for the “Perfobur” System. Journal of Mining Institute. 2019;240:694−700. https://doi.org/10.31897/pmi.2019.6.694
12. Коротаев Ю.А., Алпатов А.Н., Соболев А.В., Мялицин Н.Ю. Исследование систематических погрешностей зацепления героторного механизма, спрофилированного от исходного контура рейки. Известия Тульского государственного университета. Технические науки. 2017;8(1):112–120.
13. Коротаев Ю.А., Голдобин Д.А. Особенности проектирования и расчета многозаходных винтовых героторных механизмов мультифазных насосов. Известия Тульского государственного университета. Технические науки. 2016;8(2):175–182.
14. Minikaev A.F., Pronin V.A., Zhignovskaya D.V., Kuznetsov Yu.L. The Use of Computer Modelling for the Development of the Working Bodies’ Profiles for Screw Single-Rotor Compressor. Journal of International Academy of Refrigeration. 2018;(1):61−66. https://doi.org/10.17586/1606-4313-2018-17-1-61-66
15. Балденко Ф.Д., Ковалёнок А.Е. Компьютерное моделирование контактного взаимодействия рабочих органов одновинтовых гидравлических машин. Территория Нефтегаз. 2014;10:18–27.
Об авторах
С. О. КиреевРоссия
Сергей Олегович Киреев, доктор технических наук, профессор, заведующий кафедрой машин и оборудования нефтегазового комплекса
344003, г. Ростов-на-Дону, пл. Гагарина, 1
А. Р. Лебедев
Россия
Алексей Романович Лебедев, кандидат технических наук, доцент, кафедры машин и оборудования нефтегазового комплекса
344003, г. Ростов-на-Дону, пл. Гагарина, 1
М. В. Корчагина
Россия
Марина Валерьевна Корчагина, кандидат технических наук, доцент, кафедры машин и оборудования нефтегазового комплекса
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Киреев С.О., Лебедев А.Р., Корчагина М.В. Оптимизация геометрических характеристик циклоидальных профилей героторных гидромашин. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):269-282. https://doi.org/10.23947/2687-1653-2023-23-3-269-282
For citation:
Kireev S.O., Lebedev A.R., Korchagina M.V. Optimization of Geometric Characteristics of Cycloidal Profiles of Gerotor Hydraulic Machines. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):269-282. https://doi.org/10.23947/2687-1653-2023-23-3-269-282













































