Scroll to:
3D Human Motion Capture Method Based on Computer Vision
https://doi.org/10.23947/2687-1653-2023-23-3-317-328
Abstract
Introduction. The analysis of approaches to tracking the human body identified problems when capturing movements in a three-dimensional coordinate system. The prospects of motion capture systems based on computer vision are noted. In existing studies on markerless motion capture systems, positioning is considered only in two-dimensional space. Therefore, the research objective is to increase the accuracy of determining the coordinates of the human body in three-dimensional coordinates through developing a motion capture method based on computer vision and triangulation algorithms.
Materials and Methods. A method of motion capture was presented, including calibration of several cameras and formalization of procedures for detecting a person in a frame using a convolutional neural network. Based on the skeletal points obtained from the neural network, a three-dimensional reconstruction of the human body model was carried out using various triangulation algorithms.
Results. Experimental studies have been carried out comparing four triangulation algorithms: direct linear transfer, linear least squares method, L2 triangulation, and polynomial methods. The optimal triangulation algorithm (polynomial) was determined, providing an error of no more than 2.5 pixels or 1.67 centimeters.
Discussion and Conclusion. The shortcomings of existing motion capture systems were revealed. The proposed method was aimed at improving the accuracy of motion capture in three-dimensional coordinates using computer vision. The results obtained were integrated into the human body positioning software in three-dimensional coordinates for use in virtual simulators, motion capture systems and remote monitoring.
For citations:
Obukhov A.D., Dedov D.L., Surkova E.O., Korobova I.L. 3D Human Motion Capture Method Based on Computer Vision. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):317-328. https://doi.org/10.23947/2687-1653-2023-23-3-317-328
Introduction. Significant progress has currently been made in the domain of computer vision. Technologies have been developed to solve the problems of detecting objects, determining their state, geometric evaluation of the space depicted on the frame, and a lot more. As a result, computer vision has become widespread in various spheres of human activity, ranging from healthcare and education to entertainment. A rather promising direction is the use of computer vision technologies for three-dimensional reconstruction and positioning of various objects, including people. There is fairly large number of systems for determining the absolute position of a person in space, which can be divided into the following categories.
- Systems using inertial sensors and providing the determination of the amount of their movement, as well as the change of angles between them, which involves the use of gyroscopes and accelerometers [1]. A well-known representative of this category is the Noitom Mocap Perception Neuron [2], which includes up to 32 inertial sensors.
- Laser position tracking systems based on the use of base stations installed on opposite sides of the room and emitting infrared rays, which provide accurate determination of the position and orientation of sensors in space. An example of such systems is a virtual reality kit from HTC [3], which have an error of up to 0.1 mm.
- Systems using magnetic sensors [4] based on the use of a magnetic field to capture human movement, which assume the presence of wearable sensors on the user's body. This category includes Polhemus Liberty — a portable electromagnetic motion tracking system, considered one of the fastest (sampling rate — 240 Hz).
- Marker-based optical systems determine the position of objects by markers using a set of cameras. An example is Vicon, which has a fairly low error: the average absolute errors of marker tracking are 0.15 mm in static tests, and
2 mm (with corresponding angular errors of 0.3°) in dynamic tests [5]. - Marker-free optical systems based on the use of computer vision and machine learning. Examples of such technologies are Open space, MediaPipe, Movenext. With their help, human movements can be tracked with an accuracy of up to 30 mm [6].
After analyzing the listed categories of motion capture systems, it can be concluded that most of the solutions used to recognize human actions and movements involve various wearable devices, such as sensors or gloves. Most of these devices are bulky due to the large number of sensors and the need for a wired connection. Some systems have high accuracy, but they cannot be used due to the size or the presence of electromagnetic interference [7]. Inertial systems have a number of problems associated with the accumulation of errors, which limits their use only to relative positioning in space.
Therefore, optical systems for recognizing and tracking user actions are well regarded. To get information about the actions and position of the user, frames obtained from the camera are used. Among optical systems, it is worth noting those that use markers (the user may be wearing special clothes or certain labels fixed on him), which makes it difficult to use them under real conditions. They are more applicable to specially prepared premises (e.g., film studios).
Systems that do not use any markers allow users to interact more freely with the environment and are more suitable for use under real conditions. The significant disadvantages of systems in this line include relatively low accuracy, unreliability, and low performance. To a great extent, this may be due to the shortcomings of computer vision algorithms used to recognize a person in the frame, as well as the following reasons: the variability of a person’s appearance and lighting conditions, partial occlusions owing to the layering of objects in the scene, the complexity of the human skeletal structure.
As a rule, the operation of marker-free motion capture systems is based on an algorithm for evaluating a person's posture. Approaches to solving the problem of assessing a person's posture can be divided into top-bottom and bottom-up. In top-bottom approaches, first there is a detection of people in the frame, then an assessment of the pose of each person found. Algorithms that relate to the bottom-up approach, at the first stage, search for body parts in the frame, then group them into poses. As a rule, convolutional neural networks are used for this task, such as YOLO (You Look Only Once) [8], SSD (Single Shot Detection) [9], R–CNN (Region CNN) [10], and others. They provide the recognition of numerous different objects, including a person or individual body parts with high accuracy. However, one of the disadvantages of the solutions listed above is their low performance and slow operation. To solve this problem, there are special frameworks (MoveNet [11], MediaPipe [12], OpenPose [13]) that also use neural networks optimized for real-time operation.
It should be noted that the above algorithms, technologies and approaches of marker-free motion capture systems provide positioning in two-dimensional space, which makes it difficult both to determine the distance to objects and their sizes, and to track complex movements when, e.g., the user's hands are hidden by his body. Existing solutions in the field of stereo cameras can be effective, but they are not very accurate when the object is significantly removed from the camera, which happens when tracking the entire human body. In addition, they do not solve the problem of occlusions. Thus, the major line of research is the development of a method of motion capture using multiple cameras and computer vision technologies. When implementing multi-camera motion capture systems, the problem of combining objects from several images inevitably arises, i.e., the need to perform triangulation. Among the triangulation methods, linear and iterative linear algorithms can be distinguished.
Linear triangulation is the most common approach to performing reconstruction of objects in three-dimensional space, including such methods as linear-proprietary method, linear least squares method, direct linear transformation, which differ in varying degrees of resistance to noise [14].
Iterative linear methods are a more robust version of linear triangulation. Conventional linear methods may be less accurate when solving problems of triangulation of a set of points, since in this case, the minimized error has no geometric meaning (it does not take into account the shape of the skeleton and the rules for connecting points). The key idea of iterative linear methods is to adaptively change the weights of linear equations in such a way that the weighted equations correspond to errors. Iterative linear methods include L2 and L∞ triangulation [15].
Thus, within the framework of this study, the following task was set: to develop a method for capturing human movements that provides positioning the user's body in three-dimensional coordinates with minimal error and using computer vision technologies. The proposed method can be used as a replacement for existing motion capture systems, or as part of other algorithms, e.g., for the subsequent classification of a person's condition. This work was aimed at increasing the accuracy of determining the poses and coordinates of the human body in three-dimensional coordinates by developing motion capture methods based on computer vision. To achieve this goal, it was required to formalize the main stages of the process of capturing points of the human body from several cameras, integrate triangulation algorithms, choosing among them the optimal one from the point of view of accuracy, carry out the software implementation of the proposed method.
Materials and Methods. Solving the problem of 3D positioning of a person in space includes the following main stages:
- preliminary calibration of a set of cameras;
- implementation of human detection procedures in the frame, and calculation of skeletal points;
- calculation of 3D reconstruction of the human body model.
Let us look at them in more detail.
The calibration process involves the camera system taking several pictures of a calibration template, on which it is easy to identify key points with known relative positions in space. After that, internal and external parameters are calculated for each camera. Internal parameters are constant for a particular camera, external parameters depend on the location of the cameras relative to each other [16]. Therefore, this step must be performed before the first use of the camera system in a given location.
To calculate the coordinates of a point in three-dimensional space, it is necessary to know the coordinates of its projection on the images and the projective matrices of the cameras [17]. Projective matrix 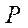 of some camera can be represented as a combination of matrices
of some camera can be represented as a combination of matrices 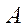 (containing the internal parameters of the camera) and
(containing the internal parameters of the camera) and 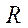 (rotation), as well as the displacement vector
(rotation), as well as the displacement vector 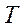 , which describe the change of coordinates from the world coordinate system to the coordinate system relative to the camera:
, which describe the change of coordinates from the world coordinate system to the coordinate system relative to the camera:
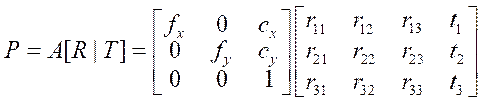 , (1)
, (1)
where
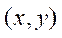 — coordinates of the projection of a 3D point on the image in pixels;
— coordinates of the projection of a 3D point on the image in pixels;
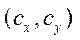 — coordinates of the central point of the camera;
— coordinates of the central point of the camera;
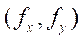 — focal length in pixels.
— focal length in pixels.
At the second stage, it is required to obtain directly the key (skeletal) points of the human body on each of their cameras. To extract skeletal body points from the frame, it is possible to use various machine learning technologies, e.g., MoveNet, MediaPipe, OpenPose, and others [18]. As part of this study, it is proposed to use a highly efficient and productive Pose module from the MediaPipe library. MediaPipe Pose uses machine learning to accurately track a person's body posture, determine 3D landmarks, and mask background segmentation on the entire body from RGB video frames. This approach makes it possible to track up to 33 points and provides real-time operation on most modern devices.
Thus, as part of the second stage, a set of 33 points is formed for each 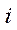 -th camera:
-th camera:
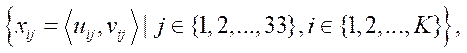 (2)
(2)
where
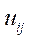 — coordinate of
— coordinate of 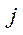 – th point on X axis in
– th point on X axis in 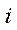 -th image;
-th image;
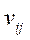 — coordinate of
— coordinate of 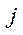 -th point on Y axis in
-th point on Y axis in 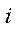 -th image;
-th image;
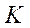 — total number of cameras and images.
— total number of cameras and images.
At the third stage, the positions of key skeletal points in three-dimensional space are calculated. To obtain data on the position of human skeletal points in space, triangulation is performed — finding the coordinates of a 3D point by the coordinates of its projections. Triangulation is one of the most important challenges in computer vision, its solution is a crucial stage in 3D reconstruction, it affects the accuracy of the entire result [19].
Epipolar geometry is fundamental for the three-dimensional reconstruction of the object points based on the position values of the projections of the points in the images from all cameras. Its main idea is that 3D points in the scene are projected onto lines in the image plane of each camera — epipolar lines. These lines correspond to the intersection of the image plane and the plane passing through the camera centers and the 3D point. This idea provides a condition for finding pairs of corresponding points on two images: if it is known that point 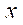 on the plane of the first image corresponds to point
on the plane of the first image corresponds to point 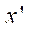 on the plane of another image, then its projection should lie on the corresponding epipolar line. According to this condition, the following relation will be valid for all corresponding pairs of points
on the plane of another image, then its projection should lie on the corresponding epipolar line. According to this condition, the following relation will be valid for all corresponding pairs of points 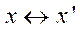 :
:
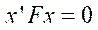 , (3)
, (3)
where 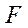 — fundamental matrix having size
— fundamental matrix having size 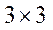 and rank equal to 2.
and rank equal to 2.
For some point 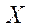 , given in three-dimensional space, the following projection formula expressed in homogeneous coordinates is valid:
, given in three-dimensional space, the following projection formula expressed in homogeneous coordinates is valid:
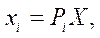 (4)
(4)
where
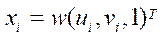 — homogeneous coordinates of some point on the plane of the
— homogeneous coordinates of some point on the plane of the 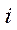 -th image (obtained from the
-th image (obtained from the 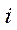 -th camera during the second stage), including the position on image
-th camera during the second stage), including the position on image 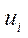 (on X axis) and
(on X axis) and 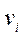 (on Y axis);
(on Y axis);
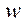 — scale factor;
— scale factor;
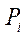 — projection matrix of
— projection matrix of 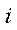 -th camera obtained at the first stage.
-th camera obtained at the first stage.
To simplify calculations, the projection matrix of the camera is often presented in the following form:
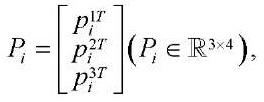 (5)
(5)
where 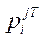 —
— 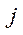 -th row of matrix
-th row of matrix 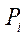 .
.
Therefore, equation (4) can be represented as follows:
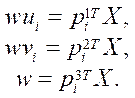 (6)
(6)
Since — scale factor, we obtain the following system of equations:
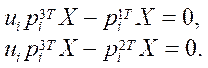 (7)
(7)
Since 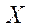 is a homogeneous representation of coordinates in three-dimensional space, then, for their calculation, it is necessary to obtain
is a homogeneous representation of coordinates in three-dimensional space, then, for their calculation, it is necessary to obtain 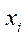 and
and 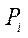 for at least two cameras. To solve the system of equations (7), 4 algorithms were considered [14]:
for at least two cameras. To solve the system of equations (7), 4 algorithms were considered [14]:
- direct linear transfer (DLT);
- linear least squares method;
- L2 triangulation;
- optimal (polynomial) method.
DLT refers to a linear triangulation algorithm, whose main advantage is the simplicity of its implementation. Specifically, in the OpenCV computer vision library there is a ready-made implementation of this algorithm in the triangulatePoints method.
The linear least squares method also refers to linear ones and consists in the fact that the system of homogeneous equations (7) is reduced to a system consisting of inhomogeneous equations, for whose solution, the least squares method is used.
L2 triangulation is an iterative method of three-dimensional reconstruction, whose solution is reduced to minimizing the reprojection error:
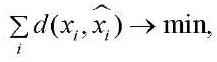 (8)
(8)
where
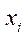 — coordinate of the projection of the estimated point in the image;
— coordinate of the projection of the estimated point in the image;
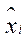 — projection coordinate calculated from formula (4) for an already determined spatial point;
— projection coordinate calculated from formula (4) for an already determined spatial point;
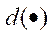 — distance between two points.
— distance between two points.
The algorithm of optimal (polynomial) triangulation refers to non-iterative approaches. To solve it, a sextic polynomial is required. The minimization criterion for performing three-dimensional reconstruction in this method can be defined as follows:
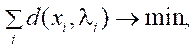 (9)
(9)
where 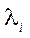 — epipolar line corresponding to point
— epipolar line corresponding to point 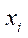 .
.
When using a two-camera system, to minimize error (9), the following sequence of actions must be performed:
- parametrize the bundle of epipolar lines in the first image using parameter
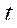 . Thus, the epipolar line in the first image can be expressed as
. Thus, the epipolar line in the first image can be expressed as 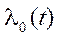 ;
; - using fundamental matrix
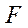 , calculate the corresponding epipolar line
, calculate the corresponding epipolar line 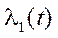 in the second image;
in the second image; - express the distance function (9) as a function of
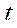 ;
; - perform a search for value
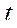 , at which (9) tends to a minimum.
, at which (9) tends to a minimum.
Using the methods of elementary calculus, it is possible to reduce the solution of the minimization problem to finding the roots of a sextic polynomial. The calculation of the assumed spatial point is performed using the direct linear transfer method (DLT) [17].
Summing up the third stage, we get that after successfully solving system (7) and obtaining the world coordinates of the key points of the target object (human body), the following set of points 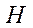 is formed:
is formed:
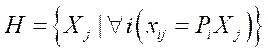 , (10)
, (10)
where 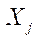 — world coordinates of the skeletal point of the human body obtained after solving the triangulation problem, expressed in centimeters.
— world coordinates of the skeletal point of the human body obtained after solving the triangulation problem, expressed in centimeters.
Thus, in this study, the optimization problem, when using two cameras, is reduced to finding triangulation method 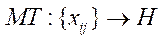 , in which the reprojection error tends to a minimum:
, in which the reprojection error tends to a minimum:
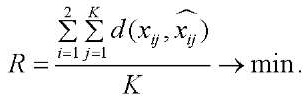 (11)
(11)
Research Results. Optimization problem (11) is solved through performing triangulation of 2D object points obtained from images of several cameras, in the framework of this study — from two cameras using various algorithms listed in the previous section.
The listed triangulation methods were implemented using OpenCV and NumPy libraries. For comparison, the algorithms were integrated into software implementing the method of three-dimensional motion capture. An example of the method for reconstructing the entire human skeleton is shown in Figure 1.
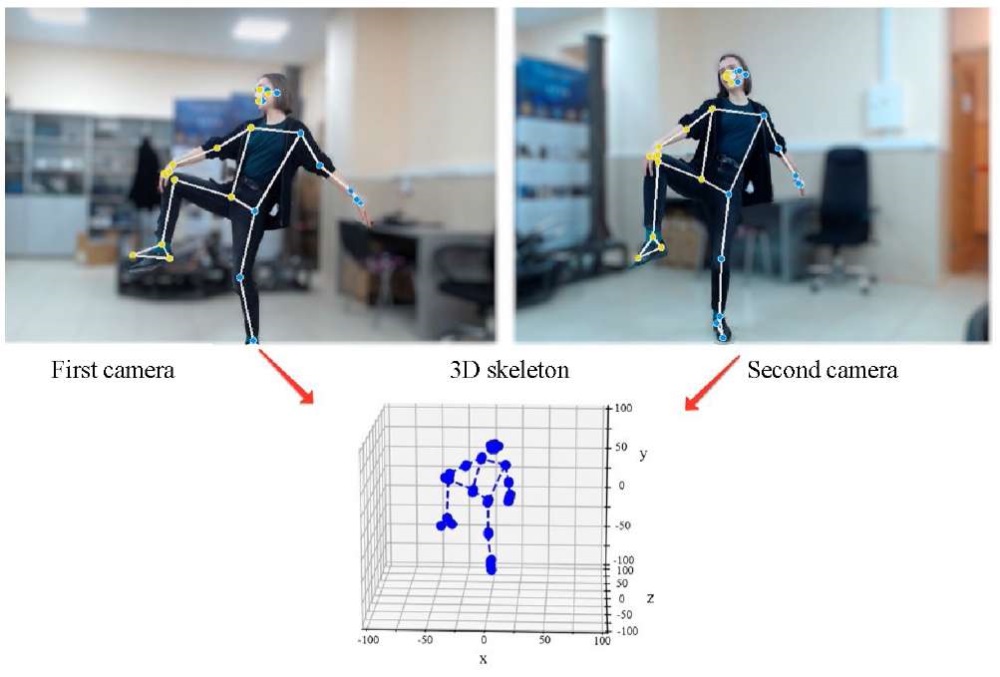
Fig. 1. Example of the method, including recognition of a person
on two cameras and construction of a 3D skeleton
Then, these algorithms were compared by the value of the reprojection error function (11) for all points of the skeleton from two images. The comparison of the selected triangulation methods by the error rate, as well as by the time of obtaining a solution (computational complexity) for the entire set of skeleton points was carried out. Summary comparative diagrams are shown in Figure 2.
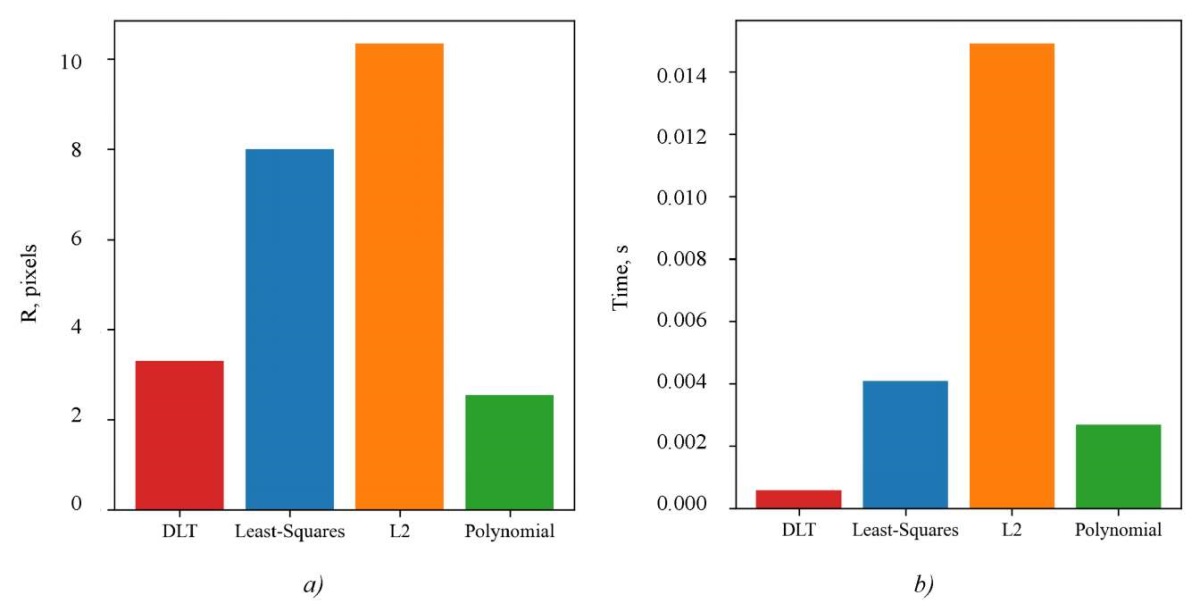
Fig. 2. Comparison of triangulation methods by metrics:
a — by reprojection error;
b — by calculation time
A number of experimental tests were also carried out for the selected triangulation methods. Under testing, the calculated lengths of the user's limbs and the absolute deviation of the obtained values from the real ones were measured for each approach. The comparison is presented in Table 1.
Table 1
Comparison of the accuracy of determining the size of limbs in the process of triangulation
|
Body segment |
DLT |
Least Squares |
L2 |
Polynomial |
Real value |
|
Forearm |
25.2 ± 1.6 |
30.8 ± 0.2 |
26.6 ± 0.5 |
24.3 ± 0.4 |
26 |
|
Shin |
42.2 ± 2.0 |
65.3 ± 1.1 |
44.6 ± 0.7 |
38.7 ± 1.8 |
41 |
|
Hip |
45.7 ± 2.7 |
59.5 ± 0.49 |
48.7 ± 1.3 |
44.1 ± 0.6 |
45 |
|
Average deviation |
2.43 |
14.58 |
2.26 |
1.67 |
0 |
|
Presented are the average values (in centimeters) after a sample of 10 measurements ± standard deviation in the sample |
|||||
The developed software includes the following modules:
- for working with input devices (cameras);
- to perform calibration and obtain basic camera parameters;
- to synchronize multiple cameras;
- for object recognition (user's body and arms);
- to analyze the location of the found skeletal points;
- to build real-time visualization.
When implementing the software, the Python programming language, OpenCV and Matplotlib libraries were used. The operation of the system was carried out in several streams: one was responsible for receiving data from cameras, the second — for visualization, the third — for sending the received world coordinates of the human body to external systems or modules. Using a unified protocol with a data package in JSON format provides integrating the software into third-party systems (e.g., Unity game development environments, Unreal Engine, etc.) [20][21].
Discussion and Conclusion. Let us analyze the results of comparing triangulation algorithms by selected metrics, shown in Figure 2 and in Table 1.
During the comparison, it was found that the optimal algorithm for three-dimensional reconstruction was the polynomial method. The error value was about 2.55 pixels. In real tests, when determining a person's height, the error was no more than 3 %, taking into account the fact that MediaPipe Pose did not fix the upper point of the head and it was calculated approximately based on the position of the eyes. When measuring limbs, the error ranged from 0.9 cm to 2.3 cm, the average was 1.67 (Table 1). Thus, real tests validate the correctness of the choice of the polynomial method.
Next, we compared the results obtained with existing studies, e.g., described in [22]. The authors also used trained networks (OpenPose) to implement a marker-free human recognition system, a camera calibration procedure, and the extraction of skeletal points, but placed cameras next to each other to simulate stereo vision. This key difference made it possible to recognize human postures within the framework of this study, when some parts of the body overlapped others. In addition, using MediaPipe Pose provided tracking 33 skeletal points, not 18, as in the OpenPose-based method. The obtained error values generally corresponded to existing studies (the best result in [22] was 2 cm), which allowed us to conclude that the proposed approach can be used in practice. Other marker-free systems, e.g., based on Kinect [23], also showed comparable results in terms of measurement error (2–5 cm). Thus, the resulting solution generally corresponded to the accuracy of existing developments.
A comparison of the calculation time of a set of points, shown in Figure 2 on the right, demonstrated that the DLT algorithm provided the highest performance. However, all algorithms showed acceptable results (to provide a speed of 30 and even 60 frames per second). Therefore, this metric was not determinative.
The developed software can be used in various subject areas primarily as a replacement for motion capture systems based on inertial sensors. The advantages of the proposed solution are low economic costs for implementation and accessibility (transition from highly specialized motion capture suits to common camera-based tools), the possibility of parallel capture of body models of several users [24].
The scientific novelty of the research consists in a comprehensive approach to formalizing the process of three-dimensional positioning of a person using computer vision technologies. It includes preliminary calibration of a set of several cameras, formalization of procedures for detecting a person in a frame using an arbitrary neural network to obtain skeletal points, as well as calculation of three-dimensional reconstruction of a human body model using various triangulation algorithms. The study presents all the necessary calculation formulas and detailed steps to achieve the goal — to increase the accuracy of determining the poses and coordinates of the human body in three-dimensional coordinates using computer vision technologies. The theoretical results obtained are quite universal and can be used for the practical implementation of motion capture systems based on various models of neural networks, and not just MediaPipe Pose.
References
1. Lind CM, Abtahi F, Forsman M. Wearable Motion Capture Devices for the Prevention of Work-Related Musculoskeletal Disorders in Ergonomics – An Overview of Current Applications, Challenges, and Future Opportunities. Sensors. 2023;23(9):4259. https://doi.org/10.3390/s23094259
2. Sers R, Forrester S, Moss E, Ward S, Ma J, Zecca M. Validity of the Perception Neuron Inertial Motion Capture System for Upper Body Motion Analysis Measurement. 2020;149:107024. http://dx.doi.org/10.1016/j.measurement.2019.107024
3. Bauer P, Lienhart W, Jost S. Accuracy Investigation of the Pose Determination of a VR System. Sensors. 2021;21(5):1622. http://dx.doi.org/10.3390/s21051622
4. Irshad MT, Nisar MA, Gouverneur P, Rapp M, Grzegorzek M. AI Approaches towards Prechtl’s Assessment of General Movements: A Systematic Literature Review. Sensors. 2020;20(18):5321. http://dx.doi.org/10.3390/s20185321
5. Merriaux P, Dupuis Y, Boutteau R, Vasseur P, Savatier X. A Study of Vicon System Positioning Performance. Sensors. 2017;17(7):1591. https://doi.org/10.3390/s17071591
6. Nakano N, Sakura T, Ueda K, Omura L, Kimura A, Iino Y, et al. Evaluation of 3D Markerless Motion Capture Accuracy Using OpenPose with Multiple Video Cameras. Frontiers in Sports and Active Living. 2020;2:50. https://doi.org/10.3389/fspor.2020.00050
7. Coronado E, Fukuda K, Ramirez-Alpizar IG, Yamanobe N, Venture G, Harada K. Assembly Action Understanding from Fine-Grained Hand Motions, a Multi-camera and Deep Learning Approach. In: Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). New York, NY: IEEE; 2021. P. 2628−2634. http://dx.doi.org/10.1109/IROS51168.2021.9636715
8. Tausif Diwan, Anirudh G, Tembhurne JV. Object Detection Using YOLO: Challenges, Architectural Successors, Datasets and Applications. Multimedia Tools and Applications. 2023;82(6):9243–9275. https://doi.org/10.1007/s11042-022-13644-y
9. Wei Liu, Anguelov D, Erhan D, Szegedy C, Reed S, Cheng-Yang Fu, et al. SSD: Single Shot MultiBox Detector. In book: Leibe B, Matas J, Sebe N, Welling M. (eds). Computer Vision – ECCV 2016. Cham: Springer. 2016;9905:21–37. https://doi.org/10.1007/978-3-319-46448-0_2
10. Bharati P, Pramanik A. Deep Learning Techniques—R-CNN to Mask R-CNN: A Survey. In book: Das A., Nayak J., Naik B., Pati S., Pelusi D. (eds). Computational Intelligence in Pattern Recognition. New York, NY: Springer. 2020;999:657–668. http://dx.doi.org/10.1007/978-981-13-9042-5_56
11. Bajpai R, Joshi D. MoveNet: A Deep Neural Network for Joint Profile Prediction across Variable Walking Speeds and Slopes. IEEE Transactions on Instrumentation and Measurement. 2021;70:1–11. http://dx.doi.org/10.1109/TIM.2021.3073720
12. Ghanbari S, Ashtyani ZP, Masouleh MT. User Identification Based on Hand Geometrical Biometrics Using Media-Pipe. In: Proc. 30th International Conference on Electrical Engineering (ICEE). New York, NY: IEEE; 2022. P. 373−378. http://dx.doi.org/10.1109/ICEE55646.2022.9827056
13. Weijian Mai, Fengjie Wu, Ziqian Guo, Yuhan Xiang, Gensheng Liu, Xiaobin Chen. A Fall Detection Alert System Based on Lightweight Openpose and Spatial-Temporal Graph Convolution Network. Journal of Physics: Conference Series. 2021;2035:012036. http://dx.doi.org/10.1088/1742-6596/2035/1/012036
14. Szeliski R. Recognition. In book: Computer Vision: Algorithms and Applications. London: Springer; 2011. P. 575–640. https://doi.org/10.1007/978-1-84882-935-0_14
15. Kahl F, Hartley R. Multiple-View Geometry Under the L∞-Norm. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2008;30(9):1603–1617. http://dx.doi.org/10.1109/TPAMI.2007.70824
16. Luhmann T, Fraser C, Maas H-G. Sensor Modelling and Camera Calibration for Close-Range Photogrammetry. ISPRS Journal of Photogrammetry and Remote Sensing. 2016;115:37−46. https://doi.org/10.1016/j.isprsjprs.2015.10.006
17. Kudinov IA, Pavlov OV, Holopov IS. Implementation of an Algorithm for Determining the Spatial Coordinates and the Angular Orientation of an Object Based on Reference Marks Using Information from a Single Camera. Computer Optics. 2015;39(3):413–419. https://doi.org/10.18287/0134-2452-2015-39-3-413-419
18. Jen-Li Chung, Lee-Yeng Ong, Meng-Chew Leow. Comparative Analysis of Skeleton-Based Human Pose Estimation. Future Internet. 2022;14(12):380. https://doi.org/10.3390/fi14120380
19. Jia Chen, Dongli Wu, Peng Song, Fuqin Deng, Ying He Y, Shiyan Pang. Multi-View Triangulation: Systematic Comparison and an Improved Method. IEEE Access. 2020;8:21017−21027. http://dx.doi.org/10.1109/ACCESS.2020.2969082
20. Obukhov A, Dedov D, Volkov A, Teselkin D. Modeling of Nonlinear Dynamic Processes of Human Movement in Virtual Reality Based on Digital Shadows. Computation. 2023;11(5):85. https://doi.org/10.3390/computation11050085
21. Abella J, Demircan E. A Multi-Body Simulation Framework for Live Motion Tracking and Analysis within the Unity Environment. In: Proc. 16th International Conference on Ubiquitous Robots (UR). New York, NY: IEEE; 2019. P. 654−659. http://dx.doi.org/10.1109/URAI.2019.8768659
22. Zago M, Luzzago M, Marangoni T, De Cecco M, Tarabini M, Galli M. 3D Tracking of Human Motion Using Visual Skeletonization and Stereoscopic Vision. Frontiers in Bioengineering and Biotechnology. 2020;8:181. https://doi.org/10.3389/fbioe.2020.00181
23. Latorre J, Llorens R, Colomer C, Alcañiz M. Reliability and Comparison of Kinect-Based Methods for Estimating Spatiotemporal Gait Parameters of Healthy and Post-Stroke Individuals. Journal of Biomechanics. 2018;72:268–273. https://doi.org/10.1016/j.jbiomech.2018.03.008
24. Obuhov AD, Volkov AA, Vekhteva NA, Patutin KI, Nazarova AO, Dedov DL. The Method of Forming a Digital Shadow of the Human Movement Process Based on the Combination of Motion Capture Systems. Informatics and Automation. 2023;22(1):168–189. https://doi.org/10.15622/ia.22.1.7
About the Authors
A. D. ObukhovRussian Federation
Artem D. Obukhov, Dr.Sci. (Eng.), Associate Professor of the Department of Automated Systems for Decision-Making Support
1, Leningradskaya St., Tambov, 392036
D. L. Dedov
Russian Federation
Denis L. Dedov, Cand.Sci. (Eng.), Senior Researche
116, Sovetskaya St., Tambov, 392000
E. O. Surkova
Russian Federation
Ekaterina O. Surkova, 4th year student of the Department of Automated Systems for Decision-Making Support
1, Leningradskaya St., Tambov, 392036
I. L. Korobova
Russian Federation
Irina L. Korobova, Cand.Sci. (Eng.), Head of the Department of Automated Systems for Decision-Making Support
1, Leningradskaya St., Tambov, 392036
Review
For citations:
Obukhov A.D., Dedov D.L., Surkova E.O., Korobova I.L. 3D Human Motion Capture Method Based on Computer Vision. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):317-328. https://doi.org/10.23947/2687-1653-2023-23-3-317-328
JATS XML














































