Scroll to:
Optimal 2D Placement of Virtual Objects in Physical Space for Augmented Reality Applications
https://doi.org/10.23947/2687-1653-2023-23-4-410-421
EDN: QPFEMG
Abstract
Introduction. Research and applied works on the placement of virtual objects in real space most often focus on issues of interactivity, integration of reality and virtuality, physical properties of virtual elements. However, the task of simultaneously free and optimal placement of objects, taking into account their size and the surrounding comfort zone, has not been sufficiently worked out. In the literature, you can find a description of a similar task — about packing in a rectangular container. In our case, the goal is not limited to the greatest possible dense placement. Two conditions should be taken into account: rigid dimensions of the objects (it is forbidden to violate them) and additional areas — comfort zones (it is undesirable to occupy them). The work aims at creating and implementing such a 2D algorithm for placing objects in physical space, which takes into account the above limitations.
Materials and Methods. Using a set of numerical methods, the authors applied the previously created 1D algorithm for the placement of objects. Calculations were based on a system of linear equations. In the one-dimensional case, the optimal placement of virtual objects was reduced to a task that did not depend on the type of comfort function. The elements of such a system were the dimensions of objects, the distances between them, as well as the distances to the edge of the embedding area, a comfort zone. The proposed 2D algorithm for optimal placement of virtual objects was implemented in the form of a program code in C# using the well-known Unity game engine. The solution was tested on gadgets in peak load mode for 5, 10, 15, 20, 25, 35, 40, 45, and 50 objects. 1.8 thousand devices were used for experiments. About 77 thousand events were analyzed. To exclude unrepresentative values, each calculation was repeated 10 times, and a z-score was performed for each value. Abnormal events (more than 3 and less than -3) were excluded.
Results. In this paper, a 2D placement algorithm that implements filling a rectangular area with virtual objects has been created. Each of the objects had a size and another characteristic — a comfort zone. The authors compiled a flowchart for the implementation of this algorithm in a given two-dimensional left-hand coordinate system. It was shown, in particular, at what stage objects were sorted by length, when their batches were formed, and arrangements were made along two axes. The first axis was horizontal, the second was directed forward from the user (this is the depth vector, or frontal measurement). The 1D-placement algorithm for the generated row provided optimal positioning the objects along X-axis based on the calculated comfort coefficient К. Calculations were made and schemes were drawn up to obtain certain comfort indicators. For each object of the first string, the displacement along Z-axis from the edge of the plane was determined so that the comfort in front was equal to the comfort along X. Starting from the 2nd row, to calculate the displacement, the presence of potential neighbors who were a row higher and had common areas along X with the object being processed, was checked. Each element of the string was set along Z-axis so that its comfort from above was the maximum of the one-sided horizontal comfort in this and the previous strings. The principle of calculating Z coordinate for a string object was presented in the form of a flowchart. The initial data for the implementation of this algorithm were 7 objects with 14 different sizes and 28 comfort zones. After the software implementation, the operation of the described 2D algorithm was tested in practice — in an augmented reality mobile application. Analytical data of user sessions was recorded. The average execution time was calculated. The hypothesis of quadratic dependence that arose during the work was tested on a personal computer. For this purpose, a similar experiment was conducted for a range of [10-10,000] objects. The hypothesis was confirmed. The algorithm can be assigned a complexity of O(n2). To compare the calculation speed, 10 of the most popular models of user devices were utilized. The results were presented in the form of a diagram. The minimum registered execution time was 0.093 ms, the maximum — 0.146 ms. Calculations showed high efficiency of the two-dimensional algorithm. Additionally, the placement schemes for different numbers and parameters of objects were visualized.
Discussion and Conclusion. The proposed algorithm of two-dimensional placement enables the user to work with a set of virtual objects with different sizes and comfort zones. Sufficiently high performance and stability are shown. On average, the algorithm is implemented in fractions of a millisecond, even with large batches of objects. Possible future focus areas:
– expansion of the approach for building 3D models and algorithms;
– inclusion of objects in the rotation algorithm for greater flexibility of their location and better use of space.
The research results can be of interest to engineers and interface designers. In the future, it is required to study the user experience and the possibilities of including additional restrictions on positioning.
Keywords
For citations:
Alpatova M.V., Rudyak Yu.V. Optimal 2D Placement of Virtual Objects in Physical Space for Augmented Reality Applications. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):410-421. https://doi.org/10.23947/2687-1653-2023-23-4-410-421. EDN: QPFEMG
Introduction. A well-known task of augmented reality (AR) applications is the placement of virtual objects in real physical space. A number of studies [1–3] focus on interactivity, the merging of real and virtual spheres. The issues of physical properties of virtual objects are also studied.
The task of such placement of objects, which would be free and optimal at the same time, taking into account not only the geometry of objects, but also comfort zones around them, has not been sufficiently worked out. In [6], the external similarity of this problem and the well-known problem of packing into a rectangular container is noted [5]. However, there is a significant difference. In the case under study, it is not enough to provide the greatest possible dense packaging. When placing virtual objects, it is required to take into account not only their rigid dimensions, which cannot be violated, but also additional areas — comfort zones. It is undesirable to occupy them. These additional areas provide getting closer to the object and performing some actions with it.
Materials and Methods. Earlier [4], the authors defined what a comfortable placement of virtual objects was, and introduced the concept of comfort function k(x). It increases monotonically from 0 to 1 at 0≤x≤1 and is equal to 1 at х>1, where x = X/D, X — distance from the edge of the object to the nearest obstacle, D — size of the comfort zone. For each measurement, the object has two one–way comfort zones D– and D+. Comfort on each side is calculated separately.
It is shown in [6] that the problem of one-dimensional placement of n virtual objects in a free region of space with length L is reduced to a system of linear equations that do not depend on the type of comfort function k(x):
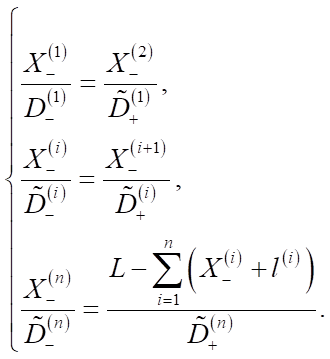
Here,
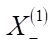 — distance of the first object from the left edge of the embedding area;
— distance of the first object from the left edge of the embedding area;
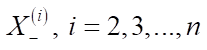 — distance between objects with numbers i and (i – 1);
— distance between objects with numbers i and (i – 1);
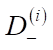 and
and 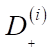 — left and right comfort zones, respectively;
— left and right comfort zones, respectively;
l(i) — object size;
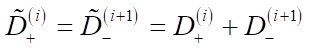 ,
,
i = 1,2,…, (n – 1).
Matrix of system (1) is strongly sparse; therefore, it is possible to avoid using not the fastest universal methods, it is easy enough to find a solution. As an example, in the first (n – 1) equalities, it is possible in each i-th equation, to express 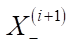 by
by 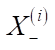 , then, substitute this into the last equation and get a linear equation with respect to
, then, substitute this into the last equation and get a linear equation with respect to 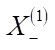 .
.
After that, values 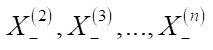 are sequentially determined from the first equation to the (n – 1)-th. The authors implemented this 1D algorithm for placing objects using numerical methods. It showed high speed and efficiency. This 1D algorithm became the basis for the scientific research described in the presented paper. The authors proposed a 2D algorithm for optimal placement of virtual objects It was implemented in the form of C# programming code using the Unity game engine, which is widely utilized to create augmented reality mobile applications [8]. During the experiment, an algorithm was run on the user's device operating in peak load mode to 5, 10, 15, 20, 25, 35, 40, 45, and 50 objects. The time spent on calculations was measured (in milliseconds). Each calculation was repeated 10 times to avoid abnormal values. In total, 1.8 thousand devices participated in the experiment, about 77 thousand events with the results were collected from them and analyzed.
are sequentially determined from the first equation to the (n – 1)-th. The authors implemented this 1D algorithm for placing objects using numerical methods. It showed high speed and efficiency. This 1D algorithm became the basis for the scientific research described in the presented paper. The authors proposed a 2D algorithm for optimal placement of virtual objects It was implemented in the form of C# programming code using the Unity game engine, which is widely utilized to create augmented reality mobile applications [8]. During the experiment, an algorithm was run on the user's device operating in peak load mode to 5, 10, 15, 20, 25, 35, 40, 45, and 50 objects. The time spent on calculations was measured (in milliseconds). Each calculation was repeated 10 times to avoid abnormal values. In total, 1.8 thousand devices participated in the experiment, about 77 thousand events with the results were collected from them and analyzed.
Filtering anomalies using z-score allowed the authors to identify values that can be defined as outliers [9]. The data was standardized, and a z-score was calculated for each value. Those with a z-score greater than 3 or less than –3 were considered abnormal. They were excluded and focused on typical and representative data.
Research Results. Thus, on X, Z plane there is a rectangular area with width 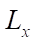 and length
and length 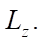 It should be filled with a certain number of virtual objects. Each object, in addition to its size
It should be filled with a certain number of virtual objects. Each object, in addition to its size 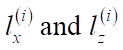 (where i — number of the object), is also characterized by comfort zones
(where i — number of the object), is also characterized by comfort zones 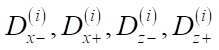 . Figure 1 shows a block diagram of the described algorithm.
. Figure 1 shows a block diagram of the described algorithm.
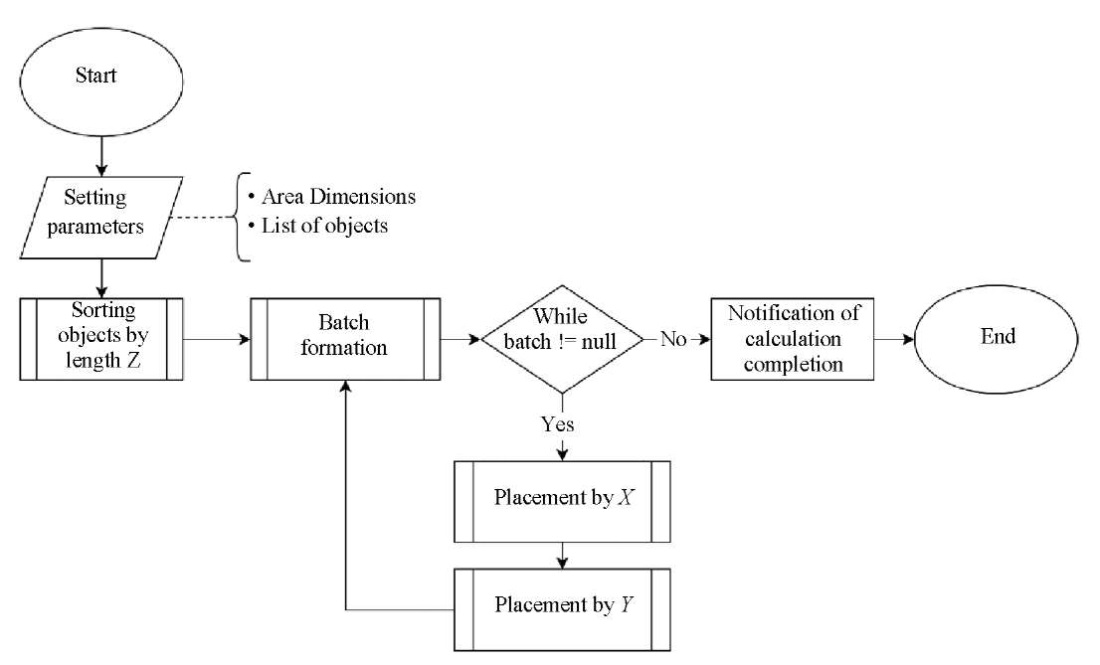
Fig. 1. Top-level 2D placement algorithm
In this work, a left-sided coordinate system is used: X-axis denotes the horizontal placement vector, Z-axis is directed forward from the user and is the depth vector, or frontal measurement [7]. Objects are placed in a horizontal plane (e.g., on the floor, countertop, etc.), therefore, the vertical Y-axis is not considered, and all illustrations assume a top view of the resulting composition.
In the lower left corner of each virtual object, a pivot is denoted. It determines the final coordinates of the object placement. Next, the set of objects is sorted in descending order by 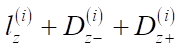 — overall length of the objects, taking into account the comfort zones located in front and behind in accordance with the coordinate axis under consideration. After sorting, objects that occupy more space in depth are located farther away from the user (or higher — for the scheme presented in the horizontal projection). A block diagram of the formation of a batch of objects is shown in Figure 2.
— overall length of the objects, taking into account the comfort zones located in front and behind in accordance with the coordinate axis under consideration. After sorting, objects that occupy more space in depth are located farther away from the user (or higher — for the scheme presented in the horizontal projection). A block diagram of the formation of a batch of objects is shown in Figure 2.
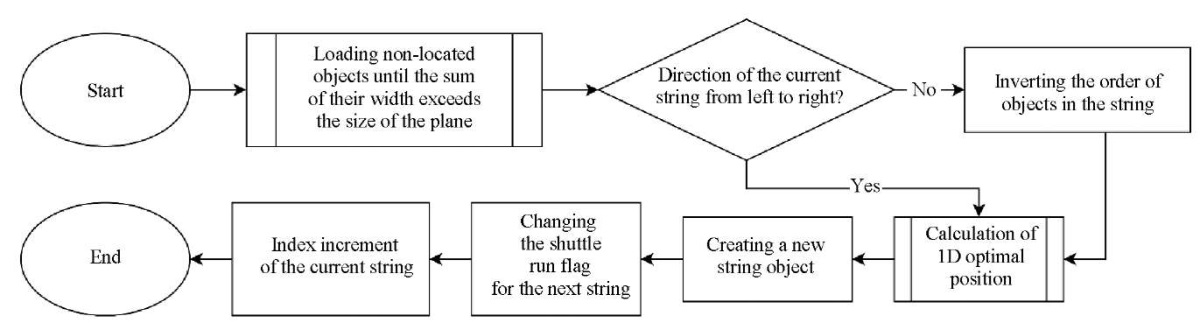
Fig. 2. Algorithm for forming a batch of objects
Then separate strings, or batches, are formed from the ordered set of objects. Each string includes the minimum number of objects, the sum of the width of which, together with the comfort zones, exceeds the width of the filled region 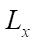 . If, when adding the next object, the calculated occupied width exceeds the horizontal size of the available space inside the rectangle, the batch is considered completed. Thus, each batch can be placed as a line within the region. Rows alternate from left to right and from right to left to mix large and small objects. This can be called a “shuttle run” (Fig. 3).
. If, when adding the next object, the calculated occupied width exceeds the horizontal size of the available space inside the rectangle, the batch is considered completed. Thus, each batch can be placed as a line within the region. Rows alternate from left to right and from right to left to mix large and small objects. This can be called a “shuttle run” (Fig. 3).

Fig. 3. Scheme of the “shuttle run” on the coordinate plane
For the formed row, 1D-placement algorithm is used, which provides for the optimal placement of a number of objects along X-axis based on the calculated comfort coefficient К, which is the same for all objects in the row. For each object of the first string, Z-axis offset from the edge of the plane is determined in such a way that the comfort in front is equal to the comfort along X:
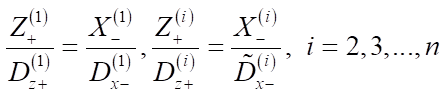 .
.
Starting from the 2nd row, to calculate Z+ indent, the presence of potential neighbors from above from the overlying row that have common sections with the current object being processed along X coordinate is checked. At the same time, each object of the placed row is installed along Z-axis in such a way that its comfort from above is the maximum of the one-sided horizontal comfort in this row and the previous rows. The algorithm for calculating Z coordinates is shown in Figure 4.
Fig. 4. Principle of calculating Z coordinate for the string object
It can be seen from the flowchart that the indent is calculated similarly for all three possible scenarios:
- indent from the edge of the plane to install the object;
- indent from the neighbor from above;
- in the absence of a neighbor in the previous string, the object closest from all previous strings along Z is taken.
New batches are formed until all objects are assigned a row, or until the physical space runs out.
The initial data for the described algorithm are systematized in Table 1. Objects are sorted by their vertical dimensions.
Table 1
Source data for the example of the operation of the described algorithm
|
Object number |
Size |
Comfort zone |
|
1 |
(7; 4) |
(4; 3; 3; 5) |
|
2 |
(10; 4) |
(4; 3; 5; 3) |
|
3 |
(5; 4) |
(2; 3; 5,25; 2,25) |
|
4 |
(12; 4) |
(2,8; 3,3; 3,8; 4,65) |
|
5 |
(5; 4) |
(2,5; 4; 1,75; 5,8) |
|
6 |
(18; 4) |
(3,2; 2,4; 5; 2,25) |
|
7 |
(11; 4) |
(2,1; 2,45; 2; 14,2) |
Table 1 corresponds to Figure 5, which demonstrates the placement of objects.
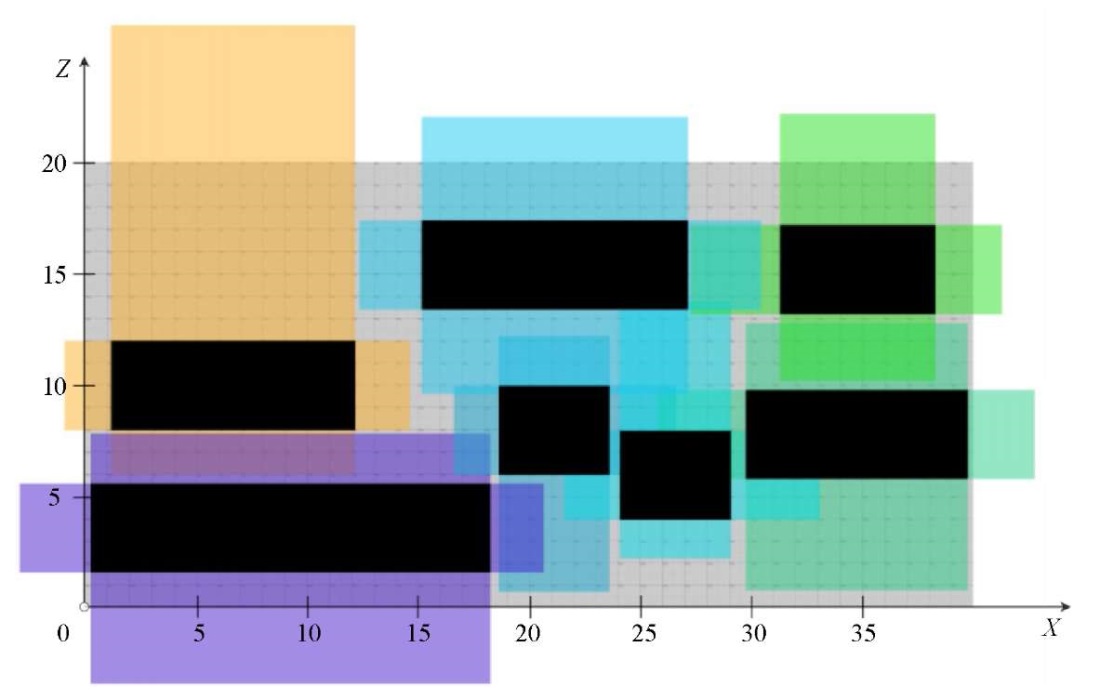
Fig. 5. Layout of the objects for the example under consideration. Top view
A gray rectangle is a free area on which objects are placed. Black areas are objects in their overall dimensions. Colored areas, with overlays, are preset comfort zones for each object. As noted above, comfort zones of objects may partially overlap and go beyond the free space, but the approach used allows for a balance so that the comfort of various objects is equally reduced.
Recall that this model includes the concept of comfort function k(x). The resulting system of equations (1) does not depend on it, and hence the optimal placement of objects. But the values of one-sided comfort of objects are determined both by their placement and by the type of function k(x). Here are two examples:
- in the case of linear function k(x), one-sided comforts of objects in the upper row of Figure 5 are equal to 0.6;
- for dependence
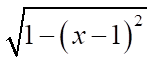 — value 0.9.
— value 0.9.
After the software execution of the described 2D algorithm, it was implemented into an augmented reality mobile application, and the analytical data of user sessions was recorded. The authors grouped information for each unique device model, for each number of objects placed in the range [10]. The average execution time was calculated (Fig. 6).
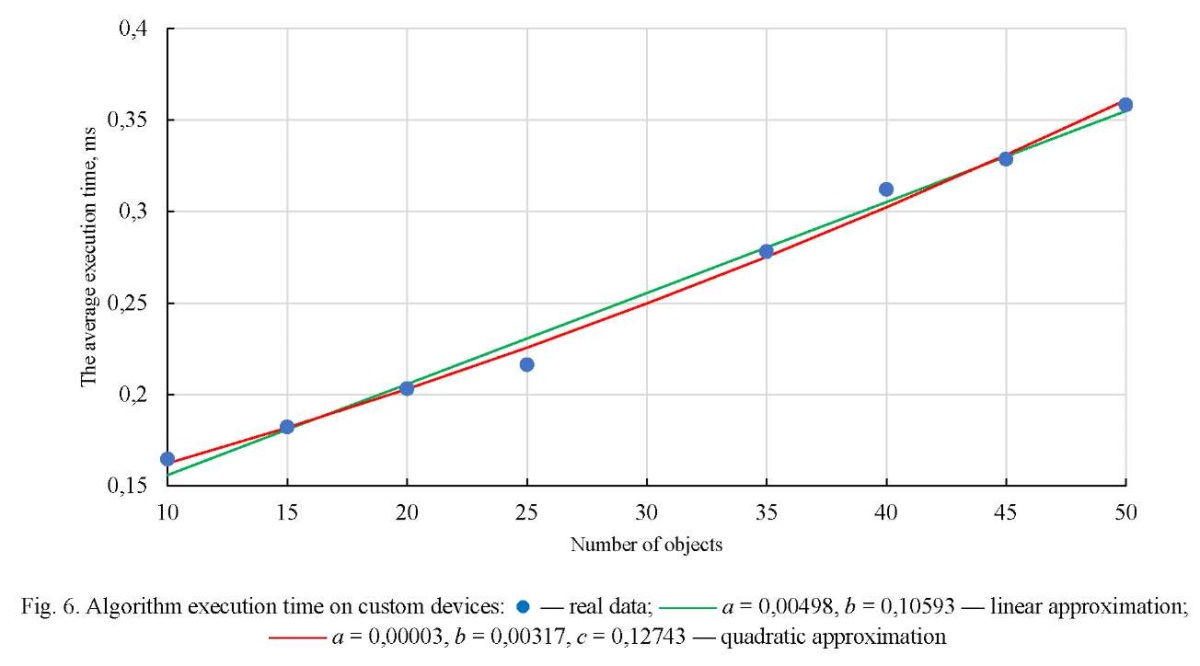
Within the specified range, it is impossible to immediately determine the exact complexity of the algorithm calculation. As can be seen from Figure 6, the data are close to linear and quadratic approximations. Using the residual sum of squares method, a quantitative estimate of both approximations was calculated and values of 0.00035 and 0.00021 were obtained, respectively [10].
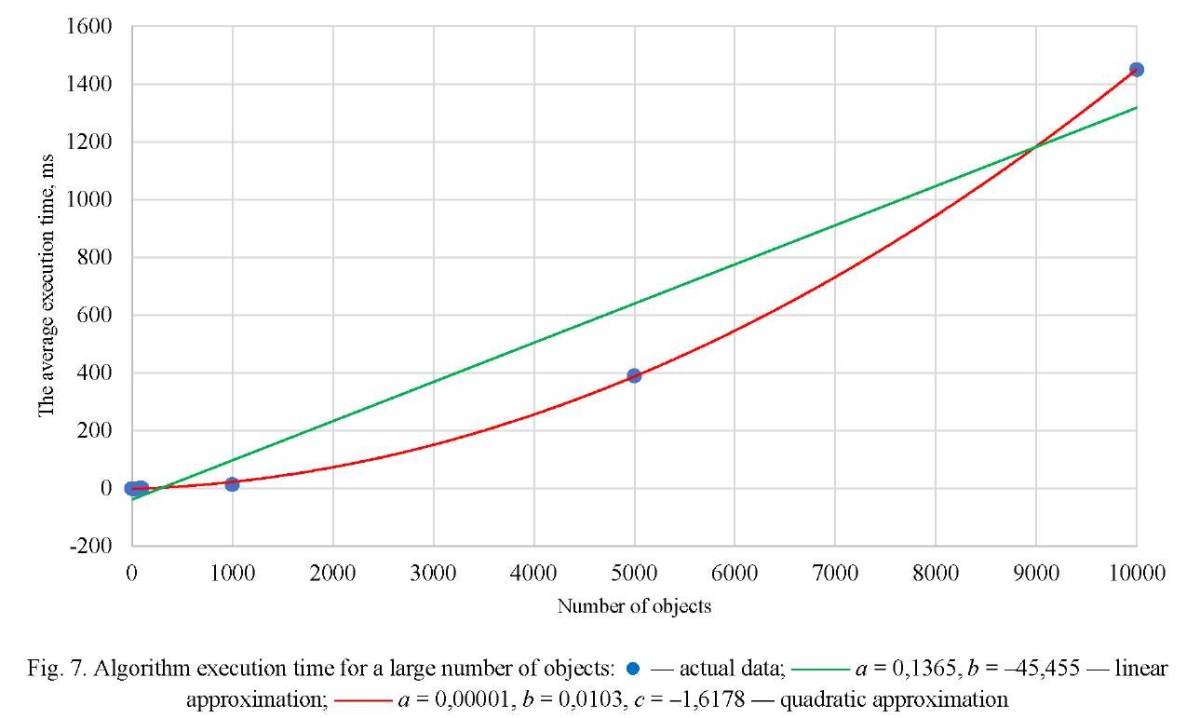
To confirm the hypothesis of quadratic dependence, a similar experiment was launched on a personal computer for a range of [ 10-10,000] objects. Figure 7 confirms the hypothesis; therefore, the algorithm can be assigned complexity O(n2). However, the situation with 10,000 objects is rather theoretical, and in practice, the user is unlikely to work with more than 1–2 dozen objects in augmented reality.
The execution time on different user devices was compared, 10 most popular models were selected, and a diagram based on the calculations results was built (Fig. 8).
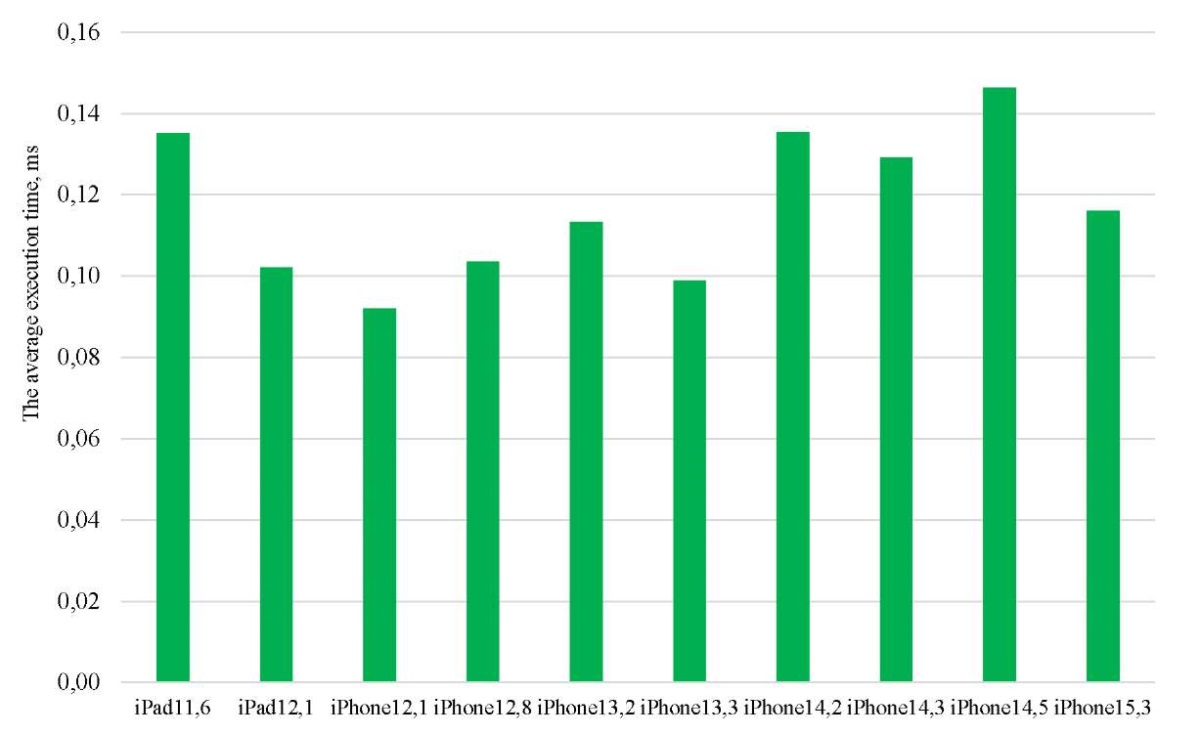
Fig. 8. Comparison of computing speed on different devices for 10 objects
The minimum registered execution time was 0.093 ms, the maximum — 0.146 ms. For this sample, the correlation between the device model and the execution time was only 0.177. This is a pretty low value.
Calculations have shown the high efficiency of the two-dimensional algorithm. This is due to the splitting of the entire set of objects into separate strings and the use of a fast one-dimensional algorithm in each string, described at the beginning of the article. This algorithm provides solving the problem with less resources and time.
Figure 9 shows additional visualizations of placement schemes for different numbers of objects and their parameters.
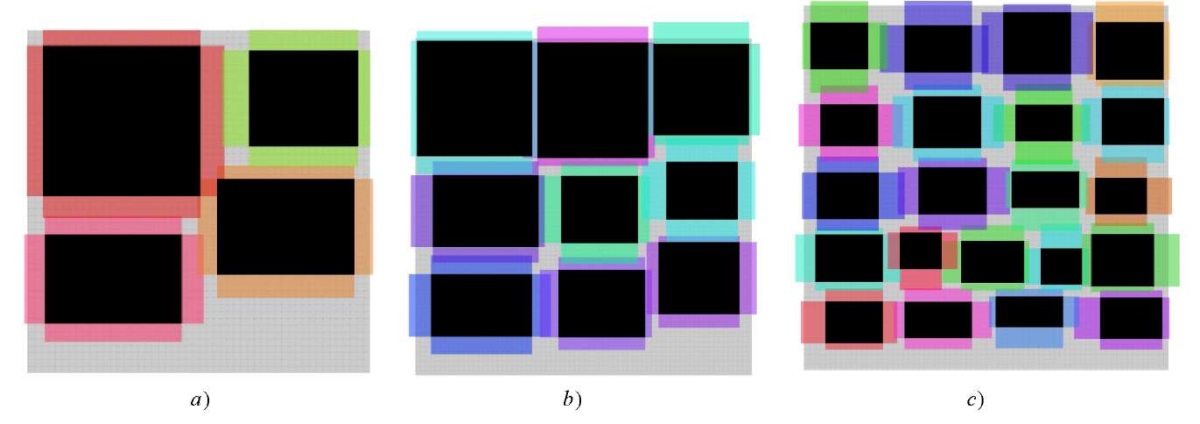
Fig. 9. Examples of placing different numbers of objects:
a — 4 objects; b — 9 objects; c — 21 objects
Thus, the proposed algorithm of two-dimensional placement provides working with a set of virtual objects. Each of them is characterized by certain sizes and comfort zones. The algorithm is designed to optimally position such objects in a rectangular physical space that recreates the user's environment.
Discussion and Conclusion. For the previously described one-dimensional problem, an effective algorithm for optimal placement of virtual objects is proposed and implemented in the program code. A model of optimal placement was constructed for the two-dimensional case. Based on it, an effective algorithm has been developed, implemented in the program code.
The performance of the algorithm, which was measured by the execution time, was analyzed. It was found that there was no significant correlation between the execution time and the device model. The average time was fractions of a millisecond even for large batches of objects. This indicated a relatively stable performance of the algorithm under various conditions. However, the possible influence of other untested factors cannot be excluded. Further research is needed to fully characterize performance dependences.
The authors outline several areas of future work to improve the performance and adaptability of the algorithm. This is, firstly, the improvement of the solution, which will allow using the full size of objects, when possible, without intersections of comfort zones. Their sizes will be reduced only if absolutely necessary. This should provide for optimal use of space and further improve the interactive user experience.
Secondly, the inclusion of rotation of elements in the algorithm will increase flexibility in their arrangement and make it possible to use space better. In addition, this will allow the algorithm to take into account more different objects, thereby expanding its practical application.
Note that in an augmented reality application, placing three or more objects by the user is a rather time-consuming task. It requires considerable time, and significantly complicates the work.
The proposed technology for placing objects in 2D allows the optimal positioning of virtual content to improve the user experience in augmented reality. Automated location calculation reduces manual work and makes it possible to focus on valid interaction with AR.
Scientific research in this direction involves seamless integration of virtual and physical spaces. The results can be applied in practice by developers of augmented reality glasses who face the problem of rapid intelligent positioning of objects depending on user preferences and context. Moreover, the results of the work may be of interest to:
- engineers working on smart home systems;
- interface designers, for whom it is important to effectively and harmoniously combine controls and information on the screen.
The introduction of fuzzy logic allows developers to adapt the solution to specific tasks and use cases. In future research, it is advisable to study and apply user experience, include additional restrictions on the positioning of objects.
References
1. Yahya Ghazwani, Shamus Smith. Interaction in Augmented Reality. In: Proc. 4th International Conference on Virtual and Augmented Reality Simulations. New York, NY: Association for Computing Machinery; 2020. P. 39–44. https://doi.org/10.1145/3385378.3385384
2. Müller J, Butscher S, Feyer SP, Reiterer H. Studying Collaborative Object Positioning in Distributed Augmented Realities. In: Proc. 16th Int. Conf. on Mobile and Ubiquitous Multimedia. New York, NY: Association for Computing Machinery; 2017. P. 123–132. https://doi.org/10.1145/3152832.3152856
3. Regenbrecht HT, Wagner MT. Interaction in a Collaborative Augmented Reality Environment. In: CHI '02 Extended Abstracts on Human Factors in Computing Systems. New York, NY: Association for Computing Machinery; 2002. P. 504–505. https://doi.org/10.1145/506443.506451
4. Alpatova MV, Glazkov AV, Rudyak YuV. Mathematical Model of Rational Location of Augmented Reality Objects in User's Environment. In: Proc Int. Sci. Conf. “Smart Nations: Global Trends In The Digital Economy”. Cham: Springer; 2022. P. 248–254. https://doi.org/10.1007/978-3-030-94873-3_30
5. Gimadi EKh, Zalyubovskii VV. Bin Packing: Asymptotically Exact Approach. Russian Mathematics. (Iz. VUZ). 1997;(12(427)):25–33. URL: https://kpfu.ru/portal/docs/F1486686603/03_12.PDF (accessed: 20.09.2023). (In Russ.).
6. Alpatova MV, Rudyak YuV. Placement of Multiple Virtual Objects in Physical Space in Augmented Reality Applications. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):203–211. https://doi.org/10.23947/2687-1653-2023-23-2-203-211
7. Karev GB. Directionality in Right, Mixed and Left Handers. Cortex. 1999;35(3):423–31. https://doi.org/10.1016/S0010-9452%2808%2970810-4
8. Sung Lae Kim, Hae Jung Suk, Jeong Hwa Kang, Jun Mo Jung, Laine TH, Westlin J. Using Unity 3D to Facilitate Mobile Augmented Reality Game Development. In: Proc. IEEE World Forum on Internet of Things (WF-IoT). New York City: IEEE; 2014. P. 21–26. https://doi.org/10.1109/WF-IoT.2014.6803110
9. Warner RA. Using Z Scores for the Display and Analysis of Data. In book: Optimizing the Display and Interpretation of Data. Amsterdam: Elsevier; 2016. P. 7–51. https://doi.org/10.1016/B978-0-12-804513-8.00002-X
10. Wolfe DA. Ranked Set Sampling: Its Relevance and Impact on Statistical Inference. ISRN Probability and Statistics. 2012;2012:568385. https://doi.org/10.5402/2012/568385
About the Authors
M. V. AlpatovaRussian Federation
Marianna V. Alpatova, Senior Lecturer of the Computer Science and Information Technology Department, ScopusID
38, Bolshaya Semyonovskaya St., Moscow, 107023
Yu. V. Rudyak
Russian Federation
Yuri V. Rudyak, Dr.Sci. (Phys.-Math.), Professor of the Computer Science and Information Technology Department, ScopusID
38, Bolshaya Semyonovskaya St., Moscow, 107023
Review
For citations:
Alpatova M.V., Rudyak Yu.V. Optimal 2D Placement of Virtual Objects in Physical Space for Augmented Reality Applications. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):410-421. https://doi.org/10.23947/2687-1653-2023-23-4-410-421. EDN: QPFEMG
JATS XML














































