Перейти к:
Моделирование процессов ультразвуковой дефектоскопии в задаче поиска и визуализации внутренних дефектов в узлах агрегатов и конструкций
https://doi.org/10.23947/2687-1653-2023-23-4-433-450
EDN: RKAOTZ
Аннотация
Введение. Обратные задачи представляют собой специфический тип задач, где изучаются последствия явлений с целью определения их причин. Они широко используются в научных исследованиях, особенно тех, что имеют дело с большими объемами экспериментальных данных. В представленном исследовании рассмотрены обратные задачи в машиностроении и диагностике конструкций. Эти области требуют точных методов для выявления в различных материалах внутренних дефектов, которые могут иметь критические значения для обеспечения безопасности и эффективности использования технических конструкций. Несмотря на множество имеющихся методов дефектоскопии существует потребность в инновационных разработках, способных обеспечить ее более высокую точность и эффективность. В данном исследовании объединены различные научные методы и технологии, оно открывает новые перспективы в неразрушающем контроле для обнаружения внутренних дефектов в различных материалах и структурах. Его цель — развитие и внедрение методов неразрушающего контроля на основе нейросетевого аппарата для повышения точности идентификации дефектов, а также разработка нейросетевой модели и оценка ее эффективности для усовершенствования процесса ультразвуковой визуализации внутренних дефектов в твердых материалах. В связи с этим задача, которую предстоит решить для достижения поставленной цели, заключается в создании надежного инструмента для точной визуализации размеров, форм, местоположения и ориентации внутренних дефектов в различных материалах.
Материалы и методы. Применяется методика определения геометрических параметров дефектов в материалах с использованием неразрушающего контроля. Также используется метод, объединяющий моделирование распространения ультразвуковых волн в акустической среде и технологии искусственных нейронных сетей. Он выявляет нелинейные связи между геометрическими характеристиками дефектов и амплитудно-частотными и амплитудно-временными данными, полученными при анализе сигналов. Искусственные нейронные сети представляют собой модель, которая может обучаться на примерах, что позволяет эффективно решать задачи, которые сложно выразить в традиционных формах. В исследовании используется метод конечных разностей во временной области. Он применяется для идентификации и визуализации внутренних дефектов в материалах с использованием ультразвукового неразрушающего контроля и сверточных генеративных нейронных сетей.
Результаты исследования. Разработана сверточная нейронная сеть для визуализации внутренних дефектов с использованием техник ультразвукового неразрушающего контроля. Эта нейронная сеть успешно определяет размер дефектов, их местоположение, форму и ориентацию с высокой точностью и надежностью.
Обсуждение и заключение. Авторы подчеркивают ключевое влияние размера дефекта на точность ультразвуковой визуализации в различных сценариях. Проведенная валидация модели для трех различных случаев дефектов с разными механическими параметрами показала, что для успешной визуализации дефектов длина волны ультразвукового импульса должна быть в десятки раз меньше размера дефекта. При анализе влияния размера дефектов на точность работы нейронной сети выявлено, что ошибка визуализации увеличивается для дефектов меньшего размера.
Установлено также, что относительная скорость звука в материалах оказывает большее влияние на точность метода, чем относительная плотность материала. На основании полученных авторами результатов можно утверждать, что разработанные методики и технические решения имеют большое значение для будущих исследований в области дефектоскопии, обладают весомым потенциалом для научных и практических сфер применения.
Ключевые слова
Для цитирования:
Соболь Б.В., Соловьев А.Н., Васильев П.В., Ляпин А.А. Моделирование процессов ультразвуковой дефектоскопии в задаче поиска и визуализации внутренних дефектов в узлах агрегатов и конструкций. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):433-450. https://doi.org/10.23947/2687-1653-2023-23-4-433-450. EDN: RKAOTZ
For citation:
Sobol B.V., Soloviev A.N., Vasiliev P.V., Lyapin A.A. Modeling of Ultrasonic Flaw Detection Processes in the Task of Searching and Visualizing Internal Defects in Assemblies and Structures. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):433-450. https://doi.org/10.23947/2687-1653-2023-23-4-433-450. EDN: RKAOTZ
Введение. Обратные задачи в рамках научного исследования — это такие задачи, в которых осуществляется анализ последствий некоторых явлений или процессов с целью формулирования гипотез и выводов относительно их причинности. Обратные задачи встречаются в различных областях научных исследований, особенно в случаях, когда имеются большие объемы экспериментальных данных, позволяющие выявить характеристики и особенности процесса, который породил эти данные. Таким образом, обратные задачи предоставляют ученым возможность определить параметры процессов, недоступных при непосредственном наблюдении.
В настоящее время существует установившаяся методология решения обратных задач, которая основывается на анализе реакции системы на определенные входные воздействия. Современные подходы к решению обратных задач подразделяют их на различные категории, что облегчает их формализацию и адаптацию в зависимости от конкретной ситуации.
В машиностроении широко применяется методика решения обратных задач для диагностики механических систем. Изучение динамической реакции таких систем, включая анализ переходных характеристик, позволяет получить детальную и точную информацию о состоянии системы, что, в свою очередь, дает возможность определить ее производительность и качество.
В области диагностики конструкций и изделий растет потребность в оценке текущего состояния технических систем с целью выявления и устранения потенциальных опасностей, которые могут привести к производственным убыткам или несчастным случаям. Такие оценки могут быть даны лишь высококвалифицированными специалистами в области реинжиниринга.
С учетом этих аспектов была поставлена задача разработать и в дальнейшем оценить возможности применения нейросетевой модели для решения прикладных проблем ультразвуковой визуализации внутренних дефектов в твердых телах для различных материалов.
Существует большое количество научных работ, посвященных данной теме. Так, в [1] авторы сфокусировали свое внимание на анализе композитных материалов, содержащих дефекты. Наличие дефектов в таких композитах может существенно влиять на их эксплуатационные характеристики и поэтому представляет особый интерес для исследователей. Для поиска дефектов каждый из исследуемых объектов подвергается ультразвуковому сканированию, в ходе которого фиксируются колебания и определяются их характеристики. Следующим этапом анализа является классификация полученных характеристик с использованием искусственных нейронных сетей. Этот метод позволяет получить изображение области дефекта с высокой точностью. Такая визуализация отражает как характер, так и степень распространения дефекта в исследуемом материале. Важно отметить, что данная методика обеспечивает четкую идентификацию зоны повреждения, а полученное изображение соответствует визуальным наблюдениям.
В работе [2] представлен метод акустической эмиссии в контексте оценки композитных материалов, представляющий собой перспективное направление исследований. Особое внимание уделяется идентификации акустических сигналов, связанных с микроструктурой волокон, в условиях высокого уровня шума и с использованием пленочных датчиков. Для исследований были подготовлены многослойные композиты на основе армированного стекловолокна, изготовленные различными методами. Эксперименты включали в себя нагружение композитных образцов в статических условиях, в то время как PVDF-пленка была установлена на их поверхности. Акустические сигналы были аккуратно записаны и после этого были классифицированы при помощи искусственной нейронной сети. Результаты данного исследования говорят о возможности при помощи нейронных сетей успешно классифицировать различные механизмы разрушения в композитных материалах.
В исследовании [3] сделан анализ инцидентов обрушения, произошедших при раскопках в слоях горных пород на гидроэлектростанции Вудунде в Китае. Его авторы представили усовершенствованную модель искусственной нейронной сети (ИНС) для прогнозирования вероятности и глубины таких обрушений. Однако следует сказать, что одиночный параметр не способен обеспечить абсолютной точности предсказания глубины обрушений. В этом исследовании был предложен интегрированный метод интеллектуального прогнозирования, основанный на применении искусственных нейронных сетей. Для его разработки проведены аналитическое и статистическое исследования, что позволило определить шесть ключевых входных параметров: глубина покрытия, отношение основных и малых напряжений, индекс геологической силы, метод выемки грунта, сила поддержки и ориентация породы.
Модель ИНС была обучена с использованием данных, собранных в процессе раскопок на гидроэлектростанции Вудунде, среди них было 45 образцов для обучения и 6 тестовых образцов для верификации. Для оптимизации параметров ИНС, таких как структурные характеристики и начальные веса, был применен генетический алгоритм. После завершения этапа обучения обученная нейронная сеть была успешно применена для прогнозирования глубины обрушений на нескольких участках раскопок. Результаты прогнозов демонстрировали высокое соответствие данным, полученным в ходе наблюдений на этих участках.
В статье [4] представлен инновационный метод для детектирования дефектов в стержневых конструкциях. Он существенно отличается от других и состоит из двух этапов. Первый этап фокусируется на точной локализации дефекта в стержне. Для этого используется анализ частот и форм колебаний, связанных с исследуемым объектом. Результаты анализа форм колебаний играют решающую роль в решении задачи первого этапа. На втором этапе, после успешной локализации дефекта, создается аналитическая или конечно-элементная модель конструкции, учитывающая выявленные дефекты. С использованием этой модели проводится оценка степени повреждения стержневой конструкции. Применение данного метода проиллюстрировано на примере вычисления параметров дефекта в упругом консольном стержне. Этот расчет основан на данных экспериментальных наблюдений, полученных в конечно-элементном комплексе. Представленный алгоритм предоставляет новый инструмент для более точной и эффективной идентификации дефектов в стержневых конструкциях, что имеет большое значение для научных исследований и инженерной практики. Результаты моделирования, проведенного в рамках данного исследования, свидетельствуют о снижении ошибки прогнозирования осаждения. Это указывает на улучшение функциональной аппроксимации и, следовательно, на отличные обучающие характеристики этого метода, по сравнению с традиционными нейронными сетями с сигмоидными или другими функциями активации.
В исследовании [5] предлагается инновационный метод диагностики дефектов в механической коробке передач, основанный на анализе сигналов вибрации, полученных в ходе экспериментальных испытаний. Основное внимание уделяется раннему выявлению аномалий в работе зубчатых передач. Для эффективного анализа вибрационных сигналов используется обработка данных, ориентированная на частотно-временную область. Одним из ключевых методов является применение непрерывного вейвлет-преобразования, что позволяет извлечь статистически значимые характеристики из сигналов. С целью оптимизации процесса обработки сигналов внедряется метод выделения особенностей, который способствует определению наиболее важных параметров, что, в свою очередь, снижает вычислительную нагрузку и ускоряет процесс анализа. Для выбора оптимальных входных признаков и дальнейшего снижения вычислительной сложности исследования применяются генетические алгоритмы. Этот интеллектуальный подход способствует повышению эффективности процесса анализа данных. Следующим важным этапом в рамках исследования является оценка эффективности предлагаемого метода. Для этой цели использованы передовые технологии нейронных сетей обратного распространения. Полученные результаты и производительность классификаторов тщательно оценивались на разнообразных вибрационных сигналах, полученных в ходе экспериментальных испытаний при различных условиях работы механических зубчатых передач коробки передач.
Исследования систем неразрушающего контроля и поиска дефектов в твёрдых телах зачастую затрагивают область моделирования соответствующих процессов [6]. Основное внимание направлено на решение обратных геометрических задач, тесно связанных с теорией упругости, для их дальнейшего применения при анализе плоской прямоугольной области. Задача заключается в восстановлении характеристик круговых полостей и трещин.
Для эффективного решения обратных задач исследователи опираются на информацию, полученную о первых четырёх собственных резонансных частотах. Эти параметры представляют собой дополнительный набор данных, значительно обогащающий информацию о системе. Методика, применяемая для решения обратных задач, базируется на минимизации функционала невязки. Суть этой методики заключается в сведении к минимуму расхождения между измеренными входными данными и значениями, полученными в результате численного решения прямых задач. При этом предварительно задаются параметры дефектов в твёрдом теле.
Таким образом, исследования в области неразрушающего контроля дефектов в твёрдых телах ориентированы на разработку и применение математических методов и моделирования, что позволяет точно определять и анализировать дефекты, скрытые внутри материала. Эти исследования нашли применение в области безопасности и контроля качества технических систем. Авторы исследуют возможности применения нейросетевых технологий в решении обратных задач механики, в частности задачи двумерной визуализации внутренних дефектов. Данные методы получили широкое распространение в медицине, гражданской инженерии, неразрушающем контроле и других областях.
В работе [7] предложена система для выявления трещин в металлических конструкциях и определения их глубины на основе анализа двухмерных изображений. Основной целью данной работы было создание доступной и удобной системы контроля, более экономически выгодной альтернативы дорогостоящим измерительным устройствам. В рамках данного исследования была разработана специфическая стратегия обучения, а также рассмотрено несколько архитектур нейронных сетей, способствующих более точному выявлению трещин и оценке их глубины.
Процесс обучения нейронной сети включал в себя предоставление сети характеристик двухмерных профилей трещин, а также данных о максимальной глубине залегания трещины, измеренной с использованием лазерного микроскопа. Это позволило создать модель, которая способна точно определять глубину дефектов в материале. Следует отметить, что средняя ошибка в работе данной нейронной сети составляет всего около 18 % на тестовых образцах. Этот результат значительно превосходит итоги предыдущих работ, которые основывались на разнообразных стратегиях обучения и методиках анализа. Таким образом, данное исследование значительно повысило качество определения глубины трещин в металлических конструкциях. Его ценность заключается в разработке новых стратегии обучения и инструмента для более точной оценки глубины трещин.
В исследовании [8] подчеркивается важность наличия размеченных данных, содержащих изображения, на которых отмечены дефекты. Одним из новейших предложений в данной области является представленная модель глубокого трансферного обучения, предназначенная для извлечения характерных признаков внутренних дефектов на рентгеновских изображениях, полученных в результате инспекции авиационных композитных материалов. Эта модель представляет собой инструмент для автоматического анализа таких изображений, который позволяет оптимизировать процесс обнаружения дефектов и повысить эффективность неразрушающего контроля.
В ходе исследования была произведена проверка эффективности предложенной модели на задаче обнаружения дефектов-включений на рентгеновских изображениях. Анализ результатов экспериментов показал, что данная модель способна достигать высокой точности (96 % по метрике F1). Такие обнадеживающие результаты свидетельствуют о потенциале данного подхода и его способности давать удовлетворительные результаты в задачах по идентификации дефектов. Это открывает новые горизонты в области неразрушающего контроля и позволяет более эффективно обеспечивать безопасность и надежность композитных материалов в авиационной индустрии.
В работе [9] показан метод, который предлагает реконструкцию и визуализацию внутренних аномалий в форме трехмерных репрезентаций. Этот подход использует экономически и временно выгодную методику, известную как импульсная термография. В данном контексте представлен новаторский метод, который способен быстро и точно оценить как глубину, так и толщину внутренних аномалий с помощью односторонней инспекции. Целесообразность и эффективность данного метода успешно демонстрировались в ходе исследования композитных и стальных образцов, содержащих полузакрытые воздушные зазоры. Результаты исследования подтвердили, что при предложенном методе ошибка в оценке общего объема трехмерных аномалий составляет всего лишь 10 % для композитных образцов. Таким образом, данный инновационный метод предоставляет новые возможности для неразрушающего контроля и визуализации внутренних дефектов в различных материалах и образцах, обеспечивая при этом высокую точность и экономическую эффективность.
В работе [10] рассмотрены фундаментальные факторы, приводящие к отказам в работе твердотопливных ракетных двигателей. Один из ключевых аспектов, оказывающих критическое воздействие на целостность двигателей, заключается в явлении отслаивания на границе раздела между ракетным топливом, изоляцией и защитным слоем. Современные методы диагностики и оценки структурной целостности ракетных двигателей, как правило, ограничиваются визуальным осмотром и анализом их компонентов. Данный подход имеет свои ограничения и требует совершенствования. В этом контексте представлен новаторский алгоритм, предназначенный для выявления поверхностных дефектов обшивки, способных нарушить связь между твердым топливом и изоляцией ракетного двигателя. Для оптимизации работы нейронной сети проведен ряд тестов, в которых менялись различные параметры сети. Эти исследования позволяют достичь точности классификации в 99,08 % для класса исправных элементов, 90,66 % — для класса посторонних объектов и 99,48 % — для класса, связанного с дефектами. Полученные результаты свидетельствуют о высокой эффективности предложенного метода и его потенциале для применения в области диагностики твердотопливных ракетных двигателей.
Исследование, проведенное и опубликованное автором в статье [11], нацелено на изучение потенциала методов глубокого обучения в контексте электромагнитной инверсии. Суть данного подхода заключается в применении глубоких нейронных сетей, основанных на сверточной архитектуре, для анализа и обработки данных, полученных в рамках данной задачи. Важным аспектом этого исследования является обучение с использованием обширных наборов синтетических данных, полученных при помощи трехмерного моделирования. Глубокие нейронные сети здесь обучаются на множестве синтетических данных, представляющих собой информацию о распределении электромагнитных полей внутри объектов и сред. Эти данные предоставляют ценную информацию об их свойствах и составах, что делает метод электромагнитной инверсии более точным и эффективным. Эффективность предложенного метода была успешно продемонстрирована на различных моделях, которые имеют высокое практическое значение. К примеру, при мониторинге электромагнитного поля в области скопления углекислого газа, находящегося под землей, инверсионный метод позволяет анализировать и контролировать данное поле с использованием источника на поверхности.
Ранее авторы представленного сегодня исследования уже рассматривали задачи, сочетающие современные методы глубокого машинного обучения и хорошо зарекомендовавшие себя классические подходы к идентификации дефектов [12–14]. В нынешней же работе акцент сделан на нейросетевую модель, которая эффективно выполняет двумерную акустическую визуализацию внутренних аномалий. Этот проект выведет на новый уровень область неразрушающего ультразвукового контроля, предоставив возможность провести системный анализ с использованием численных экспериментов.
Цель представленной сегодня исследования — разработка и оценка эффективности нейросетевой модели для улучшения ультразвуковой визуализации внутренних дефектов в твердых материалах. Для выявления нелинейных связей между геометрическими характеристиками дефектов и сигналами ультразвукового контроля авторы предлагают использовать методику, основанную на решении обратной задачи механики твердого тела и применении искусственных нейронных сетей. Основная задача при этом заключается в создании надежного инструмента для точной визуализации размеров, форм, местоположения и ориентации внутренних дефектов в различных материалах. Численные эксперименты аппроксимируют процесс ультразвукового зондирования образцов, в которых присутствуют внутренние дефекты с различными геометрическими формами и механическими характеристиками. Эти эксперименты служат исходными данными для обучения нейронной сети и последующей проверки ее на правильность функционирования и точность. Таким образом, можно утверждать, что данное исследование охватывает широкий спектр научных методов и технологий, включая разработку нейронных сетей, моделирование ультразвуковых волн и анализ акустических данных.
Материалы и методы. В данной работе применяются многослойные искусственные нейронные сети прямого распространения (feed-forward neural networks, FFNN) и свёрточные ИНС (convolutional neural network, CNN). Для определения наиболее рациональной архитектуры сетей применяется аналитическое программное обеспечение. ИНС обучаются алгоритмами RProp (устойчивое обратное распространение) и Adam (метод адаптивной оценки моментов).
Алгоритм RProp основан на методе градиентного спуска. В отличие от стандартного алгоритма обратного распространения ошибки, RProp для подстройки весовых коэффициентов использует только знаки частных производных. Алгоритм использует обучение по эпохам, а коррекция весов происходит после обработки всего объема обучающей выборки. Весовые значения обновляются следующим образом:
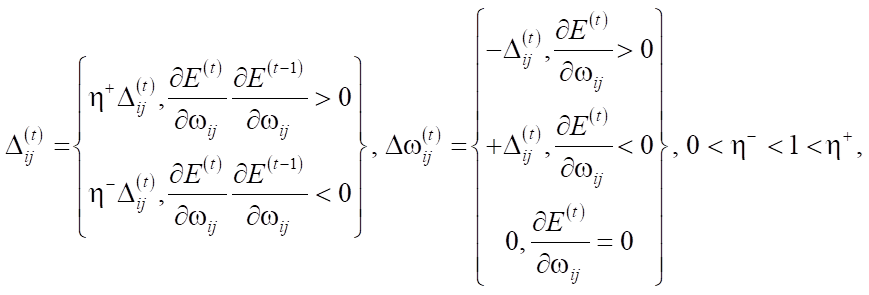
после чего происходит подстройка весов:
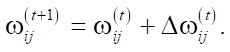
Adam (метод адаптивной оценки моментов) использует сгруппированные средние как градиентов, так и вторых моментов градиентов. Если установлены параметры w(t), а функция потерь ℒ(t), где t отражает индекс текущей итерации, пересчёт параметра алгоритмом задаётся следующим образом:
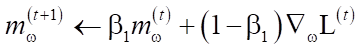
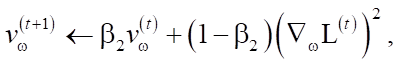
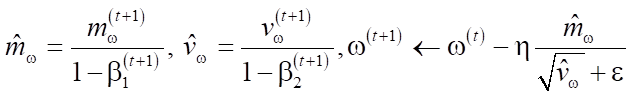
где ε является малой добавкой, используемой для предотвращения деления на 0, а β1 и β2 являются коэффициентами забывания для градиентов и вторых моментов градиентов соответственно; η — базовая скорость обучения. Возведение в квадрат и квадратный корень вычисляются поэлементно.
Изображения, обрабатываемые свёрточной ИНС, можно представить как тензор размера:
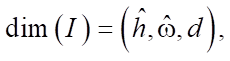
где hˆ и wˆ — размеры двумерного изображения; d — количество каналов изображения. Ядро свёртки K имеет следующие размеры:
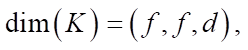
где f — сторона квадратного фильтра свёртки.
Операцию свёртки можно определить следующим образом. Объектом свёртки является двумерное изображение I. Ядро свертки K имеет размеры h × w. Результатом свертки будет:
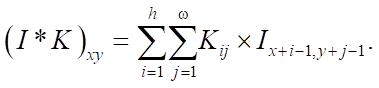
На этом операторе строится сверточный слой, который состоит из определенного набора ядер 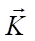 , соответствующих им смещений :
, соответствующих им смещений :
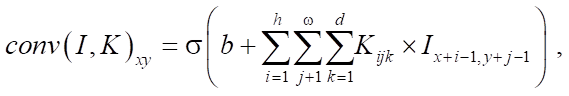
где d — индекс канала изображения; b — составляющая смещения; σ — активационная функция сверточного слоя.
Обучаемыми параметрами данного слоя являются фильтр K и смещение b.
В области машинного обучения существует несколько техник регуляризации. Для предотвращения переобучения сложных моделей ИНС с большим количеством параметров применяется метод регуляризации Тихонова (ridge regression, или L2), в машинном обучении также называемый weight decay. Коэффициентом регуляризации является λ, который управляет минимизацией нормы относительно минимизации потерь на обучающем наборе данных. Таким образом, для каждого веса w происходит прибавление к целевой функции 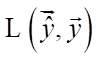 слагаемого:
слагаемого:
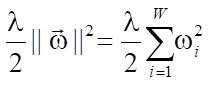 .
.
В рамках применяемого фреймворка Keras регуляризация применяется для каждого свёрточного слоя ИНС-модели.
Начальная инициализация весов проводится методом Xavier. Во время начальной установки весовых значений применяется вероятностное распределение, как равномерное, так и нормальное с дисперсией
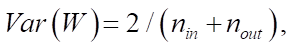
где 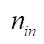 и
и 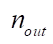 — количества нейронов в предыдущем и последующем слоях соответственно.
— количества нейронов в предыдущем и последующем слоях соответственно.
Дисперсия выходных значений линейного нейрона (без смещений) имеет вид:
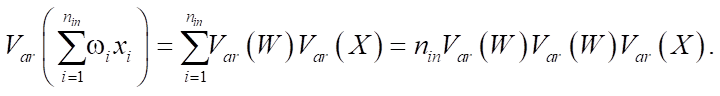
Подразумевается, что веса и входные значения не коррелируют и имеют нулевое матожидание. Из этого получаем дисперсию вероятностного распределения, на основе которого проходит первичная инициализация весов, и обеспечивающую сохранение дисперсии входных данных после прохождения через слой.
В данной работе слои батч-нормализации (Ioffe и Szegedy) активно применяются в большинстве разработанных ИНС-моделей с использованием фреймворка Keras. Метод осуществляет нормализацию входных данных таким образом, что их матожидание равно нулю, а дисперсия — единице. При этом нормализация выполняется на каждом слое для каждого пакета данных:
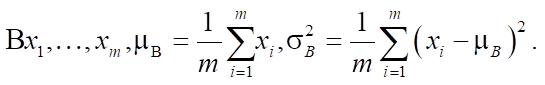
На основе этих характеристик преобразуется активационная функция:
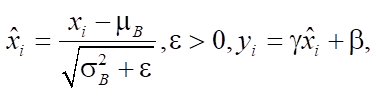
где 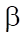 и
и 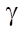 — параметры, которые возможно оптимизировать методом градиентного спуска на основе обучающего набора.
— параметры, которые возможно оптимизировать методом градиентного спуска на основе обучающего набора.
Слои Dropout применяются в ИНС-моделях в задаче идентификации дефектов на дорожном покрытии, которые служат для предотвращения переобучения. При использовании данного средства регуляризации предотвращается взаимоадаптация нейронов на этапе обучения ИНС. Данный метод блокирует (отключает) нейроны во время обучения с вероятностью. Учитывая, что 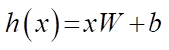 — линейная проекция входного di—мерного вектора x на dh—мерное пространство выходных значений и a(h) — активационная функция, применение Dropout к данной проекции на этапе обучения можно представить как модифицированную функцию активации
— линейная проекция входного di—мерного вектора x на dh—мерное пространство выходных значений и a(h) — активационная функция, применение Dropout к данной проекции на этапе обучения можно представить как модифицированную функцию активации
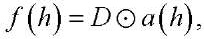
где 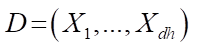 — dh-мерный вектор случайных величин
— dh-мерный вектор случайных величин 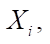 распределенных по закону Бернулли. имеет следующее распределение вероятностей:
распределенных по закону Бернулли. имеет следующее распределение вероятностей:
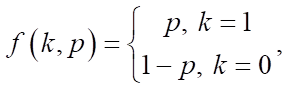
где k — все возможные выходные значения.
Применение Dropout к i-му нейрону выглядит следующим образом:
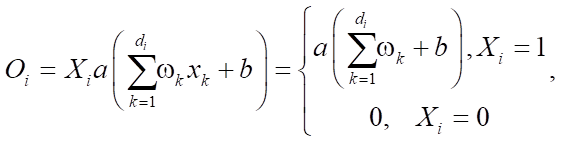
где
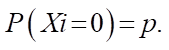
Нейронные сети, которые описаны в данной работе, принадлежат к сетям прямого распространения. Входная информация составляется из данных численных экспериментов и, проходя через сеть, формирует на выходе значения, которые оцениваются метрикой, и на основе этих данных происходит корректировка внутренних значений весов нейронной сети. Применяется итерационный подход, который обеспечивает достижение удовлетворительного уровня точности работы нейросети.
Методология идентификации дефектов. В данной работе рассматривается методика определения геометрических параметров дефектов на основе данных, полученных в процессе воздействия на исследуемый объект. Эта задача входит в область неразрушающего контроля свойств и параметров объектов, ориентированных на обратную задачу механики твердого тела. Для решения данной задачи применяется системный подход с ключевой ролью искусственных нейронных сетей. Суть данного подхода заключается в выявлении нелинейных зависимостей между различными геометрическими характеристиками дефектов, такими как их размеры, глубина расположения, угол поворота и тип, и данными, полученными в процессе анализа.
В качестве таких данных могут выступать амплитудно-частотные и амплитудно-временные характеристики сигналов, полученных в ответ на воздействие. Этот метод позволяет эффективно выявлять и оценивать параметры дефектов и обеспечивает точное и надежное контролирование состояния объектов. Искусственные нейронные сети — это вычислительная модель, используемая в машинном обучении, информатике и других исследовательских дисциплинах, которая основана на большом наборе связанных простых единиц, называемых искусственными нейронами, подобных аксонам в биологическом мозге. Связи между нейронами передают сигнал активации разной величины. Если объединённые входящие сигналы достаточно сильны, нейрон активируется и сигнал перемещается к другим нейронам, связанным с ним. Такие системы можно обучить с помощью заранее приготовленных примеров, а не явно программировать. Этот метод дает значительное преимущество в тех областях, где решения и функции трудно выразить в традиционных формах. Нейронные сети, а также другие методы машинного обучения используются для решения различных задач, которые трудно решить с помощью традиционного программирования на основе таких правил, как компьютерное зрение и распознавание речи. ИНС обычно используются для моделирования сложных связей между входами и выходами с целью нахождения закономерностей в экспериментальных или иных данных (data mining) [15][16].
Разделение технической задачи на ряд подзадач, рассматриваемых отдельно друг от друга и решаемых с применением существующих средств и подходов, позволяет говорить о системном подходе к рассматриваемой задаче идентификации. Сочетание этих задач образует целую систему, которая решает производственные проблемы комплексно.
Предлагается инновационный метод идентификации и визуализации внутренних дефектов с применением ультразвукового неразрушающего контроля (УЗНК) и сверточной генеративной нейросетевой архитектуры. Сигнал УЗНК, зарегистрированный на поверхности объекта контроля, пропускается через обученную нейронную сеть. В результате обработки сетью генерируется высококачественное изображение, представляющее собой тепловую карту, демонстрирующую внутренний дефект объекта. Для иллюстрации эффективности предложенного метода и его перспектив в промышленных приложениях в качестве объекта исследования была выбрана металлическая стальная полоса. Внутри этой полосы предполагается наличие дефектов, которые могут имитировать как полости, так и жесткие включения. Также учитывается и возможность отсутствия дефектов. Следует отметить, что характеристики дефектов, такие как форма, размер и ориентация, могут значительно варьироваться, что представляет дополнительную сложность для задачи визуализации. Методология данного подхода состоит в проведении серии численных экспериментов, на основе результатов которых обучается глубокая нейронная сеть. Для формирования обучающего набора данных выполняется систематическое изменение механических параметров, геометрических характеристик, а также положения внутренних дефектов. Особое внимание уделяется моделированию процесса распространения акустической ультразвуковой волны внутри материала.
Этот инновационный подход к идентификации и визуализации внутренних дефектов предоставляет возможность более точного и эффективного контроля за качеством материалов и изделий в различных отраслях промышленности. Его применение может способствовать повышению надежности и безопасности конечных продуктов, что является важным аспектом в современной индустрии. На основе собранных данных строится и обучается оптимальная структура нейросетевой модели. В результате нейросетевая модель может реконструировать форму, размер и положение дефекта из необработанного ультразвукового сигнала, снятого на поверхности полосы. На рис. 1 показана блок-схема исследования.
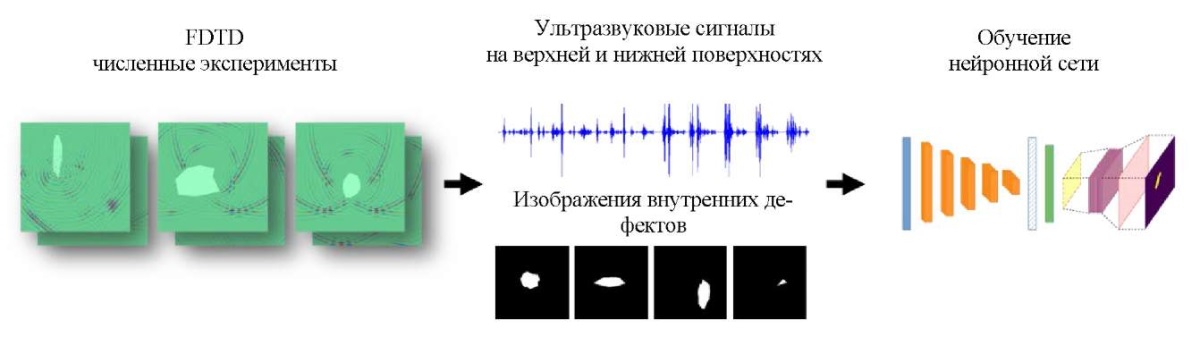
Рис. 1. Схема проведения серии численных экспериментов
с использованием метода конечных разностей во временной области (FDTD).
Фрагмент полосы в области дефекта
и распространение ультразвуковой волны (слева).
Построение набора данных, состоящего из ультразвуковых сигналов
и соответствующих бинарных изображений дефекта (в центре).
Построение архитектуры и обучение нейронной модели (справа)
Метод конечных разностей во временной области. Он был предложен Кейном Йи [17]. Решение дифференциальных уравнений в контексте моделирования сред с дисперсными и нелинейными свойствами выявляет уникальный класс методов — сеточные методы. Эти методы нашли широкое применение в разнообразных областях, начиная с геофизических задач и заканчивая задачами в оптическом диапазоне.
Один из эффективных методов исследования физических явлений в различных средах — метод конечных разностей во временной области. Он представляет собой ценный инструмент при решении акустических задач, а также может быть успешно применен в упругих средах.
Основным уравнением данной акустической модели в плоской постановке является:
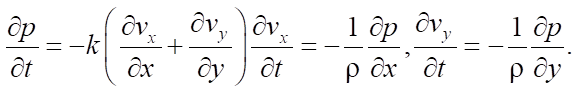
Происходит дискретизация скорости и акустического давления частиц моделируемого объекта в пространственной сетке. Путем последовательных вычислений значений этих параметров можно анализировать распространение звукового поля в течение определенного временного интервала. Этот метод обеспечивает возможность изучения различных физических процессов и явлений, предоставляя ценные данные о поведении среды с разнообразными характеристиками.
Метод конечных разностей во временной области хоть и был изначально разработан для решения акустических задач, обладает широким спектром применения и в других областях физики. В частности, он находит свое применение при моделировании распространения звука в различных средах, таких как воздух или жидкость. Такая универсальность метода делает его неотъемлемой частью научных и инженерных исследований в области физики и акустики.
Для проверки эффективности выбранной методики была разработана эталонная модель в расчетном пакете COMSOL, предназначенная для анализа распространения акустической ультразвуковой волны. В рамках данного исследования были использованы два основных численных метода: метод конечных элементов (МКЭ) и метод конечных разностей (FDTD). Модель представляет собой структуру в форме квадрата, изготовленную из стали, с присутствием внутреннего отверстия.
Значительные отличия в форме полученных сигналов объясняются различными методами задания источника ультразвуковых колебаний. В случае применения метода конечных элементов точки источника располагаются на окружности внутреннего отверстия, в то время как в методе конечных разностей во временной области источник представлен точкой, находящейся в узле сетки.
Однако следует отметить, что ограниченные размеры расчетной сетки не позволяют моделировать распространение акустических волн за пределами данной области. Для учета этого факта применяются специальные граничные условия, такие как поглощающие слои Мура или PML (Perfect Matched Layers). Эти граничные условия значительно уменьшают отражение акустических волн от границы расчетной области, что позволяет симулировать прохождение ультразвуковой волны внутрь структуры с высокой степенью точности.
Модель неразрушающего контроля. В качестве модели неразрушающего контроля используется стальная полоса, содержащая дефект. Её размер — 100x15 мм. Поглощающие слои установлены на левой и правой границах полосы. Верхняя и нижняя части прутка связаны с областями, которым заданы механические параметры воздуха. Дефекты представлены в виде выпуклых многоугольников. Разнообразие внутренних дефектов задается путем изменения количества сторон многоугольника, их длины, расстояния между вершинами и центром дефекта. Физические параметры дефектов изменяются относительно толщины полосы. Положение дефекта варьируется от 0,3 до 0,7, длина сторон — от 0,1 до 0,5. Область ввода импульса датчика расположена на верхней поверхности полосы. Колебания считываются как на верхней, так и на нижней поверхности. Таким образом, моделируется эхо- и теневой методы неразрушающего ультразвукового контроля.
В данном исследовании анализируется входной сигнал, представленный как фиксированное множество дискретных значений, зависящих от времени проведения эксперимента. Экспериментальное время было строго определено с учетом требования, чтобы зондирующий импульс, выпущенный на инициирующей стороне и направленный на противоположную поверхность тестируемого бруса, имел достаточное время для пройденного расстояния и возврата в точку источника.
Следует отметить, что использованная частота зондирующего импульса составляет 10 МГц, что обеспечивает высокую разрешающую способность экспериментальной системы. Это позволяет более точно изучать свойства бруса и его структурные характеристики, основываясь на анализе отраженного сигнала.
На рис. 2 показана схема проводимого численного эксперимента. Дефект расположен внутри стальной полосы. Источник ультразвукового сигнала обозначен красным цветом, точки считывания сигнала — зелеными метками. Сигнал также считывается в точках его излучения.
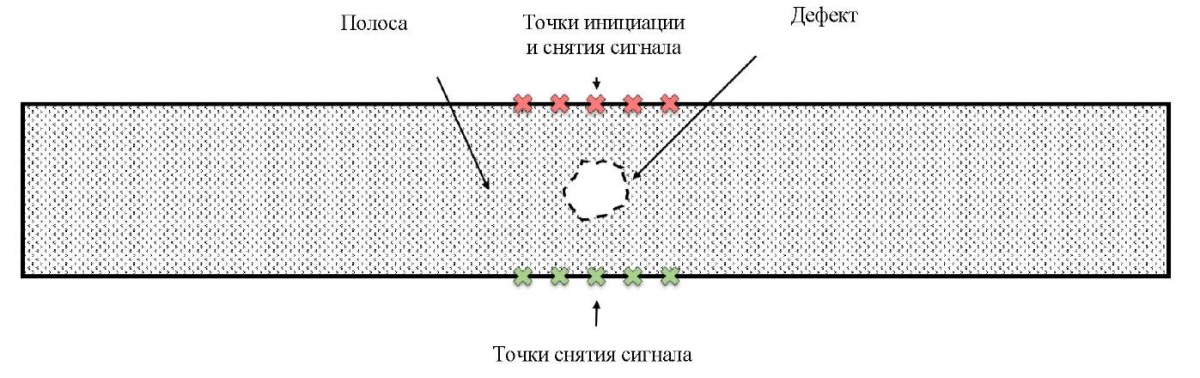
Рис. 2. Схема численного эксперимента
На рис. 3 представлены колебания ультразвуковых сигналов, полученных в указанных точках на верхней поверхности полосы (справа) и на нижней поверхности полосы (слева). Это имитирует расположение датчиков на противоположных поверхностях объекта контроля, данная модель предполагает, что датчики могут перемещаться вдоль полосы в поисках дефекта синхронно.
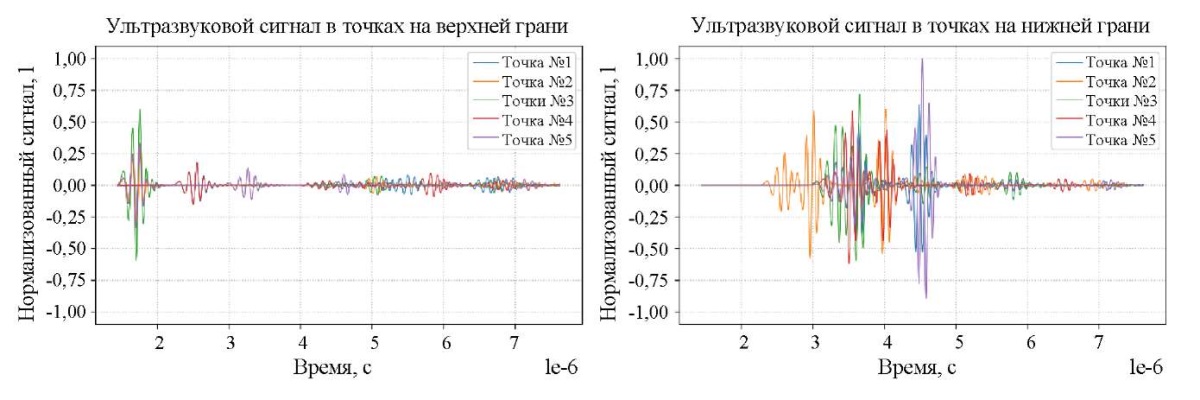
Рис. 3. Ультразвуковые сигналы на верхней и нижней поверхностях полосы,
полученные в результате численного моделирования
Модель нейронной сети. Сверточные нейронные сети (СNN) — это специальный нейросетевой инструмент для обработки дискретных данных (двумерные изображения, одномерные сигналы) [18]. В настоящее время это один из наиболее быстро развивающихся и перспективных инструментов глубокого обучения [19–21].
Сверточные нейронные сети эффективно применяются в различных областях, включая анализ видео и обработку временных рядов. Они позволяют обрабатывать временные ряды как одномерные массивы данных и выделять важные признаки в них с помощью операции свертки.
Для визуализации дефектов в объектах контроля используется архитектура модели, включающая слои одномерной свертки (Conv1D) и слои понижающей дискретизации (MaxPooling), для извлечения признаков из ультразвуковых сигналов. Затем данные передаются в полносвязный слой для анализа в контексте задачи визуализации дефектов. Вторая часть сети генерирует изображения, отображающие характеристики дефектов.
Для создания окончательного изображения дефекта данные из полносвязного слоя обрабатываются и подаются на двухмерный слой. Затем с использованием обучаемых сверточных слоев (Conv2D Transpose) формируется финальное изображение.
На рис. 4 показана архитектура сверточной нейронной сети с указанием размеров входных данных и количества сверточных фильтров для каждого слоя.
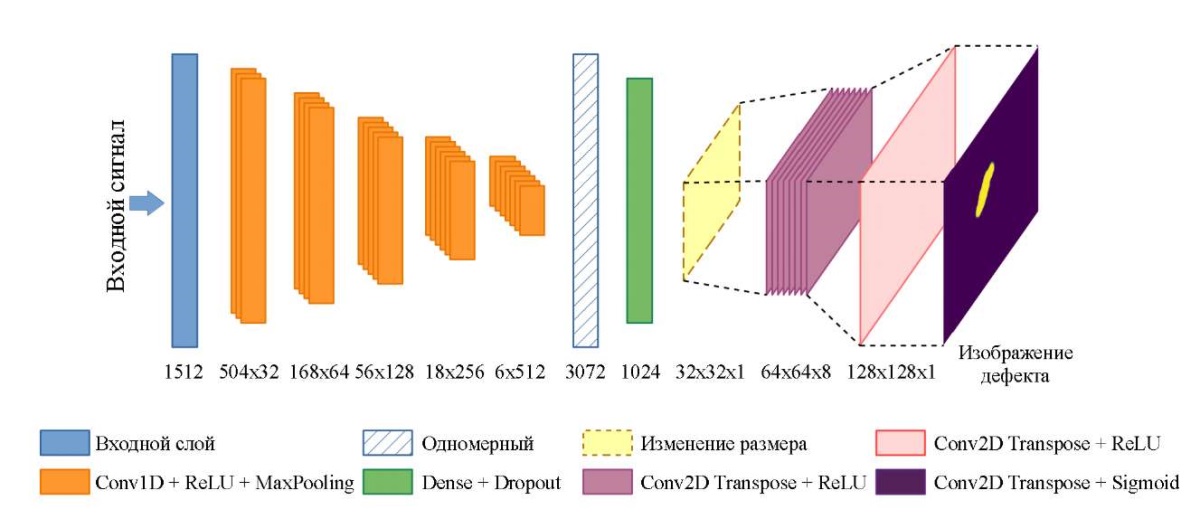
Рис. 4. Структура модели сверточной нейронной сети
Обучение и валидация модели. В рамках комплекса численных экспериментов были рассмотрены три случая. В случае А дефект моделирует полость, а параметры материала дефекта соответствуют параметрам воздуха. В случае B дефект моделирует жесткое включение и параметры дефекта имеют параметры материала, который является более жестким, чем сталь. В данном случае это карбид вольфрама. В случае C варьируются механические параметры дефектов, которые соответствуют параметрам газов, жидкостей и твердых материалов.
Для случаев A и B было решено в общей сложности 50 000 задач для различных геометрических параметров дефекта. Из них 35 000 экземпляров используются для обучения, 10 000 — для тестирования и 5 000 — для валидации. В случае C решается 60 000 задач с одинаковым процентным соотношением тестовых и валидационных образцов.
В процессе оценки производительности модели ключевыми метриками являются минимальная ошибка обучения и сокращение разрыва между ошибкой обучения и тестирования. Эффективность модели машинного обучения подвергается анализу с использованием различных методов регуляризации, таких как регуляризация Тихонова, также известная как L2-регуляризация. Инициализация весов, проводимая, например, методом Xavier, представляет собой значимый этап обучения нейронных сетей.
Одним из средств, применяемых для уменьшения внутреннего ковариационного сдвига и стабилизации обучения нейронных сетей, является метод пакетной нормализации. С целью повышения стабильности и обобщающей способности модели применяются разнообразные приемы регуляризации, такие как ранняя остановка и Dropout.
Необходимо отметить, что в данной исследовательской работе не применяется аугментация данных ввиду обширного объема обучающей выборки. Также не проводится балансировка набора данных, что, тем не менее, имеет свои преимущества в связи с нормальным распределением дефектов по размерам.
Следует подчеркнуть, что обучение нейронной сети представляет собой задачу оптимизации, где выбор соответствующей функции потерь играет важнейшую роль. Например, в задачах компьютерного зрения и семантической сегментации коэффициент схожести Жаккара может оказаться весьма значимым. В данной работе рассматривается применение коэффициента схожести Жаккара в контексте задачи обнаружения и сегментации объектов, что позволяет достичь более точных и устойчивых результатов при анализе изображений:
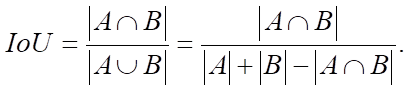
В данном контексте функция потерь выражается как обратное значение коэффициента сходства Жаккара (1–IoU) и представляет собой метрику, которая оценивает различие между двумя экземплярами. Метрика Жаккара известна в области анализа данных и машинного обучения как индикатор пересечения и сходства множеств.
Для оценки эффективности модели нейронной сети в процессе валидации данная метрика применяется как один из критериев. Она позволяет определить степень соответствия между выходом модели и эталонными данными, что важно для анализа и улучшения работы нейронных сетей в задачах обработки информации:
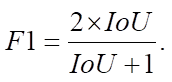
В настоящем исследовании использован один из наиболее распространенных алгоритмов оптимизации, именуемый Adam. Для решения поставленных задач машинного обучения и обучения нейронных сетей применяются одни их наиболее признанных и широко используемых библиотек — TensorFlow и Keras. Эти программные продукты выступают в настоящее время как стандартные инструменты для создания и обучения нейронных моделей и включают в себя передовые технологии в данной области.
Для достижения высокой точности работы моделей было проведено обучение в течение 30 эпох в каждом из трех рассмотренных случаев: A, B и C.
Нейросетевой подход для решения обратных задач уже зарекомендовал себя с хорошей стороны [22–24]. С углублением в область машинного обучения и последующим развитием новых методологий открываются передовые инструменты для анализа данных и решения традиционных задач в механике и дефектоскопии. Одним из значительных научных достижений в данной сфере представляется сверточная нейронная сеть, созданная специально для решения проблемы визуализации внутренних дефектов с использованием методов ультразвукового неразрушающего контроля. Примечательной характеристикой данной модели является её относительно небольшой объем, составляющий 37,2 миллиона параметров. Этот факт обеспечивает высокую эффективность процесса обучения и расширяет область её применения в разнообразных смежных областях. Для более эффективного моделирования распространения ультразвуковых волн в данном исследовании был выбран метод конечных разностей во временной области. Этот выбор метода существенно увеличил скорость вычислений по сравнению с предыдущими подходами, применяемыми в ранее проведенных научных исследованиях.
Результаты исследования. В данной работе рассматривались три состояния внутреннего дефекта. В случае А дефект моделирует полость, при этом параметры среды в области дефекта соответствуют параметрам воздуха. В случае B дефект моделирует жесткое включение, при этом параметры среды имеют параметры более жесткого материала, чем материал полосы. В данном случае это карбид вольфрама. В случае C проводится вариация механических параметров дефекта, которые соответствуют параметрам газов, жидкостей и твердых материалов.
Результаты этого исследования, представленные на рис. 5, демонстрируют эффективность нейронных сетей в анализе и восстановлении информации о дефектах. Визуализированные фрагменты полосы в области дефекта отображаются на графике. Реальный дефект обозначен сплошной черной линией, тогда как форма и положение дефекта, предсказанные нейронной сетью, представлены пунктирной красной линией. Анализ рисунка позволяет утверждать, что нейросетевая модель способна восстановить размер дефекта, точно определить его местоположение, частично воспроизвести его форму и даже установить ориентацию. Эти результаты подтверждают потенциал нейронных сетей в решении задач обработки и анализа изображений с применением высокой точности и надежности.
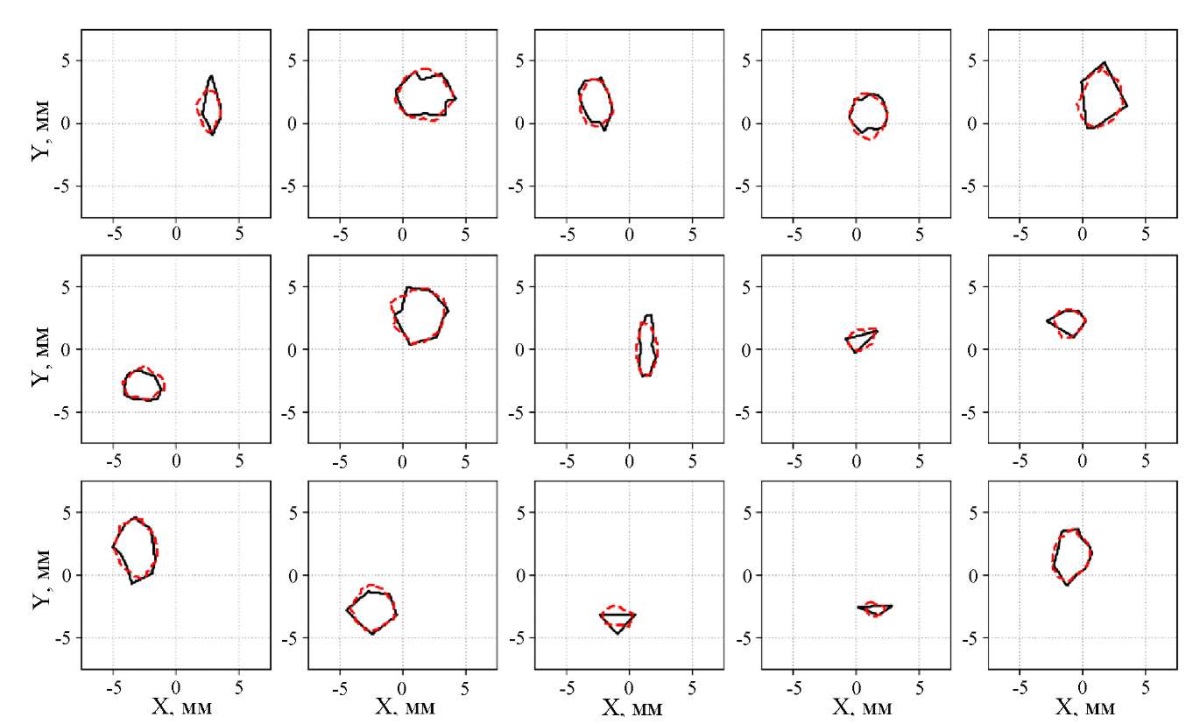
Рис. 5. Результаты визуализации дефектов.
Реальный дефект выделен черным цветом.
Прогноз нейронной сети выделен красным цветом.
Валидация проводилась для каждого из случаев. Для оценки общей эффективности модели использована метрика F1. В целом точность предложенного метода находится на высоком уровне. Среднее значение F1 для всего валидационного набора составляет 92 % для случая A, 90 % — для случая B и 85 % — для случая C.
На рис. 6 показана зависимость точности визуализации дефекта от его размера. Размер дефекта — это максимальное расстояние между вершинами многоугольника, имитирующего дефект. Полученные данные показывают, что для успешной визуализации дефектов длина волны ультразвукового импульса должна быть в десятки раз меньше размера дефекта. На рисунке также показано влияние несбалансированного набора данных на точность работы нейронной сети. Для дефектов наибольшего размера ошибка визуализации увеличивается.
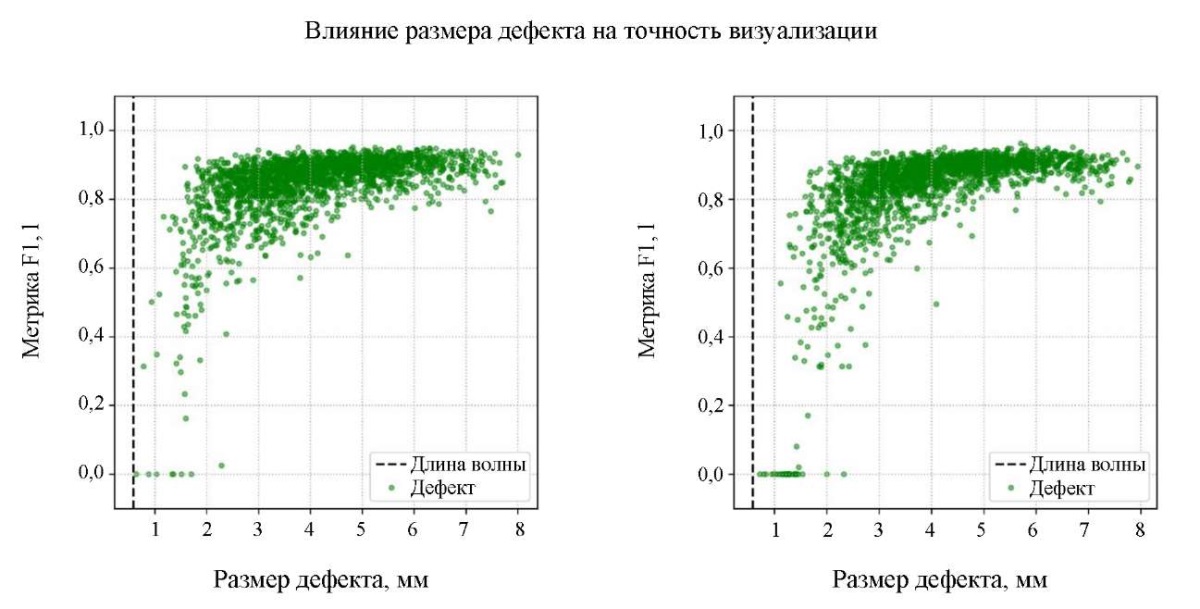
Рис. 6. Зависимость точности визуализации дефектов
от их размера для случаев A (слева) и B (справа).
Черной штриховой линией показана длина волны
зондирующего ультразвукового импульса
Авторы также проанализировали влияние механических параметров дефекта на точность их визуализации. Для каждой нейронной сети из случаев A, B и C проведена валидация на наборе данных с различными механическими параметрами дефектов. Данное исследование показывает, насколько хорошо обученные нейросетевые модели способны проводить визуализацию различных типов дефектов, в том числе дефектов, которые отсутствовали в обучающих наборах. Для простоты восприятия параметры плотности материала и скорости звука в материалах представлены как относительные:
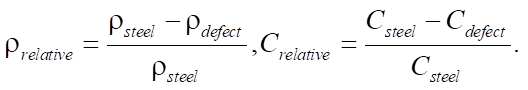
На рис. 7 показано, как точно нейросетевые модели A, B и C проводят визуализацию дефектов для широкого спектра параметров. В случае, когда нейронная сеть обучена только на наборе данных A, когда дефект моделирует полость, приемлемая точность достигается только для дефектов с 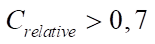 . В случае B, когда дефект моделирует жесткое включение, точность работы нейронной сети существенно ухудшается при отклонении значения
. В случае B, когда дефект моделирует жесткое включение, точность работы нейронной сети существенно ухудшается при отклонении значения 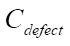 от заданного в эксперименте. В случае C, когда нейронная сеть обучалась на наборе данных с различными параметрами дефектов, результаты работы устойчивы на всей области изменения параметров. Исключением являются дефекты со значением
от заданного в эксперименте. В случае C, когда нейронная сеть обучалась на наборе данных с различными параметрами дефектов, результаты работы устойчивы на всей области изменения параметров. Исключением являются дефекты со значением 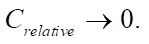 В этих случаях скорости звука в материале полосы и материале дефекта очень близки друг к другу. Также можно сделать вывод, что на точность предложенного метода в большей степени влияет изменение параметра C, чем
В этих случаях скорости звука в материале полосы и материале дефекта очень близки друг к другу. Также можно сделать вывод, что на точность предложенного метода в большей степени влияет изменение параметра C, чем 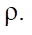 Таким образом продемонстрированы границы применения различных нейросетевых моделей для идентификации дефектов с различными механическими параметрами.
Таким образом продемонстрированы границы применения различных нейросетевых моделей для идентификации дефектов с различными механическими параметрами.
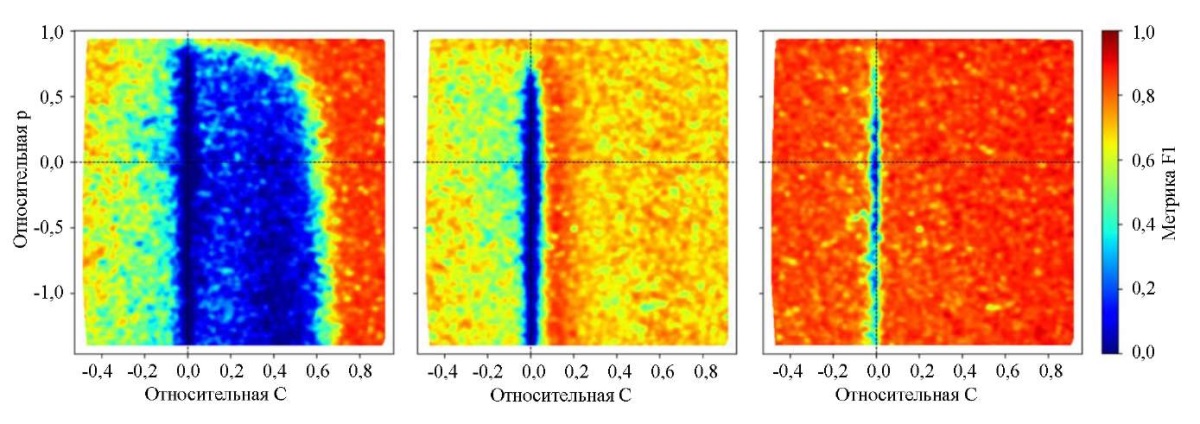
Рис. 7. Влияние параметров дефекта на точность работы нейронных сетей.
Нейронная сеть A слева, нейронная сеть B в центре, нейронная сеть C справа
Таким образом, можно заключить, что разработанная авторами модель нейронной сети представляет собой важный научный шаг в области неразрушающего контроля, обеспечивая эффективные инструменты для визуализации внутренних дефектов и создавая новые перспективы для применения в индустрии и научных исследованиях [24–25].
Обсуждение и заключение. Полученные результаты предоставляют новый взгляд на область неразрушающего контроля и его потенциал в обнаружении внутренних дефектов в различных материалах и структурах. В представленном исследовании предложен новаторский метод, основанный на применении сверточных нейронных сетей, с целью экспрессной диагностики дефектов в структуре материалов. Ключевым аспектом данной научной работы является продемонстрированная потенциальная эффективность применения сверточных нейронных сетей для повышения качества ультразвуковой визуализации. Авторы разработали модель, предназначенную для неразрушающего контроля, а также сформировали соответствующие наборы данных, используемых для обучения искусственных нейронных сетей. Эта сверточная нейросетевая модель способна не только точно определять форму, но и положение, и ориентацию внутренних дефектов в твердом материале. Полученные экспериментальные данные демонстрируют информативность ультразвукового сигнала, а также его способность точно передавать реальные характеристики внутренних дефектов.
Авторы проанализировали несколько типов дефектов, в каждом из которых уделяется особое внимание: в первом случае дефект классифицируется как А и моделируется в виде полости, во втором случае — как В и представляет собой жесткое включение, в третьем — как С, с различными механическими параметрами дефекта. Во всех сценариях исследования выявлено важное воздействие размера дефекта на точность ультразвуковой визуализации. Кроме того, полученные результаты однозначно подтверждают, что выбор частоты зондирующего сигнала имеет критическое значение и должен быть оптимизирован так, чтобы длина волны была значительно меньше размеров внутренних дефектов.
После проведения системной валидации сверточных нейронных сетей в контексте каждого из вышеупомянутых типов дефектов (A, B и C) для различных значений механических характеристик дефектов был установлен диапазон значений механических параметров дефекта, в пределах которого предложенный метод не обеспечивает достаточно качественную визуализацию.
В заключение следует отметить, что разработанные в ходе данного исследования методики и технические решения имеют большое значение для дальнейших исследований в области дефектоскопии и решения обратных задач в широком контексте научных и практических приложений.
Список литературы
1. Samanta S., Mandal A., Thingujam J.S. Application of ANN in Identifying Defects in Impacted Composite. Procedia Materials Science. 2014;6:926–930. https://doi.org/10.1016/j.mspro.2014.07.162
2. Bar H.N., Bhat M.R., Murthy C.R.L. Identification of Failure Modes in GFRP Using PVDF Sensors: ANN Approach. Composite Structures. 2004;65(2):231–237. https://doi.org/10.1016/j.compstruct.2003.10.019
3. Dong-Fang Chen, Xia-Ting Feng, Ding-Ping Xu, Quan Jiang, Cheng-Xiang Yang, Pin-Pin Yao. Use of an Improved ANN Model to Predict Collapse Depth of Thin and Extremely Thin Layered Rock Strata during Tunneling. Tunnelling and Underground Space Technology. 2016;51:372–386. https://doi.org/10.1016/j.tust.2015.09.010
4. Черпаков А.В., Акопьян В.А., Соловьев А.Н. Алгоритм многопараметрической идентификации дефектов стержневых конструкций. Техническая акустика. 2013;13:1–11.
5. Rajeswari C., Sathiyabhama B., Devendiran S., Manivannan K. A Gear Fault Identification Using Wavelet Transform, Rough Set Based GA, ANN and C4.5 Algorithm. Procedia Engineering. 2014;97:1831–1841. https://doi.org/10.1016/j.proeng.2014.12.337
6. Соловьев А.Н., Шевцов М.Ю. Реконструкция дефектов в упругих телах сочетанием генетического алгоритма и метода конечных элементов. Вестник Донского государственного технического университета. 2016;16(2):5–12. https://doi.org/10.12737/19686
7. Yasser S. Mohamed, Hesham M. Shehata, Mohamed Abdellatif, Taher H. Awad. Steel Crack Depth Estimation Based on 2D Images Using Artificial Neural Networks. Alexandria Engineering Journal. 2019;58(4):1167–1174. https://doi.org/10.1016/j.aej.2019.10.001
8. Yanfeng Gong, Hongliang Shao, Jun Luo, Zhixue Li. A Deep Transfer Learning Model for Inclusion Defect Detection of Aeronautics Composite Materials. Composite Structures. 2020;252:112681. https://doi.org/10.1016/j.compstruct.2020.112681
9. Adisorn Sirikham, Yifan Zhao, Haochen Liu, Yigeng Xu, Stewart Williams, Jörn Mehnen. Three-dimensional Subsurface Defect Shape Reconstruction and Visualisation by Pulsed Thermography. Infrared Physics & Technology. 2020;104:103151. https://doi.org/10.1016/j.infrared.2019.103151
10. Luiz Felipe Simões Hoffmann, Francisco Carlos Parquet Bizarria, José Walter Parquet Bizarria. Detection of Liner Surface Defects in Solid Rocket Motors Using Multilayer Perceptron Neural Networks. Polymer Testing. 2020;88:106559. 10.1016/j.polymertesting.2020.106559
11. Vladimir Puzyrev. Deep Learning Electromagnetic Inversion with Convolutional Neural Networks. Geophysical Journal International. 2019;218(2):817–832. https://doi.org/10.1093/gji/ggz204
12. Soloviev A.N., Sobol B.V., Vasiliev P.V. Ultrasonic and Magnetic Flow Inspection Methods of Identification of Cracks in the Pipe Coupled with Artificial Neural Networks. In book: Parinov I., Chang S.H., Jani M. (eds). Advanced Materials. Springer Proceedings in Physics. Cham: Springer; 2017. P. 381–395. https://doi.org/10.1007/978-3-319-56062-5_32
13. Soloviev A., Sobol B., Vasiliev P., Senichev A. Generative Artificial Neural Network Model for Visualization of Internal Defects of Structural Elements. In book: Parinov I., Chang S.H., Long B. (eds). Advanced Materials. Springer Proceedings in Materials. Cham: Springer; 2020. P. 587–595. https://doi.org/10.1007/978-3-030-45120-2_48
14. Sobol B.V., Soloviev A.N., Rashidova E.V., Vasiliev P.V. Identification of Crack-like Defect and Investigation of Stress Concentration in Coated Bar. PNRPU Mechanics Bulletin. 2019;(4):165–174. https://doi.org/10.15593/perm.mech/2019.4.16
15. Fang X., Luo X., Jiong Tang. Structural Damage Detection Using Neural Network with Learning Rate Improvement. Computers and Structures. 2005;83(25–26):2150–2160. https://doi.org/10.1016/j.compstruc.2005.02.029
16. Soloviev A., Sobol B., Vasiliev P. Identification of Defects in Pavement Images Using Deep Convolutional Neural Networks. In book: Parinov I., Chang S.H., Kim Y.H. (eds). Advanced Materials. Springer Proceedings in Physics. Cham: Springer; 2019. P. 615–626. https://doi.org/10.1007/978-3-030-19894-7_46
17. Kane Yee. Numerical Solution of Initial Boundary Value Problems Involving Maxwell's Equations in Isotropic Media. IEEE Transactions on Antennas and Propagation. 1966;14(3):302–307. https://doi.org/10.1109/TAP.1966.1138693
18. LeCun Y., Boser B., Denker J.S., Henderson D., Howard R.E., Hubbard W., et al. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Computation. 1989;1(4):541–551. https://doi.org/10.1162/neco.1989.1.4.541
19. Goodfellow I., Bengio Y., Courville A. Deep Learning. Cambridge, MA: MIT Press; 2016. 777 p.
20. Krizhevsky A., Sutskever I., Hinton G.E. ImageNet Classification with Deep Convolutional Neural Networks. Communications of the ACM. 2017;60(6):1097–1105. http://dx.doi.org/10.1145/3065386
21. Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. Deep Residual Learning for Image Recognition. In: Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). New York City, UA: IEEE; 2016. P. 770–778 https://doi.org/10.1109/CVPR.2016.90
22. De Angelo M., Spagnuolo M., D’Annibale F., Pfaff A., Hosche K., Misra A., et al. The Macroscopic Behavior of Pantographic Sheets Depends Mainly on Their Microstructure: Experimental Evidence and Qualitative Analysis of Damage in Metallic Specimens. Continuum Mechanics and Thermodynamics. 2019;31:1181–1203. https://doi.org/10.1007/s00161-019-00757-3
23. Nagatani Y., Okumura S., Wu S., Matsuda T. Two-dimensional Ultrasound Imaging Technique Based on Neural Network Using Acoustic Simulation. arXiv preprint. arXiv:2004.08775. 2020. https://doi.org/10.48550/arXiv.2004.08775
24. Solov’ev A.N., Sobol’ B.V., Vasil’ev P.V. Ultrasonic Location of Inner Crack Defects in a Compound Elastic Cylinder Using an Artificial Neural-Network Apparatus. Russian Journal of Nondestructive Testing. 2016;52(3):119–124. https://doi.org/10.1134/S1061830916030098
25. Soloviev A.N., Sobol B.V., Vasiliev P.V., Senichev A.V., Novikova A.I. Identification of Defects in a Coating Wedge Based on Ultrasonic Non-destructive Testing Methods and Convolutional Neural Networks. PNRPU Mechanics Bulletin. 2023;(1):111–124. https://doi.org/10.15593/perm.mech/2023.1.11
Об авторах
Б. В. СобольРоссия
Борис Владимирович Соболь, доктор технических наук, профессор, заведующий кафедрой информационных технологий, Scopus ID
344003, г. Ростов-на-Дону, пл. Гагарина, 1
А. Н. Соловьев
Россия
Аркадий Николаевич Соловьев, доктор физико-математических наук, профессор, ResearcherID, ScopusID
295015, г. Симферополь, пер. Учебный, д. 8
П. В. Васильев
Россия
Павел Владимирович Васильев, старший преподаватель кафедры информационных технологий, ScopusID
344003, г. Ростов-на-Дону, пл. Гагарина, 1
А. А. Ляпин
Россия
Александр Александрович Ляпин, доктор физико-математических наук, профессор, заведующий кафедрой информационных систем в строительстве, ScopusID
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Соболь Б.В., Соловьев А.Н., Васильев П.В., Ляпин А.А. Моделирование процессов ультразвуковой дефектоскопии в задаче поиска и визуализации внутренних дефектов в узлах агрегатов и конструкций. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):433-450. https://doi.org/10.23947/2687-1653-2023-23-4-433-450. EDN: RKAOTZ
For citation:
Sobol B.V., Soloviev A.N., Vasiliev P.V., Lyapin A.A. Modeling of Ultrasonic Flaw Detection Processes in the Task of Searching and Visualizing Internal Defects in Assemblies and Structures. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):433-450. https://doi.org/10.23947/2687-1653-2023-23-4-433-450. EDN: RKAOTZ












































