Scroll to:
Optimal Vibration Fields in Problems of Modeling Dynamic States of Technical Objects
https://doi.org/10.23947/2687-1653-2024-24-1-7-22
EDN: FAKNHP
Abstract
Introduction. Vibration interaction control is timely in production processes related to liquid and bulk media, systems of solids experiencing kinematic or force disturbances. At the same time, there is no single methodological basis for the formation of vibrational interactions. The issues of constructing optimal vibration fields of technical objects have not been addressed. The objective of the study is to develop a structural approach to the development of mathematical models in the problems of formation, evaluation, and correction of vibration fields of technical objects under conditions of intense force and kinematic loads. The task is to build vibration fields that are optimal in terms of the set of requirements, with the possibility of selecting the criterion of optimality of the vibration field of a technical object.
Materials and Methods. A structural approach was used as the basic methodology. It was based on a comparison of mechanical vibratory systems used as computational schemes of technical objects, and structural schemes of automatic control systems, which are equivalent in dynamic terms. Lagrange formalism, elements of operational calculus based on Laplace integral transformations, sections of vibration theories, algebraic methods, and the theory of spline functions were used for structural mathematical modeling.
Results. An approach to the selection of criteria for the optimality of vibration fields based on minimizing the residual of vibration fields for various required conditions was proposed. The problem was considered within the framework of a mechanical vibratory system formed by solids. It was shown that the optimal vibration field was determined by an external disturbance and was to satisfy condition Ay̅ = b. There, A — matrix mapping the operator of conditions to the shape of the vibration field at control points; b — vector of values of vibration field characteristics; “–” above y meant the vibration amplitude of the steady-state component of the coordinate. To evaluate the field with account for noisy or unreliable requirements for dynamic characteristics, the smoothing parameter was used, indicating the priority of the criterion of optimality of the vibration field shape. The construction of a field for a mechanical vibratory system showed that the value of the vibration amplitudes of generalized coordinates remained constant when the frequency of external kinematic disturbances changed. Two approaches to the correction of the field optimality criteria were considered: equalization of the vibration amplitudes of the coordinates of a technical object and the selection of an energy operator.
Discussion and Conclusion. The development of the applied theory of optimal vibration fields involved, firstly, the correlation of the energy operator and the operator of the requirements for the shape of the vibration field in the theory of abstract splines. The second pair of comparable elements was the criterion of optimality of the vibration field and a system of requirements for the characteristics of the field at control points. The structural theory of optimal vibration fields improved in this way will find application in various industries. Accurate calculations in the formation, assessment, and correction of the states of systems under vibration loading are required in the tasks of increasing the durability of structures, improving measurements in complex vibratory systems, and developing new technologies and materials.
Keywords
For citations:
Eliseev A.V., Kuznetsov N.K. Optimal Vibration Fields in Problems of Modeling Dynamic States of Technical Objects. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):7-22. https://doi.org/10.23947/2687-1653-2024-24-1-7-22. EDN: FAKNHP
Introduction. Features of vibration interactions are taken into account when creating production technologies [1]. The use of vibration methods for the intensification of production processes requires the development of mathematical modeling of the dynamic states of technical objects under conditions of vibration loading. The scientific and applied literature studies issues of the theory of vibrations and automatic control, theoretical mechanics, and dynamics of machines [2]. In particular, in the dynamics of machines, features of vibration interactions are taken into account in two types of tasks. The first one is the tasks of vibration isolation and vibroprotection [3]. The second includes tasks related to the assessment, formation, and correction of the states of technical objects under conditions of intense force or kinematic loads [4]. In the latter case, attention is drawn to the effects of vibrational interactions, which are used in the following production processes:
- transportation of rocks;
- fractionation of bulk materials;
- hardening of surfaces of long elements of aircraft structures;
- spatial orientation of parts during assembly.
Tasks of vibroprotection are related to solving the problems of railway transport safety. It is referred, specifically, to the issues of the dynamic state of the suspension elements [5], noise and vibration [6]. The problems of estimating dynamic states caused by significant loads arise when evaluating the vibration characteristics of a rail track with composite sleepers [7]. Harmful vibrations propagating in the urban environment from a moving train require control, and in this case, an assessment of complex dynamic states is also needed [8]. Similar examples are related to tracking the interactions of a wagon trolley with rails [9]. The dynamic state is formed when the sliding contact of the pantograph head and the contact wire is violated [10]. In this context, it is worth mentioning the tasks of analyzing the reaction of the rail to vertical impacts from a moving vehicle [11].
Another extensive group of tasks requiring an assessment of the dynamic states of elements is the vibration processes of production machines [12]. Thus, the dynamic state of vibration screening machines depends on the formation of dynamic states of several housings, which can be considered as solids, taking into account the nature of elastic linkage between them [13]. An essential factor determining the dynamic states of production facilities is the vibration frequency [14]. Separately, it is necessary to mention vibrating transport machines, whose dynamic state determines characteristics of movements [15].
It is worth noting the result of generalization of the tasks of assessment, formation, and correction of dynamic states of technical objects under conditions of intense loads. This approach has opened up the possibility to clarify the idea of how the distributions of the amplitudes of vibrations in the coordinates of control points depend on the connectivity of external disturbances.
Parameters of external vibration disturbances determine the possibilities of implementing dynamic effects that can act in different directions:
- constitute a danger to the performance of technical facilities;
- increase the process performance.
An example of a negative effect is exceeding the permissible values of the vibration amplitudes. Useful effects include a significant decrease in the amplitudes of coordinate vibrations and the establishment of a certain amplitude distribution.
In the tasks of vibration hardening of long-length parts, dynamic effects can be understood as the coincidence of the vibration patterns of the control points of the working bodies of vibrating production machines. This maintains the one-dimensionality and uniformity of the vibration field, which is consistent with the requirements for the dynamic quality of the interactions of the working medium and the surface of the hardened part. The required motion mode of the working body can be expressed using the conditions of equality of the vibration amplitudes of the control points. To study the concept of a vibrational field, the concept of a dynamic state at a point is generalized — at the same time, a set of points distributed over a certain variety of points of a solid body or a system of solids is considered [16].
In problems of vibrational interactions, a number of dynamic effects can be displayed using lever, elastic, and interpartial unilateral constraints. All of them are factors of specific dynamic effects that manifest themselves under the influence of external disturbances of a special configuration. To determine such configurations of external disturbances providing dynamic effects, it is proposed to develop a methodological framework that allows building mathematical models of vibration fields, taking into account the system of requirements for the features of interactions of system elements. The proposed methodological framework should have:
- an effective mathematical apparatus;
- a tool for visual display of structural features;
- capabilities to build dynamic analogies to generalize the developed methods to a broad class of physical processes.
Materials and Methods. A structural approach based on a comparison of mechanical vibratory systems and automatic control systems can serve as a methodological framework [17]. In this case, the mechanical vibratory system is considered as a design scheme of a technical object. It is compared to the structural scheme of a dynamically equivalent automatic control system. The established correspondence makes it possible to analyze and evaluate the dynamic characteristics of technical objects, taking into account the ideas about the steady-state forms of vibrations of a mechanical system based on the apparatus of the theory of automatic control [18]. The technology of structural mathematical modeling has features related to the assessment of dynamic states. Transfer functions of structural schemes are used for it. The input signals for these functions are external disturbances, the output signals are vibrations in the coordinates of the object being evaluated. Each coordinate of the system can be correlated with an indicator of the amplitude of the steady-state vibration. This allows us to consider the distribution of amplitudes over the points of the system as a vibration field of a technical object. The construction of a vibration field, taking into account a number of requirements, belongs to the class of inverse problems of dynamics, which in general may be incorrect. One of the methods for solving ill-posed problems is related to the regularization of the initial problem by introducing optimality criteria.
The listed features of the assessment of the dynamic states of technical objects indicate the need to develop a common approach in the methodology of constructing vibration fields, taking into account the criteria of optimality. At the same time, the methodology for the formation, evaluation, and correction of vibration fields with specified characteristics is not sufficiently detailed. Specifically, it is not possible to build vibration fields according to optimality criteria.
The presented research is devoted to the development of the techniques of structural mathematical modeling. For this purpose, we solve a class of specific problems of constructing vibration fields of technical objects with conditions for vibration amplitudes that reflect the requirements for dynamic effects and take into account the criteria of optimality.
Basic provisions. Formulation of the problem. A model mechanical vibratory system formed by a set of solids under conditions of vibrational loading of a kinematic origin is considered. The model system (Fig. 1) has 5 degrees of freedom, consists of 4 links in the form of solid-state rods with masses Mi, moments of inertia Ji, centers of gravity at point Oi, spaced from extreme points Аi and Аi+1 at distances l1i and l2i, where i = 1…4.
Solid bodies in the form of rods are articulated at the extreme points — these are the attachment points of elastic elements mounted on support surfaces that perform in-phase harmonic vibrations (Fig. 1).

Fig. 1. Mechanical vibratory system formed by solids A1 A2, A2 A3, A3 A4, A4 A5: A — articulation points of solids;
Оi — centers of gravity; zi — support surfaces; Ji — moments of inertia
Under the influence of external kinematic disturbances zi from the support surfaces, the system performs small steady-state vibrations relative to the static equilibrium position. External kinematic disturbances are connected
in-phase vibrations:
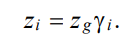 (1)
(1)
Here, zg — harmonic disturbance of type Asin(ωt), where ω — frequency and γi — connection coefficients of external disturbances; i = 1…5. In general, the connection coefficients (1) are external disturbances of a certain structure.
The required dynamic effects are provided by a set of model conditions, namely: the vibration amplitudes of the coordinates of the control points of a technical object take fixed values regardless of the frequency of external disturbances.
The task is to determine for a mechanical vibratory system such external kinematic disturbances that the corresponding vibration field at the control points satisfies a given set of conditions in the form of fixed vibration amplitudes.
Research Results
Mathematical model. To compile a system of differential equations, the coordinates {y1, y2, y3, y4, y5} of the displacements of point Аi, i = 1...5 relative to the positions of static equilibrium are studied. The following coordinates are considered along with coordinates {yi}:
- coordinates {z01, z02, z03, z04, z05}, displaying the displacements of the centers of gravity Оi of rods relative to the positions of static equilibrium;
- coordinates {φ1, φ2, φ3, φ4, φ5} of small rotation angles around the centers of gravity.
Coordinates z0i, φi, yi are related by expressions:
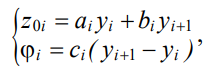 (2)
(2)
Here, 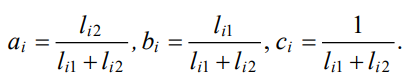
A mathematical model in the form of Lagrange differential equations of the 2nd kind is based on expressions for potential and kinematic energy. They can be represented in a matrix form using the scalar product ⟨,⟩ vectors in Rn:

Taking into account expressions (2)–(5), Lagrange equations of the 2nd kind take the form:
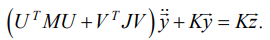 (6)
(6)
It is assumed that the initial conditions are zero. In this case, the integral Laplace transformations lead (6) to a system of algebraic equations:
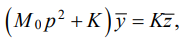 (7)
(7)
where 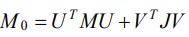 — matrix of the system, sign “–” above vectors y and z denotes the Laplace transformation [19].
— matrix of the system, sign “–” above vectors y and z denotes the Laplace transformation [19].
Using the methods of [18], algebraic system (7) can be represented as a block diagram of a dynamically equivalent automatic control system (Fig. 2).
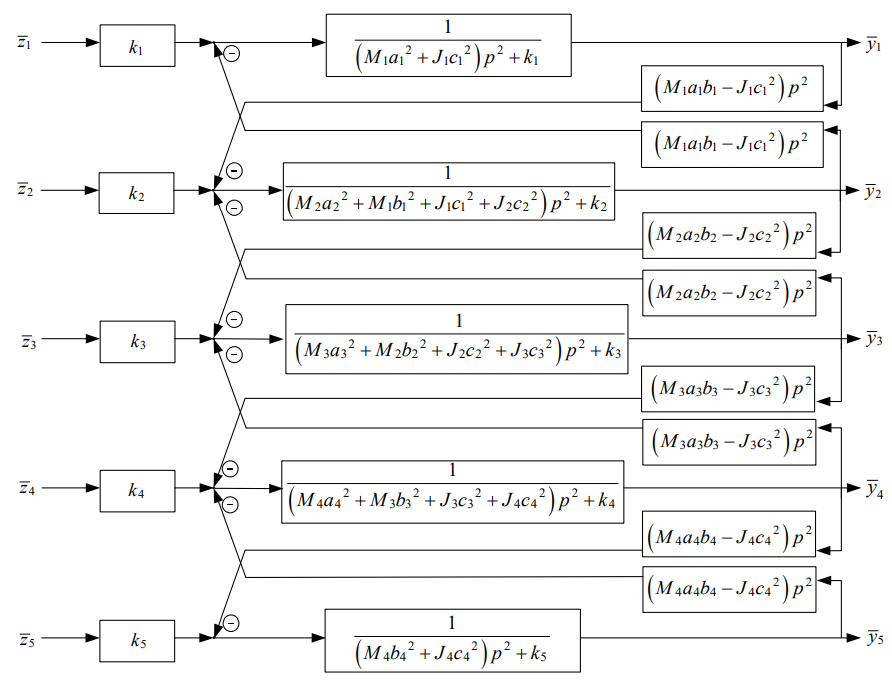
Fig. 2. Block diagram of mechanical vibratory system (Fig. 1): 
Transfer functions can be constructed based on a block diagram for a fixed set of connection coefficients γi. They are determined by the selection of an object, whose dynamic state is estimated by the expressions:
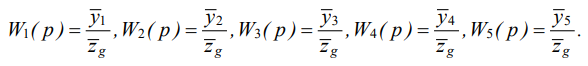 (8)
(8)
Physically, we consider the amplitude-frequency characteristics of transfer functions (8) as lever connections representing the ratio of the amplitudes of the coordinate vibrations {yi} to the vibration amplitude of the external kinematic disturbance {zg}.
Within the framework of the lever interpretation, the positive branches of the amplitude-frequency response display lever connections of the 1st kind (implemented by double-arm levers). Negative branches represent lever connections of the 2nd kind (implemented by double-arm levers). The modes of resonance and dynamic damping of vibrations display degenerate lever connections, which can be represented by conditional virtual levers with zero or infinite arms.
The selection of the structure of external kinematic disturbances through setting the connection coefficients {γi} uniquely determines the amplitudes of system coordinate vibrations. At the same time, the requirements imposed on the vibration amplitudes may:
- either imply ambiguity of the solution;
- either directly contradict each other;
- or, due to large errors, allow only partial compliance.
In these cases, criteria for the selection of external disturbances, which uniquely determine the vibration field according to the set of requirements, are needed. The logical approach for this task is based on the fact that external kinematic disturbances providing the required conditions can be determined by the criterion of optimality of vibration fields. The principle of this criterion is as follows: the vibration amplitudes of a technical object are selected in such a way that they deliver a minimum to a certain energy functional [20].
Formation of vibration fields of mechanical vibratory systems based on the optimality criterion. Within the framework of the model problem, it is assumed that a certain condition is set at points Ai1, Ai2…Aik of vibration field {yi}, i = 1…n of the mechanical vibratory system. It consists in the fact that amplitudes {yik}, k = 1…m take fixed values {y01…y0m}:
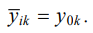 (9)
(9)
Here, k = 1…m, where m displays the number of points at which conditions for amplitudes are set; in this case, and further in the text, the sign “–” above y or z means the vibration amplitude of the steady component of the coordinate, unless otherwise specified. At the remaining points {yi, i = 1…n} / {yik, k = 1…m}, the requirements for the values of the vibration field are not set.
Needed requirements (9) can be presented in the form:
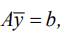 (10)
(10)
where A — matrix displaying the condition operator on the shape of the vibration field at the control points; b — vector of vibration field characteristics values [20].
In general, the conditions for vibration field (10) may be uncertain or incompatible. To rationally account for incompatible or uncertain requirements for the vibration field, a criterion of its optimality is introduced, as well as the assumption that the set of requirements can be fulfilled with some approximation.
Values 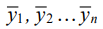 mean the vibration amplitudes of the steady-state components; therefore, for each fixed frequency ω of external disturbances z, it is possible to set a variational task of constructing an optimal vibration field, which:
mean the vibration amplitudes of the steady-state components; therefore, for each fixed frequency ω of external disturbances z, it is possible to set a variational task of constructing an optimal vibration field, which:
- delivers a minimum to the energy functional;
- displays representations of vibration patterns or values of potential or kinetic energy.
In general, the energy functional determines features of the distribution of the amplitudes of dynamic characteristics over the points of a mechanical vibratory system.
Within the framework of the considered model problem, the energy functional specified by operator Te, displays the nonuniformity of the vibration field. Its indicator is the sum of the squares of the differences in the deviations of the vibration amplitudes of nearly points:
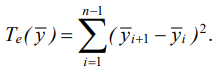 (11)
(11)
Zero value of energy functional (11) determines a uniform vibration field, whose vibration amplitudes of the points are equal to each other. Minimizing the energy functional, taking into account the specified conditions for the vibration amplitudes at the control points (10), determines the shape of the vibration field, extremely close to uniform.
We make allowance for a number of conditions:
- fixed frequency of external disturbances ω;
- vibration field is optimal in the terms of the criterion given by the energy functional;
– amplitudes of the vibration field at the control points satisfy conditions (10).
In this case, the formal formulation of the problem of constructing a vibration field can be represented as:
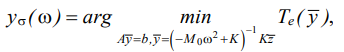 (12)
(12)
where 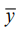 — vibration field defined by external kinematic disturbances z̅, which are considered as independent variational parameters.
— vibration field defined by external kinematic disturbances z̅, which are considered as independent variational parameters.
For fixed frequency ω, vibration field yσ(ω), which exactly satisfies the set of requirements, is formally found as solution (12) to the conditional minimization of the quadratic function (11) taking into account linear conditions (10):
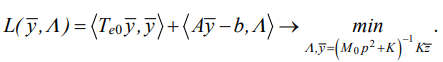 (13)
(13)
Here 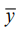 — vibration field determined by external kinematic disturbance ; Λ = (λ1, … λm) — Lagrange coefficients. Minimization in problem (13) proceeds according to the parameters of external disturbances. For fixed values of amplitudes of external disturbances, the created vibrational field
— vibration field determined by external kinematic disturbance ; Λ = (λ1, … λm) — Lagrange coefficients. Minimization in problem (13) proceeds according to the parameters of external disturbances. For fixed values of amplitudes of external disturbances, the created vibrational field 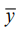 is the solution to the problem:
is the solution to the problem:
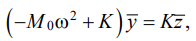 (14)
(14)
where 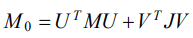 — matrix of the system.
— matrix of the system.
Vibration field 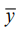 , which exactly satisfies the set values (10), can be determined under the solution to the conditional minimum problem using the Lagrange function:
, which exactly satisfies the set values (10), can be determined under the solution to the conditional minimum problem using the Lagrange function:
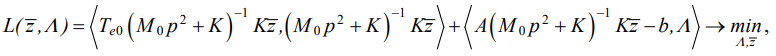 (15)
(15)
where 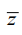 — vector of vibration amplitudes of external kinematic disturbances; Te0 — matrix defining the quadratic form of the energy functional (11).
— vector of vibration amplitudes of external kinematic disturbances; Te0 — matrix defining the quadratic form of the energy functional (11).
External disturbances 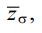 forming the required vibrational field, the Lagrange multipliers Λ are the solution of the system:
forming the required vibrational field, the Lagrange multipliers Λ are the solution of the system:
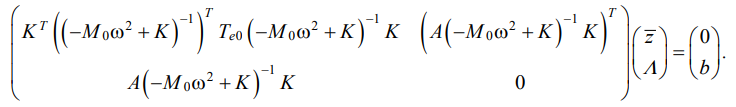 (16)
(16)
Thus, zσ — solution to the problem of conditional minimization (15), (16). The optimal vibration field yσ is determined by external disturbance zσ and has the form:
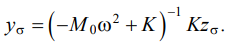 (17)
(17)
Here, yσ can be called an interpolating vibration field, since under the condition of compatibility (16), it exactly satisfies requirements (10). Taking into account the dependence on frequency ω, the compatibility and certainty of system (16) is characterized within the framework of the theorems of the existence and uniqueness of solutions to systems of equations of the theory of splines [20]. Under the condition of compatibility and certainty of the system (16) and (17), the optimal vibration field yσ exactly satisfies the set of conditions (10).
Necessary conditions (10) may contain noise, errors, or be contradictory. Taking into account contradictory or unreliable requirements, the vibration field can be constructed by solving the smoothing problem. Its result is an optimal vibration field that satisfies conditions different from the initial requirements, but close to them.
Vibration field assessment with account of noisy or unreliable dynamic performance requirements. Vibration field yσ(ω) (17) satisfying conditions (10) can be approximated using vibration field yα(ω) taking into account the unreliability or inconsistency of the necessary requirements (10):
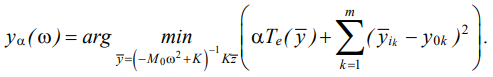 (18)
(18)
Here, 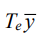 — operator displaying the criterion of optimality of the shape of the vibration field; α — smoothing parameter indicating the priority of the criterion of optimality of the shape of the vibration field in relation to the requirements of conditions (10).
— operator displaying the criterion of optimality of the shape of the vibration field; α — smoothing parameter indicating the priority of the criterion of optimality of the shape of the vibration field in relation to the requirements of conditions (10).
In expression (18), is considered as an independent variable. Vibration field yα(ω) can be called smoothing, since it approximately satisfies the necessary requirements of the system.
Vibration field yα is determined by a system of equations obtained through minimizing the Lagrange function:
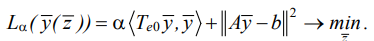 (19)
(19)
Here, 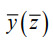 is a vibration field formed by external kinematic disturbance
is a vibration field formed by external kinematic disturbance 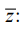
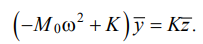 (20)
(20)
A replacement based on (20) is made:
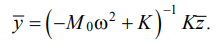 (21)
(21)
Now, the Lagrange function (19), taking into account (20) and (21), is reduced to the form:
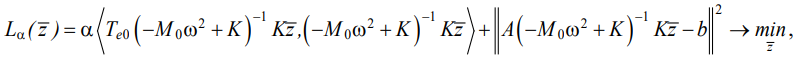 (22)
(22)
where 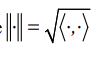 — length of the vector in Rn, expressed in terms of the scalar product
— length of the vector in Rn, expressed in terms of the scalar product 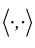 .
.
Consider the external kinematic disturbances zα. They form optimal vibration field yα, which smooths out the specified conditions (10) and is a solution to the minimization problem (22). Such disturbances are determined by the system:
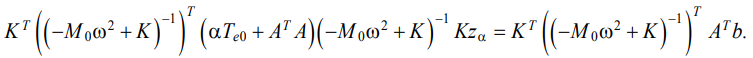 (23)
(23)
After simplifications of system (23), the desired amplitudes of kinematic disturbances zα are determined by the expression:
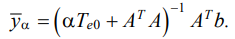 (24)
(24)
As shown above, external disturbances zα (24) are a solution to problem (23), taking into account the selection of the smoothing parameter α. These disturbances provide the construction of vibration field yα, which approximately satisfies the set of requirements (10), taking into account possible incompatibility or unreliability:
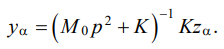 (25)
(25)
The type of vibration field yα (25) is clearly independent of the frequencies of external disturbances ω:
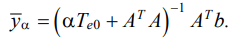 (26)
(26)
External disturbance zα, which provides the construction of an optimal smoothing vibration field yα (24), can be used to construct an interpolation vibration field yσ as α→0. The selection of smoothing parameter α is determined from the conditions of smallness of the discrepancy:
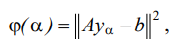 (27)
(27)
where 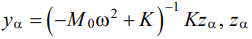 — kinematic disturbance (27).
— kinematic disturbance (27).
It should be noted that vibration field yα depends on frequency ω implicitly, through the smoothing parameter α = α(ω), whose selection is determined by the frequency of external disturbance ω and the value of discrepancy (27).
Construction of a vibration field for a mechanical oscillatory system. Computational experiment. Let the parameters of the mechanical vibratory system (Fig. 1) be given by stiffness ki, masses Mi, moments of inertia Ji and geometric characteristics l1i, l2i (Table 1).
Table 1
Parameters of the model mechanical vibratory system
|
No. |
M, kg |
J, kgm2 |
k, N/m |
l1, m |
l2, m |
|
1 |
100 |
10 |
1,000 |
1 |
1 |
|
2 |
200 |
20 |
2,000 |
1 |
1 |
|
3 |
300 |
30 |
3,000 |
1 |
1 |
|
4 |
400 |
40 |
4,000 |
1 |
1 |
As requirements for the amplitudes of the vibration field, conditions are set for the values at points Ai (Table 2).
Table 2
Vibration amplitudes at the points of the vibration field (y, m)
|
Values |
A1 |
A2 |
A3 |
A4 |
A5 |
|
Required |
0.002 |
– |
– |
– |
0.005 |
|
Smoothed out |
0.002 |
0.0027 |
0.0035 |
0.0043 |
0.005 |
Expression (11) is used as an energy functional, which can be represented using operator Te:
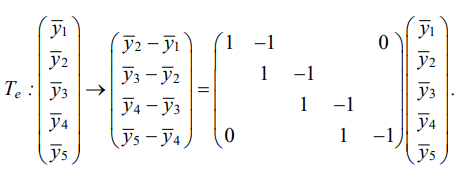
Expression  can be represented as:
can be represented as:
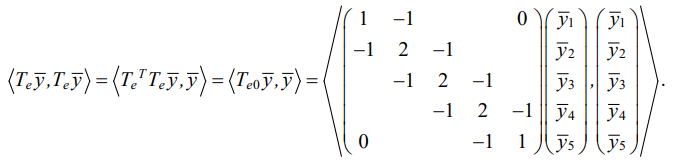
Here, Te0 — matrix that defines a quadratic shape. The value of operator 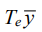 is zero on a uniform vibration field The vibration amplitudes of the points of this field are equal to each other for an external kinematic disturbance at an arbitrary frequency.
is zero on a uniform vibration field The vibration amplitudes of the points of this field are equal to each other for an external kinematic disturbance at an arbitrary frequency.
We set conditions (10) for the vibration field. For this purpose, data operator A15 can be used, which maps the amplitude values at points A1, A5 to vibration field y:
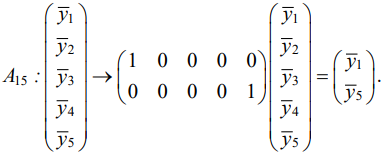
The vibration field interpolating the set values at points A1, A5 (Table 2), can be approximated using the smoothing vibration field for smoothing parameter α = 0.01. We find the difference between the values of the vibration field and the required values for the selected smoothing coefficient α. It is determined by the residual function (27), whose value is approximately 0.00001 m, where b = (0.002, 0.005)Т. The constructed vibration field, smoothing the interpolation conditions, has a linear shape (Table 2). For fixed smoothing parameter α = 0.01, the set of vibration amplitudes of the points of vibration field yα, which provides proximity to the interpolated data with residual φ(α) = 0.00001 m (Table 2), has the form of constant functions of the frequency of external disturbance ω (Fig. 3 a).
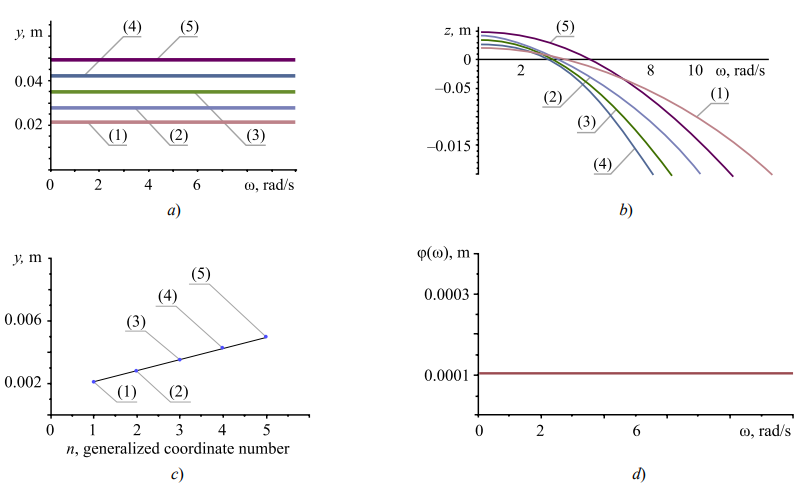
Fig. 3. Vibration field characteristics: a — values of vibration amplitudes of smoothing vibration field for frequencies of external disturbances in the range ω ∈ (0.100) rad/s; b — amplitudes of external kinematic disturbances providing the required vibration amplitudes depending on the frequency of disturbances ω; c — shape of the vibration field for frequencies in the range ω∈(0...100); (1), (5) — required values of the vibration field; (2), (3), (4) — values based on the energy approach; d — deviation φ (ω) of the vibration field from the required amplitude values at fixed points of the technical object for constant smoothing coefficient α = 0.1
In this case, the value of the vibration amplitudes of the generalized coordinates remains constant when the frequency of external kinematic disturbances zα changes. These disturbances, which are needed to provide the required amplitudes at fixed points of the vibration field, depend significantly on frequency ω of external disturbances (Fig. 3 b).
We describe a vibration field for a fixed frequency or a frequency domain in which it remains unchanged. It can be represented by a graph of a function depending on the number of the generalized coordinate or the coordinate of the point of the system in which the vibration field is estimated. The shape of the vibration field is determined by the optimality criterion. Specifically, energy functional Te0, which determines the optimality criterion, forms a linear shape of the vibration field (Fig. 3 c). It should be noted that the “interpolation” vibration field is constructed using a “smoothing” vibration field corresponding to smoothing parameter α. The deviation of the “smoothing” vibration field should be negligible. In the considered model example, for α = 0.1, the deviation of the smoothing vibration field is represented by constant φ (α) = 0.0001 m (Fig. 3 d). It should be noted that in the general case of the energy functional, the value of the smoothing coefficient α, which provides a fixed level of residual φ(α) = φ*, depends on frequency ω and the system of requirements.
Thus, the options for the formation of dynamic states of mechanical vibratory systems in the form of a vibration field satisfying a system of conditions depend on:
- energy functional reflecting the characteristics of the vibration field;
- operator displaying a set of requirements for the vibration field.
Other options for the formation of a vibration field based on the selection of an energy operator are also possible.
Correction of optimality criteria for shaping vibration fields using the weight coefficients of energy operators. The shape of the vibration field with the possibility of equalizing the vibration amplitudes of the coordinates of a technical object is considered above. There are other approaches to minimizing the amplitudes of generalized coordinates, e.g., by selecting energy operator TE in the form of an identity map:
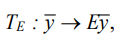
where E — identity operator.
The formation of a vibrational field based on the energy operator is associated with minimizing or zeroing the quadratic function of the amplitudes of in-phase harmonic vibrations of a fixed frequency. As a result of solving the smoothing problem, a vibration field is formed for the energy functional corresponding to unit operator TE. The amplitudes of its vibrations at points A2, A3, A4 are zero (Fig. 4 a), i.e., at points A2, A3 and A4, a dynamic vibration damping mode is implemented.

Fig. 4. Possibilities of vibration field correction: a — shape of vibration field for energy functional displays minimum possible vibration amplitudes, taking into account the necessary requirements; b — amplitudes of external kinematic disturbances zi, providing the necessary requirements for dynamic features of vibration field; c —vibration amplitudes of vibration field of technical object depending on frequency of external disturbance; d — options of vibration fields depending
on weight coefficient of energy operator Tβ
The totality of external kinematic disturbances is a solution to the problem of minimizing the energy functional, generally defined on the dynamic states of mechanical vibratory systems, taking into account the requirements for vibration amplitudes at fixed points of the vibration field (Fig. 4 b).
The characteristic property of forced kinematic disturbances, which provide the required shape of the vibration field, is an increase in the vibration amplitude when the frequency of disturbances grows (Fig. 4 c). External kinematic disturbances z provide a fixed vibration field of a technical object at various frequencies ω (Fig. 4 d). Smoothing parameter α = 0.01 provides an absolute deviation from the required values at level φ(α) = 0.000053. This shows that the totality of the vibration amplitudes at the remaining points of the vibration field determines the characteristics of the energy operator based on the required values of the vibration field amplitudes at fixed points of the mechanical vibratory system. Specifically, operator Te is aimed at forming a uniform vibration field, and operator TE is aimed at zeroing the vibration field.
Weight coefficients that display a combination of optimality criteria can be used. This allows combining the following:
- requirements for convergence of vibration amplitudes of points of vibration fields;
- requirements aimed at zeroing the vibration amplitudes of the vibration field points.
Varying the weight coefficients that determine the combination of optimal criteria for the formation of a vibration field is actually a way to correct the vibration field.
We build a family of forms of vibration fields of a technical object that meet certain conditions. For this purpose, we use a combined optimality criterion implemented by a weighted sum of energy functionals, taking into account the weight factor:
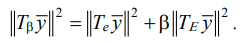 (28)
(28)
Here, β — weight factor that determines the combination of the optimality criterion based on the smallness of the amplitudes and the criterion based on the uniformity of the amplitudes of the vibration fields. The variation of the weight coefficient β leads to the construction of a family of vibration fields. The criterion of their optimality has a complex structure that takes into account the differences and absolute values of the vibration amplitudes of the points of the vibration field. The selection of a set of weight coefficients determines the appropriate forms of vibration fields, which are realized under the influence of external disturbances, which are the solution to the variational problem [20].
Based on the set of weight coefficients β, it is possible to construct optimal vibration fields that meet the requirements for vibration amplitudes at fixed points with sufficient accuracy (Table 3).
Table 3
Forms of optimal vibration fields for weight coefficients of the energy functional
|
No |
β |
α |
Residual φ(α), m |
Frequency ω, rad/s |
y1, m |
y2, m |
y3, m |
y4, m |
y5, m |
|
1 |
1 |
0.01 |
0.0000841 |
10 |
0.0019704 |
0.0009850 |
0.0009845 |
0.0019686 |
0.0049213 |
|
2 |
0.5 |
0.01 |
0.0000503 |
10 |
0.0019847 |
0.0014467 |
0.0016322 |
0.0026337 |
0.0049521 |
|
3 |
0.25 |
0.01 |
0.0000305 |
10 |
0.0019940 |
0.0018969 |
0.0022740 |
0.0032196 |
0.0049701 |
|
4 |
0.125 |
0.001 |
0.0000195 |
10 |
0.0020000 |
0.0022503 |
0.0027818 |
0.0036611 |
0.0049980 |
|
5 |
0.0625 |
0.001 |
0.0000014 |
10 |
0.0020004 |
0.0024754 |
0.0031053 |
0.0039292 |
0.0049986 |
Combining optimal criteria for the formation of vibration fields is a way to correct the dynamic states of a technical object (Fig. 4 d). Note that the found kinematic disturbances zi, considered as functions of frequency ω, have one zero each (Fig. 5 f).
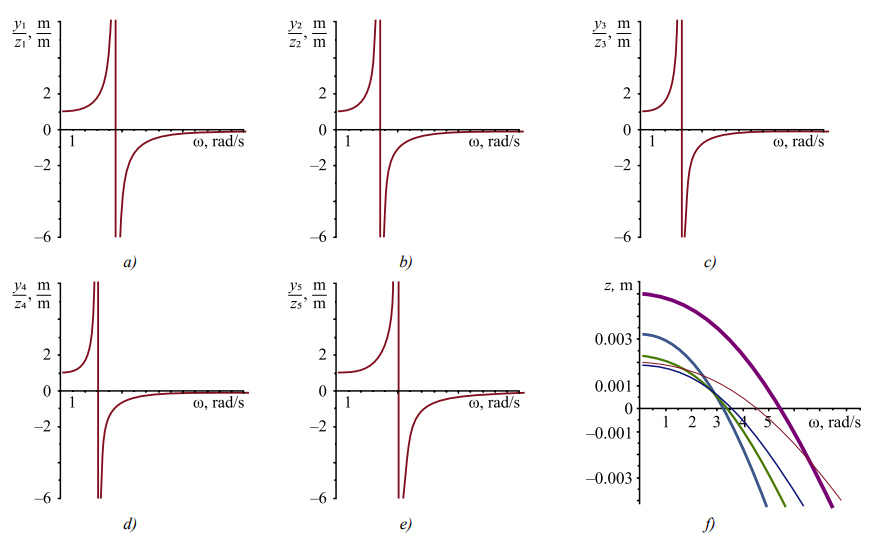
Fig. 5. Optimal vibration field characteristics for weight coefficient β = 0.25 and smoothing parameter α = 0.01:
a — ratio of the vibration amplitudes of points of optimal vibration field (yα)1 to amplitude of kinematic disturbances (zα)1;
b — ratio of amplitudes (yα)2 to (zα)2; c — ratio of amplitudes (yα)3 to (zα)3; d — ratio of amplitudes (yα)4 to (zα)4;
e — ratio of amplitudes (yα)5 to (zα)5; f — value of amplitudes of external disturbances (zα) depending on frequency ω
Amplitude ratios yi/zi, for which yi = yi (ω) and zi = zi (ω), are found on the basis of solution to the problem of determining optimal vibration fields, have one discontinuity of the 2nd kind (Fig. 5a–d).
The specified vibration amplitudes of fixed points of the vibration field of the mechanical vibration system should be provided. For this purpose, combined energy functionals with account for the weight coefficients can be selected, and, based on these indicators, the required external kinematic effects with account for the variational principles can be determined.
If the requirements for the vibration amplitudes of the vibration field are highly noisy or incompatible, it is possible to construct a vibration field that meets the requirements with a certain accuracy and is optimal for the combined criterion, but for other conditions.
Determination of the optimal criterion for shaping vibration fields based on the residual function. In general, the requirements for a vibration field can be a complex set of joint or incompatible conditions reflecting limitations on the amplitudes of displacements, velocities, and dynamic reactions, including non-retentive conditions.
Taking into account the criterion of optimality of the vibration field of a mechanical vibratory system, the set of joint conditions allows for a single solution in the form of a certain structure of external disturbances. In the case of incompatibility of conditions on the vibration field, the optimality criterion actually acts as a method of regularization of an incorrect inverse problem.
The energy functional determines the specifics of the formation of vibration fields based on the values of the vibration amplitudes of displacements, velocities, force disturbances, or reactions occurring between the elements of the system. Energy functionals can convey ideas about the maximum potential or kinetic energy, or serve as a combination of them with account for weight coefficients that act as methods for correcting vibration fields.
It is possible to add conditions according to the nature of the external kinematic or force disturbances themselves to the conditions for the values of the amplitudes of the vibration fields. They are expressed in the fact that the amplitudes of external disturbances take fixed absolute or relative values. The need to set requirements for input disturbances is due to the fact that to provide the specified forms of vibration fields, the amplitudes of external disturbances can increase indefinitely with growing frequency.
Thus, here is a complex task of selecting:
- an energy functional;
- an operator of requirements for a vibration field;
- an additional operator of requirements for external force or kinematic disturbances.
Within the framework of the development of the structural theory of the optimal vibration field, it is possible to set a generalized task of its construction:
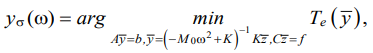
where 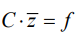 — additional connection limiting the dimension of external kinematic disturbances.
— additional connection limiting the dimension of external kinematic disturbances.
The technique for selecting an effective operator can be based on minimizing the function of additional residual, depending on the parameters of the energy operator:
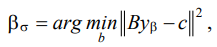
where yβ — solution to the problem of determining the vibration field with a combined optimality criterion Tβ ((28) and Fig. 4) and conditions A (10); В — operator for determining values in a set of additional points; c — vector of values at additional points.
This problem can be considered as the problem of selecting a “natural” optimality criterion [21]. Thus, the presented set of tasks and solution techniques can be the fundamental basis for the structural theory of the construction of vibration fields.
Discussion and Conclusion. Elements of the structural theory of optimal vibration fields of mechanical vibratory systems have been developed. The main components of this theory are methods for constructing vibration fields of mechanical vibratory systems based on variational principles. The basic concept is the vibration field of a mechanical vibratory system. It represents the distribution of vibration amplitudes of generalized coordinates and other dynamic characteristics of a mechanical vibratory system over the points of an object with an estimated dynamic state.
It is assumed that a system of conditions is set at a number of points of the mechanical vibratory system. It is expressed in terms of absolute or relative values of displacements, velocities, and reactions. Conditions are requirements for the characteristics of the vibration field of a mechanical vibratory system. There is also a system of conditions related to the features of external force or kinematic disturbances, and it also reflects the requirements for a set of absolute and relative values of the amplitudes of kinematic or force disturbances.
For the development of the applied theory of optimal vibration fields within the framework of structural representations, an analogy can be established between the two pairs. The first one is formed from energy operator T and condition operator A in the theory of abstract splines. The second one is formed by the criterion of optimality of the vibration field and a system of requirements for the characteristics of the vibration field at control points.
Interpolation, smoothing and mixed splines are distinguished within the framework of the theory of variational spline approximation. Within the framework of the concepts of vibration fields of mechanical vibratory systems based on structural representations, the role of the spline is performed by a set of amplitudes of external force and kinematic disturbances, and the role of interpolation conditions is performed by a set of requirements for the amplitudes of input or output signals.
It can be assumed that there are differences between the vibration fields of technical objects under conditions of external forced or kinematic disturbances, which are considered as a key factor in the formation of a dynamic state. At the same time, when constructing a vibration field, it is considered natural to estimate energy ratios depending on generalized coordinates. Their values are determined by an external force or kinematic disturbance. In fact, we need to find two vectors — generalized coordinates and external disturbances.
We take into account the variational approach, as well as the set of requirements for the vibration field and external disturbances. We present the problem of determining external disturbances that form a set of dynamic states in the form of a vibration field with account for a system of conditions. In this interpretation, we are talking about the optimization problem in different formulations within the framework of variational principles. Specifically, it is possible to set tasks similar to the tasks of constructing a smoothing or mixed spline. It depends on the compatibility of the conditions for the input and output signals. We note the following an essential feature of the problems of constructing vibration fields: the frequency of an external disturbance is a parameter of the optimization problem, and in the case of systems with concentrated parameters, amplitude vectors serve as elements of an n-dimensional Cartesian space.
Analogies between the tasks of approximation and construction of vibration fields provide developing techniques for the formation, assessment, and correction of dynamic states of technical objects.
The improved structural theory of optimal vibration fields will be in demand in the aviation and space industries. Its apparatus can be used to maintain flight safety and durability of structures. In addition, it is logical to use this approach in mechanical engineering, electronics, and the development of medical equipment. The theory will allow solving the problems of forming, evaluating, and correcting the states of technical systems and devices under conditions of vibration loading. Another area of its practical application is the creation and improvement of measuring methods and means of complex vibratory systems. We also believe that mathematical models of optimal vibration fields are of interest for the development of new technologies and materials, in particular, materials with high damping, which can reduce the level of vibrations and noise in technical systems.
As the main limitation of the technique, it is necessary to indicate that vibrations in the coordinates of an object, which are steady-state forms of harmonic vibrations or vibrations of a fixed amplitude, are considered.
References
1. Juan Carlos A Jauregui Correa, Alejandro A Lozano Guzman. Chapter One — Fundamentals of Mechanical Vvibrations. Mechanical Vibrations and Condition Monitoring. Cambridge, MA: Academic Press; 2020. P. 1–26. https://doi.org/10.1016/B978-0-12-819796-7.00001-9
2. Jalal Torabi, Jarkko Niiranen. Nonlinear Finite Element Free and Forced Vibrations of Cellular Plates Having Lattice-Type Metamaterial Cores: A Strain Gradient Plate Model Approach. Mechanical Systems and Signal Processing. 2023;192:110224. https://doi.org/10.1016/j.ymssp.2023.110224
3. Keigo Ikeda, Kota Kamimori, Ikkei Kobayashi, Jumpei Kuroda, Deigo Uchino, Kazuki Ogawa, et al. Basic Study on Mechanical Vibration Suppression System Using 2-Degree-of-Freedom Vibration Analysis. Vibration. 2023;6(2):407–420. https://doi.org/10.3390/vibration6020025
4. Bolshakov RS. Features of Vibration States of Transport and Technological Machines. Dynamic Reactions and Forms of Interaction of Elements. Novosibirsk: Nauka; 2020. 411 p. (In Russ.).
5. Dumitriu M, Apostol II. Influence of Interference between Vertical and Roll Vibrations on the Dynamic Behaviour of the Railway Bogie. Vibration. 2022;5(4):659–675. https://doi.org/10.3390/vibration5040039
6. Sehner M, Seidi-Nigsch M, Valdés Nava LE, Loy H. Vibration Mitigation: Under-Ballast Mats in Heavy-Haul Applications. Practice Periodical on Structural Design and Construction. 2023;28(4):05023004. https://doi.org/10.1061/PPSCFX.SCENG-1258
7. Zhenhang Zhao, Ying Gao, Chenghui Li. Research on the Vibration Characteristics of a Track’s Structure Considering the Viscoelastic Properties of Recycled Composite Sleepers. Applied Sciences. 2020;11(1):150. https://doi.org/10.3390/app11010150
8. Yu Zou, Yongpeng Wen, Qian Sun. Study on the Urban Rail Transit Sleeper Spacing Considering Vehicle System. MATEC Web of Conferences. 2019;296:01008. https://doi.org/10.1051/matecconf/201929601008
9. Yoshino Sh, Abe K, Koro K. An Analytic Solution of Mathematical Expectation for Bogie-Track Interaction Problems. Mechanical Engineering Journal. 2023;10(3):22–00300. https://doi.org/10.1299/mej.22-00300
10. Wenping Chu, Yang Song. Study on Dynamic Interaction of Railway Pantograph–Catenary Including Reattachment Momentum Impact. Vibration. 2020;3(1):18–33. https://doi.org/10.3390/vibration3010003
11. Maryam El Moueddeb, François Louf, Pierre-Alain Boucard, Franck Dadié, Gilles Saussine, Danilo Sorrentino. An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range. Vibration. 2022;5(2):326–343. https://doi.org/10.3390/vibration5020019
12. Korendiy V, Kachur O, Predko R, Kotsiumbas O, Stotsko R, Ostashuk M. Generating Rectilinear, Elliptical, and Circular Oscillations of a Single-Mass Vibratory System Equipped with an Enhanced Twin Crank-Type Exciter. Vibroengineering Procedia. 2023;51:8–14. https://doi.org/10.21595/vp.2023.23657
13. Krot P, Shiri H, Dąbek P, Zimroz R. Diagnostics of Bolted Joints in Vibrating Screens Based on a Multi-Body Dynamical Model. Materials. 2023;16(17):5794. https://doi.org/10.3390/ma16175794
14. Vishwa Priya Vellingiri, Udhayakumar Sadasivam. Effect of Vibrator Parameters and Physical Characteristics of Parts on Conveying Velocity. Strojniški vestnik — Journal of Mechanical Engineering. 2023;69(7–8):352–363. https://doi.org/10.5545/sv-jme.2022.510
15. Korendiy V, Gursky V, Kachur O, Dmyterko P, Kotsiumba O, Havrylchenko O. Mathematical Model and Motion Analysis of a Wheeled Vibro-Impact Locomotion System. Vibroengineering Procedia. 2022;41:77–83. https://doi.org/10.21595/vp.2022.22422
16. Krupenin V, Astashev V. Properties of Vibration Fields in a Two-Dimensional Lattice Structure Colliding with an Obstacle. In: EJ Sapountzakis, M Banerjee, P Biswas, E Inan (eds). Proc. 14th Int. Conf. on Vibration Problems (ICOVP). Singapore: Springer; 2020. P. 473–485. https://doi.org/10.1007/978-981-15-8049-9_30
17. Karnovsky IA, Lebed E. Structural Theory of Vibration Protection Systems. In book: Theory of Vibration Protection. Cham: Springer; 2016. 708 p. https://doi.org/10.1007/978-3-319-28020-2_12
18. Eliseev AV. Structural Mathematical Modeling Applications in Technological Machines and Transportation Vehicles. Hershey, PA: IGI Global; 2023. 288 p. https://doi.org/10.4018/978-1-6684-7237-8
19. Sarah Saeed. Laplace Transform: Basics and Main Properties. In book: J García (ed). Encyclopedia of Electrical and Electronic Power Engineering. Amsterdam: Elsevier; 2023. P. 645–651. https://doi.org/10.1016/B978-0-12-821204-2.00062-3
20. Bezhaev AYu, Vasilenko VA. Variational Theory of Splines. New York, NY: Springer; 2001. 208 p. https://doi.org/10.1007/978-1-4757-3428-7
21. Vasilenko VA, Elyseev AV. Abstract Splines with the Tension as the Functions of Parameters in Energy Operator. Siberian Journal of Computational Mathematics. 1998;1(4):301–311. URL: https://www.mathnet.ru/
22. links/be5b8fe7cfea1927a6fff34630f7de33/sjvm311.pdf (accessed: 11.12.2023).
About the Authors
A. V. EliseevRussian Federation
Andrey V. Eliseev, Cand.Sci. (Eng.), Associate Professor of the Department of Mechanical Engineering Design and Standardization, Associate Professor of the Mathematics Department
15, ul. Chernyshevskogo, Irkutsk, 664074
83, Lermontov St., Irkutsk, 664074
N. K. Kuznetsov
Russian Federation
Nikolai K. Kuznetsov, Dr.Sci. (Eng.), Professor, Head of the Department of Mechanical Engineering Design and Standardization
83, Lermontov St., Irkutsk, 664074
Review
For citations:
Eliseev A.V., Kuznetsov N.K. Optimal Vibration Fields in Problems of Modeling Dynamic States of Technical Objects. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):7-22. https://doi.org/10.23947/2687-1653-2024-24-1-7-22. EDN: FAKNHP
JATS XML














































