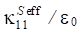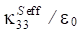Scroll to:
On a Method for Calculating Bending and Shear Vibrations of a Porous Piezoelement in the Low-Frequency Region
https://doi.org/10.23947/2687-1653-2024-24-2-148-158
EDN: VPUERG
Abstract
Introduction. Devices for collecting and storing energy from the external environment are low-power sources of electric energy that are actively used. The autonomous devices for monitoring the damaged condition of various structures include them as well. The working element of these devices is a piezoelectric generator (PEG) — a converter of mechanical energy into electrical energy. The design of PEG is associated with the preliminary construction of their mathematical and computer models, with the help of which the calculation and optimization of structures is carried out. One of the ways to model and calculate PEG is to develop approximate calculation methods based on applied theories. The applied theories for calculating bending vibrations of multilayer piezoactive plates are known and previously developed in the literature. However, in the scientific literature there is not enough information about bending and shear vibrations as a tool for improving the efficiency of engineering calculations of the described structures. The objective of this work was to develop an applied method for calculating bending and shear vibrations of piezoceramic plates, including porous ones.
Materials and Methods. Piezoceramics PZT-4, including porous ones, were used as the piezoactive material of the plate. When using porous ceramics, the rigidity of the structure decreased to a greater extent than the piezoelectric modules, which made it possible to obtain a more effective PEG under mechanical action. The mathematical formulation was carried out within the framework of the linear theory of electroelasticity with plate polarization in thickness. The sides of the plate were electrodated, the right side was fixed, and a smooth contact in the vertical wall was set on the left side. Steady-state vibrations of the plate were caused by pressure on the front surfaces of the plate or the difference in electrical potentials at the electrodes. To calculate the characteristics of PEG, the authors proposed an applied theory based on hypotheses about the distribution of characteristics of the stress-strain state and the electric field.
Results. Transverse vibrations of a piezoceramic plate in the low-frequency region (below the first bending-shear resonance) were studied. Due to the fact that the mathematical formulation was considered within the framework of the linear theory of elasticity, the problem was divided into the sum of two. The first one took into account the mechanical effect: a distributed load and a transverse force at the left end acted on the front surfaces of the plate, and the potentials at the electrodes were zero. In the second task, there were no mechanical loads, but the potential difference was set at the electrodes. Based on hypotheses about the distribution of deformations, mechanical stresses and electric potential, both problems were reduced to a system of ordinary differential equations and boundary conditions. Comparison with the results of calculations by the finite element method in the ACELAN package showed the adequacy of the proposed applied theory in the low-frequency region.
Discussion and Conclusion. Since the formulation of the problem was considered in the linear theory of electroelasticity, and the low-frequency region was studied, the work succeeded in dividing the problem of bending-shear vibrations of a porous piezoceramic plate into two: bending — with mechanical action at zero potentials, and shear — when setting the potential difference and zero mechanical action. The corresponding hypotheses about bending and shear were used. Two systems of ordinary differential equations and boundary conditions, which were solved analytically without the use of “heavy” finite element packages, were constructed. To compare the results and confirm the adequacy of the proposed method, the finite element modeling of such tasks was carried out in a specialized ACELAN package. The comparison showed that the error in determining displacements and electric potential when using this approach, in the case of setting mechanical loads and potential differences, did not exceed 6%. The method developed in the paper can be applied in the design of piezoelectric generators for energy storage in the low-frequency region.
Keywords
For citations:
Soloviev A.N., Chebanenko V.A., Oganesyan P.A., Fomenko E.I. On a Method for Calculating Bending and Shear Vibrations of a Porous Piezoelement in the Low-Frequency Region. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148-158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158. EDN: VPUERG
Introduction. Piezoelectric generators (PEG) are used to convert mechanical energy into electrical energy, followed by its accumulation. One of the application areas of PEG is the creation of low-power autonomous renewable sources of electric energy. The working element of the PEG is a piezoceramic element of a certain shape. The shape and type of deformation of this element determine the piezomodule, which characterizes the conversion of mechanical deformation energy into electrical energy. Thus, piezomodule d33 is associated with tension-and-compression along the axis of polarization, d31 — with the same deformation in the transverse direction to this axis, d15 — with shear. The use of porous ceramics makes it possible to create more efficient PEG. This is due to the fact that the elastic modules of porous ceramics decrease significantly stronger with increasing porosity than piezomodules. Thus, under the same mechanical load, the deformation amplitude of porous ceramics is greater; therefore, the output electric potential is also greater.
PEG calculation can be performed by the finite element method implemented in ANSYS, ACELAN, COMSOL, and others packages. For piezoelectric elements, one or two sizes of which are significantly smaller than others (plates, rods), applied calculation theories can be constructed based on hypotheses about the distribution of mechanical and electric fields. Without the use of “heavy” finite element packages, applied theories make it possible to model various devices based on piezoactive materials. Piezoelectric, piezomagnetic and composite piezomagnetoelectric materials are considered as such materials. The construction of these theories is based on the acceptance of hypotheses about the distribution of mechanical, electric and magnetic fields. These hypotheses are related to the vibration mode of elastic and piezoactive elements of PEG. The most common designs are active and semipassive bimorphs based on multilayer plates, polarized in thickness with electrodes on the front faces, performing transverse bending vibrations. A number of papers are devoted to the study of devices with shear deformation of piezoelectric elements. An electric model with piezoelectric defining equations of mode d15 and a single-degree-of-freedom model were combined to describe the energy collection characteristics of a piezoelectric cantilever in a shear mode in operation [1]. The proposed model is used to simulate the frequency dependence of the output peak voltage and power. The results show a good agreement with the experiment and the finite element calculation in ANSYS. In [2], a piezoelectric shear mode energy converter was developed to use the energy of a pressurized water flow. It converts the energy of the flow into electrical energy through piezoelectric conversion with vibration of the piezoelectric film. A finite element model has been developed to estimate the generated voltage of a piezoelectric film, which is in good agreement with the conducted field experiment. A one-dimensional fully coupled beam vibration model based on Timoshenko-type hypotheses, which provides a single common basis for energy analysis in shear and bending modes, is presented in [3]. In [4], the effect of the inhomogeneity of the properties of the plate under shear and torsional vibrations of its central part was studied. In experimental work [5], a multilayer cylindrical piezoelectric shear actuator (MCPSA) operating in shear mode d15, was presented for precision actuation under high mechanical load. The actuator was made of piezoelectric ceramic rings Pb(Zr,Ti)O3 (PZT-51), which were concentrically assembled together in an electrically parallel connection with alternately positive and negative polarization in the axial direction. In [6], metamaterial of identical elementary cells was created, an artificial prototype of a device with characteristic patterned electrodes and piezoceramic subunits arranged in a row was designed and manufactured, which, as proven, ideally generated the synthetic shear deformation of the face. At the same excitation voltage, there was an increase in the displacement of the shear type by more than an order of magnitude, compared to the previous volumetric elements in mode d15. In the static formulation in [7], the field of electromechanical coupling in the shear-bending mode for an annular piezoelectric plate was theoretically established. In accordance with the classical theory of elastic plates of small bending and piezoelectric defining equations, an analytical solution of the bending deformation of the piezoactuator under the action of an electric field and a concentrated or evenly distributed mechanical load was achieved. The mechanism of generating bending deformation was explained by axisymmetric shear deformation, which additionally caused bending deformation of one piezoelectric plate in the form of a ring. This mechanism differs significantly from the mechanism of piezoelectric bimorphic or unimorphic drives, which were previously reported. The design of the annular piezoactuator has been optimized. In [8], a one-dimensional model was used to construct a sensor response function based on shear resonators (quartz cuts) of a bulk acoustic wave, which are promising for in-line measurements of fluid viscosity, e.g., in industrial processes. In [9], using the finite element method, a piezoelectric flying height control converter was investigated using a shear model deformation. In [10], the theory of a functionally graded plate
with four-unknown shear deformations was used to express the displacement component. The distribution of the electric potential was a linear function of thickness. The plate was under mechanical load and electrical voltage. The basic equations and boundary conditions were derived using the virtual work principle. The analysis of stresses and deformations from the design parameters was performed. The electromechanical analysis of the stability loss of a piezoelectric nanoplate under shear using a modified theory of paired stresses with different boundary conditions was studied in [11]. To take into account the electrical effects, an external electrical voltage was applied to the piezoelectric nanoplate. A simplified theory of the first-order shear deformation was used. The basic differential equations were obtained using the Hamilton principle and nonlinear Von Karman deformations. Finally, the results showed that the effect of external electrical voltage on the critical shear load arising on the piezoelectric nanoplate was insignificant. In [12], using a combination of two classical approaches to modeling the nonlinear behavior of piezoelectric materials, a piezoelectric shear drive for an atomic-force microscope was investigated. Specifically, the novelty of the proposed method was in the fact that it combined two sources of nonlinearity of the field-dependent model from Müller and Zhang with the frequency-dependent model from Damjanović. The numerical results obtained using the finite element method (FEM) were compared to the experiment.
Vibrations in which there is shear in addition to bending are less studied in the scientific literature, i.e., piezomodule d15, is the “working” one, whose value decreases with increasing porosity, but to a lesser extent than elastic modules. The latter circumstance makes it possible to build an efficient energy conversion device. Therefore, the development of an applied theory of PEG calculation using porous piezoceramics based on simplified models without “heavy” finite element packages seems to be a highly relevant task. The objective of this work was to construct an applied calculation method for steady-state transverse vibrations in the low-frequency region of a porous piezoceramic plate characterized by both shear and bending.
Materials and Methods. The PEG under study was a piezoceramic plate (length l, thickness h), polarized in thickness, cantilevered on the right side, the left side was attached to an inertial mass that performed vertical vibrations and was fixed in the horizontal direction. The electrodes were located on the sides of the plate; therefore, with a potential difference on them and no mechanical load, the principal deformation in the low-frequency region was shear. Vibrations whose frequency was less than the frequency of the first resonance were considered.
Mathematical formulation of the problem
The mathematical formulation of the problem is described by a system of differential equations [13] and the corresponding boundary conditions.
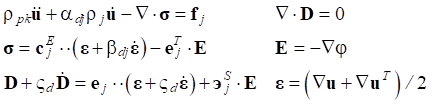 (1)
(1)
When considering porous ceramics of connectivity 3–0, equations (1) use effective physical constants determined through the ACELAN-COMPOS package [14]. These effective properties based on representative volumes (Fig. 1) were obtained in [15]. They are presented in Table 1.

Fig. 1. Representative volumes in ACELAN-COMPOS package [14]
Table 1
Effective properties of porous ceramics
|
% of porosity |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
7,500 |
6,750 |
6,000 |
5,250 |
4,500 |
3,750 |
3,000 |
2,250 |
1,500 |
|
|
13.9 |
11.56 |
9.25 |
6.85 |
5.05 |
3.34 |
2.07 |
1.26 |
0.68 |
|
|
7.78 |
6.15 |
4.66 |
3.14 |
2.10 |
1.16 |
0.62 |
0.28 |
0.13 |
|
|
7.43 |
5.82 |
4.25 |
2.82 |
1.7 |
1.06 |
0.52 |
0.24 |
0.1 |
|
|
11.5 |
9.53 |
7.23 |
5.42 |
3.91 |
2.72 |
1.63 |
0.91 |
0.47 |
|
|
2.56 |
2.23 |
1.83 |
1.44 |
1.10 |
0.74 |
0.44 |
0.23 |
0.1 |
|
|
15.1 |
13.38 |
11.37 |
9.59 |
7.68 |
5.93 |
3.93 |
2.30 |
1.25 |
|
|
–5.2 |
–4.23 |
–3.14 |
–2.07 |
–1.32 |
–0.75 |
–0.43 |
–0.21 |
–0.1 |
|
|
12.7 |
10.96 |
8.96 |
6.91 |
5.00 |
3.30 |
1.95 |
1.00 |
0.44 |
|
|
730 |
663 |
582 |
509 |
439 |
349 |
263 |
191 |
122 |
|
|
635 |
567 |
492 |
413 |
345 |
270 |
199 |
130 |
75 |
According to Table 1, the dependences of effective elastic modules and piezomodules on the percentage of porosity [15] are plotted. They are shown in Figure 2.
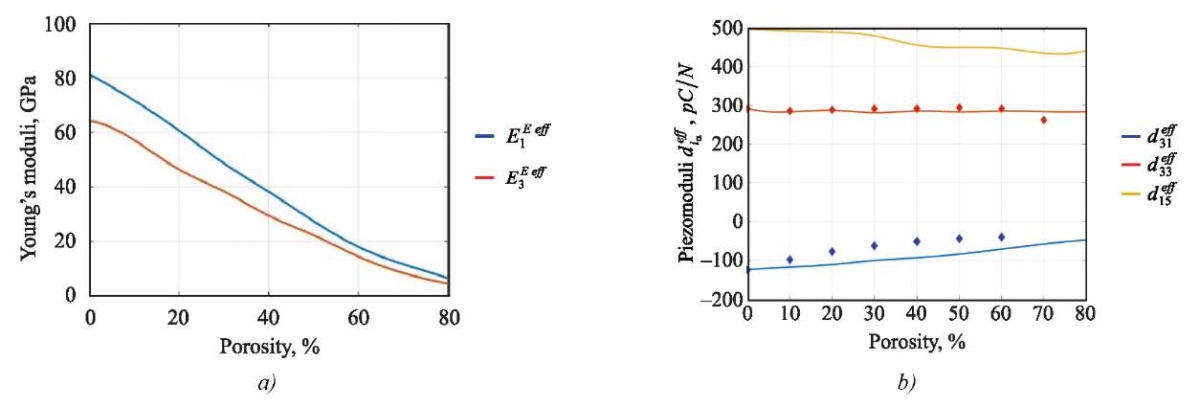
Fig. 2. Dependences of values on percentage of porosity [15]:
a — elastic models; b — piezomodules [15]
In accordance with the results shown in Figure 2, elastic modulus E1 decreases significantly faster than piezomodule d15.
Building an applied theory
The developed calculation method consists of solving two problems: in the first, bending under the effect of a mechanical load with zero potential difference is considered; in the second, the shear caused by a potential difference in the absence of a mechanical load is modeled. In both cases, the absence of charges on the front faces of the plate is taken into account. Under the action of a mechanical load and an electrical potential difference, the results of the two tasks add up due to the linearity of the task.
The action of the mechanical load, the potentials on the electrodes are zero. Hypotheses of the Kirchhoff-Love type are accepted regarding the equality of normal stresses to zero, and for displacements:
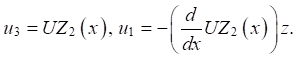 (2)
(2)
The distribution of electric potential over the thickness is assumed to be quadratic and symmetrical:
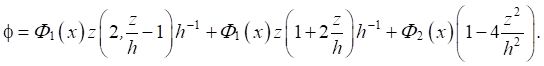 (3)
(3)
To take into account the boundary conditions at the ends of the plate (x = 0, l), an expression for the transverse force is obtained:
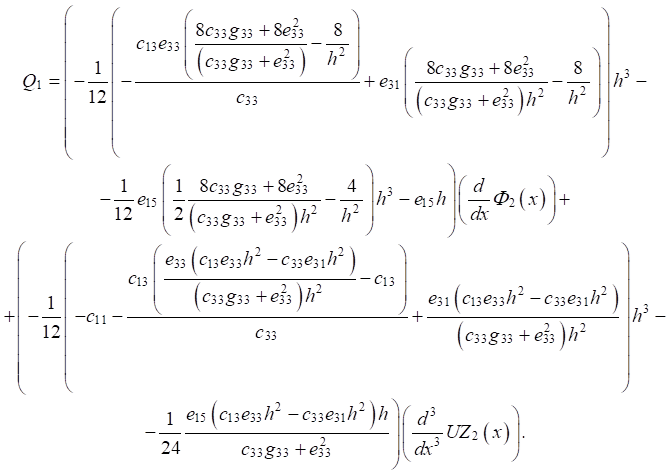 (4)
(4)
Taking into account the equality of the normal component of the electric induction vector on the front faces (z = ±h) to zero, the equations for the unknown deflection UZ2(x) and distribution of the electric potential Ф2(x) have the form:
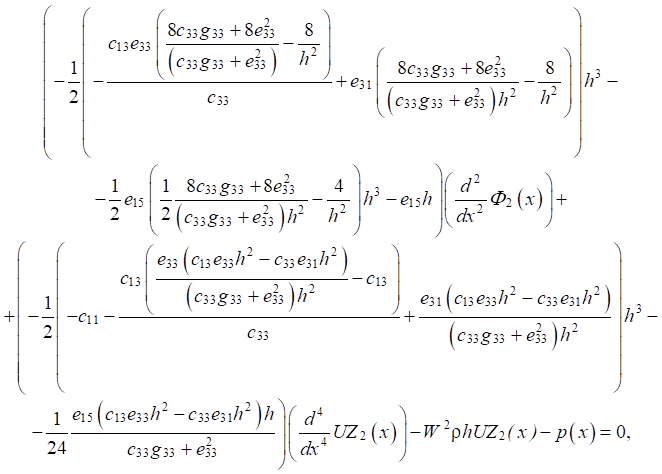 (5)
(5)
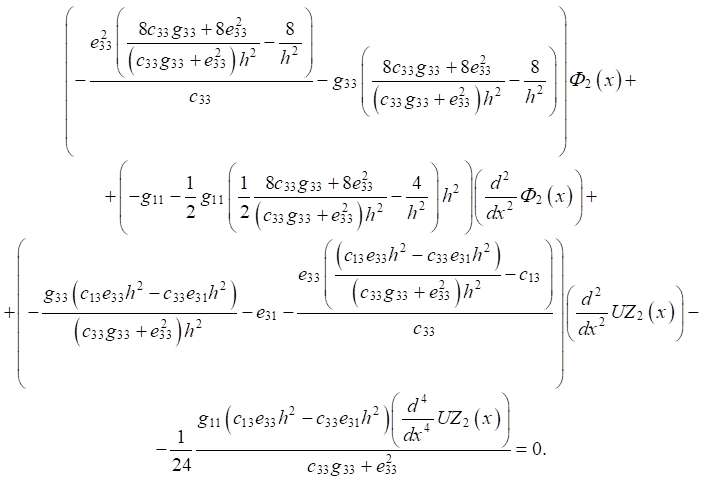 (6)
(6)
The potential difference is set, the mechanical load is zero. Independence of lateral displacement from thickness, equality of the longitudinal displacement to zero, and the quadratic distribution of the electric potential over the thickness are assumed (3):
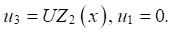 (7)
(7)
Expression for the transverse force:
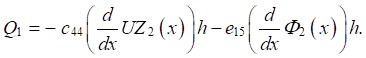 (8)
(8)
Taking into account the equality of the normal component of the electric induction vector on the front faces (z = ±h) to zero, the equations for the unknown deflection UZ2(x) and distribution of the electric potential Ф2(x) have the form:
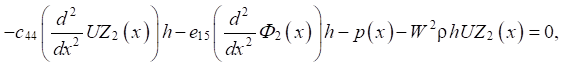 (9)
(9)
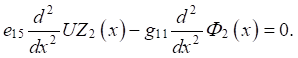 (10)
(10)
Research Results. The results of calculations based on the proposed applied theories were compared to the calculations of piezoelectric element vibrations (l = 0.1 m, h = 0.01 m) at a frequency equal to 100 s-1 by the finite element method in ACELAN [16].
In the first problem, defined by equations (5) and (6), when specifying a uniformly distributed load p(x) = 1000 Pa⸳m and with boundary conditions:
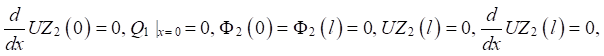 (11)
(11)
the following results were obtained, shown in Figures 3, 4.
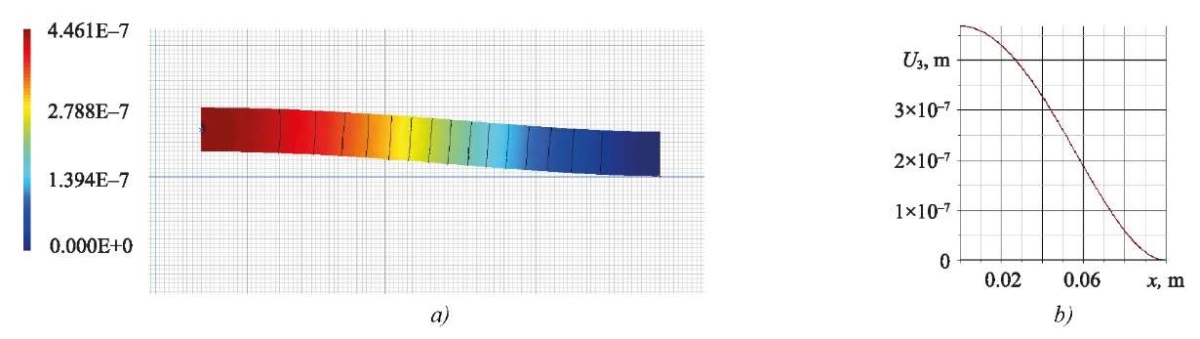
Fig. 3. Vertical displacement in ACELAN in the first problem:
a — distribution; b — graph on the upper boundary
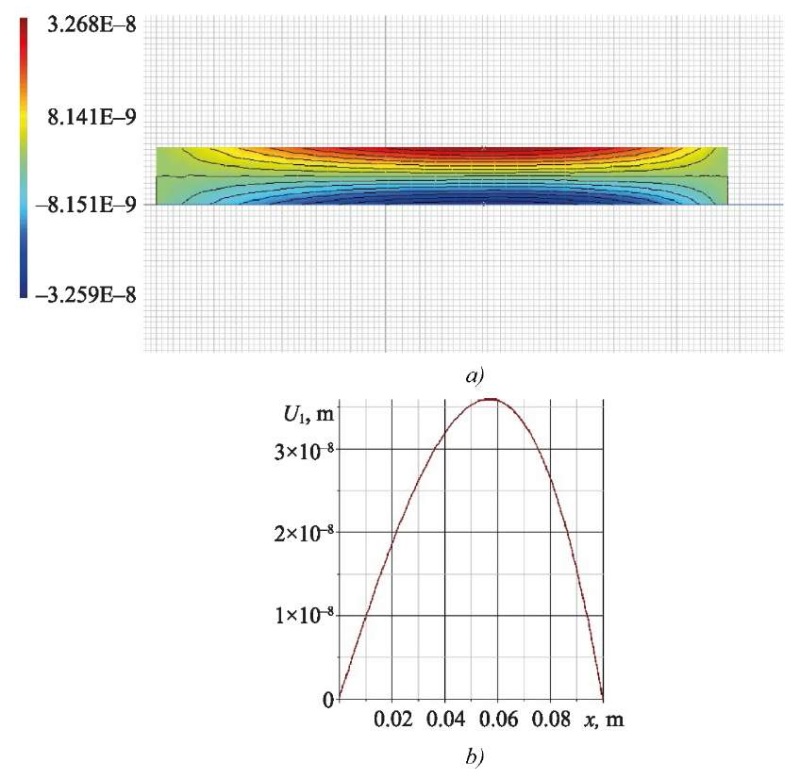
Fig. 4. Horizontal displacement in ACELAN in the first problem:
a — distribution; b—graphon the upper boundary
The calculations showed that the error in determining the vertical displacement was 5.8%, and for the horizontal displacement, it was 1.2%.
In the second problem, defined by equations (8) and (9), when setting zero load p(x) ≡ 0, potential difference V0 = 100 W and with boundary conditions:
 (12)
(12)
the following results were obtained, shown in Figures 5, 6.
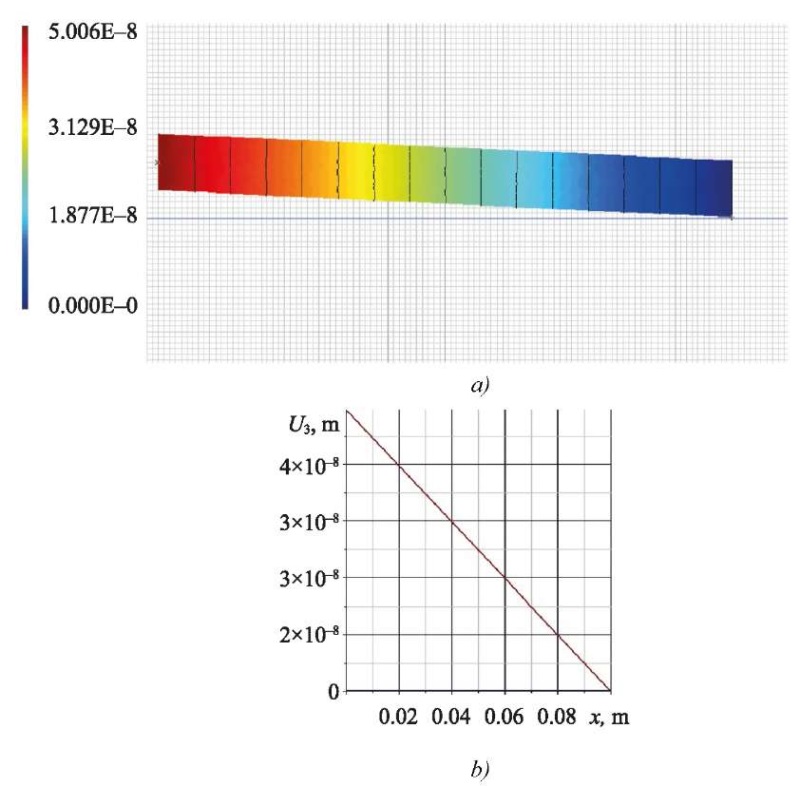
Fig. 5. Vertical displacement in ACELAN in the second problem:
a — distribution; b—graphon the upperboundary
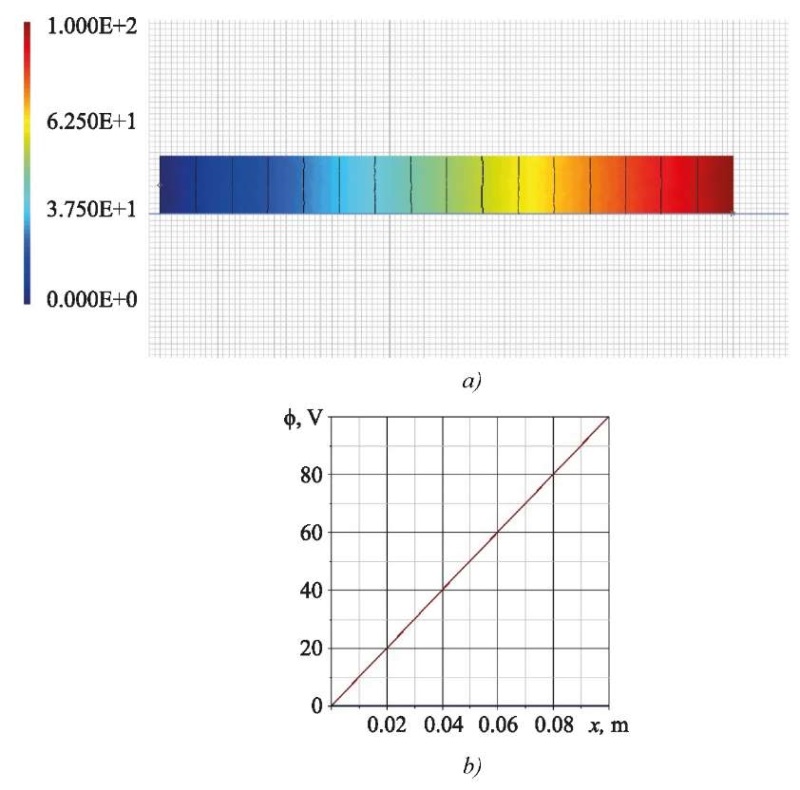
Fig. 6. Electric potential in ACELAN in the second problem:
a—distribution;
b—dependenceon the longitudinalcoordinatein the middle of the thickness
The calculations showed that the error in determining the vertical displacement was 0.8%, and for the electric potential, it was less than 1%. It should be noted that the values of the horizontal displacement calculated in ACELAN turned out to be three orders of magnitude less than the maximum vertical displacement, which indicated the adequacy of the hypothesis (7).
When setting mechanical loads and potential differences, the error of the proposed method turned out to be about 6 % for the displacement and electrical potential components.
Discussion and Conclusion. As noted in the cited literature, the simultaneous use of bending and shear of a piezoelectric element can significantly increase its efficiency. In addition, the use of porous ceramics, due to different dependences of elastic modules and piezomodules on the percentage of porosity, also improves the output characteristics of PEG.
In this paper, due to the linear formulation in the theory of electroelasticity, it was possible to develop an applied theory for calculating bending-shear vibrations of a piezoelectric element in the low-frequency region, which consisted of solving two problems: in the first, mechanical loads operated at zero potentials, and in the second, on the contrary, there were zero mechanical loads, and a potential difference was set. Based on various hypotheses about the distribution of mechanical and electric fields, two boundary value problems for systems of ordinary differential equations were obtained, which were solved analytically. The results of the calculation of displacements and electric potential were compared using the proposed method and the FEM implemented in the ACELAN package. These calculations validated the applicability of the proposed method, the error for which in calculating the above characteristics was 6%. This accuracy is sufficient for engineering calculations; therefore, the proposed method can be applied in the design of piezoelectric devices, including the collection and storage of energy. Further development of this applied theory will be aimed at covering a wider frequency range, including the first flexural shear resonance.
References
1. Liang Zhou, Jing Sun, Xuejun Zheng, Shuifeng Deng, Jihe Zhao, Jihe Zhao, et al. A Model for the Energy Harvesting Performance of Shear Mode Piezoelectric Cantilever. Sensors and Actuators A: Physical. 2012;179:185–192. http://doi.org/10.1016/j.sna.2012.02.041
2. Dung-An Wang, Nine-Zeng Liu. A Shear Mode Piezoelectric Energy Harvester Based on a Pressurized Water Fow. Sensors and Actuators A: Physical. 2011;167(2):449–458. https://doi.org/10.1016/j.sna.2011.03.003
3. Shreya Banerjee, Sitikantha Roy. A Timoshenko like Model for Piezoelectric Energy Harvester with Shear Mode. Composite Structures. 2018;204:677–688. https://doi.org/10.1016/j.compstruct.2018.07.117
4. Yanping Kong, Jinxi Liu. Vibration Confinement of Thickness-Shear and Thickness-Twist Modes in a Functionally Graded Piezoelectric Plate. Acta Mechanica Solida Sinica. 2011;24(4):299–307. https://doi.org/10.1016/S0894-9166(11)60031-1
5. Xiangyu Gao, Xudong Xin, Jingen Wu, Zhaoqiang Chu, Shuxiang Dong. A Multilayered-Cylindrical Piezoelectric Shear Actuator Operating in Shear (d15) Mode. Applied Physics Letters. 2018;112:152902. http://doi.org/10.1063/1.5022726
6. Jikun Yang, Qiang Huan, Yang Yu, Jingen Wu, Zhaoqiang Chu, Mohammadjavad Pourhosseiniasl, et al. Tailoring Artificial Mode to Enable Cofired Integration of Shear-type Piezoelectric Devices. Advanced Science. 2020;7(17):2001368. https://doi.org/10.1002/advs.202001368
7. Zejun Yu, Shuxiang Dong, Daining Fang. Theoretical Analysis on Shear-Bending Deflection of a Ring-Shape Piezoelectric Plate. AIP Advances. 2016;6(2):025124. https://doi.org/10.1063/1.4943219
8. Ewald Benesa, Helmut Nowotny, Stefan Braun, Stefan Radel, Martin Greöschl. Analytical Sensor Response Function of Viscosity Sensors Based on Layered Piezoelectric Thickness Shear Resonators. Physics Procedia. 2015;70:236–240. http://doi.org/10.1016/j.phpro.2015.08.144
9. Hui Lia, Shengnan Shenb, Kensuke Amemiya, Bo Liu, Hejun Du. Simulation of Piezoelectric Flying Height Control Slider Using Shear-Mode Deformation. Physics Procedia. 2011;16:101–110. https://doi.org/10.1016/j.phpro.2011.06.115
10. Zenkour AM, Alghanmi RA. Stress Analysis of a Functionally Graded Plate Integrated with Piezoelectric Faces via a Four-Unknown Shear Deformation Theory. Results in Physics. 2019;12:268–277. https://doi.org/10.1016/j.rinp.2018.11.045
11. Mohammad Malikan. Electro-Mechanical Shear Buckling of Piezoelectric Nanoplate Using Modified Couple Stress Theory Based on Simplified First Order Shear Deformation Theory. Applied Mathematical Modelling. 2017;48:196–207. https://doi.org/10.1016/j.apm.2017.03.065
12. Bo Xue, Emmanuel Brousseau, Chris Bowen. Modelling of a Shear-type Piezoelectric Actuator for AFM-based Vibration-assisted Nanomachining. International Journal of Mechanical Sciences. 2023;243:108048. https://doi.org/10.1016/j.ijmecsci.2022.108048
13. Belokon’ AV, Eremeev VA, Nasedkin AV, Solov’ev AN. Partitioned Schemes of the Finite-Element Method for Dynamic Problems of Acoustoelectroelasticity. Journal of Applied Mathematics and Mechanics. 2000;64(3):367–377. https://doi.org/10.1016/S0021-8928(00)00059-9
14. Kudimova AB, Nadolin DK, Nasedkin AV, Nasedkina AA, Oganesyan PA, Soloviev AN. Finite Element Homogenization of Piezocomposites with Isolated Inclusions Using Improved 3-0 Algorithm for Generating Representative Volumes in ACELAN-COMPOS Package. Materials Physics and Mechanics. 2020;44(3):392–403. https://doi.org/10.18720/MPM.4432020_10
15. Nasedkin AV, Oganesyan PA, Soloviev AN. Analysis of Rosen Type Energy Harvesting Devices from Porous Piezoceramics with Great Longitudinal Piezomodulus. Zeitschrift für Angewandte Mathematik und Mechanik. 2021;101(3):e202000129. https://doi.org/10.1002/zamm.202000129
16. Nasedkin AV, Skaliukh AS, Soloviev AN. ACELAN Package and Finite Element Modeling of Hydroacoustic Piezoelectric Transducers. Bulletin of Higher Education Institutes. North-Caucasian Region. Natural Sciences. 2001;S1:122–125. (In Russ.).
About the Authors
A. N. SolovievRussian Federation
Arkadiy N. Soloviev, Dr.Sci. (Phys.-Math.), Professor of the Mathematics and Physics Department; Professor of the Theoretical and Applied Mechanics Department; Chief Researcher
8, Uchebnyi Lane, Simferopol); D1, Gagarin sq., Rostov-on-Don, 344003; 105/42, Bolshaya Sadovaya Str., Rostov-on-Don, 344006
V. A. Chebanenko
Russian Federation
Valery A. Chebanenko, Cand.Sci. (Phys.-Math.), Senior Researcher, Laboratory of Transport, Composite Materials and Structures, Southern Research Cente
41, Chekhova Av., Rostov-on-Don, 344006
P. A. Oganesyan
Russian Federation
Pavel A. Oganesyan, Cand.Sci. (Phys.-Math.), Associate Professor of the Mathematical Modeling Department, Institute of Mathematics, Mechanics and Computer Science
8a, Milchakova Str., Rostov-on-Don, 344058
E. I. Fomenko
Russian Federation
Elizaveta I. Fomenko, graduate student of the Mathematical Modeling Department, Institute of Mathematics, Mechanics and Computer Science,
8a, Milchakova Str., Rostov-on-Don, 344058
Review
For citations:
Soloviev A.N., Chebanenko V.A., Oganesyan P.A., Fomenko E.I. On a Method for Calculating Bending and Shear Vibrations of a Porous Piezoelement in the Low-Frequency Region. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148-158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158. EDN: VPUERG
JATS XML




 , kg/m³
, kg/m³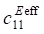 , 10¹⁰, N/m²
, 10¹⁰, N/m²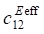 , 10¹⁰, N/m²
, 10¹⁰, N/m²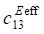 , 10¹⁰, N/m²
, 10¹⁰, N/m²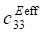 , 10¹⁰, N/m²
, 10¹⁰, N/m²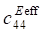 , 10¹⁰, N/m²
, 10¹⁰, N/m²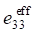 , C/m²
, C/m²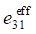 , C/m²
, C/m²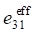 , C/m²
, C/m²