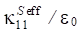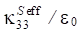Перейти к:
Об одном методе расчета изгибных и сдвиговых колебаний пористого пьезоэлемента в низкочастотной области
https://doi.org/10.23947/2687-1653-2024-24-2-148-158
EDN: VPUERG
Аннотация
Введение. Устройства сбора и накопления энергии из внешней среды представляют собой маломощные источники электрической энергии, которые активно используются, в том числе в автономных приборах мониторинга поврежденного состояния различных конструкций. Рабочим элементом этих устройств является пьезоэлектрический генератор (ПЭГ) — преобразователь механической энергии в электрическую. Конструирование ПЭГ связано с предварительным построением их математических и компьютерных моделей, с помощью которых производится расчет и оптимизация конструкций. Одним из способов моделирования и расчета ПЭГ является разработка приближенных методов расчета на основе прикладных теорий. В литературе известны и ранее разработаны прикладные теории расчета изгибных колебаний многослойных пьезоактивных пластин. Однако информации об изгибно-сдвиговых колебаниях, как инструменте повышения эффективности инженерных расчетов описанных конструкций, в научной литературе недостаточно. Целью настоящей работы являлась разработка прикладного метода расчета изгибных и сдвиговых колебаний пьезокерамических пластин, в том числе пористых.
Материалы и методы. В качестве пьезоактивного материала пластины используется пьезокерамика PZT-4, в том числе пористая. При использовании пористой керамики жесткость конструкции уменьшается в большей степени, чем пьезомодули, что позволяет получить более эффективный ПЭГ при механическом воздействии. Математическая постановка осуществлена в рамках линейной теории электроупругости при поляризации пластины по толщине. Боковые стороны пластины электродированы, правая сторона закреплена, а на левой задан гладкий контакт в вертикальной стенке. Установившиеся колебания пластины вызываются давлением на лицевые поверхности пластины или разностью электрических потенциалов на электродах. Для расчета характеристик ПЭГ в работе предлагается прикладная теория, основанная на гипотезах о распределении характеристик напряженно-деформированного состояния и электрического поля.
Результаты исследования. Рассмотрены поперечные колебания пьезокерамической пластины в низкочастотной области (ниже первого изгибно-сдвигового резонанса). В силу того, что математическая постановка рассмотрена в рамках линейной теории упругости, задача разделилась на сумму двух. В первой учитывалось механическое воздействие: на лицевые поверхности пластины действует распределенная нагрузка и поперечная сила на левом конце, а потенциалы на электродах равны нулю. Во второй задаче механические нагрузки отсутствовали, но задавалась разность потенциалов на электродах. На основе гипотез о распределении деформаций, механических напряжений и электрического потенциала обе задачи были сведены к системе обыкновенных дифференциальных уравнений и граничных условий. Сравнение с результатами расчетов методом конечных элементов в пакете ACELAN показали адекватность предложенной прикладной теории в низкочастотной области.
Обсуждение и заключение. Поскольку постановка задачи рассматривалась в линейной теории электроупругости и изучалась низкочастотная область, в работе удалось задачу об изгибных и сдвиговых колебаниях пластины из пористой пьезокерамики разделить на две: изгибную — с механическим воздействием при нулевых потенциалах и сдвиговую — при задании разности потенциалов и нулевом механическом воздействии. Использованы соответствующие гипотезы об изгибе и сдвиге, построены две системы обыкновенных дифференциальных уравнений и граничных условий, которые решаются аналитически без использования «тяжелых» конечно-элементных пакетов. Для сравнения результатов и подтверждения адекватности предложенного метода проведено конечно-элементное моделирование таких задач в специализированном пакете ACELAN. Это сравнение показало, что ошибка в определении смещений и электрического потенциала при использовании этого подхода, в случае задания механических нагрузок и разности потенциалов, не превышает 6 %. Разработанный в статье метод может быть применен при проектировании пьезоэлектрических генераторов накопления энергии в низкочастотной области.
Ключевые слова
Для цитирования:
Соловьев А.Н., Чебаненко В.А., Оганесян П.А., Фоменко Е.И. Об одном методе расчета изгибных и сдвиговых колебаний пористого пьезоэлемента в низкочастотной области. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148-158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158. EDN: VPUERG
For citation:
Soloviev A.N., Chebanenko V.A., Oganesyan P.A., Fomenko E.I. On a Method for Calculating Bending and Shear Vibrations of a Porous Piezoelement in the Low-Frequency Region. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148-158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158. EDN: VPUERG
Введение. Пьезоэлектрические генераторы (ПЭГ) используются для преобразования механической энергии в электрическую с последующим ее накоплением. Одна из областей применения ПЭГ — создание маломощных автономных возобновляемых источников электрической энергии. Рабочим элементом ПЭГ является пьезокерамический элемент определенной формы. Форма и тип деформации этого элемента определяют пьезомодуль, который характеризует преобразование механической энергии деформации в электрическую. Так пьезомодуль d33 связан с растяжением-сжатием вдоль оси поляризации, d31 — с такой же деформацией в поперечном направлении к этой оси, d15 — со сдвигом. Использование пористой керамики позволяет создавать более эффективные ПЭГ. Это связано с тем, что модули упругости пористой керамики с ростом пористости убывают значительно сильнее, чем пьезомодули. Таким образом при одной и той же механической нагрузке амплитуда деформации у пористой керамики будет больше, следовательно, выходной электрический потенциал также больше.
Расчет ПЭГ может быть произведен методом конечных элементов, реализованном в пакетах ANSYS, ACELAN, COMSOL и других. Для пьезоэлементов, один или два размера которых значительно меньше других (пластины, стержни), могут быть построены прикладные теории расчета на основе гипотез о распределении механического и электрического полей. Без применения «тяжелых» конечно-элементных пакетов прикладные теории позволяют моделировать различные устройств на основе пьезоактивных материалов. В качестве таких материалов рассматривались пьезоэлектрические, пьезомагнитные и композиционные пьезомагнитоэлектрические. Построение этих теорий основано на принятии гипотез о распределении механических, электрических и магнитных полей. Эти гипотезы связаны с характером колебаний упругих и пьезоактивных элементов ПЭГ. Наиболее распространенными конструкциями являются активные и полупассивные биморфы на основе многослойных пластин, поляризованные по толщине с электродами на лицевых поверхностях, совершающие поперечные изгибные колебания. Исследованию устройств со сдвиговой деформацией пьезоэлементов посвящен ряд работ. Электрическая модель с пьезоэлектрическими определяющими уравнениями режима d15 и модель с одной степенью свободы объединены для описания характеристик сбора энергии пьезоэлектрического кантилевера в сдвиговом режиме в работе [1]. Предлагаемая модель используется для моделирования частотной зависимости выходного пикового напряжения и мощности. Результаты показывают хорошее совпадение с экспериментом и конечно-элементным расчетом в ANSYS. В работе [2] разработан пьезоэлектрический преобразователь энергии сдвигового режима для использования энергии потока воды под давлением. Он преобразует энергию потока в электрическую энергию путем пьезоэлектрического преобразования с колебанием пьезоэлектрической пленки. Разработана модель конечных элементов для оценки генерируемого напряжения пьезоэлектрической пленки, которая хорошо согласуется с проведенным натурным экспериментом. Одномерная полностью связанная модель колебания балки на основе гипотез типа Тимошенко, которая предоставляет единую общую основу для анализа энергии в режиме сдвига и изгиба, представлена в работе [3]. В работе [4] изучается влияние неоднородности свойств пластины при сдвиговых и крутильных колебаниях ее центральной части. В экспериментальной работе [5] был представлен многослойно-цилиндрический пьезоэлектрический сдвиговый актуатор (MCPSA), работающий в режиме сдвига d15, для прецизионного срабатывания при большой механической нагрузке. Актуатор был изготовлен из пьезоэлектрических керамических колец Pb(Zr,Ti)O3 (PZT-51), которые были концентрически собраны вместе в электрически параллельном соединении с попеременно положительной и отрицательной поляризацией в осевом направлении. В работе [6] создан метаматериал из идентичных элементарных ячеек, спроектирован и изготовлен искусственный прототип устройства с характерными узорчатыми электродами и расположенными в ряд пьезокерамическими субъединицами, который, как доказано, идеально генерирует синтетическую деформацию сдвига грани. При том же напряжении возбуждения наблюдается усиление смещения сдвигового типа более чем на порядок, по сравнению с предыдущими объемными элементами в режиме d15. В статической постановке в работе [7] теоретически установлено поле электромеханической связи в сдвигово-изгибающем режиме для кольцеобразной пьезоэлектрической пластины. В соответствии с классической теорией упругих пластин малого изгиба и пьезоэлектрическими определяющими уравнениями было достигнуто аналитическое решение изгибной деформации пьезоактюатора под действием электрического поля и концентрированной или равномерно распределенной механической нагрузки. Механизм создания изгибной деформации объясняется осесимметричной сдвиговой деформацией, которая дополнительно вызывает изгибную деформацию одной пьезоэлектрической пластины в форме кольца. Этот механизм существенно отличается от механизма пьезоэлектрических биморфных или униморфных приводов, о которых сообщалось ранее. Проведена оптимизация конструкции кольцеобразного пьезоактуатора. В работе [8] на основе одномерной модели строится функция отклика датчика на основе сдвиговых резонаторов (срезы кварца) объемной акустической волны, которые перспективны для поточных измерений вязкости жидкости, например, в промышленных процессах. В работе [9] с помощью метода конечных элементов исследовался пьезоэлектрический преобразователь управления высотой полета с использованием деформации модели сдвига. В [10] теория функционально-градиентной пластины с четырьмя неизвестными сдвиговой деформации применяется для выражения компоненты смещения. Распределение электрического потенциала представляет собой линейную функцию по толщине. Пластина находится под механической нагрузкой и электрическим напряжением. Основные уравнения и граничные условия выводятся с использованием принципа виртуальной работы. Проведен анализ напряжений и деформаций от параметров конструкции. Электромеханический анализ потери устойчивости пьезоэлектрической нанопластины при сдвиге с использованием модифицированной теории парных напряжений с различными граничными условиями изучался в работе [11]. Чтобы учесть электрические эффекты, к пьезоэлектрической нанопластине прикладывали внешнее электрическое напряжение. Была использована упрощенная теория сдвиговой деформации первого порядка. Основные дифференциальные уравнения были получены с использованием принципа Гамильтона и нелинейных деформаций Фон-Кармана. В итоге результаты показали, что влияние внешнего электрического напряжения на критическую сдвиговую нагрузку, возникающую на пьезоэлектрической нанопластине, незначительно. В работе [12] с помощью комбинации двух классических подходов моделирования нелинейного поведения пьезоэлектрических материалов исследуется пьезоэлектрический привод сдвигового типа для атомно-силового микроскопа. В частности, новизна предлагаемого метода состоит в том, что он сочетает в себе два источника нелинейности полезависимой модели Мюллера и Чжана с частотно-зависимой моделью Дамьяновича. Численные результаты, полученные с помощью метода конечных элементов (МКЭ), сравниваются с экспериментом.
Менее исследованы в научной литературе колебания, в которых кроме изгиба присутствует сдвиг, т.е. «рабочим» является пьезомодуль d15, значение которого убывает с увеличением пористости, но в меньшей степени, чем упругие модули. Последнее обстоятельство позволяет построить эффективное устройство преобразования энергии. Поэтому разработка прикладной теории расчета ПЭГ с использованием пористой пьезокерамики на основе упрощенных моделей без использования «тяжелых» конечно-элементных пакетов представляется весьма актуальной задачей. Целью настоящей работы явилось построение прикладного метода расчета для установившихся поперечных колебаний в низкочастотной области пористой пьезокерамической пластины, характеризующиеся как сдвигом, так и изгибом.
Материалы и методы. Исследуемый ПЭГ представляет собой пьезокерамическую пластину (длина l, толщина h), поляризованную по толщине, консольно-закрепленную по правой боковой стороне, левая боковая сторона прикреплена к инерционной массе, которая совершает вертикальные колебания и закреплена в горизонтальном направлении. Электроды расположены на боковых сторонах пластины, поэтому при разности потенциалов на них и отсутствии механической нагрузки, основной деформацией в низкочастотной области является сдвиг. Рассматриваются колебания, частота которых меньше частоты первого резонанса.
Математическая постановка задачи
Математическая постановка задачи описывается системой дифференциальных уравнений [13] и соответствующими граничными условиями.
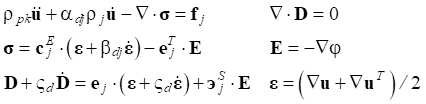 (1)
(1)
При рассмотрении пористой керамики связности 3–0 в уравнениях (1) используются эффективные физические константы, определенные с помощью пакета ACELAN-COMPOS [14]. Эти эффективные свойства на основе представительных объемов (рис. 1) получены в работе [15] и представлены в таблице 1.

Рис. 1. Представительные объемы в пакете ACELAN-COMPOS [14]
Таблица 1
Эффективные свойства пористой керамики
|
% пористости |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
7 500 |
6 750 |
6 000 |
5 250 |
4 500 |
3 750 |
3 000 |
2 250 |
1 500 |
|
|
13,90 |
11,56 |
9,25 |
6,85 |
5,05 |
3,34 |
2,07 |
1,26 |
0,68 |
|
|
7,78 |
6,15 |
4,66 |
3,14 |
2,10 |
1,16 |
0,62 |
0,28 |
0,13 |
|
|
7,43 |
5,82 |
4,25 |
2,82 |
1,87 |
1,06 |
0,52 |
0,24 |
0,10 |
|
|
11,50 |
9,53 |
7,23 |
5,42 |
3,91 |
2,72 |
1,63 |
0,91 |
0,47 |
|
|
2,56 |
2,23 |
1,83 |
1,44 |
1,10 |
0,74 |
0,44 |
0,23 |
0,10 |
|
|
15,10 |
13,38 |
11,37 |
9,59 |
7,68 |
5,93 |
3,93 |
2,30 |
1,25 |
|
|
–5,20 |
–4,23 |
–3,14 |
–2,07 |
–1,32 |
–0,75 |
–0,43 |
–0,21 |
–0,10 |
|
|
12,70 |
10,96 |
8,96 |
6,91 |
5,00 |
3,30 |
1,95 |
1,00 |
0,44 |
|
|
730 |
663 |
582 |
509 |
439 |
349 |
263 |
191 |
122 |
|
|
635 |
567 |
492 |
413 |
345 |
270 |
199 |
130 |
75 |
По данным таблицы 1 построены зависимости эффективных упругих модулей и пьезомодулей от процента пористости [15], которые представлены на рис. 2.
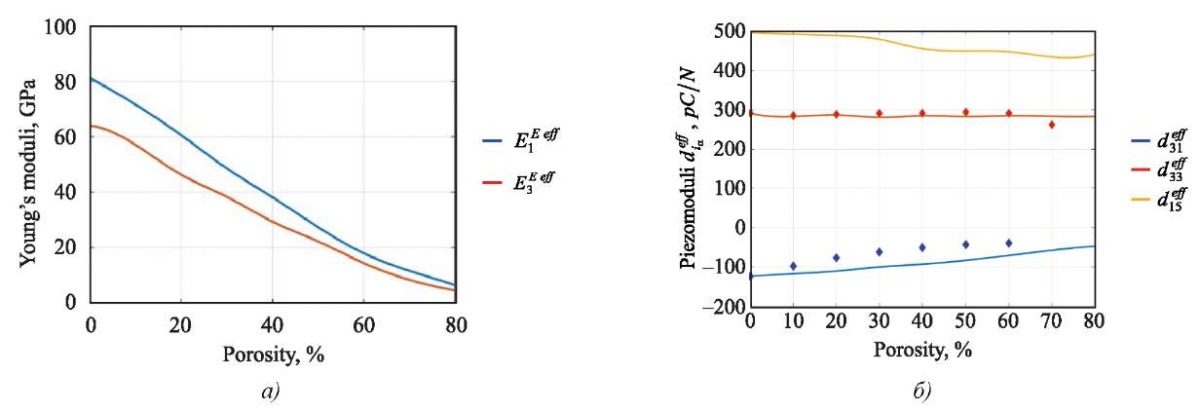
Рис. 2. Зависимости значений от процента пористости [15]:
а — упругих моделей; б — пьезомодулей
В соответствии с результатами, представленными на рис. 2, модуль упругости E1 убывает значительно быстрей, чем пьезомодуль d15.
Построение прикладной теории
Построенный метод расчета состоит из решения двух задач: в первой рассматривается изгиб под действием механической нагрузки при нулевой разности потенциалов, во второй — моделируется сдвиг, вызванный разностью потенциалов при отсутствии механической нагрузки. В обоих случаях учитывается отсутствие зарядов на лицевых поверхностях пластины. При действии механической нагрузки и разности электрических потенциалов результаты двух задач складываются в силу линейности задачи.
Действие механической нагрузки, потенциалы на электродах равны нулю. Принимаются гипотезы типа Кирхгофа-Лява относительно равенства нулю нормальных напряжений, а для перемещений:
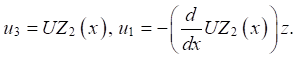 (2)
(2)
Распределение электрического потенциала по толщине предполагается квадратичным и симметричным:
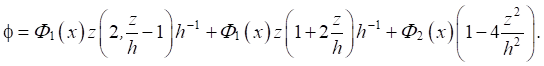 (3)
(3)
Для учета граничных условий на концах пластины (x = 0, l) получено выражение для поперечной силы:
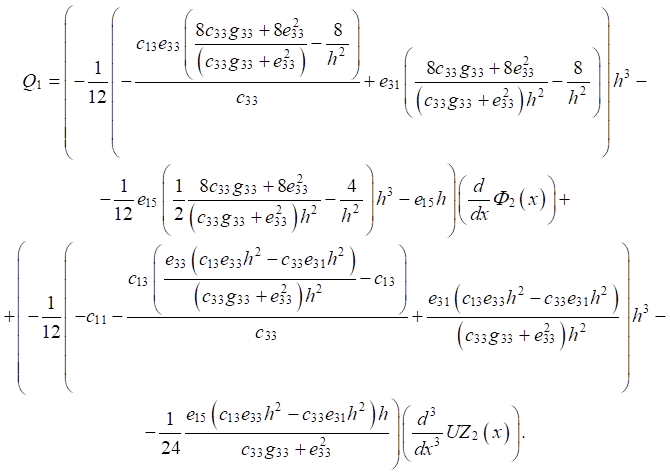 (4)
(4)
С учетом равенства нулю нормальной компоненты вектора электрической индукции на лицевых поверхностях (z = ±h), уравнения для неизвестного прогиба UZ2(x) и распределения электрического потенциала Ф2(x) имеют вид:
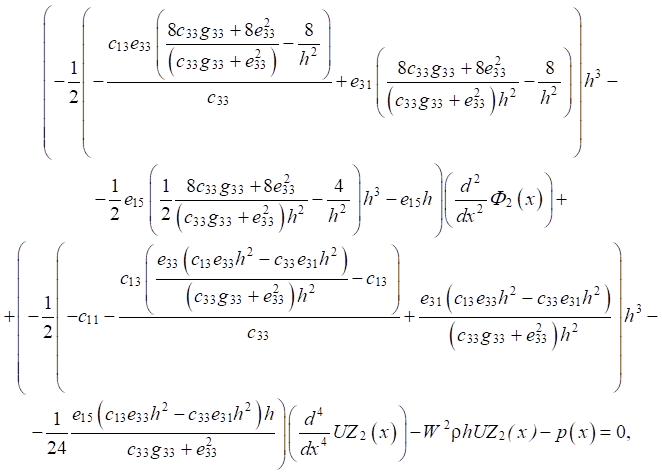 (5)
(5)
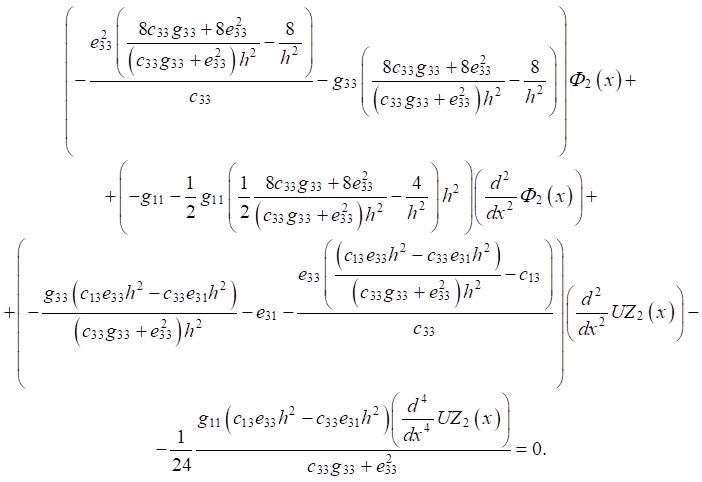 (6)
(6)
Задана разность потенциалов, механическая нагрузка равна нулю. Предполагается независимость поперечного смещения от толщины и равенство нулю продольного перемещения и квадратичное распределение электрического потенциала по толщине (3):
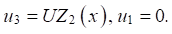 (7)
(7)
Выражение для поперечной силы:
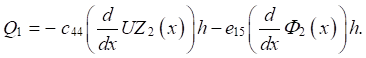 (8)
(8)
С учетом равенства нулю нормальной компоненты вектора электрической индукции на лицевых поверхностях (z = ±h), уравнения для неизвестного прогиба UZ2(x) и распределения электрического потенциала Ф2(x) имеют вид:
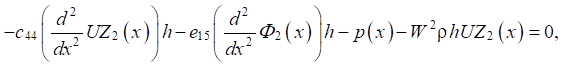 (9)
(9)
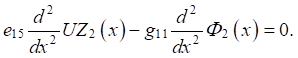 (10)
(10)
Результаты исследования. Проведено сравнение результатов расчетов по предложенным прикладным теориям с расчетами колебаний пьезоэлемента (l = 0,1 м, h = 0,01 м) на частоте равной 100 с-1 методом конечных элементов в ACELAN [16].
В первой задаче, определяемой уравнениями (5) и (6), при задании равномерно распределенной нагрузки p(x) = 1000 Па·м и с граничными условиями:
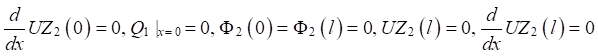 (11)
(11)
получены следующие результаты, представленные на рис. 3, 4.
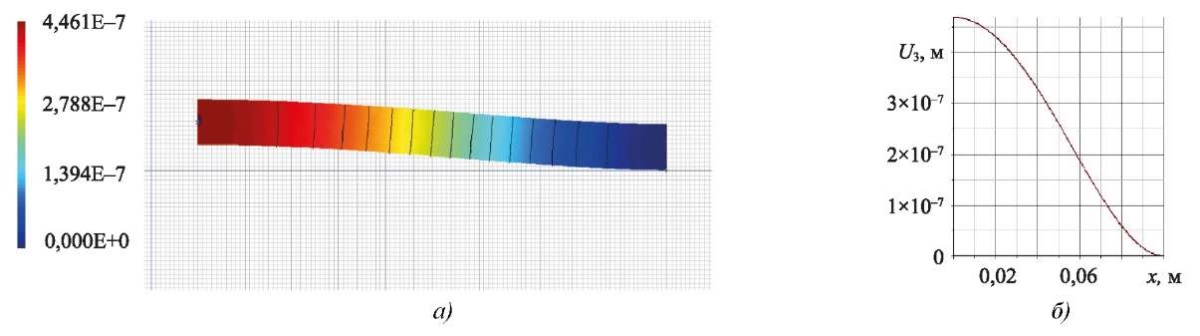
Рис. 3. Вертикальное смещение в ACELAN в первой задаче:
а — распределение; б — график на верхней границе
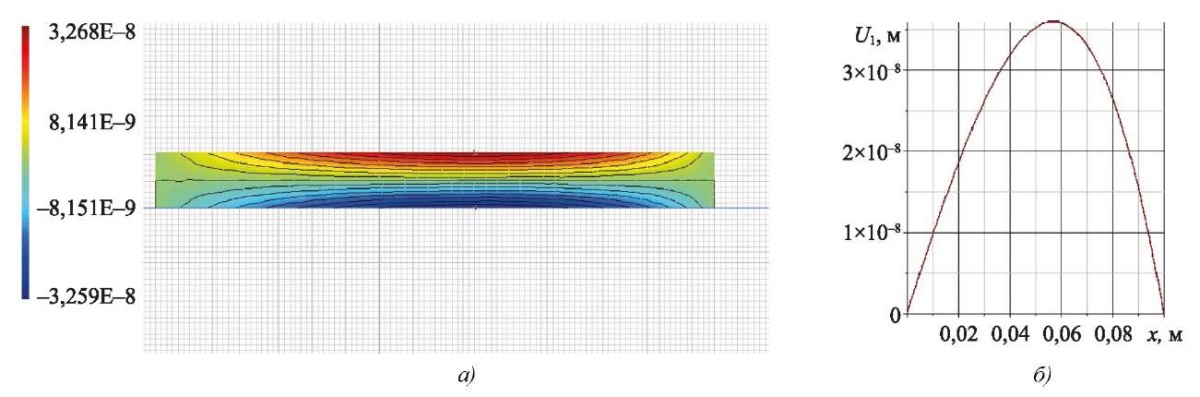
Рис. 4. Горизонтальное смещение в ACELAN в первой задаче:
а — распределение; б — график на верхней границе
Расчеты показали, что погрешность в определении вертикального смещения — 5,8 %, а для горизонтального смещения составляет 1,2 %.
Во второй задаче, определяемой уравнениями (8) и (9), при задании нулевой нагрузки p(x) ≡ 0, разности потенциалов V0 = 100 В и граничными условиями:
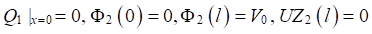 (12)
(12)
получены следующие результаты, представленные на рис. 5, 6.
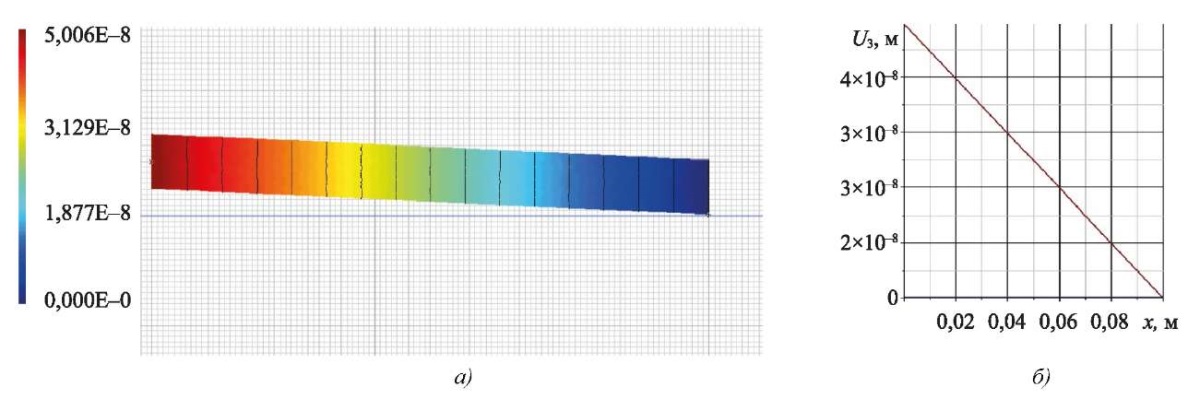
Рис. 5. Вертикальное смещение в ACELAN во второй задаче:
а — распределение; б — график на верхней границе
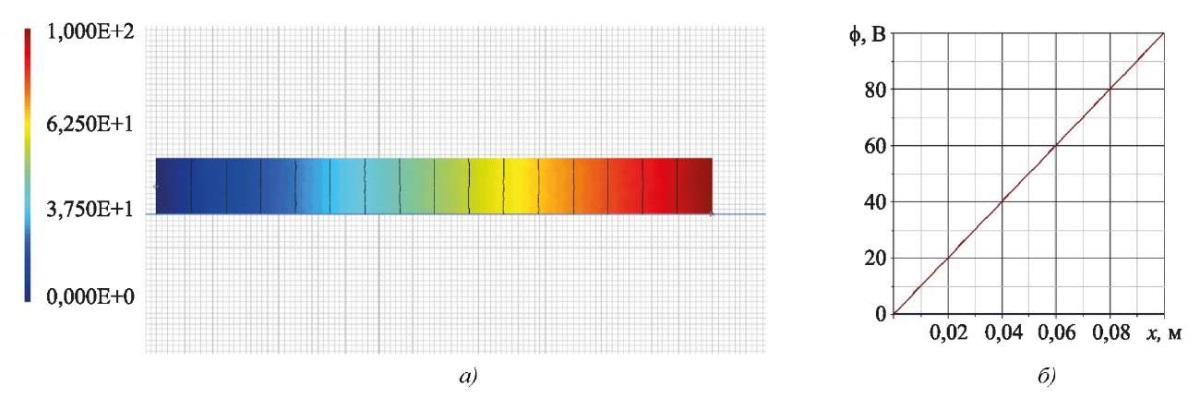
Рис. 6. Электрический потенциал в ACELAN во второй задаче:
а — распределение;
б — зависимость от продольной координаты в середине толщины
Расчеты показали, что погрешность в определении вертикального смещения составляет 0,8 %, а для электрического потенциала — менее 1 %. Следует отметить, что значения горизонтального смещения, рассчитанные в ACELAN, оказались на три порядка меньше максимального вертикального смещения, что говорит об адекватности гипотезы (7).
При задании механических нагрузок и разности потенциалов погрешность предложенного метода оказалась порядка 6 % для компонент перемещения и электрического потенциала.
Обсуждение и заключение. Как отмечалось в цитируемой литературе, одновременное использование изгиба и сдвига пьезоэлемента может значительно повысить его эффективность. Кроме этого, использование пористой керамики в силу различных зависимостей упругих модулей и пьезомодулей от процента пористости также улучшает выходные характеристики ПЭГ.
В настоящей работе в силу линейной постановки в теории электроупругости удалось построить прикладную теорию расчета изгибно-сдвиговых колебаний пьезоэлемента в низкочастотной области, которая состоит из решения двух задач: в первой действуют механические нагрузки при нулевых потенциалах, а во второй — наоборот — нулевые механические нагрузки и задана разность потенциалов. На основе различных гипотез о распределении механического и электрического полей получены две краевые задачи для систем обыкновенных дифференциальных уравнений, которые решались аналитически. Проведено сравнение результатов расчета смещений и электрического потенциала по предложенному методу и с помощью МКЭ, реализованного в пакете ACELAN. Эти расчеты подтвердили применимость предложенного метода, погрешность для которого в вычислении вышеуказанных характеристик составила 6 %. Такой точности достаточно для инженерных расчетов, поэтому предложенный метод может быть применен при проектировании пьезоэлектрических устройств, в том числе при сборе и накоплении энергии. Дальнейшее развитие этой прикладной теории будет направлено на охват более широкого частотного диапазона, включая первый изгибно-сдвиговый резонанс.
Список литературы
1. Liang Zhou, Jing Sun, Xuejun Zheng, Shuifeng Deng, Jihe Zhao, Jihe Zhao, et al. A Model for the Energy Harvesting Performance of Shear Mode Piezoelectric Cantilever. Sensors and Actuators A: Physical. 2012;179:185–192. http://doi.org/10.1016/j.sna.2012.02.041
2. Dung-An Wang, Nine-Zeng Liu. A Shear Mode Piezoelectric Energy Harvester Based on a Pressurized Water Fow. Sensors and Actuators A: Physical. 2011;167(2):449–458. https://doi.org/10.1016/j.sna.2011.03.003
3. Shreya Banerjee, Sitikantha Roy. A Timoshenko like Model for Piezoelectric Energy Harvester with Shear Mode. Composite Structures. 2018;204:677–688. https://doi.org/10.1016/j.compstruct.2018.07.117
4. Yanping Kong, Jinxi Liu. Vibration Confinement of Thickness-Shear and Thickness-Twist Modes in a Functionally Graded Piezoelectric Plate. Acta Mechanica Solida Sinica. 2011;24(4):299–307. https://doi.org/10.1016/S0894-9166(11)60031-1
5. Xiangyu Gao, Xudong Xin, Jingen Wu, Zhaoqiang Chu, Shuxiang Dong. A Multilayered-Cylindrical Piezoelectric Shear Actuator Operating in Shear (d15) Mode. Applied Physics Letters. 2018;112:152902. http://doi.org/10.1063/1.5022726
6. Jikun Yang, Qiang Huan, Yang Yu, Jingen Wu, Zhaoqiang Chu, Mohammadjavad Pourhosseiniasl, et al. Tailoring Artificial Mode to Enable Cofired Integration of Shear-type Piezoelectric Devices. Advanced Science. 2020;7(17):2001368. https://doi.org/10.1002/advs.202001368
7. Zejun Yu, Shuxiang Dong, Daining Fang. Theoretical Analysis on Shear-Bending Deflection of a Ring-Shape Piezoelectric Plate. AIP Advances. 2016;6(2):025124. https://doi.org/10.1063/1.4943219
8. Ewald Benesa, Helmut Nowotny, Stefan Braun, Stefan Radel, Martin Greöschl. Analytical Sensor Response Function of Viscosity Sensors Based on Layered Piezoelectric Thickness Shear Resonators. Physics Procedia. 2015;70:236–240. http://doi.org/10.1016/j.phpro.2015.08.144
9. Hui Lia, Shengnan Shenb, Kensuke Amemiya, Bo Liu, Hejun Du. Simulation of Piezoelectric Flying Height Control Slider Using Shear-Mode Deformation. Physics Procedia. 2011;16:101–110. https://doi.org/10.1016/j.phpro.2011.06.115
10. Zenkour AM, Alghanmi RA. Stress Analysis of a Functionally Graded Plate Integrated with Piezoelectric Faces via a Four-Unknown Shear Deformation Theory. Results in Physics. 2019;12:268–277. https://doi.org/10.1016/j.rinp.2018.11.045
11. Mohammad Malikan. Electro-Mechanical Shear Buckling of Piezoelectric Nanoplate Using Modified Couple Stress Theory Based on Simplified First Order Shear Deformation Theory. Applied Mathematical Modelling. 2017;48:196–207. https://doi.org/10.1016/j.apm.2017.03.065
12. Bo Xue, Emmanuel Brousseau, Chris Bowen. Modelling of a Shear-type Piezoelectric Actuator for AFM-based Vibration-assisted Nanomachining. International Journal of Mechanical Sciences. 2023;243:108048. https://doi.org/10.1016/j.ijmecsci.2022.108048
13. Белоконь А.В., Еремеев В.А., Наседкин А.В., Соловьев А.Н. Блочные схемы метода конечных элементов для динамических задач акустоэлектроупругости. Прикладная математика и механика. 2000;64(3):381–393. URL: https://pmm.ipmnet.ru/ru/Issues/2000/3 (дата обращения: 04.03.2024).
14. Kudimova AB, Nadolin DK, Nasedkin AV, Nasedkina AA, Oganesyan PA, Soloviev AN. Finite Element Homogenization of Piezocomposites with Isolated Inclusions Using Improved 3-0 Algorithm for Generating Representative Volumes in ACELAN-COMPOS Package. Materials Physics and Mechanics. 2020;44(3):392–403. https://doi.org/10.18720/MPM.4432020_10
15. Nasedkin AV, Oganesyan PA, Soloviev AN. Analysis of Rosen Type Energy Harvesting Devices from Porous Piezoceramics with Great Longitudinal Piezomodulus. Zeitschrift für Angewandte Mathematik und Mechanik. 2021;101(3):e202000129. https://doi.org/10.1002/zamm.202000129
16. Наседкин А.В., Скалиух А.С., Соловьев А.Н. Пакет ACELAN и конечно-элементное моделирование гидроакустических пьезопреобразователей. Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. Спецвыпуск. Математическое моделирование. 2001;S1:122–125.
Об авторах
А. Н. СоловьевРоссия
Аркадий Николаевич Соловьев, доктор физико-математических наук, профессор кафедры математики и физики; профессор кафедры теоретической и прикладной механики; главный научный сотрудник
г. Симферополь, пер. Учебный, д. 8 ; 344003, г. Ростов-на-Дону, пл. Гагарина, 1; 344006, г. Ростов-на-Дону, ул. Большая Садовая, 105/42
В. А. Чебаненко
Россия
Валерий Александрович Чебаненко, кандидат физико-математических наук, старший научный сотрудник лаборатории транспорта, композиционных материалов и конструкций федерального исследовательского центра «Южный научный центр Российской академии наук»
344006, г. Ростов-на-Дону, пр. Чехова, 41
П. А. Оганесян
Россия
Павел Артурович Оганесян, кандидат физико-математических наук, доцент кафедры математического моделирования института математики, механики и компьютерных наук им. И.И. Воровича
344058, г. Ростов-на-Дону, ул. Мильчакова, 8 а
Е. И. Фоменко
Россия
Елизавета Ивановна Фоменко, магистрант кафедры математического моделирования института математики, механики и компьютерных наук им. И.И. Воровича
344058, Ростов-на-Дону, ул. Мильчакова, 8 а
Рецензия
Для цитирования:
Соловьев А.Н., Чебаненко В.А., Оганесян П.А., Фоменко Е.И. Об одном методе расчета изгибных и сдвиговых колебаний пористого пьезоэлемента в низкочастотной области. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148-158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158. EDN: VPUERG
For citation:
Soloviev A.N., Chebanenko V.A., Oganesyan P.A., Fomenko E.I. On a Method for Calculating Bending and Shear Vibrations of a Porous Piezoelement in the Low-Frequency Region. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148-158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158. EDN: VPUERG




 , kg/m³
, kg/m³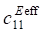 , 10¹⁰, N/m²
, 10¹⁰, N/m²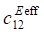 , 10¹⁰, N/m²
, 10¹⁰, N/m²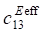 , 10¹⁰, N/m²
, 10¹⁰, N/m²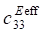 , 10¹⁰, N/m²
, 10¹⁰, N/m²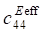 , 10¹⁰, N/m²
, 10¹⁰, N/m²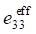 , C/m²
, C/m²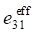 , C/m²
, C/m²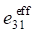 , C/m²
, C/m²