Перейти к:
Реализация цифровой модели тепловых характеристик на основе температурного поля
https://doi.org/10.23947/2687-1653-2024-24-2-178-189
EDN: EYQXQZ
Аннотация
Введение. Компьютерное моделирование позволяет инженерам принимать обоснованные проектные решения за счет точной оценки тепловых характеристик объектов проектирования. Актуальным направлением научных исследований и разработок является реализация технологии цифровых двойников в процессе проектирования технических объектов. Для этого необходимо разрабатывать компьютерные модели, точность которых соответствует требованиям, предъявляемым к цифровым двойникам. Однако в научной литературе недостаточно широко представлены результаты исследований, направленных на реализацию технологии цифровых двойников в процессе проектирования. В основном рассматриваются общие вопросы, связанные с применением цифровых двойников в различных отраслях промышленности. Поэтому целью данного исследования явилась разработка цифровой модели и сравнительный анализ точности расчетов тепловых характеристик объекта проектирования.
Материалы и методы. В качестве основного инструмента для проведения исследования выступает предложенная авторами методика разработки компьютерной модели тепловых характеристик для реализации технологии цифровых двойников. Численное решение реализовано путем построения тепловой модели для расчета температурного поля на основе метода конечных элементов в системе инженерного анализа «Ansys» от компании «Ansys Inc» (США). Для аналитического решения применяется разработанная на основе метода пространства состояний компьютерная модель тепловых характеристик, реализованная в модуле «Ansys Twin Builder». Модель пространства состояний приводится в соответствие с поведением исходной тепловой модели путем приближения передаточной функции к пошаговому отклику тепловой нагрузки с применением метода векторной аппроксимации во временной области. Верификация построенной аналитической модели выполнялась в системе инженерных расчетов «MATLAB» от компании «The MathWorks» (США). Исследования проводились для станка модели 400V производства предприятия ООО «НПО «Станкостроение» г. Стерлитамак (Россия).
Результаты исследования. Разработана цифровая модель, позволяющая с высокой точностью выполнить расчет тепловых характеристик объекта проектирования. Результаты сравнительного анализа показывают высокую степень соответствия значений тепловых характеристик, полученных с помощью предложенной цифровой модели, результатам численного моделирования. Максимальная погрешность расчета тепловых характеристик не превышает 0,1 °C.
Обсуждение и заключение. Компьютерное моделирование, сочетающее численные методы расчета и научный подход, основанный на технологии цифровых двойников, позволяют получить результат максимально приближенный к результатам экспериментов. Предложенная в исследовании цифровая модель является эффективным решением, поскольку позволяет выполнить расчеты для оценки тепловых характеристик в режиме реального времени, что является одним из важнейших требований при реализации технологии цифровых двойников.
Ключевые слова
Для цитирования:
Позевалкин В.В., Поляков А.Н. Реализация цифровой модели тепловых характеристик на основе температурного поля. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):178-189. https://doi.org/10.23947/2687-1653-2024-24-2-178-189. EDN: EYQXQZ
For citation:
Pozevalkin V.V., Polyakov A.N. Implementation of a Digital Model of Thermal Characteristics Based on the Temperature Field. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):178-189. https://doi.org/10.23947/2687-1653-2024-24-2-178-189. EDN: EYQXQZ
Введение. Компьютерное моделирование традиционно является эффективным инструментом для решения тепловых проблем на ранней стадии проектирования сложных технических объектов. Однако решение проблемы требует точной оценки тепловых характеристик объекта проектирования для снижения негативных эффектов, вызванных повышением температуры [1]. При этом одним из эффективных инструментов для предварительной оценки тепловых характеристик является имитационное моделирование в системе инженерного анализа на основе передовых цифровых решений и разработок. Например, в работе [2] авторов Jianying Xiao и Kaiguo Fan представлен разработанный цифровой двойник для определения тепловых характеристик. Принцип работы двойника заключается в моделировании теплового поведения объекта путем отображения и коррекции тепловых граничных условий. Результаты эксперимента показали высокую точность модели (более 95 %), что существенно для повышения точности моделирования тепловых характеристик и тепловой оптимизации. Поэтому актуальным направлением научных исследований и разработок в области моделирования является применение систем искусственного интеллекта [3] и цифровых двойников [4]. Например, в работе [3] авторов Haoran Yi и др. для повышения точности анализа тепловых характеристик предложена интерактивная модель коррекции тепловых граничных условий на основе нейронной сети. Результаты экспериментов показывают, что точность расчета температурного поля превышает 98 %, а точность прогнозирования тепловой деформации — 96 %, что эффективно повышает точность моделирования. Кроме того, в работе [5] авторов Курганова Н.В. и др. отмечено, что цифровые двойники часто применяются с целью совершенствования физических прототипов сложных технических объектов, поскольку позволяют не только обеспечить информационное сопровождение процесса проектирования, но и принимать эффективные проектные решения на основе наработок в области искусственного интеллекта.
Одной из характерных особенностей технологии цифровых двойников является то, что для имитационного моделирования часто применяются компьютерные модели пониженного порядка [6]. Поэтому разработка компьютерных моделей является одним из базовых условий в реализации технологии цифровых двойников [7]. Понижение порядка моделей — эффективный и понятный с математической точки зрения подход для преодоления ограничений времени выполнения многомерных имитационных моделей. Например, в работе [8] авторов Мирзаев Д.А. и др. предложена простая аналитическая модель тепловых полей для разработки цифровых двойников процесса промышленной дуговой сварки. Авторы Бордачев Е.В. и Лапшин В.П. в своей работе [9] представили результаты математического моделирования температуры в зоне контакта инструмента и изделия при токарной обработке металлов. Такой подход позволяет получить точную оценку тепловых характеристик, соответствующую результатами численных экспериментов в режиме реального времени. В работе [10] авторы Schröder C. и Matthias V. представили модель пониженного порядка и предложили новую процедуру балансировки модели, основанную на преобразовании сдвига состояния. В заключении представили результаты сравнительного анализа с результатами из источников литературы, полученных с помощью серии численных экспериментов.
Применение линейной и инвариантной по времени компьютерной модели пониженного порядка позволяет обеспечить быстрое моделирование при сохранении высокой точности расчетов [11]. При разработке компьютерной модели выполняется аппроксимация [12] передаточной функции для приближения модели пространства состояний к пошаговому отклику исходной тепловой модели [13]. Поскольку пошаговый отклик тепловой нагрузки получен из исходной тепловой модели, то цифровая модель должна предоставить те же значения тепловых характеристик.
Однако несмотря на то, что в последнее время наблюдается рост интереса к цифровому двойнику, в научной литературе недостаточно широко представлены результаты исследований, связанных с реализацией цифровых решений в процессе проектирования технических объектов. На основе систематического обзора литературы и тематического анализа публикаций по цифровым двойникам выявлен один из ключевых пробелов в знаниях, связанный с разработкой математического, программного и методического обеспечения высокоточных компьютерных моделей в рамках реализации технологии цифровых двойников.
В этой связи целью исследования являлась разработка компьютерной модели пониженного порядка и анализ эффективности её применения в составе цифровой модели для точного расчета тепловых характеристик сложных технических объектов проектирования.
Для достижения поставленной цели требовалось построить тепловую модель и выполнить расчет температурного поля объекта проектирования, сгенерировать независимые пошаговые отклики тепловой нагрузки с помощью разработанного программного сценария [14], реализовать цифровую модель для расчета тепловых характеристик, определить погрешность расчетов, полученных с помощью численного и аналитического решений и провести сравнительный анализ полученных результатов моделирования.
Материалы и методы. Построение температурного поля объекта моделирования выполнялось для однородного изотропного тела на основе уравнения нестационарной теплопроводности:
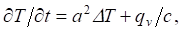 (1)
(1)
где T — температура (°C); t — время (с); 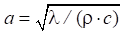 — коэффициент температуропроводности (м2/с); λ — коэффициент теплопроводности (Вт/м·°C); c — удельная теплоемкость (Дж/кг·°C); ρ — плотность материала (кг/м3); ∆ — оператор Лапласа; qv — объемная мощность тепловыделения (Вт/м3).
— коэффициент температуропроводности (м2/с); λ — коэффициент теплопроводности (Вт/м·°C); c — удельная теплоемкость (Дж/кг·°C); ρ — плотность материала (кг/м3); ∆ — оператор Лапласа; qv — объемная мощность тепловыделения (Вт/м3).
Тепловой поток в процессе теплопередачи принимался равным количеству теплоты, переносимой через произвольную поверхность площадью S в единицу времени t, что выражается следующим уравнением:
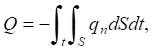 (2)
(2)
где Q — тепловой поток (Вт); qn — плотность теплового потока (Вт/м2); S — площадь поверхности (м2).
Плотность теплового потока при теплоотдаче определялась по формуле:
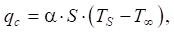 (3)
(3)
где α — коэффициент теплоотдачи (Вт/(м2·°C)); TS — температура поверхности (°C); T∞ — температура окружающей среды (°C).
В этой связи, для расчета температурного поля объекта моделирования по формуле (1), задавались тепловые потоки (2) и (3), которые определяли количество теплоты, проходящее через поверхность в единицу времени.
В качестве объекта моделирования был выбран компонент (рис. 1) металлорежущего станка модели «400V» производства предприятия ООО «НПО «Станкостроение» (Россия, г. Стерлитамак) в виде сверлильной головки.
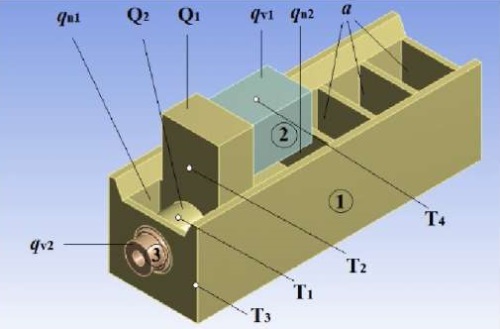
Рис. 1. Геометрическая модель объекта в «Ansys Design Modeler»:
1 — корпус; 2 — электродвигатель; 3 — шпиндельный узел;
Q — тепловые потоки; qv — объемная мощность тепловыделений;
qn — плотности тепловых потоков; a — коэффициент теплоотдачи;
T1–T4 — температурные датчики
Поскольку для расчета температурного поля учитывалось количество теплоты, выделяемое в основном электродвигателем (электромагнитные потери) и шпиндельным узлом (механические потери на трение), то в качестве внутренних источников тепла принимались электродвигатель qv1 и шпиндельный узел qv2, вблизи которых задавались соответствующие тепловые потоки Q1 и Q2. Плотности тепловых потоков qn1, qn2 назначались для поверхностей, расположенных вблизи электродвигателя и шпиндельного узла соответственно.
Конвекция задавалась коэффициентом теплоотдачи α с учетом условий теплообмена (свободная конвекция в воздухе). Поскольку станок контактирует с газообразной средой (воздух), то количество теплоты, отданное нагретой поверхностью окружающей среде в единицу времени t, прямо пропорционально разности температуры поверхности TS и среды T∞ в зависимости от S площади теплоотдающей поверхности (3).
При построении тепловой модели объекта (твердого тела), состоящего из однородного материала (конструкционная сталь) с постоянными теплофизическими свойствами и наличием внутренних источников тепла, назначались следующие начальные и граничные условия:
- начальные условия учитывали фиксацию постоянной температуры по всей поверхности объекта моделирования (t= 0: T = T0 = const);
- граничные условия второго рода задавались тепловыми потоками электродвигателя (Q1), шпиндельного узла (Q2), плотностью теплового потока (qn1) от электродвигателя к передней стенке корпуса и (qn2) к внутренним поверхностям;
- граничные условия третьего рода задавались коэффициентом теплоотдачи (α) для поверхностей, расположенных внутри корпуса сверлильной головки;
- граничные условия четвертого рода для контактных соединений поверхностей учитывали идеальный тепловой контакт и отсутствие термического сопротивления:
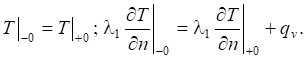 (4)
(4)
Тепловые потоки (Q1, Q2), плотности тепловых потоков (qn1, qn2), как и объемная мощность тепловыделения (qv1, qv2), назначались в соответствии с известными рекомендациями по металлорежущим станкам [1]. Граничные условия, как и тепловые потоки, задавались для наружных поверхностей. Поэтому учитывалось, что взаимосвязи тепловых полей присутствовали только между внешними поверхностями.
Дифференциальное уравнение (1), совместно с начальными и граничными условиями второго (2), третьего (3) и четвертого (4) рода, представляет собой математическую формулировку поставленной задачи. Поставленная задача решалась с помощью методов численного и аналитического моделирования.
Численное решение выполнялось на основе метода конечных элементов в системе инженерного анализа «Ansys», которая разрабатывается американской компанией «Ansys Inc» (США) и поставляется фирмой «МЦД», авторизованным дистрибьютором «Ansys» в России. Геометрическая модель (рис. 1) объекта импортировалась в проект «Ansys Workbench» с добавлением блока анализа переходного температурного поля «Transient Thermal». При численном решении выполнялась калибровка параметров моделирования и граничных условий тепловой модели (таблица 1) для приближения модельных значений температуры к экспериментальным данным.
Таблица 1
Граничные условия (параметры) тепловой модели
|
Параметр |
Мощность тепловыделений |
Тепловые потоки |
Плотности тепловых потоков |
Коэффициент теплоотдачи |
|||
|
qv1, Вт/м³ |
qv2, Вт/м³ |
Q1, Вт |
Q2, Вт |
qn1, Вт/м² |
qn2, Вт/м² |
а, Вт/(м²·°С) |
|
|
Значение |
6 500 |
1 000 |
28 |
15 |
32 |
18 |
15 |
В модуле «Ansys Mechanical» назначались начальные (начальная температура T0=24 °С) и граничные (таблица 1) условия для построенной сеточной модели, выполнялось построение температурного поля (рис. 2). При этом коэффициент теплопроводности принимался равным λ=60,5 Вт/(м °С) и назначался таковым для конструкционной стали.
Тепловая модель объекта включала два контактных соединения для электродвигателя и гильзы шпинделя с корпусом сверлильной головки и содержала 7 тепловых граничных условий. Построенная сеточная модель состояла из 16 309 элементов и 58 527 узлов.
Общее время моделирования 21 600 секунд (6 часов) разбивалось на интервалы (1 час) и шаги ∆t = 360 секунд (6 минут), всего N = 60 шагов, в пределах которых параметры тепловой модели (граничные условия) принимались как постоянные и независящие от времени.
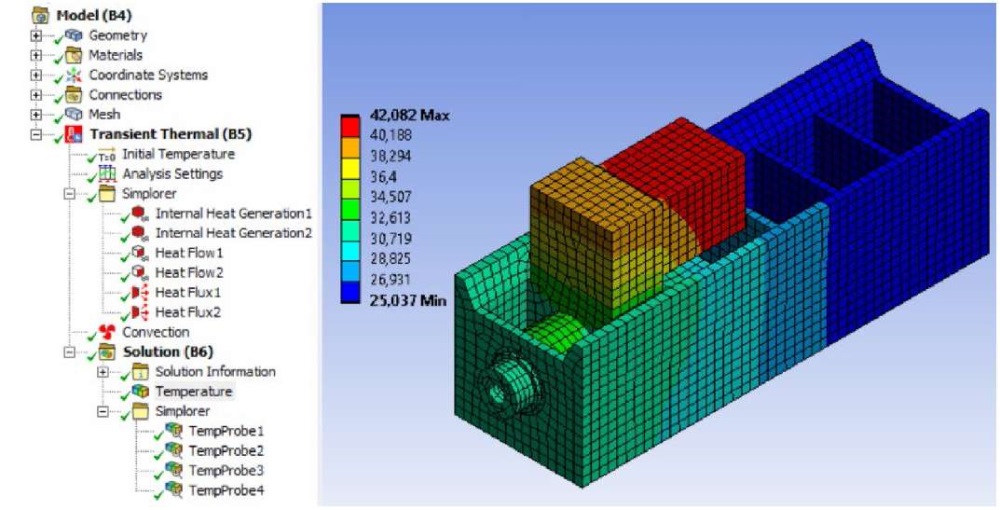
Рис. 2. Температурное поле объекта в «Ansys Mechanical»
Расчет температурного поля требовался для генерации независимого пошагового отклика тепловой нагрузки, содержащего информацию об изменении температуры по времени (тепловые характеристики) для каждого параметра (таблица 1) тепловой модели в отдельности:
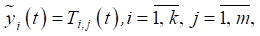 (5)
(5)
где k — количество температурных датчиков; m — количество параметров тепловой модели.
Генерация пошагового отклика выполнялась в модуле «Ansys Mechanical» с применением расширения «Application Customization Toolkit (ACT)», которое поддерживает внедрение пользовательских сценариев. Это позволило разработать программный сценарий на языке программирования «Python» с целью автоматической генерации специального набора файлов, содержащих независимые пошаговые отклики [14].
Аналитическое решение выполнялось на основе метода пространства состояний путем построения модели тепловых характеристик по формуле:
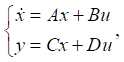 (6)
(6)
где 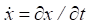 — производная вектора x состояний по времени t; y и u — векторы выходных и входных данных соответственно; A, B, C, D — матрицы постоянных коэффициентов.
— производная вектора x состояний по времени t; y и u — векторы выходных и входных данных соответственно; A, B, C, D — матрицы постоянных коэффициентов.
В уравнении (6), вектор x = (x1, x2, …, xN)T содержит переменные состояния, вектор входа u = (qv1, qv2, Q1, Q2, qn1, qn2, T01, T02, …, T0k)T значения параметров тепловой модели (граничные и начальные условия), вектор выхода y = (T1, T2, …, Tk)T значения тепловых характеристик.
Модель передаточной функции выражается следующим уравнением:
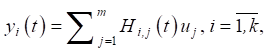 (7)
(7)
где H — матричная комплексная передаточная функция.
Матричная передаточная функция H получена путем применения к формуле (6) преобразования Лапласа, что выражается следующим уравнением:
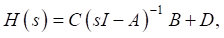 (8)
(8)
где s — комплексная переменная Лапласа; I — единичная диагональная матрица.
Передаточная функция (8) отражает зависимость преобразования Лапласа выходной переменной
Y(s) = H(s)U(s) от преобразования Лапласа входной переменной U(s) модели (6) при нулевых начальных условиях x(0) = x0 = 0. При этом размерность матрицы передаточной функции H зависит от величины выхода k = 4 и размерности входной величины m = 10, что соответствует размерности исходного пошагового отклика (5). Поэтому модель (6) приводилась в соответствие с поведением исходной тепловой модели путем приближения ее передаточной функции (7) к пошаговому отклику (5) с применением метода векторной аппроксимации [15].
Для построения матриц коэффициентов модели (6) выполнялся обратный переход от передаточной функции (8) к модели в пространстве состояний. В этом случае, передаточная функция (8) принимает вид уравнения, в знаменателе которого содержится характеристический полином степени l = 4 (порядок системы), а в числителе полином степени z = l – 1:
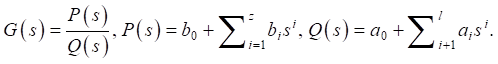 (9)
(9)
где a и b коэффициенты полиномов Q(s) и P(s) соответственно.
Корни полиномов Q(s) и P(s) представляют собой полюса и нули передаточной функции (8) соответственно. Метод неопределённых множителей применялся к уравнению (9) для разложения каждого элемента матрицы H на элементарные дроби. Обозначив полюса характеристического полинома через pi, получаем уравнение следующего вида:
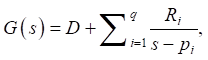 (10)
(10)
где
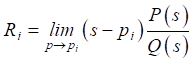 — матрица размерностью (k × m); q — количество полюсов.
— матрица размерностью (k × m); q — количество полюсов.
Ранг матрицы Ri обозначался через ri и выполнялось ее разложение на произведение двух матриц с полным рангом столбца и строки соответственно:
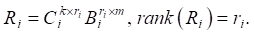 (11)
(11)
Матрицы модели (6) являются диагональными, размерностью An×n, Bn×m, Ck×n, Dk×m (n = 56) и содержат элементы, которые получены непосредственно из коэффициентов передаточной функции (10).
Матрицы A системы и B управления содержат следующие коэффициенты:
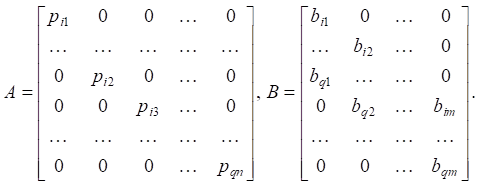 (12)
(12)
Матрицы C выхода и D прямой связи содержат следующие коэффициенты:
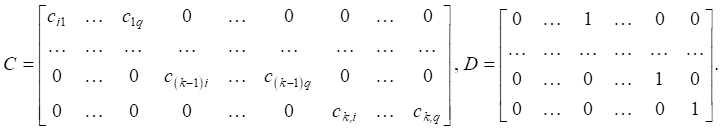 (13)
(13)
Такой подход позволил выполнить переход от модели в форме передаточной функции (8) к модели в пространстве состояний (6). Алгоритмы перехода также реализованы в системе инженерных расчетов «MATLAB», коммерческой компании «The MathWorks» (США), в виде специальных функции «ss2tf()» и «tf2ss()».
Для получения значений тепловых характеристик решалась задача Коши для системы обыкновенных дифференциальных уравнений, поскольку в формуле (6) переменная 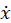 является производной от вектора состояний температурного поля по времени t. Решение системы уравнений (6) было получено с помощью метода Рунге-Кутты четвертого порядка.
является производной от вектора состояний температурного поля по времени t. Решение системы уравнений (6) было получено с помощью метода Рунге-Кутты четвертого порядка.
Верификация построенной аналитической модели выполнялась путем проведения серии вычислительных экспериментов с применением, разработанной в системе «MATLAB» прикладной программы, которая включала реализацию метода Рунге-Кутты четвертого порядка (рис. 3). Вычислительные эксперименты проводились на персональном компьютере (процессор AMD Ryzen 5 5600U with Radeon Graphics 2.30 GHz, оперативная память 16,0 ГБ, тип системы 64-разрядная операционная система Windows 10 Pro версия 21H2), характеристики которого являются базовыми для современной вычислительной техники.
Построенная аналитическая модель и применение метода Рунге-Кутты четвертого порядка для решения системы дифференциальных уравнений позволило с высокой точностью вычислить значения тепловых характеристик (рис. 3). Поскольку максимальные значения погрешности, то есть разность между модельными значениями тепловых характеристик, полученных с помощью численного (FE-Model) и аналитического (LTI-Model) решений, не превысили 0,72 °С на всем интервале моделирования.
Линейная и инвариантная по времени (Linear and Time-Invariant, LTI) компьютерная модель пониженного порядка (Reduced Order Model, ROM) разрабатывалась в модуле «Ansys Twin Builder» системы инженерного анализа «Ansys» на основе температурного поля объекта и сгенерированного в модуле «Ansys Mechanical» пошагового отклика. ссс
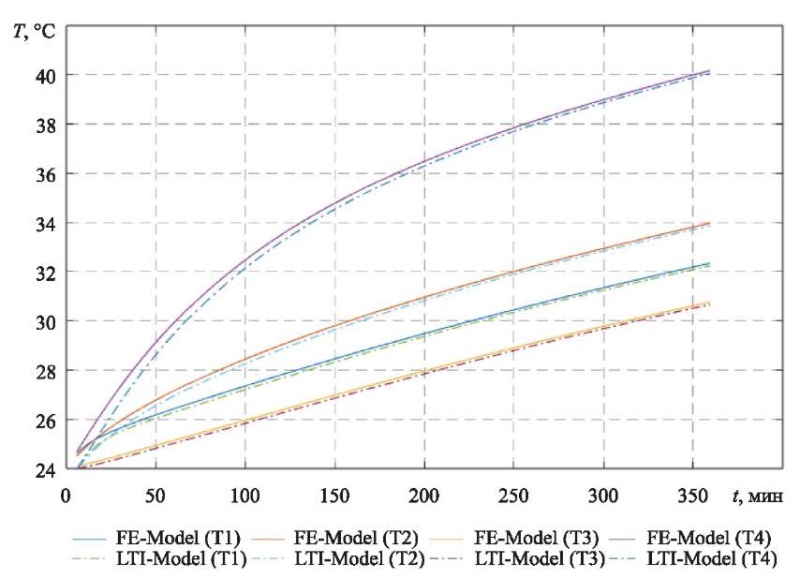
Рис. 3. Графики тепловых характеристик в системе «MATLAB»
Реализация цифровой модели тепловых характеристик на основе температурного поля с применением векторной аппроксимации заключается в последовательном выполнении семи основных этапов:
Этап 1. Импорт геометрической модели объекта и построение тепловой модели в системе инженерного анализа;
Этап 2. Расчет температурного поля объекта на основе построенной тепловой модели;
Этап 3. Генерация независимого пошагового отклика по результатам численного моделирования тепловых характеристик объекта;
Этап 4. Применение алгоритма векторной аппроксимации для получения полюсов и нулей передаточной функции модели пространства состояний;
Этап 5. Построение модели пространства состояний по известной передаточной функции;
Этап 6. Разработка компьютерной модели тепловых характеристик;
Этап 7. Реализация цифровой модели объекта.
Таким образом предложенная цифровая модель, содержащая компьютерную модель для точной оценки тепловых характеристик сложных технических объектов проектирования, была получена путем последовательного выполнения всех представленных выше этапов.
Результаты исследования. Разработанная компьютерная модель (Thermal_SG400V_SML1) содержит 6 входов и 4 выхода (рис. 4), что позволяет выявить взаимосвязь между параметрами тепловой модели и значениями тепловых характеристик. В качестве входных данных компьютерной модели приняты объемная мощность тепловыделений (qv1, qv2), тепловые потоки (Q1, Q2) и плотности тепловых потоков (qn1, qn2). В качестве выходных данных выступают тепловые характеристики (T1–T4). Компьютерная модель входит в состав цифровой модели (рис. 4 а) тепловых характеристик, реализованной в модуле «Ansys Twin Builder».
Значения параметров цифровой модели, представленные в табличном виде (рис. 4 в), подаются на вход компьютерной модели (рис. 4 а) с помощью компонентов «STEP». Графический модуль демонстрирует значения тепловых характеристик (рис. 4 б), полученных на выходе компьютерной модели.
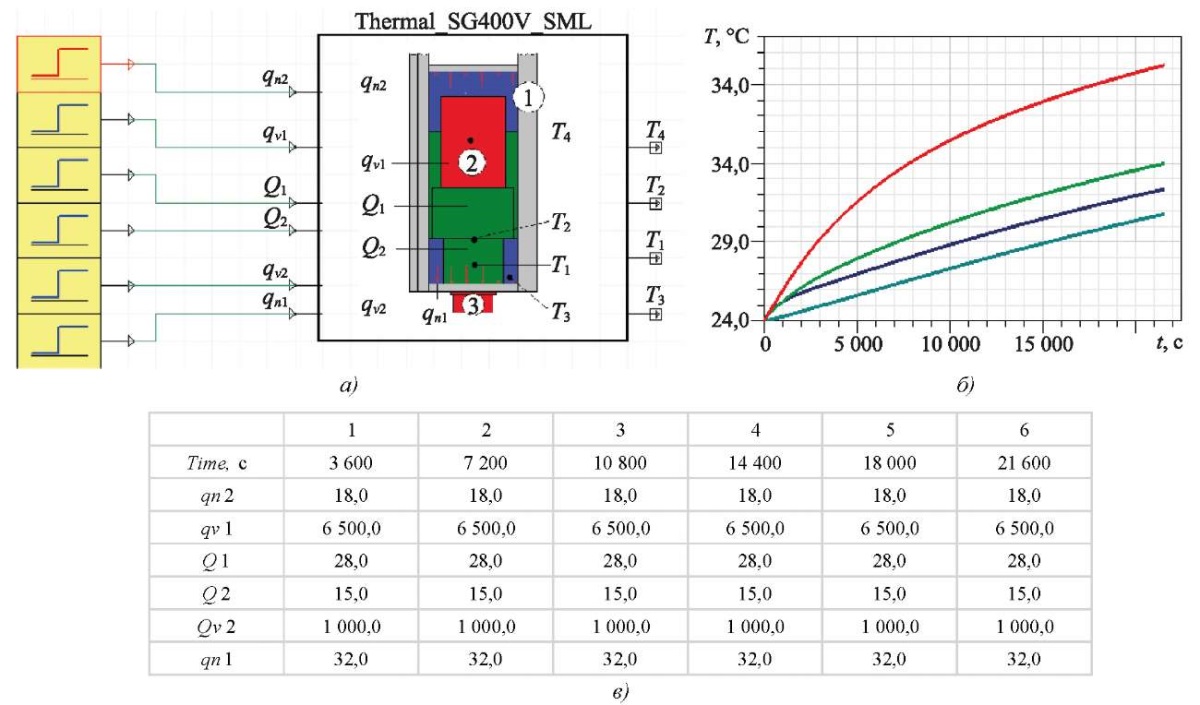
Рис. 4. Реализация цифровой модели в системе «Ansys Twin Builder»:
а — компьютерная модель тепловых характеристик;
б — модуль графического представления результатов;
в — модуль контроля входных данных компьютерной модели
При разработке компьютерной модели задавались пределы размерности от 2 до 4 порядка, значения целевой ошибки ε = 5×10–3 и допуск для нулевого порядка ε0 = 2×10–3. Остальные параметры устанавливались автоматически, поскольку метод векторной аппроксимации максимально автоматизирован в сравнении с остальными методами, которые поддерживаются в модуле «Ansys Twin Builder».
В процессе разработки компьютерной модели модуль «Ansys Twin Builder» автоматически генерирует специальную матрицу ошибок аппроксимации 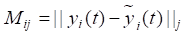 во временной области, каждый элемент которой отражает разность между значениями тепловых характеристик пошагового отклика (5) и передаточной функции (7) модели в пространстве состояний, что выражается следующим уравнением:
во временной области, каждый элемент которой отражает разность между значениями тепловых характеристик пошагового отклика (5) и передаточной функции (7) модели в пространстве состояний, что выражается следующим уравнением:
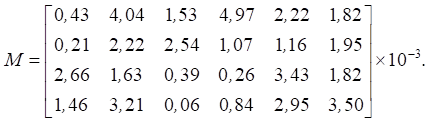 (14)
(14)
В данном случае максимальная относительная ошибка не превышает значение ε = 4,97×10–3. При этом все остальные значения ошибок оказались меньше указанного ε = 5×10–3 предела. Нулевое значение ошибки в матрице (14) означает, что вход был проигнорирован в связи с очень малым вкладом.
Оценка точности расчета тепловых характеристик с применением предложенной цифровой модели выполнялась путем сравнительного анализа результатов, полученных с помощью численного и аналитического решений. Сравнительный анализ проводился по критерию максимальной погрешности. Максимальная погрешность ΔTmax, то есть разность между значениями тепловых характеристик, полученных с помощью численного и аналитического решений для всех температурных датчиков, в каждый момент времени рассчитывается по формуле:
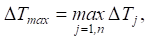 (15)
(15)
где ΔTj = |Tj,f – Tj,d| — погрешность; Tj,f и Tj,d — значения температуры конечно-элементной и цифровой моделей соответственно 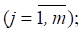 m — количество температурных датчиков.
m — количество температурных датчиков.
Для оценки точности цифровой модели выполнялся расчет погрешностей, результаты которого представлены в виде поверхности (рис. 5 а) и линейного графика (рис. 5 б) максимальной погрешности по времени. Поверхность (рис. 5 а) представляет собой расчетные значения погрешности ΔTj для каждого температурного датчика (dT1, dT2, dT3, dT4) в отдельности и в каждый момент времени на всем интервале моделирования.
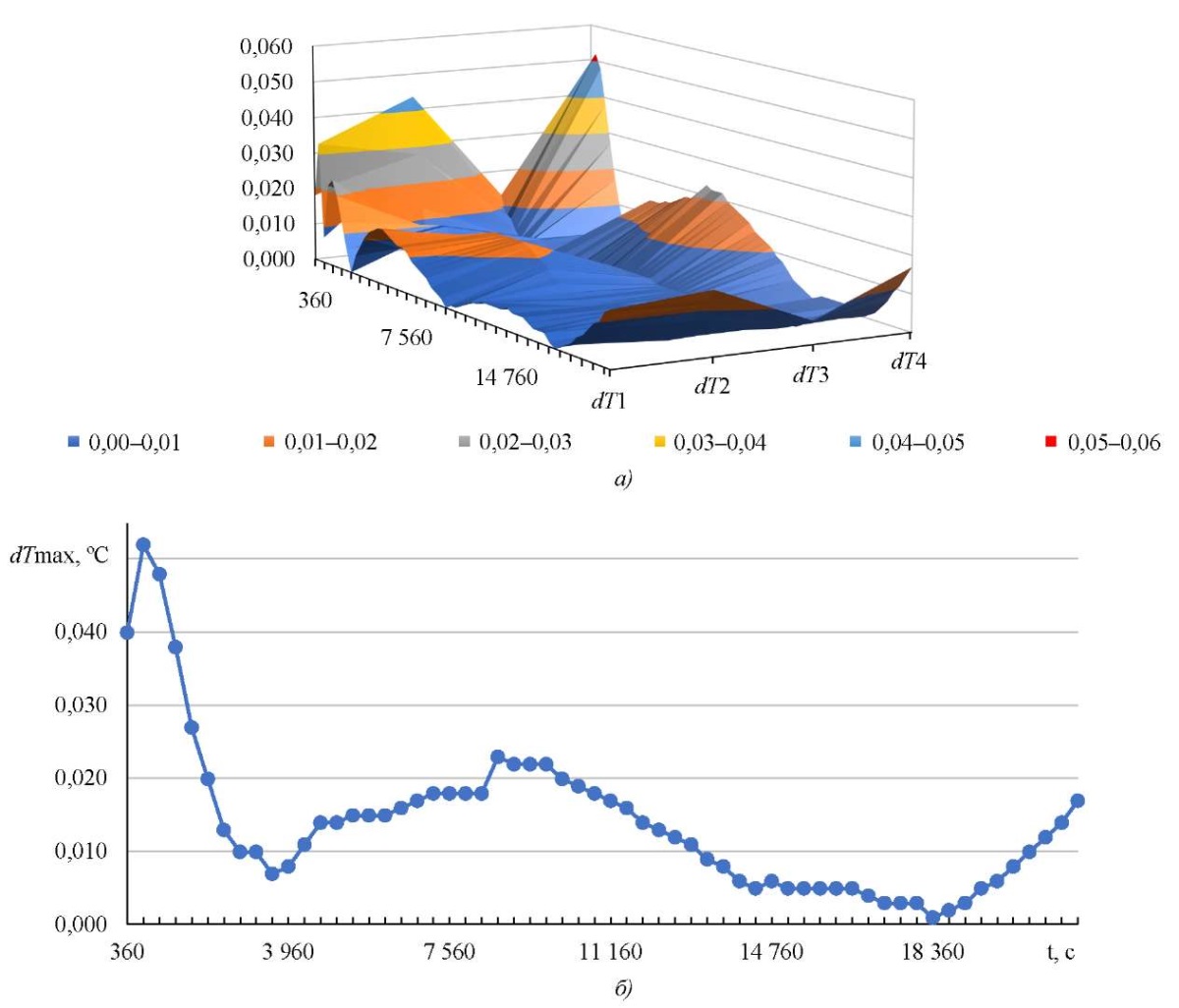
Рис. 5. Погрешности расчета тепловых характеристик:
а — погрешность для каждого температурного датчика;
б — максимальная погрешность для всех температурных датчиков
График (рис. 5 б) показывает, что для выбранного интервала времени максимальная погрешность ΔTmax не превышает 0,1 °C. Погрешность расчета тепловых характеристик для каждого температурного датчика в отдельности (рис. 5 а) также не превышает заданных пределов.
Обсуждение и заключение. Полученные результаты вычислительных экспериментов и проведенный сравнительный анализ подтверждают эффективность применения предложенной цифровой модели, которая позволяет с высокой точностью ΔTmax = 0,052 °С выполнить расчет тепловых характеристик, для дальнейшего проведения процедур анализа и идентификации тепловой модели.
На температурное поле объекта проектирования влияет множество факторов, что осложняет определение номинальных значений тепловых граничных условий. Для решения данной проблемы в исследовании сначала анализируются ключевые технологии, задействованные в реализации цифрового двойника сложного технического объекта, затем строятся тепловая модель и компьютерная модель пониженного порядка LTI ROM переходного температурного поля. Разработанная компьютерная модель применяется в составе цифровой модели, которая позволяет получить точную оценку тепловых характеристик объекта проектирования и тем самым повысить эффективность выполнения проектных процедур в процессе автоматизированного проектирования сложных технических объектов.
Точность и эффективность вычислений компьютерной модели пониженного порядка и исходной тепловой модели полного порядка оценивается путем сравнительного анализа результатов моделирования. Результаты вычислительных экспериментов показывают, что с точки зрения точности расчетов компьютерные модели пониженного порядка и конечно-элементные модели полного порядка в основном сопоставимы по точности, а максимальная погрешность расчетов находится в пределах допустимого диапазона и не превышает 0,1 °C.
Полученные в ходе вычислительных экспериментов результаты не противоречат результатам, представленным в источниках научной литературы по схожей тематике и позволяют сделать вывод о том, что применение предложенной цифровой модели эффективно для оценки тепловых характеристик сложных технических объектов в режиме реального времени, что является одним из важнейших условий для реализации технологии цифровых двойников.
Однако изменение температурного поля сложного технического объекта по-прежнему зависит от многих факторов. Поэтому в дальнейших исследованиях необходимо разработать компьютерные модели тепловых деформаций и ввести эффективные алгоритмы оптимизации на основе искусственного интеллекта, чтобы обеспечить надежность результатов моделирования, полученных с помощью цифровых двойников.
Список литературы
1. Бушуев В.В., Кузнецов А.П., Сабиров Ф.С., Хомяков В.С., Молодцов В.В. Проблемы точности и эффективности современных металлорежущих станков. СТИН. 2016;(2):6–16. https://doi.org/10.3103/S1068798X16090070
2. Jianying Xiao, Kaiguo Fan. Research on the Digital Twin for Thermal Characteristics of Motorized Spindle. The International Journal of Advanced Manufacturing Technology. 2022;119:5107–5118. https://doi.org/10.1007/s00170-021-08508-y
3. Haoran Yi, Kaiguo Fan. Co-Simulation-Based Digital Twin for Thermal Characteristics of Motorized Spindle. The International Journal of Advanced Manufacturing Technology. 2023;125(9–10):4725–4737. https://doi.org/10.1007/s00170-023-11060-6
4. Kuo Liu, Lei Song, Wei Han, Yiming Cui, Yongqing Wang. Time-Varying Error Prediction and Compensation for Movement Axis of CNC Machine Tool Based on Digital Twin. IEEE Transactions on Industrial Informatics. 2022;18(1):109–118. https://doi.org/10.1109/TII.2021.3073649
5. Курганова Н.В., Филин М.А., Черняев Д.С., Шаклеин А.Г., Намиот Д.Е. Внедрение цифровых двойников как одно из ключевых направлений цифровизации производства. International Journal of Open Information Technologies. 2019;7(5):105–115. http://injoit.org/index.php/j1/article/view/748
6. Jones D, Snider C, Nassehi A, Yon J, Hicks B. Characterising the Digital Twin: A Systematic Literature Review. CIRP Journal of Manufacturing Science and Technology. 2020;29A:36–52. https://doi.org/10.1016/j.cirpj.2020.02.002
7. Aumann Q, Benner P, Saak J, Vettermann J. Model Order Reduction Strategies for the Computation of Compact Machine Tool Models. In: Proc. 3rd International Conference on Thermal Issues in Machine Tools. Cham: Springer; 2023. P. 132–145. https://doi.org/10.1007/978-3-031-34486-2_10
8. Мирзаев Д.А., Окишев К.Ю., Мирзоев А.А. Простая аналитическая модель тепловых полей для разработки цифровых двойников процесса промышленной дуговой сварки. Вестник Южно-Уральского государственного университета. Серия: Математика. Механика. Физика. 2023;15(1):76–86. https://doi.org/10.14529/mmph230109
9. Бордачев Е.В., Лапшин В.П. Математическое моделирование температуры в зоне контакта инструмента и изделия при токарной обработке металлов. Advanced Engineering Research (Rostov-on-Don). 2019;19(2):130–137. https://doi.org/10.23947/1992-5980-2019-19-2-130-137
10. Schröder C, Matthias V. Balanced Truncation Model Reduction with a Priori Error Bounds for LTI Systems with Nonzero Initial Value. Journal of Computational and Applied Mathematics. 2023;420:114708. https://doi.org/10.1016/j.cam.2022.114708
11. Xaver Thiem, Kauschinger B, Ihlenfeldt S. Online Correction of Thermal Errors Based on a Structure Model. International Journal of Mechatronics and Manufacturing Systems. 2019;12(1):49–62. https://doi.org/10.1504/IJMMS.2019.097852
12. Клочков Ю.В., Николаев А.П., Ищанов Т.Р., Андреев А.С. Векторная аппроксимация в МКЭ для оболочки вращения при учете сдвиговых деформаций. Проблемы машиностроения и надежности машин. 2020;(4):35–43. https://doi.org/10.31857/S0235711920040070
13. Xiao Hu, Scott Stanton, Long Cai, Ralph E White. A Linear Time-Invariant Model for Solid-Phase Diffusion in Physics-Based Lithium Ion Cell Models. Journal of Power Sources. 2012;214:40–50. https://doi.org/10.1016/j.jpowsour.2012.04.040
14. Поляков А.Н., Позевалкин В.В. Программный модуль генерации входных данных для построения цифровых моделей. Свидетельство о гос. регистрации программы для ЭВМ 2023660032. 2023. 1 с.
15. Гурарий М.М., Жаров М.М., Русаков С.Г., Ульянов С.Л., Ходош Л.С. Эффективный алгоритм реализации метода векторной аппроксимации в задачах идентификации передаточных функций динамических систем. Мехатроника, автоматизация, управление. 2015;16(9):579–584. https://doi.org/10.17587/mau.16.579-584
Об авторах
В. В. ПозевалкинРоссия
Владимир Владимирович Позевалкин, кандидат технических наук, старший преподаватель кафедры прикладной информатики в экономике и управлении
460018, г. Оренбург, пр. Победы, 13
А. Н. Поляков
Россия
Александр Николаевич Поляков, доктор технических наук, профессор, заведующий кафедрой технологии машиностроения, металлообрабатывающих станков и комплексов
460018, г. Оренбург, пр. Победы, 13
Рецензия
Для цитирования:
Позевалкин В.В., Поляков А.Н. Реализация цифровой модели тепловых характеристик на основе температурного поля. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):178-189. https://doi.org/10.23947/2687-1653-2024-24-2-178-189. EDN: EYQXQZ
For citation:
Pozevalkin V.V., Polyakov A.N. Implementation of a Digital Model of Thermal Characteristics Based on the Temperature Field. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):178-189. https://doi.org/10.23947/2687-1653-2024-24-2-178-189. EDN: EYQXQZ












































