Scroll to:
Numerical Solution to the Problem of Thermal Conductivity in a Porous Plate with a Topology of Triply Periodic Minimal Surfaces
https://doi.org/10.23947/2687-1653-2025-25-1-23-31
EDN: YYGRFP
Abstract
Introduction. Thermal performance of materials based on triply periodic minimal surfaces (TPMS) is becoming increasingly important in view of the growing interest in materials with special thermophysical properties and their applications in engineering, energy, and other fields. Since these materials have unique structural and functional characteristics, understanding the relationship between their geometry and thermal parameters plays a key role in optimizing their use. Despite the considerable attention paid to the problem, the study of the relationship between the geometry of porous structures and their thermal characteristics remains incomplete. Existing scientific papers cover only individual options, and a complete understanding of the effect of complex micro- and macrostructure on thermal conductivity requires further study. The current gap in scientific knowledge is the lack of systematization and generalization of existing data, which complicates the development of universal approaches to calculating thermal conductivity in such materials. The objective of this study was to develop simplified formulas for calculating the effective thermal conductivity of porous structures based on S-type TPMC cells proposed by Fisher and Koch. The authors also set the task of analyzing the heat-conducting process in a plate with given porosity parameters. This will improve the understanding of the thermodynamic processes occurring in such systems.
Materials and Methods. To achieve the stated objectives, mathematical modeling was performed, including the solution to the boundary value problem taking into account the identified correlations. A cellular structure made of PETG plastic and having pores consisting of identical repeating elements was considered. These elements formed a three-dimensional minimal surface that corresponded to the Fisher-Koch model. The analysis was performed using two methods: calculations in MathCAD based on the finite difference method, and modeling in ANSYS using the finite element method. In this case, the effect of the geometric parameters of the porous structure on its thermal characteristics was taken into account.
Results. The research results represented a numerical solution to the thermal conductivity problem for a porous plate, taking into account the symmetrical boundary conditions of the first kind, and the presence of internal heat sources that remained constant in time and considered the topological features of the material. In the course of the study, temperature distributions were obtained, both in the spatial coordinate and in time. The change in heat flow depending on variations in the plate porosity coefficient was estimated. The graphs of isotherm distribution and their speed of movement were constructed and analyzed, which allowed for a deeper understanding of the heat transfer dynamics in the system under consideration.
Discussion and Conclusion. The obtained mathematical dependences demonstrate the degree and nature of the effect of porosity on the distribution of heat flux density. It has been found that changes in the porosity of the plate can both increase and decrease the intensity of heat transfer, which provides reaching the required values of thermal resistance of the material. The obtained results are consistent with the findings presented in other studies on similar topics, which opens up opportunities for their application in further research. These results can be useful in designing thermal protection systems for heat-generating equipment, as well as for heat and mass transfer paths of heat-mechanical equipment and other applications. The solutions are presented in an accessible and understandable form, which makes them easy to use for a wide range of researchers and engineers, and does not require expensive software or specialized computing equipment.
Keywords
For citations:
Gubareva K.V., Eremin A.V. Numerical Solution to the Problem of Thermal Conductivity in a Porous Plate with a Topology of Triply Periodic Minimal Surfaces. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):23-31. https://doi.org/10.23947/2687-1653-2025-25-1-23-31. EDN: YYGRFP
Introduction. Porous materials are widely used in various industries, such as metallurgy [1], microelectronics [2], and construction [3]. Their unique properties, due to the presence of cavities and voids filled with gases that conduct heat poorly, make them ideal for use in the production of thermal insulation [4]. The urgency of this problem is related to the need to improve energy efficiency in various areas, which is an important aspect in the context of sustainable development. In light of this, in [4], the authors developed an energy- and resource-saving technology for producing an effective porous heat and sound insulation structural material, which emphasizes the importance of research in this area.
A comparative analysis of the literature shows that the problem raised by the authors has been sufficiently studied, but there are still a number of aspects that require more in-depth study. Paper [5] presents modern porous thermal insulation materials, including the use of silicate raw materials in their production. In [6], various types of porous material matrices are studied, and it is emphasized that the geometric size of the sample (specifically, its thickness, optimal for sound absorption — about 20 mm) significantly affects their characteristics. In addition, it should be noted that porous materials have a lower mass compared to homogeneous media, which makes them mostly attractive for use under conditions of mass and size restrictions, such as the aviation [7] and space industries [8]. In the context of the petrochemical industry, studies conducted by Mazitov A.A. [9] demonstrated the capabilities of a new web application for mathematical modeling of non-stationary oil flow in a porous medium, which emphasizes the importance of porous materials in this area as well. Paper [10] clearly demonstrated the relevance of the analysis of the mechanical properties of porous plastics, since an applied methodology for calculating the vibrations of piezoceramic porous plates was developed using the finite element method.
Despite their advantages, such as low weight, high strength characteristics and predictable thermal properties, porous materials have disadvantages related to the stochastic distribution of pores and the anisotropy of their properties, which complicates the mathematical and physical analysis of transport processes. In this regard, the analysis of a material with a porous structure created on the basis of triply periodic minimal surfaces (TPMS) is of considerable interest, since it demonstrates predictable properties depending on the geometric characteristics of the elementary cells.
Thermal properties of materials based on TPMP are actively studied in scientific circles [11]. To model the processes occurring in porous media, both numerical [12] and analytical methods are used. However, one of the main problems remains the search for a qualitative connection between the thermophysical characteristics [13] and the geometry of porous media [14]. In this context, the study of the temperature field in porous bodies, taking into account their geometric characteristics and cell porosity, as well as the application of modern numerical methods and algorithms, is an area with high potential and considerable topicality. The development of numerical algorithms capable of describing the behavior of temperature by coordinate and time, as well as heat flow depending on changes in the porosity coefficient, allows for a more accurate and effective approach to the design of heat exchangers and the development of thermal protection of equipment.
Thus, the objectives of this research were to study the process of thermal conductivity in a porous plate with a given porosity made of PETG plastic, and to search for dependences to determine the coefficient of effective thermal conductivity of such materials based on Fischer-Koch S cells. To achieve this goal, a problem of thermal conductivity in a porous plate was formulated and solved, and an analysis of the obtained solutions was performed. The results of this study can be useful for practitioners in the design of heat exchangers and in other areas of application.
Materials and Methods. The object of the study is a porous plate made of PETG material with a wall thickness of 0.0001 m. Its heat capacity is 1,050 J/(kg⸱K), density is 1300 kg/m3, and thermal conductivity is 0.2 W/(m⸱K). Figure 1 shows a sketch of this plate created using the ANSYS software package. The plate is formed from elementary Fisher-Koch cells in the S topology. The initial conditions are set as follows: the temperature at the initial moment of time T0 = 20°C, the temperature on the plate surface is TCT = 100°C, and the power of the heat source is 500 W/m3.
Mathematical Formulation of the Problem. The mathematical formulation of the problem under consideration is as follows: (1) – (4) [15]:
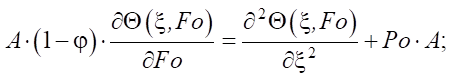 (1)
(1)
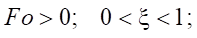
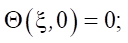 (2)
(2)
 (3)
(3)
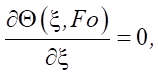 (4)
(4)
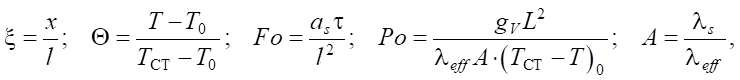
where Θ — relative excess temperature; ξ — dimensionless coordinate; Fo — Fourier criterion (dimensionless time); Po — Pomerantsev criterion; T — temperature, °C; x — coordinate, m; τ — time, s; ТСТ — wall temperature, °C; T0 — initial temperature, °C; l — cell size, m; A — coefficient; qV — power of internal heat source, W/m3; as = λs / cρs — thermal diffusivity coefficient.
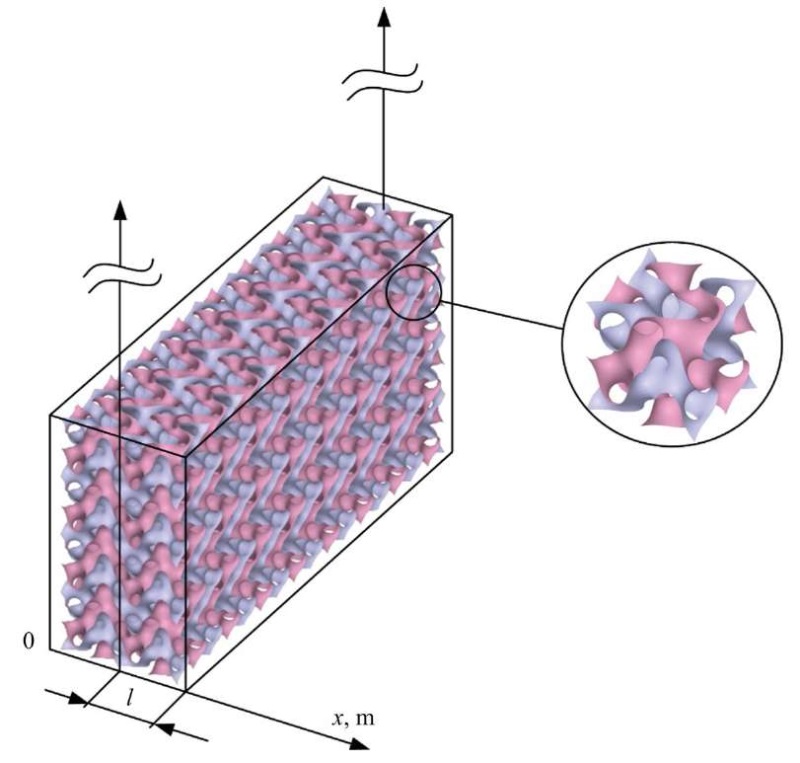
Fig. 1. Plate illustration
Research Methods. In the study of thermal conductivity in porous materials, a combination of two approaches was used: representative volume elementary (RVE) and computational homogenization. This methodology was implemented on Fisher-Koch S TPMP cells to calculate the effective thermal conductivity [15]. The effective thermal conductivity coefficient of the material was determined from formula [16]:
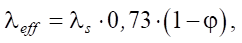
where λs — thermal conductivity coefficient of the frame material; φ — porosity [17].
The density of the porous material was determined from formula [18]:
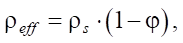
where ρs — density value of the material from which the cell is made.
The geometric characteristics of the cellular structure are the determining factors on which the degree of porosity of the material depends. They were calculated using the mathematical expression:
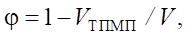
where VТПМП — cell volume; V — cube volume.
Numerical Solution. The solution to problem (1) – (4) was obtained by the finite difference method [19]. According to this method, a space-time grid with coordinate steps Δξ and time steps ΔFo is introduced. In this case:
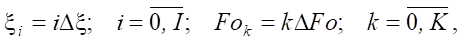 (5)
(5)
where I, K — number of steps along coordinate ξ and time Fo, respectively.
On grid (5), the grid functions 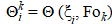 are introduced [20]. Using the explicit approximation scheme of differential operators, problem (1) – (4) takes the following form [21]:
are introduced [20]. Using the explicit approximation scheme of differential operators, problem (1) – (4) takes the following form [21]:
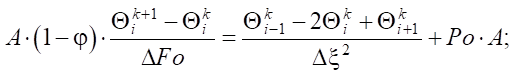
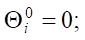
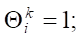

2.5 million grid cells were used in the calculations.
Two key limitations were established during the calculations. First of all, the PETG material was characterized by constant and predetermined thermal parameters. It was also assumed that heat exchange occurred exclusively on surfaces with specified boundary conditions, while the remaining cell faces were thermally insulated.
In the course of the study, it was found that using a grid containing 2.5 to 3.0 million cells leads to an optimal solution to the problem. Increasing the number of grid elements does not significantly affect the accuracy of the solution, but drastically increases the time costs and complexity of the process.
To confirm the correctness of the results obtained in the MathCAD environment, the authors conducted additional modeling in the ANSYS system. The dynamics of temperature changes is graphically presented in Figure 2.
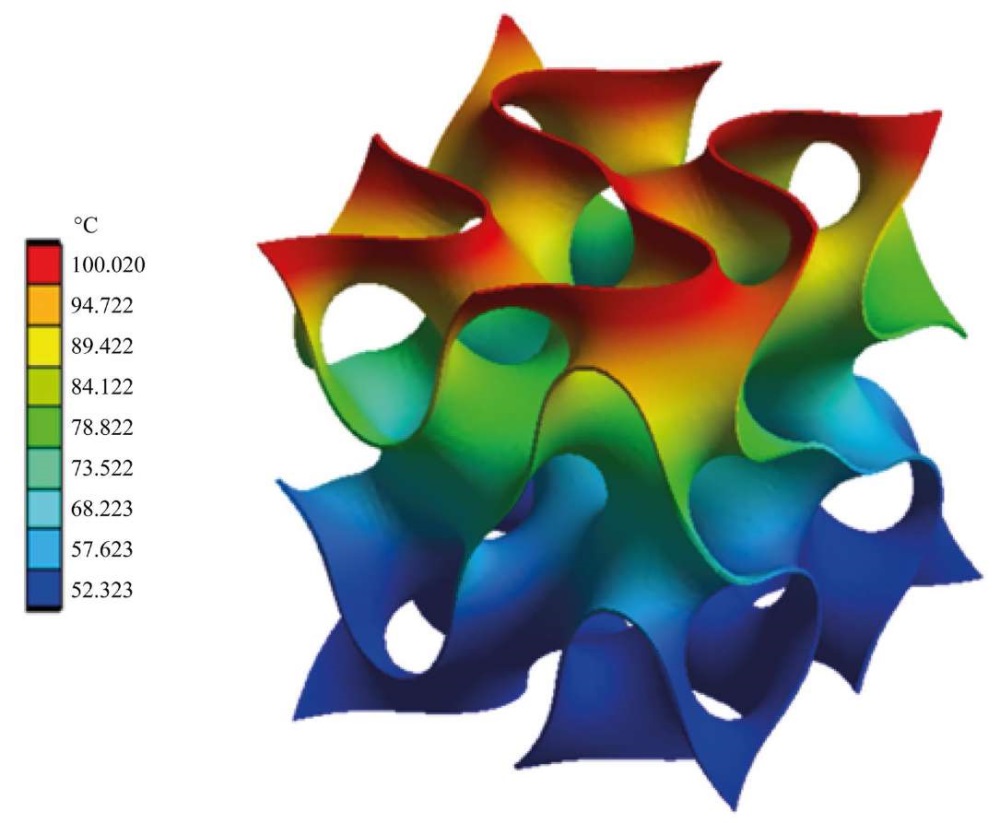
Fig. 2. Change in temperature in the cell
Research Results. Figure 3 shows the calculation results obtained by the finite element method (FEM) and the finite difference method (FDM). The analysis of the results allows us to conclude that the dimensionless temperatures obtained by the two methods are in satisfactory agreement. By analyzing the computational experiments, it is established that the Fisher-Koch S-type TPMP cell retains its structure (there are no internal intersections, complete filling of pores, etc.) in the wall thickness range 0 < δ < 0.002 m. The time evolution of isotherms and the dynamics of their speed mode are shown in Figures 4, 5. A notable feature is that in the process of time development, each isothermal line is formed on the surface with a characteristic initial speed inherent in it. It is noteworthy that an increase in the porosity of the material causes an increase in the heat flow over the entire time interval of the research, which is clearly demonstrated in Figure 5. The dependence of the heat flow density on time with varying porosity is shown in Figure 6.
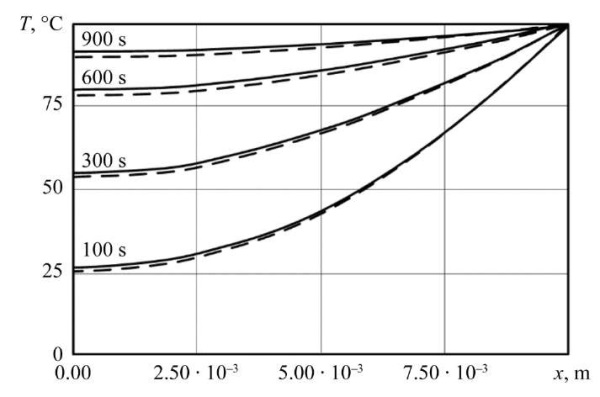
Fig. 3. Temperature distribution by coordinate: – solution according to FDM;
– solution according to FDM;  – solution according to FEM
– solution according to FEM
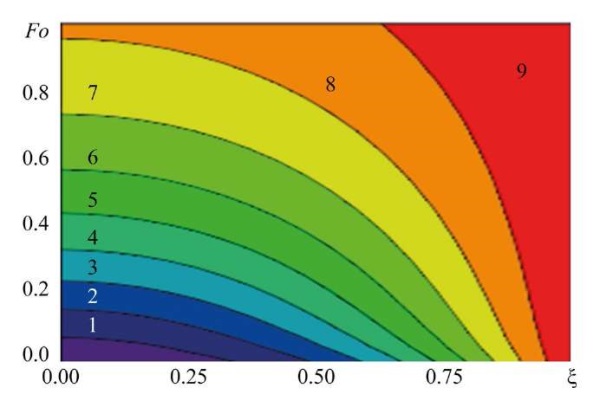
Fig. 4. Graphs of isotherm motion at coordinates depending on time at:
Ѳ = 0.1 (1); 0.2 (2); 0.3 (3); 0.4 (4); 0.5 (5); 0.6 (6); 0.7 (7); 0.8 (8); 0.9 (9)
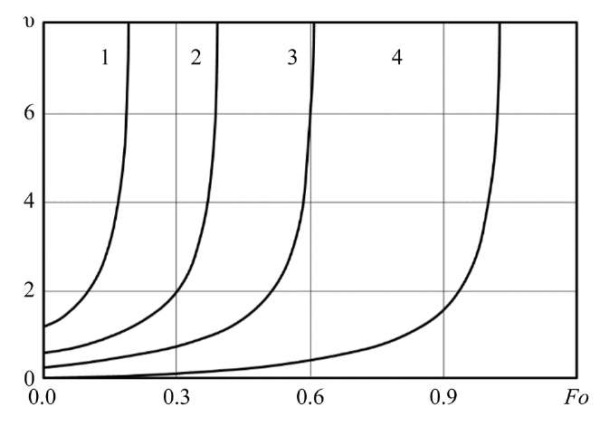
Fig. 5. Distribution of isotherm velocities in a porous plate at:
Ѳ = 0.2 (1); 0.5 (2); 0.7 (3); 0.9 (4)
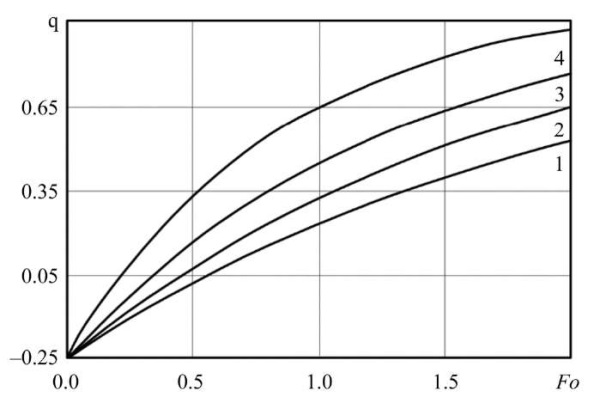
Fig. 6. Heat-flux density distribution at:
φ = 0.75 (1); 0.80 (2); 0.85 (3); 0.90 (4);
Discussion and Conclusion. In the course of the study, a mathematical model of heat transfer for a flat porous plate based on the Fisher-Koch prefractal S type TPMP was developed. The accuracy of the solution was confirmed by comparison with alternative calculation methods, such as finite-difference and finite-element analysis. The maximum deviation of the results according to the Chebyshev norm did not exceed 3%.
One of the significant advantages of the proposed approach is the ability to calculate the temperature distribution and heat losses in porous media without using complex computer programs and expensive computing equipment. The expressions obtained for the temperature function significantly simplify the process of engineering calculations of heat transfer in such materials.
The numerical modeling results, consistent with fundamental studies on thermal conductivity [20], methods for specifying boundary and initial conditions [15], as well as with various approaches to numerical calculations [11], open up new prospects for further scientific research. In particular, the developed approach can be applied to the analysis of one-dimensional heat transfer in porous media, including the calculation of temperature distribution, heat fluxes, and effective thermal conductivity coefficients of materials based on TPMP.
References
1. Kem AYu. Surface Magnetic Properties and Fractality of Fe-P Powder Material – Iron Analogue Received by Porous Workpiece Forging. Vestnik of Don State Technical University. 2011;11(2):174–180. URL: https://www.vestnik-donstu.ru/jour/article/view/707 (accessed: 25.10.2024).
2. Yi-Lung Cheng, Chih-Yen Lee. Porous Low-Dielectric-Constant Material for Semiconductor Microelectronics. In book: Nanofluid Flow in Porous Media. MSh Kandelousi, S Ameen, M Shaheer Akhtar, Hyung-Shik Shin (eds). London: InTech; 2020. 244 p. https://doi.org/10.5772/intechopen.81577
3. Su-Gwang Jeong, Jeonghun Lee, Seong Jin Chang, Sumin Kim. Thermal and Structural Behavior of Thermal Inertia-Reinforced Mortars for Building Envelope Applications. Construction and Building Materials. 2023;384:131452. https://doi.org/10.1016/j.conbuildmat.2023.131452
4. Maslov AA, Mironov SG, Poplavskaya TV, Kirilovskiy SV, Tsyryulnikov IS. Effect of Porous Inserts on Aerodynamics of Flying Vehicles. Journal of Physics: Conference Series. 2019;1382:012023. https://doi.org/10.1088/1742-6596/1382/1/012023
5. Goltzman BM, Yatsenko EA, Gerashchenko VS, Komunzhieva NYu, Yatsenko LA, Smoliy VA, et al. Porous Heat-Insulating Materials Based on Various Types of Silicate Raw Materials. Bulletin of Higher Educational Institutions. North Caucasus Region. Technical Sciences. 2020;(1):55–60. https://doi.org/10.17213/1560-3644-2020-1-55-60
6. Shashkeev KA, Shuldeshov EM, Popkov OV, Kraev ID, Yurkov GYu. Porous Sound-Absorbing Materials (review). Proceedings of VIAM. 2016;42(6):46–56. https://doi.org/10.18577/2307-6046-2016-0-6-6-6
7. Gasanov SK. Polymeric Composite Materials for Aircraft and Space Equipment. International Research Journal. 2014;28(9):29–30. https://research-journal.org/en/archive/9-28-2014-september (accessed: 25.10.2024).
8. Péter Ádám, Levente Dudás, Ottó Temesi, András Nagy, Katalin Sinkó. Porous Aluminum Oxide Insulation Materials Tested in Space Mission. CEAS Space Journal. 2023;15:671–680. https://doi.org/10.1007/s12567-022-00473-w
9. Mazitov AA. Web Application for Mathematical Modeling of Unsteady Oil Flow in Porous Medium. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):422–432. https://doi.org/10.23947/2687-1653-2023-23-4-422-432
10. Soloviev AN, Chebanenko VA, Oganesyan PA, Fomenko EI. On a Method for Calculating Bending and Shear Vibrations of a Porous Piezoelement in the Low-Frequency Region. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148–158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158
11. Prosviryakov EYu, Ledyankina OA, Goruleva LS. Exact Solutions to the Navier–Stokes Equations for Describing the Flow of Multicomponent Fluids with Internal Heat Generation. Russian Aeronautics. 2024;67(1):60–69. https://doi.org/10.3103/S1068799824010070
12. Ershkov S, Leshchenko D, Prosviryakov E. Correction: A Novel Type of ER3BP Introducing Milankovitch Cycles or Seasonal Irradiation Processes Influencing onto Orbit of Planet. Archive of Applied Mechanics. 2023;93:823–824. https://doi.org/10.1007/s00419-022-02328-6
13. Pavlenko A, Koshlak H. Production of Porous Material with Projected Thermophysical Characteristics. Metallurgical and Mining Industry. 2015;(7):123–127.
14. Chaniot J, Moreaud M, Sorbier L, Fournel T, Becker J-M. Tortuosimetric Operator for Complex Porous Media Characterization. Image Analysis and Stereology. 2019;38(1):25–41. https://doi.org/10.5566/ias.203915
15. Bragin DM, Popov AI, Eremin AV, Olatuyi OJ, Zinina SA, Shulga AS. Thermal Conductivity of a Porous Material with an Ordered Structure. In: Proc. 4th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency. New York City: IEEE; 2022. P. 858–861. https://doi.org/10.1109/SUMMA57301.2022.9973913
16. Mingwei Tian, Sukang Zhu, Ning Pan. Measuring the Thermophysical Properties of Porous Fibrous Materials with a New Unsteady-State Method. Journal of Thermal Analysis and Calorimetry. 2011;107:395–405. https://doi.org/10.1007/s10973-011-1581-y
17. Bicer Ayse, Kar Filiz. A Model for Determining the Effective Thermal Conductivity of Porous Heterogeneous Materials. International Journal of Thermophysics. 2019;40:9. https://doi.org/10.1007/s10765-018-2468-y
18. Dong Niu, Hongtao Gao. Thermal Conductivity of Ordered Porous Structures Coupling Gas and Solid Phases: A Molecular Dynamics Study. Materials. 2021;14(9):2221. https://doi.org/10.3390/ma14092221
19. Chau KV, Gaffney JJ. A Finite‐Difference Model for Heat and Mass Transfer in Products with Internal Heat Generation and Transpiration. Journal of Food Science. 2006;55(2):484–487. https://doi.org/10.1111/j.1365-2621.1990.tb06792.x
20. Formalev VF, Reviznikov DL. Numerical Methods. Мoscow: Fizmatlit; 2004. 400 p. (In Russ.)
21. Verzhbitsky VM. Fundamentals of Numerical Methods. Мoscow: Vysshaya shkola; 2002. 840 p. (In Russ.)
About the Authors
K. V. GubarevaRussian Federation
Kristina V. Gubareva, Cand.Sci. (Eng.), Associate Professor of the Department of Industrial Thermal Power Engineering
Scopus ID: 57216361463
244, Molodogvardeyskaya Str., Samara, 443100
A. V. Eremin
Russian Federation
Anton V. Eremin, Dr.Sci. (Eng.), Associate Professor, Vice-rector for Integration Projects, Head of the Department of Industrial Thermal Power Engineering
Scopus ID: 56395547000
244, Molodogvardeyskaya Str., Samara, 443100
Review
For citations:
Gubareva K.V., Eremin A.V. Numerical Solution to the Problem of Thermal Conductivity in a Porous Plate with a Topology of Triply Periodic Minimal Surfaces. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):23-31. https://doi.org/10.23947/2687-1653-2025-25-1-23-31. EDN: YYGRFP
JATS XML














































