Перейти к:
Численное решение задачи теплопроводности в пористой пластине с топологией трижды периодических минимальных поверхностей
https://doi.org/10.23947/2687-1653-2025-25-1-23-31
EDN: YYGRFP
Аннотация
Введение. Термические характеристики материалов, созданных на базе трижды периодических минимальных поверхностей (ТПМП), становятся все более важными в свете роста интереса к материалам с особыми теплофизическими свойствами и их применениям в инженерии, энергетике и других областях. Поскольку эти материалы обладают уникальными структурными и функциональными характеристиками, понимание взаимосвязи между их геометрией и теплофизическими параметрами играет ключевую роль в оптимизации их использования. Несмотря на значительное внимание, уделенное проблеме, исследование взаимосвязи между геометрией пористых структур и их термическими характеристиками остается неполным. Существующие научные работы охватывают лишь отдельные варианты, а полное понимание влияния сложной микро- и макроструктуры на теплопроводность требует дальнейшего изучения. Существующий пробел в научном знании заключается в недостаточной систематизации и обобщении существующих данных, что затрудняет разработку универсальных подходов к расчету теплопроводности в таких материалах. Целью данного исследования являлась разработка упрощенных формул для расчета показателя эффективной теплопроводности пористых структур, основанных на ТПМП-ячейках типа S, предложенных Фишером и Кохом. Авторы также ставили задачу анализа теплопроводного процесса в пластине с заданными параметрами пористости. Это позволит улучшить понимание термодинамических процессов, происходящих в таких системах.
Материалы и методы. Для достижения поставленных целей проведено математическое моделирование, включающее решение граничной задачи с учетом выявленных корреляций. Рассматривается ячеистая конструкция, изготовленная из PETG-пластика и имеющая поры, состоящие из одинаковых повторяющихся элементов. Эти элементы формируют трехмерную минимальную поверхность, которая соответствует модели Фишера-Коха. Анализ проводился с использованием двух методов: расчеты в MathCAD, основанные на методе конечных разностей, и моделирование в ANSYS методом конечных элементов. При этом учитывалось влияние геометрических параметров пористой структуры на ее теплофизические характеристики.
Результаты исследования. Результаты исследования представляют собой численное решение задачи теплопроводности для пористой пластины, принимая во внимание симметричные граничные условия первого рода и наличие внутренних источников тепла, которые остаются постоянными во времени и учитывают топологические особенности материала. В ходе работы были получены распределения температуры как по пространственной координате, так и во времени. Оценено изменение теплового потока в зависимости от вариаций коэффициента пористости пластины. Построены и проанализированы графики распределения изотерм и скорости их перемещения, что позволяет более глубоко понять динамику теплопередачи в рассматриваемой системе.
Обсуждение и заключение. Полученные математические зависимости демонстрируют степень и характер влияния пористости на распределение плотности теплового потока. Было установлено, что изменения в пористости пластины могут как увеличить, так и уменьшить интенсивность теплопереноса, что позволяет достигать необходимых значений термического сопротивления материала. Полученные результаты согласуются с выводами, изложенными в других исследованиях аналогичной тематики, что открывает возможности для их применения в дальнейших исследованиях. Эти результаты могут быть полезны при проектировании систем тепловой защиты для тепловыделяющего оборудования, а также для тепломассообменных трактов тепломеханического оборудования и других приложений. Решения представлены в доступной и понятной форме, что облегчает их использование как для широкого круга исследователей, так и инженеров, и не требует привлечения дорогостоящего программного обеспечения или специализированной вычислительной техники.
Ключевые слова
Для цитирования:
Губарева К.B., Еремин А.В. Численное решение задачи теплопроводности в пористой пластине с топологией трижды периодических минимальных поверхностей. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):23-31. https://doi.org/10.23947/2687-1653-2025-25-1-23-31. EDN: YYGRFP
For citation:
Gubareva K.V., Eremin A.V. Numerical Solution to the Problem of Thermal Conductivity in a Porous Plate with a Topology of Triply Periodic Minimal Surfaces. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):23-31. https://doi.org/10.23947/2687-1653-2025-25-1-23-31. EDN: YYGRFP
Введение. Пористые материалы находят широкое применение в различных отраслях промышленности, таких как металлургия [1], микроэлектронная промышленность [2] и строительная индустрия [3]. Их уникальные свойства, обусловленные наличием полостей и пустот, заполненных плохо проводящими тепло газами, делают их идеальными для использования в производстве тепловой изоляции [4]. Актуальность данной проблемы связана с необходимостью повышения энергоэффективности в различных сферах, что является важным аспектом в условиях устойчивого развития. В свете этого в статье [4] авторами была разработана энерго- и ресурсосберегающая технология получения эффективного пористого тепло- и звукоизоляционного конструкционного материала, что подчеркивает важность исследований в данной области.
Сравнительный анализ литературы показывает, что проблема, поднятая авторами, достаточно исследована, однако остается ряд аспектов, требующих более глубокого изучения. В работе [5] представлены современные пористые теплоизоляционные материалы, включая применение силикатного сырья в их производстве. Авторы в [6] исследовали различные типы матриц пористых материалов и подчеркнули, что геометрический размер образца (в частности, его толщина, оптимальная для звукопоглощения — около 20 мм) значительно влияет на их характеристики. Кроме того, необходимо отметить, что пористые материалы имеют меньшую массу по сравнению с однородными средами, что делает их особенно привлекательными для использования в условиях массогабаритных ограничений, таких как авиационная [7] и космическая отрасли [8]. В контексте нефтехимической промышленности, исследования, проведенные Мазитовым А.А. [9], продемонстрировали возможности нового веб-приложения для математического моделирования нестационарного течения нефти в пористой среде, что подчеркивает значимость пористых материалов и в этой области. В работе [10] наглядно показана актуальность анализа механических свойств пористых пластиков, так как была разработана прикладная методология расчета колебаний пьезокерамических пористых пластин с использованием метода конечных элементов.
Несмотря на свои преимущества, такие как малая масса, высокие прочностные характеристики и предсказуемые теплофизические свойства, пористые материалы имеют недостатки, которые связаны со стохастическим распределением пор и анизотропией их свойств, что усложняет математический и физический анализ процессов переноса. В этой связи анализ материала с пористой структурой, созданного на основе трижды периодических минимальных поверхностей (ТПМП), представляет значительный интерес, так как он демонстрирует предсказуемые свойства в зависимости от геометрических характеристик элементарных ячеек.
Изучение тепловых свойств материалов на основе ТПМП активно ведется в научных кругах [11]. Для моделирования процессов, происходящих в пористых средах, применяются как численные [12], так и аналитические методы. Однако одной из основных проблем остается поиск качественной связи между теплофизическими характеристиками [13] и геометрией пористых сред [14]. В этом контексте исследование температурного поля в пористых телах с учетом их геометрических характеристик и пористости ячеек, а также применение современных численных методов и алгоритмов, представляют собой область с высоким потенциалом и значительной актуальностью. Разработка численных алгоритмов, способных описывать поведение температуры по координате и во времени, а также теплового потока в зависимости от изменений коэффициента пористости, позволят более точно и эффективно подходить к проектированию теплообменников и разработке тепловой защиты оборудования.
Таким образом, целями настоящего исследования стали изучение процесса теплопроводности в пористой пластине с заданной пористостью из пластика PETG и поиск зависимостей для определения коэффициента эффективной теплопроводности таких материалов на основе ячеек типа Фишера-Коха S. Для достижения поставленной цели была сформулирована и решена задача теплопроводности в пористой пластине, а также проведен анализ полученных решений. Результаты данного исследования могут быть полезны для практиков в проектировании теплообменников и в других сферах применения.
Материалы и методы. Объектом исследования является изготовленная из материала PETG пористая пластина толщиной стенки 0,0001 м. Её теплоемкость составляет 1 050 Дж/(кг⸱К), плотность — 1 300 кг/м3, а теплопроводность — 0,2 Вт/(м⸱К). На рис. 1 представлен эскиз данной пластины, созданный с помощью программного комплекса Ansys. Пластина сформирована из элементарных ячеек Фишера-Коха в топологии S. Начальные условия задаются следующим образом: температура в начальный момент времени T0 = 20 °C, температура на поверхности пластины — TСТ = 100 °C, а мощность источника теплоты — 500 Вт/м3.
Математическая постановка задачи. Математическая формулировка рассматриваемой задачи имеет вид (1) – (4) [15]:
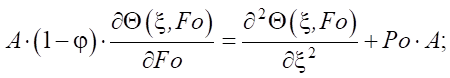 (1)
(1)
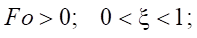
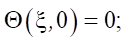 (2)
(2)
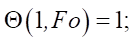 (3)
(3)
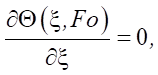 (4)
(4)
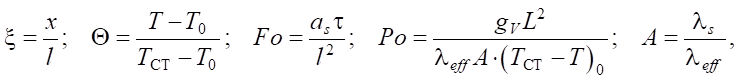
где Θ — относительная избыточная температура; ξ — безразмерная координата; Fo — критерий Фурье (безразмерное время); Po — критерий Померанцева; T — температура, °C; x — координата, м; τ — время, с; ТСТ — температура стенки, °C; T0 — начальная температура, °C; l — размер ячейки, м; A — коэффициент; qV — мощность внутреннего источника теплоты, Вт/м3; as = λs / cρs — коэффициент температуропроводности.

Рис. 1. Иллюстрация пластины
Методы исследования. При исследовании теплопроводности в пористых материалах была применена комбинация двух подходов — репрезентативного элементарного объема (RVE) и вычислительной гомогенизации. Данная методология реализована на ТПМП-ячейках Фишера-Коха типа S для расчета эффективной теплопроводности [15]. Эффективный коэффициент теплопроводности материала определялся по формуле [16]:
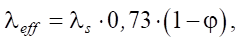
где λs — коэффициент теплопроводности материала каркаса; φ — пористость [17].
Плотность пористого материала определялась по формуле [18]:
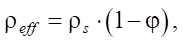
где ρs — значение плотности материала, из которого изготовлена ячейка.
Геометрические характеристики ячеистой структуры являются определяющими факторами, от которых зависит степень пористости материала, и были вычислены с помощью математического выражения:
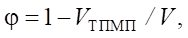
где VТПМП — объем ячейки; V — объем куба.
Численное решение. Решение задачи (1) – (4) было получено методом конечных разностей [19]. Согласно данному методу, вводится пространственно-временная сетка с шагами по координате Δξ и по времени ΔFo. При этом:
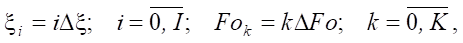 (5)
(5)
где I, K — число шагов по координате ξ и времени Fo соответственно.
На сетке (5) вводятся сеточные функции 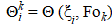 [20]. Применяя явную схему аппроксимации дифференциальных операторов, задача (1) – (4) принимает следующий вид [21]:
[20]. Применяя явную схему аппроксимации дифференциальных операторов, задача (1) – (4) принимает следующий вид [21]:

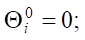
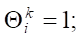
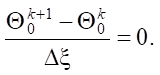
При расчете было использовано 2,5 млн. ячеек сетки.
При проведении расчетов были установлены два ключевых ограничения. Прежде всего, материал PETG характеризуется неизменными и заранее определенными теплофизическими параметрами. Также было принято, что теплообмен происходит исключительно на поверхностях с заданными граничными условиями, в то время как остальные грани ячейки теплоизолированы.
В ходе проведения исследования было установлено, что использование сетки, содержащей от 2,5 до 3,0 миллиона ячеек, приводит к оптимальному результату решения задачи. Повышение числа элементов сетки не оказывает значительного влияния на точность решения, однако существенно увеличивает затраты времени и сложность процесса.
Чтобы подтвердить корректность результатов, полученных в среде MathCAD, авторы провели дополнительное моделирование в системе ANSYS. Динамика температурных изменений графически представлена на рис. 2.

Рис. 2. Изменение температуры в ячейке
Результаты исследования. На рис. 3 представлены результаты расчетов, полученные методом конечных элементов и методом конечных разностей. Анализ результатов позволяет заключить об удовлетворительном совпадении безразмерных температур, полученных двумя методами. Путем анализа вычислительных экспериментов установлено, что ТПМП-ячейка типа Фишера-Коха S сохраняет структуру (не происходит внутренних пересечений, полного заполнения пор и др.) в диапазоне толщины стенки 0 < δ < 0,002 м. Временная эволюция изотерм и динамика их скоростного режима отображены на рис. 4, 5. Примечательной особенностью является то, что в процессе временного развития каждая изотермическая линия формируется на поверхности с характерной начальной скоростью, присущей именно ей. Примечательно, что повышение пористости материала приводит к усилению теплового потока на всем временном интервале исследования, что наглядно продемонстрировано на рис. 5. Зависимость плотности теплового потока от времени при варьировании пористости представлена на рис. 6.
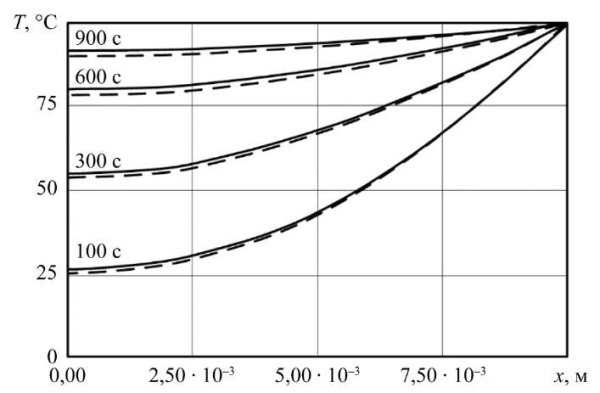
Рис. 3. Распределение температуры по координате: – решение по МКР;
– решение по МКР; – решение по МКЭ
– решение по МКЭ
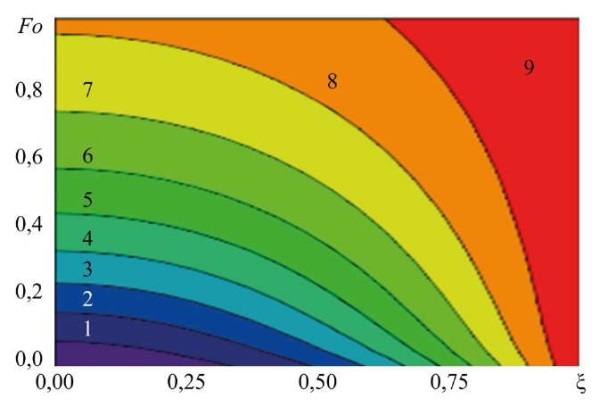
Рис. 4. Графики движения изотерм при координате в зависимости от времени
при: Ѳ = 0,1 (1); 0,2 (2); 0,3 (3); 0,4 (4); 0,5 (5); 0,6 (6); 0,7 (7); 0,8 (8); 0,9 (9)
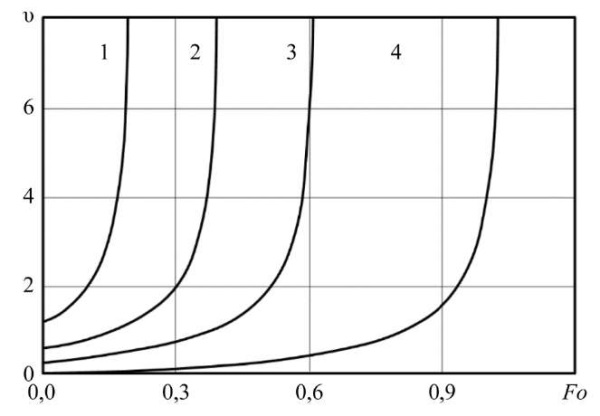
Рис. 5. Распределение скоростей изотерм в пористой пластине
при Ѳ = 0,2 (1); 0,5 (2); 0,7 (3); 0,9 (4)
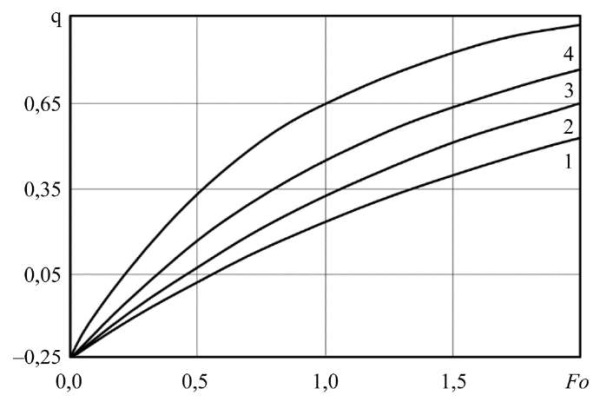
Рис. 6. Распределение плотности теплового потока
при φ = 0,75 (1); 0,80 (2); 0,85 (3); 0,90 (4);
Обсуждение и заключение. В ходе исследования была разработана математическая модель теплопередачи для плоской пористой пластины, основанной на предфрактале Фишера-Коха S типа ТПМП. Точность решения была подтверждена путем сопоставления с альтернативными методами расчета, такими как конечно-разностный и конечно-элементный анализ. Максимальное отклонение результатов по норме Чебышева не превышало 3 %.
Одним из значительных преимуществ предложенного подхода является возможность расчета распределения температур и тепловых потерь в пористых средах без использования сложных компьютерных программ и дорогостоящего вычислительного оборудования. Полученные выражения для температурной функции существенно упрощают процесс инженерных расчетов теплопереноса в подобных материалах.
Результаты численного моделирования, согласующиеся с фундаментальными исследованиями теплопроводности [20], методами задания граничных и начальных условий [15], а также с различными подходами к численным расчетам [11], открывают новые перспективы для дальнейших научных изысканий. В частности, разработанный подход может быть применён для анализа одномерного теплопереноса в пористых средах, включая расчёт распределения температур, тепловых потоков и эффективных коэффициентов теплопроводности материалов на основе ТПМП.
Список литературы
1. Кем А.Ю. Исследование магнитных свойств и фрактальности поверхности порошкового Fе — P материала — аналога технического железа, полученного горячей объемной штамповкой пористой заготовки. Вестник Донского государственного технического университета. 2011;11(2):174–180. URL: https://www.vestnik-donstu.ru/jour/article/view/707 (дата обращения: 25.10.2024).
2. Yi-Lung Cheng, Chih-Yen Lee. Porous Low-Dielectric-Constant Material for Semiconductor Microelectronics. In book: Nanofluid Flow in Porous Media. MSh Kandelousi, S Ameen, M Shaheer Akhtar, Hyung-Shik Shin (eds). London: InTech; 2020. 244 p. https://doi.org/10.5772/intechopen.81577
3. Su-Gwang Jeong, Jeonghun Lee, Seong Jin Chang, Sumin Kim. Thermal and Structural Behavior of Thermal Inertia-Reinforced Mortars for Building Envelope Applications. Construction and Building Materials. 2023;384:131452. https://doi.org/10.1016/j.conbuildmat.2023.131452
4. Maslov AA, Mironov SG, Poplavskaya TV, Kirilovskiy SV, Tsyryulnikov IS. Effect of Porous Inserts on Aerodynamics of Flying Vehicles. Journal of Physics: Conference Series. 2019;1382:012023. https://doi.org/10.1088/1742-6596/1382/1/012023
5. Гольцман Б.М., Яценко Е.А., Геращенко В.С., Комунжиева Н.Ю., Яценко Л.А., Смолий В.А. и др. Пористые теплоизоляционные материалы на основе различных видов силикатного сырья. Известия высших учебных заведений. Северо-Кавказский регион. Технические наук. 2020;(1):55–60. https://doi.org/10.17213/1560-3644-2020-1-55-60
6. Шашкеев К.А., Шульдешов Е.М., Попков О.В. Краев И.Д., Юрков Г.Ю. Пористые звукопоглощающие материалы (обзор). Труды ВИАМ. 2016;42(6):46–56. https://doi.org/10.18577/2307-6046-2016-0-6-6-6
7. Гасанов С.К. Полимерные композиционные материалы для авиационной и космической техники. Международный научно-исследовательский журнал. 2014;28(9):29–30. URL: https://research-journal.org/archive/9-28-2014-september (дата обращения: 25.10.2024).
8. Péter Ádám, Levente Dudás, Ottó Temesi, András Nagy, Katalin Sinkó. Porous Aluminum Oxide Insulation Materials Tested in Space Mission. CEAS Space Journal. 2023;15:671–680. https://doi.org/10.1007/s12567-022-00473-w
9. Мазитов А.А. Web-приложение для математического моделирования нестационарного течения нефти в пористой среде. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):422–432. https://doi.org/10.23947/2687-1653-2023-23-4-422-432
10. Соловьев А.Н., Чебаненко В.А., Оганесян П.А., Фоменко Е.И. Об одном методе расчета изгибных и сдвиговых колебаний пористого пьезоэлемента в низкочастотной области. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):148–158. https://doi.org/10.23947/2687-1653-2024-24-2-148-158
11. Prosviryakov EYu, Ledyankina OA, Goruleva LS. Exact Solutions to the Navier–Stokes Equations for Describing the Flow of Multicomponent Fluids with Internal Heat Generation. Russian Aeronautics. 2024;67(1):60–69. https://doi.org/10.3103/S1068799824010070
12. Ershkov S, Leshchenko D, Prosviryakov E. Correction: A Novel Type of ER3BP Introducing Milankovitch Cycles or Seasonal Irradiation Processes Influencing onto Orbit of Planet. Archive of Applied Mechanics. 2023;93:823–824. https://doi.org/10.1007/s00419-022-02328-6
13. Pavlenko A, Koshlak H. Production of Porous Material with Projected Thermophysical Characteristics. Metallurgical and Mining Industry. 2015;(7):123–127.
14. Chaniot J, Moreaud M, Sorbier L, Fournel T, Becker J-M. Tortuosimetric Operator for Complex Porous Media Characterization. Image Analysis and Stereology. 2019;38(1):25–41. https://doi.org/10.5566/ias.203915
15. Bragin DM, Popov AI, Eremin AV, Olatuyi OJ, Zinina SA, Shulga AS. Thermal Conductivity of a Porous Material with an Ordered Structure. In: Proc. 4th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency. New York City: IEEE; 2022. P. 858–861. https://doi.org/10.1109/SUMMA57301.2022.9973913
16. Mingwei Tian, Sukang Zhu, Ning Pan. Measuring the Thermophysical Properties of Porous Fibrous Materials with a New Unsteady-State Method. Journal of Thermal Analysis and Calorimetry. 2011;107:395–405. https://doi.org/10.1007/s10973-011-1581-y
17. Bicer Ayse, Kar Filiz. A Model for Determining the Effective Thermal Conductivity of Porous Heterogeneous Materials. International Journal of Thermophysics. 2019;40:9. https://doi.org/10.1007/s10765-018-2468-y
18. Dong Niu, Hongtao Gao. Thermal Conductivity of Ordered Porous Structures Coupling Gas and Solid Phases: A Molecular Dynamics Study. Materials. 2021;14(9):2221. https://doi.org/10.3390/ma14092221
19. Chau KV, Gaffney JJ. A Finite‐Difference Model for Heat and Mass Transfer in Products with Internal Heat Generation and Transpiration. Journal of Food Science. 2006;55(2):484–487. https://doi.org/10.1111/j.1365-2621.1990.tb06792.x
20. Формалев В.Ф., Ревизников Д.Л. Численные методы. Москва: Физматлит; 2004. 400 с.
21. Вержбицкий В.М. Основы численных методов. Москва: Высшая школа; 2002. 840 с.
Об авторах
К. B. ГубареваРоссия
Кристина Владимировна Губарева, кандидат технических наук, доцент кафедры промышленной теплоэнергетики
Scopus ID: 57216361463
443100, г. Самара, ул. Молодогвардейская, д. 244
А. В. Еремин
Россия
Антон Владимирович Еремин, доктор технических наук, доцент, проректор по интеграционным проектам, заведующий кафедрой промышленной теплоэнергетики
Scopus ID: 56395547000
443100, г. Самара, ул. Молодогвардейская, д. 244
Рецензия
Для цитирования:
Губарева К.B., Еремин А.В. Численное решение задачи теплопроводности в пористой пластине с топологией трижды периодических минимальных поверхностей. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):23-31. https://doi.org/10.23947/2687-1653-2025-25-1-23-31. EDN: YYGRFP
For citation:
Gubareva K.V., Eremin A.V. Numerical Solution to the Problem of Thermal Conductivity in a Porous Plate with a Topology of Triply Periodic Minimal Surfaces. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):23-31. https://doi.org/10.23947/2687-1653-2025-25-1-23-31. EDN: YYGRFP












































