Scroll to:
Using Surrogate Models in the Construction of a Pareto-Optimal Positioning Electropneumatic Actuator with Discrete Pneumatic Valves
https://doi.org/10.23947/2687-1653-2025-25-1-52-64
EDN: OETHVA
Abstract
Introduction. Pneumatic actuators are widely used in industry due to their reliability, simplicity of design, and ability to operate under complex conditions. However, when solving positioning problems, the use of traditional proportional valves is often redundant, which causes an unjustified increase in cost and complexity of the design. The application of simpler discrete distributors faces the problem related to the need to reach a compromise between their switching frequency and positioning accuracy.
Existing studies mainly focus on optimizing individual performance indicators of pneumatic actuators and do not offer effective methods for finding a compromise between conflicting criteria. Using classical methods for constructing a Pareto set for multicriteria optimization requires significant computational resources, which complicates their practical application.
The research objective is to develop a methodology for multicriteria optimization of the parameters of a positioning electropneumatic actuator with discrete distributors based on the construction of a Pareto set using surrogate models, which provides finding the optimal balance between switching frequency and positioning accuracy.
Materials and Methods. The research was conducted on a model of a positioning pneumatic actuator with discrete distributors, implemented in MATLAB Simulink. The Latin hypercube method was used to analyze the parameters, which provided uniform filling of the parameter space. To reduce computational costs, surrogate models, built using neural networks, were used. Sliding control was selected as a control algorithm, which effectively compensated for external disturbances and uncertainties of the system.
Results. The optimization of control parameters has shown the possibility of reaching high positioning accuracy with a minimum frequency of distributor switching. The use of the Latin hypercube method provided a uniform distribution of the calculation points, which made it possible to construct an accurate surrogate model. It has been experimentally proven that the proposed approach reduces computational costs by 48%, while maintaining high accuracy of modeling and analysis.
Discussion and Conclusion. The research results confirm that sliding control is an effective solution for discrete pneumatic drives in the context of multicriteria optimization. The developed approach makes it possible to significantly reduce the frequency of switching distributors without substantial losses in the quality of transients, which helps to extend the service life of equipment and increase the reliability of automated systems. The use of surrogate models and neural network technology opens up new prospects for faster design of complex systems.
Keywords
For citations:
Sheykin M.O., Cherkasskikh S.N., Shilin D.V., Fedenkov V.V. Using Surrogate Models in the Construction of a Pareto-Optimal Positioning Electropneumatic Actuator with Discrete Pneumatic Valves. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):52-64. https://doi.org/10.23947/2687-1653-2025-25-1-52-64. EDN: OETHVA
Introduction. Pneumatic drives are widely used in various industries due to the simplicity of their design, the ability to provide high speeds of movement of controlled objects, environmental friendliness, fire safety, and the ability to work in aggressive environments.
In systems oriented to tracking, proportional valves are in routine used to control the pneumatic actuator, which provide continuous regulation. However, when the basic task of the pneumatic actuator is to arrange the output element in a specified position, rather than following a given trajectory, the use of such distributors may be redundant. In this case, it is advisable to consider the application of simpler discrete valves [1].
Existing research papers suggest various approaches to positioning control, including algorithms using pulse-width modulation, as well as sliding and predictive control principles [2]. Improvement in positioning accuracy is reached either by modifying the control algorithm near the breaking point [3], or by implementing specialized mechanical or hydraulic braking devices [4]. However, despite the improvement in accuracy, the use of braking devices significantly complicates the design, which in turn can negate the advantages of using discrete pneumatic valves [5].
The analysis of the current state of research has revealed significant gaps in the understanding of the problem. First of all, there is no holistic approach to assessing the efficiency of various structures of positional electropneumatic drives with discrete valves. In addition, the issue of reaching a compromise between the frequency of switching distributors and the quality of positioning has not been sufficiently studied. Existing methods of multicriteria optimization of parameters of such systems do not provide the required efficiency. Authors of publications often focus on individual aspects of quality, such as accuracy or speed. Little attention is paid to the relationship between increasing the accuracy of positioning and increasing the frequency of switching distributors, which directly affects equipment wear and service life.
The pneumatic actuator considered in this paper does not have special braking devices, and the positioning of the output link at a given point is performed exclusively by switching discrete pneumatic distributors at the right moments in time, according to the applied control algorithms. This provides for the simplicity of the design and low cost of the solution, but leads to frequent switching of pneumatic distributors. The strictness of the requirements for the quality of the transient process, in turn, inevitably leads to an increase in the number of switches.
Thus, there is a need to find a trade-off decision that takes into account two contradictory criteria: positioning accuracy and intensity of the distributors. The construction of the Pareto front will allow us to determine a set of unimprovable solutions, where it is impossible to improve one quality indicator without degrading the other, which will provide the developer with the opportunity to make a justified selection of system parameters. However, traditional methods for constructing the Pareto set require multiple calculations of complex dynamic models [6], which makes the process extremely labor-intensive and time-consuming.
The use of surrogate models in constructing the Pareto set [7] opens up new horizons for solving this problem, although it requires the development of specialized methods adapted to a specific class of pneumatic devices.
This research is aimed at developing a methodology for multicriteria optimization of the parameters of a positional electropneumatic drive with discrete valves, based on the use of surrogate models, which provide for an effective search for trade-off decisions between the switching frequency and the quality of positioning. To accomplish this purpose, it is necessary to develop a methodology of creating a surrogate model for assessing the quality indicators of a positional electropneumatic drive. It is also required to create an algorithm for multicriteria optimization of drive parameters using a surrogate model and conduct a study of the efficiency of the proposed approach on a specific drive design.
Materials and Methods. This paper examines a positional pneumatic drive with discrete pneumatic distributors without special braking devices. It is shown in Figure 1. It contains a single-rod, double-acting pneumatic cylinder controlled by four 2/2 pneumatic distributors. Using four 2/2 pneumatic distributors instead of two 3/2 pneumatic distributors allows for better dynamic characteristics of the pneumatic drive with an acceptable increase in the cost of the design.
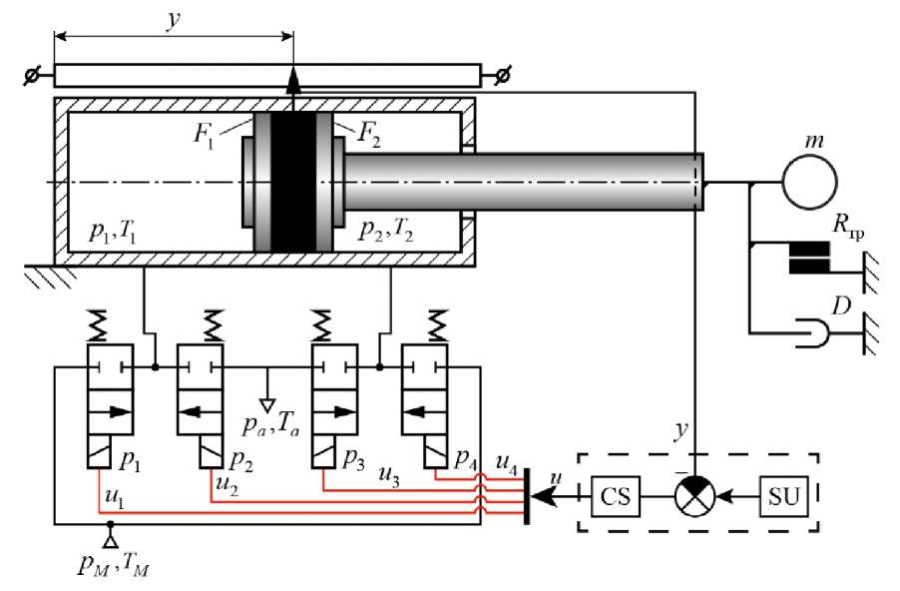
Fig. 1. Pneumatic actuator circuit with discrete distributors
To control discrete pneumatic distributors, a control system (CS) is used, shown in Figure 2. It implements the principle of sliding control in accordance with the input signal determined by the setup unit (SU). The sliding mode provides robust control, allowing the system to effectively cope with the uncertainties and disturbances characteristic of pneumatic systems.
The basic idea of the method is to make the system move along a predetermined trajectory, called a “sliding surface” [8]. When the system gets on this trajectory, it starts to “slide” along it to the desired target, ignoring numerous external actions.
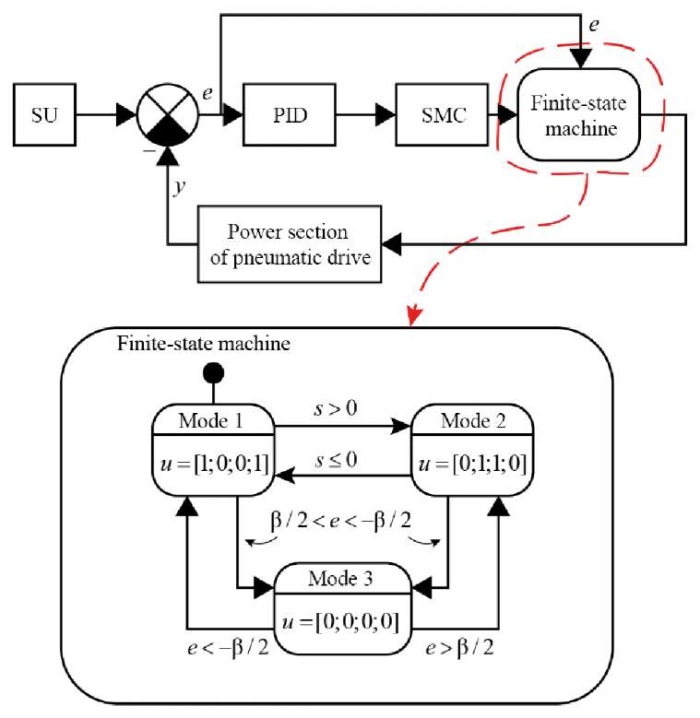
Fig. 2. Control system structure
In this paper, we use the sliding straight line described by the equation:
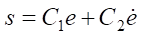 ,
,
where s — switch function; e — control error; ė — rate of error change; C1 and C2 — positive coefficients determining the slope and characteristics of the sliding straight line.
Control consists of two parts: one part keeps the system on the desired trajectory, and the other quickly brings it back if something tries to mislead the system [9]. This second part can cause rapid unwanted oscillations.
The control signal from the sliding mode controller is fed to the input of the finite-state machine, which generates the corresponding combinations of control actions for the pneumatic distributors. The system implements three main operating modes: piston extension (P1 and P4 are active), piston retraction (P2 and P3 are active), and braking (P1 and P2 are active). The braking mode, in which the charge pressure is supplied to both cavities of the pneumatic cylinder, is switched on when the control error reaches values from the range [ –β/2; +β/2], where β — width of the braking corridor.
The mathematical model of the pneumatic power part includes the equation of the dynamic balance of forces on the piston of the pneumatic cylinder, the equations of filling and emptying the cavities of the pneumatic cylinder, and the equations of mass flows for the discharge and exhaust cavities [10].
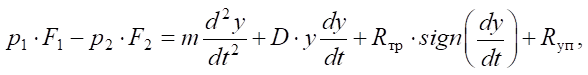
where p1, p2 — pressure in the piston and rod cavities of the pneumatic cylinder; F1, F2 — piston and rod areas of the piston; m — reduced mass; Rтр — Coulomb friction force; D — coefficient of viscous friction; Rуп — reaction force of stops in the pneumatic cylinder; y — piston displacement.
The reaction of the stops limiting the piston movement can be calculated using the following formulas:
for the case when the piston approaches the lower stop (at y < –0.5H):
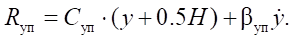
For the case when the piston is within the working stroke (at –0.5H ≤ y ≤ 0.5H):
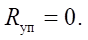
For the case when the piston approaches the upper stop (at y > 0.5H ):
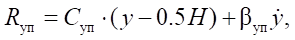
where H — stroke of the pneumatic cylinder piston; Cуп, βуп — coefficients of rigidity and dissipation of the contact interaction of the pneumatic cylinder piston with the stop, respectively.
The equation for filling and emptying the left cavity has the form [11]:
 (1)
(1)
where k — adiabatic index; R — specific gas constant; Тм, T1 — air temperature in the line and in the left cavity of the pneumatic cylinder; G1, G2 — mass air flow rates through the pneumatic distributors P1 and P2, respectively. The value takes into account the selection of the origin of y coordinates, as well as the dead volume of the left part of the pneumatic cylinder, including the volume of the supply line and is determined by the expression:

Mass flow rates G1 and G2 for an adiabatic process are calculated using the Saint-Venant – Wantzel equation [12]:
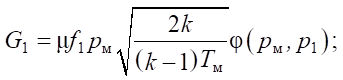 (2)
(2)
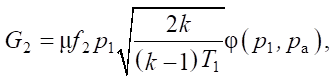 (3)
(3)
where pм, pa — line and atmospheric pressure; μ — flow rate coefficient, f1, f2 — areas of the throttle slots of pneumatic distributors P1 and P2, respectively.
Flow function φ(pa, pb) for a diatomic ideal gas is defined as follows:
at the subcritical flow regime (when pa / pb > 0.528):
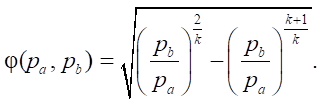
under critical and supercritical flow conditions (when pa / pb ≤ 0.528):
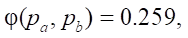
where k — adiabatic index (for a diatomic gas usually k = 1.4).
Temperature Т 1 during the adiabatic emptying process is equal to:
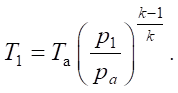 (4)
(4)
Substituting (1), (2) and (3) into (4), we obtain:
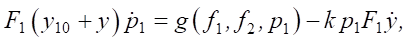
where
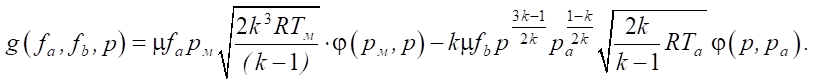
The processes of filling and emptying the right cavity are described by the following equation:
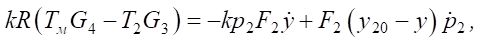 (5)
(5)
where T2 — air temperature in the right cavity of the pneumatic drive; G3, G4 — mass air flow rates through pneumatic distributors P3 and P4 respectively. Value y2 is determined by the formula:
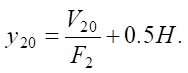
In the expression, V20 — dead volume of the right cavity of the hydraulic cylinder, including the volume of the exhaust line. Temperature T2 during the adiabatic emptying process is equal to:
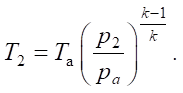 (6)
(6)
Mass flows G3 and G4 are equal to:
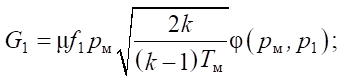 (7)
(7)
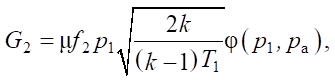 (8)
(8)
where f3, f4 — areas of the throttle gaps of pneumatic distributors P3 and P4, respectively.
Substituting (6), (7) and (8) into (5), we obtain:
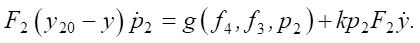
The presented mathematical model of the pneumatic drive was subsequently implemented in the MATLAB Simulink software package (Fig. 3). Numerical modeling of the system was performed considering the parameters, whose values are presented in Table 1.

Fig. 3. Model of a pneumatic drive with discrete pneumatic valves in MATLAB Simulink
Table 1
Values of Model Parameters for Numerical Simulation
|
Parameter |
Value |
|
Reduced mass at the end of the rod, kg |
6 |
|
Main line pressure, bar |
4 |
|
Exhaust pressure, bar |
1 |
|
Pneumatic cylinder piston diameter, mm |
32 |
|
Pneumatic cylinder rod diameter, mm |
12 |
|
Working environment temperature, K |
293.15 |
|
Breakaway friction force, N |
20 |
|
Sliding friction force, N |
15 |
|
Coefficient of viscous friction, mm/s |
350 |
The proposed method for constructing the Pareto set for the pneumatic drive structure under consideration is presented in the form of an algorithm in Figure 4 and includes several stages.
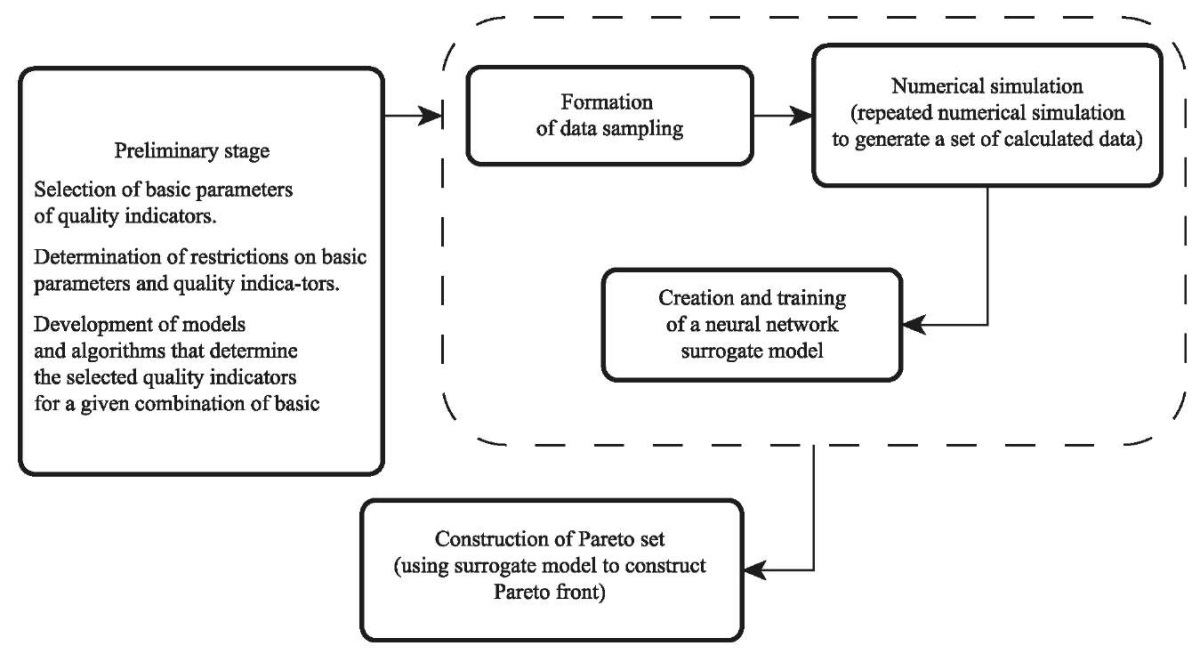
Fig. 4. Algorithm for constructing Pareto set
Selection of basic parameters of quality indicators.
Determination of restrictions on basic parameters and quality indicators.
Development of models and algorithms that allow determining the selected quality indicators for a given combination of basic parameters.
Numerical modeling (repeated numerical modeling to create a set of calculated data).
Creation and training of a neural network surrogate model.
Construction of the Pareto set (use of a surrogate model to construct the Pareto front).
At the preliminary stage, quality indicators are selected that evaluate the perfection of the system under study. For a comprehensive assessment of the quality of the transient process, a generalized integral quadratic estimate can be used [1]:
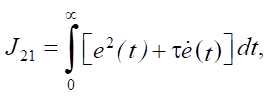
where e — transient component of the error, normalized from 0 to 1; τ — weight coefficient.
Improving the quality of the transient process is related to an increase in the number of switchings of the pneumatic distributors n. In this regard, it is of interest to study the limiting capabilities of the pneumatic drive structure for two conflicting quality indicators J21 and n. At the preliminary stage, quality indicators are selected that evaluate the efficiency of the system under study. Thus, a space of quality indicators in which the surface corresponding to the Pareto front will be identified, is formed.
From the design parameters of the system, a group of basic parameters is identified. It determines the main control characteristics: slope coefficients of the sliding line C1 and C2, response time of the distributors, and width of the braking corridor. The ranges of variation of these parameters determine the search space for optimal solutions. They are presented in Table 2.
Table 2
Intervals of Values of Variable Parameters
|
Coefficient С1 |
1.0–4.0 |
|
Coefficient С2 |
0.1–1.0 |
|
Distributor response time, ms |
5–45 |
|
Size of the braking corridor, mm |
2–4 |
To calculate the vector of quality indicators based on the vector of basic parameters, corresponding models are formed. For the case under consideration, a nonlinear dynamic model was used, which includes both a power pneumatic part and a control system based on sliding modes.
At the next stage, the parameter space is filled with computation points, in which the vector of quality indicators will be calculated. In this case, the number of points should be minimal to reduce computational costs, but sufficient to provide for the desired accuracy of the surrogate model. An important requirement is also the uniform distribution of points in the parameter space.
To construct a surrogate model, various methods of filling the parameter space were investigated: random sampling, the Latin hypercube method (LHC), the Sobol method, and the grid method. Figure 5 shows a comparison of filling a two-dimensional space by the uniform direct search method and the LHC method. Despite the apparent visual uniformity, direct search provides worse filling quality compared to the LHC method.
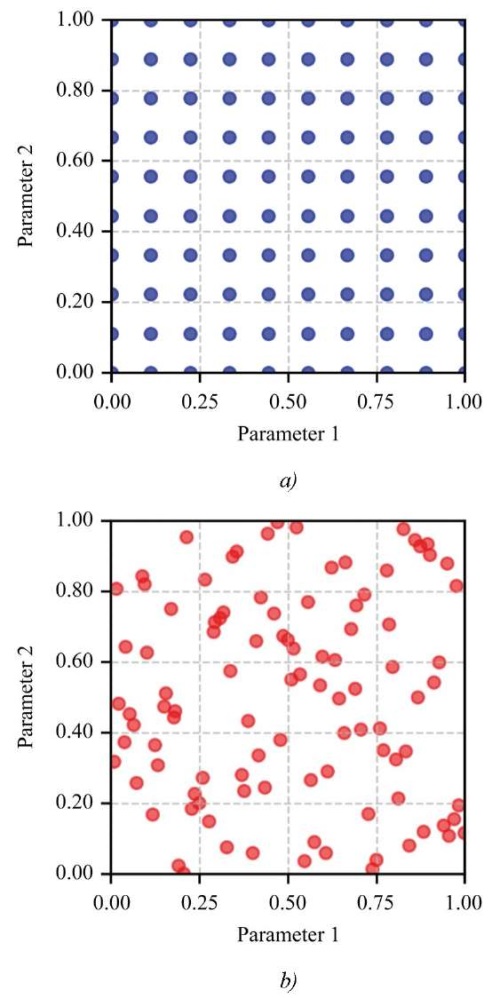
Fig. 5. Filling the parameter space with computation points:
a — uniform filling; b — filling by the LHC method
To quantitatively assess the uniformity of the parameter space coverage, a metric method [2] was developed based on the comparison of the specific average distance between nearby points. The method includes normalization of the parameters in a single hypercube, generation of points by the studied filling method, and calculation of the Monte Carlo coefficient. This coefficient is the ratio of the actual average distance between nearby points to the expected average distance:
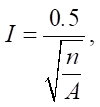
where n — number of real points; A — area of the region (in the case under consideration, A = 1).
For the selected combinations of parameters, parallel calculations of the model and calculations of quality indicators were performed, which made it possible to form a data set for constructing a surrogate model. The research used a direct propagation neural network of the following architecture [3][13]: an input layer (3 inputs with data normalization), two fully connected layers (16 and 8 neurons) with ReLU activation functions, an output layer for regression. The network was trained using the ADAM algorithm, which provided adaptive adjustment of the learning rate and efficient work with noisy data.
At the final stage, the Pareto front was constructed by the NSGA-II evolutionary algorithm [4][14], which used the quality indicator estimates obtained through the surrogate model. This algorithm provided for the efficient identification of a set of non-dominated solutions in the quality criteria space [15].
Research Results. The developed method was tested on a positional pneumatic drive with discrete distributors. At the first stage, a study on the dynamic characteristics of the control system was conducted. Figure 6 shows transient processes demonstrating the key features of the drive operation. The analysis of the graphs shows symmetry in the number of switchings of the control signal during the forward and reverse stroke, which indicates the stability of the control algorithm. At the same time, asymmetry is observed in the positioning accuracy: for the forward stroke of the system, the control error reaches 1.5 mm, which is explained by the design features of the single-rod pneumatic cylinder.
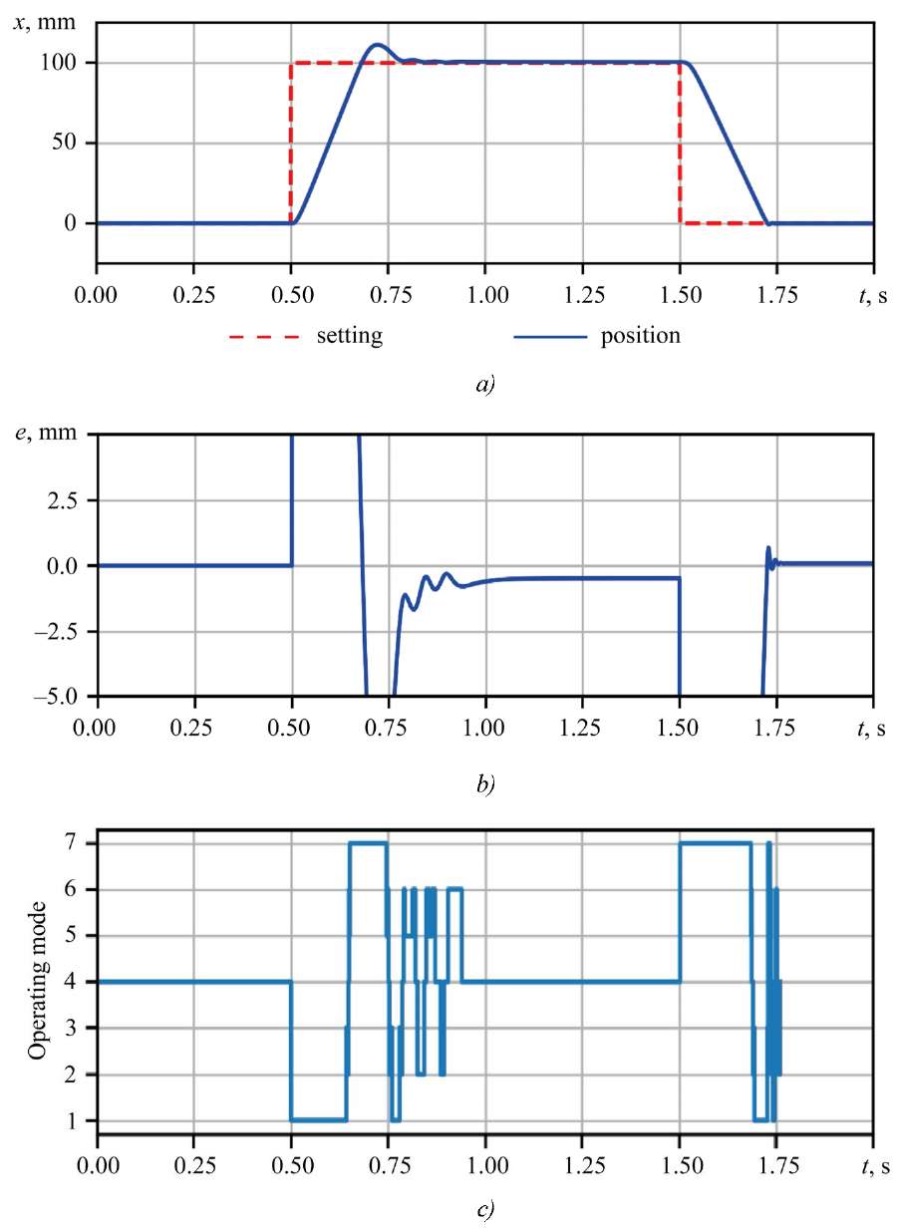
Fig. 6. Transient processes of pneumatic drive with discrete pneumatic distributors:
a — transient process; b — control error; c —switching modes
An assessment of the effect of the system parameters on transient processes has established that reducing the width of the braking corridor increases the positioning accuracy, accompanied by an increase in the number of switchings of the pneumatic distributors. Similarly, an acceleration of the response speed of the pneumatic distributors increases the positioning accuracy, but leads to an increase in the oscillation of the transient process and a growth of the number of switchings. At the same time, the magnitude of the displacement did not have a significant effect on the transient process, which indicated the linearity of the system in a wide range of working displacements and confirmed the efficiency of the control algorithm.
When constructing a surrogate model, the parameter area was filled with computation points, with preference given to the Latin hypercube method, which provides for a uniform distribution of points compared to direct enumeration, random sampling, the Sobol method, and the network method. The calculation of the Monte Carlo coefficient (Table 3) demonstrated that the Latin hypercube method was characterized by the smallest dispersion of distances between nearby points, which made it possible to form a sample of 2,500 combinations of basic parameters. The application of surrogate models compromised the labor intensity of constructing the Pareto set, which resulted in a 48% reduction in calculation time. The surrogate model was built on the basis of neural network technology, while the analysis of various approaches to the formation of a training data sample confirmed the feasibility of using the Latin hypercube method.
Table 3
Comparison of Uniformity of Parameter Space Coverage by Different Sampling Methods
|
Sampling method |
Monte Carlo coefficient |
|
Random sampling |
1.024 |
|
Latin hypercube method |
0.997 |
|
Sobol's method |
0.980 |
For each combination of basic parameters, a mathematical model was calculated with the definition of quality indicators, which made it possible to consider the set of calculated points of each iteration of the algorithm as a generation. Within the framework of the non-dominant sorting procedure, unimprovable solutions were identified that formed the Pareto front of zero rank, and the remaining points formed the Pareto front of the first rank. Subsequent generation of the next generation was performed by operations similar to crossover, mutation and selection, while a fixed generation size was maintained by cutting off the least high-quality options. The optimization algorithm terminated when the maximum number of generations or the required convergence level was reached. The result of the algorithm implemented using the evolutionary algorithm NSGA-II was the Pareto front. It is shown in Figure 7, reflecting unimprovable solutions with a balance between the number of switchings of pneumatic distributors and the quality of the transient process. At the same time, a small steepness of the front provides for considerable reduction of the number of switchings without significant deterioration of the transient characteristics.
Using a neural network with 4 hidden intermediate layers and a training sample consisting of 2,500 points allowed us to provide for an average accuracy of the surrogate model equal to 91%, with a maximum deviation of 12%. An additional increase in the number of points by 50% has led to an increase in the accuracy of the surrogate model by 15%.
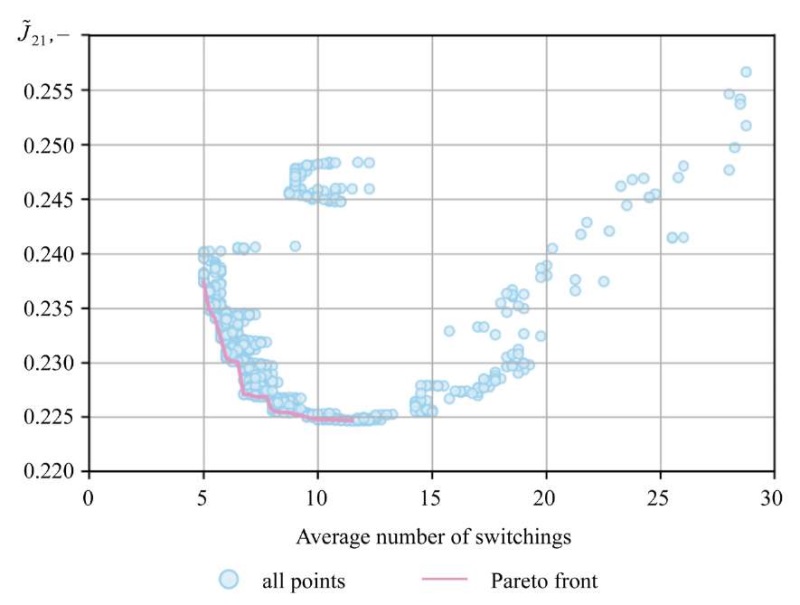
Fig. 7. Pareto set for a pneumatic actuator with discrete distributors
Discussion and Conclusion. The obtained results indicate high stability of the control algorithm, providing symmetrical switching of signals during forward and reverse strokes, which confirms correctness of the approach applied to pneumatic drive control. The revealed asymmetry of positioning accuracy, expressed in an error of up to 1.5 mm for forward stroke, indicates the need for further optimization of the design features of the pneumatic cylinder.
The analysis of the effect of system parameters on dynamic characteristics has shown that the compromise between positioning accuracy and the number of switchings of pneumatic distributors requires an optimal selection of the width of the braking corridor and the speed of the distributors. The use of the Latin hypercube method to form a training sample has provided for uniform filling of the parametric space, which is confirmed by calculations of the Monte Carlo coefficient.
The use of replacement surrogate models built on the basis of neural network technologies made it possible to compromise the labor intensity of constructing the Pareto set and reduce the calculation time by 48%, which indicates the prospects of this approach in optimization problems. The efficiency of the evolutionary algorithm NSGA-II used to construct the Pareto front is validated through obtaining trade-off decisions that provide for a balance between the number of switchings of pneumatic distributors and the quality of the transient process.
Reaching an average accuracy of the replacement model at 91% and reducing the maximum deviation to 12% when using a neural network with 4 hidden layers demonstrates the high efficiency of neural network technologies. At the same time, an increase in accuracy by 15% with an expansion of the training sample by 50% indicates the potential for further improvement of the accuracy of the models.
Thus, the results of the conducted research confirm the potential of the proposed method for increasing the efficiency of positional pneumatic drives with discrete distributors, and determine promising directions for further optimization research in this area.
References
1. Youssry M, Elmayyah W, Mabrouk M. Position Control of a Pneumatic Cylinder Actuator Using Modified PWM Algorithm. Journal of Engineering Science and Military Technologies. 2020;4(1):121–126. http://doi.org/10.21608/ejmtc.2020.31861.1145
2. Nguyen T, Leavitt J, Jabbari F, Bobrow JE. Accurate Sliding-Mode Control of Pneumatic Systems Using Low-Cost Solenoid Valves. IEEE/ASME Transactions on Mechatronics. 2007;12(2):216–219. https://doi.org/10.1109/TMECH.2007.892821
3. Bone GM, Xue M, Flett J. Position Control of Hybrid Pneumatic–Electric Actuators Using Discrete-Valued Model-Predictive Control. Mechatronics. 2014;25:1–10. https://doi.org/10.1016/j.mechatronics.2014.10.009
4. Anh Dao, Sidorenko VS, Dymochkin DD. Study on Positioning Accuracy of Automated Pneumatic Drive with an Outer Brake. Vestnik of Don State Technical University. 2015;15(4):46–53. https://doi.org/10.12737/16077
5. Grishchenko VI, Sidorenko VS. Modeling of the Positioning Process of Actuators of Technology Equipment with Discrete Pneumohydraulic Device and Pneumatic Communication Lines. Vestnik of Don State Technical University. 2009;(S2):81–90.
6. Podinovskiy VV, Nogin VD. Pareto-Optimal Solutions to Multicriteria Problems. Moscow: Fizmatlit; 2007. 256 p. (In Russ.)
7. Diaz-Manriquez A, Toscano G, Barron-Zambrano JH, Tello-Leal E. A Review of Surrogate Assisted Multiobjective Evolutionary Algorithms. Computational Intelligence and Neuroscience. 2016;2016:9420460. http://doi.org/10.1155/2016/9420460
8. Yongping Pan, Chenguang Yang, Lin Pan, Haoyong Yu. Integral Sliding Mode Control: Performance, Modification, and Improvement. IEEE Transactions on Industrial Informatics. 2018;14(7):3087–3096. https://doi.org/10.1109/TII.2017.2761389
9. Sheykin MO, Cherkasskikh SN. Experimental Study of a Pneumatic Actuator with a Fuzzy Logic Controller. In: Proc. XII All-Russian Scientific and Technical Conference “Hydraulic Machines, Hydraulic Drives and Hydropneumatic Automation. Current Status and Development Prospects”. St. Petersburg: Politekh-Press; 2022. P. 257–267.
10. Sheykin MO, Cherkasskikh SN, Shilin DV. Application of Sliding Mode Control in Pneumatic Actuators. Gidravlika. 2024;(23):24–32. (In Russ.)
11. Incremona GP, Rubagotti M, Ferrara A. Sliding Mode Control of Constrained Nonlinear Systems. IEEE Transactions on Automatic Control. 2017;62(6):2965–2972. https://doi.org/10.1109/TAC.2016.2605043
12. Ley C. Applied Directional Statistics: Modern Methods and Case Studies. London: Chapman & Hall/CRC Press; 2018. 318 p. https://doi.org/10.1201/9781315228570
13. Raisch A, Sawodny O. Analysis and Optimal Sizing of Pneumatic Drive Systems for Handling Tasks. Mechatronics. 2019;59:168–177. https://doi.org/10.1016/j.mechatronics.2019.04.003
14. Yagoubi M, Bederina H. Surrogate-Assisted NSGA-II Algorithm for Expensive Multiobjective Optimization. In: Proceedings of the Companion Conference on Genetic and Evolutionary Computation. New York, NY: Association for Computing Machinery; 2023. P. 431–434. https://doi.org/10.1145/3583133.3590746
15. Deb K, Pratap A, Agarwal S, Meyarivan T. A Fast and Elitist Multi-Objective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation. 2002;6(2):182–197. https://doi.org/10.1109/4235.996017
About the Authors
M. O. SheykinRussian Federation
Maxim O. Sheykin, Junior Researcher of the Hydromechanics and Hydraulic Machines Department
17, Krasnokazarmennaya Str., Moscow, 111250
S. N. Cherkasskikh
Russian Federation
Sergey N. Cherkasskikh, Cand.Sci. (Eng.), Associate Professor of the Hydromechanics and Hydraulic Machines Department
Scopus ID: 12038974200
17, Krasnokazarmennaya Str., Moscow, 111250
D. V. Shilin
Russian Federation
Denis V. Shilin, Cand.Sci. (Eng.), Associate Professor of the Hydromechanics and Hydraulic Machines Department
Scopus ID: 57204153776
Researcher ID: AAA-2033-2019
17, Krasnokazarmennaya Str., Moscow, 111250
V. V. Fedenkov
Russian Federation
Vladimir V. Fedenkov, Dr.Sci. (Eng.), Professor of the Hydromechanics and Hydraulic Machines Department
17, Krasnokazarmennaya Str., Moscow, 111250
Review
For citations:
Sheykin M.O., Cherkasskikh S.N., Shilin D.V., Fedenkov V.V. Using Surrogate Models in the Construction of a Pareto-Optimal Positioning Electropneumatic Actuator with Discrete Pneumatic Valves. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):52-64. https://doi.org/10.23947/2687-1653-2025-25-1-52-64. EDN: OETHVA













































