Scroll to:
Approximate Synthesis of Н∞ – Controllers in Nonlinear Dynamic Systems over a Semi-Infinite Time Period
https://doi.org/10.23947/2687-1653-2025-25-2-152-164
EDN: IHQRUT
Abstract
Introduction. Problems and methods of finding Н∞ – control are the basis of modern control theory. They are actively used to develop robust controllers, especially in aircraft control systems under limited external actions. These methods allow for adapting control systems to changing environmental conditions, which is critically important for providing the reliability and safety of aircraft operation. Current research is aimed at improving approaches to the synthesis of controllers covering both linear and nonlinear dynamic systems. In this context, special attention is paid to the integration of new mathematical methods, such as linear matrix inequalities and frequency analysis, which allows for optimizing the system response to various external actions and providing protection against unexpected conditions. It is important to note that, despite the progress made in this area, significant problems remain unsolved regarding the analysis and synthesis of controllers for nonlinear systems. This necessitates further research and development in this promising area. In this paper, in order to fill the existing gap, sufficient conditions for the existence of control for one of the frequently encountered classes of nonlinear systems are formulated and proven, which will then be used as a theoretical basis for developing approximate algorithms for finding it.
Materials and Methods. The basic research tool was the Н∞ – control synthesis methods based on the minimax approach, which consisted in finding the control law under the worst external action. In this context, it was proposed to prove sufficient conditions for the existence of control using the extension principle. However, due to the computational difficulties that might arise when applying those conditions, it was decided to simplify the initial formulation of the problem. The simplification process was performed by approximate replacing the nonlinear system with another nonlinear system, which was similar in structure to the linear one, using the factorization procedure. This approach made it possible to use the solution of the Riccati equation, whose coefficients depended on the state vector, for the synthesis of controllers. To solve model examples and applied problems, a software package was developed using the MATLAB mathematical package.
Results. The article solved the problem of synthesis of Н∞ – control of the state of nonlinear continuous dynamic systems, linear in control and disturbance. Sufficient conditions for the existence of Н∞ – control were formulated and proved on the basis of the extension principle. An approximate method was proposed that provided solving the problem of finding control laws for dynamic systems that were nonlinear in state, similar to the methods used for linear systems. Analytical solutions were found for two model examples, which were illustrated by graphs of transient processes to demonstrate the results of numerical modeling of the considered nonlinear dynamic systems in the presence of external actions.
Discussion and Conclusion. The proposed approximate algorithm for synthesizing state and output controllers guarantees the required quality of transient processes and asymptotic stability of closed nonlinear control systems. This significantly expands the class of dynamic systems for which it is possible to synthesize controllers capable of resisting various external actions. The methods presented in this paper can be effectively applied to solve a variety of control problems, including the design of autopilots and automatic navigation systems for aircraft, even under conditions of limited external actions.
Keywords
For citations:
Panteleev A.V., Yakovleva A.A. Approximate Synthesis of Н∞ – Controllers in Nonlinear Dynamic Systems over a Semi-Infinite Time Period. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):152-164. https://doi.org/10.23947/2687-1653-2025-25-2-152-164. EDN: IHQRUT
Introduction. Methods of modern control theory play an important role in the development of complex aerospace systems, providing their efficient operation. To achieve high productivity, stability and efficiency of such systems, it is necessary to develop algorithms for synthesizing controllers capable of operating under conditions of uncertainty in the description of external influences. The modern foundation for their development include the state space method, frequency analysis, and the approach based on linear matrix inequalities [1]. To solve problems of finding optimal control, sufficient optimality conditions in the form of the Bellman equation and the relations following from it in special cases are usually applied. Linear matrix inequalities can be used to search for Н∞ – controllers. They determine the existence of a regulator that satisfies certain performance criteria and provides the stability of the system to external influences. These criteria are usually associated with a norm, which is a measure of the sensitivity of the system to external disturbances. These criteria are usually related to Н∞ – norm, which is a measure of the sensitivity of the system to external disturbances. The problem is to find a regulator that minimizes this norm, while providing the stability of the system and satisfying the quality criterion of control. The solution method is based on finding the extremum of a convex objective function, where the conditions are presented in the form of linear matrix inequalities [2]. By using this method, it is possible to reduce the solution of complex systems of linear and nonlinear algebraic matrix equations of a certain type to the solution of convex optimization problems. However, the solution of linear matrix inequalities can be difficult when considering complex technical problems.
An alternative method based on stochastic minimax is presented in the anisotropic theory of stochastic robust control described in [3]. The main idea in applying this method is that robustness in stochastic control is reached by explicitly including different noise distribution scenarios in a single performance indicator to be optimized. Statistical uncertainty is expressed through entropy, and the robust quality indicator is selected in such a way as to make it possible to quantify the system's ability to suppress the worst external impact. The application of such an approach to solving complex systems of interrelated equations requires the development and use of specialized algorithms.
It should be noted that methods of Н∞ – optimization are used to solve numerous different applied problems, such as aircraft [4], helicopter [5], quadcopter [6] and multi-agent systems [7] control, robot stabilization [8], rocket engine design [9], where, when compared to other controllers, these methods show good results and lower error values under limited disturbances. It is also worth mentioning their use in filtering problems [10], state vector estimation [11] and neural network design [12]. Thus, the development and advancement of Н∞ – optimization methods are highly topical issues for research. Previously, the authors considered the problems of synthesizing Н∞ – controller [13] and Н∞ – observer [14] for linear dynamic systems, for the solution of which sufficient optimality conditions based on the expansion principle were used. Their application made it possible to justify the synthesis procedures and, as a result, to form step-by-step algorithms for solving problems.
Despite significant achievements in this area, a number of problems related to the analysis and synthesis of controllers for nonlinear systems remain unsolved. In this regard, the paper considers the problem of synthesis of controllers for nonlinear dynamic systems, linear in control and disturbance, on a semi-infinite time interval. The research objective is to formulate and prove sufficient conditions for the existence of control. This will not only create a basis for new research and development, but also fill existing gaps in the field of knowledge. Specifically, the work provides for the use of sufficient conditions as a theoretical justification for the formulation of approximate control search algorithms for the class of dynamic systems under consideration. To test the efficiency of the proposed algorithm, two model examples will be solved.
Materials and Methods. Let there be a mathematical model of the control object:
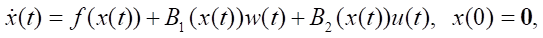 (1)
(1)
and the model of the measuring system:
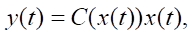 (2)
(2)
where x ∈ Rn —state vector, u ∈ Rq —control vector, w ∈ Rp — external influences vector, y ∈ Rm — output vector, t ∈ T = [0, ∞) — current time, 0 — zero matrix-column of dimensions (n × 1). Assume that the continuously differentiable vector function f(x) of dimensions (n × 1), as well as the matrix functions B1(x) of dimensions (n × p), B2(x) of dimensions (n × q), C(x) of dimensions (m × n) are given. The model of the object is described by an equation that is nonlinear in state, but linear with respect to control and external influences.
It is implied that:
- w(.) ∈ L2[0,∞), u(.) ∈ L2[0,∞);
- m≤n, rg С(x) = m;
- the origin of coordinates x≡ 0 is the equilibrium point, e.g., f(0) = 0;
- B1(x) ≠O, B2(x) ≠O;
where O — zero matrix of corresponding dimensions.
An indicator describing the current behavior of the control object model (1) with measuring system (2) is defined:
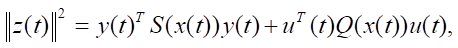 (3)
(3)
where for all x ∈ Rn Q(x) > 0 — symmetric positive definite square matrix of order q, and S(x) > 0 — symmetric non-negative definite square matrix of order m. Functional (3) is quadratic in control, but non-quadratic in state.
Note that we are considering models of an object and a measuring system, the matrices in which depend on the state vector.
It is required to ensure the correctness of the condition:
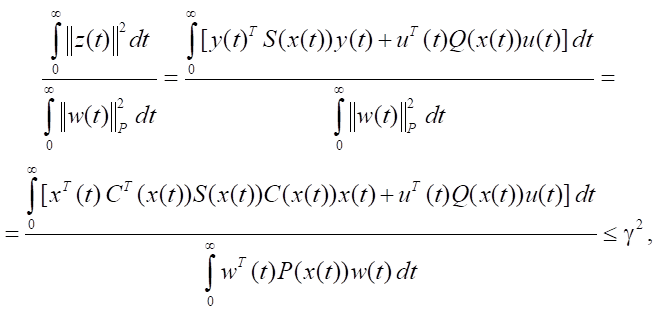 (4)
(4)
where ∀ x ∈ Rn P(x) > 0 — symmetric square matrix of order p, γ > 0 — some number. As an additional condition, the necessity of fulfilling the property of asymptotic stability of the closed system “object-controller” is considered. Note that it is important to find the smallest value of parameter γ* that provides the preservation of the required properties of the closed system. This is possible only if the conditions of minimizing the numerator and maximizing the denominator of the expression are simultaneously fulfilled (4).
We rewrite condition (4) in the form:
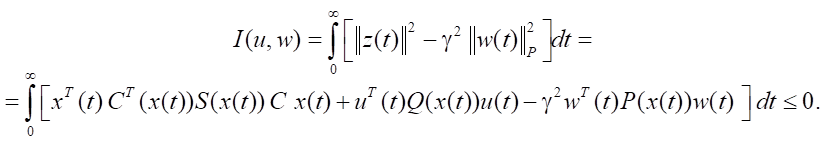 (5)
(5)
This means that it is required to provide that inequality (5) is satisfied while minimizing control costs under conditions of maximum counteraction of external influences (disturbances).
Sufficient conditions for the existence of Н∞ – controllers
Assume that function V(x) ∈ C¹(Rn) is known. Let us define the function:
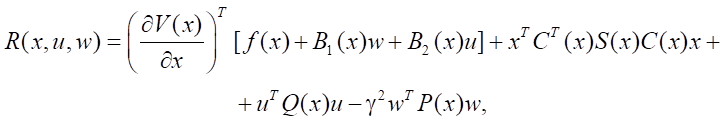 (6)
(6)
where
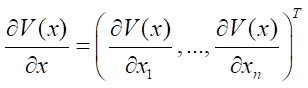 .
.
Theorem. If there exists function V(x) ∈ C¹(Rn), satisfying conditions V(0) = 0 and
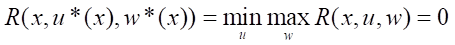
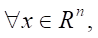 (7)
(7)
where
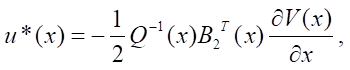
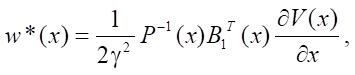 (8)
(8)
and function V(x) is determined by solving a partial differential equation:
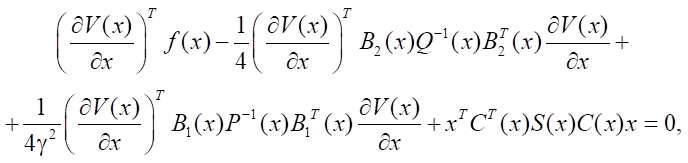 (9)
(9)
then condition (4) is satisfied.
Proof. Suppose that the conditions of the theorem are satisfied. We find
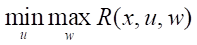 ,
,
applying the required conditions for an unconditional extremum, since no restrictions are imposed on the variables u, w:
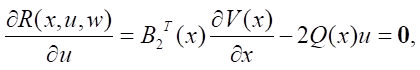
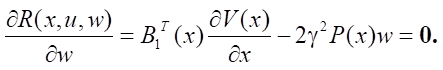
Solving the matrix equations, we obtain:
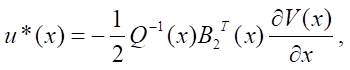
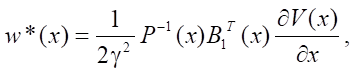
where u*(x), w*(x) — control structures of the object model and external influence (disturbance).
Since
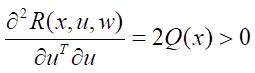
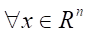
is true, then the sufficient conditions for the minimum in control are satisfied. Also true are the sufficient conditions that guarantee the achievement of the maximum external influence w,
since
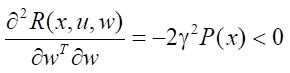
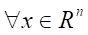 .
.
In this case
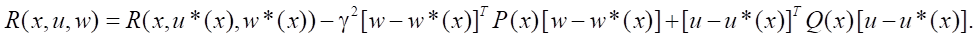
From this we get
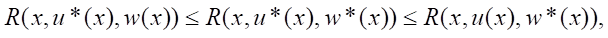 (10)
(10)
i.e., the conditions for the presence of a saddle point are satisfied.
Assume that function V(x) ∈ C¹(Rn) satisfies conditions V(0) = 0 and R(x, u*(x), w*(x)) = 0.
Then the relation that is fulfilled along the trajectories of system (1) is valid, namely:
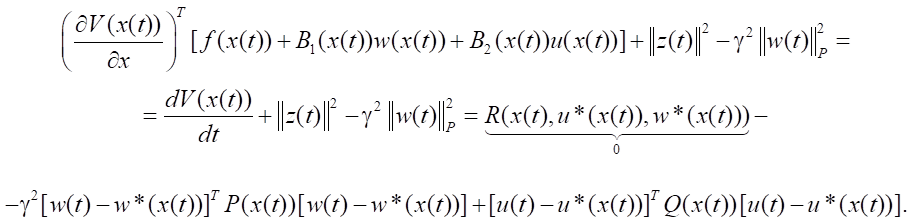
For u = u*(x), let us rewrite the left side of the inequality (10), i.e.,
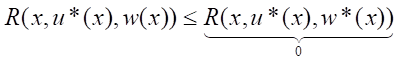 ,
,
in the form:
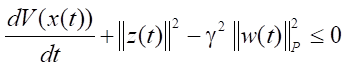 .
.
By integrating the left and right sides of the resulting inequality over the time interval from 0 to t1, we obtain:
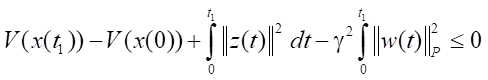 .
.
Since it is required to provide the fulfillment of the condition of asymptotic stability of the closed system, then x(t1) → 0 when t1 → +∞, therefore V(x(t1)) → V(0) = 0. Since x(0) = 0 then V(x(0)) → V(0) = 0. From this we can conclude that when t1 → +∞ the inequality is valid:
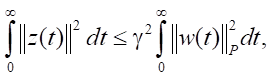
indicating that condition (4) is satisfied, which was to be proved.
As a remark, we emphasize that when conditions P(x) = E,
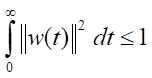 ,
,
i.e., the energy of external influences is limited, an inequality of the form
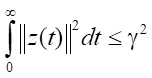 is valid.
is valid.
Approximate synthesis of Н∞ – state-based controllers using the SDRE method
Due to the nonlinearity of equation (9) and difficulties in obtaining its solution, a method based on the algebraic Riccati equation with coefficients dependent on the state vector is used for further analysis [15].
As a result of applying the factorization operation, we obtain a nonlinear system transformed to a structure similar to a linear one, with matrices dependent on the state vector.
It is known [16] that if f(0) = 0 and f(x) ∈ C¹(Rn), then there exists matrix function A(x), such that:
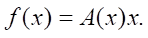 (11)
(11)
Notes
1. The factorization procedure for n= 1 in unique ∀x≠ 0, i.e., A(x) = f(x) / x = a(x).
2. For n> 1, the factorization procedure yields a non-unique result [16]. For example, for n= 2, there are at least two options: f(x) = A1(x)x and f(x) = A2(x)x, i.e., for a system of the form:
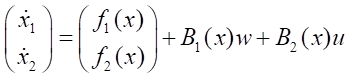
we obtain
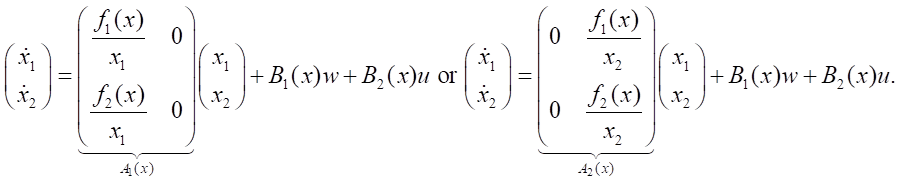
3. If there are two parametrization options, i.e., f(x) = A1(x)x= A2(x)x, then there is an infinite family of options of the form [16]: A(x, α) = αA1(x) + (1 – α)A2(x) ∀α. The selection of parameter α allows for flexibility in designing the control system. The solution to the Riccati equation and the corresponding control become functions of this parameter.
As a result of factorization, the mathematical model of system (1) takes the form:
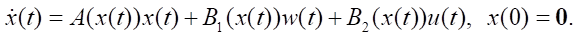 (12)
(12)
On the trajectories of system (12), functional (5) is specified.
It is assumed that system (12) is controllable and observable, i.e., ∀x ∈ Rn the conditions are fulfilled point-to-point [16]:
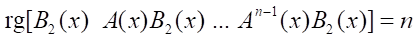 ,
,
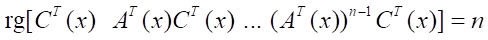 .
.
Equation (9) takes the form:
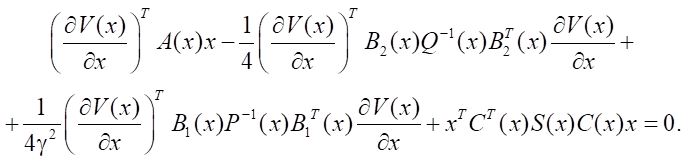 (13)
(13)
Assume that
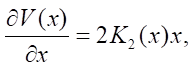 (14)
(14)
where K2(x) > 0 unknown matrix function (for fixed x ∈ Rn, matrix K2(x) is a symmetric positive definite numerical matrix). Thus, an assumption is made not about the type of function V(x), but only about the structure of its partial derivative.
Then, the control structures of the object and disturbance take the form:
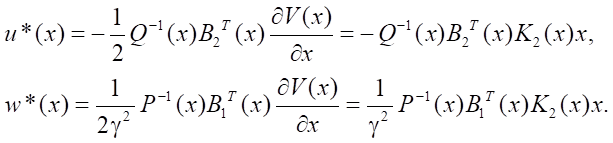 (15)
(15)
Equation (13) takes the form:
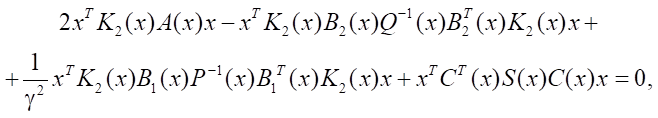
or
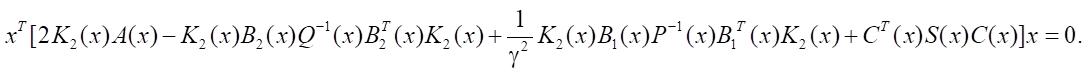
Applying the transpose operation, we obtain:
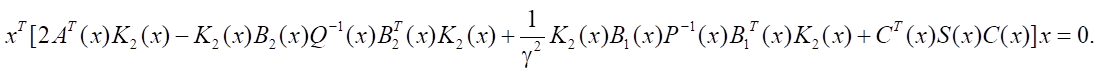
Summing up the last two expressions, we arrive at the equality:
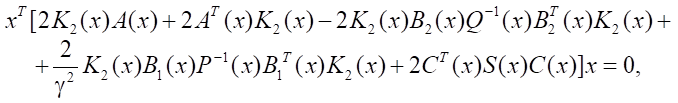
or finally:
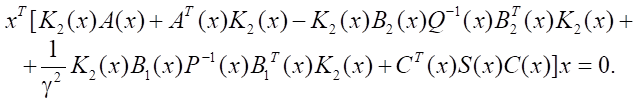 (16)
(16)
Note that due to the dependence of all matrices on the state vector, the equality of the zero matrix in square brackets does not follow from (16).
By analogy with the case of a linear stationary system, it is proposed to solve the algebraic Riccati equation, all matrices in which are functions of the system's state vector (State Dependent Riccati Equation, SDRE). In this case, a positive definite solution to the Riccati equation is sought, generating a control law that guarantees that the system will be asymptotically stable in the vicinity of the equilibrium position. To check this property, the stability criterion by the roots of the characteristic equation, checked point-to-point, or the Routh–Hurwitz criterion, is used.
In the problem under consideration, it is proposed to solve the equation:
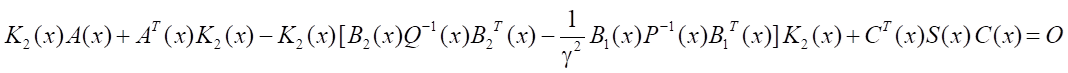 , (17)
, (17)
i.e., to look for matrix K2(x) > 0, that satisfies the Riccati equation, whose coefficients depend on x. Equation (17) is solved repeatedly for fixed x ∈ Rn. The coordinates of the state vector are determined in the process of integrating the differential equation (12) together with the controls of the object and the disturbances:
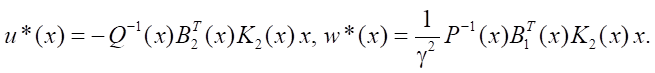 (18)
(18)
In this case, the solution to the Riccati equation must be such that the criterion
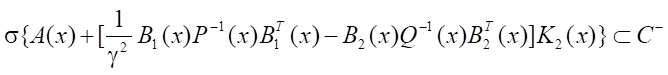
∀x ∈ Rn, is satisfied, where σ– matrix spectrum, C– — open left half-plane of the complex plane. Note that the stability criterion of a closed system can be replaced by checking the point-to-point fulfillment of the Routh-Hurwitz criterion.
Algorithm for approximate synthesis of Н∞ – controllers of state
Step 1. Set parameter γ > 0.
Step 2. Find the solution to the equation:
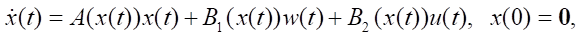
with controls
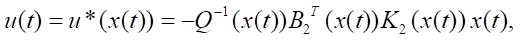
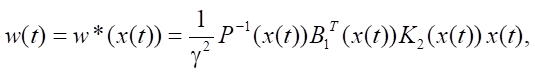
one of the numerical methods of integration with constant step h (explicit Euler method, Euler-Cauchy method, Adams-Bashforth, Milne, Hamming methods of various orders).
In this case, for each of the discrete moments of time ti = ih, i = 0, 1, 2, …, solve the Riccati equation:
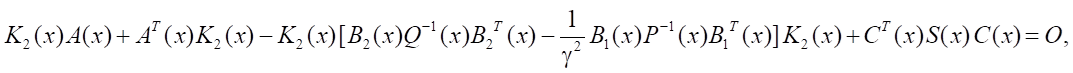
for x = x(ti ). As a result, find matrix K2(x) and use it to form control laws.
Step 3. Find the minimum γ*. To do this, it is required to consistently decrease γ until the stability property of solutions of the differential equation
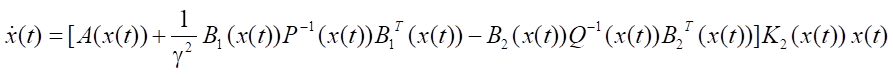 ,
,
describing the dynamics of the system with the obtained controls, remains valid.
Research Results. To test the efficiency of the proposed approximate algorithm for synthesizing Н∞ – state-based controllers, two model examples were solved.
Model example No. 1. A one-dimensional case is considered, when equations (1), (2) and functional (5) have the form:
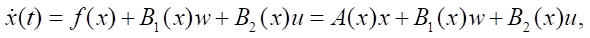
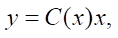
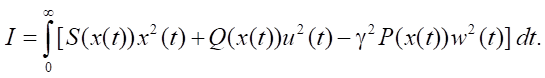
Solution. The control structures follow from (18):
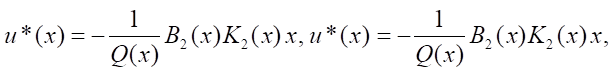
and equation (17) has the form:
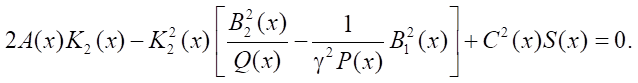
Let us write the resulting quadratic equation in canonical form:
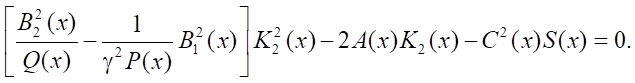
The solution is as follows:
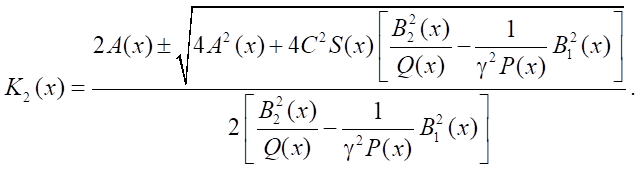
Since K2 > 0, then
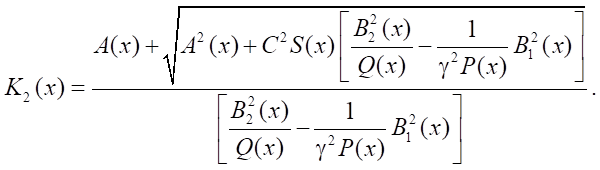
Let us take a closer look at a particular case:
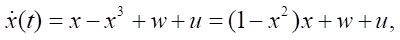
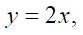
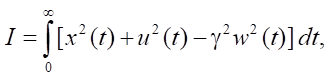
where A(x) = (1 – x²), B1(x) = 1, B2(x) = 1, C(x) = 2, Q(x) = 1, S(x) = 1, P(x) = 1.
Then (omitting the dependence on х) we get:
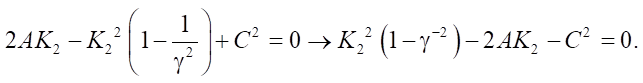
Roots of the quadratic equation:
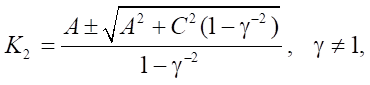
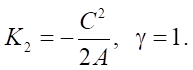
Note that when considering the case γ ≠ 1, it is not yet possible to exclude the extra roots, since A(x) and (1 – γ⁻²) can change the sign.
As a result, we obtain the control structures:
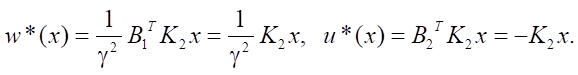
In this case, the equation of the closed system has the form:
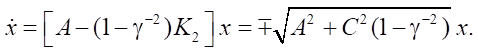
To provide asymptotic stability, we take the minus sign, and in the expression for K2 − plus. For this example, we get:
- if γ≠1, then
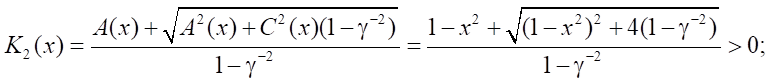
- if functions A(x), C(x) are not equal to zero simultaneously, then discriminant A²(x) + C² (x)( 1– γ⁻²).
Then,
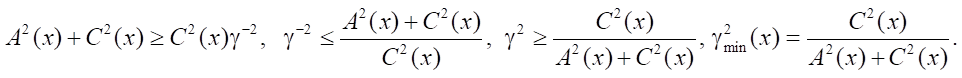
For the example being solved
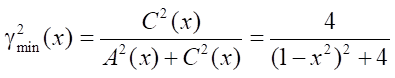 ,
,
i.e., for each current x, there is its own value 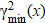 .
.
For γ = γmin, x = 0, x(0) = 0 is satisfied (the condition of asymptotic stability is not satisfied, but x(t) ≡ 0 is valid).
For γ = γmin we have
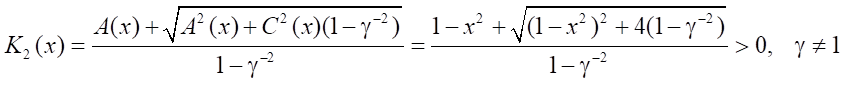 .
.
If γ = 1, then
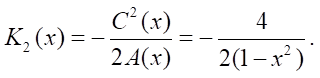
To fulfill condition K2 > 0, condition A(x) = 1 – x² < 0 that defines set |x| < 1 of possible functioning of the system must be fulfilled.
Modeling. For modeling under different initial conditions, finite time interval T = [0, 20] was selected, since all transient processes in a closed system are practically completed.
According to Figures 1–3, the value of the state vector asymptotically tends to zero for different initial conditions, which indicates the stability of the system and the correct selection of parameters, under which the system retains the property of stability subject to any given limited disturbances.
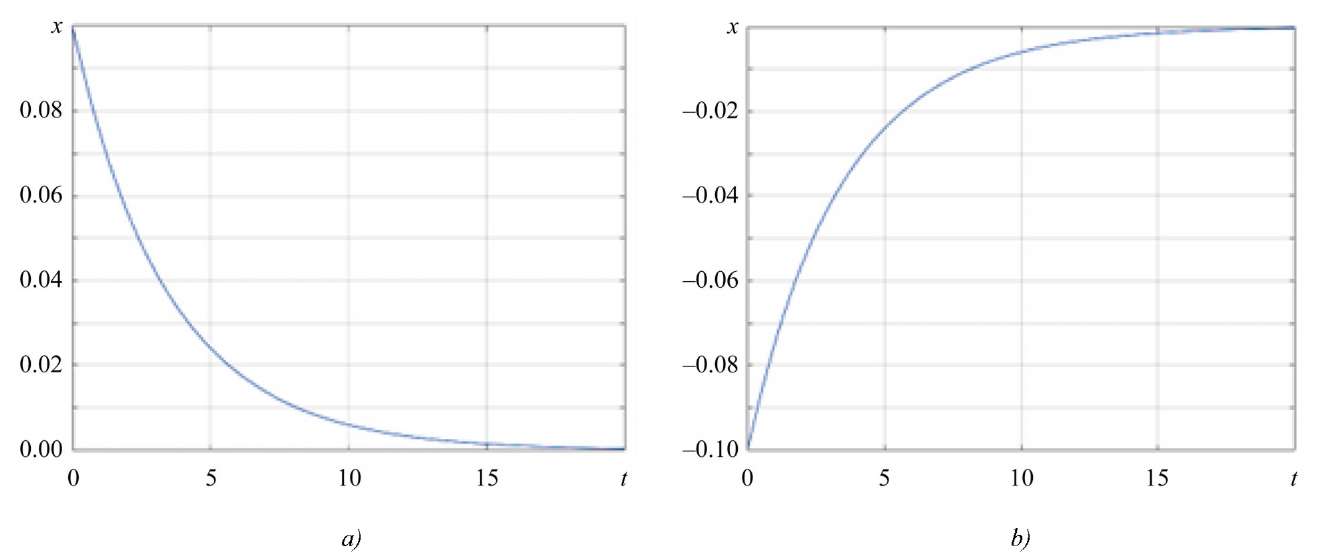
Fig. 1. Change of the state vector:
a — for initial state x0 = 0.1; b — for initial state x0 = –0.1
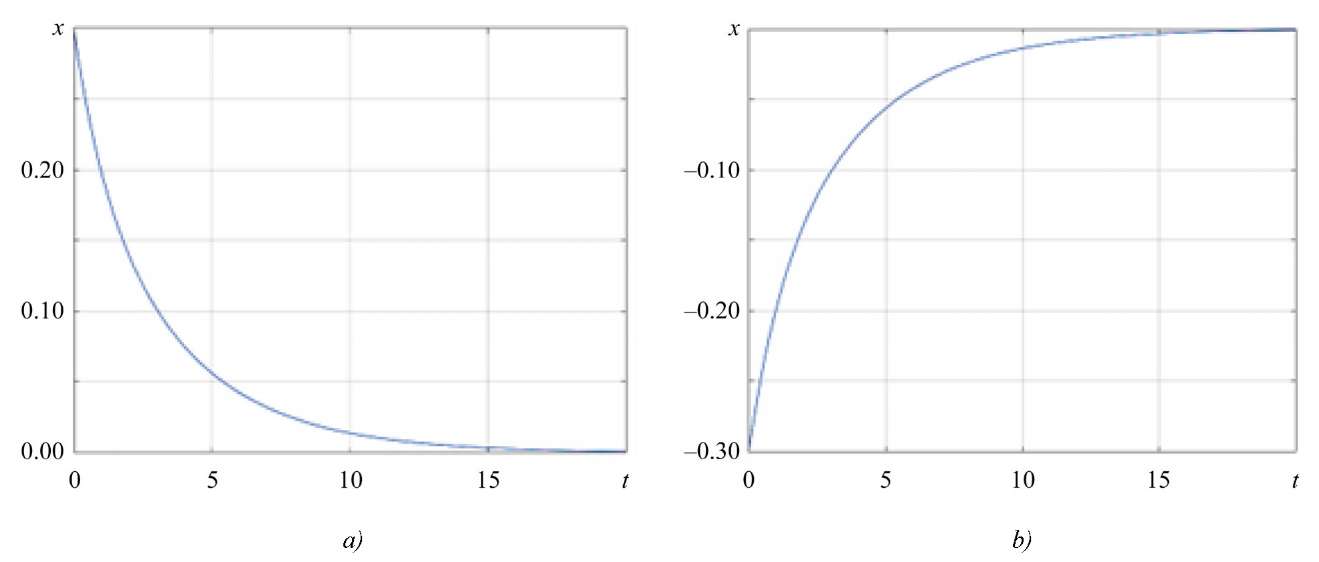
Fig. 2. Change of the state vector:
a — for initial state x0 = 0.3; b — for initial state x0 = –0.3
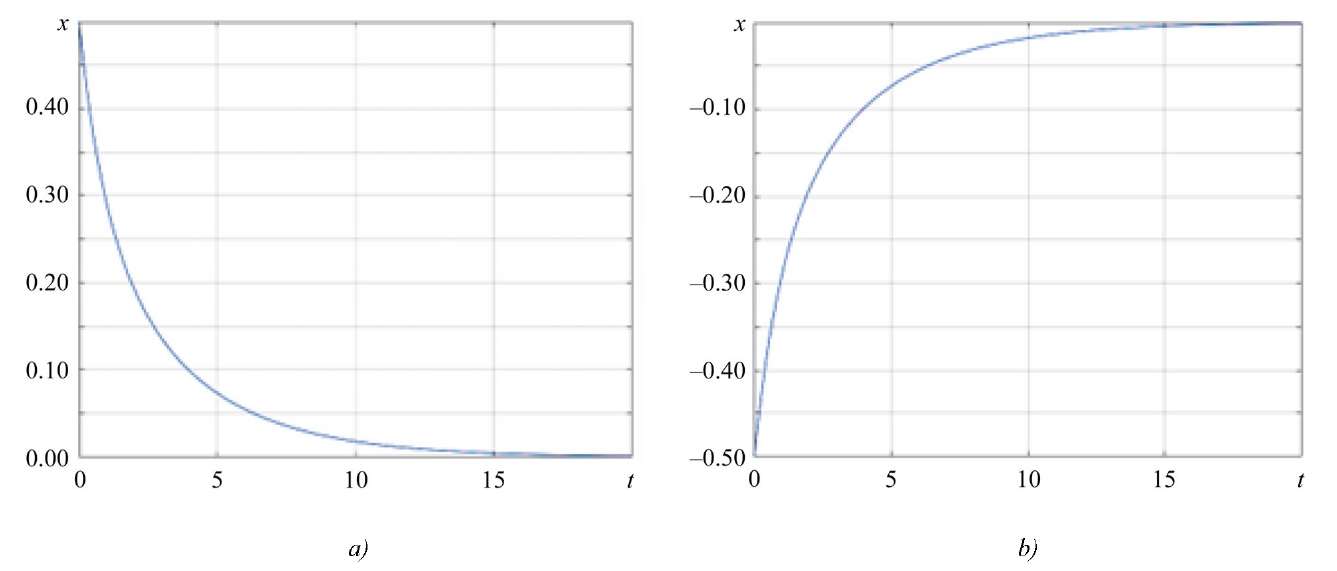
Fig. 3. Change of the state vector:
a — for initial state x0 = 0.5; b — for initial state x0 = –0.5
Model example No. 2. One of the options of the two-dimensional case is considered, when equations (1), (2) and functional (5) have the form:
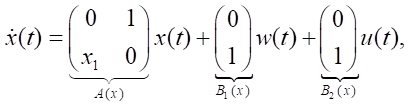
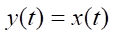 ,
,

i.e., C(x) = E2, S(x) = E2, Q(x) = 1, P(x) = 1.
Solution. The control structures of the object and the disturbance follow from (18):
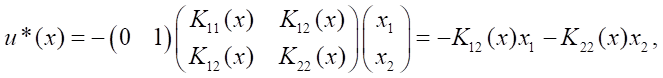
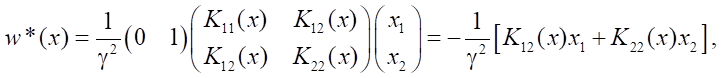
and equation (17) has the form:
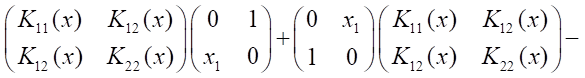
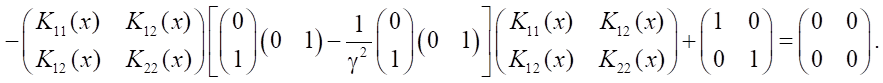
From here,
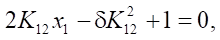
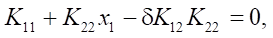
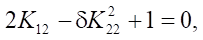
where
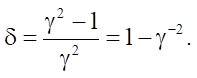
Solution to the first equation 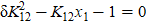 has the form:
has the form:
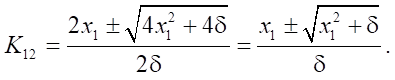
Solution to the third equation:
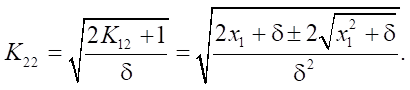
Solution to the second equation:
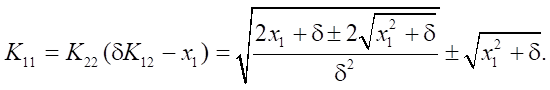
In the obtained solutions, positive signs were selected taking into account condition K2 > 0.
Modeling. To model the system, it is required to select the minimum possible value γ, so that it satisfies (4) and at the same time guarantees the asymptotic stability of the closed system. In example 1, the value of parameter γ was found analytically, but a problem arose with determining the value of the optimal parameter γ*, therefore value γ, used in the modeling, was selected experimentally. When γ* = 1.5, the system remained stable according to expression (19). For modeling, the time interval T = [0, 10] was selected, since transient processes in the closed system decayed fairly quickly. Modeling was performed for various initial conditions.
According to Figures 4–5, it can be concluded that the coordinates of the state vector asymptotically tend to zero. This result is observed for each of the initial conditions considered. This indicates that the system is stable, and its parameters are selected correctly, which allows maintaining the property of stability under any initial conditions and under the worst disturbances.
The initial conditions significantly affect the trajectories of the change in the coordinates of the state vector, but from Figures 4–5, it is clear that the proposed approach allows us not only to compensate for external disturbances, but also to stabilize the trajectory of motion.
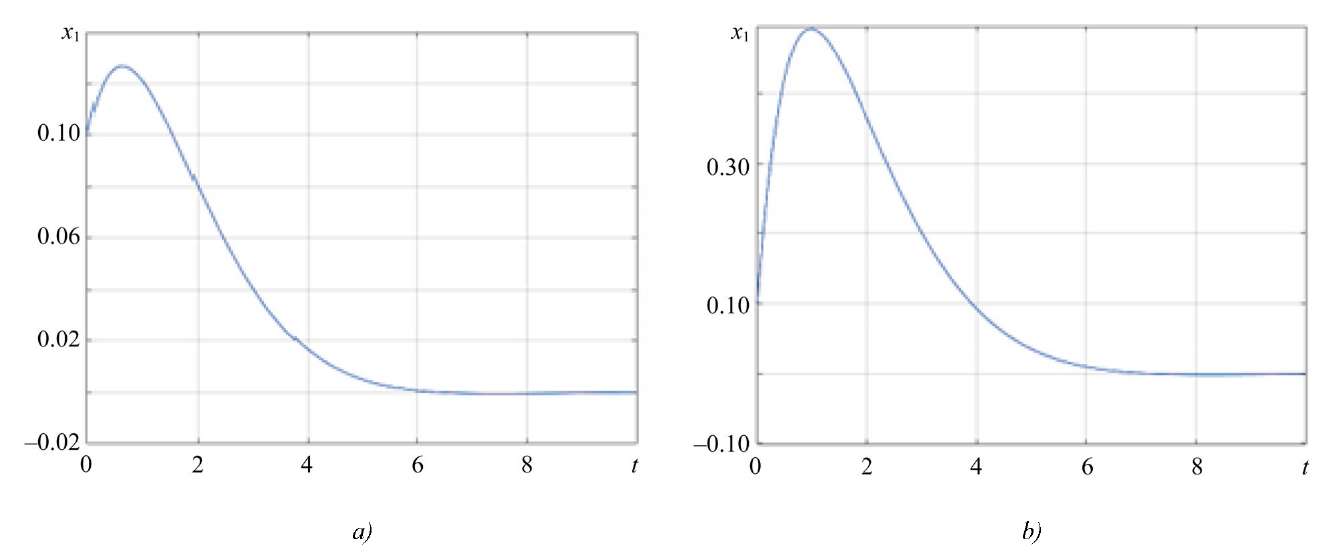
Fig. 4. Change of x1(t):
a — for initial state x0 = (0,1; 0,1)T; b — for initial state x0 = (0,1; 1)T
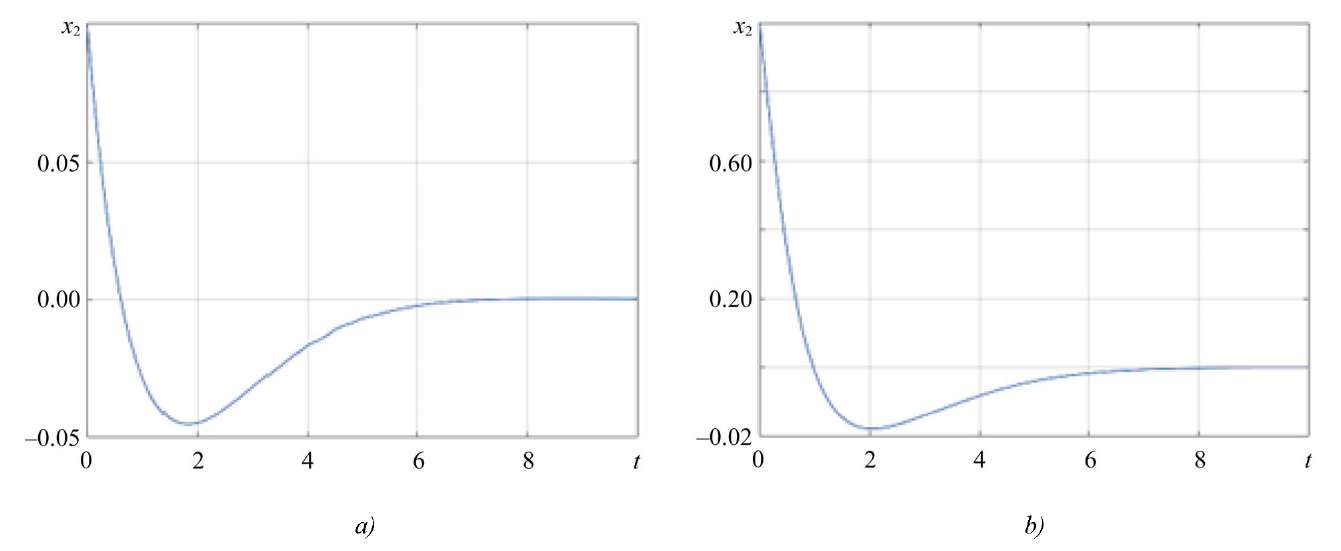
Fig. 5. Change of x2(t):
a — for initial state x0 = (1; 0,1)T; b — for initial state x0 = (1; 1)T
Discussion of the Results. As a result of the study, sufficient Н∞ – control conditions were formulated and substantiated, an approximate solution method was developed. The method proposed within the framework of the problem was tested on two model examples. The simulation results allow us to conclude that the use of the developed controller synthesis method guarantees the required quality of transient processes and provides asymptotic stability of closed systems.
Conclusion. The results and methods proposed in this paper can be applied to solve control problems of varying complexity — from designing simple autopilots to developing complex automatic navigation systems for manned and unmanned aerial vehicles. This emphasizes the prospects of using the proposed approach and makes it an attractive option for further research.
References
1. Kurdyukov AP, Andrianova OG, Belov AA, Gol'din DA. In between the LQG/H2- and H∞-Control Theories. Automation and Remote Control. 2021(4):8–76. https://doi.org/10.31857/S0005231021040024
2. Wanigasekara C, Liruo Zhang, Swain A. H∞ State-Feedback Consensus of Linear Multi-Agent Systems. In: Proc. 17th International Conference on Control & Automation. Piscataway, NJ: IEEE Xplore; 2022. P. 710–715. https://doi.org/10.1109/ICCA54724.2022.9831897
3. Banavar RN, Speyer JL. A Linear-Quadratic Game Approach to Estimation and Smoothing. In: Proc. the American Control Conference. New York City: IEEE; 1991. P. 2818–2822. https://doi.org/10.23919/ACC.1991.4791915
4. Chodnicki M, Pietruszewski P, Wesołowski M, Stępień S. Finite-Time SDRE Control of F16 Aircraft Dynamics. Archives of Control Sciences. 2022;32(3):557–576. https://doi.org/10.24425/acs.2022.142848
5. Panteleev A, Yakovleva A. Approximate Methods of H-infinity Control of Nonlinear Dynamic Systems Output. MATEC Web of Conferences. XXII International Conference on Computational Mechanics and Modern Applied Software Systems (CMMASS 2021). 2022;362:012021. https://doi.org/10.1051/matecconf/202236201021
6. Hamza A, Mohamed AH, Badawy A. Robust H-infinity Control for a Quadrotor UAV. AIAA SCITECH 2022 Forum. Reston, VA: AIAA; 2022. https://doi.org/10.2514/6.2022-2033
7. Fei Han, Qianqian He, Yanhua Song, Jinbo Song. Outlier-Resistant Observer-Based Н∞ – Consensus Control for Multi-Rate Multi-Agent Systems. Journal of the Franklin Institute. 2021;358(17):8914–8928. https://doi.org/10.1016/j.jfranklin.2021.08.048
8. Junfeng Long, Wenye Yu, Quanyi Li, Zirui Wang, Dahua Lin, Jiangmiao Pang. Learning H-Infinity Locomotion Control. A rXiv preprint arXiv. 2024;2404:14405. https://doi.org/10.48550/arXiv.2404.14405
9. Fayin Chen, Wei Xue, Yong Tang, Tao Wang. A Comparative Research of Control System Design Based on H-Infinity and ALQR for the Liquid Rocket Engine of Variable Thrust. International Journal of Aerospace Engineering. 2023;(2):1–12. https://doi.org/10.1155/2023/2155528
10. Yazdkhasti S, Sabzevari D, Sasiadek JZ. Adaptive H-infinity Extended Kalman Filtering for a Navigation System in Presence of High Uncertainties. Transactions of the Institute of Measurement and Control. 2022;45(8):1430–1442. https://doi.org/10.1177/01423312221136022
11. Balandin DV, Biryukov RS, Kogan MM. Multicriteria Optimization of Induced Norms of Linear Operators: Primal and Dual Control and Filtering Problems. Journal of Computer and Systems Sciences International. 2022;61(2):176–190. http://doi.org/10.1134/S1064230722020046
12. Aalipour A, Khani A. Data-Driven H-infinity Control with a Real-Time and Efficient Reinforcement Learning Algorithm: An Application to Autonomous Mobility-on-Demand Systems. arXiv:2309.08880. https://doi.org/10.48550/ARXIV.2309.08880
13. Panteleev AV, Yakovleva AA. Sufficient Conditions for H-infinity Control on the Finite Time Interval. Journal of Physics: Conference Series. 2021;1925:012024. https://doi.org/10.1088/1742-6596/1925/1/012024
14. Panteleev AV, Yakovleva AA. Sufficient Conditions for the Existence of Н∝-infinity State Observer for Linear Continuous Dynamical Systems. Modelling and Data Analysis. 2023;13(2):36–63. https://doi.org/10.17759/mda.2023130202
15. Çimen T. State-Dependent Riccati Equation (SDRE) Control: A Survey. IFAC Proceedings Volumes. 2008;41(2):3761–3775. https://doi.org/10.3182/20080706-5-KR-1001.00635
16. Cloutier JR, D’Souza CN, Mracek CP. Nonlinear Regulation and Nonlinear H∞ Control via the StateDependent Riccati Equation Technique: Part 1, Theory. In: Proc. International Conference on Nonlinear Problems in Aviation and Aerospace. Daytona Beach, FL: Embry-Riddle Aeronautical University Press; 1996. P. 117–131. URL: https://clck.ru/3M4kki (accessed: 04.02.2025).
About the Authors
A. V. PanteleevRussian Federation
Andrei V. Panteleev, Dr.Sci. (Phys.-Math.), Full Professor, Head of the Department of Mathematical Cybernetics, Institute of Information Technology and Applied Mathematics
4, Volokolamskoe Shosse, Moscow, 125993
A. A. Yakovleva
Russian Federation
Aleksandra A. Yakovleva, Postgraduate Student of the Department of Mathematical Cybernetics, Institute of Information Technology and Applied Mathematics
4, Volokolamskoe Shosse, Moscow, 125993
New sufficient conditions for the existence of Н∞ – control for continuous nonlinear systems that are linear in control and disturbance are determined. The proposed method is based on the minimax approach and the extension principle. An algorithm is developed that simplifies the procedure for synthesizing Н∞ – controllers based on an approximate replacement of a nonlinear system with a simpler system similar in structure to a linear one. The results of the study open up new possibilities for solving various control problems, e.g., problems of stabilizing aircraft of different classes in the presence of external actions.
Review
For citations:
Panteleev A.V., Yakovleva A.A. Approximate Synthesis of Н∞ – Controllers in Nonlinear Dynamic Systems over a Semi-Infinite Time Period. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):152-164. https://doi.org/10.23947/2687-1653-2025-25-2-152-164. EDN: IHQRUT













































