Перейти к:
Приближенный синтез Н∞ – регуляторов в нелинейных динамических системах на полубесконечном промежутке времени
https://doi.org/10.23947/2687-1653-2025-25-2-152-164
EDN: IHQRUT
Аннотация
Введение. Задачи и методы нахождения Н∞ – управления являются основой современной теории управления и активно используются для разработки робастных регуляторов, особенно в системах управления летательными аппаратами под ограниченными внешними воздействиями. Эти методы позволяют адаптировать системы управления к изменяющимся условиям окружающей среды, что критически важно для обеспечения надежности и безопасности работы летательных аппаратов. Текущие исследования направлены на усовершенствование подходов к синтезу регуляторов, охватывающих как линейные, так и нелинейные динамические системы. В этом контексте особое внимание уделяется интеграции новых математических методов, таких как линейные матричные неравенства и частотный анализ, что позволяет оптимизировать отклик системы на различные внешние воздействия и гарантировать защиту от непредвиденных условий. Важно отметить, что, несмотря на достигнутые успехи в данной области, остаются нерешенными значительные проблемы, касающиеся анализа и синтеза регуляторов для нелинейных систем. Это создает необходимость в дальнейших исследованиях и разработках в этой перспективной области. В данной работе с целью заполнения существующего пробела сформулированы и доказаны достаточные условия существования управления для одного из часто встречающихся классов нелинейных систем, которые затем будут использоваться в качестве теоретического обоснования для разработки приближенных алгоритмов его нахождения.
Материалы и методы. В качестве основного инструмента исследования используются методы синтеза Н∞ – управления, основанные на минимаксном подходе, заключающемся в нахождении закона управления в условиях наихудшего внешнего воздействия. В этом контексте предлагается доказать достаточные условия существования управления, используя принцип расширения. Однако из-за вычислительных трудностей, которые могут возникнуть при применении этих условий, было решено упростить исходную постановку задачи. Процесс упрощения осуществлялся путем приближенной замены нелинейной системы на другую нелинейную систему, которая по своей структуре схожа с линейной, с помощью процедуры факторизации. Такой подход позволяет применять решение уравнения Риккати, коэффициенты которого зависят от вектора состояния, для синтеза регуляторов. Для решения модельных примеров и прикладных задач был разработан программный комплекс с использованием математического пакета MATLAB.
Результаты исследования. В статье решена проблема синтеза Н∞ – управления состоянием нелинейных непрерывных динамических систем, линейных по управлению и возмущению; сформулированы и на основе принципа расширения доказаны достаточные условия существования Н∞ – управления. Предложен приближенный метод, позволяющий решать задачу нахождения законов управления для динамических систем, нелинейных по состоянию, аналогичный методам, применяемым для линейных систем. Найдены аналитические решения двух модельных примеров, которые проиллюстрированы графиками переходных процессов для демонстрации результатов численного моделирования рассмотренных нелинейных динамических систем в присутствии внешних воздействий.
Обсуждение и заключение. Предложенный приближенный алгоритм синтеза регуляторов по состоянию и выходу гарантирует необходимое качество переходных процессов и асимптотическую устойчивость замкнутых нелинейных систем управления. Это значительно расширяет класс динамических систем, для которых возможно синтезирование регуляторов, способных противостоять различным внешним воздействиям. Методы, изложенные в данной работе, могут быть эффективно применены для решения множества задач управления, включая проектирование автопилотов и автоматических навигационных систем для летательных аппаратов, даже в условиях ограниченного воздействия извне.
Ключевые слова
Для цитирования:
Пантелеев А.В., Яковлева А.А. Приближенный синтез Н∞ – регуляторов в нелинейных динамических системах на полубесконечном промежутке времени. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):152-164. https://doi.org/10.23947/2687-1653-2025-25-2-152-164. EDN: IHQRUT
For citation:
Panteleev A.V., Yakovleva A.A. Approximate Synthesis of Н∞ – Controllers in Nonlinear Dynamic Systems over a Semi-Infinite Time Period. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):152-164. https://doi.org/10.23947/2687-1653-2025-25-2-152-164. EDN: IHQRUT
Введение. Методы современной теории управления играют важную роль в разработке сложных авиационно-космических систем, обеспечивая их эффективное функционирование. Для достижения высокой производительности, устойчивости и эффективности таких систем необходимо разработать алгоритмы синтеза регуляторов, способных работать в условиях неопределенности описания внешних воздействий. Современной основой для их разработки являются метод пространства состояний, частотный анализ и подход на основе линейных матричных неравенств [1]. Для решения задач нахождения оптимального управления обычно применяются достаточные условия оптимальности в форме уравнения Беллмана и вытекающие из него соотношения в частных случаях. Для поиска Н∞ – регуляторов могут быть использованы линейные матричные неравенства. Они применяются для определения существования регулятора, который удовлетворяет определенным критериям производительности и обеспечивает устойчивость системы к внешним воздействиям. Эти критерии обычно связаны с Н∞ – нормой, которая является мерой чувствительности системы к внешним возмущениям. Суть проблемы заключается в нахождении такого регулятора, который минимизирует эту норму, обеспечивая при этом устойчивость системы и удовлетворение критерию качества управления. Метод решения основывается на нахождении экстремума выпуклой целевой функции, где условия представлены в виде линейных матричных неравенств [2]. Благодаря использованию данного метода имеется возможность свести решение сложных систем линейных и нелинейных алгебраических матричных уравнений определенного вида к решению задач выпуклой оптимизации. Однако решение линейных матричных неравенств может быть затруднительно при рассмотрении сложных технических задач.
Альтернативный метод, основанный на стохастическом минимаксе, представлен в анизотропийной теории стохастического робастного управления, описанной в [3]. Основная идея при использовании данного метода заключается в том, что робастность при стохастическом управлении достигается с помощью явного включения различных сценариев распределения шума в единый показатель качества, подлежащий оптимизации. Статистическая неопределенность выражается через энтропию, а показатель робастного качества выбирается таким образом, чтобы дать возможность количественно оценить способность системы подавлять наихудшее внешнее воздействие. Применение такого подхода для решения сложных систем взаимосвязанных уравнений требует разработки и использования специализированных алгоритмов.
Следует отметить, что методы Н∞ – оптимизации находят применение при решении множества различных прикладных задач, например, управления самолетом [4], вертолетом [5], квадрокоптером [6] и мультиагентными системами [7], стабилизации роботов [8], проектирования ракетных двигателей [9], где при сравнении с другими регуляторами данные методы показывают хорошие результаты и меньшее значение ошибок при наличии ограниченных возмущений. Также стоит упоминания их использование в задачах фильтрации [10], оценивания вектора состояния [11] и проектирования нейронных сетей [12]. Таким образом, разработка и развитие Н∞ – методов оптимизации является актуальной темой для исследований. Ранее авторами рассматривалась задачи синтеза Н∞ – регулятора [13] и Н∞ – наблюдателя [14] для линейных динамических систем, для решения которых использовались достаточные условия оптимальности на основе принципа расширения. Их применение позволило обосновать процедуры синтеза и, как следствие, сформировать пошаговые алгоритмы решения задач.
Несмотря на значительные достижения в данной области, ряд проблем, связанных с анализом и синтезом регуляторов для нелинейных систем, остаются нерешенными. В связи с этим, в настоящей работе рассматривается задача синтеза регуляторов для нелинейных динамических систем, линейных по управлению и возмущению, на полубесконечном промежутке времени. Целью исследования является формулировка и доказательство достаточных условий существования управления, что позволит не только создать основу для новых исследований и разработок, но и восполнить существующие пробелы в области знаний. В частности, в работе предусмотрено использование достаточных условий в качестве теоретического обоснования для формулировки приближенных алгоритмов поиска управления для рассматриваемого класса динамических систем. Для проверки эффективности предложенного алгоритма будет решено два модельных примера.
Материалы и методы. Пусть имеется математическая модель объекта управления
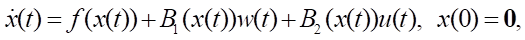 (1)
(1)
и модель измерительной системы
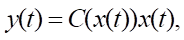 (2)
(2)
где x ∈ Rn — вектор состояния, u ∈ Rq — вектор управления, w ∈ Rp — вектор внешних воздействий, y ∈ Rm — вектор выхода, t ∈ T = [0, ∞) — текущее время, 0 — нулевая матрица-столбец размеров (n × 1). Будем считать заданными непрерывно-дифференцируемую векторную функцию f(x) размеров (n × 1), а также матричные функции B1(x) размеров (n × p), B2(x) размеров (n × q), C(x) размеров (m × n). Модель объекта описывается уравнением, нелинейным по состоянию, но линейным относительно управления и внешних воздействий.
Подразумевается, что:
- w(.) ∈ L2[0,∞), u(.) ∈ L2[0,∞);
- m≤n, rg С(x) = m;
- начало координат x≡0 есть точка равновесия, т.е. f(0) = 0;
- B1(x) ≠O, B2(x) ≠O;
где O — нулевая матрица соответствующих размеров.
Определен показатель, описывающий текущее поведение модели объекта управления (1) с измерительной системой (2):
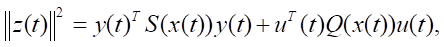 (3)
(3)
где для всех x ∈ Rn Q(x) > 0 — симметрическая положительно определенная квадратная матрица порядка q, а S(x) > 0 — симметрическая неотрицательно-определенная квадратная матрица порядка m. Функционал (3) является квадратичным по управлению, но неквадратичным по состоянию.
Заметим, что рассматриваются модели объекта и измерительной системы, матрицы в которых зависят от вектора состояния.
Требуется обеспечить справедливость условия:
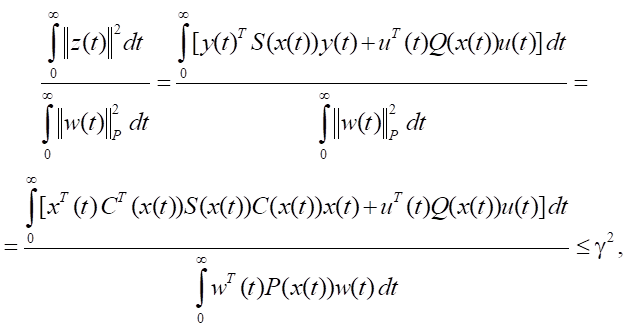 (4)
(4)
где ∀ x ∈ Rn P(x) > 0 — симметрическая квадратная матрица порядка p, γ > 0 — некоторое число. В качестве дополнительного условия рассматривается необходимость выполнения свойства асимптотической устойчивости замкнутой системы «объект-регулятор». Заметим, что важно найти наименьшую величину параметра γ*, обеспечивающего сохранение требуемых свойств замкнутой системы. Это возможно лишь при одновременном выполнении условий минимизации числителя и максимизации знаменателя выражения (4).
Условие (4) перепишем в форме
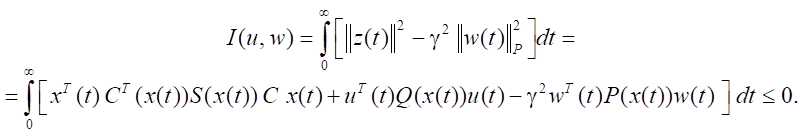 (5)
(5)
Это означает, что требуется обеспечить выполнение неравенства (5) при минимизации затрат на управление в условиях максимального противодействия внешних воздействий (возмущений).
Достаточные условия существования Н∞ – регуляторов
Предположим, что известна функция V(x) ∈ C¹(Rn). Определим функцию
 (6)
(6)
где
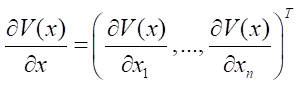 .
.
Теорема. Если существует функция V(x) ∈ C¹(Rn), удовлетворяющая условиям V(0) = 0 и
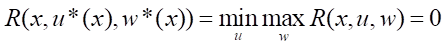
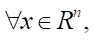 (7)
(7)
где
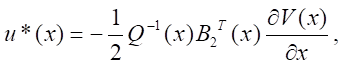
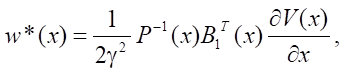 (8)
(8)
а функция V(x) определяется решением уравнения с частными производными:
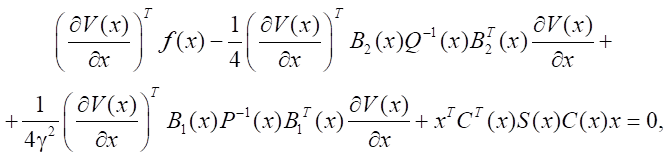 (9)
(9)
то условие (4) удовлетворяется.
Доказательство. Предположим, что условия теоремы выполняются. Найдем
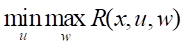 ,
,
применяя необходимые условия безусловного экстремума, поскольку ограничений на переменные u, w не наложено:
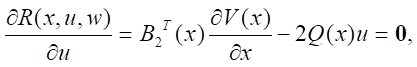
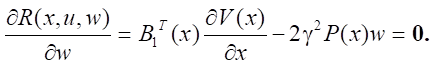
Решая матричные уравнения, получаем:

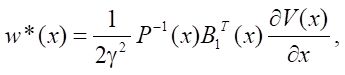
где u*(x), w*(x) — структуры управления моделью объекта и внешним воздействием (возмущением).
Так как справедливо
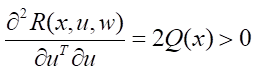
 ,
,
то достаточные условия минимума по управлению выполняются. Также справедливы достаточные условия, гарантирующие достижение максимума по внешнему воздействию w, поскольку
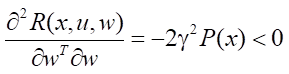
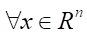 .
.
В таком случае:
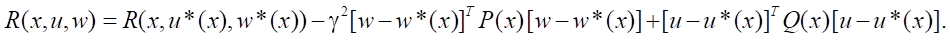
Отсюда получим:
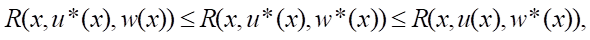 (10)
(10)
т.е. выполняются условия наличия седловой точки.
Предположим, что функция V(x) ∈ C¹(Rn) удовлетворяет условиям V(0) = 0 и R(x, u*(x), w*(x)) = 0.
Тогда справедливо соотношение, выполняющееся вдоль траекторий системы (1), а именно:
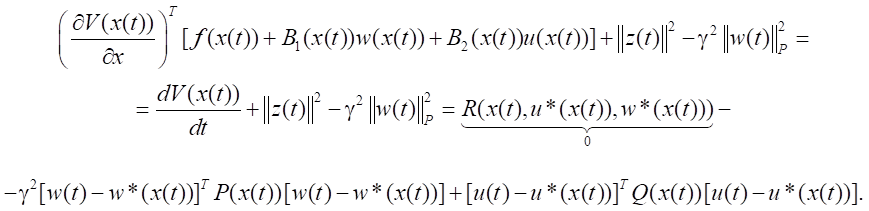
При u = u*(x) перепишем левую часть неравенства (10), т.е.
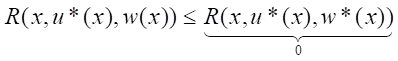 ,
,
в виде:
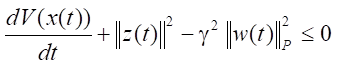 .
.
Проинтегрировав левую и правую части полученного неравенства на промежутке времени от 0 до t1, получим:
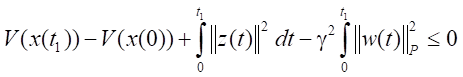 .
.
Так как требуется обеспечить выполнение условия асимптотической устойчивости замкнутой системы, то x(t1) → 0 при t1 → +∞, поэтому V(x(t1)) → V(0) = 0. Поскольку x(0) = 0 то V(x(0)) → V(0) = 0. Отсюда можно сделать вывод о том, что при t1 → +∞ справедливо неравенство:
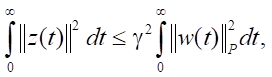
свидетельствующее о выполнении условия (4), что и требовалось доказать.
В качестве замечания подчеркнем, что при выполнении условий P(x) = E,
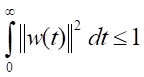 ,
,
т.е. ограниченности энергии внешних воздействий, справедливо неравенство вида
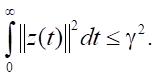
Приближенный синтез Н∞ – регуляторов по состоянию методом SDRE
Вследствие нелинейности уравнения (9) и трудностей в получении его решения, для дальнейшего анализа применяется метод, основанный на алгебраическом уравнении Риккати с коэффициентами, зависящими от вектора состояния [15].
В результате применения операции факторизации получим нелинейную систему, преобразованную к структуре, похожей на линейную, с матрицами, зависящими от вектора состояния.
Известно [16], что если f(0) = 0 и f(x) ∈ C¹(Rn), то существует матричная функция A(x), такая что:
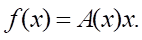 (11)
(11)
Замечания
1. Процедура факторизации для n=1 единственная ∀x ≠ 0, т.е. A(x) = f(x) / x = a(x).
2. При n>1 процедура факторизации дает неединственный результат [16]. Например, при n = 2 имеются, по крайней мере, два варианта: f(x) = A1(x)x и f(x) = A2(x)x, т.е. для системы вида:
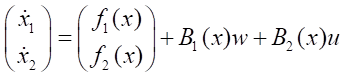 .
.
Получаем:
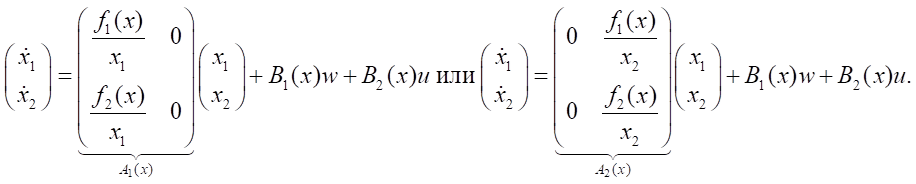
3. Если имеются два варианта параметризации, т.е. f(x)=A1(x)x = A2(x)x, то имеется бесконечное семейство вариантов вида [16]: A(x, α) = αA1(x) + (1 – α)A2(x) ∀α. Выбор параметра α позволяет обеспечить гибкость при проектировании системы управления. Решение уравнения Риккати и соответствующее управление становятся функциями этого параметра.
В результате факторизации математическая модель системы (1) принимает вид:
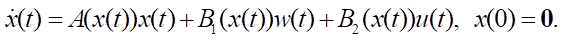 (12)
(12)
На траекториях системы (12) задан функционал (5).
Предполагается, что система (12) является управляемой и наблюдаемой, т.е. ∀x ∈ Rn поточечно выполняются условия [16]:
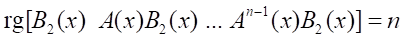 ,
,
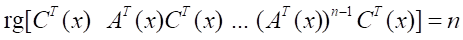 .
.
Уравнение (9) принимает вид:
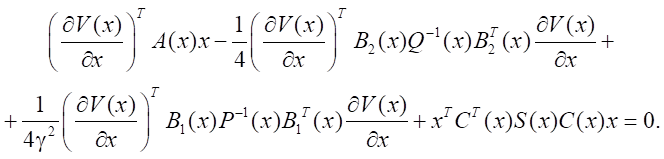 (13)
(13)
Предположим, что:
 (14)
(14)
где K2(x) > 0 — неизвестная матричная функция (при фиксированном x ∈ Rn матрица K2(x) является симметрической положительно определенной числовой матрицей). Таким образом, делается предположение не о виде функции V(x), а только о структуре ее частной производной.
Тогда структуры управления объектом и возмущением принимают вид:
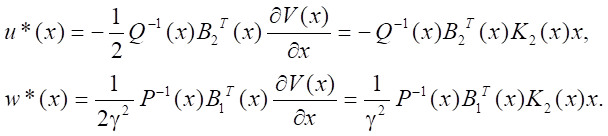 (15)
(15)
Уравнение (13) принимает вид:
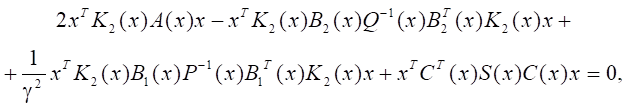
или
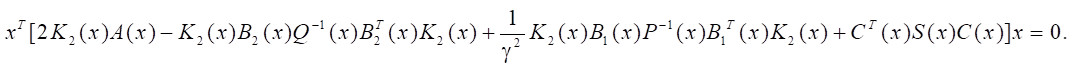
Применяя операцию транспонирования, получаем:
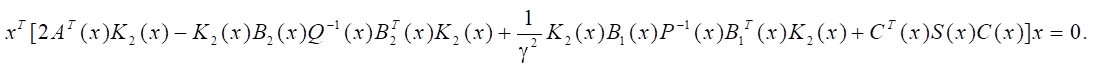
Суммируя два последних выражения, приходим к равенству:
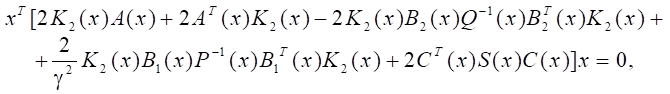
или окончательно:
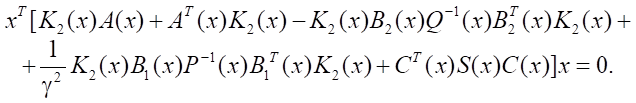 (16)
(16)
Заметим, что в силу зависимости всех матриц от вектора состояния, из (16) не следует равенство нулевой матрице выражения в квадратных скобках.
По аналогии со случаем линейной стационарной системы предлагается решать алгебраическое уравнение Риккати, все матрицы в котором являются функциями вектора состояния системы (State Dependent Riccati Equation, SDRE). При этом ищется положительно определенное решение уравнения Риккати, порождающее закон управления, гарантирующий то, что система будет асимптотически устойчива в окрестности положения равновесия. Для проверки этого свойства используется критерий устойчивости по корням характеристического уравнения, проверяемый поточечно, или критерий Рауса-Гурвица.
В рассматриваемой задаче предлагается решать уравнение:
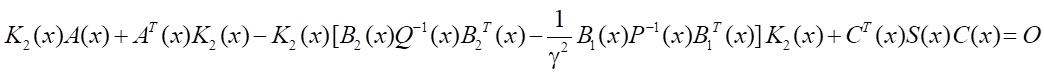 , (17)
, (17)
т.е. искать матрицу K2(x) > 0, которая удовлетворяет уравнению Риккати, коэффициенты которого зависят от x. Уравнение (17) решается многократно при фиксированном x ∈ Rn. Координаты вектора состояния определяются в процессе интегрирования дифференциального уравнения (12) совместно с управлениями объектом и возмущениями:
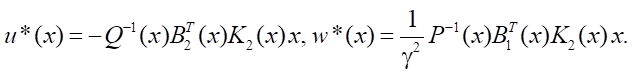 (18)
(18)
При этом решение уравнения Риккати должно быть таким, чтобы удовлетворялся критерий
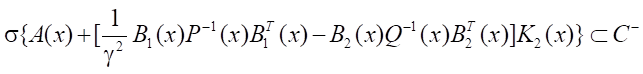
∀x ∈ Rn, где σ — спектр матрицы, C– — открытая левая полуплоскость комплексной плоскости. Заметим, что критерий устойчивости замкнутой системы можно заменить проверкой поточечного выполнения критерия Рауса-Гурвица.
Алгоритм приближенного синтеза Н∞ – регуляторов по состоянию
Шаг 1. Задать параметр γ > 0.
Шаг 2. Найти решение уравнения
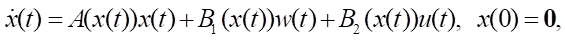
с управлениями
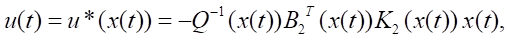
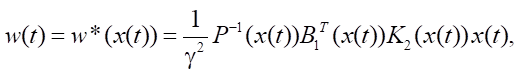
одним из численных методов интегрирования с постоянным шагом h (явным методом Эйлера, методом Эйлера–Коши, методами Адамса–Бэшфорта, Милна, Хэмминга различных порядков).
При этом для каждого из дискретных моментов времени ti = ih, i = 0, 1, 2, … решить уравнение Риккати:
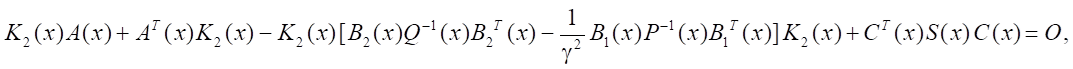
при x = x(ti ). В результате найти матрицу K2(x) и использовать ее при формировании законов управления.
Шаг 3. Найти минимальное γ*. Для этого требуется последовательно уменьшать γ пока свойство устойчивости решений дифференциального уравнения
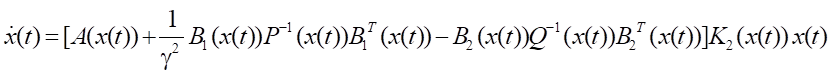 ,
,
описывающего динамику системы с полученными управлениями, остается справедливым.
Результаты исследования. Для проверки эффективности предложенного приближенного алгоритма синтеза Н∞ – регуляторов по состоянию решены два модельных примера.
Модельный пример №1. Рассмотрен одномерный случай, когда уравнения (1), (2) и функционал (5) имеют вид:
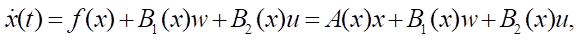
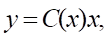
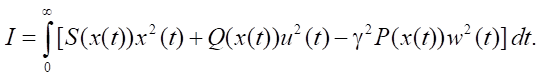
Решение. Структуры управления следуют из (18):
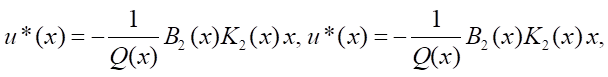
а уравнение (17) имеет форму:
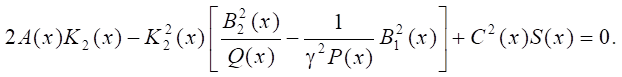
Запишем полученное квадратное уравнение в канонической форме:
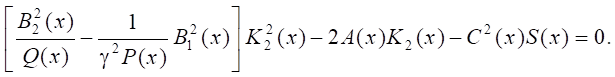
Решение имеет вид:
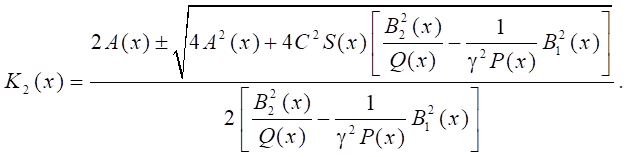
Поскольку K2 > 0, то:
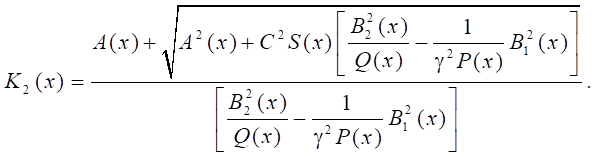
Рассмотрим подробнее частный случай:

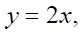
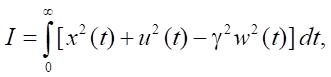
где A(x) = (1 – x²), B1(x) = 1, B2(x) = 1, C(x) = 2, Q(x) = 1, S(x) = 1, P(x) = 1.
Тогда (опуская зависимость от х) получаем:
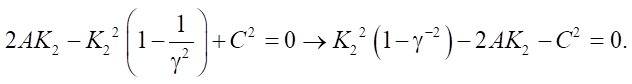
Корни квадратного уравнения
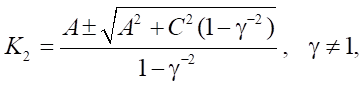
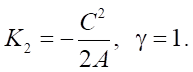
Заметим, что при рассмотрении случая γ ≠ 1 пока невозможно исключить лишние корни, так как A(x) и (1 – γ⁻²) могут изменять знак.
В результате получаем структуры управления:
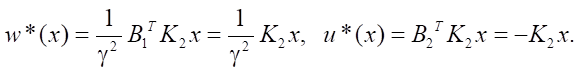
При этом уравнение замкнутой системы имеет вид:
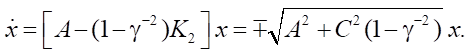
Для обеспечения асимптотической устойчивости берем знак минус, а в выражении для K2 — плюс. Для данного примера получаем:
- если γ≠1, то
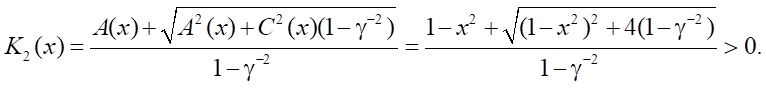
- если функции A(x), C(x) не равны нулю одновременно, то дискриминант A²(x)+C² (x)(1 – γ⁻²).
Тогда
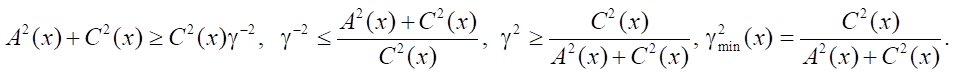
Для решаемого примера
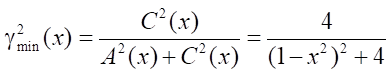 ,
,
т.е. при каждом текущем x имеется свое значение 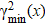 .
.
При γ = γmin выполняется x = 0, x(0) = 0 (условие асимптотической устойчивости не выполняется, но справедливо x(t) ≡ 0).
При γ = γmin имеем
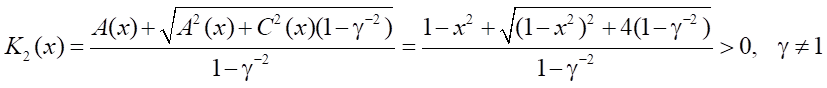 .
.
Если γ = 1, то
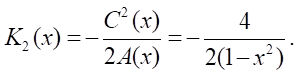
Для выполнения условия K2 > 0 требуется выполнение условия A(x) = 1 – x² < 0 задающее множество |x| < 1 возможного функционирования системы.
Моделирование. Для моделирования при различных начальных условиях был выбран конечный промежуток времени T = [0, 20], поскольку все переходные процессы в замкнутой системе практически завершаются.
Согласно рис. 1–3, значение вектора состояния асимптотически стремится к нулю для различных начальных условий, что свидетельствует об устойчивости системы и правильном выборе параметров, при которых система сохраняет свойство устойчивости при любых заданных ограниченных возмущениях.
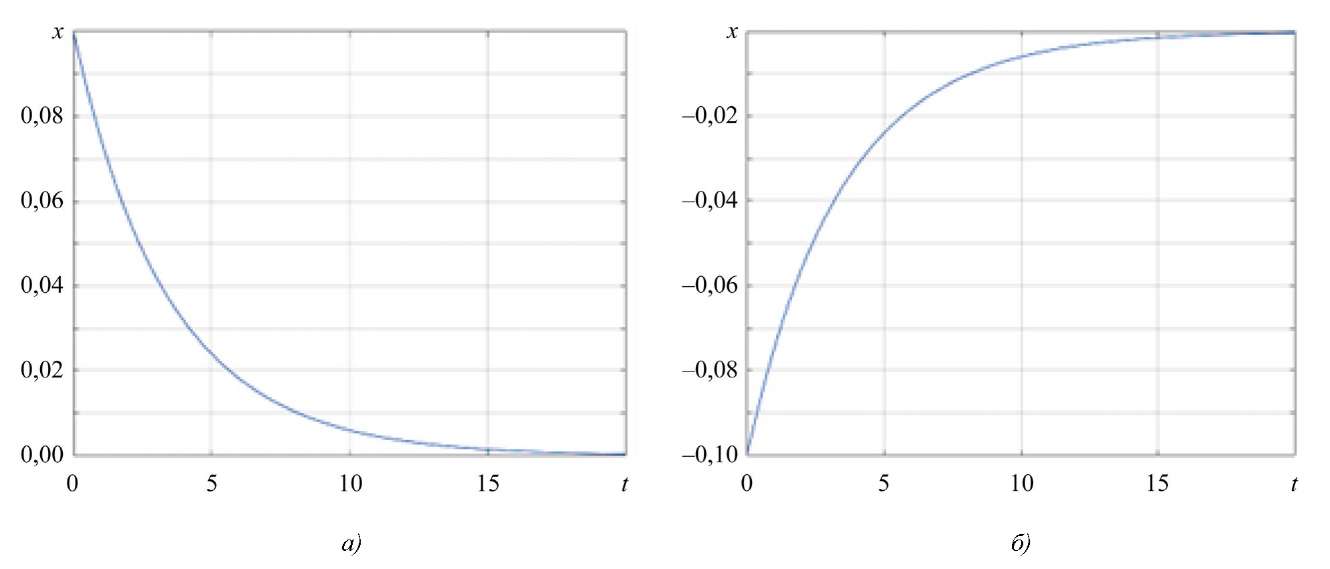
Рис. 1. Изменение вектора состояния:
а — для начального состояния x0 = 0,1; б — для начального состояния x0 = –0,1
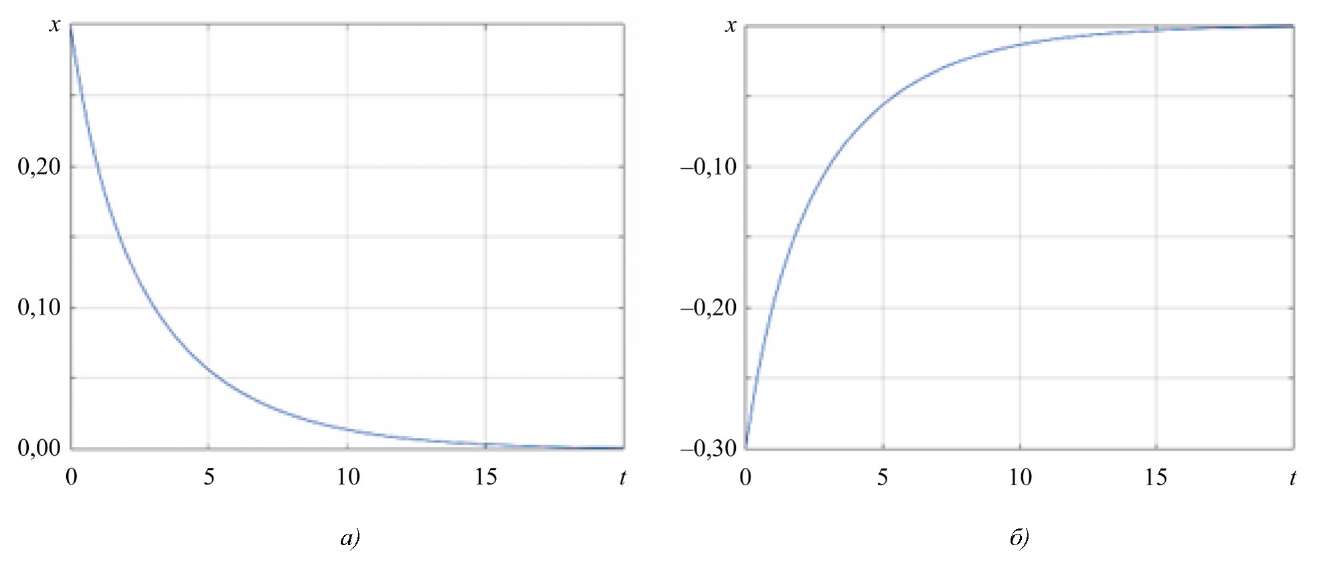
Рис. 2. Изменение вектора состояния:
а — для начального состояния x0 = 0,3; б — для начального состояния x0 = –0,3
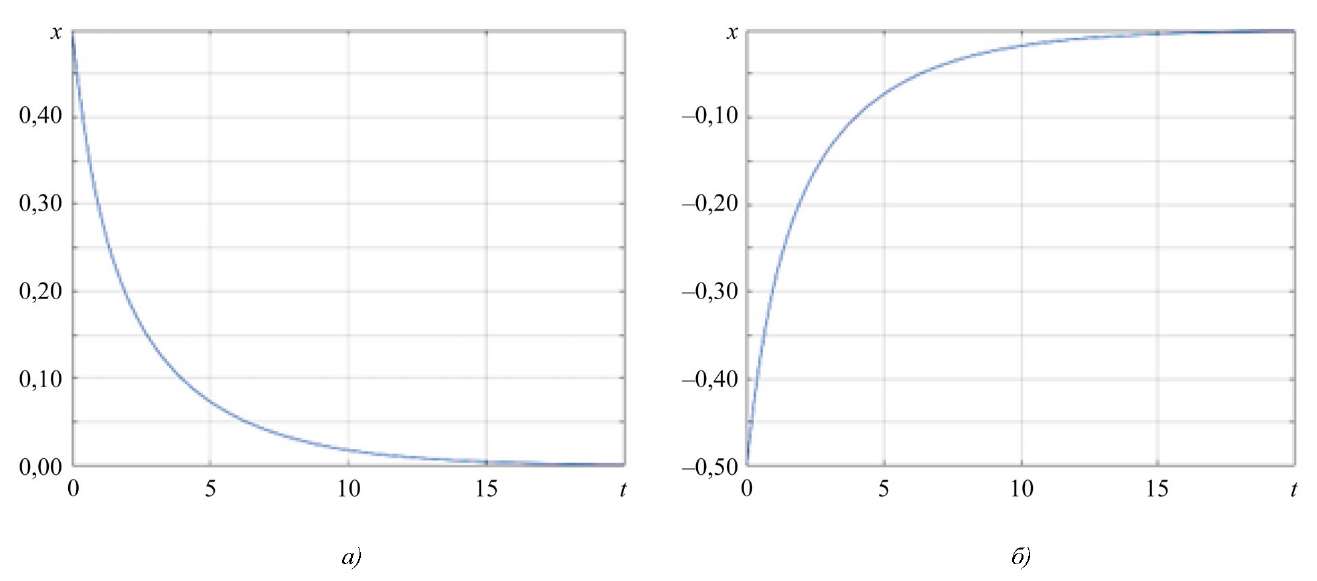
Рис. 3. Изменение вектора состояния:
а — для начального состояния x0 = 0,5; б — для начального состояния x0 = –0,5
Модельный пример № 2. Рассмотрен один из вариантов двумерного случая, когда уравнения (1), (2) и функционал (5) имеют вид:
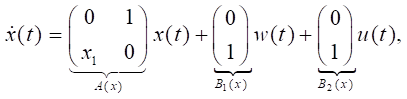
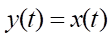 ,
,
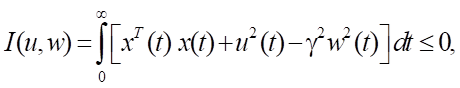
т.е. C(x) = E2, S(x) = E2, Q(x) = 1, P(x) = 1.
Решение. Структуры управления объектом и возмущением следуют из (18):
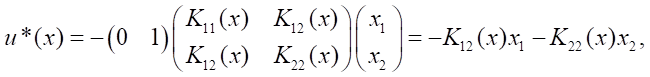
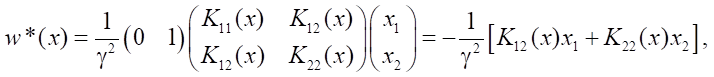
и уравнение (17) имеет форму:
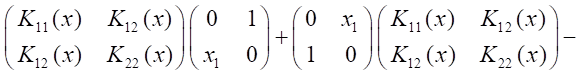
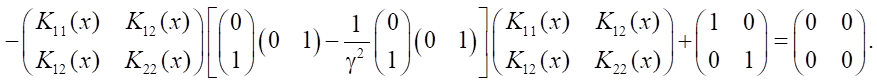
Отсюда
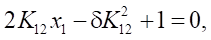
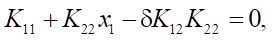
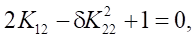
где
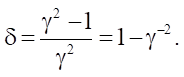
Решение первого уравнения 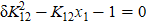 имеет вид:
имеет вид:
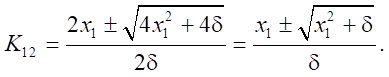
Решение третьего уравнения:

Решение второго уравнения:
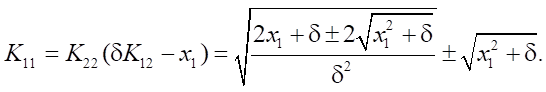
В полученных решениях выбраны положительные знаки с учетом условия K2 > 0.
Моделирование. Для моделирования системы требуется подобрать такое минимально возможное значение γ, чтобы оно удовлетворяло (4) и в то же время гарантировало асимптотическую устойчивость замкнутой системы. В примере 1 аналитически была найдена величина параметра γ, но возникла проблема с определением значения оптимального параметра γ*, поэтому значение γ, используемое при моделировании, было выбрано экспериментально. При γ* = 1,5 сохраняется устойчивость системы согласно выражению (19). Для моделирования был выбран интервал времени T = [0, 10], так как переходные процессы в замкнутой системе затухают достаточно быстро. Моделирование проводилось для различных начальных условий.
Согласно рис. 4–5, можно сделать вывод, что координаты вектора состояния асимптотически стремятся к нулю. Данный результат наблюдается для каждого из рассмотренных начальных условий. Это свидетельствует о том, что система устойчива, а ее параметры подобраны корректно, что позволяет сохранять свойство устойчивости при любых начальных условиях и в условиях наихудших возмущений.
Начальные условия существенно влияют на траектории изменения координат вектора состояния, но из рис. 4–5 видно, что предложенный подход позволяет не только компенсировать внешние возмущения, но и стабилизировать траекторию движения.
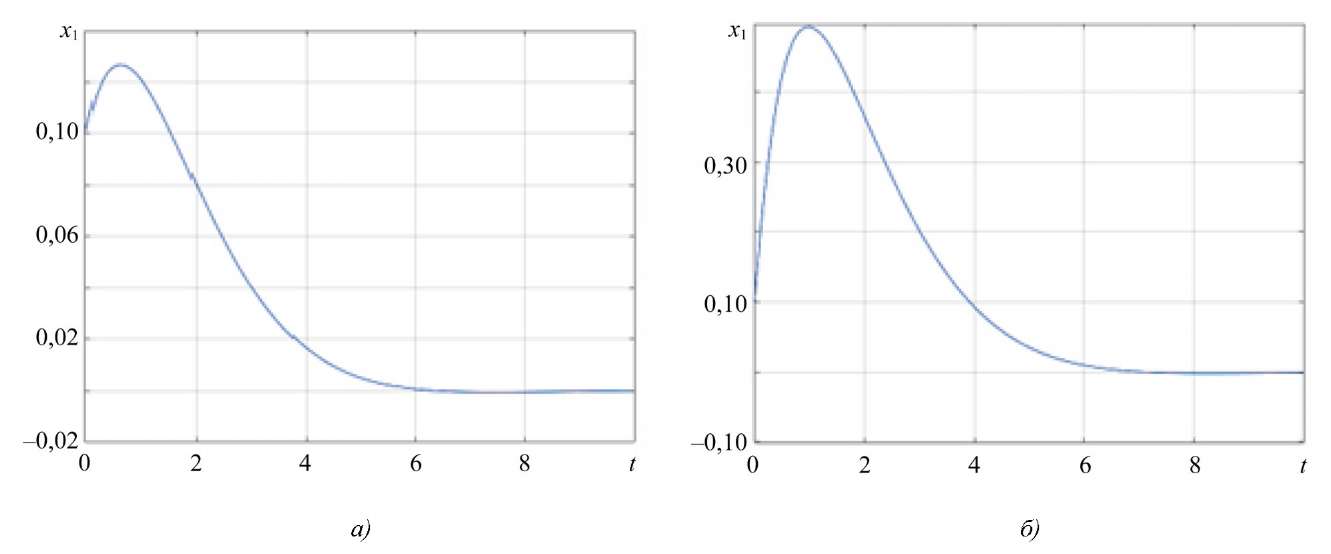
Рис. 4. Изменение x1(t):
а — для начального состояния x0 = (0,1; 0,1)T; б — для начального состояния x0 = (0,1; 1)T
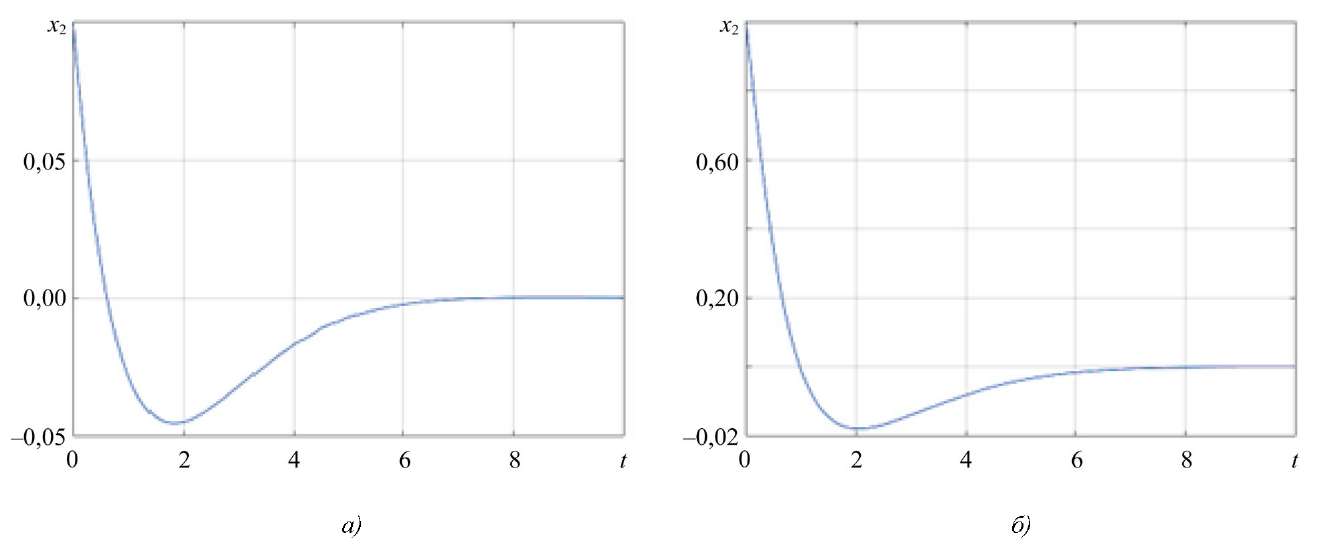
Рис. 5. Изменение x2(t):
а — для начального состояния x0 = (1; 0,1)T; б — для начального состояния x0 = (1; 1)T
Обсуждение и заключение. В результате работы были сформулированы и обоснованы достаточные условия Н∞ – управления, предложен приближенный метод решения. Предложенный в рамках задачи метод был проверен на двух модельных примерах. Результаты моделирования позволяют заключить, что использование разработанного метода синтеза регулятора гарантирует необходимое качество переходных процессов и обеспечивает асимптотическую устойчивость замкнутых систем.
Результаты и методы, предложенные в данной работе, могут быть применены для решения задач управления различной сложности — от проектирования простых автопилотов до разработки сложных систем автоматической навигации для пилотируемых и беспилотных летательных аппаратов. Это подчеркивает перспективность использования предложенного подхода и делает его привлекательным вариантом для дальнейших исследований.
Список литературы
1. Курдюков А.П., Андрианова О.Г., Белов А.А., Гольдин Д.А. Между LQG/H2 и H∞ теориями управления. Автоматика и телемеханика. 2021;(4):8–76. https://doi.org/10.31857/S0005231021040024
2. Wanigasekara C, Liruo Zhang, Swain A. H∞ State-Feedback Consensus of Linear Multi-Agent Systems. In: Proc. 17th International Conference on Control & Automation. Piscataway, NJ: IEEE Xplore; 2022. P. 710–715. https://doi.org/10.1109/ICCA54724.2022.9831897
3. Banavar RN, Speyer JL. A Linear-Quadratic Game Approach to Estimation and Smoothing. In: Proc. the American Control Conference. New York City: IEEE; 1991. P. 2818–2822. https://doi.org/10.23919/ACC.1991.4791915
4. Chodnicki M, Pietruszewski P, Wesołowski M, Stępień S. Finite-Time SDRE Control of F16 Aircraft Dynamics. Archives of Control Sciences. 2022;32(3):557–576. https://doi.org/10.24425/acs.2022.142848
5. Panteleev A, Yakovleva A. Approximate Methods of H-infinity Control of Nonlinear Dynamic Systems Output. MATEC Web of Conferences. XXII International Conference on Computational Mechanics and Modern Applied Software Systems (CMMASS 2021). 2022;362:012021. https://doi.org/10.1051/matecconf/202236201021
6. Hamza A, Mohamed AH, Badawy A. Robust H-infinity Control for a Quadrotor UAV. AIAA SCITECH 2022 Forum. Reston, VA: AIAA; 2022. https://doi.org/10.2514/6.2022-2033
7. Fei Han, Qianqian He, Yanhua Song, Jinbo Song. Outlier-Resistant Observer-Based Н∞ – Consensus Control for Multi-Rate Multi-Agent Systems. Journal of the Franklin Institute. 2021;358(17):8914–8928. https://doi.org/10.1016/j.jfranklin.2021.08.048
8. Junfeng Long, Wenye Yu, Quanyi Li, Zirui Wang, Dahua Lin, Jiangmiao Pang. Learning H-Infinity Locomotion Control. A rXiv preprint arXiv. 2024;2404:14405. https://doi.org/10.48550/arXiv.2404.14405
9. Fayin Chen, Wei Xue, Yong Tang, Tao Wang. A Comparative Research of Control System Design Based on H-Infinity and ALQR for the Liquid Rocket Engine of Variable Thrust. International Journal of Aerospace Engineering. 2023;(2):1–12. https://doi.org/10.1155/2023/2155528
10. Yazdkhasti S, Sabzevari D, Sasiadek JZ. Adaptive H-infinity Extended Kalman Filtering for a Navigation System in Presence of High Uncertainties. Transactions of the Institute of Measurement and Control. 2022;45(8):1430–1442. https://doi.org/10.1177/01423312221136022
11. Balandin DV, Biryukov RS, Kogan MM. Multicriteria Optimization of Induced Norms of Linear Operators: Primal and Dual Control and Filtering Problems. Journal of Computer and Systems Sciences International. 2022;61(2):176–190. http://doi.org/10.1134/S1064230722020046
12. Aalipour A, Khani A. Data-Driven H-infinity Control with a Real-Time and Efficient Reinforcement Learning Algorithm: An Application to Autonomous Mobility-on-Demand Systems. arXiv:2309.08880. https://doi.org/10.48550/ARXIV.2309.08880
13. Panteleev AV, Yakovleva AA. Sufficient Conditions for H-infinity Control on the Finite Time Interval. Journal of Physics: Conference Series. 2021;1925:012024. https://doi.org/10.1088/1742-6596/1925/1/012024
14. Panteleev AV, Yakovleva AA. Sufficient Conditions for the Existence of Н∝-infinity State Observer for Linear Continuous Dynamical Systems. Modelling and Data Analysis. 2023;13(2):36–63. https://doi.org/10.17759/mda.2023130202
15. Çimen T. State-Dependent Riccati Equation (SDRE) Control: A Survey. IFAC Proceedings Volumes. 2008;41(2):3761–3775. https://doi.org/10.3182/20080706-5-KR-1001.00635
16. Cloutier JR, D’Souza CN, Mracek CP. Nonlinear Regulation and Nonlinear H∞ Control via the State-Dependent Riccati Equation Technique: Part 1, Theory. In: Proc. International Conference on Nonlinear Problems in Aviation and Aerospace. Daytona Beach, FL: Embry-Riddle Aeronautical University Press; 1996. P. 117–131. URL: https://clck.ru/3M4kki (accessed: 04.02.2025).
Об авторах
А. В. ПантелеевRussian Federation
Андрей Владимирович Пантелеев, доктор физико-математических наук, профессор, заведующий, кафедра «Математическая кибернетика» института информационных технологий и прикладной математики
125993, г. Москва, Волоколамское шоссе, д. 4
А. А. Яковлева
Russian Federation
Александра Алексеевна Яковлева, аспирант, кафедра «Математическая кибернетика»
125993, г. Москва, Волоколамское шоссе, д. 4
Предложены новые достаточные условия существования Н∞ – управления для непрерывных нелинейных систем, линейных по управлению и возмущению. Предложенный метод основан на минимаксном подходе и принципе расширения. Разработан алгоритм, упрощающий процедуру синтеза Н∞ – регуляторов, на основе приближенной замены нелинейной системы более простой системой, похожей по структуре на линейную. Результаты исследования открывают новые возможности решения различных задач управления, например, задач стабилизации летательных аппаратов разных классов при наличии внешних воздействий.
Рецензия
Для цитирования:
Пантелеев А.В., Яковлева А.А. Приближенный синтез Н∞ – регуляторов в нелинейных динамических системах на полубесконечном промежутке времени. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):152-164. https://doi.org/10.23947/2687-1653-2025-25-2-152-164. EDN: IHQRUT
For citation:
Panteleev A.V., Yakovleva A.A. Approximate Synthesis of Н∞ – Controllers in Nonlinear Dynamic Systems over a Semi-Infinite Time Period. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):152-164. https://doi.org/10.23947/2687-1653-2025-25-2-152-164. EDN: IHQRUT
JATS XML














































