Scroll to:
Related dynamic axisymmetric thermoelectroelasticity problem for a long hollow piezoceramic cylinder
https://doi.org/10.23947/2687-1653-2022-22-2-81-90
Abstract
Introduction. The article studies the problem of investigation of coupled nonstationary thermoelectroelastic fields in piezoceramic structures. The main approaches related to the construction of a general solution to the initial non-selfadjoint equations describing the process under consideration are briefly outlined. The work aims at constructing a new closed solution to the axisymmetric thermoelectroelasticity problem for a long piezoceramic cylinder.
Materials and Methods. A long hollow cylinder whose electrodated surfaces were connected to a measuring device with large input resistance was considered. On the cylindrical surfaces of the plate, a time-varying temperature was given. The hyperbolic theory of Lord–Shulman thermo-electro-elasticity was used. The closed solution is constructed using a generalized method of finite integral transformations.
Results. The developed calculation algorithm makes it possible to determine the stress–strain state of the cylinder, its temperature, and electric fields. In addition, it becomes possible to investigate the coupling of fields in a piezoceramic cylinder, as well as to analyze the effect of relaxation of the heat flow on the fields under consideration.
Discussion and Conclusion. The use of assumptions about the equality of the components of the temperature stress tensor and the absence of temperature effect on the electric field allowed us to formulate a self-adjoint initial system of equations and construct a closed solution.
Keywords
For citations:
Shlyakhin D.A., Kalmova M.A. Related dynamic axisymmetric thermoelectroelasticity problem for a long hollow piezoceramic cylinder. Advanced Engineering Research (Rostov-on-Don). 2022;22(2):81-90. https://doi.org/10.23947/2687-1653-2022-22-2-81-90
Introduction. Recently, different-purpose technical devices made of piezoceramic material have become widespread. Here, devices whose operation is based on the effect of the coupling of elastic, electric and temperature fields hold a specific place [1]. Various theories of thermoelectroelasticity were developed to describe their work taking into account the coupling of fields [2–4]. At the same time, for a better description and evaluation of non-stationary processes in structures, it was required to construct analytical solutions. However, the mathematical formulation of the problems under consideration included a system of non-self-adjoint partial differential equations, whose integration was difficult to treat mathematically.
To solve this problem, as a rule, equations are investigated in an uncoupled form [5][6], infinitely long bodies are analyzed [7–11], or thermoelectroelasticity problems are considered in a quasi-static formulation [12][13].
In this paper, we consider a coupled dynamic thermoelectroelasticity problem for an infinitely long hollow piezoceramic cylinder. As a result of the transformation of the initial calculated ratios, it was possible to form a self-adjoint system of equations, the integration of which was carried out by the method of incomplete separation of variables in the form of a generalized finite integral transformation [13].
Materials and Methods. Let a hollow, long, loose in the radial plane, piezoceramic cylinder occupy area Ω in the cylindrical coordinate system 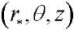 :
: 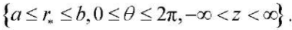
On the cylindrical surfaces, the temperature is given in the form of the following nonstationary functions (boundary conditions of the 1st kind) — 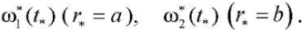
The internal electrodated surface is grounded, and the external one is connected to a measuring device with a large input resistance (electric idle mode.
The mathematical formulation of the axisymmetric problem under consideration in dimensionless form includes differential equations of motion, electrostatics, and thermal balance based on the hyperbolic Lord–Shulman theory, as well as the boundary conditions [2][7][15]:
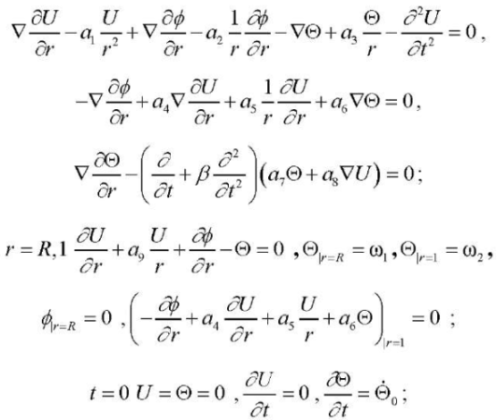 (1) , (2), (3)
(1) , (2), (3)
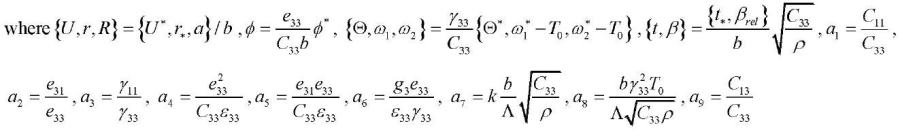
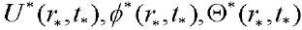 — accordingly, the radial component of the displacement vector, the electric field potential, and the temperature increment in dimensional form;
— accordingly, the radial component of the displacement vector, the electric field potential, and the temperature increment in dimensional form;
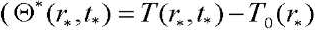 — current temperature and temperature of the initial state of the body;
— current temperature and temperature of the initial state of the body;
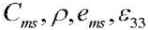 — elastic moduli, density, piezo module, and permittivity coefficient of electroelastic anisotropic material;
— elastic moduli, density, piezo module, and permittivity coefficient of electroelastic anisotropic material;
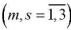 ;
;
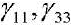 — components of the temperature stress tensor
— components of the temperature stress tensor 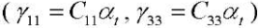 ;
;
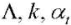 — coefficients of thermal conductivity, volumetric heat capacity, and linear thermal expansion of the material;
— coefficients of thermal conductivity, volumetric heat capacity, and linear thermal expansion of the material;
 — component of the pyroelectric coefficient tensor;
— component of the pyroelectric coefficient tensor;
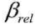 — relaxation time;
— relaxation time;
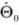 — the rate of temperature change known at the initial moment;
— the rate of temperature change known at the initial moment;
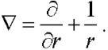
In the case of grounding of the inner surface of a piezoceramic element, electrical voltage 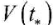 is determined by the potential on its outer surface:
is determined by the potential on its outer surface:
 (4)
(4)
When constructing a general solution at the first stage of the study, the radial component of the electric field intensity vector is determined as a result of integrating the electrostatics equation:
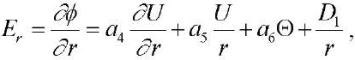 (5)
(5)
where D1 — integration constant.
Substituting (5) into (1)–(3) allows us to formulate a new problem with respect to functions 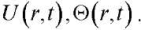 In this case, the condition of the absence of a radial component of the electric field induction vector on the outer cylindrical surface of the element (the last equality (2)) is fulfilled at D1 = 0 ; and the condition of grounding of the inner surface
In this case, the condition of the absence of a radial component of the electric field induction vector on the outer cylindrical surface of the element (the last equality (2)) is fulfilled at D1 = 0 ; and the condition of grounding of the inner surface 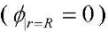 is satisfied as a result of integration (5).
is satisfied as a result of integration (5).
At the next stage of the solution, the inhomogeneous boundary conditions (2) are reduced to a form that allows further use of the procedure for incomplete separation of variables by the method of finite integral transformations. To do this, new functions u(r,t), N(r,t) related to 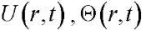 are introduced:
are introduced:
 (6)
(6)
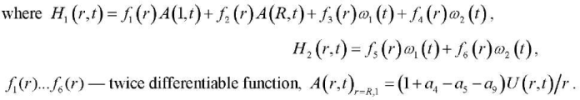
Substituting (6) into the calculated ratios (1)–(3) with respect to functions 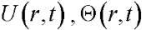 when the following conditions are met:
when the following conditions are met:
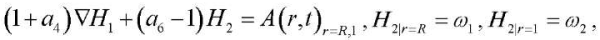 (7)
(7)
allows us to get a new boundary value problem with respect to function u(r,t), N(r,t)
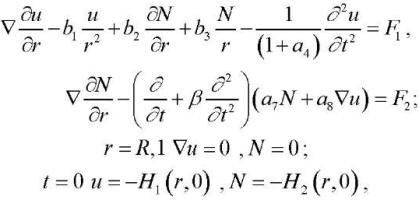 (8), (9), (10)
(8), (9), (10)
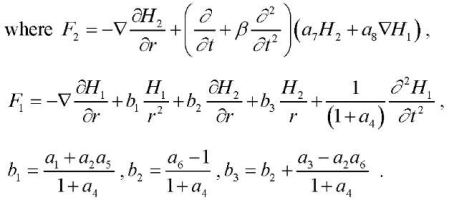
It should be noted here that A(r,t) is a function of the displacements of the cylindrical surfaces of the cylinder. Initially, A(r,t) is equated to zero with its subsequent determination and refinement H1, F1, F2.
Further transformations of the calculated ratios (8)–(10) are associated with the use of the following assumptions: b1 = 1, b3 = 0, and the introduction of a thermoelastic potential
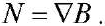 (11)
(11)
Condition b1 = 1 can be accepted without a large error, since for piezoceramic materials b1 = 0.94 ÷ 0.98, and dependence b3 = 0 is fulfilled in the case of equality of the components of the temperature stress tensor
(γ11 = γ33) and the absence of temperature influence on the electric field g3 = 0.
As a result, the following task is formed regarding u(r,t), B(r,t):
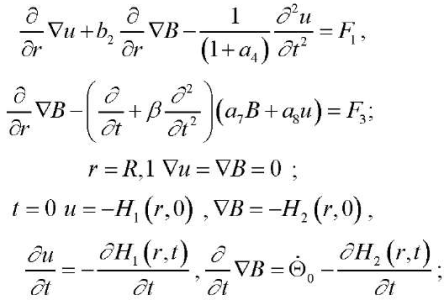 (12), (13), (14)
(12), (13), (14)
where
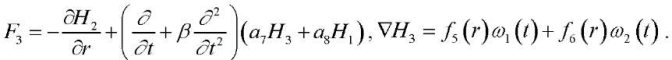
The initial boundary value problem (12)–(14) is solved using the structural algorithm of the generalized finite integral transformation (FIT) [14]. At the same time, it is possible to use single-component unknown transformation kernel K(λi,r) for this task:
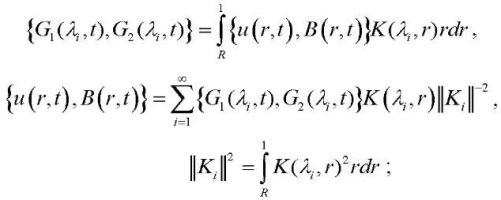 (15), (16)
(15), (16)
where λi — eigenvalues forming a countable set.
As a result of using the FIT algorithm [14], we obtain problems with respect to the transformation kernel K(λi,r):
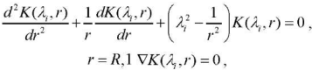 (17), (18)
(17), (18)
and transform G1(λi,t), G2(λi,t):
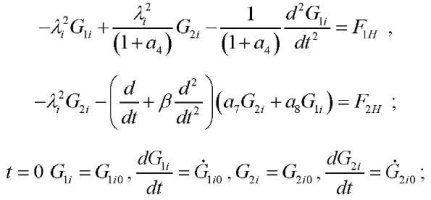 (19), (20)
(19), (20)
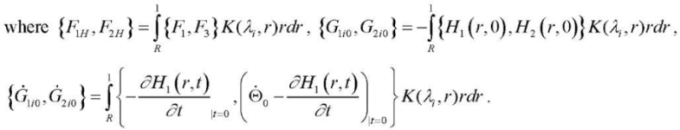
The general solution to problem (17), (18) has the form:
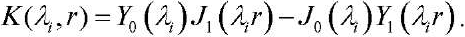 (21)
(21)
Here, eigenvalues λi are determined using the following transcendental equation:
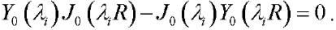
The system of differential equations (19) is reduced to the following resolving equation of the 4th order with respect to G1(λi,t):
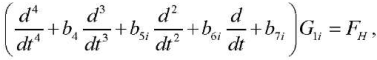 (22)
(22)
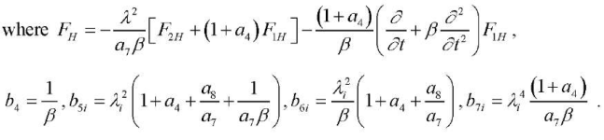
Since the characteristic equation corresponding to (22),
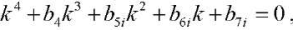
is valid, then it, from the condition of the oscillating solution for G1(λi,t), has two real roots (k1i,k2i) and two complex-conjugate roots
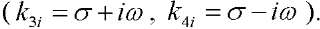
In this case, the general solution to equation (22) has the form:
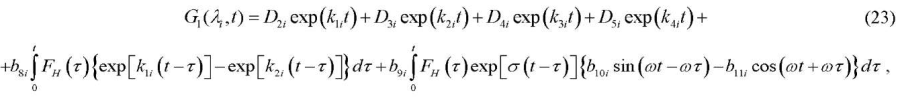 (23)
(23)
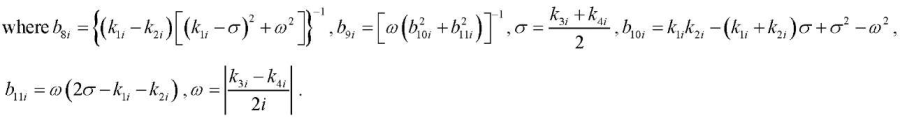
Function G2(λi,t) is determined from the first equation of system (19). Substitution of the obtained expressions for the transforms under the boundary conditions (20) makes it possible to determine the integration constants D2i...D5i (19).
Substitution of G1(λi,t), G2(λi,t) into (16), (11), (6) allows us to get the final expressions for functions 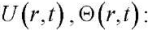
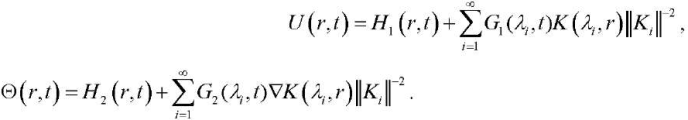 (24)
(24)
At the final stage of the study, functions H1(r,t), H2(r,t) are determined through solving the following differential equations:
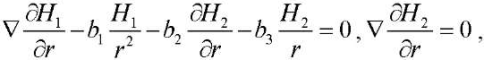 (25)
(25)
which makes it possible to significantly simplify the right parts (F1,F2) of the calculated ratios (8).
Substitution of expressions for H1, H2 in (25) enables to form systems of equations with respect to functions f1(r)...f6(r), that are determined when the conditions are satisfied (7).
The potential of the electric field of a piezoceramic cylinder is determined from integrating equality (5) and satisfying the next-to-last boundary condition (2):
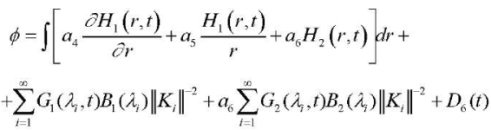 (26)
(26)
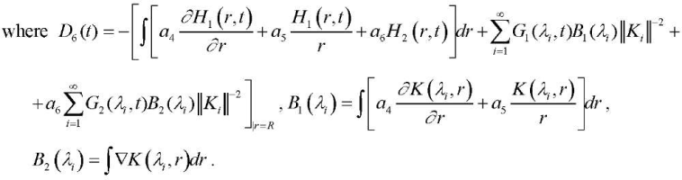
The obtained calculated relations (24), (26) satisfy differential equations (1) and boundary conditions (2), (3), i.e., they are a closed solution to the problem under consideration.
Research Results. As an example, we considered a radially polarized piezoceramic cylinder (b = 0.02 m, R = 0.8) of PZT–4 composition, having the following physical characteristics [10]: ρ = 7500 kg/m3,
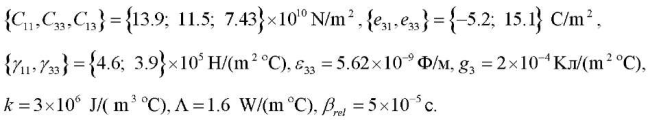
A temperature load acts on the inner surface 
of the piezoceramic cylinder:
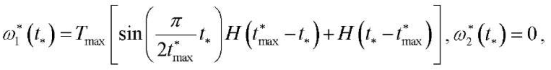
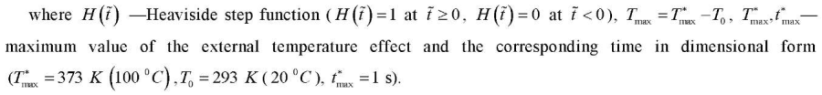
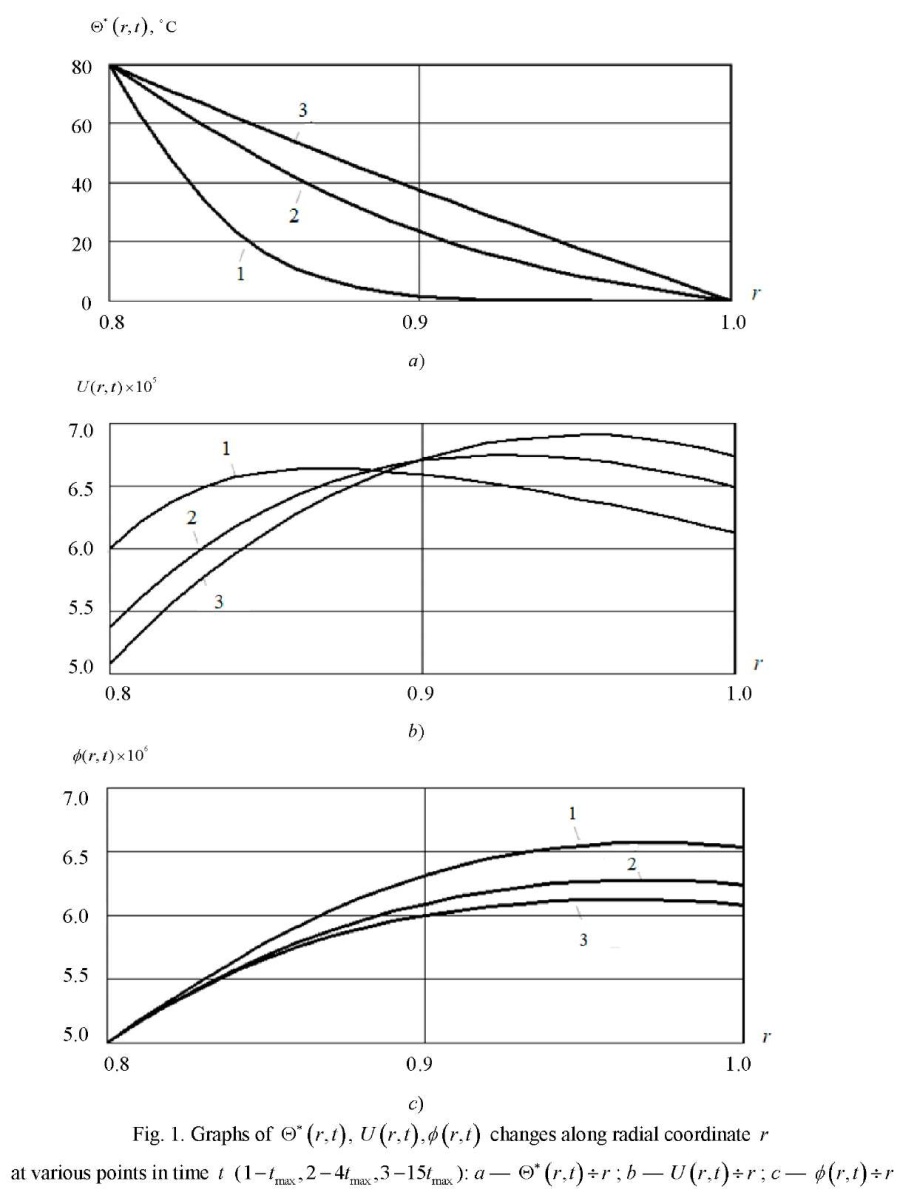
Figure 1 shows graphs of changes in functions 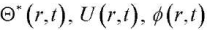 along radial coordinate r at various points in time t. The numbers 1−3 respectively indicate the results obtained at the following time values
along radial coordinate r at various points in time t. The numbers 1−3 respectively indicate the results obtained at the following time values
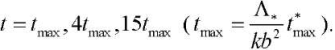
Analysis of the calculation results allows us to draw the following conclusions:
- sufficiently large value of the coefficient of linear thermal expansion αt of the piezoceramic material causes rapid heating of the cylinder;
- radial displacements on the inner cylindrical surface (r = R) ) at the first stage of the study (t = tmax) take the greatest values, followed by a decrease over time. The reverse pattern is observed with respect to the displacements at r = 1.
The degree of coupling of thermoelectroelastic fields is most conveniently analyzed using the coefficient
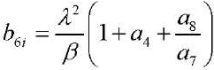
from equality (21). Here, α4 determines the coupling of electroelastic fields, and 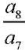 — the effect of the rate of change in the volume of the body on its temperature field.
— the effect of the rate of change in the volume of the body on its temperature field.
Figure 2 shows displacement graph U(1, t) in time t taking into account (solid line) and without taking into account (dotted line) the induced electric field.
It should be noted that the preliminary polarization of piezoceramics causes the formation of a more “rigid” material (α4 = 0.353) and, accordingly, a decrease in displacements during deformation of the cylinder.
The coupling of temperature and electroelastic fields in a piezoceramic cylinder can be neglected due to the small value
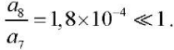
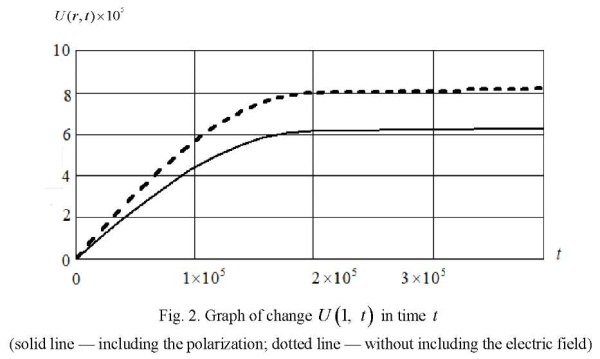
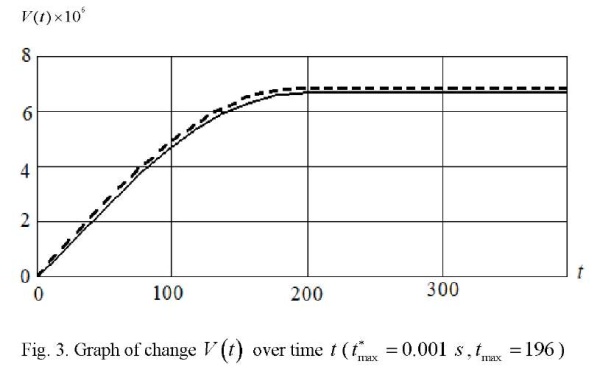
Figure 3 shows graphs of changes in electrical voltage V(t) over time, taking into account (solid line) and without taking into account (dotted line, 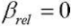 the heat flow relaxation.
the heat flow relaxation.
The calculation results show that for the problem under consideration, the refined hyperbolic Lord-Shulman theory should be used at a high rate of change in the temperature load
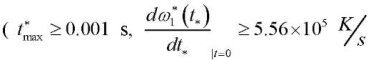
and at lower speeds — the classical theory of thermoelectroelasticity 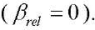
Discussion and Conclusion. The constructed new closed solution to the coupled dynamic problem with satisfaction of the boundary conditions of thermal conductivity of the 1st kind made it possible to determine all the components of thermoelectroelastic fields in a long piezoceramic cylinder. The advantage of the presented calculation algorithm is that there is no need to approximate the temperature function when studying the equation of motion, in contrast to the uncoupled formulation of the problem. At the same time, the effect of the rate of change in the volume of a piezoceramic body on its temperature field can be neglected.
References
1. Кульчин, Ю. Н. Распределенные волоконно-оптические измерительные системы / Ю. Н. Кульчин. — Москва : Физматгиз, 2001. — 272 с.
2. Lord, H. W. A generalized dynamical theory of thermoelasticity / H. W. Lord, Y. Shulman // Journal of the Mechanics and Physics of Solids. — 1967. — Vol. 15. — P. 299–309. https://doi.org/10.1016/0022-5096(67)90024-5
3. Green, A. E. Thermoelasticity without energy dissipation / A. E. Green, P. M. Naghdi // Journal of Elasticity. — 1993. — Vol. 31. — P. 189–208. https://doi.org/10.1007/BF00044969
4. Montanaro, A. Some theorems of incremental thermoelectroelasticity / A. Montanaro // Archives of Mechanics. — 2010. — Vol. 62. — P. 49–72.
5. Kulikov, G. M. Coupled thermoelectroelastic stress analysis of piezoelectric shells / G. M. Kulikov, A. A. Mamontov, S. V. Plotnikova // Composite Structures. — 2015. — Vol. 124. — P. 65–76. https://doi.org/10.1016/j.compstruct.2014.12.045
6. Abbas, I. A. LS model on electro-magneto-thermoelastic response of an infinite functionally graded cylinder / I. A. Abbas, A. M. Zenkour // Composite Structures. — 2013. — Vol. 96. — P. 89–96. https://doi.org/10.1016/j.-compstruct.2012.08.046
7. Ватульян, А. О. Плоские волны и фундаментальные решения в линейной термоэлектроупругости / А. О. Ватульян, А. Ю. Кирютенко, А. В. Наседкин // Прикладная механика и техническая физика. — 1996. — Т. 37, № 5 (219). — С. 135–142.
8. Ватульян, А. О. Динамическая задача термоэлектроупругости для функционально-градиентного слоя / А. О. Ватульян, С. А. Нестеров // Вычислительная механика сплошных сред. — 2017. — Т. 10, № 2. — С. 117–126. https://doi.org/10.7242/1999-6691/2017.10.2.10
9. Saadatfar, M. Piezoelectric hollow cylinder with thermal gradient / M. Saadatfar, A. S. Razavi // Journal of Mechanical Science and Technology. — 2009. — Vol. 23. — P. 45–53. https://doi.org/10.1007/s12206-008-1002-8
10. Khorsand, M. Dynamic analysis of a functionally graded piezoelectric spherical shell under mechanical and thermal shocks / M. Khorsand // Mechanical Engineering Science. — 2014. — Vol. 228. — P. 632–645. https://doi.org/10.1177/0954406213489445
11. Thermoelectroelastic response of a piezoelectric cylinder with D symmetry under axisymmetric mechanical and thermal loading/ M. Ishihara, Y. Ootao, Y. Kameo, T. Saito // Mechanical Engineering Journal. — 2017. — Vol. 4. — Р. 16–00609. https://doi.org/10.1299/mej.16-00609
12. Shlyakhin, D. A. Uncoupled problem of thermoelectroelasticity for a cylindrical shell / D. A. Shlyakhin, M. A. Kalmova // In: Proc. XXX Russian-Polish-Slovak Seminar Theoretical Foundation of Civil Engineering (RSP 2021). — 2022. — Vol. 189. — P. 263–271. https://doi.org/10.1007/978-3-030-86001-1_31
13. Шляхин, Д. А. Нестационарная задача термоэлектроупругости для длинного пьезокерамического цилиндра / Д. А. Шляхин, М. А. Кальмова // Вестник Пермского национального исследовательского политехнического университета. Механика. — 2021. — № 2. — С. 181–190. https://doi.org/10.15593/perm.mech/2021.2.16
14. Сеницкий, Ю. Э. Многокомпонентное обобщенное конечное интегральное преобразование и его приложение к нестационарным задачам механики / Ю. Э. Сеницкий // Известия вузов. Математика. — 1991. — № 4. — С. 57–63.
15. Гринченко, В. Т. Механика связанных полей в элементах конструкций / В. Т. Гринченко, А. Ф. Улитко, Н. А. Шульга. — Киев : Наукова думка, 1989. — 279 с.
About the Authors
D. A. ShlyakhinRussian Federation
244, Molodogvardeyskaya St., Samara
M. A. Kalmova
Russian Federation
244, Molodogvardeyskaya St., Samara
Review
For citations:
Shlyakhin D.A., Kalmova M.A. Related dynamic axisymmetric thermoelectroelasticity problem for a long hollow piezoceramic cylinder. Advanced Engineering Research (Rostov-on-Don). 2022;22(2):81-90. https://doi.org/10.23947/2687-1653-2022-22-2-81-90












































