Перейти к:
Применение блока инерциальных датчиков для оценивания положения и управления движением экзоскелета нижних конечностей
https://doi.org/10.23947/2687-1653-2022-22-3-204-213
Аннотация
Введение. Исследуется задача управления движением экзоскелета нижних конечностей. Для ее решения предлагается задействовать программное управление и управление в виде обратной связи. Формирование управления в виде обратной связи требует оценки состояния экзоскелета (углы поворота, угловые скорости и ускорения звеньев). Рассматривается возможность применения блока инерциальных датчиков для оценки угловых скоростей и ускорений звеньев экзоскелета. Цель работы — определить законы формирования управления движением экзоскелета, которые обеспечат устойчивость программного движения и будут использовать измерения энкодеров, микромеханических гироскопов и акселерометров.
Материалы и методы. Ранее выполненное математическое моделирование динамики экзоскелета задействовали при формировании программного управления. Предложили оснастить экзоскелет блоками инерциальных датчиков. Это решение позволяет оценивать вектор состояния экзоскелета и использовать данные оценки в цепи обратной связи. Описали математическую модель измерений указанных датчиков. Предложенный вариант пригоден для систем управления трехзвенными экзоскелетами нижних конечностей и может быть расширен для многозвенных.
Результаты исследования. Предложены новые законы управления движением экзоскелета, основанные на математической модели динамики системы и использующие измерительную информацию с энкодеров и инерциальных датчиков. В математическом пакете Wolfram Mathematica выполнено численное моделирование движения экзоскелета. Его итоги подтвердили работоспособность предложенного управления и возможность использования блока инерциальных датчиков для оценки состояния экзоскелета. Приводятся результаты численного моделирования для следующих программных движений: подъем экзоскелета из положения сидя в вертикальное и стабилизация вертикального положения равновесия.
Обсуждение и заключения. Предлагаемое управление применимо в экзоскелетах для медицинских приложений (например, в задаче вертикализации пациентов с нарушениями функций опорно-двигательного аппарата). Показана возможность использования измерительной информации, полученной от блоков инерциальных датчиков, в задаче оценки состояния звеньев экзоскелета. Применение инерциальных датчиков позволит определять угловое ускорение звеньев экзоскелета, избегая численного дифференцирования измерительной информации, полученной от энкодеров. Оценки углового ускорения позволяют вводить в систему управления обратную связь по угловым ускорениям, что открывает возможность улучшить переходные процессы при управлении движением экзоскелета.
Ключевые слова
Для цитирования:
Сайпулаев Г.Р., Сайпулаев М.Р., Меркурьев И.В., Адамов Б.И., Гарсиа Р.Б. Применение блока инерциальных датчиков для оценивания положения и управления движением экзоскелета нижних конечностей. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):204-213. https://doi.org/10.23947/2687-1653-2022-22-3-204-213
For citation:
Saypulaev G.R., Saypulaev M.R., Merkuryev I.V., Adamov B.I., Garcia R.B. Application of an Inertial Sensor Unit for Position Estimation and Motion Control of the Lower-Extremity Powered Exoskeleton. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):204-213. https://doi.org/10.23947/2687-1653-2022-22-3-204-213
Введение. Разработка и применение экзоскелетов — устройств, предназначенных для облегчения движения и повышения двигательной эффективности человека, — перспективное направление развития робототехники.
Экзоскелеты все шире применяются в промышленности [1], военном деле [2], медицине [3] и других областях. Этим обусловлена актуальность исследований, посвященных их схемотехническому и конструкционному исполнению, оптимизации энергозатрат, траектории движения, динамике, управлению.
В представленной работе рассматривается активный экзоскелет нижних конечностей человека с жесткой конструкцией силового каркаса. Его используют для реабилитации пациентов с нарушениями функций опорно-двигательного аппарата.
При разработке таких экзоскелетов возникает необходимость решения взаимосвязанных научно-технических задач. В их числе:
- формирование скелетной схемы;
- математическое моделирование движения экзоскелета [4–6];
- оптимизация движения звеньев на основе математической модели кинематики и динамики1;
- рациональное построение двигательной системы [7][8];
- разработка алгоритмов управления [9–11] и оценивания [13][14].
Все перечисленные задачи связывает проблема поиска управляющих воздействий для программного движения. Их источником может быть, во-первых, динамическая модель системы. Во-вторых, они формируются в виде пропорционального интегрально-дифференциального (ПИД) регулятора, используемого для стабилизации программного движения. Возможна также комбинация двух способов. При этом для формирования управления по принципу обратной связи (в частности в виде ПИД регулятора) важную роль играют алгоритмы оценивания состояния динамической системы и набор датчиков, показатели которых используются в алгоритмах.
Для получения информации о положении звеньев экзоскелетов их оснащают энкодером или гироскопом [9–14]. Другие возможные варианты: акселерометр, магнитометр, потенциометр, датчики момента, силы, биосигналов и др.
В [13] на каждом звене экзоскелета предлагается использовать по одному блоку инерциальных датчиков, состоящих из гироскопов и акселерометров. Такое решение позволит оценивать углы поворота, угловые скорости и ускорения. При этом модель измерений получается нелинейной, что усложняет структуру систем управления и наблюдения.
Цель работы — улучшение управления экзоскелетом за счет использования двух инерциальных блоков, закрепленных на каждом звене экзоскелета. Такой подход позволяет оценивать углы поворота, угловые скорости и ускорения экзоскелета. С помощью предлагаемого варианта расположения гироскопов и акселерометров можно получить линейную модель измерений, что откроет пути для упрощения системы управления и применения теории оптимального оценивания линейных систем [15]. Это, в свою очередь, станет базой для совершенствования управления движением экзоскелета. Критерий улучшения качества управления — уменьшение отклонений угловых скоростей звеньев от программного движения.
Материалы и методы. Рассмотрим кинематическую схему экзоскелета с жесткой конструкцией силового каркаса при симметричном движении ног в сагиттальной плоскости (рис. 1).
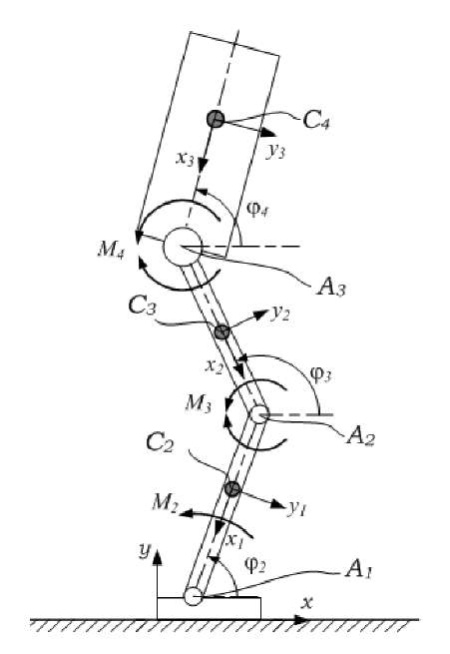
Рис. 1. Кинематическая схема экзоскелета нижних конечностей в сагиттальной плоскости
C2, C3, C4 — центры масс голеней, бедер и корпуса соответственно; А1, А2, А3 — шарниры, соединяющие звенья экзоскелета; φ2, φ3, φ4 — углы поворота звеньев экзоскелета; М2, М3, М4 — управляющие моменты, создаваемые приводами, расположенными в шарнирах А1, А2, А3 соответственно. Для описания движения вводится система координат xyz. Ось x направлена вдоль опорной поверхности, y — вдоль местной вертикали к опорной поверхности. Ось z дополняет координатные оси до правой декартовой системы координат.
В качестве основы для построения системы управления движением экзоскелета используем динамическую модель из [6].
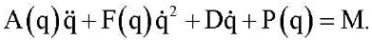 (1)
(1)
Здесь:
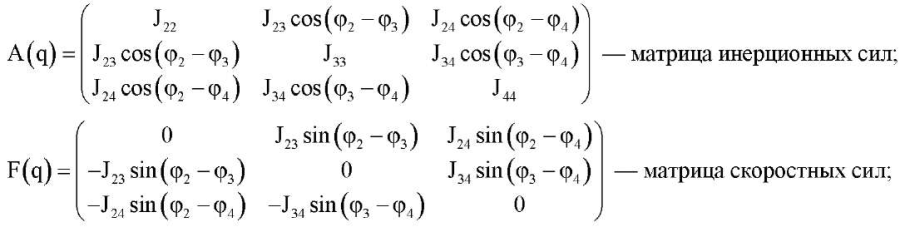
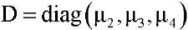 — диагональная матрица диссипативных сил, характеризующих линейное трение в шарнирах;
— диагональная матрица диссипативных сил, характеризующих линейное трение в шарнирах;
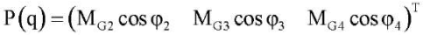 — вектор-столбец моментов, возникающих от действия сил тяжести;
— вектор-столбец моментов, возникающих от действия сил тяжести;
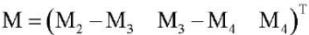 — вектор-столбец управляющих моментов, создаваемых приводами, которые расположены в шарнирах звеньев экзоскелета;
— вектор-столбец управляющих моментов, создаваемых приводами, которые расположены в шарнирах звеньев экзоскелета;
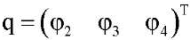 — вектор-столбец обобщенных координат, состоящий из углов поворота звеньев экзоскелета;
— вектор-столбец обобщенных координат, состоящий из углов поворота звеньев экзоскелета;
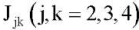 — моменты инерции звеньев экзоскелета;
— моменты инерции звеньев экзоскелета;
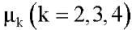 — коэффициенты линейного трения в шарнирах звеньев экзоскелета;
— коэффициенты линейного трения в шарнирах звеньев экзоскелета;
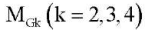 — максимальные величины моментов гравитационных сил, воспринимаемые выходными звеньями приводов.
— максимальные величины моментов гравитационных сил, воспринимаемые выходными звеньями приводов.
Пусть заданы законы изменения углов и их производные при программном движении:
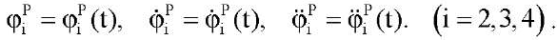 (2)
(2)
Для управления движением экзоскелета предлагается формировать управляющие воздействия в виде суммы управляющих моментов:
- при программном управлении
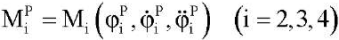 ;
; - ПИД регулятора
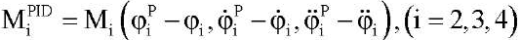
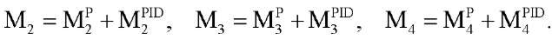 (3)
(3)
Для программного управления значения управляющих воздействий MiP можно рассчитать по формулам [7]:
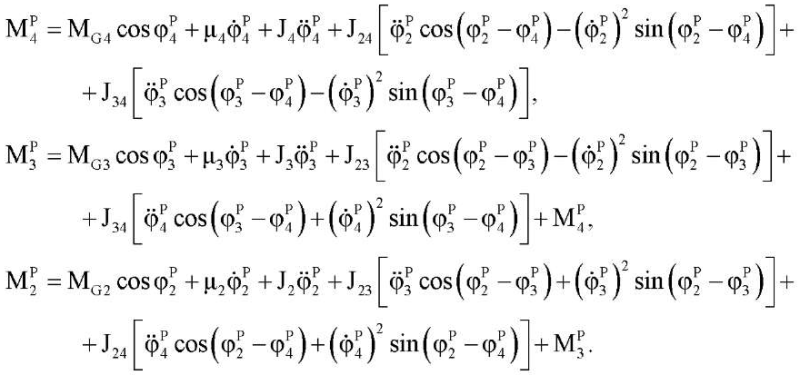 (4)
(4)
Величины MiPID вычисляются по принципу обратной связи (в форме ПИД регулятора):
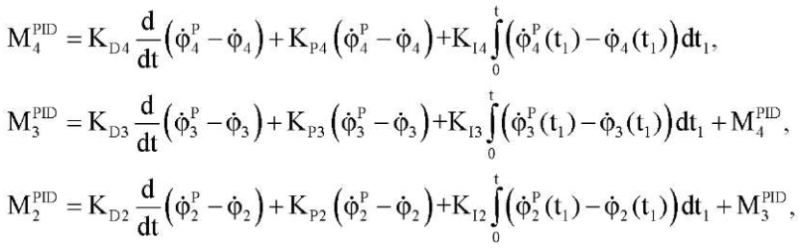 (5)
(5)
или
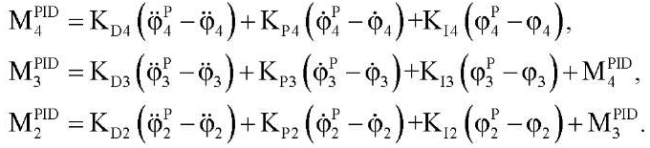 (6)
(6)
Здесь коэффициенты ПИД регулятора KPi, Kit, KDi (i = 2, 3, 4) могут быть:
- постоянными (их находят из условий устойчивости);
- функциями времени (находят из решения задач оптимального управления) [9][13].
Одна из проблем формирования управляющих воздействий в виде ПИД регулятора — возможные погрешности при дифференцировании измерительной информации. Чтобы их избежать, используем:
- энкодеры (для измерения текущих углов поворота φi звеньев экзоскелета);
- блоки инерциальных датчиков из микромеханических гироскопов (для измерения угловых скоростей) и акселерометров (для оценки угловых скоростей
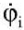 и ускорений
и ускорений 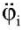 ).
).
Модель измерений углов поворота с помощью энкодеров можно представить в виде:
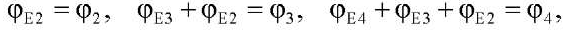 (7)
(7)
где φE2. φE3. φE4 — показания энкодеров, расположенных в шарнирах А1, А2, А3 (рис. 1).
Модель измерений угловых скоростей с помощью микромеханических гироскопов можно записать в виде:
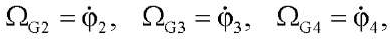 (8)
(8)
где ΩG2, ΩG3, ΩG4 — показания гироскопов, закрепленных на звеньях экзоскелета.
Для оценки угловых скоростей и ускорений с помощью акселерометров можно использовать по два двухосевых акселерометра, которые расположены на противоположных концах каждого из звеньев. Они измеряют в проекциях на оси xiyi (i = 1, 2, 3) кажущиеся ускорения, связанные с соответствующими звеньями.
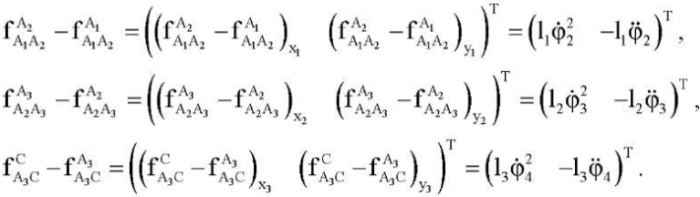 (9)
(9)
Здесь
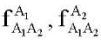 — векторы показаний двухосевых акселерометров, закрепленных на звене A1A2 и расположенных в точках A1 и A2 соответственно;
— векторы показаний двухосевых акселерометров, закрепленных на звене A1A2 и расположенных в точках A1 и A2 соответственно;
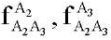 — векторы показаний двухосевых акселерометров, закрепленных на звене A2A3 и расположенных в точках A2 и A3 соответственно;
— векторы показаний двухосевых акселерометров, закрепленных на звене A2A3 и расположенных в точках A2 и A3 соответственно;
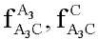 — векторы показаний двухосевых акселерометров, закрепленных на звене A3C и расположенных в точках A3 и C соответственно;
— векторы показаний двухосевых акселерометров, закрепленных на звене A3C и расположенных в точках A3 и C соответственно;
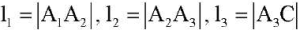 — расстояния между парами акселерометров, закрепленных на звеньях A1A2, A2A3, и A3C соответственно.
— расстояния между парами акселерометров, закрепленных на звеньях A1A2, A2A3, и A3C соответственно.
Объединим уравнения (7)–(9) и запишем формулы для оценки углов поворота, угловых скоростей и ускорений:
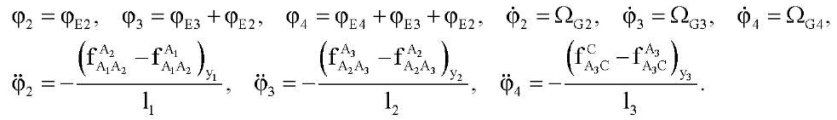 (10)
(10)
Для коррекции оценок модулей угловых скоростей можно использовать уравнения:
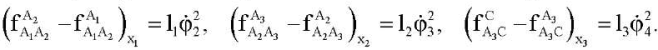 (11)
(11)
Таким образом, для оценки углов поворота, угловых скоростей и угловых ускорений звеньев экзоскелета можно обработать измерения фильтром скользящего среднего, алгоритмом фильтра Калмана и др. [10][13][15].
В самом простом варианте замыкания цепи обратной связи при формировании управления получим выражения для управляющих моментов:
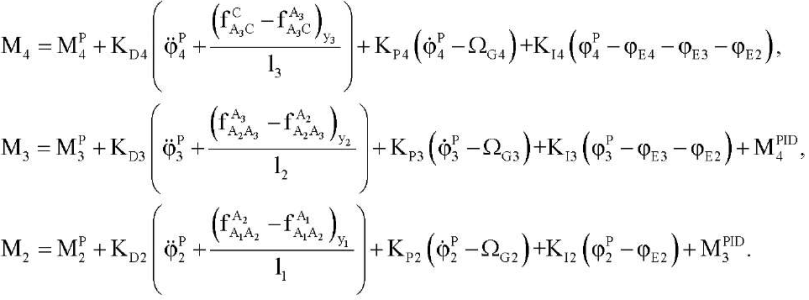 (12)
(12)
Введение в систему управления обратной связи по угловым ускорениям позволяет применить диагонализацию матрицы инерционных сил для снижения перекрестного влияния между обобщенными координатами.
Смоделируем движения экзоскелета для проверки работоспособности предложенного закона управления. В качестве программного движения рассмотрим:
- смену положения из сидячего в стоячее [7];
- стабилизацию вертикального положения экзоскелета при начальных отклонениях звеньев от вертикали.
Результаты исследования. Для численного моделирования системы возьмем параметры математической модели экзоскелета из [6][7]. Рассмотрим частный случай, выбрав одинаковые коэффициенты ПИД регулятора для каждого привода:
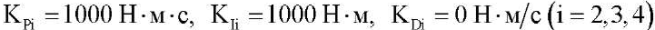
На рис. 2 приведены зависимости от времени для углов поворота и угловых скоростей звеньев экзоскелета. Их получили при управляющих моментах, соответствующих подъему из положения сидя. Как видно из рис. 2 а, по окончании движения углы поворота каждого звена равны φ2 = φ3 = φ4 = 90°, что соответствует стоянию.
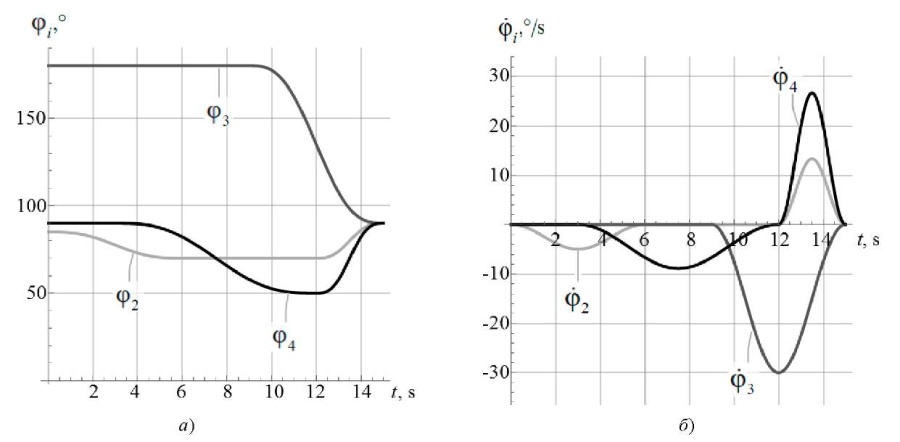
Рис. 2. Результаты моделирования подъема из положение сидя без начальных отклонений от программного движения в углах поворота звеньев экзоскелета: а — углы поворота звеньев; б — угловые скорости звеньев
Теперь рассмотрим случай с отклонениями около 20° в углах поворота звеньев по сравнению с начальным положением, заданным в программном движении. Результаты моделирования подъема из положения сидя приведены на рис. 3. Как и на рис. 2, по окончании времени движения значения углов поворота равны φ2 = φ3 = φ4 = 90°. Следовательно, использование комбинации программного управления и управления в виде ПИД регулятора точно приводит экзоскелет к требуемому положению.
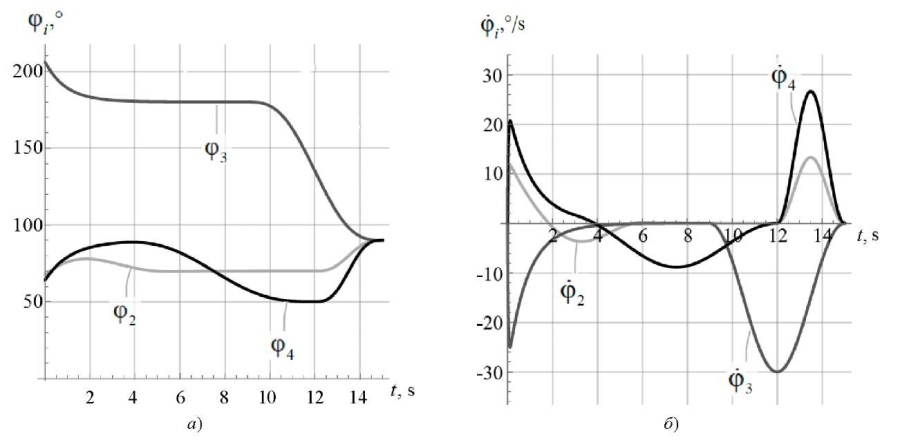
Рис. 3. Результаты моделирования подъема из положения сидя при начальных отклонениях от программного движения в углах поворота звеньев экзоскелета: а — углы поворота звеньев; б — угловые скорости звеньев
Таким образом, при моделировании программного движения показана работоспособность предложенного закона формирования управляющих воздействий, описанного в (4) и (12).
Вертикальное положение экзоскелета неустойчиво без управления, поэтому возмущающие факторы могут обусловить отклонения от равновесия вплоть до падения экзоскелета.
Проверим работоспособность предложенного управления в задаче стабилизации вертикального положения экзоскелета. Значения для программного движения: 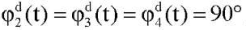 . Рассмотрим случай, когда в углах поворота звеньев есть отклонения около 20° от вертикального положения (рис. 4).
. Рассмотрим случай, когда в углах поворота звеньев есть отклонения около 20° от вертикального положения (рис. 4).
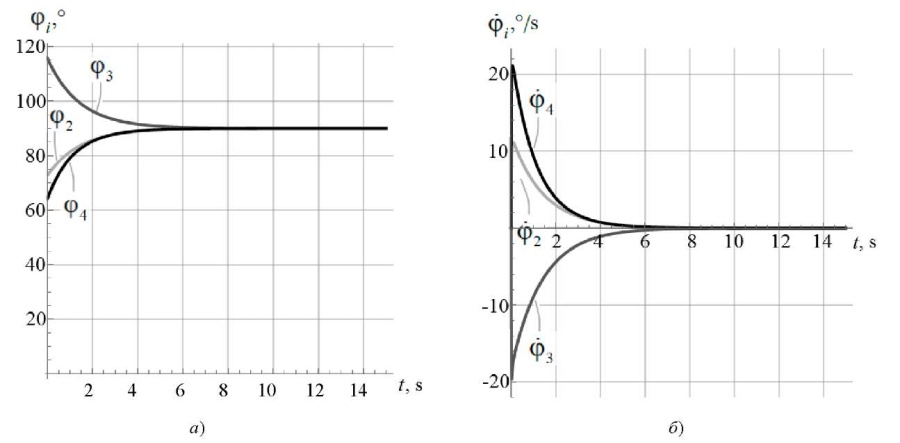
Рис. 4. Результаты моделирования стабилизации вертикального положения при начальных отклонениях от программного движения в углах поворота звеньев экзоскелета: а — углы поворота звеньев; б — угловые скорости звеньев
Из рис. 4 видно, что предложенное управление обеспечивает стабилизацию вертикального положения звеньев экзоскелета.
Для сравнения приведем результаты моделирования стабилизации вертикального положения при использовании следующих значений коэффициентов ПИД регулятора:
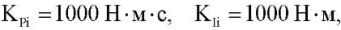
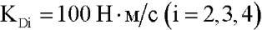 (рис. 5).
(рис. 5).
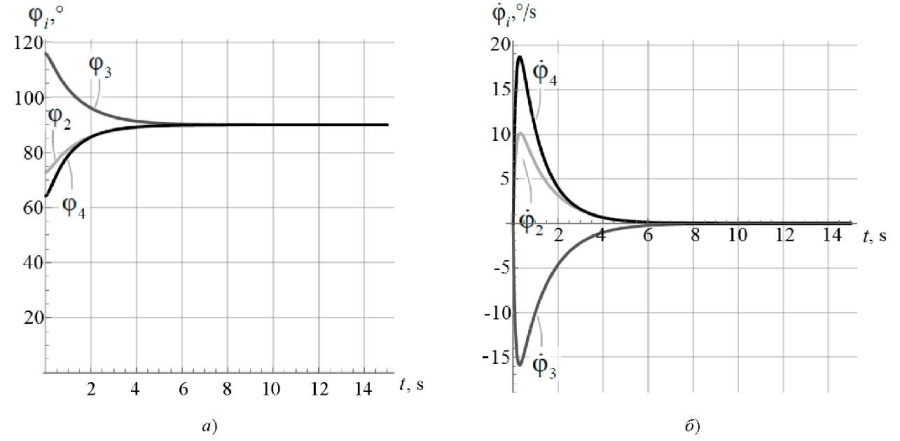
Рис. 5. Результаты моделирования стабилизации вертикального положения при начальных отклонениях от программного движения в углах поворота звеньев экзоскелета: а — углы поворота звеньев; б — угловые скорости звеньев
Из рис. 5 видно, что при использовании дифференциального звена 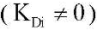 регулятора можно снизить выбросы в зависимостях угловых скоростей звеньев экзоскелета по сравнению со случаем
регулятора можно снизить выбросы в зависимостях угловых скоростей звеньев экзоскелета по сравнению со случаем 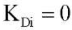 (рис. 4 б).
(рис. 4 б).
Итак, рассмотрена возможность управления звеньями экзоскелета нижних конечностей с использованием показаний энкодеров и блоков инерциальных датчиков (микромеханических гироскопов и акселерометров). Результаты моделирования доказывают действенность данного подхода.
Обсуждение и заключения. Предлагаемое решение задачи управления движением экзоскелета может быть использовано в медицинских приложениях, в том числе для вертикализации пациентов с нарушениями функций опорно-двигательного аппарата.
Итак, данные блоков инерциальных датчиков можно использовать в задаче оценивания состояния звеньев экзоскелета — их угловых скоростей и ускорений. При этом нет необходимости в численном дифференцировании измерительной информации энкодеров. Таким образом, в систему управления можно вводить обратную связь по угловым ускорениям, что позволяет улучшать переходные процессы при управлении движением экзоскелета.
1. Оптимизация времени вертикализации экзоскелета по критерию энергоэффективности / С. Ф. Яцун [и др.] // Вибрационные технологии, мехатроника и управляемые машины. Курск : Изд-во Юго-Зап. гос. ун-та, 2016. Ч. 2. С. 151–160.
Список литературы
1. Exoskeletons for Industrial Application and Their Potential Effects on Physical Work Load / M. P. De Looze, T. Bosch, F. Krause [et al.] // Ergonomics. — 2015. — Vol. 59. — P. 671–681. https://doi.org/10.1080/00140139.2015.1081988
2. Геворкян, А. А. Роботизированная механотерапия: возможность применения экзоскелета для нижних конечностей у пациентов с нарушением функции ходьбы при рассеянном склерозе / А. А. Геворкян, С. В. Котов, В. Ю. Лиждвой // Альманах клинической медицины. — 2020. — Т. 48, № 1. — С. 7–12.
3. Экзоскелет — состояние проблемы и перспективы внедрения в систему абилитации и реабилитации инвалидов (аналитический обзор) / А. А. Воробьев, О. А. Засыпкина, П. С. Кривоножкина [и др.] // Вестник Волгоградского государственного медицинского университета. — 2015. — Вып. 2 (54). — С. 9–17.
4. Трехзвенная математическая модель для задачи стабилизации вертикальной позы человека / И. В. Новожилов, А. В. Терехов, А. В. Забелин [и др.] // Математическое моделирование движений человека в норме и при некоторых видах патологии. — Москва : Изд-во механико-математического факультета МГУ. — 2005. — С. 7–20.
5. Моделирование процессов вставания экзоскелета из положения сидя / С. И. Савин, С. Ф. Яцун, А. С. Яцун, Г. Я. Пановко // Проблемы машиностроения и надежности машин. — 2016. — Т. 3. — С. 19–24.
6. Saypulaev, M. R. Development of the Lower Extremity Exoskeleton Dynamics Model Using in the Task of the Patient Verticalization / M. R. Saypulaev, Yu. Yu. Zuev, G. R. Saypulaev // Journal of Physics: Conference Series. — 2021. — Vol. 2096. — Art. 0120421. https://doi.org/10.1088/1742-6596/2096/1/012042
7. Zuev, Yu. Yu. Laws of Motion of the Lower Extremities and Structural-parametric Synthesis of Electro-Hydraulic Executive Modules of the Active Exoskeleton According to the Criterion of Energy Sufficiency / Yu. Yu. Zuev, M. R. Saypulaev, V. Doni // Journal of Physics: Conference Series. — 2021. — Vol. 2096. — Art. 012044. 10.1088/1742-6596/2096/1/012044
8. Яцун, С. Ф. Определение параметров приводов биоинженерных мехатронных модулей для экзоскелета нижних конечностей человека / С. Ф. Яцун, А. Н. Рукавицин // Известия Юго-Западного государственного университета. — 2012. — Т. 2, № 1. — С. 196–200.
9. Savin, S. I. Energy-Efficient Algorithm of Control of Exoskeleton Verticalization / S. I. Savin, A. S. Yatsun, S. F. Yatsun // Journal of Machinery Manufacture and Reliability. — 2017. — Vol. 46. — P. 512–517.
10. A Robust Adaptive-Fuzzy-Proportional-Derivative Controller for a Rehabilitation Lower Limb Exoskeleton / N. Aliman, R. Ramli, S. M. Haris [et al.] // International Journal of Engineering Science and Technology. — 2022. — Vol. 35. — Art. 101097. 10.1016/j.jestch.2022.101097
11. Adaptive Particle Swarm Optimization of PID Gain Tuning for Lower-Limb Human Exoskeleton in Virtual Environment / M. S. Amiri, R. Ramli, M. F. Ibrahim [et al.] // Mathematics. — 2020. — Vol. 8. — Art. 2040. 10.3390/math8112040
12. Development and Control of an Electro-Hydraulic Actuator System for an Exoskeleton Robot / Dongyoung Lee, Buchun Song, Sang Yong Park, Yoon Su Baek // Applied Sciences. — 2019. — Vol. 9. — Art. 4295. 10.3390/app9204295
13. Lora-Millan, J. S. An IMUs-Based Extended Kalman Filter to Estimate Gait Lower Limb Sagittal Kinematics for the Control of Wearable Robotic Devices / J. S. Lora-Millan, A. F. Hidalgo, E. Rocon // IEEE Access. — 2021. — Vol. 9. — P. 144540–144554. 10.1109/ACCESS.2021.3122160
14. Minimizing Human-Exoskeleton Interaction Force by Using Global Fast Sliding Mode Control / Duong Mien Ka, Cheng Hong, Tran Huu Toan, Jing Qiu // International Journal of Control, Automation and Systems. — 2016. — Vol. 14. — P. 1064–1073. 10.1007/s12555-014-0395-7
15. Балакришнан, А. В. Теория фильтрации Калмана / А. В. Балакришнан. — Москва : Книга по требованию. — 2021. — 164 с.
Об авторах
Г. Р. СайпулаевРоссия
Сайпулаев Гасан Русланович, аспирант и ассистент кафедры «Робототехника, мехатроника, динамика и прочность машин»
ScopusID
111250, г. Москва, ул. Красноказарменная, 14
М. Р. Сайпулаев
Россия
Сайпулаев Муса Русланович, аспирант кафедры «Робототехника, мехатроника, динамика и прочность машин»
ScopusID
111250, г. Москва, ул. Красноказарменная, 14
И. В. Меркурьев
Россия
Меркурьев Игорь Владимирович, заведующий кафедрой «Робототехника, мехатроника, динамика и прочность машин»
ScopusID
111250, г. Москва, ул. Красноказарменная, 14
Б. И. Адамов
Россия
Адамов Борис Игоревич, доцент кафедры «Робототехника, мехатроника, динамика и прочность машин»
ScopusID
111250, г. Москва, ул. Красноказарменная, 14
Р. Б. Гарсиа
Россия
Гарсиа Ройлан Бельо, аспирант кафедры «Робототехника, мехатроника, динамика и прочность машин»
111250, г. Москва, ул. Красноказарменная, 14
Рецензия
Для цитирования:
Сайпулаев Г.Р., Сайпулаев М.Р., Меркурьев И.В., Адамов Б.И., Гарсиа Р.Б. Применение блока инерциальных датчиков для оценивания положения и управления движением экзоскелета нижних конечностей. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):204-213. https://doi.org/10.23947/2687-1653-2022-22-3-204-213
For citation:
Saypulaev G.R., Saypulaev M.R., Merkuryev I.V., Adamov B.I., Garcia R.B. Application of an Inertial Sensor Unit for Position Estimation and Motion Control of the Lower-Extremity Powered Exoskeleton. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):204-213. https://doi.org/10.23947/2687-1653-2022-22-3-204-213













































