Scroll to:
Analytical Estimation of the Natural Oscillation Frequency of a Planar Lattice
https://doi.org/10.23947/2687-1653-2022-22-4-315-322
Abstract
Introduction. A new scheme of a flat statically determinate regular lattice is proposed. The lattice rods are hinged.
The study aims at deriving a formula for the dependence on the number of panels of the first natural oscillation frequency of nodes endowed with masses, each of which has two degrees of freedom in the lattice plane. The rigidity of all rods is assumed to be the same, the supports (movable and fixed hinges) — nondeformable.
Another objective of the study is to find the dependence of the stresses in the most compressed and stretched rods on the number of panels in an analytical form.
Materials and Methods. An approximate Dunkerley’s method was used to determine the lower bound for the lattice natural frequency. The lattice rigidity was found in analytical form according to Maxwell-Mohr formula. The rod stresses and the reactions of the supports were determined from the equilibrium equations compiled for all lattice nodes. Generalization of the result to an arbitrary number of panels was performed by induction using Maple symbolic math operators for analytical solutions to a number of problems for lattices with different number of panels.
Results. The lower analytical estimate of the first oscillation frequency was in good agreement with the numerical solution for the minimum frequency of the oscillation spectrum of the structure. Formulas were found for the stresses in four most compressed and stretched rods and their linear asymptotics. All required transformations were made in the system of Maple symbolic math.
Discussion and Conclusions. The obtained dependence of the first frequency of lattice oscillations on the number of panels, mass and dimensions of the structure has a compact form and can be used as a test problem for numerical solutions and optimization of the structure.
Keywords
For citations:
Kirsanov M.N. Analytical Estimation of the Natural Oscillation Frequency of a Planar Lattice. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):315-322. https://doi.org/10.23947/2687-1653-2022-22-4-315-322
Introduction. Lattice structures are widely used in mechanical engineering as load-bearing or enclosing elements. The procedure of calculating the natural frequencies of lattice vibrations is traditionally based on numerical evaluations, which, as a rule, use the finite element technique with application-specific packages. Analytical methods are used much less frequently. The development of mathematical packages of symbolic mathematics (Maple, Wolfram Mathematica, Derive, Maxima, etc.) enables to search for such solutions for regular systems in which it is possible to take into account the order of regularity (the number of periodic structures of the construct, specifically, the number of panels) in the solution. The study aims at finding analytical dependence of the lower boundary of the first part of the lattice structure on the number of panels. The dependence of the solution on the number of panels expands significantly the scope of the formula and makes it possible to optimize the design by any parameter. For the first time, R. Hutchinson and N. Fleck were engaged in the problem of the existence and calculation of statically definable regular truss systems [1][2]. In [3][4], such constructions were studied in connection with optimization problems. There are also analytical solutions in the form of finite formulas for the programs of regular planar [5–7] and spatial trusses [8]. Reference book [9] provides formulas for deflections and displacements of supports for flat trusses and lattices with an arbitrary number of panels. In [10–13], lower estimates of the first natural frequency of flat trusses were obtained, found by induction for an arbitrary order of a regular structure.
There is another line of analytical research of structures [14–16]. In these works, the solution is in the Maple system in the form of trigonometric series.
In this paper, the induction method has been used, which consists in generalizing a number of separate calculations of lattices with a consistently increasing number of panels for the case of an arbitrary number of panels. All transformations used Maple symbolic math operators. The object of the study was a new scheme of a regular statically definable flat lattice of rectangular shape in the form of an asymmetric truss on two supports. The task was to deduce the analytical dependence of the fundamental vibration frequency of the structure on the number of panels. The derived formula can be used in optimization problems and for estimating numerical solutions of such large-order structures, for which numerical calculations may contain errors associated with the round-off accumulation.
Materials and Methods. There are 5(n + 1) nodes, including three support nodes (one for fixing the left support, two — for the right bars modeling a fixed hinge), in a truss with length (2n – 1)a and height 4h. The number of rods, including three support rods, is N = 10n + 4. The truss is statically definable. When calculating the vibration frequencies of the structure, it is assumed that the mass of the truss is concentrated in the nodes.
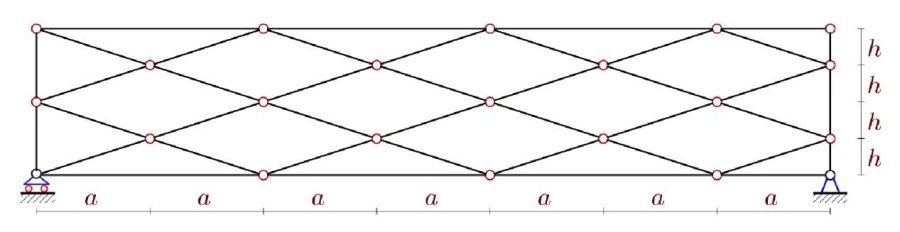
Fig. 1. Lettice diagram, n=4 (the author's figure)
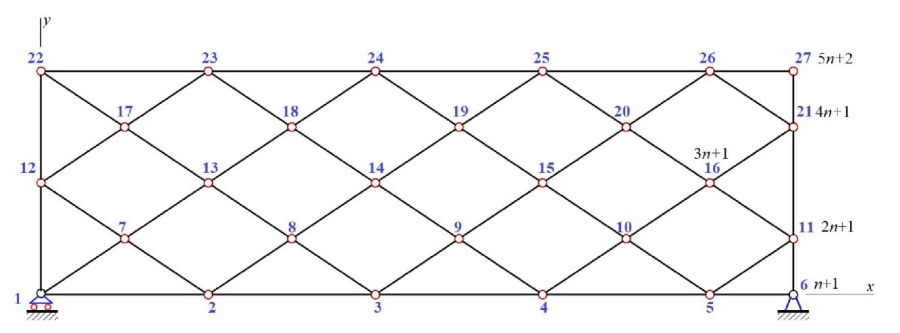
Fig. 2. Lattice numbering, n=5 (the author's figure)
The force calculation is performed in the Maple system according to the program [17]. The nodes and rods of the truss are numbered (Fig. 2). The origin of coordinates is in the left support. Coordinates are set in cycles.
The lattice structure is established by the order of connection of the rods in the nodes. To do this, special lists Фа = [ i1,i2] of numbers i1,i2 of the rod ends α = 1,..,N are introduced. The rods of the lower outer contour, specifically, have the following node numbers at the ends: Фi = [ i,i + 1], i = 1,..,n. The numbers of the ends of the other rods of the lattice are set in the same way. The system of equilibrium equations of nodes in projections on the coordinate axis is compiled in matrix form GS = B, S — vector of all rod stresses, including three reactions of the supports, B — vector of external nodal loads. System matrix G consists of guiding cosines of stresses. In this case, the same stress is applied to different rod ends and are multidirectional:
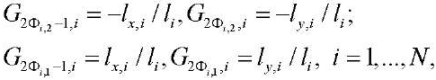
where
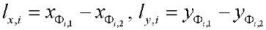 — projections of conditional vectors of rods on the coordinate axis,
— projections of conditional vectors of rods on the coordinate axis,
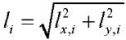 — length of rod i = 1,..,N.
— length of rod i = 1,..,N.
The lattice rod stresses can be obtained from solving a system of equations in symbolic or numerical form.
Research Results. Consider the stress state of the lattice in the case of loading at all angles by vertical stresses P (Fig. 1). Figure 3 shows a distribution pattern in the rods of the structure. The thicknesses of the segments in the Figure are conditionally proportional to the modules of the corresponding stresses. Compressed rods are highlighted in blue, stretched rods — in red. The stress values are attributed to magnitude P of the load on the node, rounded to two significant digits. The most stretched rod was expected to be in the middle of the lower belt, the most compressed one — in the lower rod on the right side of the structure.
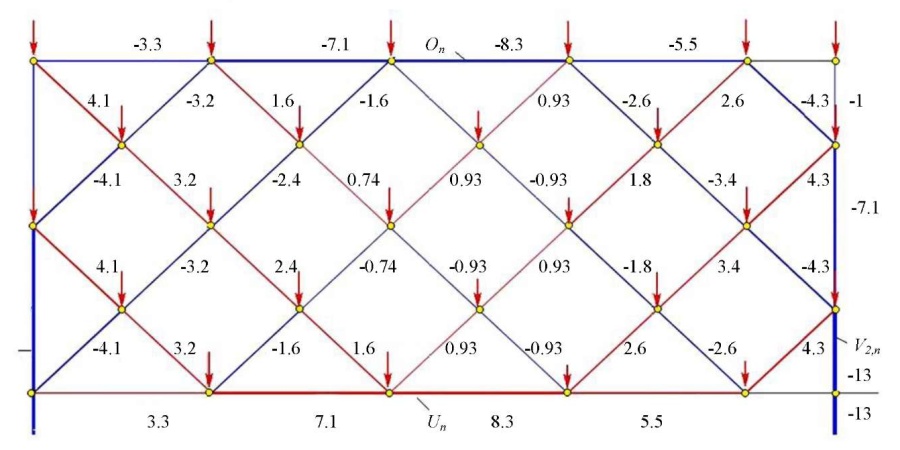
Fig. 3. Stress distribution on the lattice rods, a=4m, h=3m, n=5 (the author's figure)
The analytical dependences of the stresses in the most compressed and stretched rods on the number of panels are obtained by induction from the generalization of the sequences of individual solutions. Say, for stress V1,n in the lower rod of the left side of the lattice, the sequence of values for lattices of order n = 1, 2, 3, ... has the form: V1,n / P = –2, –12, –28, –54, –84, –126, –170, –228, –286, –360,... . The recurrent equation for the common term of this sequence is given by operator rgf_findrecur of the Maple system:
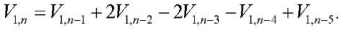
Solving the equation using rsolve operator:
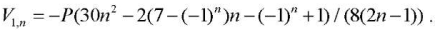
Other expressions for critical stresses are found in the same way:
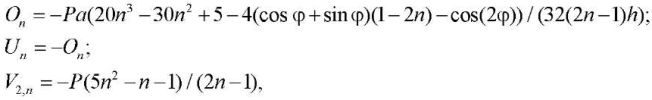
where φ = πn / 2. It is of interest to note that stresses V1,n and V2,n do not depend on the size of a and h.
The analytical form of solutions allows us to find their asymptotics using Maple operator limit:
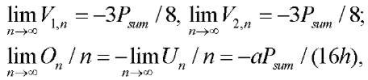
where Psum = 5nP — total load on the lattice. For stresses V1,n and V2,n in the rods on the sides of the lattice, the as-ymptotes are horizontal, for stresses On and Un on the upper and lower belts, they are inclined.
Natural frequency. Of the entire spectrum of natural vibration frequencies of a structure, the first, lowest frequency is the most important for assessing its dynamic behavior. Its value is included in most solutions to the problems of structural dynamics. This value is required, among other things, to assess the seismic characteristics of the structure. The lower bound of the first frequency for regular structures in the form of a dependence on the number of panels can be obtained analytically.
When determining the natural vibration frequencies of the structure, a simplified model of the inertial properties of the truss is adopted. It is assumed that the rods of the lattice have no mass, and the entire mass is distributed evenly across the nodes. Neglecting the movement of the supports, we get the total number of degrees of freedom equal to K = 10n. Donkerley’s formula [13] for estimating the lower bound of the first frequency has the form:
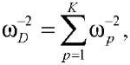 (1)
(1)
where ωp — partial frequencies of the structure. Partial frequencies of mass vibrations are determined from the equation:
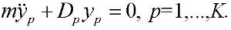 (3)
(3)
Here, yp = yp (t) — coordinate of node p; ÿp — acceleration; Dp — rigidity, inverse compliance δp = 1 / Dp . Compliance can be calculated using the Maxwell-Mohr formula:
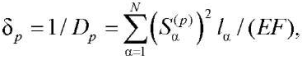 (4)
(4)
where Sα(p) — stress in the rod with number α from the action of the vertical unit force applied to node p, where the mass is located. The rigidity rate and partial frequency depend on the place where the mass is located. For harmonic vibrations 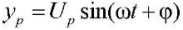 from (3),
from (3), 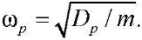
follows. The substitution of this expression in (4) gives a formula for estimating the first frequency only by partial frequencies of mass vibrations:
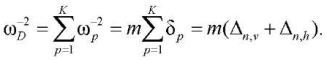 (5)
(5)
The amounts for vibrations in the vertical Δn,v and horizontal Δn,h directions are separately allocated. Successive calculation of the vibration frequencies of lattices of various orders shows that coefficient Δn,v in (5) has the form:
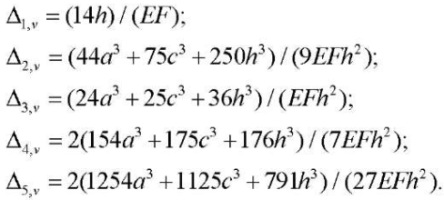
In general, for vertical partial frequencies:
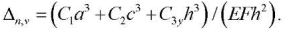 (6)
(6)
For partial frequencies horizontally:
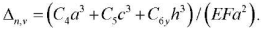 (7)
(7)
Using Maple operator rgf_findrecur, we obtain a homogeneous recurrent equation of the seventh order to determine the coefficient for a3:
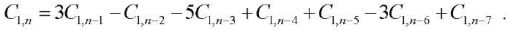
The solution to the equation is given by rsolve operator:
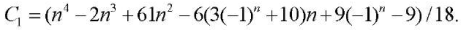 (8)
(8)
Other coefficients are found in the same way:
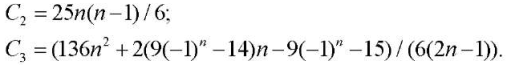 (9)
(9)
Similarly:
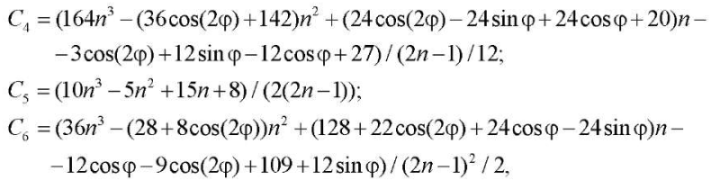 (10)
(10)
where φ = πn / 2.
As a result, the expression for the lower estimate of the first frequency follows from (5–7):
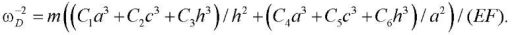 (11)
(11)
Estimation of the solution error (11) is possible from comparison to the minimum frequency of the entire spectrum of lattice natural frequencies obtained numerically. The spectrum of a system with many degrees of freedom is found from solving the eigenvalue problem of the matrix. Differential equations of mass dynamics of a structure with a number of degrees of freedom K are written in matrix form:
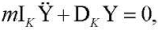 (12)
(12)
where DK — truss rigidity matrix, Y — mass displacement vector, IK — unity matrix. Let BK be the matrix, inverse of DK. Multiplying (12) from the left by BK, gives the equation:
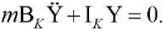 (13)
(13)
Connection Ϋ = –ω2Y is valid for harmonic vibrations with frequency ω. Hence, from (13), the problem of eigen-values follows: BKY = λY, where λ = 1 (ω2m) — the eigenvalues of matrix BK. The elements of the compliance matrix are found from the Maxwell-Mohr formula. To calculate the eigenvalues of a matrix in the Maple system, Eigen-values operator from LinearAlgebra package is used. In general, the solution to this problem can be obtained only in numerical form.
Example. The steel lattice has panel length a = 2m, height h = 1m, masses in nodes m = 300 kg, rod rigidity EF = 0.8 ∙ 105 kN. Figure 4 shows the dependences of the first frequency on the number of panels obtained numerically and analytically.
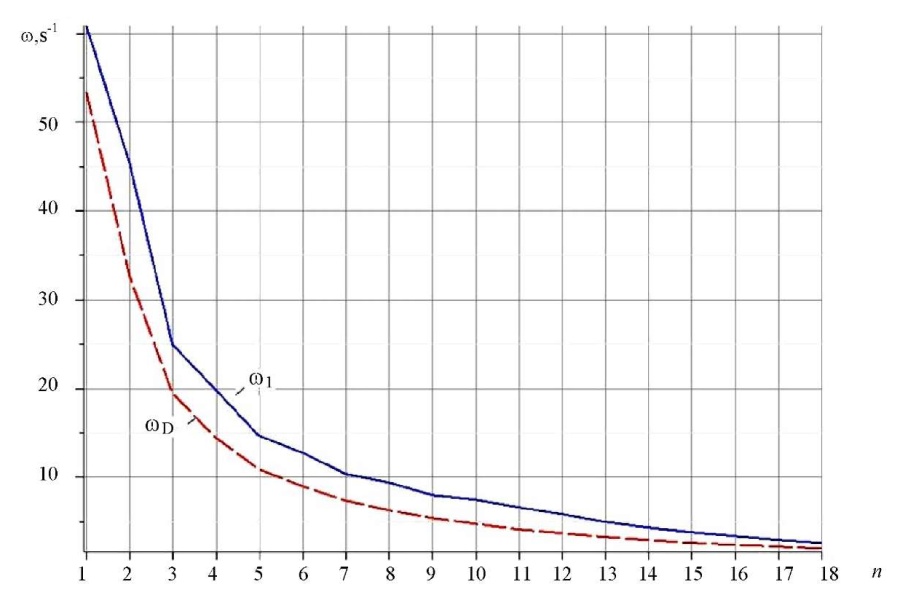
Fig. 4. Comparison of the first natural vibration frequency of lattice ω1 and its lower analytical estimate ωD depending on the number of panels (the author's figure)
Relative error ε = (ω1 – ωD) / ω1, depending on the number of panels (Fig. 5), shows that with an increase in the number of panels, the error, starting from n =1, increases, and then monotonously and quickly decreases. This is particularly important when using the obtained formula through calculating lattices with a large number of panels, for which the numerical count starts to gain an error associated with the accumulation of rounding errors, and the cost of computer resources is growing rapidly.
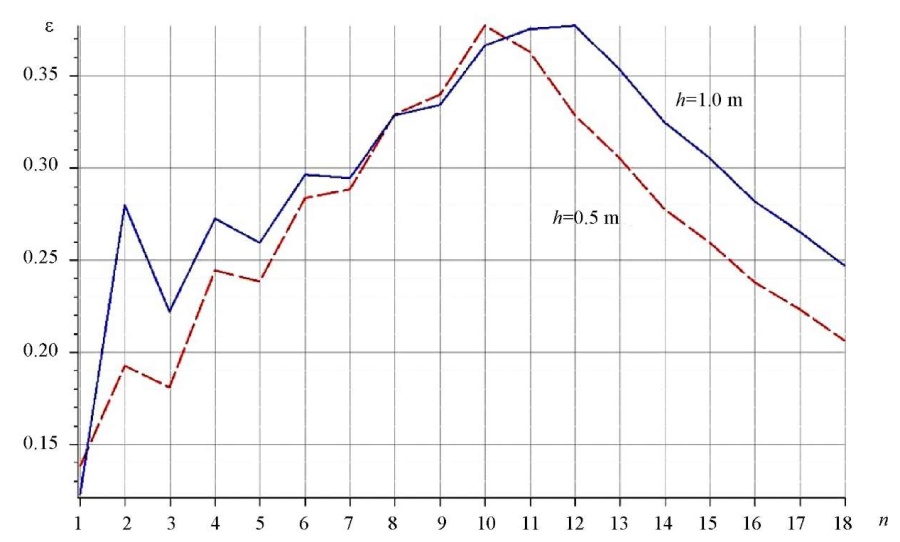
Fig. 5. The error of the analytical solution for the natural frequency depending on the number of panels and height h (the author's figure)
Discussion and Conclusions. A scheme of a statically definable plane lattice was proposed. The task was to obtain an analytical expression of the lower bound of the first natural vibration frequency of a lattice truss for an arbitrary number of panels in the structure. The solution was obtained by induction in the Maple system. The presence of extrema on the constructed curves made it possible to optimize the number of lattice panels by choosing the highest accuracy of the estimate and selecting the required vibration frequency. The proposed study took into account horizontal mass vibrations. Considering horizontal vibrations somewhat complicated the final calculation formula, making it more cumbersome. In addition to the Donkerley’s method used, there was a more accurate Rayleigh energy method for evaluating the first frequency, which gave an estimate of the first frequency from above. However, even this solution in the case under consideration had an unnecessarily cumbersome appearance and was not given here.
References
1. Hutchinson, R. G. Microarchite0ctured Cellular Solids — the Hunt for Statically Determinate Periodic Trusses / R. G. Hutchinson, N. A. Fleck // ZAMM Journal for Applied Mathematics and Mechanics. — 2005. — Vol. 85. — P. 607–617. doi: 10.1002/zamm.200410208
2. Hutchinson, R. G. The Structural Performance of the Periodic Truss / R. G. Hutchinson, N. A. Fleck // Journal of the Mechanics and Physics of Solids. — 2006. — Vol. 54. — Р. 756 –782. doi: 10.1016/J.JMPS.2005.10.008
3. Kaveh, A. Optimal Analysis of Structures by Concepts of Symmetry and Regularity / A. Kaveh. — Vienna : Springer, 2013. — 463 р. doi: 10.1007/978-3-7091-1565-7
4. Kaveh, A. Truss Optimization with Natural Frequency Constraints Using a Hybridized CSS–BBBC Algorithm with Trap Recognition Capability / A. Kaveh, A. Zolghadr // Computers & Structures. — 2012. — Vol. 102–103. — Р. 14–27. doi: 10.1016/J.COMPSTRUC.2012.03.016
5. Ovsyannikova, V. M. Dependence of Deformations of a Trapezous Truss Beam on the Number of Panels / V. M. Ovsyannikova // Structural Mechanics and Structures. — 2020. — Vol. 3 (26). — Р. 13–20.
6. Ilyushin, A. S. The Formula for Calculating the Deflection of a Cmpound Externally Statically Indeterminate Frame / A. S. Ilyushin // Structural Mechanics and Structures. — 2019. — Vol. 22. — Р. 29–38.
7. Qiao Dai. Analytical Dependence of Planar Truss Deformations on the Number of Panels / Qiao Dai // AlfaBuild. — 2021. — Vol. 17. — Р. 1701. URL: https://alfabuild.spbstu.ru/userfiles/files/AlfaBuild/AlfaBuild_2021_17/1701.pdf?ysclid=lcomt14c9t623424160
8. Kirsanov, M. N. The Stress-Strain State of a Rectangular Covering Spatial Truss / M. N. Kirsanov // Construction of Unique Buildings and Structures. — 2020. — Vol. 91. — Р. 9104.
9. Kirsanov, M. Trussed Frames and Arches: Schemes and Formulas / M. Kirsanov. — UK : Cambridge Scholars Publishing Lady Stephenson Library, 2020. — 178 р.
10. Petrichenko, E. A. Lower Bound of the Natural Oscillation Frequency of the Fink Truss / E. A. Petrichenko // Structural Mechanics and Structures. — 2020. — Vol. 3 (26). — Р. 21–29.
11. Petrenko, V. F. The Natural Frequency of a Two-Span Truss / V. F. Petrenko // AlfaBuild. — 2021. — Vol. 20. — Р. 2001.
12. Vorobev, O. V. Bilateral Analytical Estimation of the First Frequency of a Plane Truss / O. V. Vorobev // Construction of Unique Buildings and Structures. — 2020. — Vol. 92. — Р. 9204.
13. Vorobyev, O. About Methods of Obtaining Analytical Solution for Eigenfrequencies Problem of Trusses / O. Vorobyev // Structural Mechanics and Structures. — 2020. — Vol. 24. — Р. 25–38.
14. Goloskokov, D. P. Approximate Analytical Solutions in the Analysis of Thin Elastic Plates / D. P. Goloskokov, A. V. Matrosov // AIP Conference Proceedings. — 2018. — Vol. 1959. — Art. 070012. doi: 10.1063/1.5034687
15. Goloskokov, D. P. Approximate Analytical Approach in Analyzing an Orthotropic Rectangular Plate with a Crack / D. P. Goloskokov, A. V. Matrosov // Materials Physics and Mechanics. — 2018. — Vol. 36. — Р. 137–141.
16. Goloskokov, D. P. Comparison of Two Analytical Approaches to the Analysis of Grillages / D. P. Goloskokov, A. V. Matrosov // In: Proc. 2015 Int. Conf. “Stability and Control Processes” in Memory of V. I. Zubov (SCP). — 2015. — Р. 382–385. doi: 10.1109/SCP.2015.7342169
17. Buka-Vaivade, K. Calculation of Deformations of a Cantilever-Frame Planar Truss Model with an Arbitrary Number of Panels / K. Buka-Vaivade, M. N. Kirsanov, D. O. Serdjuks // Vestnik MGSU. — 2020. — Vol. 15. — P. 510–517. doi: 10.22227/1997-0935.2020.4.510-517
About the Author
M. N. KirsanovRussian Federation
14, Krasnokazarmennaya St.
Moscow
Review
For citations:
Kirsanov M.N. Analytical Estimation of the Natural Oscillation Frequency of a Planar Lattice. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):315-322. https://doi.org/10.23947/2687-1653-2022-22-4-315-322













































