Перейти к:
Расчёт угловых координат для системы управления двухзвенным манипулятором промышленного робота
https://doi.org/10.23947/2687-1653-2022-22-4-346-352
Аннотация
Введение. Одной из задач двухзвенных манипуляторов промышленных роботов, выполняющих перемещение рабочего органа по сложным траекториям (например, роботов-сварщиков), является необходимость тщательного программирования их движения. Для этих целей используются методы ручного программирования или методы обучения. Эти методы достаточно трудоёмки и требуют высокой квалификации обслуживающего персонала. Возможным вариантом решения проблемы программирования перемещений манипулятора является моделирование движения с расчётом угловых координат. Это может способствовать упрощению геометрической адаптации манипулятора в процессе отладки управляющей программы.
Поэтому целью работы явился расчет координат для программирования системы управления двухзвенным манипулятором, действующим в угловой системе координат и перемещающим рабочий орган по сложной траектории (например, при сварке автомобильных кузовов).
Материалы и методы. Рассмотрен двухзвенный манипулятор робота, действующий в угловой системе координат и предназначенный для циклически повторяющихся действий. Манипулятор состоит из двух вращающихся звеньев: «плеча» и «локтя», которые закреплены на основании. Основание может вращаться, что обеспечивает третью степень свободы. Такая конфигурация увеличивает рабочую область манипулятора и минимизирует площадь для его размещения на производстве. Перемещение рабочего органа манипулятора может выполняться, если кинематика обеспечивает его позиционирование по трём декартовым и трём угловым координатам. Для программного управления роботами, в том числе роботами-сварщиками, действующими в угловой системе координат и выполняющими движение рабочего органа по сложной траектории, требуется расчёт угловых координат перемещения рабочего органа двухзвенного шарнирного манипулятора. Система управления роботом должна определять положение инструмента в угловой системе координат, преобразуя его для удобства пользователя в координаты x, y и z декартовой системы координат.
Результаты исследования. Получены соотношения угловых и декартовых координат, которые можно использовать для расчёта при программировании системы управления двухзвенным манипулятором промышленного робота и организации обмена информацией между пользователем и системой управления, а также для проверки точности и отладки перемещения рабочего органа промышленного робота с использованием обратной связи.
Обсуждение и заключения. Представленные результаты работы могут быть использованы для программного управления роботом-сварщиком, действующим в угловой системе координат и выполняющим сложную траекторию перемещения рабочего органа двухзвенного шарнирного манипулятора (захвата). Манипулятор, действующий в угловой системе координат, можно использовать для контактной точечной сварки при перемещении рабочего органа по сложной траектории с применением позиционной или позиционно-контурной системы управления. Эти системы с помощью технологических команд управляют перемещением рабочего органа по заданной траектории.
Ключевые слова
Для цитирования:
Глушко С.П. Расчёт угловых координат для системы управления двухзвенным манипулятором промышленного робота. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):346-352. https://doi.org/10.23947/2687-1653-2022-22-4-346-352
For citation:
Glushko S.P. Calculation of Angular Coordinates for the Control System of a Two-Link Industrial Robot Manipulator. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):346-352. https://doi.org/10.23947/2687-1653-2022-22-4-346-352
Введение. Промышленные роботы используются для автоматизированного управления пространственной ориентацией орудий и объектов труда в различных технологических процессах1 [1–7]. Промышленный робот, как правило, включает манипулятор, имеющий несколько степеней подвижности, и устройство числового программного управления приводами. Манипулятор используется для перемещения захвата или инструмента по заданной траектории в заданные точки технологического пространства2 [1–3].
При разработке программ управления перемещениями захвата или инструмента промышленного робота по сложным траекториям (например, для роботов-сварщиков) используются сложные по организации и техническому оснащению методы обучения.
Для упрощения программирования системы управления двухзвенным манипулятором промышленного робота, перемещающего рабочий орган по сложной траектории (например, при сварке автомобильных кузовов), можно использовать моделирование его перемещений с расчётом угловых координат. Это упростит геометрическую адаптацию манипулятора и процесс разработки и отладки его управляющих программ.
Цель работы — расчёт угловых координат для программирования работы системы управления двухзвенным манипулятором, действующим в угловой системе координат и перемещающим рабочий орган по сложной траектории.
Материалы и методы. На практике используются четыре основных типа манипуляторов, которые действуют в цилиндрической, сферической, прямоугольной или угловой системах координат.
На рис. 1 показана рабочая область манипулятора робота, действующего в угловой системе координат. Манипулятор состоит из двух вращающихся звеньев — «плеча» и «локтя», которые закреплены на основании. Основание может вращаться, что обеспечивает третью степень свободы. Такая конфигурация увеличивает рабочую область манипулятора и минимизирует площадь для его размещения на производстве.
Манипулятор, действующий в угловой системе координат, можно использовать для контактной точечной сварки при перемещении горелки по сложной траектории. Для выполнения контактной точечной сварки чаще всего используются роботы с позиционной или позиционно-контурной системой управления. Эти системы с помощью технологических команд управляют перемещением горелки по заданной траектории при заданной ее ориентации с постоянной скоростью.
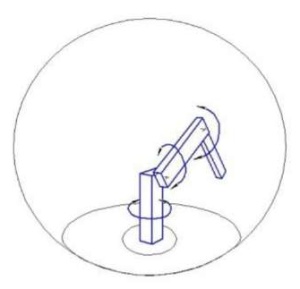
Рис. 1. Рабочая область манипулятора, действующего в угловой системе координат (рисунок автора)
При этом работа подвижных узлов манипулятора в зоне сварки может быть усложнена влиянием выделяемого тепла. Частично эта проблема решается применением водяного охлаждения горелок с автономными устройствами охлаждения. Для полного устранения этой проблемы потребуется дополнительно решить тепловую задачу с моделированием теплового процесса для определения и компенсации температурных расширений, вызванных нагревом электрическим разрядом или электрической дугой [8].
Результаты исследования. Для разработки программы управления роботом, который действует в угловой системе координат (рис. 1), необходимо выполнить расчет угловых координат перемещения рабочего органа манипулятора (захвата) [1–4][6][7]. На рис. 2 приведена его схема, состоящая из двух стержней 1 и 2, которые соединены сферическим шарниром 3 и плоским шарниром 4. Вся конструкция устанавливается на основании 5. Стержни манипулятора имеют длину 𝑙1 и 𝑙2. Шарнир 3 может вращаться в горизонтальной плоскости (угол α) и в вертикальной плоскости (угол β). Шарнир 4 вращается в вертикальной плоскости (угол γ).
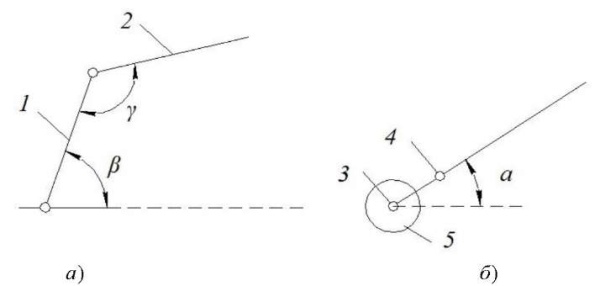
Рис. 2. Конструкция двухзвенного шарнирного манипулятора:
а — главный вид; б — вид сверху (рисунок автора)
На рис. 3 показана схема двухзвенного шарнирного манипулятора в виде полусферы с радиусом 𝑅=𝑙1+𝑙2 и с вырезанной полусферой с радиусом r, который определяется эмпирически при отладке работы манипулятора.
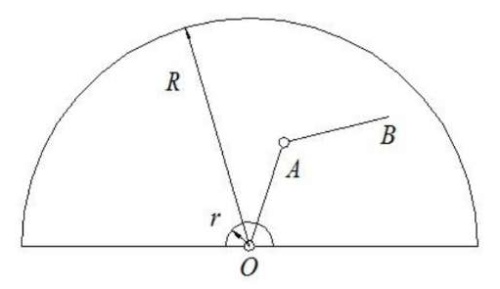
Рис. 3. Схема двухзвенного шарнирного манипулятора (рисунок автора)
Система управления манипулятором должна задавать положение инструмента в угловой системе координат и для удобства пользователя преобразовывать его в параметры декартовой системы координат.
Принимаем основание конструкции (точку О) за начало декартовой системы координат и располагаем её оси как показано на рис. 4.
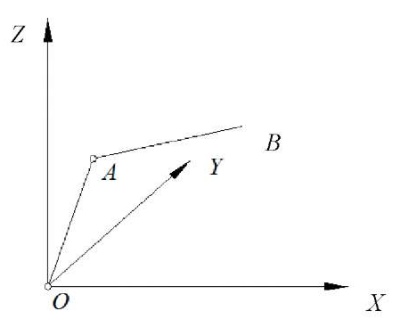
Рис. 4. Прямоугольная система координат с центром в точке O (рисунок автора)
Угол α проекции отрезка OB на плоскость XOY показан на рис. 5.
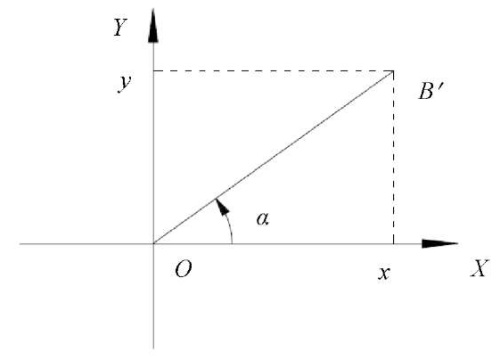
Рис. 5. Определение угла проекции отрезка OB на плоскость XOY (рисунок автора)
Угол α определяем по формуле:

где x и y — координаты точки B.
Знак «+» следует ставить, если y будет больше или равно нулю, а знак «–», когда y будет меньше нуля.
Углы на плоскости 𝑍𝑂𝐵´ 𝛽1, 𝛽2 и γ между осями координат и рычагами 𝑙1 и 𝑙2 показаны на рис. 6.
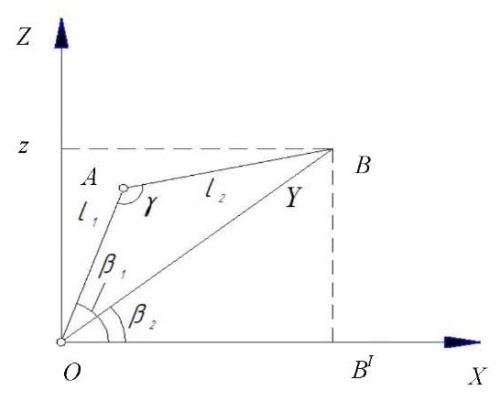
Рис. 6. Определение углов 𝛽1, 𝛽2 и γ (рисунок автора)
Формулы для определения углов 𝛽1, 𝛽2 и γ найдём, пользуясь теоремой косинусов:
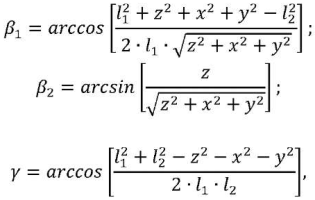
где x, y и z — координаты точки B.
Полученные соотношения можно использовать для расчёта угловых координат при разработке программ управления двухзвенным манипулятором промышленного робота, решения задач позиционного или контурно-позиционного управления с применением датчиков обратной связи для непрерывного контроля и корректировки промежуточных точек траектории перемещения манипулятора3 и управления двигателями приводов [5][6].
Так как динамические системы роботов, в том числе двухзвенных манипуляторов, действующих в угловой системе координат, характеризуются нелинейностями и подвержены возмущениям, то с целью устранения ошибок при воспроизведении траектории перемещения рабочего органа манипулятора предлагаемый расчёт угловых координат может быть дополнен решениями с использованием следующих методов:
- нейросетевого моделирования [9];
- имитационного исследования системы роботизированной руки для обнаружения и оценки неисправностей [10];
- эквивалентного принципа переменной структуры скользящего режима для точного восстановления произвольных нелинейных неисправностей [11];
- генетического алгоритма для решения задачи планирования траектории [12];
- генерации совместных траекторий для роботизированных манипуляторов с возможностью предотвращения столкновений [13].
Для управления двухзвенным шарнирным манипулятором со сложными траекториями его перемещения перспективно применение адаптивного управления с датчиками обратной связи, сигналы с которых обрабатываются и, по результатам обработки, принимаются решения о дальнейших действиях.
Структура аппаратной части предлагаемой системы управления (рис. 7) включает: приводы звеньев манипулятора, датчики углового положения звеньев манипулятора, датчики температуры узла крепления горелки, программируемый логический контроллер, осуществляющий функции управления манипулятором.
В промышленных роботах используются электрические, гидравлические и пневматические приводы с поступательным и вращательным движением. Наибольшее распространение в робототехнике получил электрический привод, который отличают широкий диапазон мощностей двигателей, удобство в регулировании скорости и удобство в автоматизации процессов управления.
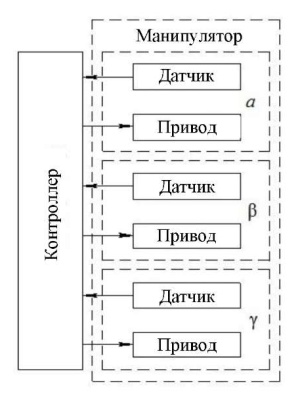
Рис. 7. Структура аппаратной части системы управления многозвенным шарнирным манипулятором (рисунок автора)
Для контроля угловых перемещений в многозвенных шарнирных механизмах манипуляторов с адаптивными системами управления, выполняющими сложные траектории, рекомендуется использовать датчики углового положения — энкодеры. С их помощью можно измерять параметры перемещения инструмента или обрабатываемого объекта, углы их поворота, направление перемещения, скорость вращения вала электродвигателя или редуктора, угловое положение по отношению к нулевой метке, направление вращения.
В адаптивных системах управления можно использовать инкрементальные (инкрементные) и абсолютные энкодеры. Инкрементальные энкодеры отличаются простотой, надежностью и относительно низкой стоимостью. Абсолютные энкодеры сложнее и дороже, но они позволяют определять углы поворота осей звеньев в любой момент времени сразу после включения питания, причём, даже в неподвижном состоянии звеньев. Абсолютные энкодеры также позволяют определять углы поворота осей звеньев при отключении и последующем восстановлении питания и не требуют возврата устройства в начальное положение. При этом на сигналы абсолютных энкодеров не оказывают влияния помехи и вибрации. В последних разработках адаптивных систем управления появились инерциальные датчики [14], имеющие ряд усовершенствований для компенсации ошибок системы управления перемещениями манипулятора.
Обсуждение и заключения. Проведен расчёт угловых координат для программирования работы системы управления двухзвенным манипулятором, действующим в угловой системе координат и перемещающим рабочий орган по сложной траектории. Полученные в работе соотношения угловых и декартовых координат можно использовать для расчёта и контроля угловых перемещений и программирования систем управления двухзвенными манипуляторами промышленных роботов, перемещающих рабочие органы по сложным траекториям.
Расчёт угловых координат для управления двухзвенным манипулятором промышленного робота, представленный в данной работе в виде решения геометрической задачи позиционирования, можно также использовать при моделировании аналогичного манипуляционного устройства или при построении системы управления таким манипулятором и организации обмена информацией между пользователем и системой управления, а также для проверки точности и отладки перемещения рабочего органа промышленного робота с использованием обратной связи.
1. Козырев Ю. Г. Промышленные роботы: основные типы и технические характеристики: учебное пособие. М., 2015. 560 с.
2. То же.
3. Глушко С. П., Частиков А. П., Корниенко В. Г., Тотухов К. Е. Программная система тестирования и отладки управляющих программ для робототехнического комплекса: свидетельство о государственной регистрации программы для ЭВМ № 2011611987, поступ. 11.01.11 опубл. 04.03.11.
Список литературы
1. Горитов, А. Н. Программирование промышленных роботов без остановки производственного цикла / А. Н. Горитов // Доклады Томского государственного университета систем управления и радиоэлектроники. — 2009. — № 1 (19). — Ч. 1. — С. 61–64.
2. Горитов, А. Н. Синтез управляемых механических устройств с применением экспертной системы / А. Н. Горитов, И. В. Колотаев // Доклады Томского государственного университета систем управления и радиоэлектроники. — 2009. — № 1 (19). — Ч. 1. — С. 72–76.
3. Горитов, А. Н. Сглаживание траектории перемещения рабочего инструмента робота манипулятора / А. Н. Горитов, С. М. Алферов // Известия Томского политехнического университета. — 2006. — Т. 309, № 8. — С. 176—179.
4. Горитов, А. Н. Моделирование адаптивных мехатронных систем / А. Н. Горитов, А. М. Кориков. — Томск : В-Спектр, 2007. — 350 с.
5. Босинзон, М. А. Автоматизированные мехатронные модули линейных и вращательных перемещений металлообрабатывающих станков / М. А. Босинсон // Приводная техника. — 2002. — № 1. — С. 10–19.
6. Букреев, В. Г. Алгоритм планирования траектории движения следящего многокоординатного электропривода / В. Г. Букреев, Н. В. Гусев // Известия высших учебных заведений. Электромеханика. — 2003. — № 3. — С. 16–20.
7. Гусев, Н. В. Алгоритмическое обеспечение систем управления следящими электроприводами / Н. В. Гусев // Научно-технический и учебно-образовательный журнал: Известия высших учебных заведений. Электромеханика. — 2006. — № 3. — С. 57–60.
8. Глушко, С. П. Моделирование теплового процесса центробежной биметаллизации внутренней поверхности втулок / С. П. Глушко, Д. Л. Поправка, Н. С. Абрамов // Сварочное производство. — 2009. — № 6. — С. 30–35.
9. Uglev, V. A. Automated Education: Tendency for Scientific Approaches Convergence / V. A. Uglev, D. I. Suchinin // In: Proc. 2nd International Conference on Applied Social Science Research (ICASSR2 014). — 2014. — P. 20–23. doi: 10.2991/icassr-14.2014.6
10. Xing-Gang Yan. Nonlinear Robust Fault Reconstruction and Estimation Using Sliding Mode Observers / Xing-Gang Yan, Ch. Edwards // Automatica. — 2007. — Vol. 43. — P. 1605–1614. doi: 10.1016/j.automatica.2007.02.008
11. Jing He. Fault Reconstruction Based on Sliding Mode Observer for Nonlinear Systems / Jing He, Changfan Zhang // Mathematical Problems in Engineering. — 2012. — Vol. 2012. — Art. 451863. doi: 10.1155/2012/451843
12. A Direct Approach to Solving Trajectory Planning Problems Using Genetic Algorithms with Dynamics in Complex Environments / F. J. Abu-Dakka, F. J. Valero, J. L. Suñer, V. A. Mata // Robotica. — 2015. — Vol. 33. — P. 669–683. doi: 10.1017/S0263574714000393
13. On-Line Path Planning with Collision Avoidance for Coordinate- Controlled Robotic Manipulators / T. Kivelä, J. Mattila, J. Puura, S. Launis // In: Proc. ASME/BATH 2017 Symposium on Fluid Power and Motion Control. — 2017. — P. 1–10. doi: 10.1115/FPMC2017-4297
14. Titterton, D. H. Strapdown Inertial Navigation Technology, 2nd ed. / D. H. Titterton, J. L. Weston // MPG Books Ltd.: Bodmin, Cornwall, UK; 2004. — 558 p.
Об авторе
С. П. ГлушкоРоссия
Сергей Петрович Глушко, доцент кафедры, кандидат технических наук, доцент
кафедра «Инженерия систем управления, материалов и технологий в
машиностроении»
350072
ул. Московская, д. 2
Краснодар
Рецензия
Для цитирования:
Глушко С.П. Расчёт угловых координат для системы управления двухзвенным манипулятором промышленного робота. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):346-352. https://doi.org/10.23947/2687-1653-2022-22-4-346-352
For citation:
Glushko S.P. Calculation of Angular Coordinates for the Control System of a Two-Link Industrial Robot Manipulator. Advanced Engineering Research (Rostov-on-Don). 2022;22(4):346-352. https://doi.org/10.23947/2687-1653-2022-22-4-346-352












































