Scroll to:
On the Construction of Mathematical Models of the Membrane Theory of Convex Shells
https://doi.org/10.23947/2687-1653-2023-23-1-17-25
Abstract
Introduction. The paper considers the issues of constructing mathematical models of the momentless equilibrium stress state of elastic convex shells using methods of the complex analysis. At the same time, shells with a piecewise smooth (ribbed) lateral surface were considered for the first time. The work objective was to find classes of shells for which it is possible to build meaningful mathematical models.
Materials and Methods. Using the methods of the theory of the discontinuous Riemann-Hilbert problem for generalized analytic functions, a criterion for the unconditional solvability of the corresponding static problem for the equilibrium equation of a convex shell with a ribbed lateral surface has been obtained. This criterion, combined with the methods of the theory of generalized analytical functions, is a tool for constructing mathematical models of the state of momentless stress equilibrium of elastic convex shells.
Results. A method has been developed for constructing mathematical models of the momentless equilibrium stress state of a convex shell under the action of a variable external load and the condition of stress concentration at the corner points of the median surface. The introduction of a vector parameter, as well as the concepts of “order of quasi-correctness” and “quasi-stability”, into the boundary condition provided both quantitative and qualitative comparison of mathematical models. Classes of shells have been found for which the description of mathematical models is given in terms of the geometry of the boundary in the vicinity of the corner points of the median surface. The obtained result, when applied to shallow convex shells, provides a geometric criterion of quasi-stability. It is established that for a shallow shell, which is not quasi-stable, the only adequate mathematical model is a probabilistic one.
Discussion and Conclusions. The proposed method for constructing a two-parameter family of problems with a modified boundary condition makes it possible to simulate the momentless equilibrium stress state for fairly wide classes of convex shells with a piecewise-smooth lateral surface under a sleeve connection. At the same time, the developed algorithm for calculating the boundary condition index allowed us to answer the question of the existence of an adequate mathematical model for a shell with a side surface of an arbitrary configuration, and for shells of a special type (specifically, shallow or shells of revolution), to formulate a geometric criterion for the existence of a mathematical model.
Keywords
For citations:
Tyurikov E.V. On the Construction of Mathematical Models of the Membrane Theory of Convex Shells. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):17-25. https://doi.org/10.23947/2687-1653-2023-23-1-17-25
Introduction. The issues considered in the paper were studied and described in the works of I. N. Vekua [1][2] and A. L. Goldenveizer [3][4], who initiated the application of methods of the theory of generalized analytical functions to the momentless (membrane) theory of thin elastic shells and the theory of surface bending. To date, the final results in this direction have been obtained for convex shells with a smooth edge (i.e., with a smooth boundary of its median surface). The most significant of them — the correctness and quasi-correctness of the key problem with a static boundary condition with simply connected and multiply connected median surfaces — are consequences of the fact that the index of the corresponding Riemann-Hilbert problem is an invariant of the connectivity of the surface. The author's application of I. N. Vekua's methods to the problems of the theory of convex shells with a piecewise smooth edge1 [5][6] recognized a connection between the “geometry” of the median surface in the vicinity of its angular point and the picture of the solvability of the corresponding Riemann-Hilbert problems with a discontinuous coefficient of the boundary condition. The use of these methods in [7–9] allowed us to obtain an effective formula for the index under some additional geometric conditions on the angular points of the surface, and, as a consequence, the geometric criterion of quasi-correctness of the main boundary problem.
The purpose of this work is to construct mathematical models of the momentless equilibrium stress state of convex shells with ribbed side surfaces based on the geometric criterion of quasi-correctness of the main boundary problem.

satisfying the Riemann–Hilbert condition
 (2)
(2)
where

As is known [11], the static boundary value problem of the momentless theory for an elastic convex shell with a ribbed side surface in the mathematical formulation is problem R , where w(z) — a complex stress function, F(z) — a complex-valued function of the external load. In this case, the condition  is equivalent to the stress concentration condition at the corner points of the median surface. We will construct a mathematical model of the equilibrium state of the shell based on the results on the solvability of problem R for a surface of a special type
is equivalent to the stress concentration condition at the corner points of the median surface. We will construct a mathematical model of the equilibrium state of the shell based on the results on the solvability of problem R for a surface of a special type

Definition 2. Corner point p(v) is called an instability point of problem R , if sector T(v) contains a special direction.
We introduce the notation: ν , σ — one-sided limits at corner point p(v) of the unit vector tangent to L , where vector σ sets main direction k2 on the surface at point p , and inside corner v is given by pair (−ν,σ) .
Statement 1. If the direction of vector r at point p(v) coincides with the direction of vector ν , then point q = J(p) is a special node of boundary condition (2) if and only if:
 (4)
(4)
If vector v is replaced by vector σ , then:
 (5)
(5)
Where t — the only positive root of the equation:
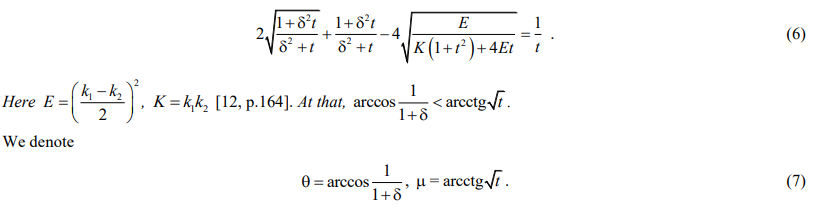
The consequence of statement 1 is statement 2.
Statement 2. Corner point p(v) is a point of instability of problem R if and only if:
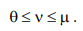 . (8)
. (8)

The condition that the solution to problem R belongs to class H* is the boundedness condition of the integral of the shell stretching energy [13, p. 83] in the vicinity of the corner point.
From formulas (9), (10), statement 4 follows.

Remark 3. As it is easy to see, formulas (9), (10) together with statement 4 are valid in the case:

Based on the obvious graphical analysis of equation (6), we conclude:


Consider 1-canonical dome S. Statement 4 is true.
Statement 4. If in each of the corner points p(v) of dome S, the following condition is met:


Discussion and Conclusions. The results obtained can be used to construct mathematical models of thin and shallow shells of the positive Gaussian curvature with ribbed side surfaces. The most complete and advanced results of both linear and nonlinear elastic shell theory are obtained for thin shallow shells. A detailed discussion of the concept of “shallow shell”, as well as a description of various versions of the theory is given in [15, p. 29]. The linear theory of flat convex curves was developed by I.N. Vekua [2, 16]. Within the framework of this theory, the issue of the realization of the equilibrium stress state of a shallow shell with a ribbed side surface, when a static boundary condition of a general form is met, is reduced to problem R discussed above.
Let P be a shallow shell [2, p. 164] with a ribbed side surface, S — its median surface with a piecewise smooth edge. We assume that at each corner point of surface S , the condition of strong shallowness k1 = k2 is satisfied, which is equivalent to the following:
 (19)
(19)

The method proposed above can be used to construct mathematical models of the theory of thin shallow shells with ribbed side surfaces of any configuration. To do this, it is enough to use the results3 on the solvability of problem R for spherical domes with a piecewise smooth edge. Let us consider for definiteness, the median surface S under the assumption that all the corner points p( ) of the boundary are “outgoing”, that is,
) of the boundary are “outgoing”, that is,  <
< . In this case, a corner point on a spherical surface is a special node of the boundary condition if and only if
. In this case, a corner point on a spherical surface is a special node of the boundary condition if and only if  . It follows that the “outgoing” corner point of the median surface of the shallow shell is an instability point if one of the following conditions is met:
. It follows that the “outgoing” corner point of the median surface of the shallow shell is an instability point if one of the following conditions is met:  Thus, formula (9) for the index can serve as validation for the following hypothesis:
Thus, formula (9) for the index can serve as validation for the following hypothesis:
if problem R for a shallow convex shell is unconditionally solvable in a given class of solutions, then its quasicorrectness order is a discrete random variable taking integer values K , K +1 ,…, K N+ , where N — the number of instability points, K — the number given by a set of corner points and a selection of continuous vector parameter r .
In conclusion, we note that the same reasoning can serve as validation for this hypothesis, but carried out for regular convex surfaces satisfying the condition of local symmetry [17] at corner points.
1. Tyurikov EV. Obobshchennaya granichnaya zadacha Goldenveizera dlya bezmomentnykh sfericheskikh kupolov. In: Proc. XIV Int. Conf. “Sovremennye problemy mekhaniki sploshnoi sredy. Rostov-on-Don. P. 290–293. (In Russ.)
2. Tyurikov EV. Obobshchennaya granichnaya zadacha Goldenveizera dlya bezmomentnykh sfericheskikh kupolov.
3. Tyurikov EV. Obobshchennaya granichnaya zadacha Goldenveizera dlya bezmomentnykh sfericheskikh kupolov.
References
1. Vekua IN. Generalized Analytical Functions. Moscow: Fizmatlit; 1988. 512 p. (In Russ.)
2. Vekua IN. Nekotorye obshchie metody postroeniya razlichnykh variantov v teorii obolochek. Moscow: Fizmatlit; 1982. 288 p. (In Russ.)
3. Goldenveizer AL. O primenenii reshenii zadachi Rimana–Gil'berta k raschetu bezmomentnykh obolochek. Journal of Applied Mathematics and Mechanics. 1951;15:149–166. (In Russ.)
4. Goldenveizer AL. Teoriya tonkikh uprugikh obolochek. Moscow: Nauka; 1976. 512 p. (In Russ.)
5. Tyurikov EV. Boundary Value Problems in the Theory of Infinitesimal Bendings of Surfaces of Positive Curvature with Piecewise Smooth Boundary. Sbornik: Mathematics. 1977;32:385–400.
6. Tyurikov EV. Obshchii sluchai smeshannoi granichnoi zadachi membrannoi teorii vypuklykh obolochek. Issledovaniya po sovremennomu analizu i matematicheskomu modelirovaniyu. 2011;5:225–229. (In Russ.)
7. Muskhelishvili NI. Singulyarnye integral'nye uravneniya. Moscow: Fizmatlit; 1968. 511 p. (In Russ.)
8. Vekua IN. Sistemy differentsial'nykh uravnenii pervogo poryadka ehllipticheskogo tipa i granichnye zadachi s primeneniem k teorii obolochek. Sbornik: Mathematics. 1952;31:217–314. (In Russ.)
9. Tyurikov EV. The Canonical Form of the Main Boundary Value Problem of the Membrane Theory of Convex Shells. Global and Stochastic Analysis. 2020;7:209–218.
10. Tyurikov EV. A Geometric Analogue of the Vekua–Goldenveizer Problem. Doklady Mathematics. 2009;79:83–86. https://doi.org/10.1134/S1064562409010256
11. Tyurikov EV. One Case of Quasi–Correctness of the Canonical Boundary Value Problem of the Membrane Theory of Convex Shells. Global and Stochastics Analysis. 2021;8:45–52.
12. Vekua IN. Osnovy tenzornogo analiza i teorii kovariantov. Moscow: Fizmatlit; 1978. 296 p. (In Russ.)
13. Landau LD, Lifshits EM. Teoreticheskaya fizika. Teoriya uprugosti. Moscow: Fizmatlit; 1965. 204 p. (In Russ.)
14. Tyurikov EV, Polyakov AS. On One Case of Quasi–Correctness of the Static Boundary Value Problem for Shells of Rotation. Journal of Physics: Conference Series. 2021;2131:022130. https://doi.org/10.1088/1742-6596/2131/2/022130
15. Voronich II. Matematicheskie problemy nelineinoi teorii pologikh obolochek. Moscow: Nauka; 1989. 376 p. (In Russ.)
16. Vekua IN. Teoriya tonkikh pologikh obolochek peremennoi tolshchiny. Tbilisi: Metsniereba; 1965. 101 p. (In Russ.)
17. Tyurikov EV. One Case of Extended Boundary Value Problem of the Membrane Theory of Convex Shells by I. N. Vekua. Issues of Analysis. 2021;7(S):153–162. https://doi.org/10.15393/j3.art.2018.5471
About the Author
E. V. TyurikovRussian Federation
Evgeniy V Tyurikov, professor of the Advanced Mathematics Department, associate professor
1, Gagarin sq., Rostov-on-Don
Review
For citations:
Tyurikov E.V. On the Construction of Mathematical Models of the Membrane Theory of Convex Shells. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):17-25. https://doi.org/10.23947/2687-1653-2023-23-1-17-25
JATS XML














































