On the Construction of Mathematical Models of the Membrane Theory of Convex Shells

Introduction. The issues considered in the paper were studied and described in the works of I. N. Vekua [1][2] and A. L. Goldenveizer [3][4], who initiated the application of methods of the theory of generalized analytical functions to the momentless (membrane) theory of thin elastic shells and the theory of surface bending. To date, the final results in this direction have been obtained for convex shells with a smooth edge (i.e., with a smooth boundary of its median surface). The most significant of them — the correctness and quasi-correctness of the key problem with a static boundary condition with simply connected and multiply connected median surfaces — are consequences of the fact that the index of the corresponding Riemann-Hilbert problem is an invariant of the connectivity of the surface. The author's application of I. N. Vekua's methods to the problems of the theory of convex shells with a piecewise smooth edge¹ [5][6] recognized a connection between the “geometry” of the median surface in the vicinity of its angular point and the picture of the solvability of the corresponding Riemann-Hilbert problems with a discontinuous coefficient of the boundary condition. The use of these methods in [7–9] allowed us to obtain an effective formula for the index under some additional geometric conditions on the angular points of the surface, and, as a consequence, the geometric criterion of quasi-correctness of the main boundary problem.

The purpose of this work is to construct mathematical models of the momentless equilibrium stress state of convex shells with ribbed side surfaces based on the geometric criterion of quasi-correctness of the main boundary problem.

satisfying the Riemann–Hilbert condition

(2)

where

As is known [11], the static boundary value problem of the momentless theory for an elastic convex shell with a ribbed side surface in the mathematical formulation is problem R , where w(z) — a complex stress function, F(z) — a complex-valued function of the external load. In this case, the condition is equivalent to the stress concentration condition at the corner points of the median surface. We will construct a mathematical model of the equilibrium state of the shell based on the results on the solvability of problem R for a surface of a special type

Definition 2. Corner point p(v) is called an instability point of problem R , if sector T(v) contains a special direction.

We introduce the notation: ν , σ — one-sided limits at corner point p(v) of the unit vector tangent to L , where vector σ sets main direction k2 on the surface at point p , and inside corner v is given by pair (−ν,σ) .

Statement 1. If the direction of vector r at point p(v) coincides with the direction of vector ν , then point q = J(p) is a special node of boundary condition (2) if and only if:

(4)

If vector v is replaced by vector σ , then:

(5)

Where t — the only positive root of the equation:

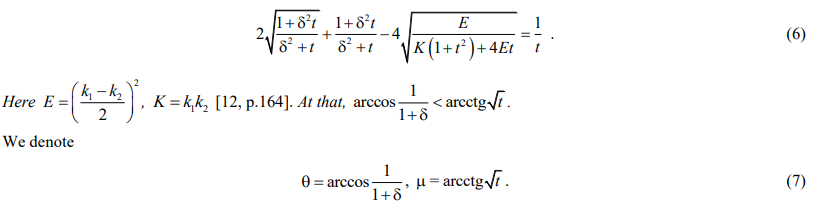
The consequence of statement 1 is statement 2.

Statement 2. Corner point p(v) is a point of instability of problem R if and only if:

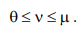. (8)

The condition that the solution to problem R belongs to class H* is the boundedness condition of the integral of the shell stretching energy [13, p. 83] in the vicinity of the corner point.

From formulas (9), (10), statement 4 follows.

Remark 3. As it is easy to see, formulas (9), (10) together with statement 4 are valid in the case:

Based on the obvious graphical analysis of equation (6), we conclude:

Consider 1-canonical dome S. Statement 4 is true.

Statement 4. If in each of the corner points p(v) of dome S, the following condition is met:

Discussion and Conclusions. The results obtained can be used to construct mathematical models of thin and shallow shells of the positive Gaussian curvature with ribbed side surfaces. The most complete and advanced results of both linear and nonlinear elastic shell theory are obtained for thin shallow shells. A detailed discussion of the concept of “shallow shell”, as well as a description of various versions of the theory is given in [15, p. 29]. The linear theory of flat convex curves was developed by I.N. Vekua [2, 16]. Within the framework of this theory, the issue of the realization of the equilibrium stress state of a shallow shell with a ribbed side surface, when a static boundary condition of a general form is met, is reduced to problem R discussed above.

Let P be a shallow shell [2, p. 164] with a ribbed side surface, S — its median surface with a piecewise smooth edge. We assume that at each corner point of surface S , the condition of strong shallowness k1 = k2 is satisfied, which is equivalent to the following:

(19)

The method proposed above can be used to construct mathematical models of the theory of thin shallow shells with ribbed side surfaces of any configuration. To do this, it is enough to use the results³ on the solvability of problem R for spherical domes with a piecewise smooth edge. Let us consider for definiteness, the median surface S under the assumption that all the corner points p() of the boundary are “outgoing”, that is, < . In this case, a corner point on a spherical surface is a special node of the boundary condition if and only if  . It follows that the “outgoing” corner point of the median surface of the shallow shell is an instability point if one of the following conditions is met:   Thus, formula (9) for the index can serve as validation for the following hypothesis:

if problem R for a shallow convex shell is unconditionally solvable in a given class of solutions, then its quasicorrectness order is a discrete random variable taking integer values K , K +1 ,…, K N+ , where N — the number of instability points, K — the number given by a set of corner points and a selection of continuous vector parameter r .

In conclusion, we note that the same reasoning can serve as validation for this hypothesis, but carried out for regular convex surfaces satisfying the condition of local symmetry [17] at corner points.