Scroll to:
Method for Solving the Problem of Load Movement over the Ice Cover of a Reservoir along a Complex Trajectory
https://doi.org/10.23947/2687-1653-2023-23-1-34-40
Abstract
Introduction. The development of the polar regions of the World Ocean contributed to an increased interest in studying wave processes in water bodies with ice cover caused by the action of a mobile load. In most papers of domestic and foreign scientists, the ice sheet was considered as an elastic or viscoelastic plate loaded with a rectilinearly moving vertical force. However, when modeling the impact of vehicles on the ice cover, it is of interest to investigate problems in which the force moves along a more complex trajectory. Therefore, this study aims at developing a method for studying the behavior of the ice cover under the action of a force moving along a trajectory of a complex shape, obeying an arbitrary law of motion.
Materials and Methods. A method for solving problems of the action of an arbitrarily moving force on the ice cover of a reservoir of finite depth filled with an inviscid incompressible fluid is proposed. The ice cover was considered as a viscoelastic plate lying on the surface of a liquid in a state of potential flow. A concentrated force moving along an arbitrary closed trajectory and being periodic in time was applied to the upper surface of the plate. Hydrodynamic pressure acted on the lower surface of the plate from the liquid side. Due to the periodicity of the load applied to the plate, an integral time transformation was used to solve differential equations describing the behavior of this system. Further, using traditional methods, formulas were obtained for calculating stresses and displacements in the plate and components of the velocity vector of liquid particles. These formulas were presented in the form of an iterated integral. Numerical methods were used to calculate integrals.
Results. Calculations showed that the deflection of the ice cover increased markedly with the growth of speed and tangential acceleration of the load movement. An increase in the relaxation time of ice and a decrease in the radius of the trajectory of the load also caused an increase in deflection. The distribution of the fluid particle velocity vector over the depth of the reservoir was calculated.
Discussion and Conclusions. The proposed method has shown its efficiency in solving problems about the impact of a moving load on the ice cover of a reservoir. With its help, the influence of the curvature of the trajectory of motion and the mechanical properties of ice, the kinematic characteristics of the movement of the load on the deflection of the ice cover was investigated. The method simulates the impact of vehicles on the ice cover of a reservoir. The results of its application can be used under the construction of ice roads or airdromes on ice.
For citations:
Galaburdin A.V. Method for Solving the Problem of Load Movement over the Ice Cover of a Reservoir along a Complex Trajectory. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):34-40. https://doi.org/10.23947/2687-1653-2023-23-1-34-40
Introduction. Recently, in connection with the development of the northern territories and areas of the World Ocean, great attention has been paid to the studying the behavior of the ice cover under the action of external load. A large number of works by domestic and foreign scientists are devoted to these issues. The impact of a pulsed moving load on a viscoelastic floating plate was considered in [1]. The effect of a moving load on the ice cover frozen to the channel walls was presented in [2, 3]. The fluctuations of the ice cover caused by a load moving at a constant speed were considered in [4]. The behavior of a semi-infinite ice sheet under the action of a uniformly moving load on it was studied in [5]. The propagation of waves excited along a channel with an ice cover was discussed in [6]. In [7], nonlinear models were used in simulation. The monograph [8] presented the results of studies of surface waves in a sea with a floating broken and solid ice cover. The ice failure under the action of a moving load was considered in [9]. In the above works, the rectilinear load movement was mainly considered. The objective of this study was to develop a method for solving the problem of the impact of a force moving across the ice cover in an arbitrary way. Achieving this goal makes it possible to more accurately simulate the impact on the ice cover of vehicles, whose movement often occurs along rather complex trajectories and according to a complex law.
Problem Statement. The oscillations of an infinite ice cover lying on the surface of a reservoir of finite depth under the action of a force moving arbitrarily along a closed trajectory were considered. The ice cover was modeled by a thin viscoelastic plate, whose mechanical properties were described by the Kelvin-Voigt model. The reservoir was filled with an incompressible liquid.
Materials and Methods. The ice cover bending was described by the differential equation [7]:
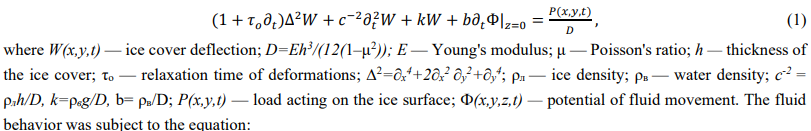
∆Ф=0.
Boundary conditions at the ice-water interface at z=0 and at the bottom of the reservoir z=–H (H — reservoir depth) had the form:

It was supposed that force P (x, y, t) moved along an arbitrary closed trajectory γ in an arbitrary way. It was assumed that P=P(s(t)), where s — arc coordinate measured from some fixed point of the curve γ. If function s(t) was periodic with period T, then it was quite obvious that value P(s(t)), would also be periodic, and also with period T. The parametric assignment of the trajectory was taken as:

where t — time.
Considering the steady-state process and applying the integral transformation with respect to variables x and y as well as the final integral transformation with respect to t on the interval [0; T], we obtained:
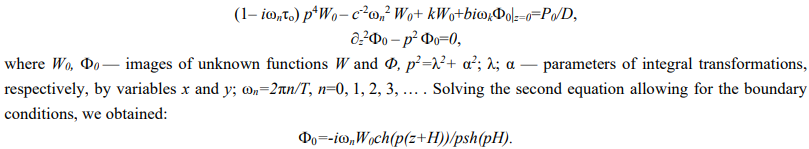
Then, the first equation followed:

The moving concentrated force was approximated by the function:

where ε — parameter.
Further, by performing quite obvious transformations, we got:

Knowing W, it was possible to determine formulas for calculating the components of the displacement vector and the stress tensor at any point of the ice cover using available ratios.
In the numerical implementation of the proposed method, a problem arose related to the need to calculate integrals. One of them as a subintegral function had a strongly oscillating function for sufficiently large n, and the second was improper with an infinite upper limit.
To calculate integrals from strongly oscillating functions, a quadrature formula was used, obtained by the cubic spline method [11]:

where ℎ𝑗 — lengths of elementary segments into which the interval was divided [a; b]; S(x) — approximation of f(x) by cubic spline, 𝑀𝑗 = 𝑆̕̕(𝑥𝑗).

When calculating the sum of a series, the Lanczos sigma multiplier method was used to accelerate its convergence.
Research Results. The calculations were carried out for the case of the action of a single concentrated force that moved along a closed curve, shown in Figure 1:

It was assumed that the thickness of the ice cover was h=0.25 m, Young's modulus of the plate material E=500,000,000 N/m2 , Poisson's ratio μ=1/3, ice density ρ=900kg/m3 , water density ρ=1,000 kg/m3 , reservoir depth H=5 m, ε=2.5. The radii determining the shape of the force trajectory were assumed to be R1=15 m, R2=9 m, R3=3 m (Fig. 1).

Fig. 1. Trajectory of the concentrated force
Figure 2 shows the change in the deflection of the ice cover (a), as well as the maximum values of normal stresses (at z=±h) Sx and Sy (b and c) and at the movement speed of single concentrated force v =7.4022 m/s and tangential acceleration wt=0.

Fig. 2. Change in deflection and stresses of the ice cover: a — change in deflection; b — change in stress Sx; c — change in stress Sy
On these graphs, the red dot indicates the place of application of force, and the blue color indicates the trajectory of movement (the author's figure).
Figure 3 shows the dependence of the change in the maximum value of the deflection of the ice cover on the force speed rate (а) at the moment t=T/2. The position of the force on the trajectory at the moment is marked by a red dot (Fig. 1), while the tangential acceleration wt=0. Two graphs are given, one of which corresponds to the radius of the trajectory R1=15 m (solid line), and the second — to radius R1=5 m (dotted line). Graph b in Figure 3 shows the dependence of the maximum value of the ice cover deflection on the tangential acceleration rate at moment t=T at the point of the trajectory (2; 0) in Figure 1 at speed v=0. The graph in Figure 3 shows the dependence of the maximum deflection value on the value of the strain relaxation time.

Fig. 3. Dependences of the ice cover deflection on: a — speed; b — tangential acceleration; c — relaxation time
The liquid behavior is shown in Figure 4. It illustrates the distribution of the speed vector of liquid particles over the depth of the reservoir at t=T/2, force speed v=3.7011 m/s and acceleration wt=0.

Fig. 4. Distribution of the speed vector of liquid particles over the reservoir depth
Discussion and Conclusions. The influence of the movement trajectory curvature and the mechanical properties of ice on the ice cover deflection, speed and acceleration of the load movement was investigated. Calculations have shown that the deflection of the ice cover depends significantly on the movement speed of the force and acceleration of movement.
However, the nature of qualitative changes in displacements and stresses in the ice cover caused by the action of a moving force with a change in speed and acceleration of movement changed slightly.
Mechanical properties of ice, specifically, the relaxation time, had a noticeable effect on the deflection of the ice cover.
The results obtained and the proposed method for solving such problems can be used in the construction of ice roads or airfields on ice. Moreover, the proposed solution method has shown its effectiveness and can be used to solve other similar problems.
References
1. Wang K, Hosking RJ, Milinazzo F. Time-Dependent Response of a Floating Viscoelastic Plate to an Impulsively Started Moving Load. Journal of Fluid Mechanics. 2004;521:295–317. https://doi.org/10.1017/S002211200400179X
2. Shishmarev K, Khabakhpasheva T, Korobkin A. The Response of Ice Cover to a Load Moving along a Frozen Channel. Applied Ocean Research. 2016;59:313–326. https://doi.org/10.1016/j.apor.2016.06.008
3. Shishmarev KA. Problem Formulation of Ice Plate Viscoelastic Oscillations in a Channel Caused by a Moving Load. Izvestiya of Altai State University. 2015;1–2:189–194.
4. Kozin VM, Zemlyak VL, Kozhaev AV. Influence of Physical and Mechanical Properties of Ice on the Parameters of Resonant Flexural-Gravity Waves. Scholarly Notes of KNASTU. 2019;37:36–45.
5. Tkacheva LA. Behavior of a Semi-Infinite Ice Cover under a Uniformly Moving Load. Journal of Applied Mechanics and Technical Physics. 2018;59:258–272. https://doi.org/10.15372/PMTF20180109
6. Korobkin A, Khabakhpasheva T, Papin A. Waves Propagating along a Channel with Ice Cover. European Journal of Mechanics – B/Fluids. 2014;47:166–175. https://doi.org/10.1016/j.euromechflu.2014.01.007
7. Guyenne P, Pǎrǎu EI. Computations of Fully Nonlinear Hydroelastic Solitary Waves on Deep Water. Journal of Fluid Mechanics. 2012;713:307–329. https://doi.org/10.1017/jfm.2012.458
8. Bukatov AE, Bukatov AA, Zharkov VV, et al. Rasprostranenie poverkhnostnykh voln v ledovykh usloviyakh. Sevastopol: FGBUN FITS MGI; 2019. 204 p. (In Russ.)
9. Malenko ZhB, Yaroshenko AA. Bending-Gravity Waves in the Sea with an Ice Cover from Moving Disturbances. Marine Intellectual Technologies. 2021;4:157–161. https://doi.org/10.37220/MIT.2021.52.2.086
10. Galaburdin AV. Infinite Plate Loaded with Normal Force Moving along a Complex Path. Advanced Engineering Research (Russia). 2020;20:370−381. https://doi.org/10.23947/2687-1653-2020-20-4-370-381
About the Author
A. V. GalaburdinRussian Federation
Alexander V Galaburdin, associate professor of the Mathematics and Computer Sciences Department, Cand.Sci. (Phys.-Math.), associate professor
1, Gagarin sq., Rostov-on-Don, 344003
Review
For citations:
Galaburdin A.V. Method for Solving the Problem of Load Movement over the Ice Cover of a Reservoir along a Complex Trajectory. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):34-40. https://doi.org/10.23947/2687-1653-2023-23-1-34-40
JATS XML














































