Перейти к:
Двухкритериальный метод обеспечения ресурсосбережения в краевом и туманном слоях сети
https://doi.org/10.23947/2687-1653-2023-23-1-85-94
Аннотация
Введение. В настоящее время концепции туманных и краевых вычислений используются широким кругом приложений самой различной направленности. Одной из ключевых проблем организации вычислений в группах мобильных устройств, составляющих краевой/туманный слой, является обеспечение выполнения миссии на основе наличия заряда батареи. В связи с этим к настоящему времени представлено немало разработок, направленных на энергосбережение систем устройств. Однако очень важный аспект остается за рамками рассмотрения проблемы ресурсосбережения, а именно — вопрос сбережения остаточного ресурса вычислительного устройства. Целью данного исследования является формализация задачи распределения нагрузки как двухкритериальной задачи оптимизации и выбор базового метода ее решения.
Материалы и методы. В рамках данной статьи предлагается подход к ресурсосбережению на основе оценивания двух критериев устройств: ресурса батареи и остаточного ресурса вычислительного устройства. Остаточный ресурс вычислительного устройства может быть оценен при помощи значений вероятности безотказной работы устройства или как величина, обратная интенсивности отказов с учетом того, что при моделировании используется экспоненциальный закон распределения отказов. На основе этого сформулирована модель задачи двухкритериальной оптимизации с учетом динамики топологии сети в процессе выполнения пользовательской миссии. Динамика топологии отражена в модели как последовательность топологий, каждая из которых соответствует определенному отрезку времени функционирования системы.
Результаты исследования. На основании представленной модели задачи двухкритериальной оптимизации предложен метод обеспечения ресурсосбережения в краевом и туманном слое сети, отражающий специфику динамических слоев сети, а также учитывающий важность критериев оценивания расхода ресурсов устройств. Проведен эксперимент, позволяющий оценить влияние способа распределения задач по сетевому кластеру на вероятность безотказной работы устройств и на средний остаточный ресурс.
Обсуждение и заключения. Проведенный эксперимент демонстрирует целесообразность применения разработанного метода, поскольку распределение задач по исполняющим устройствам оказывает существенное влияние (до 25 % по итогам эксперимента) на средний остаточный ресурс вычислительного устройства.
Ключевые слова
Для цитирования:
Клименко А.Б. Двухкритериальный метод обеспечения ресурсосбережения в краевом и туманном слоях сети. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):85-94. https://doi.org/10.23947/2687-1653-2023-23-1-85-94
For citation:
Klimenko A.B. Two-Criteria Technique for the Resource-Saving Computing in the Fog and Edge Network Tiers. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):85-94. https://doi.org/10.23947/2687-1653-2023-23-1-85-94
Введение. В настоящее время широкое применение нашли приложения, использующие краевой и туманный сегменты сети [1–5]. Распределенные вычисления, выполняемые на узлах этих сегментов, имеют существенное отличие от распределенных вычислений, выполняемых в облачных структурах, а именно — относительно высокую динамику топологии и, помимо этого, наличие определенных расстояний между используемыми узлами. Это приводит к необходимости учета данного параметра при моделировании времени информационных обменов между исполняемыми задачами. Существование динамики топологии объясняется тем, что устройства края сети — это, как правило, пользовательские устройства (включая разного рода датчики, смартфоны, ноутбуки и т.д.), которые принадлежат определенным людям и могут быть перемещены, выключены, доступ к данным/ресурсам может быть запрещен. Все они при этом находятся в зависимости от наличия заряда батареи (источника питания) [6][7]. Туманный слой сети менее динамичен, однако и для него характерно все перечисленное в той или иной степени: наличие определенного расстояния между узлами с присутствием транзитных участков сети, возможная мобильность самих узлов. Например, в случае обработки данных группами мобильных устройств. Интересным примером в этом смысле являются группы низкоорбитальных спутников, которые к настоящему времени используются для обработки данных, но при этом узлы смещаются относительно поверхности Земли с достаточно высокой скоростью (время доступа — порядка нескольких минут) и, следовательно, возникает вопрос о маршрутизации и передаче результатов обработки на наземные станции [8].
В рамках вопросов ресурсосбережения используемых устройств в динамичных слоях сети был опубликован ряд работ [9–11], в которых внимание акцентируется на энергосбережении. Как правило, модель предполагает наличие зависимости потребляемой энергии устройства от его загруженности [12]. При этом вне фокуса исследований остался такой важный фактор как сбережение остаточного вычислительного ресурса устройства [13].
Остаточный вычислительный ресурс устройства — это величина, тесно связанная с такими надежностными характеристиками, как вероятность безотказной работы и гамма-процентная наработка на отказ. Также средний остаточный ресурс, с учетом использования экспоненциального закона распределения интенсивности отказов, характеризуется следующим выражением:
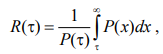 (1)
(1)
где P (x) — вероятность безотказной работы (ВБР) объекта в течение времени x .
Для экспоненциального закона распределения ресурса ВБР определяется как:
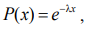 (2)
(2)
где 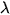 — интенсивность отказов,
— интенсивность отказов, 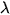 > 0 .
> 0 .
Тогда согласно формуле (1), средний остаточный ресурс определяется по следующей формуле:
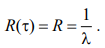 (3)
(3)
При этом имеются работы, посвященные связи величин ВБР, гамма-процентной наработки на отказ и среднего остаточного ресурса от температуры вычислительного элемента устройства, которая, в свою очередь, описана как функция от загруженности устройства [14–16]. Задача ресурсосбережения устройства также может быть поставлена как задача максимизации среднего остаточного ресурса устройства.
Таким образом, проблема ресурсосбережения рассматривается в современных работах либо как задача минимизации расхода электроэнергии устройств, либо как задача сбережения остаточного вычислительного ресурса.
Однако в современных условиях целесообразно говорить о двухкритериальной оптимизации расхода ресурсов устройств по следующим причинам:
- электроэнергия — восполняемый, но критичный для выполнения миссии устройства ресурс, будь то датчик информационно-управляющей системы или управляемое мобильное устройство;
- остаточный вычислительный ресурс определяет длительность целесообразной эксплуатации устройства, а время эксплуатации, соответственно, складывается из миссий, выполненных устройством.
Поэтому целью данного исследования являлась разработка метода ресурсосбережения для устройств динамичных слоев сети, в рамках которого бы оценивание проводилось на основании двух критериев — расхода электроэнергии и расхода вычислительного ресурса устройства.
Материалы и методы. Определим понятие «миссия группы устройств» как заранее определенную последовательность решения группой устройств комплекса вычислительных задач, связанных информационными обменами. Миссия группы устройств может быть описана ациклическим графом, вершины которого будут взвешены трудоемкостями задач, а дуги, соответственно, будут определять ограничения следования и объемы данных, передаваемых задачами. Пусть миссия описывается графом W = {wl , zl , I }, где wl — трудоемкость задачи, zl — доля задачи, выполненная к моменту смены топологий, I — матрица объемов данных, передаваемых между задачами. Группа устройств в динамическом слое сети описывается набором графов, каждый из которых определяет топологию сети в момент времени ti . Будем считать, что время выполнения миссии включает некоторый временной интервал с дискретными моментами времени [t0, t1, …tk], каждому из которых соответствует граф топологии Gi={, H}, j=1…m, pij — производительность j-го узла i-й топологии, eij — энергоресурс j-го узла i-й топологии, Rij — средний остаточный вычислительный ресурс j-го узла i-й топологии, m — число устройств в группе, H — матрица сетевых соединений между узлами. Также примем допущение о том, что в каждый последующий момент времени ti+1 для графов Gi+1 и Gi справедливо следующее: по меньшей мере одна из вершин, принадлежащая Gi , будет содержаться в Gi+1, что необходимо для продолжения выполнения миссии.
Также будем считать, что обеспечивается, в случае изменения графа топологии в момент времени ti+1, возможность переназначения задач, которые в i-й топологии выполнялись на узлах, переставших существовать в i+1 момент времени, на любые из узлов топологии i+1, имеющиеся в наличии. При этом сделаем допущение о том, что перенесенные на новые узлы задачи начинают выполняться на том же месте, где было прервано их исполнение.
Оценивание остаточного вычислительного ресурса будет реализовано следующим образом: для оценки ВБР устройства туманного слоя будем использовать выражения, предложенные в [17][18]:
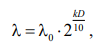 (4)
(4)
где D — загрузка вычислителя (в долях).
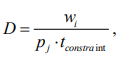 (5)
(5)
где wi — трудоемкость выполняемой работы.
Соответственно может быть оценена ВБР (t), а также средний остаточный ресурс:
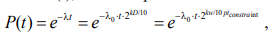 (6)
(6)
где tconstraint — ограничение по времени, за которое должна быть выполнена задача узлом, чтобы уложиться в ограничение по времени выполнения миссии tm.
При оценивании остаточного энергетического ресурса также будем полагать, что расход энергии пропорционален загруженности вычислительного узла и больше энергетических затрат не имеется:
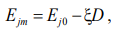 (7)
(7)
где Ej0 — исходный уровень энергии в наличии; Ejm — остаточный уровень; 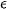 — коэффициент, выражающий зависимость между нагрузкой вычислительного элемента и его энергозатратами.
— коэффициент, выражающий зависимость между нагрузкой вычислительного элемента и его энергозатратами.
Результатом работы двухкритериального метода обеспечения ресурсосбережения будет последовательность распределений нерешенных еще задач миссии за время [t0, ti-1] по топологии Gi с учетом того, что часть задач, находящихся в процессе решения на узлах, наследуемых из топологии Gi-1, остаются на своих местах и не переносятся: A = { Ai } ;
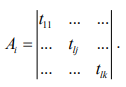 (8)
(8)
Матрица А описывает распределение нерешенных задач, для которых zl<1. При этом количество узлов соответствует новой топологии Gi. Узлы, унаследованные от топологии Gi-1, перенумеровываются и занимают индексы, начиная с 1. Поскольку выполнение миссии может включать более одной топологии, проведем декомпозицию задачи следующим образом: воспользуемся «жадной» стратегией и будем полагать, что удовлетворяющее решение (минимизация ресурсопотребления, оцениваемое двумя выбранными критериями) может быть получено, если для каждой топологии мы будем выбирать наилучшее решение.

Рассмотрим возможную приоритетность сформулированных целевых функций. Для каждой отдельно взятой топологии необходимо минимизировать как расход электроэнергии, так и расход вычислительного ресурса. В некоторых частных случаях может быть достигнуто совпадение целей оптимизации для двух критериев. Например, задача распределяется на узел таким образом, что обеспечит ему минимальную загруженность вычислительного элемента и при этом минимальный расход энергопотребления.
Однако, такая ситуация возможна не всегда. Например, имеется узел, загруженный менее прочих вычислениями, но при этом его энергоресурс практически исчерпан. Назначая на него задачу, мы ставим выполнение миссии под угрозу (либо необходима смена топологий по мере окончания запаса электроэнергии), а назначая задачу на узел более загруженный, мы ухудшаем значение критерия остаточного вычислительного ресурса. Противоположная ситуация также может иметь место: узел с большим остаточным энергоресурсом может иметь низкий остаточный вычислительный ресурс как результат участия в предыдущих миссиях устройств.
Поэтому целесообразно провести ранжирование целевой функции (ЦФ) по важности, на основе чего выбрать дальнейший метод решения.
Для миссий, критически важных к выполнению, ведущую роль играет ресурс батареи устройства [19–21]. Соответственно, ЦФ, определяющая остаточный вычислительный ресурс, может быть сведена к дополнительному ограничению. Невыполненные задачи миссии будут дораспределяться в зависимости от остаточного заряда батареи.
Следует отметить, что и для миссий, не обладающих критичностью выполнения, справедливо сказанное выше. В случае, если устройство лишится заряда батареи, не выполнив миссию, оно может быть утеряно. Тогда оптимизация вычислительного ресурса станет бессмысленной.
С другой стороны, сводя остаточный вычислительный ресурс к ограничению, решение может быть не получено вовсе по причине отсутствия доступных узлов, характеристики которых бы ему удовлетворяли.
Результаты исследования. Многокритериальные задачи оптимизации, как правило, сводят к решению одной и более однокритериальных задач. В данном случае более целесообразно оставить одну ЦФ, а вторую представить в качестве ограничения.
Для рассматриваемой системы выполнение миссии критично для каждого узла, поэтому преобразуем ЦФ по энергопотреблению в ограничение, выполнение которого отсечет неприемлемые варианты по распределению задач по узлам. Далее в рамках полученного множества узлов распределение будет происходить с минимизацией расхода остаточного вычислительного ресурса.
Опишем основные этапы двухкритериального метода обеспечения ресурсосбережения, как основного результата проведенного исследования:
- на имеющейся Gi-топологии выбрать узлы, обладающие достаточным для завершения миссии без смены топологии энергоресурсом;
- произвести распределение задач миссии по выбранным узлам таким образом, чтобы для незанятых узлов, к которым будут прикреплены нерешенные еще задачи, минимизировать расход вычислительного ресурса.
Допустимо ранжирование узлов, полученных на первом шаге метода, по убыванию наличия энергоресурса. Но тогда, распределяя задачи в первую очередь по узлам с максимальным количеством энергоресурса, может возникать ухудшение значений критерия остаточного вычислительного ресурса.
Проиллюстрируем зависимость значений ВБР устройств от выбора узла для решения задачи (в данном эксперименте сравниваем состояния узлов при передаче поступающих данных и при их обработке). Топология представлена на рис. 1.
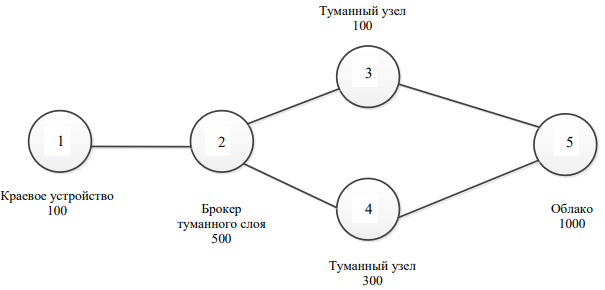
Рис. 1. Экспериментальный фрагмент топологии сети
Эксперимент проводится для 10 временных отрезков, каждый из которых по 100 часов при следующих значениях параметров: Wreceive (объем получаемых задачей данных) — 500 ед., Wsend (объем отправляемых задачей данных) — 100 ед., Wprocess (трудоемкость обработки данных) — 150 ед., Tdecl (время, отводимое на решение задачи) — 50 ед.
Далее приведены графики ВБР-узлов в зависимости от того, обрабатывает ли узел данные или только передает их (рис. 2–5).
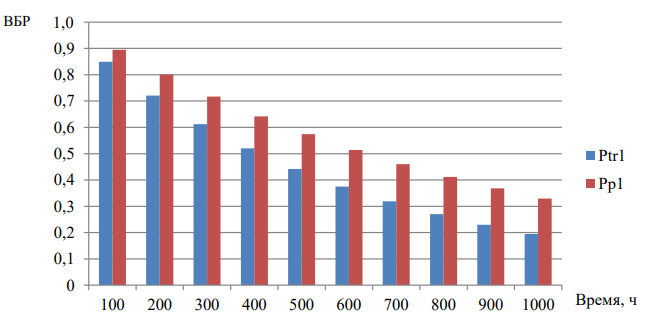
Рис. 2. Сравнение значений ВБР для узла 1 при обработке данных (Pp1) и при передаче данных (Ptr1)
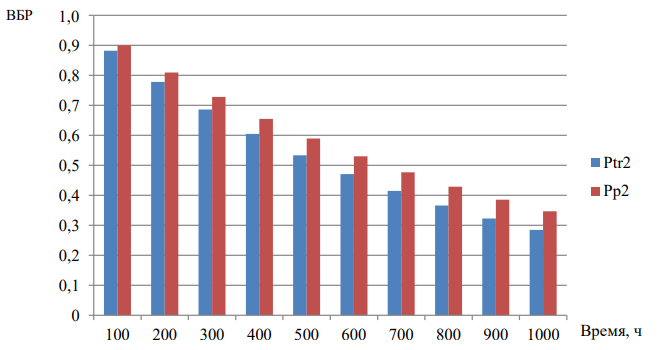
Рис. 3. Сравнение значений ВБР для узла 2 при обработке данных (Pp2) и при передаче данных (Ptr2)
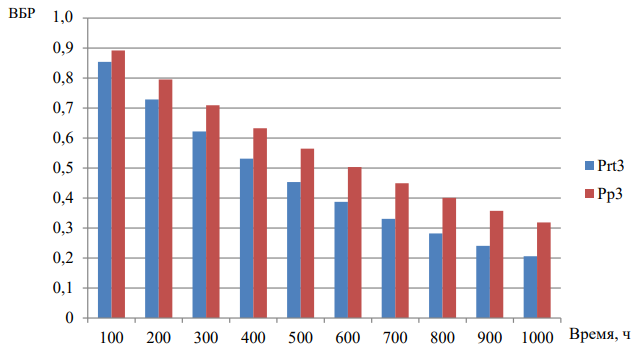
Рис. 4. Сравнение значений ВБР для узла 3 при обработке данных (Pp3) и при передаче данных (Ptr3)
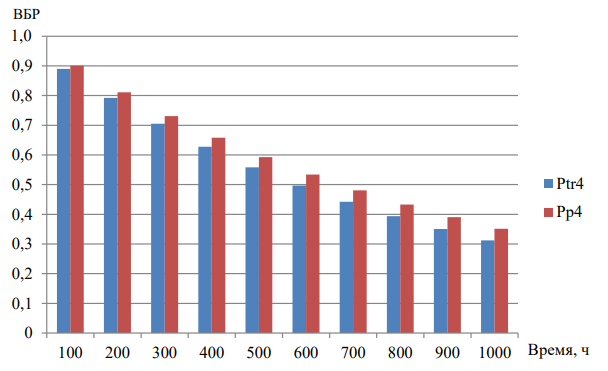
Рис. 5. Сравнение значений ВБР для узла 4 при обработке данных (Pp4) и при передаче данных (Ptr4)
Далее на рис. 6 представлено сравнение различий в значениях среднего остаточного вычислительного ресурса.
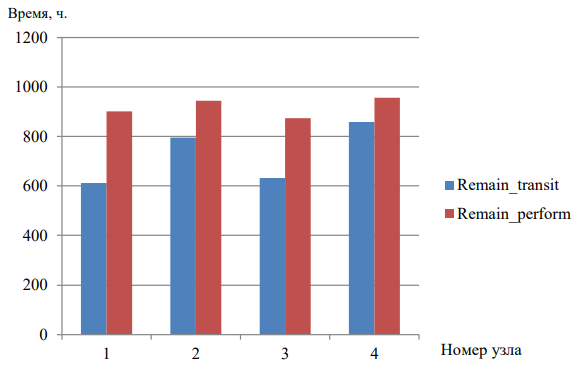
Рис. 6. Сравнение значений среднего остаточного ресурса для узлов 1–4 при транзите данных (Remain_transit) и при обработке данных (Remain_perform)
Обсуждение и заключения. В статье предложен двухкритериальный метод обеспечения ресурсосбережения в краевом и туманном слоях сети, который отличается от ранее представленных в предметной области организации распределенных вычислений в динамических слоях сети тем, что учитывает одновременно состояние батареи устройства (что критично для выполнения миссии) и остаточный ресурс вычислительного устройства (что влияет на длительность целесообразного использования устройства за пределами выполняемой миссии).
В основу разработанного метода положена сформулированная задача двухкритериальной оптимизации, которую затем предлагается свести к однокритериальной, переведя ЦФ остатка энергоресурса в ограничение.
Отсекая узлы, заранее не подходящие по уровню заряда батареи, далее распределение задач происходит по критерию остаточного вычислительного ресурса.
Проведенный эксперимент позволяет сравнить результаты распределения задачи по узлам при наличии информационных взаимодействий между задачами. Наглядно показано, что способ распределения задач существенно влияет на величину остаточного ресурса вычислительного устройства (до 25 %). Таким образом, возможны улучшения показателей ресурсопотребления устройств, участвующих в вычислениях в краевом и туманном слоях сети.
Список литературы
1. Mehbub Alam, Nurzaman Ahmed, Rakesh Matam, et al. L3Fog: Fog Node Selection and Task Offloading Framework for Mobile IoT. In: Proc. IEEE Conference on Computer Communications Workshops — IEEE INFOCOM 2022. P. 1-6. https://doi.org/10.1109/INFOCOMWKSHPS54753.2022.9798118
2. Abdelfettah Maatoug, Ghalem Belalem, Saïd Mahmoudi. A Location-Based Fog Computing Optimization of Energy Management in Smart Buildings: DEVS Modeling and Design of Connected Objects. Frontiers of Computer Science. 2023;17:172501. https://doi.org/10.1007/s11704-021-0375-z
3. Abohamama A.S., Amir el Ghamry, Eslam Hamouda. Real-Time Task Scheduling Algorithm for IoT-Based Applications in the Cloud–Fog Environment. Journal of Network and Systems Management. 2022;30(4):54. https://doi.org/10.1007/s10922-022-09664-6
4. Saad Ahmad Khan, Muhammad Abdullah, Waheed Iqbal, et al. Efficient Job Placement Using Two-Way Offloading Technique over Fog-Cloud Architectures. Cluster Computing. 2022;154:1–19. http://dx.doi.org/10.1007/s10586-022-03750-9
5. Rajasi Gore, Shashwati Banerjea, Neeraj Tyagi. A Heterogeneous Soft-Hard Fusion Framework on Fog Based Private SaS Model for Smart Monitoring of Public Restrooms. Journal of Ambient Intelligence and Humanized Computing. 2022. Vol. 63. https://doi.org/10.1007/s12652-022-04401-y
6. Haibo Wang, Hongli Xu, He Huang, et al. Robust Task Offloading in Dynamic Edge Computing. IEEE Transactions on Mobile Computing. 2021;22:500–514. https://doi.org/10.1109/TMC.2021.3068748
7. Enlu Liu, Xiaoheng Deng, Zhi Cao, et al. Design and Evaluation of a Prediction-Based Dynamic Edge Computing System. In: Proc. 2018 IEEE Global Communications Conference (GLOBECOM). 2018. P. 1–6. https://doi.org/10.1109/GLOCOM.2018.8647199
8. Fraire J.A., Gerstacker C., Hermanns H., et al. On the Scalability of Battery‐Aware Contact Plan Design for LEO Satellite Constellations. International Journal of Satellite Communications and Networking. 2020;39:193–204. https://doi.org/10.1002/sat.1374
9. Yung-Ting Chuang, Chiu-Shun Hsiang. A Popularity-Aware and Energy-Efficient Offloading Mechanism in Fog Computing. The Journal of Supercomputing. 2022;78:1–24. https://doi.org/10.1007/s11227-022-04626-w
10. Ida Syafiza Binti, Taizir EH El-Gorashi, Mohamed OI Musa, et al. Energy Efficient Fog Based Healthcare Monitoring Infrastructure. IEEE Access. 2020;8:197828–197852. https://doi.org/10.1109/ACCESS.2020.3033555
11. Fatemah S. Behbehani, Taisir El-Gorashi, Jaafar M.H. Elmirghani. Power Minimization in Vehicular Cloud Architecture. arXiv:2102.09011. 2021. https://doi.org/10.48550/arXiv.2102.09011
12. Shilpa B. Kodli, Sujatha Terdal. Survey on Energy Efficient-Load Balancing in Cloud. International Journal of Computer Applications. 2022;184(25):15-24. http://dx.doi.org/10.5120/ijca2022922301
13. Фудухин А.В. Прогнозирование надежности электронных устройств после длительного хранения. Математические машины и системы. 2004;4:164–170.
14. Klimenko A.B., Melnik E.V. A Method of Improving the Reliability of the Nodes Containing Ledger Replicas. In book: Silhavy R, Silhavy P, Prokopova Z. (eds.) Software Engineering Application in Informatics. 2021. P. 584–592. https://doi.org/10.1007/978-3-030-90318-3_47
15. Klimenko A., Melnik E. Information and Control Systems with Distributed Ledger Usage: A Reliability Issue. In book: Radek Silhavy (ed.) Artificial Intelligence in Intelligent Systems. Springer; 2021. P. 133–144. https://doi.org/10.1007/978-3-030-77445-5_12
16. Melnik E., Safronenkova I., Kapustyan S. The Efficiency Improvement of Robots Group Operation by Means of Workload Relocation. In: Proc. Int. Conf. on Interactive Collaborative Robotics. 2021;450:126–137. https://doi.org/10.1007/978-3-030-87725-5_11
17. Мельник Э.В., Горелова Г.В. Эффект выравнивания вычислительной нагрузки процессорных устройств в высоконадежных распределенных информационно-управляющих системах. Мехатроника, автоматизация, управление. 2012;11:29–35.
18. Каляев И.А., Мельник Э.В. Децентрализованные системы компьютерного управления. Ростов-на-Дону: Изд. ЮНЦ РАН; 2011. 196 с.
19. Preedipat Sattayasoonthorn, Jackrit Suthakorn. Battery Management for Rescue Robot Operation. In: Proc. 2016 IEEE Int. Conf. on Robotics and Biomimetics (ROBIO). 2016. P. 1227–1232. https://doi.org/10.1109/ROBIO.2016.7866493
20. Vinay Jadhav, Surendra Bhosale. Battery Management System for Drones. In: Proc. Int. Conf. on Electrical Electronics and Data Communication. 2022. URL: https://www.researchgate.net/publication/362889754_Battery_Management_System_for_Drones (дата обращения: 10.12.2022).
21. Wei Liu, Tobias Placke, Chau K.T. Overview of Batteries and Battery Management for Electric Vehicles. Energy Reports. 2022;8:4058–4084. https://doi.org/10.1016/j.egyr.2022.03.016
Об авторе
А. Б. КлименкоРоссия
Клименко Анна Борисовна, доцент кафедры «Фундаментальная и прикладная математика», кандидат технических наук
117534, Москва, ул. Кировоградская, д. 25 корп 2
Рецензия
Для цитирования:
Клименко А.Б. Двухкритериальный метод обеспечения ресурсосбережения в краевом и туманном слоях сети. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):85-94. https://doi.org/10.23947/2687-1653-2023-23-1-85-94
For citation:
Klimenko A.B. Two-Criteria Technique for the Resource-Saving Computing in the Fog and Edge Network Tiers. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):85-94. https://doi.org/10.23947/2687-1653-2023-23-1-85-94












































