Перейти к:
Анализ напряженно-деформированного состояния цилиндра с переменными модулями упругости на основе трехмерных уравнений теории упругости
https://doi.org/10.23947/2687-1653-2023-23-2-113-120
Аннотация
Введение. Функционально-градиентные материалы находят большое применение, т.к. неоднородность свойств позволяет управлять прочностью и жесткостью контрукций. Этим вызван большой интерес к данной теме в мировой научной литературе. Построение решения таких задач существенно зависит от типа граничных условий. В настоящей работе рассматривается равновесие тонкостенного кругового цилиндра, механические свойства которого заменяются вдоль радиуса. На цилиндрических поверхностях заданы однородные граничные условия, которые до этого не рассматривались, воздействие оказывается на торцах. Математическая постановка задачи осуществляется в линейной теории упругости в рамках осесимметричной деформации. В работе построены выражения для компонент напряженно-деформированного состояния цилиндра, в которых некоторые коэффициенты находятся из решения полученной системы линейных алгебраических уравнений.
Материалы и методы. Материал цилиндра является линейно упругим, модуль упругости которого линейно зависит от радиальной координаты. Основным методом исследования является ассимптотический метод, в котором в качестве малого параметра выступает половина логарифма отношения внешнего и внутреннего радиусов. Для построения характеристик напряженно-деформированного состояния цилиндра применены итерационные процессы.
Результаты исследования. Для линейно-упругого функционально-градиентного полого тонкостенного цилиндра получены однородные решения краевой задачи. Анализ этих решений позволяет раскрыть характер напряженно-деформированного состояния в стенке цилиндра. С этой целью проведен асимптотический анализ решений, получены соотношения для перемещений и напряжений. Установлено, что эти решения соответствуют пограничному слою, при этом их первые члены определяют краевой эффект Сен-Венана, аналогичный теории плит.
Обсуждение и заключение. Построенное с помощью асимптотического разложения аналитическое решение задачи о равновесии неоднородного по радиусу тонкостенного цилиндра может быть использовано для численного решения конкретной задачи. Для этого нужно решить полученные системы линейных алгебраических уравнений и определить соответствующие коэффициенты. Полученные асимптотические представления позволяют анализировать трехмерное напряженно-деформированное состояние. Выбор количества членов разложения позволяет рассчитать перемещения и напряжения с заданной степенью точности. Этот анализ может быть полезен при оценке адекватности прикладных методов расчета, применяемых в инженерной практике.
Ключевые слова
Для цитирования:
Исмайылова Д.Д. Анализ напряженно-деформированного состояния цилиндра с переменными модулями упругости на основе трехмерных уравнений теории упругости. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):113-120. https://doi.org/10.23947/2687-1653-2023-23-2-113-120
For citation:
Ismayilova J.J. Analysis of Stress-Strain State of a Cylinder with Variable Elasticity Moduli Based on Three-Dimensional Equations of Elasticity Theory. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):113-120. https://doi.org/10.23947/2687-1653-2023-23-2-113-120
Введение. Функционально-градиентные материалы находят широкое применение в различных конструкциях. Благодаря зависимости механических свойств от координат можно управлять напряженно-деформированным состоянием (НДС) деталей. Примером использования такой неоднородности может служить цилиндр, механические свойства которого зависят от радиуса. При этом интерес может представлять цилиндр как отдельная конструкция, так и являющийся подтелом составного тела, например, соединяющий две среды с сильно различающимися свойствами. При расчете НДС тонкостенного цилинда используются некоторые прикладные теории. При этом важно знать оценку их адекватности. Особенно в случае неоднородных свойств она может быть осуществлена с помощью компьютерного моделирования или асимптотического анализа на основе трехмерной постановки. Последним определяется актуальность настоящего исследования.
Изучению НДС полых цилиндрических тел в рамках линейной теории упругости посвящен ряд исследований. В [1][2] на основе метода сплайн-коллокации и метода конечных элементов изучено механическое поведение радиально-неоднородного цилиндра в трехмерной постановке. В [3] изучено НДС цилиндра, свойства которого зависят от радиуса, нагруженного равномерным внутреннем давлением. В [4] проведено аналитическое исследование для функционально-градиентного пьезоэлектрического цилиндра. В [5] построено точное решение для радиально-неоднородного полого цилиндра с экспоненциальным модулем Юнга, постоянным коэффициентом Пуассона и степенным модулем Юнга. В [6][7] c помощью метода прямого интегрирования получено аналитическое решение осесимметричной задачи термоупругости для сплошного цилиндра, когда коэффициент линейного теплового расширения является произвольной функцией от радиуса. В [8] разработана общая асимптотическая теория трансверсально-изотропного однородного полого цилиндра. Для трансверсальноизотропного однородного цилиндра получены новые группы решений. Приведено сравнение построенных решений с решениями, построенными с помощью прикладных методов расчета. В [9][10] изучены некоторые краевые задачи теории упругости для функционально-градиентного изотропного и трансверсально-изотропного (плоскость изотропии перпендикулярна оси) цилиндра, в случае, когда модули упругости являются произвольными непрерывными функциями от радиуса цилиндра. В [11] проведен анализ задачи изгибной деформации для радиально-неоднородного цилиндра. Анализ этих работ показывает, что не для всех типов граничных условий на цилиндрических поверхностях имееются асимптотические представления решений.
В настоящей работе на основе асимптотического анализа трехмерных уравнений теории упругости изучаются особенности НДС тонкостенного цилиндра, свойства которого линейно меняются вдоль радиуса. При этом внутренняя граница закреплена в осевом направлении и свободна в радиальном направлении.
Достижение этой цели было получено с помощью нескольких шагов: асимптотическое интегрирование дифференциальных уравнений и построение однородных решений; вывод формул для компонент вектора перемещений и тензора напряжений; учет краевых условий на торцевых поверхностях.
Материалы и методы. Рассматривается радиально-неоднороднополый тонкостенный цилиндр 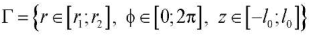 в цилиндрической системе координат r, ф, z с началом на его оси. Задача о его равновесии, в случае закрепления цилиндрических поверхностей вдоль оси и нулевых нормальных напряжений, решается в осесимметричной постановке при действии напряжений на его торцах.
в цилиндрической системе координат r, ф, z с началом на его оси. Задача о его равновесии, в случае закрепления цилиндрических поверхностей вдоль оси и нулевых нормальных напряжений, решается в осесимметричной постановке при действии напряжений на его торцах.
Краевая задача состоит из уравнений равновесия [8]:
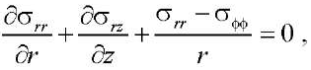 (1)
(1)
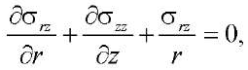 (2)
(2)
где σrr, σrz, σфф, σzz — компоненты тензора напряжений.
Определяющие соотношения [8]:
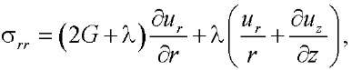 (3)
(3)
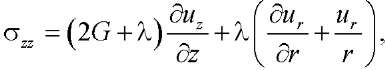 (4)
(4)
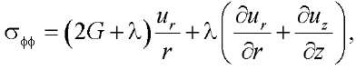 (5)
(5)
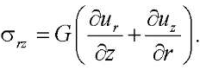 (6)
(6)
Здесь ur = ur(r, z), uz = uz(r, z) — компоненты вектора перемещений.
Параметры Ламе изменяются по линейному закону вдоль радиуса:
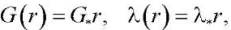 (7)
(7)
где G*, l* — константы.
После подстановки (3)–(7) в уравнения (1), (2) безразмерная система уравнений принимает вид:
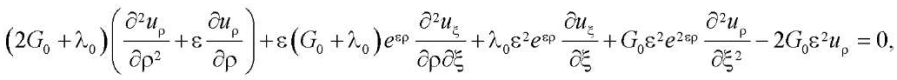 (8)
(8)
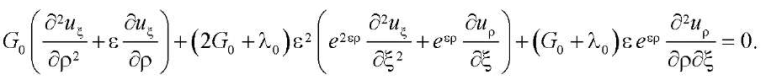 (9)
(9)
Здесь:
 — новые безразмерные координаты;
— новые безразмерные координаты;
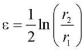 — малый параметр в случае тонкостенности;
— малый параметр в случае тонкостенности;
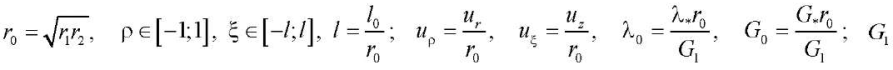
— некоторый параметр, имеющий размерность напряжения. Рассмотрим задачу, в которой на боковых поверхностях цилиндра заданы однородные граничные условия:
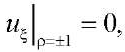 (10)
(10)
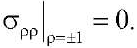 (11)
(11)
К торцам цилиндра приложены напряжения:
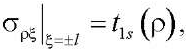 (12)
(12)
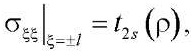 (13)
(13)
(s =1; 2).
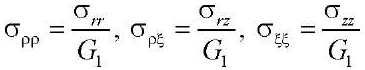 — безразмерные напряжения.
— безразмерные напряжения.
Компоненты вектора напряжений t1s (ρ), t2s (ρ), (s =1;2) удовлетворяют условиям равновесия.
Для построения однородных решений компоненты вектора смещений будем искать в виде:
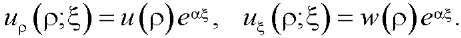 (14)
(14)
Подставляя представления (14) в систему (8)–(11), получим:
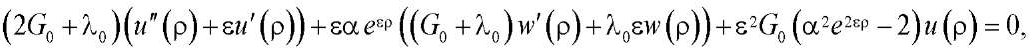 (15)
(15)
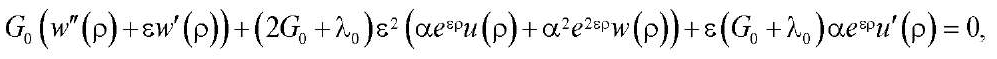 (16)
(16)
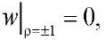 (17)
(17)
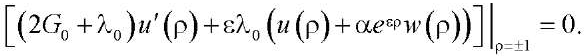 (18)
(18)
Исследуем краевые задачи (15)–(18) при ε→0. Для решения (15)–(18) при ε→0 воспользуемся асимптотическом методом [9–13].
Ненулевые решения (15)–(18) соответствуют третьему итерационному процессу, компоненты вектора смещений будем искать в виде разложений по малому параметру:
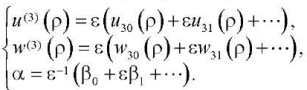 (19)
(19)
После подстановки разложений (19) в уравнения (15)–(18) для членов первого порядка имеем:
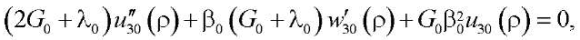 (20)
(20)
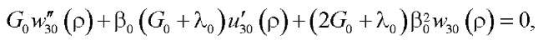 (21)
(21)
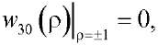 (22)
(22)
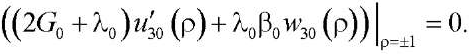 (23)
(23)
Следуя [13], спектральная задача (20)–(23) соответствует потенциальному решению для плиты. Таким образом решения представляются в виде:
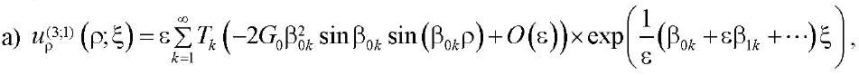 (24)
(24)
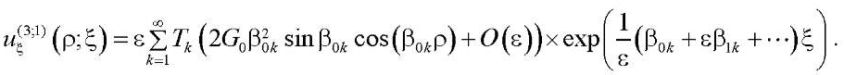 (25)
(25)
Здесь β0k является решением уравнения:
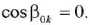 (26)
(26)
Напряжения, соответствующие решениям (24) и (25), имеют вид:
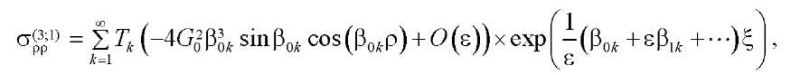 (27)
(27)
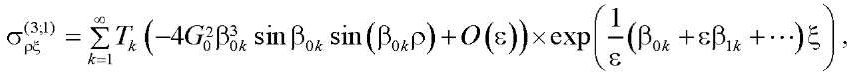 (28)
(28)
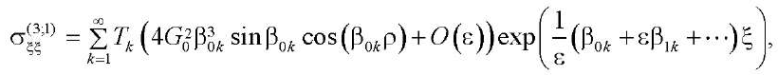 (29)
(29)
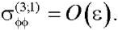 (30)
(30)
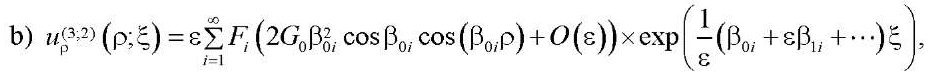 (31)
(31)
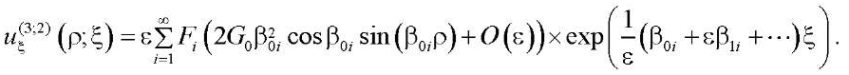 (32)
(32)
Здесь β0k является решением уравнения:
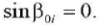 (33)
(33)
Напряжения, соответствующие решениям (31) и (32), имеют вид:
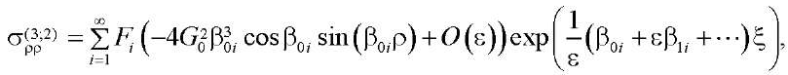 (34)
(34)
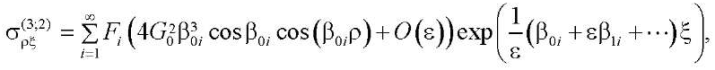 (35)
(35)
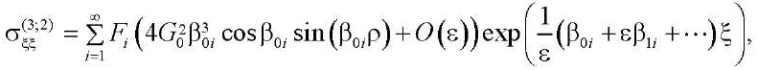 (36)
(36)
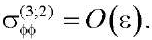 (37)
(37)
Общее решение (15)–(18) будет суперпозицией решений (24), (25), (31), (32):
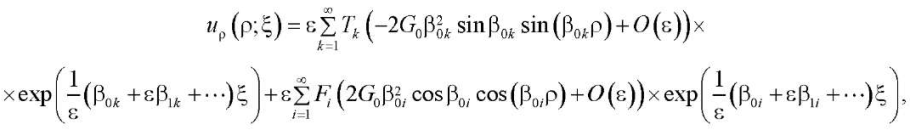 (38)
(38)
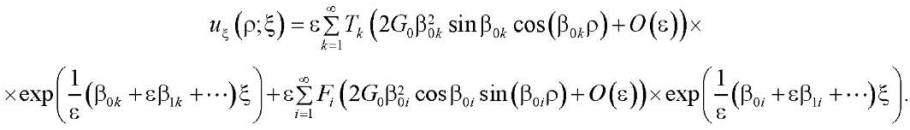 (39)
(39)
Решения (24), (25), (31), (32) имеют характер пограничного слоя. При удалении от торцов решения (24), (25), (31), (32) экспоненциально убывают.
Чтобы определить константы Tk, Fi, воспользуемся вариационным принципом Лагранжа. Вариационный принцип принимает вид [8]:
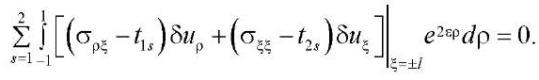 (40)
(40)
Подставляя (24–36) в (40), имеем:
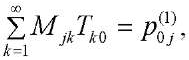 (41)
(41)
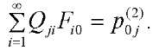 (42)
(42)
Здесь:
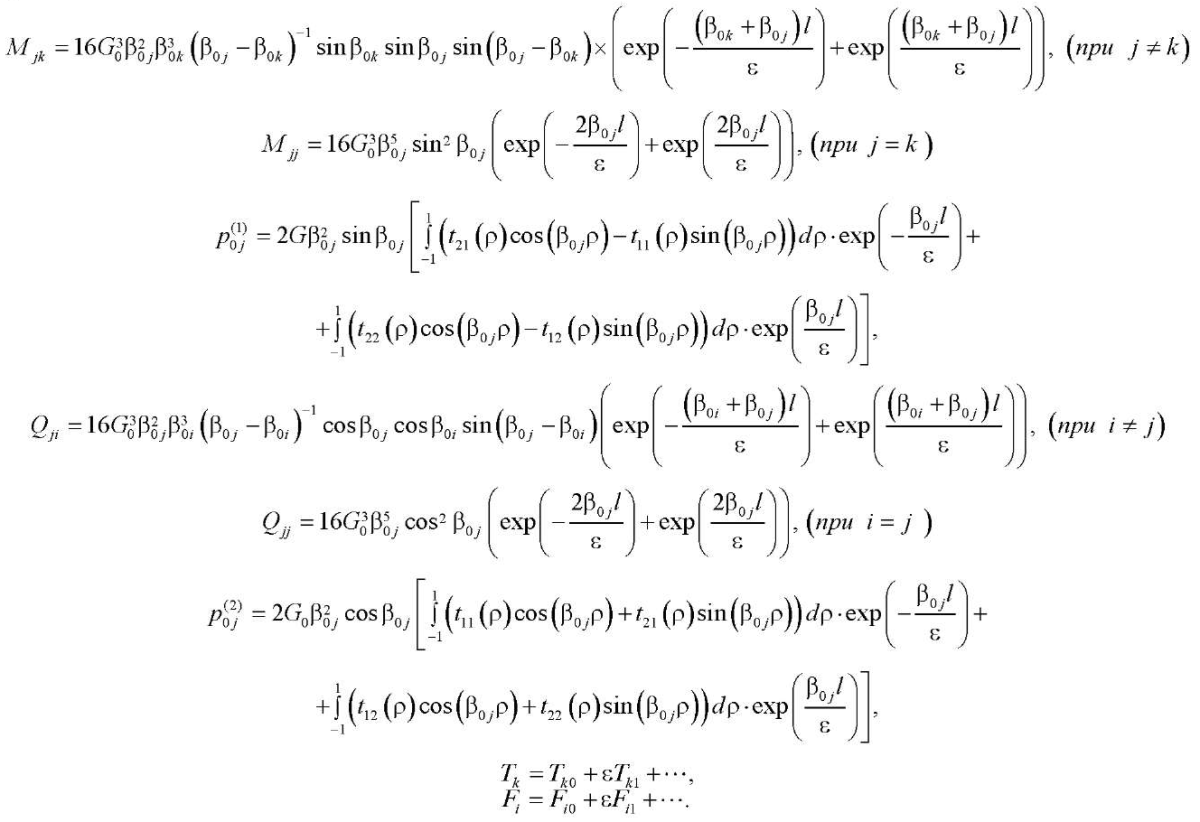
Постоянные Tkp, Fip (p = 1, 2,…) находятся из систем линейных алгебраических уравнений (41), (42), аналогичные которым изучены в [13].
Результаты исследований. В работе в осесимметричной постановке рассмотрено решение задачи линейной теории упругости для функционально-градиентного полого тонкостенного цилиндра, свойства которого изменяются по толщине по линейному закону. На боковых поверхностях цилиндра заданы однородные перекрестные граничные условия, на торцах задан вектор напряжений. Построенные однородные решения удовлетворяют граничным условиям на цилиндрических поверхностях. Для их построения использован асимптотический подход на основе разложения по малому параметру, характеризующему относительную толщину цилиндра. Для учета неоднородных граничных условий на торцах получены системы линейных алгебраических уравнений, аналогичные изученным в литературе. Показано, что построенные решения НДС имеют погранслойный характер, который соответствует краевому эффекту, аналогичному теории неоднородных плит, носящему имя Сен-Венана.
Обсуждение и заключение. Обычно при изучении НДС тонкостенных конструкций строятся прикладные методы расчета, снижающие размерность задачи. В этой связи актуальной является задача определения диапазона геометрических и механических параметров, в которых эти методы дают приемлемую точность. Построенные в работе на основе асимптотического анализа решения трехмерных уравнений позволяют оценить адекватность таких прикладных теорий с заданным наперед порогом точности. Кроме того, эти решения могут найти применение при оценке численных решений задач для конструкций с функционально-градиентными материалами.
Список литературы
1. Grigorenko A.Ya., Yaremchenko S.N. Analysis of the Stress-Strain State of Inhomogeneous Hollow Cylinders. International Applied Mechanics. 2016;52(4):342–349. https://doi.org/10.1007/s10778-016-0757-3
2. Grigorenko A.Ya., Yaremchenko S.N. Three-Dimensional Analysis of the Stress-Strain State of Inhomogeneous Hollow Cylinders Using Various Approaches. International Applied Mechanics. 2019;55(5):487–494. https://doi.org/10.1007/s10778-019-00970-2
3. Tutuncu N., Temel B. A Novel Approach to Stress Analysis of Pressurized FGM Cylinders, Disks and Spheres. Composite Structures. 2009;91(3):385–390. https://doi.org/10.1016/j.compstruct.2009.06.009
4. Hong-Liang Dai, Li Hong, Yi-Ming Fu, et al. Analytical Solution for Electromagnetothermoelastic Behaviors of a Functionally Graded Piezoelectric Hollow Cylinder. Applied Mathematical Modelling. 2010;34(2):343–357. https://doi.org/10.1016/j.apm.2009.04.008
5. Theotokoglou E.E., Stampouloglou I.H. The Radially Nonhomogeneous Elastic Axisymmentric Problem. International Journal of Solids and Structures. 2008;45(25–26):6535–6552. https://doi.org/10.1016/j.ijsolstr.2008.08.011
6. Tokovyy Yu., Chyzh A., Chien-Ching Ma. Axisymmetric Thermal Stresses in a Radially-Inhomogeneous Elastic Cylinder Subjected to with-Respect-to-Length Varying Thermal Loadings. In: Proc. 11th Int. Congress on Thermal Stresses. Palermo: Poguro edizioni; 2016. P. 263–266.
7. Tokovyy Yu., Chien-Ching Ma. Elastic Analysis of Inhomogeneous Solids: History and Development in brief. Journal of Mechanics. 2019;35(5):613–626. https://doi.org/10.1017/jmech.2018.57
8. Mekhtiev M.F. Asymptotic Analysis of Spatial Problems in Elasticity. Singapore: Springer; 2019. 241 p. URL: https://link.springer.com/book/10.1007/978-981-13-3062-9 (accessed: 10.02.2023).
9. Akhmedov N.K. Axisymmetric Problem of the Elasticity Theory for the Radially Inhomogeneous Cylinder with a Fixed Lateral Surface. Applied and Computational Mechanics. 2021;7(2):599–610.
10. Ахмедов Н.К., Акперова С.Б. Асимптотический анализ трехмерной задачи теории упругости для радиально-неоднородного трансверсально-изотропного полого цилиндра. Известия РАН. Механика твердого тела. 2011;4:170–180. URL: https://mtt.ipmnet.ru/ru/Issues/2011/4/170 (дата обращения: 10.20.2023).
11. Akhmedov N.K., Akbarova S.B. Behavior of Solution of the Elasticity Problem for a Radial Inhomogeneous Cylinder with Small Thickness. Eastern-European Journal of Enterprise Technologies Applied Mechanics. 2021;6/7(114):29–42. https://doi.org/10.15587/1729-4061.2021.247500
12. Akhmedov N.K., Sofiyev A.H. Asymptotic Analysis of Three-Dimensional Problem of Elasticity Theory for Radially Inhomogeneous Transversally-Isotropic Thin Hollow Spheres. Thin-Walled Structures. 2019;139:232–241. https://doi.org/10.1016/j.tws.2019.03.022
13. Устинов Ю.А. Математическая теория поперечно-неоднородных плит. Ростов-на Дону: ООО «ЦВВР»; 2006. 257 с.
Об авторе
Д. Д. ИсмайыловаАзербайджан
Джалала Джамшид кызы Исмайылова, докторант кафедры общих технических наук и технологий
AZ2003, Азербайджан, г. Гянджа, ул. Гейдар Алиев, 187
Рецензия
Для цитирования:
Исмайылова Д.Д. Анализ напряженно-деформированного состояния цилиндра с переменными модулями упругости на основе трехмерных уравнений теории упругости. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):113-120. https://doi.org/10.23947/2687-1653-2023-23-2-113-120
For citation:
Ismayilova J.J. Analysis of Stress-Strain State of a Cylinder with Variable Elasticity Moduli Based on Three-Dimensional Equations of Elasticity Theory. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):113-120. https://doi.org/10.23947/2687-1653-2023-23-2-113-120













































