Scroll to:
Buckling of Rectangular Plates under Nonlinear Creep
https://doi.org/10.23947/2687-1653-2023-23-3-257-268
Abstract
Introduction. The task of analyzing the stability of plates and shells under creep conditions is critical for structural elements made of materials with the property of aging, which are under the action of long-term loads, since the loss of stability can occur abruptly and long before the exhaustion of the strength resource of the material. Currently, the issues of joint consideration of geometric nonlinearity and creep in the problems of buckling plates remain poorly studied, existing software systems do not provide such calculations. The objective of this work is to develop an algorithm for calculating the stability of rectangular plates with initial deflection, which are subjected to loads in the middle plane, taking into account geometric nonlinearity and creep.
Materials and Methods. When obtaining the resolving equations, the geometric and static equations of the theory of flexible elastic plates were taken as the basis. Physical equations were derived from the assumption that total strains were equal to the sum of elastic strains and creep deformations. Finally, the problem was reduced to a system of two differential equations, in which the desired functions were the stress and deflection functions. The resulting system of equations was solved numerically using the finite-difference method in combination with the method of successive approximations and the Euler method. As the boundary conditions for the stress function, the frame analogy was used, as in the case of a plane problem of elasticity theory.
Results. The solution to the problem for a plate compressed in one direction by a uniformly distributed load has been presented. The nature of the growth of displacements at different load rates and initial deflection was studied. It has been established that when the vertical displacements reach values comparable to the thickness of the plate, their growth rate begins to decay even at a load greater than the long-term critical one.
Discussion and Conclusion. The results of stability analysis using the developed algorithm show that the growth of plate deflection under the considered boundary conditions is limited, stability loss is not observed at any load values not exceeding the instantaneous critical one. This indicates the possibility of long-term safe operation of such structures with a load less than instant critical one.
Keywords
For citations:
Yazyev S.B., Chepurnenko A.S. Buckling of Rectangular Plates under Nonlinear Creep. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):257-268. https://doi.org/10.23947/2687-1653-2023-23-3-257-268
Introduction. Much attention is paid to the stability analysis of thin-walled structures in the form of plates and shells, since such structures are widely used in construction and other branches of technology [1–3]. One of the challenges in the field of calculating plates and shells is the analysis of their stress-strain state under creep conditions, which is confirmed by a significant number of works published recently on this problem in domestic and foreign sources. Thus, in [4–8], the issues of buckling under creep of composite thin-walled structures were investigated. In [9], the problem of stability of functionally gradient plates was considered, taking into account the dependence of material properties on temperature. In [10], stochastic analysis methods were applied to the problem of buckling composite plates. In [11–17], the issues of stability of viscoelastic plates and shells under the influence of dynamic and tracking loads were discussed, and [18] dealt with plates of medium thickness, taking into account the dependence of material properties on time. Mathematical difficulties arising in solving these problems led to the fact that numerous researchers limited themselves to linear laws of viscoelastic deformation or considered the case of steady-state creep. The finite element method opens up great possibilities in solving the problems of calculating plates and shells taking into account creep. However, modern computational complexes, such as ANSYS, Abaqus, LIRA, etc., contain a limited set of rheological models applicable to specific materials in a fixed range of stresses and temperatures. There is a need for alternative calculation methods suitable for arbitrary laws of viscoelastic deformation, including nonlinear ones.
This work was aimed at constructing a system of resolving equations for the problem of buckling rectangular plates with nonlinear viscoelastic properties under the action of forces in the middle plane, taking into account large displacements, as well as an algorithm for its solution. Note that the problem of the stability of structural elements, taking into account creep, cannot be solved as a problem of pure stability. Its solution requires the presence of disturbances in the form of initial irregularities. Generally, the initial imperfections are given in the form of the initial loss or eccentricities of the application of loads.
Materials and Methods. Let us consider the calculation method on the example of a plate with an initial deflection w0(x,y), compressed by a distributed load p [kN/m] in the x-axis direction and having a hinge support along the contour (Fig. 1).
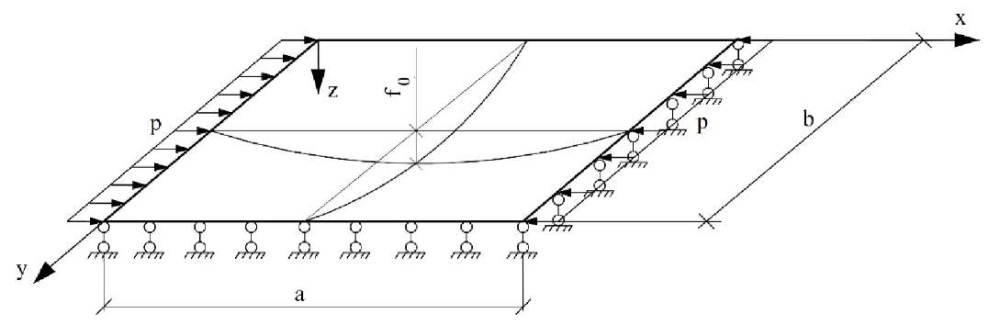
Fig. 1. Computational scheme
In the case under consideration, in the presence of creep, if compared to the theory of elastic flexible plates, the difference manifests itself only in the form of physical equations. Total deformations can be presented as the sum of deformations of the middle plane (passing into the surface) and bending deformations caused by changes in the curvature of the middle surface:
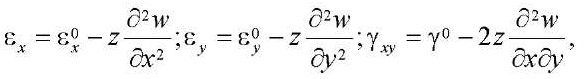 (1)
(1)
where
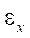 and
and 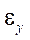 — total linear deformations;
— total linear deformations;
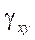 — total angular deformations;
— total angular deformations;
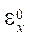 and
and 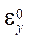 — linear deformations of the middle surface;
— linear deformations of the middle surface;
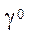 — angular deformations of the middle surface.
— angular deformations of the middle surface.
For deformations of the middle surface, the equation of continuity of deformations can be written [19]:
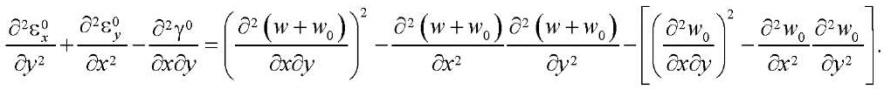 (2)
(2)
For materials with viscoelastic properties, total deformations can be represented as:
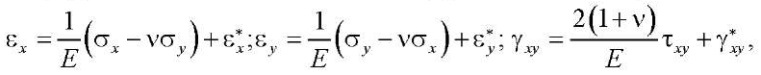 (3)
(3)
where
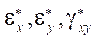 — creep deformations;
— creep deformations;
E — modulus of elasticity;
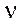 — Poisson's ratio;
— Poisson's ratio;
σx, σy, τxy — values of stress components in the corresponding directions.
Having expressed the stress components in (3) through deformations, we write down the physical relations in the inverse form:
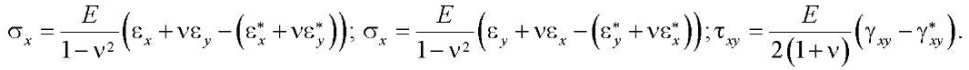 (4)
(4)
The relationship of internal force factors and stresses is determined by integral relations:
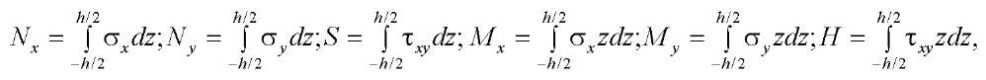 (5)
(5)
where
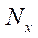 and
and 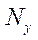 — linear longitudinal forces;
— linear longitudinal forces;
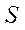 — linear shear forces;
— linear shear forces;
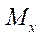 and
and 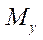 — linear bending moments;
— linear bending moments;
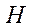 — linear torques;
— linear torques;
h — plate thickness.
Next, we substitute (1) in (4), as well as (4) in (5). As a result, we get:
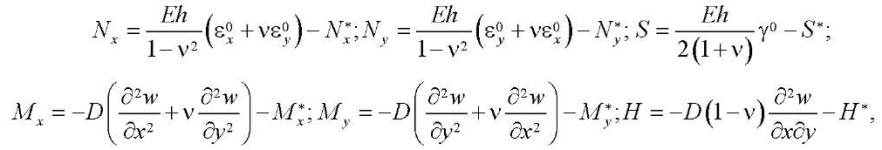 (6)
(6)
where
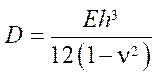 — cylindrical rigidity of the plate,
— cylindrical rigidity of the plate,
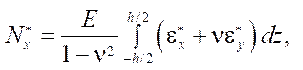
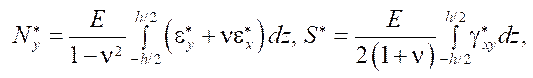
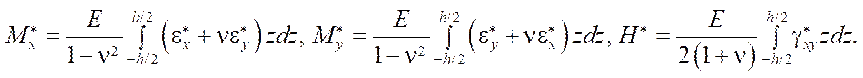
Values  have the dimension of internal forces and determine the contribution of creep deformations to the redistribution of forces.
have the dimension of internal forces and determine the contribution of creep deformations to the redistribution of forces.
Static equations of the flexible plate theory have the form [19]:
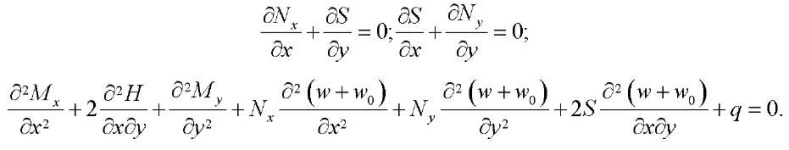 (7)
(7)
Here, q — normal load on the surface of the plate, which is zero in this problem.
It is possible to satisfy the first two static equations using the Airy stress functions, introduced by the formulas:
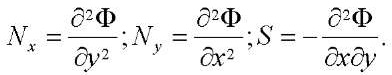 (8)
(8)
After substituting the last three equalities from (6) into the last static equation in (7) and taking into account (8), we obtain the first resolving equation:
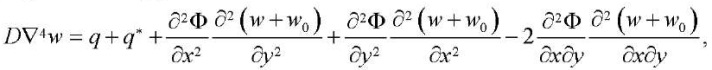 (9)
(9)
where
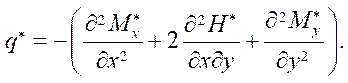
To obtain the second resolving equation, it is required to express the deformation of the median surface from (6):
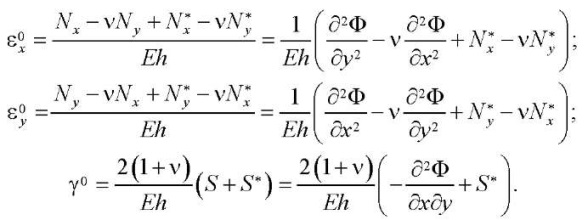 (10)
(10)
Substituting (10) into (2), we get:
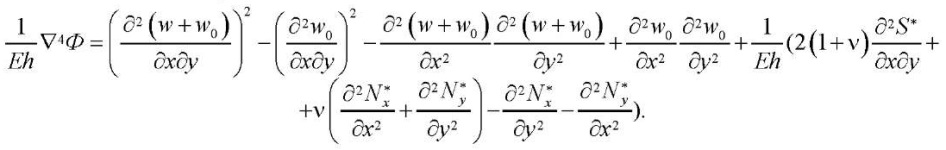 (11)
(11)
Thus, for the problem under consideration, a system of resolving equations is obtained from two fourth-order differential equations (9) and (11). Equations (9) and (11) are nonlinear. In the resulting equations, values 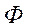 and w are functions of the coordinates x, y, and time t. Explicitly, there is no time in these equations, the time dependence is laid down in creep deformations
and w are functions of the coordinates x, y, and time t. Explicitly, there is no time in these equations, the time dependence is laid down in creep deformations 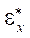 ,
, 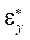 ,
, 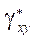 , which are taken into account by the introduction of integral quantities
, which are taken into account by the introduction of integral quantities 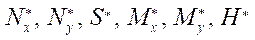 .
.
For the calculation scheme shown in Figure 1, the boundary conditions are written as:
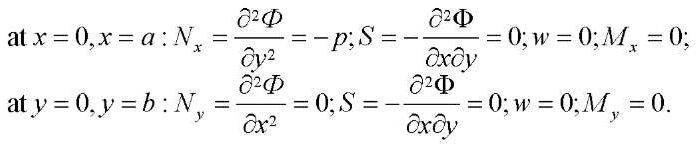 (12)
(12)
Equation (11) for small displacements, in the case of a plate made of elastic material, is a biharmonic equation that is used to solve the plane problem of the theory of elasticity in stresses. Frame analogy can serve as the boundary conditions for the stress function for the biharmonic equation. The plate contour is considered as a frame, and the stress function on the contour are equal to the bending moment M in it, and its derivative along the normal to the contour is the longitudinal force N. Plots M and N in the frame can be constructed in one of the basic systems of the force method (BSFM). The basic system, as well as the diagrams of the bending moment and longitudinal force in the frame are shown in Figure 2.
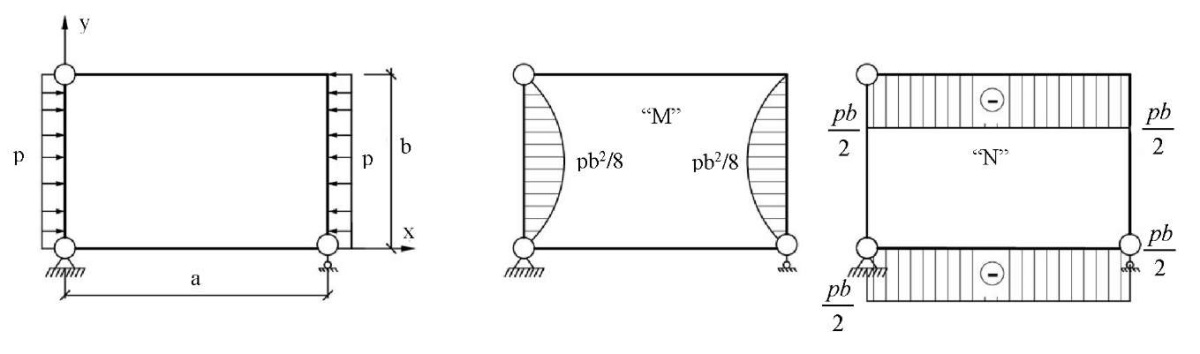
Fig. 2. BSFM and diagrams of the bending moment and longitudinal forces
If the vertical displacements do not exceed a quarter of the plate thickness, then it is possible to assume the forces in the middle surface independent
of the coordinates x and y (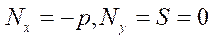 ) and use the linearized equation for calculations:
) and use the linearized equation for calculations:
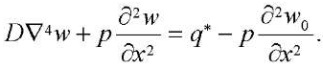 (13)
(13)
The analytical solution to the system of equations (9) and (11) is associated with great difficulties. The authors propose to solve this system numerically. The finite-difference method (FDM) was used in combination with the method of successive approximations. The Euler method was applied to determine creep deformation in the time domain. As the first stage, the solution for the elastic plate was performed. Load p was applied stepwise with small steps. At the initial load values, deflections w1 were calculated by solving the simplified equation (13). Then, the calculated values w1 were substituted into the differential equation (11). This provided determining the stress function. The next step was to solve the differential equation (9) using the known values of function Ф, which made it possible to determine the nodal values of deflections 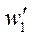 . After that, the values (11
. After that, the values (11 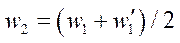 were substituted into equation (11). The iterative process was repeated at each step until the relative discrepancy with the norms of the vectors of the nodal values of deflections
were substituted into equation (11). The iterative process was repeated at each step until the relative discrepancy with the norms of the vectors of the nodal values of deflections 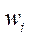 and
and  was greater than the specified value (the authors assumed it to be equal to 0.1 %). For the second load step, the initial value
was greater than the specified value (the authors assumed it to be equal to 0.1 %). For the second load step, the initial value 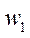 in each node was the final result obtained in the first step. The calculation technique in the time domain, taking into account creep, was similar. The time interval, at which the process was investigated, was divided into steps ∆t. In the case of setting the law of viscoelastic deformation in differential form, the values of creep deformations at step t + ∆t were calculated on the basis of the known rate of their growth at time t using the Euler approximation:
in each node was the final result obtained in the first step. The calculation technique in the time domain, taking into account creep, was similar. The time interval, at which the process was investigated, was divided into steps ∆t. In the case of setting the law of viscoelastic deformation in differential form, the values of creep deformations at step t + ∆t were calculated on the basis of the known rate of their growth at time t using the Euler approximation:
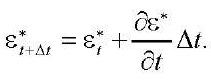 (14)
(14)
The block diagram of the creep calculation algorithm is shown in Figure 3.
Note that the system of equations (9) and (11) provides using schemes of a higher order of accuracy, e.g., the fourth-order Runge-Kutta method. At the same time, to achieve the same accuracy of the results, you can set noticeably large time steps. However, with an increase in the step, there is a chance of not catching the effects of unsteady creep at the initial moments of time. And with the same time step, the Runge-Kutta method, in comparison to the Euler method, requires four times more operations to be performed.

Fig. 3. Block diagram of the creep calculation algorithm
Research Results. A polyvinyl chloride polymer plate with dimensions a =2 m, b = 2 m, h = 1 cm at E = 1480 MPa, ν = 0.3 was considered. The nonlinear Maxwell-Gurevich equation was adopted as the law determining the rate of creep strain growth:
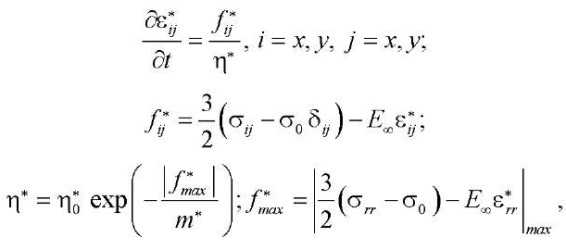 (15)
(15)
where
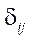 — Kronecker symbol;
— Kronecker symbol;
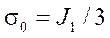 ,
, 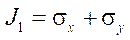 — first invariant of the stress tensor;
— first invariant of the stress tensor;
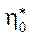 , E∞ and
, E∞ and 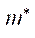 — rheological parameters of the material, called the initial relaxation viscosity, the modulus of high elasticity, and the modulus of velocity.
— rheological parameters of the material, called the initial relaxation viscosity, the modulus of high elasticity, and the modulus of velocity.
Indices rr in formula (15) indicate the direction of the primary stresses.
For PVC, the authors took the values of rheological parameters from [20]:
E∞ = 5.99∙103 MPa, 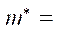 12.6 MPa,
12.6 MPa, 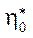 = 5.44·107 MPa·s.
= 5.44·107 MPa·s.
The shape of the initial deflection w0(x,y) was taken in accordance with the first form of the loss of stability of the plate made of elastic material:
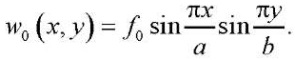 (16)
(16)
For a plate made of elastic material without initial imperfections, the critical load, in the case of the whole ratio of sides a/b, was determined from the formula [19]:
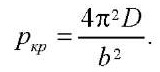 (17)
(17)
To verify the developed calculation algorithm, the first step was to solve the elastic test problem and compare the results to the calculation in the finite element LIRA-CAD package (Fig. 4). The value of the arrow of the initial deflection f0 was set to 0.15 mm. The grid size when using the FDM was 20×20, the number of load steps was 200. When calculating in the LIRA-CAD PC, the plate was divided by triangular finite elements with a triangulation step of 0.1 m. The load step size was assumed to be the same as when using the FDM. The value of the critical load for the elastic plate, calculated from formula (17), was 1340 N/m. Table 1 shows a comparison of vertical displacements in the center of the plate for different load values obtained by the author's method and using the finite element method (FEM). The deflections calculated using two alternative methods are quite close, except for the load of 1330 N/m. The deviation at this load value can be explained by the fact that when approaching the critical load, the movements rush to infinity.
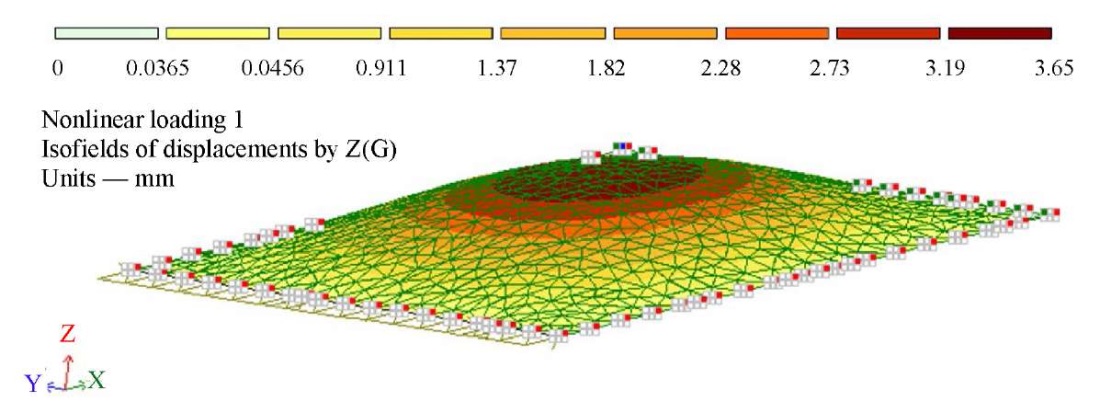
Fig. 4. Isofield of vertical displacements in LIRA-CAD PC (p = 1330 N/m)
Table 1
Comparison of calculation results using the author's method and with the help of FEM
|
p, N/m |
w∙103, mm |
|
|
LIRA-CAD |
the authors’ method |
|
|
133 |
16 |
16 |
|
266 |
37 |
37 |
|
399 |
63 |
63 |
|
532 |
98 |
99 |
|
665 |
146 |
148 |
|
798 |
218 |
221 |
|
931 |
336 |
342 |
|
1,064 |
562 |
578 |
|
1,197 |
1,163 |
1229 |
|
1,330 |
3,646 |
4,229 |
In [21], the possibility of transition from the solution of the elastic problem of calculating plates to the solution at the end of the creep process is shown. The value of the long-term critical load p∞ can be obtained by replacing the cylindrical stiffness D of the elastic plate with the long-term cylindrical stiffness D∞, which is determined from the formula:
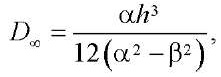 (18)
(18)
where
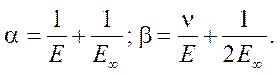
For viscoelastic rods and round plates, it has been previously established that in case p < p∞, the growth of displacements in time slows down, and the deflection arrow comes to a finite value. If p = p∞, deflections grow at a constant rate. At p > p∞, the rate of deflection growth increases.
The authors also analyzed the nature of the growth of deflections over time for p < p∞, p = p∞ and p > p∞ for different values of the maximum initial loss f0. The deflection curves over time in the center of the plate at p = 0.9 p∞, p = p∞ and p = 1.1 p∞ are shown respectively in Figures 5–7.
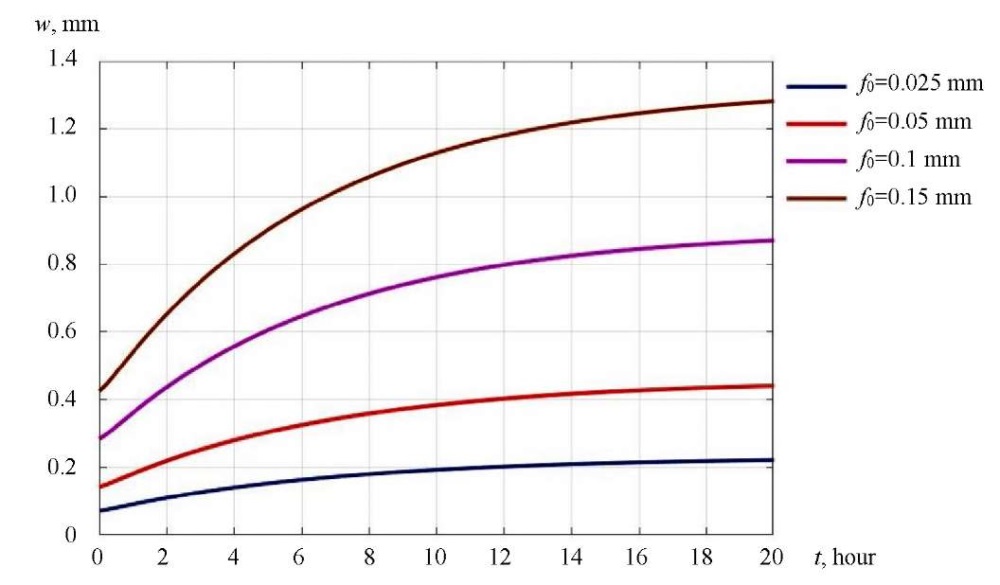
Fig. 5. Deflection curves over time in the center of the plate at p = 0.9p∞

Fig. 6. Deflection curves over time in the center of the plate at p = p∞
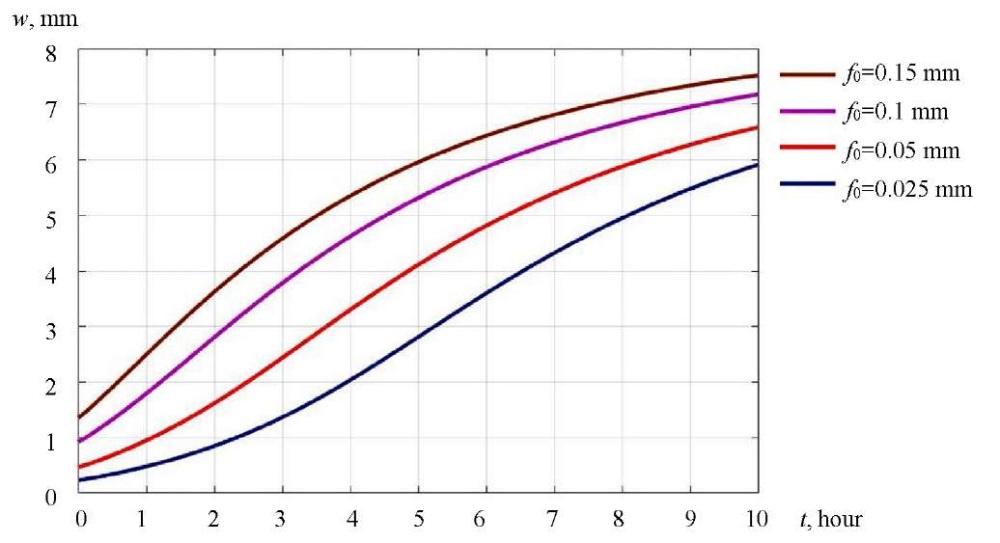
Fig. 7. Deflection curves over time in the center of the plate at p = 1.1 p∞
Discussion and Conclusion. It can be seen from Fig. 5 that at p < p∞, the deflection arrow always comes to the final value, regardless of the values of the initial imperfections. At the same time, at p ≥ p∞, the pattern of deflection growth obtained in [21] occurs only with small displacements. When deflections reach values exceeding about a quarter of the plate thickness, the rate of deformation growth begins to decrease even in the case of loads exceeding the long-term critical one. It should also be noted that there is a complete absence of a section with an increasing rate of displacement growth for plates with large initial curvatures. The identified effects can be explained by the redistribution of efforts 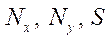 in the middle surface.
in the middle surface.
Summarizing the above, we can conclude that the vertical movements of the plate pivotally supported along the contour, under the action of a compressive load on one axis, always come to a final value if the load does not exceed the instantaneous critical one. In other words, with the considered fastening and loading, the plate is in stable equilibrium under creep conditions.
The obtained equations and the calculation algorithm make it possible to calculate plates made of arbitrary viscoelastic materials for any fastening options. The law of the relationship between stresses and creep deformations can also be set arbitrarily.
References
1. Yankovskii AP. Refined Deformation Model for Metal-Composite Plates of Regular Layered Structure in Bending under Conditions of Steady-State Creep. Mechanics of Composite Materials. 2017;52(6):715–732. https://doi.org/10.1007/s11029-017-9622-7
2. Yankovskii AP. The Steady Creeping Difficulty Reinforced the Metal-Composite Plates Loaded in the Plane. Mathematical Models and Computer Simulations. 2010;22(8);55–66. URL: https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mm&paperid=3007&option_lang=rus (accessed: 18.05.2023).
3. Khoroshun LP, Babich DV. Ustoichivost' pryamougol'nykh plastin iz sloistogo kompozitnogo materiala pri dlitel'noi povrezhdaemosti komponentov. Prikladnaya mekhanika. 2010;46(12):67–75. (In Russ.)
4. Zhongyu Lu, Guijun Xian, Khuram Rashid. Creep Behavior of Resin Matrix and Basalt Fiber Reinforced Polymer (BFRP) Plate at Elevated Temperatures. Journal of Composites Science. 2017;1(1):3. https://doi.org/10.3390/jcs1010003
5. Pawlus D. Stability of Three-Layered Annular Plate with Composite Facings. Applied Composite Materials. 2017;24(1):141–158. https://doi.org/10.1007/s10443-016-9518-z
6. Rouzegar J, Gholami M. Creep and Recovery of Viscoelastic Laminated Composite Plates. Composite Structures. 2017;181:256–272. https://doi.org/10.1016/j.compstruct.2017.08.094
7. Gräfe M, Dietsch P, Winter S. CLT under In-Plane Loads: Investigation on Stress Distribution and Creep. In: Proc. INTER International Network on Timber Engineering Research. Karlsruhe: Timber Scientific Publishing; 2018. P. 289−306. URL: https://mediatum.ub.tum.de/doc/1533836/document.pdf (accessed: 18.05.2023).
8. Pawlus D. Dynamic Behaviour of Three-Layered Annular Plates with Viscoelastic Core under Lateral Loads. Journal of Theoretical and Applied Mechanics. 2015;53(4):775–788. https://doi.org/10.15632/jtam-pl.53.4.775
9. Sharma K. Kumar D., Elastoplastic Stability and Failure Analysis of FGM Plate with Temperature Dependent Material Properties under Thermomechanical Loading. Latin American Journal of Solids and Structures. 2017;14(7):1361–1386. https://doi.org/10.1590/1679-78253747
10. Kumar RR, Mukhopadhyay T, Pandey KM, Dey S. Stochastic Buckling Analysis of Sandwich Plates: The Importance of Higher Order Modes. International Journal of Mechanical Sciences. 2019;152:630–643. https://doi.org/10.1016/j.ijmecsci.2018.12.016
11. Kosheleva E. Dynamic Stability of a Viscoelastic Plate. MATEC Web of Conferences. 2017;117:00086. https://doi.org/10.1051/matecconf/201711700086
12. Abramovich H. Stability and Vibrations of Thin-Walled Composite Structures. Cambridge: Woodhead Publishing; 2017. 770 p.
13. Kirsanov MN. Buckling of a Plate of Nonlinear Rheological Mwith Variable Loading. Bulletin of the Tatar State Humanitarian and Pedagogical University. 2011;24:19–22. URL: https://cyberleninka.ru/article/n/vypuchivanieplastiny-iz-nelineynogo-reologicheskogo-materiala-pri-peremennom-nagruzhenii (accessed: 18.05.2023).
14. Abdikarimov RA, Zhgutov VM. Geometrically Nonlinear Mathematical Simulation the Viscoelastic Gently Sloping Variable-Thickness Shells’ Dynamic Steadiness. Magazine of Civil Engineering. 2011;(6):12–22. https://cyberleninka.ru/article/n/geometricheski-nelineynoe-matematicheskoe-modelirovanie-dinamicheskoyustoychivosti-vyazkouprugih-pologih-obolochek-peremennoy/viewer (accessed: 18.05.2023).
15. Abdikarimov RA, Khudayarov BA. Dinamicheskaya ustoichivost' vyazkouprugikh gibkikh plastin peremennoi zhestkosti pri osevom szhatii. Prikladnaya mekhanika. 2014;50(4): 41–51. (In Russ.)
16. Abdikarimov RA, Verlan AF, Goroshko IO. Chislennoe issledovanie dinamicheskoi ustoichivosti vyazkouprugikh ortotropnykh pryamougol'nykh plastin s peremennoi zhestkost'yu. Моделювання та інформаційні технології. 2011;60:10–17. (In Russ.)
17. Robinson MTA, Adali S. Nonconservative Stability of Viscoelastic Plates Subject to Triangularly Distributed Follower Loads. Journal of Theoretical and Applied Mechanics. 2017;55(3):1015–1027. https://doi.org/10.15632/jtampl.55.3.1015
18. Jafari N, Azhari M. Stability Analysis of Arbitrarily Shaped Moderately Thick Viscoelastic Plates Using Laplace– Carson Transformation and a Simple HP Cloud Method. Mechanics of Time-Dependent Materials. 2017;21(3):365–381. https://doi.org/10.1007/s11043-016-9334-8
19. Chepurnenko AS, Yazyev BM, Savchenko AA. Calculation for the Circular Plate on Creep Considering Geometric Nnonlinearity. Procedia Engineering. 2016;150:1680–1685. https://doi.org/10.1016/j.proeng.2016.07.150
20. Chepurnenko AS, Andreev VI, Beskopylny AN, Jazyev BM. Determination of Rheological Parameters of Polyvinylchloride at Different Temperatures. MATEC Web of Conferences. 2016;67:06059. https://doi.org/10.1051/matecconf/20166706059
21. Andreev VI, Yazyev BM, Chepurnenko AS. Axisymmetric Bending of a Round Elastic Plate in Case of Creep. Vestnik MGSU. 2014;(5):16–24. URL: https://cyberleninka.ru/article/n/osesimmetrichnyy-izgib-krugloy-gibkoyplastinki-pri-polzuchesti (accessed: 18.05.2023).
About the Authors
S. B. YazyevRussian Federation
Serdar B. Yazyev, Dr.Sci. (Eng.), Associate Professor, Associate Professor of the Structural Mechanics and Theory of Structures Department
1, Gagarin sq., Rostov-on-Don, 344003
A. S. Chepurnenko
Russian Federation
Anton S. Chepurnenko, Dr.Sci. (Eng.), Associate Professor, Professor of the Structural Mechanics and Theory of Structures Department
1, Gagarin sq., Rostov-on-Don, 344003
Review
For citations:
Yazyev S.B., Chepurnenko A.S. Buckling of Rectangular Plates under Nonlinear Creep. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):257-268. https://doi.org/10.23947/2687-1653-2023-23-3-257-268













































