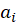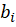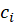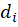Scroll to:
Automation of the Formation of a Mathematical Formulation of Kinetics for Multistage Chemical Reactions and Numerical Solution to a Direct Problem
https://doi.org/10.23947/2687-1653-2023-23-4-398-409
EDN: PDPGGO
Abstract
Introduction. The basis for research, analysis and mathematical optimization of any chemical process is an adequate mathematical model that takes into account the kinetics of the object. Kinetic analysis is a challenge in chemical technology, since it allows for optimizing synthesis processes and predicting their efficiency. Numerous chemical processes involve several stage reactions. For successful design and optimization, a mathematical model that describes each stage is needed. Creating such a model manually can be time-consuming and costly, since it requires processing a large amount of information. The modern level of automation makes it possible to accelerate the obtaining of a mathematical formulation of the kinetics of multistage reactions. In this case, working with data is greatly simplified, and the probability of making mistakes is reduced. The resulting mathematical model can be applied for further analysis and optimization of the process. The paper considers the industrial reaction of catalytic reforming of gasoline, which occupies an important place in the modern scheme of oil refining, since it is a source of high-octane components of commercial gasolines and individual aromatic hydrocarbons. This process is characterized by the participation of a large number (up to 300) of various hydrocarbons, a change in the number of moles, and non-isothermality in it. Mathematical modeling of such processes involves detailing the stages to the required level. The detailing of up to 173 stages is considered. In this setting, automation of the formation of a mathematical formulation of kinetics for catalytic reforming of gasoline has not been carried out before. Therefore, the presented work aimed at implementing effective numerical methods and algorithms for automating the building of a mathematical model taking into account kinetics, thermodynamics, and changes in the number of moles.
Materials and Methods. The mathematical formulation of the kinetics of multistage reactions was developed on the basis of the mass action law. The kinetic parameters values were taken from literary sources. The direct kinetics problem was solved using algorithms: the Gear method, the Runge-Kutta method of the 4th order, and the scipy.odeint() method of the Python language. The automation concept was implemented using the IDEF0 methodology. The software was written in the Python programming language.
Results. A new software was created to automate the process of forming a mathematical model, taking into account the kinetics, thermodynamics, and the volume of the reaction mixture. The program results were presented by the example of catalytic reforming of gasoline. The model implemented the possibility of taking into account the intermediate heating of the mixture in the reactor cascade. Numerical values of temperature changes corresponding to industrial data were obtained.
Discussion and Conclusion. The results obtained through modeling chemical transformations in the cascade of gasoline catalytic reforming reactors confirmed the exothermic nature of the reaction. The developed software product provides displaying changes in the concentrations of reactants, as well as temperature variations in the reactor, and it can be used in scientific research organizations for the analysis of multistage catalytic processes. The results of the reaction kinetics modeling will be used in the subsequent optimization of the process conditions in production.
Keywords
For citations:
Lysenko N.A., Koledina K.F. Automation of the Formation of a Mathematical Formulation of Kinetics for Multistage Chemical Reactions and Numerical Solution to a Direct Problem. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):398-409. https://doi.org/10.23947/2687-1653-2023-23-4-398-409. EDN: PDPGGO
Introduction. Studies on the kinetics of multistage chemical processes is of theoretical and practical importance, since it allows for revealing the mechanism of reactions and carrying out control. At the same time, it becomes possible to accelerate target or slow down side chemical reactions. Kinetic analysis, being an important task of chemical engineering, contributes to the optimization of synthesis processes and the prediction of their effectiveness [1–3]. A great many chemical processes are multistage reactions. For their effective design and optimization, it is required to have a mathematical model describing all stages [4][5]. Manual formation of such a model can be very time-consuming and costly, since it implies processing a large amount of information [6].
The object of the study is the industrial process of catalytic reforming of gasoline. The target product of the reaction — reformate — provides obtaining the bulk of commercial gasoline. The remaining components are products of isomerization, catalytic cracking, and alkylation. Most oil refineries in Russia and worldwide use catalytic reforming units [7][8]. Catalytic reforming of gasoline makes it possible to obtain aromatic hydrocarbons (xylene, toluene, benzene), which can then be used in the petrochemical industry [9][10]. However, for commercial gasoline, the presence of aromatic hydrocarbons in the product is limited by environmental criteria. Therefore, detailed complex kinetics, demonstrating the step-by-step formation of components, is able to operate the process conditions to control the yield of the product and limit the content of aromatic hydrocarbons. The process of catalytic reforming of gasoline is carried out in a reactor unit consisting of three consecutive reactors, between which furnaces are installed to heat the mixture. This is a necessity since the reaction is endothermic. In the mathematical formulation of the reactor unit, it is required to take into account the variation of temperature and volume of the reaction mixture along with changes in the concentrations of the components from the conditional contact time of the catalyst and the reaction mixture.
Automation of modeling of such complex processes makes it possible to significantly speed up obtaining a mathematical formulation of the kinetics of multistage reactions, reduce the probability of errors, and simplify the process of working with data [11]. In general, automation of the formation of a mathematical formulation for multistage chemical reactions is an important tool for effective process management in various industries, as well as for achieving more accurate and efficient implementation of chemical reactions in the laboratory.
Thus, the study aimed at developing a software product to help automate the formation of a mathematical formulation of multistage chemical reactions, taking into account the kinetics, thermodynamics and changes in the volume of the reaction mixture, as well as obtaining a numerical solution of the compiled mathematical model.
To achieve the research goal, the following tasks were solved in this work:
- development of a software module for the formation of a mathematical formulation of kinetics using the Python programming language;
- development of a software module for numerical solution to a direct problem according to a compiled mathematical formulation using the Python programming language;
- obtaining the results of the software product for the reaction of catalytic reforming of gasoline.
Materials and Methods. Mathematically, this process can be described by a system of ordinary nonlinear differential equations with initial data, which is a mathematical model. Considering that the catalytic reforming of gasoline is an exothermic reaction with a change in the volume of the reaction mixture, the model of multistage chemical kinetics can be considered in the following context:
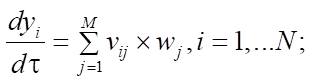 (1)
(1)
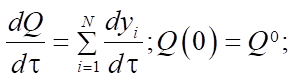 (2)
(2)
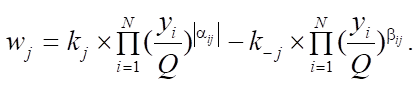 (3)
(3)
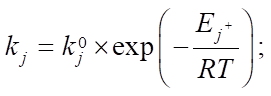
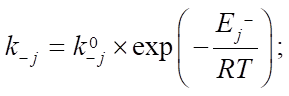 (4)
(4)
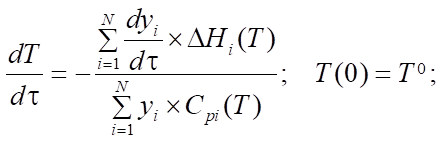 (5)
(5)
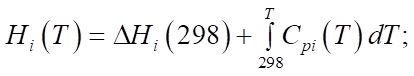 (6)
(6)
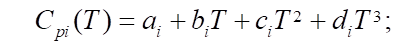 (7)
(7)
with initial conditions at
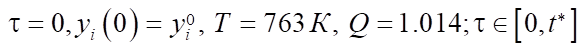 [11].
[11].
In this formula of reaction kinetics there are a number of variables and coefficients that determine the concentration of reagents, contact time and reaction rate. Specifically, Q and 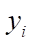 (concentrations of reaction reagents) can be expressed in mol/l or in fractions, and variable
(concentrations of reaction reagents) can be expressed in mol/l or in fractions, and variable 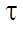 , showing the conditional contact time of the reaction mixture with the catalyst, in kg×min/mol or kg of the catalyst. The formula also includes the following indicators: the number of stages M (173 stages) and the number of substances N (38 substances), as well as stoichiometric matrix
, showing the conditional contact time of the reaction mixture with the catalyst, in kg×min/mol or kg of the catalyst. The formula also includes the following indicators: the number of stages M (173 stages) and the number of substances N (38 substances), as well as stoichiometric matrix 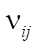 .
. 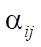 — these are all negative elements of matrix
— these are all negative elements of matrix 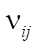 at the intersection of the
at the intersection of the 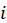 -th row and the j-th column, and
-th row and the j-th column, and 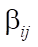 — all positive elements of matrix
— all positive elements of matrix 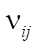 at the intersection of the
at the intersection of the 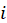 -th row and the j-th column. The rate of the j-th reaction stage
-th row and the j-th column. The rate of the j-th reaction stage 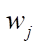 can be expressed in 1/min or in mol/(kg×min), and the rate constants of stages
can be expressed in 1/min or in mol/(kg×min), and the rate constants of stages 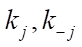 — in 1/min. In addition, the formula specifies pre-exponential factors
— in 1/min. In addition, the formula specifies pre-exponential factors 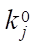 ,
, 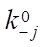 , expressed in 1/min, the activation energies of the forward and reverse reactions
, expressed in 1/min, the activation energies of the forward and reverse reactions 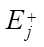 ,
, 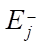 , expressed in kcal/mol, gas constant R and temperature T, measured in Kelvins. The period of reaction t* is determined by the time required to complete it in minutes, and the enthalpy of the formation of the i-th component
, expressed in kcal/mol, gas constant R and temperature T, measured in Kelvins. The period of reaction t* is determined by the time required to complete it in minutes, and the enthalpy of the formation of the i-th component 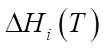 is measured in J/mol. The specific heat capacity
is measured in J/mol. The specific heat capacity 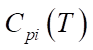 of the i-th component, measured in J/(mol×K), can be expressed in terms of the coefficients of the temperature dependence of the heat capacity of this component, which are indicated by letters
of the i-th component, measured in J/(mol×K), can be expressed in terms of the coefficients of the temperature dependence of the heat capacity of this component, which are indicated by letters 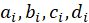 [12]. i — serial number of the substance involved in the reaction.
[12]. i — serial number of the substance involved in the reaction.
When modeling chemical transformations of catalytic reforming of gasoline, it is required to take into account a large number of individual hydrocarbons. Therefore, in the article, group components are used in the model for the separation of types of hydrocarbons and the number of carbon atoms in the structure of the molecule: Al — aromatic hydrocarbons; ACPl — five-membered naphthenes; ACHl — six-membered naphthenes; iPl — paraffin isomers; nPl — normal paraffins. Here, l — number of carbon atoms in the molecular structure. Table 1 shows the average coefficients of the temperature dependence of the heat capacity of the group components that are used in the calculations.
Table 1
Coefficients of temperature dependence of group components
|
l |
Hydrocarbon group |
|
|
|
|
|
1 |
nP1 |
34.942 |
–0.03996 |
0.19184 |
–0.153 |
|
2 |
nP2 |
28.146 |
0.043447 |
0.18946 |
–0.1908 |
|
3 |
nP3 |
28.277 |
0.116 |
0.19597 |
–0.2327 |
|
4 |
nP4 |
20.56 |
0.2815 |
–0.013143 |
–0.09457 |
|
5 |
IP4 |
6.772 |
0.34147 |
–0.10271 |
–0.03685 |
|
6 |
nP5 |
26.671 |
0.32324 |
0.04282 |
–0.1664 |
|
7 |
iP5 |
–0.881 |
0.47498 |
–0.24797 |
0.06751 |
|
8 |
nP6 |
25.924 |
0.41927 |
–0.012491 |
–0.1592 |
|
9 |
iP6 |
–7.123 |
0.58327 |
–0.30338 |
0.06802 |
|
10 |
nP7 |
26.984 |
0.50387 |
–0.04748 |
–0.1684 |
|
11 |
iP7 |
19.245 |
0.55072 |
–0.14055 |
–0.08248 |
|
12 |
nP8 |
29.053 |
0.58016 |
–0.057103 |
–0.1955 |
|
13 |
iP8 |
–3.367 |
0.75824 |
–0.38216 |
0.05736 |
|
14 |
nP9 |
29.687 |
0.66821 |
–0.096492 |
–0.2001 |
|
15 |
iP9 |
68.581 |
0.44754 |
0.31908 |
–0.5118 |
|
16 |
nP10 |
31.78 |
0.74489 |
–0.10945 |
–0.2267 |
|
17 |
iP10 |
–46.17 |
1.108 |
–0.70316 |
0.1787 |
|
18 |
nP11 |
125.21 |
0.31401 |
0.79137 |
–0.9141 |
|
19 |
iP11 |
–8.791 |
1.0548 |
–0.5778 |
0.1192 |
|
20 |
ACH6 |
13.783 |
0.20742 |
0.53682 |
–0.6301 |
|
21 |
ACH7 |
4.296 |
0.42716 |
0.21058 |
–0.3999 |
|
22 |
ACH8 |
–51.866 |
0.78827 |
–0.35255 |
–0.006855 |
|
23 |
ACH9 |
–120.89 |
1.2728 |
–1.0794 |
0.4035 |
|
24 |
ACH10 |
90.421 |
0.23264 |
0.94595 |
–1.057 |
|
25 |
ACH11 |
–65.48 |
1.1809 |
–0.68379 |
0.1458 |
|
26 |
ACP6 |
–9.939 |
0.42528 |
0.012521 |
–0.1886 |
|
27 |
ACP7 |
–28.514 |
0.58607 |
–0.094379 |
–0.1644 |
|
28 |
ACP8 |
–69.713 |
0.92602 |
–0.62526 |
0.2049 |
|
29 |
ACP9 |
–116.73 |
1.3097 |
–1.2439 |
0.5292 |
|
30 |
ACP10 |
–67.341 |
1.0922 |
–0.704 |
0.1906 |
|
31 |
ACP11 |
–68.23 |
1.187 |
–0.7575 |
0.2018 |
|
32 |
A6 |
–31.368 |
0.4746 |
–0.31137 |
0.08524 |
|
33 |
A7 |
–24.097 |
0.52187 |
–0.29827 |
0.06122 |
|
34 |
A8 |
–17.36 |
0.5647 |
–0.26293 |
0.01122 |
|
35 |
A9 |
–10.933 |
0.64349 |
–0.27829 |
–0.01443 |
|
36 |
A10 |
–24.187 |
0.79716 |
–0.48265 |
0.1341 |
|
37 |
A11 |
–26.717 |
0.91044 |
–0.53876 |
0.1203 |
|
38 |
H2 |
29.07 |
–0.0836 |
0.1064 |
0.5752 |
Equations (1), (3) and (4) describe changes in reagent concentrations in the process, and in system (2), molar fractions are used to describe changes in the molar flow rate of the mixture. In (5), the dependence of the reaction temperature change on the thermodynamic characteristics of substances is considered. In (6), (7), the dependence for calculating the enthalpy of formation of the i-th component and the specific heat capacity is given.
In this model, the direct problem (solving a system of differential equations) is both rigid and non-rigid. The Gear method used to solve the catalytic reforming model is based on backward differentiation [13–15]. To compare the results and identify the optimal method, an explicit one-step Runge-Kutta numerical integration fourth-order method and an explicit numerical integration method scipy.odeint() of the Python programming language were used.
The concept of automating the formation of a mathematical formulation of kinetics for multistage chemical reactions and a numerical solution method is illustrated using the IDEF0 methodology.
Figure 1 shows a contextual diagram of the process of automating the formation of a mathematical formulation of kinetics for multistage chemical reactions and solutions by numerical method.
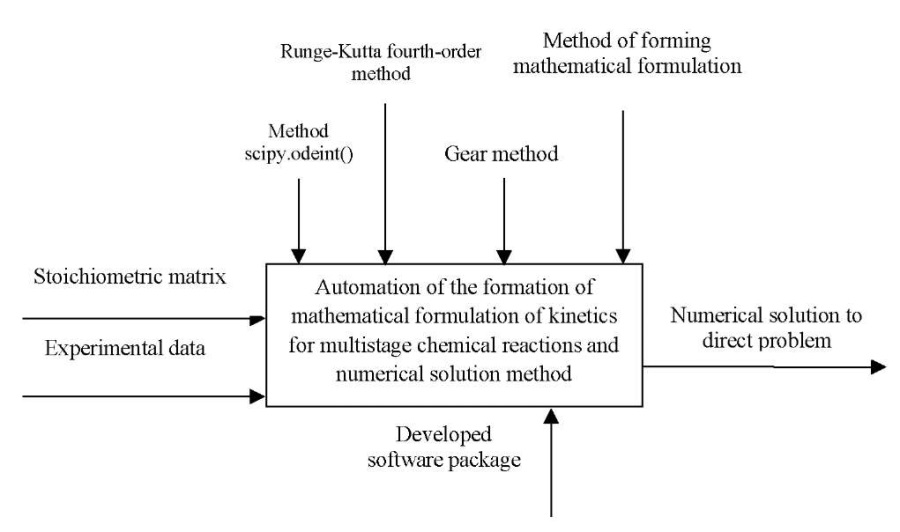
Fig. 1. Context diagram
“Automation of the formation of mathematical formulation of kinetics
for multistage chemical reactions and a numerical solution method”
The input parameters are the stoichiometric reaction matrix and experimental data. These include initial data on the concentration of substances, temperature, pre-exponential multiplier, activation energies. The result of solving the problem is a numerical solution to the direct problem. The controls are numerical methods for comparing the results, as well as the method of forming a mathematical description. The mechanism is the developed software package for automating the mathematical formulation of the kinetics of multistage reactions and solving a direct problem. Figure 2 shows the decomposition of the process of automating the formation of a mathematical formulation of kinetics for multistage chemical reactions and solutions by numerical method into stages:
- formation of mathematical formulation;
- direct problem solution.
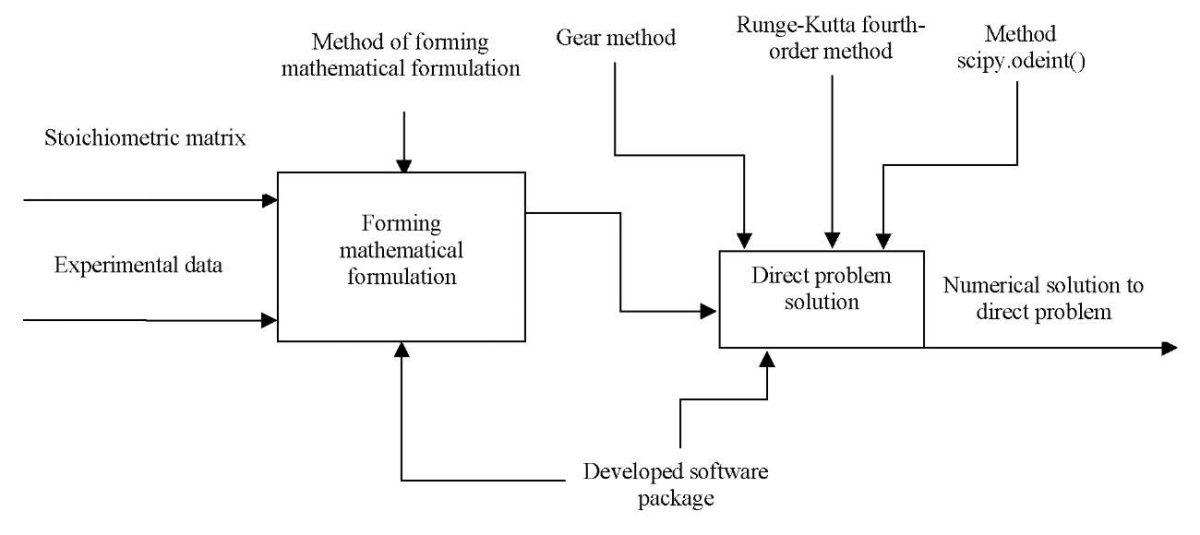
Fig. 2. Stages of the problem solution
“Automation of the formation of mathematical formulation of kinetics
for multistage chemical reactions and a numerical solution method”
The developed software package capabilities are represented by the features described below.
With the help of the program, you can create a kinetic model of a multistage chemical reaction and present its solution by the previously described methods, using a given stoichiometric matrix. If the reaction is exothermic and there is a change in the volume of the reaction mixture, two complementary equations are added to the system of differential equations to describe these changes.
The mathematical model of catalytic reforming of gasoline is a system of differential equations (DES) of form (1)–(7), consisting of 40 differential equations with respect to the number of group components, temperature dependence, and the mole change equation.
The basic functionality of the program is:
- main application window with the output of the mathematical formulation according to the stoichiometric matrix entered by the user;
- window with visualization of the solution: for each numerical method (Python-odeint, fourth-order Runge-Kutta, Gear method), the operating time, an array of time t and the solution of a system of differential equations at each moment of time are displayed, which are graphs of changes in the concentration of substances, changes in the reaction temperature or the volume of the reaction mixture.
Research Results. The catalytic reforming reaction took place in three reactors, between which a heating furnace was located. The initial temperature of the first reactor was 766 K (493°C). For the first 9.6 conditional hours, the reaction proceeded in the first reactor, the temperature dropped. After that, heating took place in the furnace between the two reactors to 763 K (490°C), and the chemical process passed into the second reactor. In the second reactor, the process occurred in the time interval from 9.6 to 32.3 conventional hours, the temperature decreased. Before proceeding to reactor 3, the mixture was heated in the second intermediate furnace to 768 K (495°C) and flew in this reactor in the time interval from 32.3 to 60 conventional hours.
Figures 3–5 show the kinetic curves of the hydrocarbon groups involved in the reaction and obtained using the Gear method. The intermittent transitions on the graphs indicate that the mixture is moving from one reactor to another with intermediate heating.
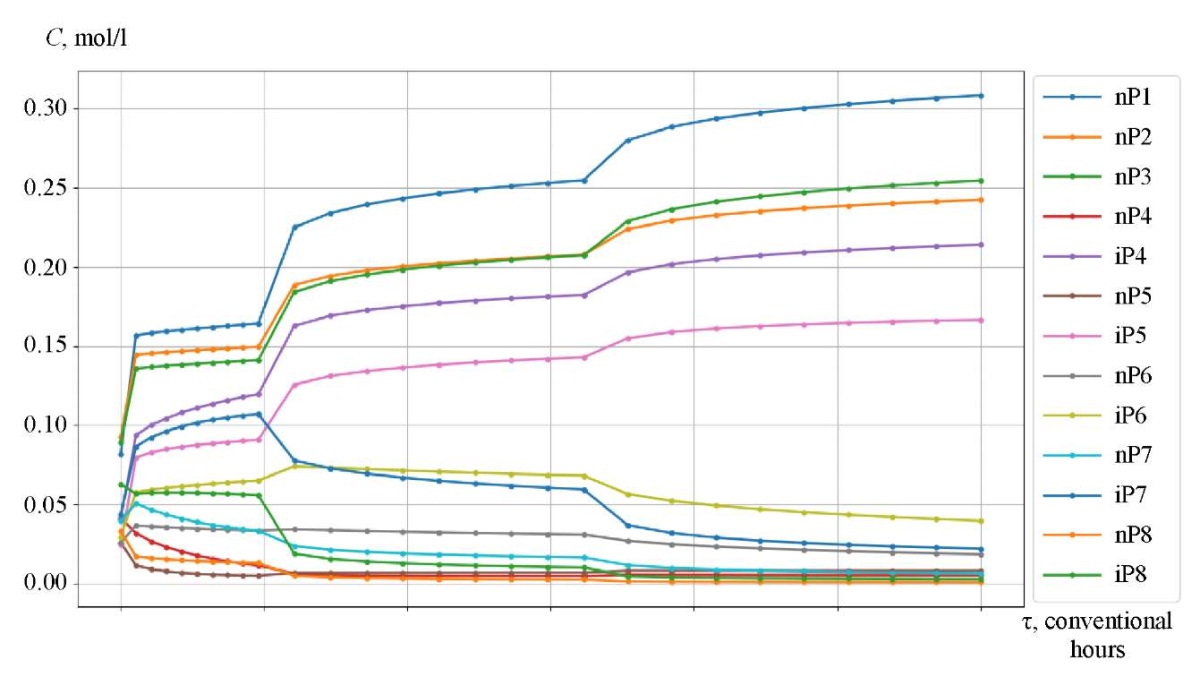
Fig. 3. Kinetic curves of catalytic reforming of gasoline
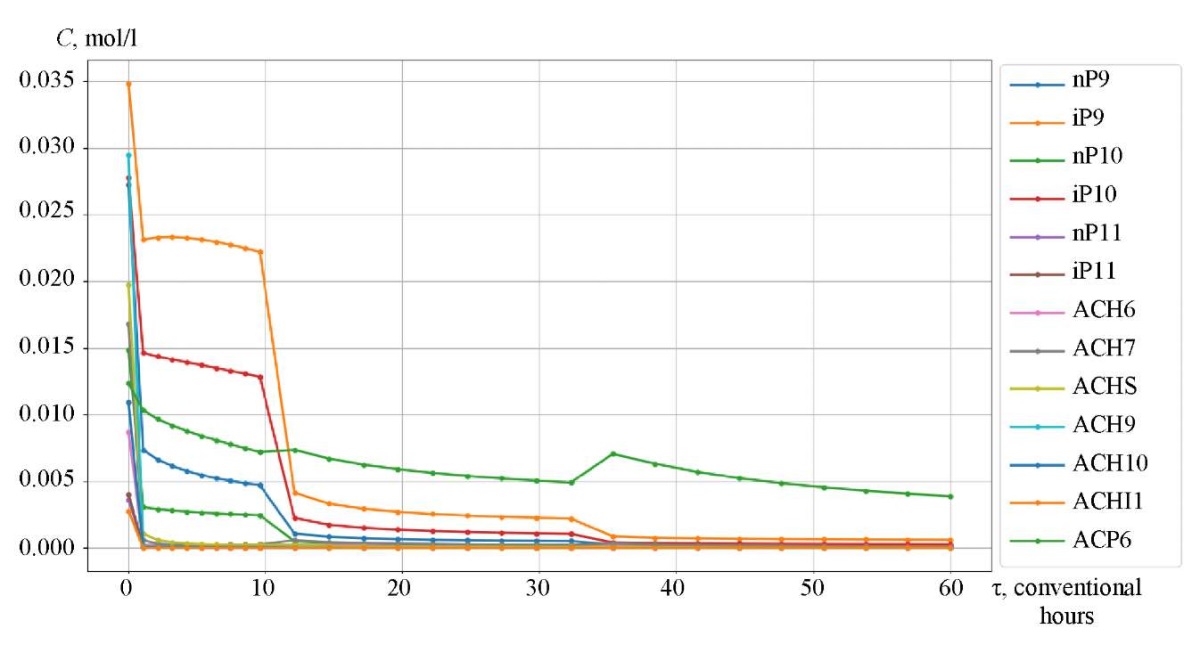
Fig. 4. Kinetic curves of catalytic reforming of gasoline
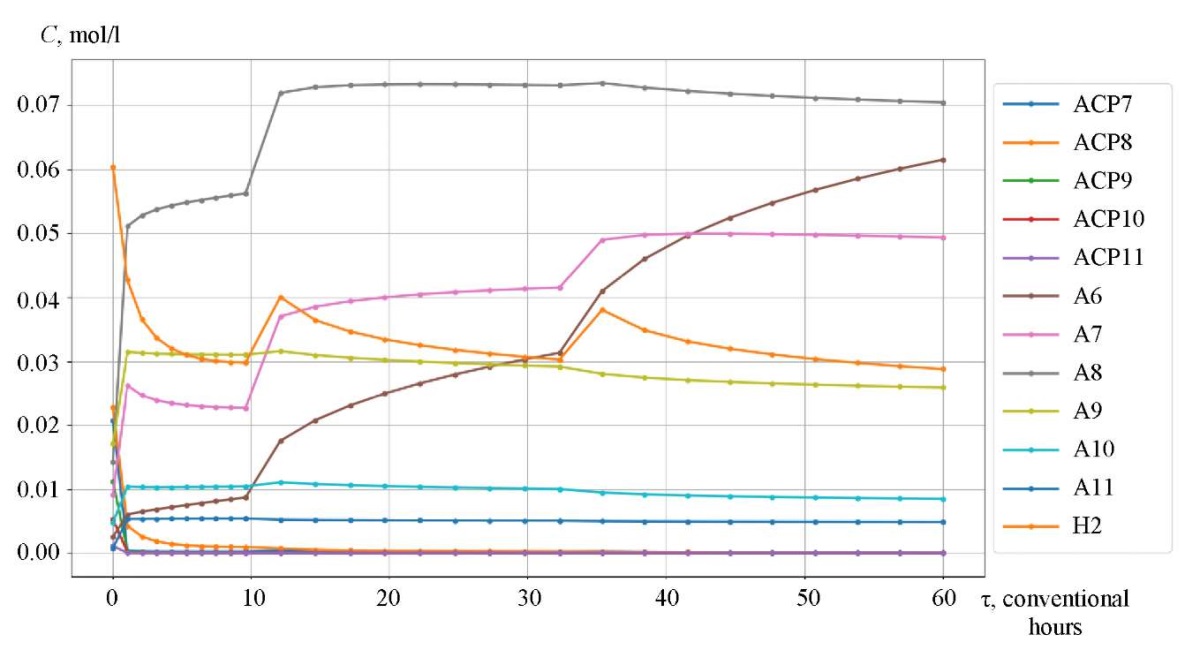
Fig. 5. Kinetic curves of catalytic reforming of gasoline
The curves of changes in the concentrations of the group components are given depending on the time of contact of the reaction mixture with the catalyst (Fig. 3–5). As an example, symbol nP1 stands for normal paraffin with one carbon atom, and symbol A9 — stands for aromatic hydrocarbon with nine carbon atoms. Figures 6 and 7 show, respectively, the curves of changes in temperature and volume of the reaction mixture of the catalytic reforming reaction of gasoline.
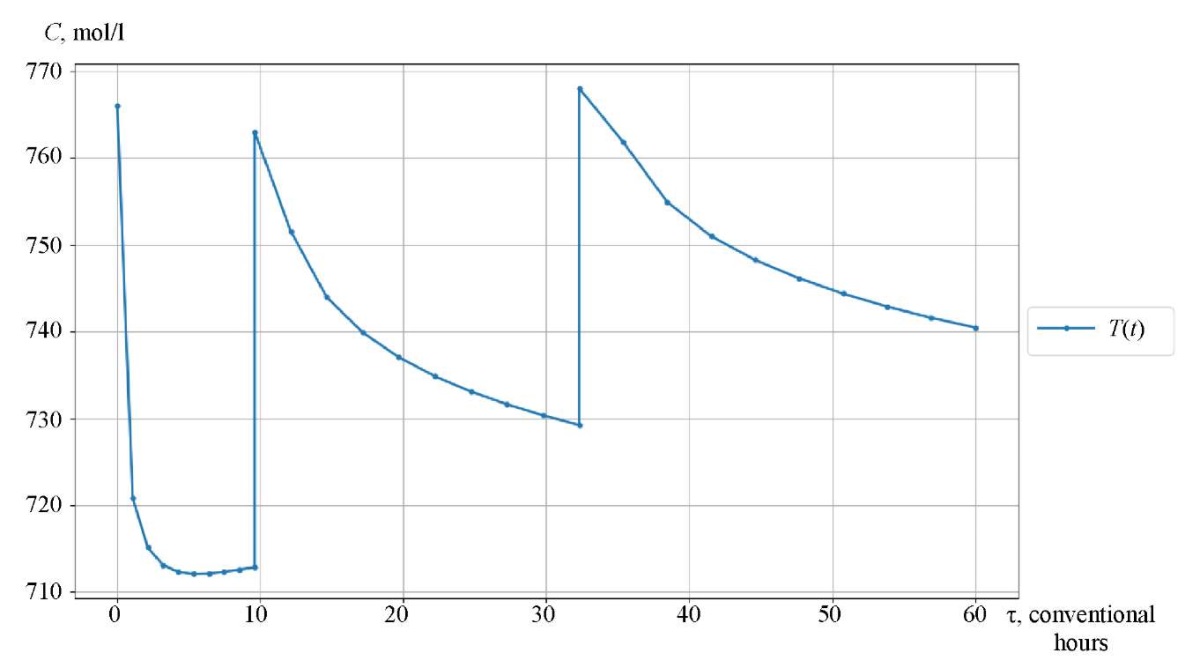
Fig. 6. Temperature curve
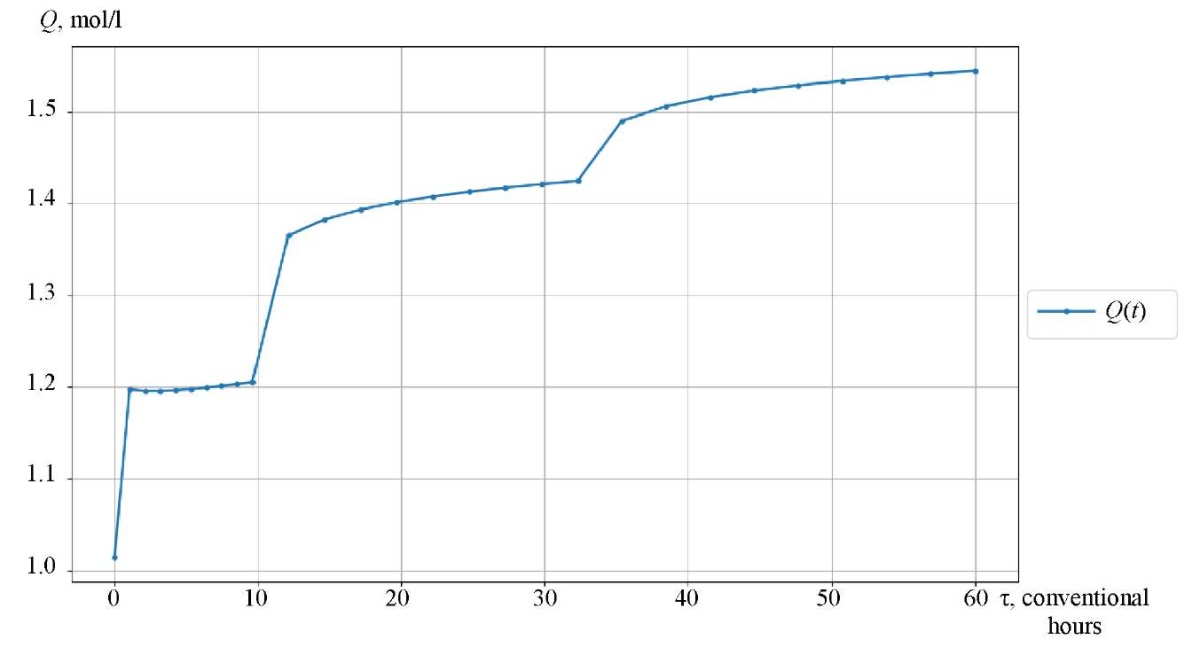
Fig. 7. Reaction mixture volume change curve
Discussion and Conclusion. In the presented work, a software module for the formation of a mathematical formulation of kinetics for complex multistage reactions has been developed. This makes it possible to analyze complex processes, including industrial, to consider various possible mechanisms in an acceptable time.
The developed software module for the numerical solution of a direct kinetic problem provides monitoring the dynamic change in the concentrations of components and the process temperatures in the case of its non-isothermality. In addition to the presented graphs of changes in component concentrations, measurements of the operating time of each of the three implemented methods were made. According to the scipy.odeint() method, the solution to the direct problem lasted 80.5 seconds; according to the Runge-Kutta fourth-order method — 111.8 seconds. The most optimal time, equal to 39.8 seconds, was shown by the Gear method. This confirms that Gear's method is optimized for working with rigid systems of differential equations.
The implemented approach was applied to modeling the industrial process of catalytic reforming of gasoline. Automation of the formation of a mathematical formulation of kinetics and the implementation of a numerical solution to a direct problem allowed us to develop a kinetic model of a detailed scheme of chemical transformations in an acceptable time, and obtain concentration and temperature profiles in the process reactors corresponding to industrial data.
References
1. Naryshkin DG. Computer Mathematics in the Course “Physical Chemistry”. Modern Information Technologies and IT-Education. 2012;(8):430–440. (In Russ.)
2. Qi Han, Xian-Tai Zhou, Xiao-Qi He, Hong-Bing Ji. Mechanism and Kinetics of the Aerobic Oxidation of Benzyl Alcohol to Benzaldehyde Catalyzed by Cobalt Porphyrin in a Membrane Microchannel Reactor. Chemical Engineering Science. 2021;245:116847. https://doi.org/10.1016/j.ces.2021.116847
3. Gheorghe Maria. A CCM-Based Modular and Hybrid Kinetic Model to Simulate the Tryptophan Synthesis in a Fed-Batch Bioreactor Using Modified E. Coli Cells. Computers and Chemical Engineering. 2021;153:107450. https://doi.org/10.1016/j.compchemeng.2021.107450
4. Fayzullin MR, Balaev AV. Computer-Aided System for Kinetic Studies of Complex Chemical Reactions. Bulletin of BSU. 2008;13(3-1):835–839.
5. Khamidullina ZA, Ismagilova AS, Spivak SI. Analysis Informativity of Kinetic Parameters of Complex Chemical Reactions. Herald of TvSU. Series “Chemistry”. 2020;39(1):70–80. https://doi.org/10.26456/vtchem2020.1.9
6. Koledina KF, Gubaydullin IM, Koledin SN. Mathematical Modeling and Computational Aspects of Multi-Criteria Optimization of the Conditions of a Laboratory Catalytic Reaction. Numerical Analysis and Applications. 2022;15:104–111. http://doi.org/10.1134/S1995423922020033
7. Zainullin RZ, Koledina KF, Akhmetov AF, Gubaidullin IM. Kinetics of the Catalytic Reforming of Gasoline. Kinetics and Catalysis. 2017;58(3):279–289. https://doi.org/10.1134/S0023158417030132
8. Zainullin RZ, Koledina KF, Akhmetov AF, Gubaidullin IM. Possible Ways of Upgrading Reactor Unit of Catalytic Reforming Based on Kinetic Model. Electronic Scientific Journal of Oil and Gas Business. 2018;(6):78–97.
9. Brasseur GP, Jacob DJ. Modeling of Atmospheric Chemistry. Cambridge: Cambridge University Press; 2017. 606 p. https://doi.org/10.1017/9781316544754
10. Gubaydullin I, Koledina K, Sayfullina L. Mathematical Modeling of Induction Period of the Olefins Hydroalumination Reaction by Diisobutylaluminiumchloride Catalyzed with Cp2ZrCl2. Engineering Journal. 2014;18(1):13 – 24. https://doi.org/10.4186/ej.2014.18.1.13
11. Meshalkin VP, Dovi VG, Soboleva IV. Method and Algorithm for Bayesian Estimation of Kinetic Parameters of Chemical Processes with Fluctuating Independent Variables. Theoretical Foundations of Chemical Engineering. 2009;43(6):861 – 868. http://doi.org/10.1134/S0040579509060037
12. Safiullina LF, Koledina KF, Gubaydullin IM, Zaynullin RZ. Study of a Mathematical Model of Gasoline Catalytic Reforming by Sensitivity Analysis Methods. Numerical Methods and Programming. 2020;21(4):440–451. https://doi.org/10.26089/NumMet.v21r435 (In Russ.)
13. Murphy JA. Physical Organic Chemistry. Beilstein Journal of Organic Chemistry. 2010;(6):1025. https://doi.org/10.3762/bjoc.6.116
14. Zaynullin RZ, Koledina KF, Gubaydullin IM, Akhmetov AF, Koledin SN. Kinetic Model of Catalytic Gasoline Reforming with Consideration for Changes in the Reaction Volume and Thermodynamic Parameters. Kinetics and Catalysis. 2020;61:613–622. https://doi.org/10.1134/S002315842004014X
15. Safiullina LF, Gubaydullin IM, Uzyanbaev RM, Musina AE. Computational Aspects of Simplification of Mathematical Models of Chemical Reaction Systems. Journal of Physics: Conference Series. 2019;1368:042022. http://doi.org/10.1088/1742-6596/1368/4/042022
About the Authors
N. A. LysenkoRussian Federation
Nikita A. Lysenko, undergraduate student of the Information Technology and Applied Mathematics Department, ResearcherID
1, Kosmonavtov St., Ufa, 450064
K. F. Koledina
Russian Federation
Kamila F. Koledina, Dr.Sci. (Phys.-Math.), Professor of the Information Technology and Applied Mathematics Department; Senior Researcher, Laboratory of Mathematical Chemistry, ResearcherID, ScopusID
1, Kosmonavtov St., Ufa, 450064
141, pr. Oktyabrya, Ufa, 450075
Review
For citations:
Lysenko N.A., Koledina K.F. Automation of the Formation of a Mathematical Formulation of Kinetics for Multistage Chemical Reactions and Numerical Solution to a Direct Problem. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):398-409. https://doi.org/10.23947/2687-1653-2023-23-4-398-409. EDN: PDPGGO
JATS XML