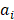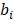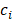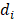Перейти к:
Автоматизация формирования математического описания кинетики для многостадийных химических реакций и численное решение прямой задачи
https://doi.org/10.23947/2687-1653-2023-23-4-398-409
EDN: PDPGGO
Аннотация
Введение. Основой для исследования, анализа и математической оптимизации любого химического процесса является адекватная математическая модель, учитывающая кинетику объекта. Кинетический анализ в химической технологии является важной задачей, поскольку позволяет оптимизировать процессы синтеза и прогнозировать их эффективность. Многие химические процессы включают в себя несколько стадийных реакций. Для успешного проектирования и оптимизации необходима математическая модель, которая описывает каждую стадию. Создание такой модели вручную может быть трудоемким и затратным процессом, требующим обработки большого объема информации. Современный уровень автоматизации позволяет ускорить получение математического описания кинетики многостадийных реакций. В этом случае значительно упрощается работа с данными и уменьшается вероятность совершения ошибок. Полученная математическая модель может быть применена для последующего анализа и оптимизации процесса. В работе рассмотрена промышленная реакция каталитического риформинга бензина, занимающая важное место в современной схеме переработки нефти, поскольку является источником высокооктановых компонентов товарных бензинов и индивидуальных ароматических углеводородов. Данный процесс характеризуется участием в нем большого числа (до 300) различных углеводородов, изменением числа молей и неизотермичностью. Математическое моделирование таких процессов предполагает детализацию стадий до необходимого уровня. Рассмотрена детализация до 173 стадий. В такой постановке задачи автоматизация формирования математического описания кинетики для каталитического риформинга бензинов ранее не проводилась. Поэтому целью представленной работы явилась реализация эффективных численных методов и алгоритмов для автоматизации формирования математической модели с учётом кинетики, термодинамики и изменения числа молей.
Материалы и методы. Математическое описание кинетики многостадийных реакций разрабатывается на основе закона действующих масс. Значения кинетических параметров взяты из литературных источников. Решение прямой задачи кинетики проводилось с применением следующих алгоритмов: метод Гира, Рунге-Кутты 4 порядка и метод scipy.odeint() языка Python. Концепция автоматизации реализована с помощью методологии IDEF0. Программное обеспечение написано на языке программирования Python.
Результаты исследования. Создано новое программное обеспечение для автоматизации процесса формирования математической модели с учетом кинетики, термодинамики и учета объема реакционной смеси. Приведены результаты работы программы на примере каталитического риформинга бензина. Реализована возможность учета в модели промежуточного подогрева смеси в каскаде реакторов. Получены численные значения изменения температуры, соответствующие промышленным данным.
Обсуждение и заключение. Результаты, полученные при моделировании химических превращений в каскаде реакторов каталитического риформинга бензина, подтвердили экзотермический характер реакции.
Разработанный программный продукт позволяет отобразить изменения концентраций веществ реакции, а также изменение температуры в реакторе и может быть использован в научных исследованиях организаций для анализа многостадийных каталитических процессов. Результаты моделирования кинетики реакции будут использоваться в последующей оптимизации условий проведения процесса на производстве.
Ключевые слова
Для цитирования:
Лысенко Н.А., Коледина К.Ф. Автоматизация формирования математического описания кинетики для многостадийных химических реакций и численное решение прямой задачи. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):398-409. https://doi.org/10.23947/2687-1653-2023-23-4-398-409. EDN: PDPGGO
For citation:
Lysenko N.A., Koledina K.F. Automation of the Formation of a Mathematical Formulation of Kinetics for Multistage Chemical Reactions and Numerical Solution to a Direct Problem. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):398-409. https://doi.org/10.23947/2687-1653-2023-23-4-398-409. EDN: PDPGGO
Введение. Изучение кинетики многоступенчатых химических процессов имеет теоретическое и практическое значение, поскольку позволяет раскрыть механизм реакций и осуществить контроль. При этом становится возможным ускорять целевые или замедлять побочные химические реакции. Кинетический анализ, будучи важной задачей химической технологии, способствует оптимизации процессов синтеза и прогнозированию их эффективности [1–3]. Многие химические процессы являются многостадийными реакциями. Для их эффективного проектирования и оптимизации необходимо иметь математическую модель, описывающую все стадии [4][5]. Ручное формирование такой модели может быть очень трудоемким и затратным процессом, так как подразумевает под собой обработку большого объема информации [6].
Объектом исследования является промышленный процесс каталитического риформинга бензина. Целевой продукт реакции — риформат — позволяет получать основную массу товарного бензина. Остальные составляющие являются продуктами изомеризации, каталитического крекинга и алкилирования. Большинство нефтеперерабатывающих заводов в России и мире используют установки каталитического риформинга [7][8]. Каталитический риформинг бензина позволяет получать ароматические углеводороды (ксилол, толуол, бензол), которые затем могут быть использованы в нефтехимической отрасли [9][10]. Однако для товарного бензина присутствие в продукте ароматических углеводородов ограничивается по экологическим критериям. Поэтому детализированная сложная кинетика, показывающая постадийное образование компонент, позволит управлять условиями процесса для контроля выхода продукта и ограничения содержания ароматических углеводородов. Процесс каталитического риформинга бензина проводится в реакторном блоке, состоящем из трех последовательных реакторов, между которыми установлены печи для нагрева смеси. Это является необходимостью, так как данная реакция — эндотермическая. При математическом описании реакторного блока необходимо, наряду с изменениями концентраций компонент от условного времени контакта катализатора и смеси реакции, учитывать изменение температуры и объема реакционной смеси.
Автоматизация моделирования таких сложных процессов позволяет значительно ускорить получение математического описания кинетики многостадийных реакций, снизить вероятность ошибок и упростить процесс работы с данными [11]. В целом автоматизация формирования математического описания для многостадийных химических реакций является важным инструментом для эффективного управления процессами в различных отраслях промышленности, а также для достижения более точной и эффективной реализации химических реакций в лаборатории.
Таким образом, целью исследования являлась разработка программного продукта, помогающего автоматизировать формирование математического описания многостадийных химических реакций с учётом кинетики, термодинамики и изменения объёма реакционной смеси, а также получение численного решения составленной математической модели.
Для достижения цели исследования в данной работе решались следующие задачи:
- разработка программного модуля формирования математического описания кинетики с использованием языка программирования Python;
- разработка программного модуля численного решения прямой задачи согласно составленному математическому описанию с использованием языка программирования Python;
- получение результатов работы программного продукта для реакции каталитического риформинга бензина.
Материалы и методы. Математически указанный процесс может быть описан системой обыкновенных нелинейных дифференциальных уравнений с начальными данными, которая и является математической моделью. Учитывая, что каталитический риформинг бензина является неизотермической реакцией с изменением объема реакционной смеси, модель многоступенчатой химической кинетики может быть рассмотрена в следующем контексте:
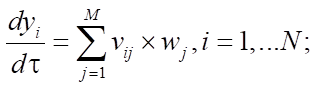 (1)
(1)
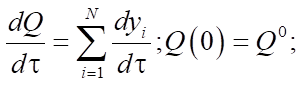 (2)
(2)
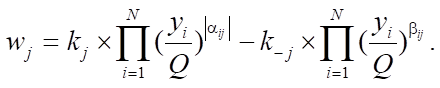 (3)
(3)
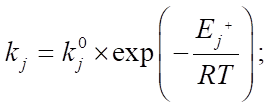
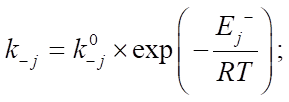 (4)
(4)
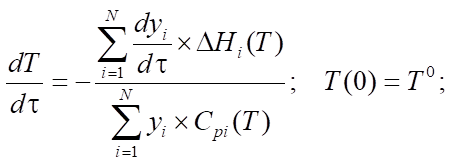 (5)
(5)
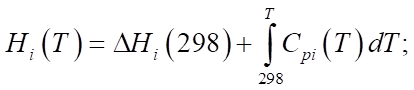 (6)
(6)
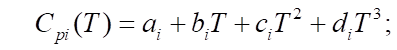 (7)
(7)
с начальными условиями при
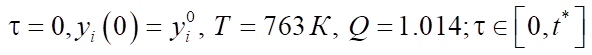 [11].
[11].
В данной формуле реакционной кинетики имеется ряд переменных и коэффициентов, которые определяют концентрацию реагентов, время контакта и скорость реакции. Конкретно Q и 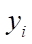 (концентрации реагентов реакции) могут быть выражены в моль/л или в долях, а переменная
(концентрации реагентов реакции) могут быть выражены в моль/л или в долях, а переменная 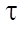 , показывающая условное время контакта реакционной смеси с катализатором, в кг×мин/моль или кг катализатора. В формуле также задействованы показатели: количество стадий M (173 стадии) и количество веществ N (38 веществ), а также стехиометрическая матрица
, показывающая условное время контакта реакционной смеси с катализатором, в кг×мин/моль или кг катализатора. В формуле также задействованы показатели: количество стадий M (173 стадии) и количество веществ N (38 веществ), а также стехиометрическая матрица 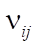 .
. 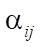 — это все отрицательные элементы матрицы
— это все отрицательные элементы матрицы 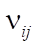 на пересечении i-ой строки и j-го столбца, а
на пересечении i-ой строки и j-го столбца, а 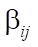 — все положительные элементы матрицы
— все положительные элементы матрицы 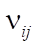 на пересечении
на пересечении 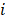 -ой строки и j-го столбца. Скорость j-ой стадии реакции
-ой строки и j-го столбца. Скорость j-ой стадии реакции 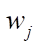 может быть выражена в 1/мин или в моль/(кг×мин), а константы скоростей стадий
может быть выражена в 1/мин или в моль/(кг×мин), а константы скоростей стадий 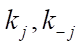 — в 1/мин. Кроме этого, в формуле указаны предэкспоненциальные множители
— в 1/мин. Кроме этого, в формуле указаны предэкспоненциальные множители 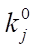 ,
, 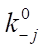 , выраженные в 1/мин, энергии активации прямой и обратной реакции
, выраженные в 1/мин, энергии активации прямой и обратной реакции 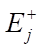 ,
, 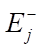 , выраженные в ккал/моль, газовая постоянная R и температура T, измеряемая в Кельвинах. Продолжительность реакции t* определяется временем, которое требуется для её завершения в минутах, а энтальпия образования i-го компонента
, выраженные в ккал/моль, газовая постоянная R и температура T, измеряемая в Кельвинах. Продолжительность реакции t* определяется временем, которое требуется для её завершения в минутах, а энтальпия образования i-го компонента 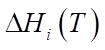 измеряется в Дж/моль. Удельную теплоемкость
измеряется в Дж/моль. Удельную теплоемкость 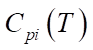 i-го компонента, измеряемую в Дж/(моль×К), можно выразить через коэффициенты температурной зависимости теплоемкости данного компонента, которые обозначены буквами
i-го компонента, измеряемую в Дж/(моль×К), можно выразить через коэффициенты температурной зависимости теплоемкости данного компонента, которые обозначены буквами 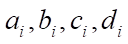 [12]. i — порядковый номер вещества, участвующего в реакции.
[12]. i — порядковый номер вещества, участвующего в реакции.
При моделировании химических превращений каталитического риформинга бензина необходимо учитывать большое число индивидуальных углеводородов. Поэтому в работе применяются групповые компоненты в модели по выделению типов углеводородов и числу атомов углерода в структуре молекулы: Al — ароматические углеводороды; ACPl — пятичленные нафтены; ACHl — шестичленные нафтены; iPl — изомеры парафинов; nPl — нормальные парафины. Здесь l — количество атомов углерода в структуре молекулы. В таблице 1 приведены усредненные значения коэффициентов температурной зависимости теплоемкости групповых компонент, которые будут применяться в расчетах.
Таблица 1
Коэффициенты температурной зависимости групповых компонент
|
l |
Группа углеводородов |
|
|
|
|
|
1 |
nP1 |
34,942 |
–0,03996 |
0,19184 |
–0,153 |
|
2 |
nP2 |
28,146 |
0,043447 |
0,18946 |
–0,1908 |
|
3 |
nP3 |
28,277 |
0,116 |
0,19597 |
–0,2327 |
|
4 |
nP4 |
20,56 |
0,2815 |
–0,013143 |
–0,09457 |
|
5 |
IP4 |
6,772 |
0,34147 |
–0,10271 |
–0,03685 |
|
6 |
nP5 |
26,671 |
0,32324 |
0,04282 |
–0,1664 |
|
7 |
iP5 |
–0,881 |
0,47498 |
–0,24797 |
0,06751 |
|
8 |
nP6 |
25,924 |
0,41927 |
–0,012491 |
–0,1592 |
|
9 |
iP6 |
–7,123 |
0,58327 |
–0,30338 |
0,06802 |
|
10 |
nP7 |
26,984 |
0,50387 |
–0,04748 |
–0,1684 |
|
11 |
iP7 |
19,245 |
0,55072 |
–0,14055 |
–0,08248 |
|
12 |
nP8 |
29,053 |
0,58016 |
–0,057103 |
–0,1955 |
|
13 |
iP8 |
–3,367 |
0,75824 |
–0,38216 |
0,05736 |
|
14 |
nP9 |
29,687 |
0,66821 |
–0,096492 |
–0,2001 |
|
15 |
iP9 |
68,581 |
0,44754 |
0,31908 |
–0,5118 |
|
16 |
nP10 |
31,78 |
0,74489 |
–0,10945 |
–0,2267 |
|
17 |
iP10 |
–46,17 |
1,108 |
–0,70316 |
0,1787 |
|
18 |
nP11 |
125,21 |
0,31401 |
0,79137 |
–0,9141 |
|
19 |
iP11 |
–8,791 |
1,0548 |
–0,5778 |
0,1192 |
|
20 |
ACH6 |
13,783 |
0,20742 |
0,53682 |
–0,6301 |
|
21 |
ACH7 |
4,296 |
0,42716 |
0,21058 |
–0,3999 |
|
22 |
ACH8 |
–51,866 |
0,78827 |
–0,35255 |
–0,006855 |
|
23 |
ACH9 |
–120,89 |
1,2728 |
–1,0794 |
0,4035 |
|
24 |
ACH10 |
90,421 |
0,23264 |
0,94595 |
–1,057 |
|
25 |
ACH11 |
–65,48 |
1,1809 |
–0,68379 |
0,1458 |
|
26 |
ACP6 |
–9,939 |
0,42528 |
0,012521 |
–0,1886 |
|
27 |
ACP7 |
–28,514 |
0,58607 |
–0,094379 |
–0,1644 |
|
28 |
ACP8 |
–69,713 |
0.92602 |
–0,62526 |
0,2049 |
|
29 |
ACP9 |
–116,73 |
1,3097 |
–1,2439 |
0,5292 |
|
30 |
ACP10 |
–67,341 |
1,0922 |
–0,704 |
0,1906 |
|
31 |
ACP11 |
–68,23 |
1,187 |
–0,7575 |
0,2018 |
|
32 |
A6 |
–31,368 |
0,4746 |
–0,31137 |
0,08524 |
|
33 |
A7 |
–24,097 |
0,52187 |
–0,29827 |
0,06122 |
|
34 |
A8 |
–17,36 |
0,5647 |
–0,26293 |
0,01122 |
|
35 |
A9 |
–10,933 |
0,64349 |
–0,27829 |
–0,01443 |
|
36 |
A10 |
–24,187 |
0,79716 |
–0,48265 |
0,1341 |
|
37 |
A11 |
–26,717 |
0,91044 |
–0,53876 |
0,1203 |
|
38 |
H2 |
29,07 |
–0,0836 |
0,1064 |
0,5752 |
Уравнения (1), (3) и (4) описывают изменения концентраций реагентов в процессе, а в системе (2) используются мольные доли для описания изменения мольного расхода смеси. В (5) рассматривается зависимость изменения температуры реакции от термодинамических характеристик веществ. В (6), (7) приведена зависимость для расчета энтальпии образования i-го компонента и удельной теплоемкости.
В данной модели прямая задача (решение системы дифференциальных уравнений) является как жесткой, так и нежесткой. Метод Гира, используемый для решения модели каталитического риформинга, основан на дифференцировании назад [13–15]. Для сравнения результатов и выявления оптимального метода использовались явный одношаговый метод численного интегрирования Рунге-Кутты четвертого порядка и явный метод численного интегрирования scipy.odeint() языка программирования Python.
Концепцию автоматизации формирования математического описания кинетики для многостадийных химических реакций и численного метода решений проиллюстрируем с помощью методологии IDEF0.
На рис. 1 представлена контекстная диаграмма процесса автоматизации формирования математического описания кинетики для многостадийных химических реакций и решения численным методом.
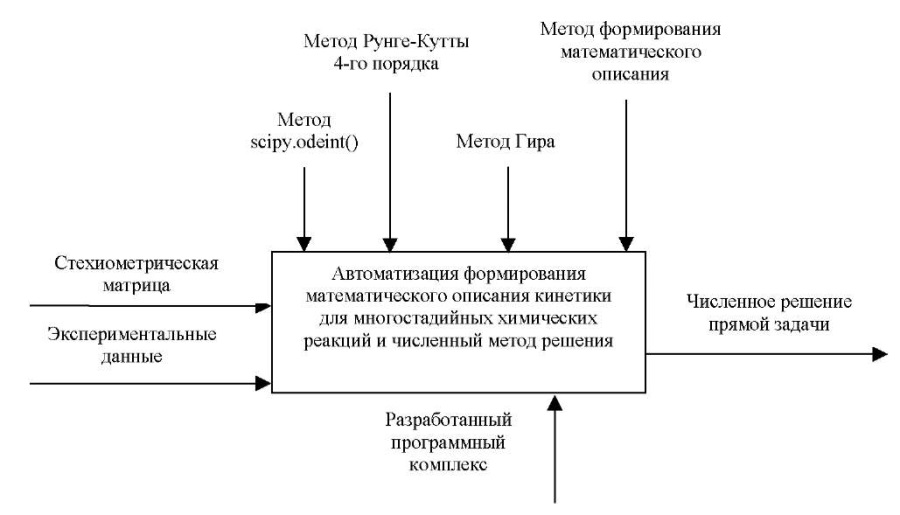
Рис. 1. Контекстная диаграмма
«Автоматизация формирования математического описания кинетики
для многостадийных химических реакций и численный метод решения»
Входные параметры — стехиометрическая матрица реакции и экспериментальные данные. В их число входят начальные данные по концентрации веществ, температуре, предэкспоненциальным множителям, энергиям активации. Результатом решения задачи является численное решение прямой задачи. В качестве элементов управления выступают численные методы для сравнения результатов, а также метод формирования математического описания (СОНДУ). В качестве механизма выступает разработанный программный комплекс автоматизации математического описания кинетики многостадийных реакций и решения прямой задачи. На рис. 2 приведена декомпозиция процесса автоматизации формирования математического описания кинетики для многостадийных химических реакций и решения численным методом на этапы:
- формирование математического описания;
- решение прямой задачи.
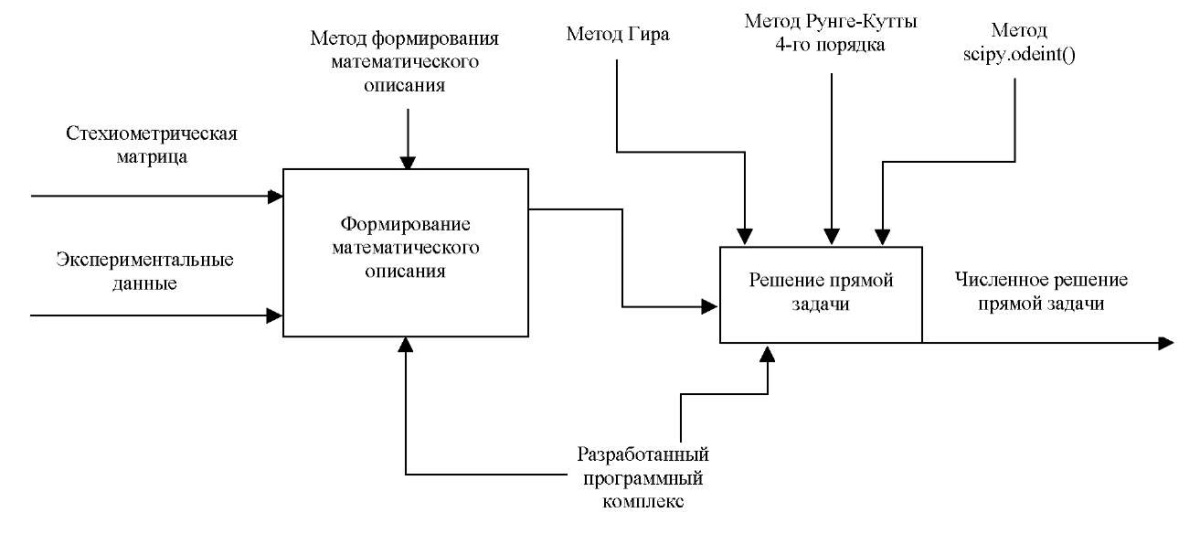
Рис. 2. Этапы решения задачи
«Автоматизация формирования математического описания кинетики
для многостадийных химических реакций и численный метод решения»
Возможности разработанного программного комплекса представлены описанными ниже особенностями.
При помощи программы можно создать кинетическую модель многостадийной химической реакции и представить её решение методами, описанными ранее, используя заданную стехиометрическую матрицу. Если реакция неизотермическая и происходит изменение объема реакционной смеси, к системе дифференциальных уравнений добавляются два дополнительных уравнения для описания этих изменений.
Математическая модель каталитического риформинга бензина представляет собой систему дифференциальных уравнений (СДУ) вида (1)–(7), состоящую из 40 дифференциальных уравнений по числу групповых компонент, температурной зависимости и уравнения изменения молей.
Основной функционал программы представляет собой:
- главное окно приложения c выводом математического описания по стехиометрической матрице, введенной пользователем;
- окно с визуализацией решения: для каждого численного метода (Python-odeint, Рунге-Кутта 4-го порядка, метод Гира) выводится время работы, массив времени t и решение системы дифференциальных уравнений в каждый момент времени, которое представляет собой графики изменения концентрации веществ, изменения температуры реакции или объёма реакционной смеси.
Результаты исследования. Реакция каталитического риформинга протекает в трех реакторах, между которыми располагается нагревательная печь. Начальная температура первого реактора равна 766 K (493 °C). Первые 9,6 условных часа реакция протекает в первом реакторе, температура падает. После этого происходит нагревание в печи между двух реакторов до 763 K (490 °C) и химический процесс переходит во второй реактор. Во втором реакторе процесс протекает в интервале времени от 9,6 до 32,3 условных часа, температура понижается. Прежде чем перейти к 3 реактору, смесь нагревается во второй промежуточной печи до 768 K (495 °C) и протекает в этом реакторе в интервале времени от 32,3 до 60 условных часа.
На рис. 3–5 изображены кинетические кривые групп углеводородов, участвующие в реакции и полученные с помощью метода Гира. Скачкообразные переходы на графиках свидетельствуют о том, что смесь переходит из одного реактора в другой с промежуточным нагревом.
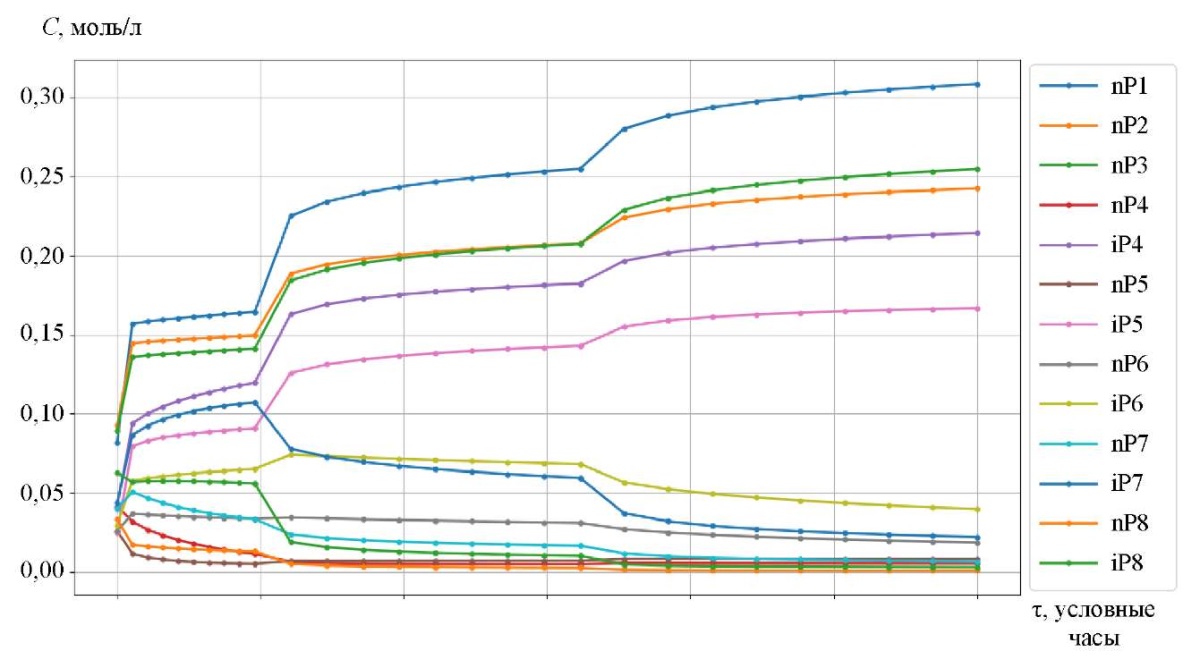
Рис. 3. Кинетические кривые каталитического риформинга бензина
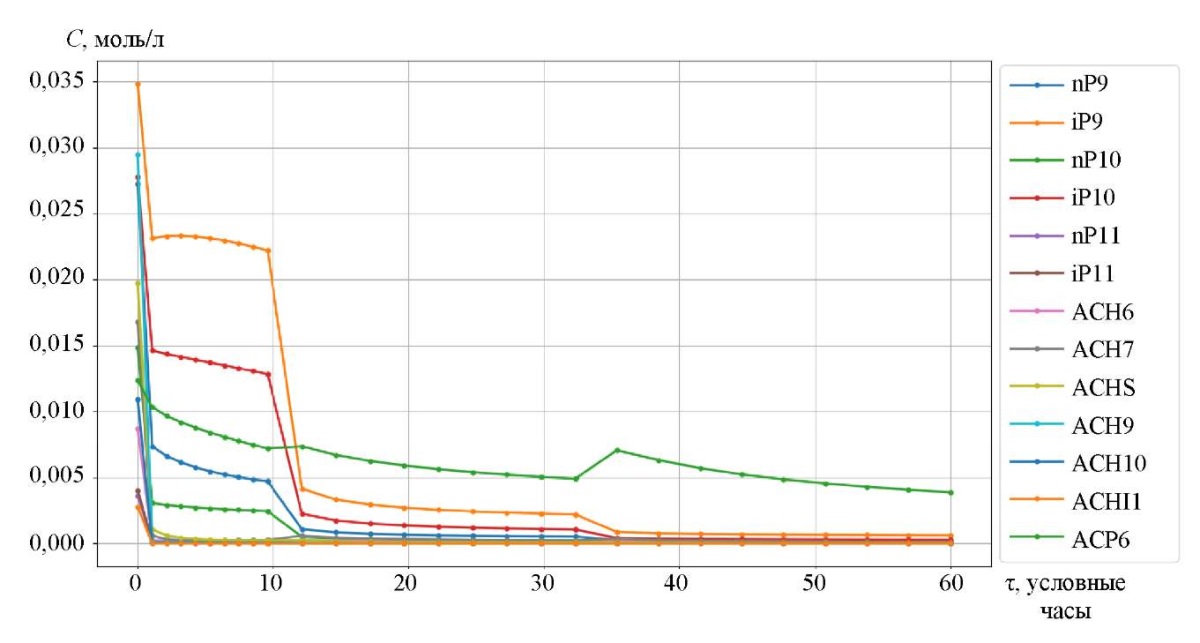
Рис. 4. Кинетические кривые каталитического риформинга бензина
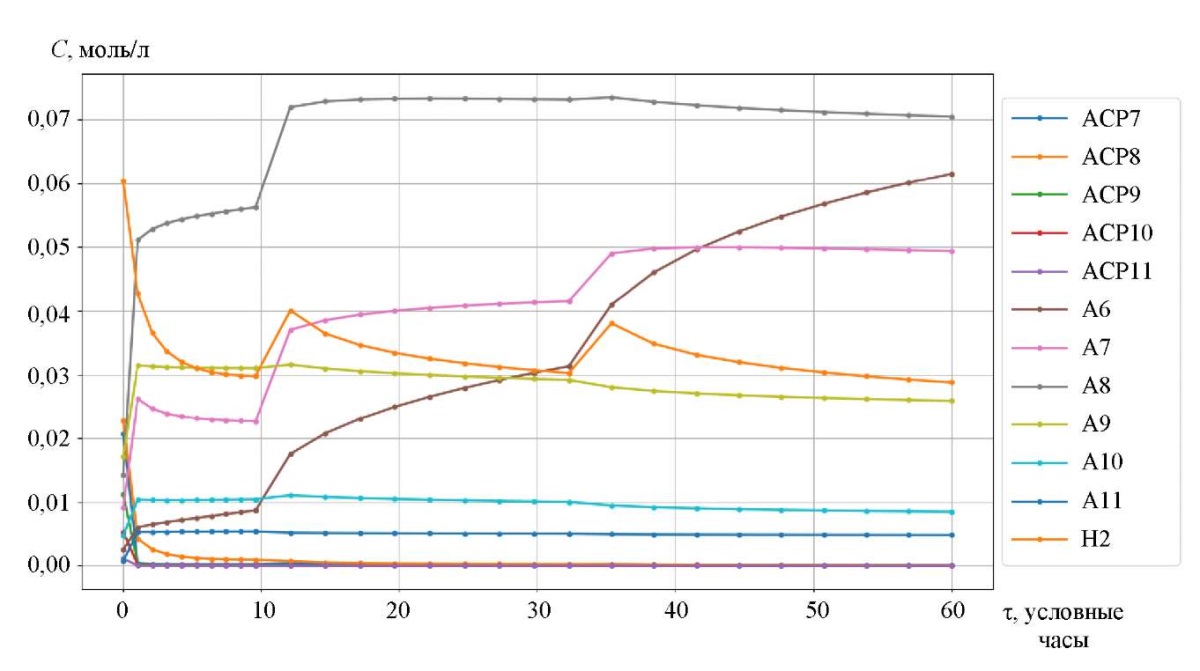
Рис. 5. Кинетические кривые каталитического риформинга бензина
Кривые изменения концентраций групповых компонент приведены в заисимости от времени контакта реакционной смеси с катализатором (рис. 3–5). Например, символ nP1 обозначает нормальный парафин с одним атомом углерода, а символ A9 — ароматический углеводород с девятью атомами углерода. На рис. 6 и 7 представлены соответственно кривые изменения температуры и объема реакционной смеси реакции каталитического риформинга бензина.
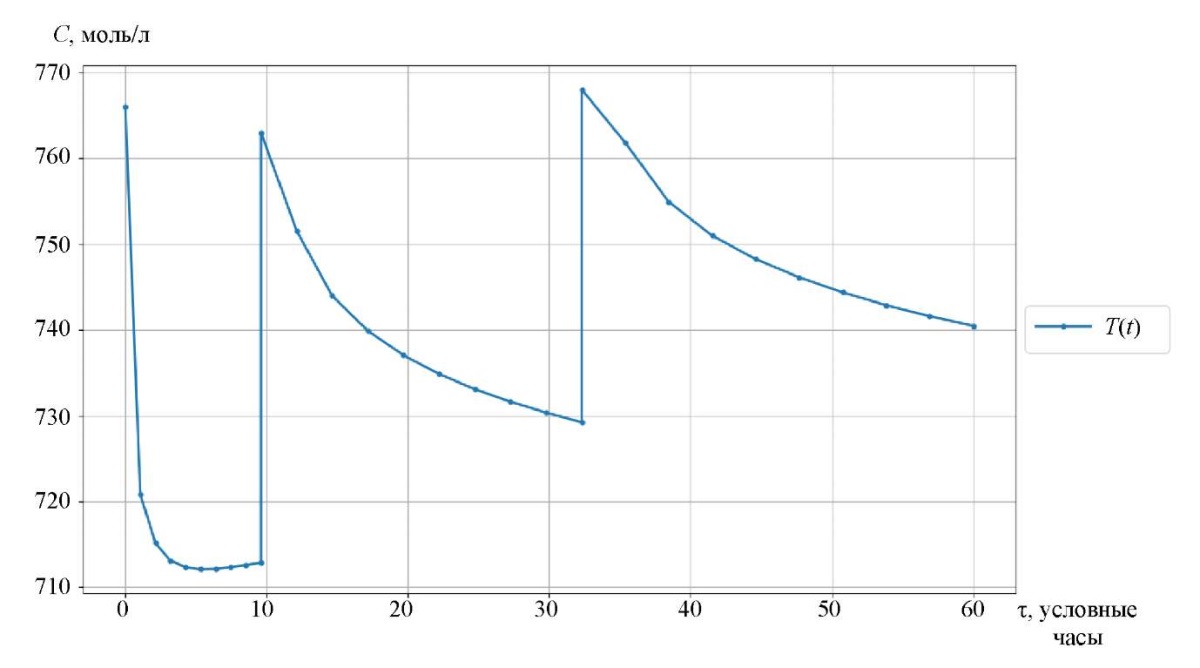
Рис. 6. Кривая изменения температуры
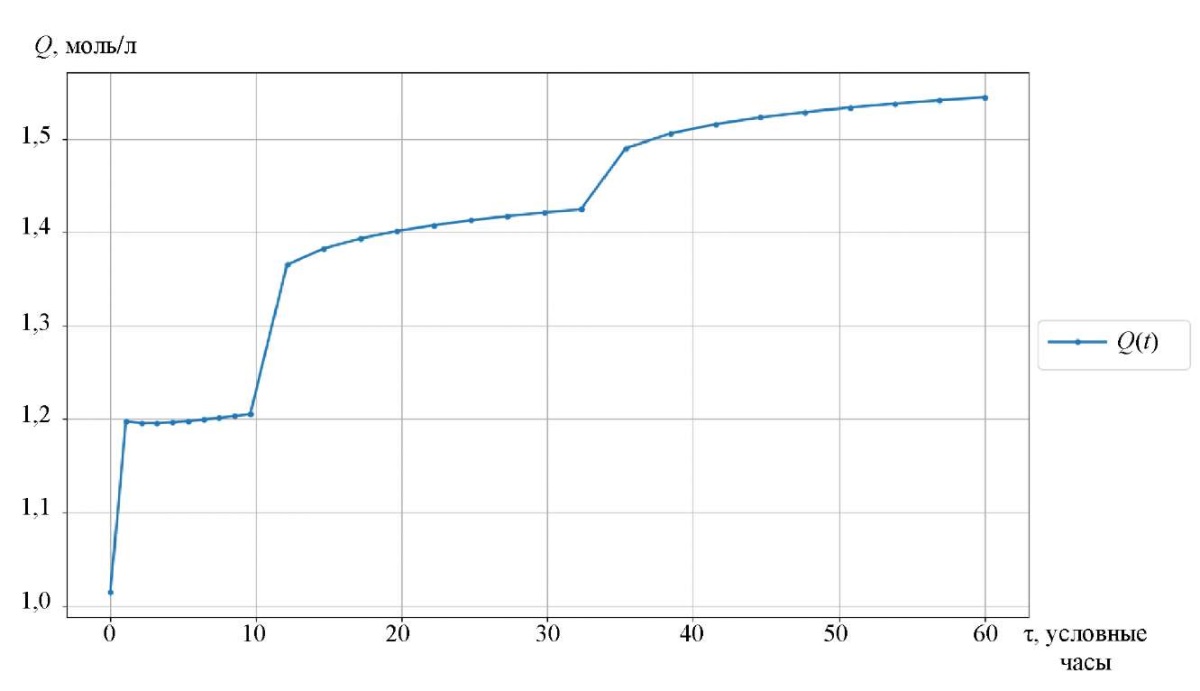
Рис. 7. Кривая изменения объема реакционной смеси
Обсуждение и заключение. В представленной работе разработан программный модуль формирования математического описания кинетики для сложных многостадийных реакций. Это позволяет анализировать сложные, в том числе промышленные процессы, рассматривать разные возможные механизмы за приемлемое время.
Разработанный программный модуль численного решения прямой кинетической задачи позволяет отслеживать динамическое изменение концентраций компонент и температуры процесса в случае его неизотермичности. Помимо представленных графиков изменения концентраций компонент, произведены замеры времени работы каждого из трех реализованных методов. По методу scipy.odeint() решение прямой задачи длилось 80,5 секунды, по методу Рунге-Кутты 4-го порядка — 111,8 секунд. Наиболее оптимальное время, равное 39,8 секунды, показал метод Гира. Это подтверждает, что метод Гира оптимизирован для работы с жесткими системами дифференциальных уравнений.
Реализованный подход применен для моделирования промышленного процесса каталитического риформинга бензина. Автоматизация формирования математического описания кинетики и реализация численного решения прямой задачи позволили в приемлемые сроки разработать кинетическую модель детализированной схемы химических превращений и получить концентрационные и температурные профили в реакторах процесса, соответствующие промышленным данным.
Список литературы
1. Нарышкин Д.Г. Компьютерная математика в курсе "Физическая химия". Современные информационные технологии и ИТ-образование. 2012;(8):430–440. URL: https://cyberleninka.ru/article/n/kompyuternaya-matematika-v-kurse-fizicheskaya-himiya/viewer (дата обращения: 15.08.2023).
2. Qi Han, Xian-Tai Zhou, Xiao-Qi He, Hong-Bing Ji. Mechanism and Kinetics of the Aerobic Oxidation of Benzyl Alcohol to Benzaldehyde Catalyzed by Cobalt Porphyrin in a Membrane Microchannel Reactor. Chemical Engineering Science. 2021;245:116847. https://doi.org/10.1016/j.ces.2021.116847
3. Gheorghe Maria. A CCM-Based Modular and Hybrid Kinetic Model to Simulate the Tryptophan Synthesis in a Fed-Batch Bioreactor Using Modified E. Coli Cells. Computers and Chemical Engineering. 2021;153:107450. https://doi.org/10.1016/j.compchemeng.2021.107450
4. Файзуллин М.Р., Балаев А.В. Автоматизированная система исследования кинетики сложных химических реакций. Вестник Башкирского университета. 2008;13(3–1):835–839.
5. Хамидуллина З.А., Исмагилова А.С., Спивак С.И. Анализ информативности кинетических параметров сложных химических реакций. Вестник Тверского государственного университета. Серия: химия. 2020;39(1):70–80. https://doi.org/10.26456/vtchem2020.1.9
6. Koledina K.F., Gubaydullin I.M., Koledin S.N. Mathematical Modeling and Computational Aspects of Multi-Criteria Optimization of the Conditions of a Laboratory Catalytic Reaction. Numerical Analysis and Applications. 2022;15:104–111. http://doi.org/10.1134/S1995423922020033
7. Zainullin R.Z., Koledina K.F., Akhmetov A.F., Gubaidullin I.M. Kinetics of the Catalytic Reforming of Gasoline. Kinetics and Catalysis. 2017;58(3):279–289. https://doi.org/10.1134/S0023158417030132
8. Зайнуллин Р.З., Коледина К.Ф., Ахметов А.Ф., Губайдуллин И.М. Возможные пути модернизации реакторного блока каталитического риформинга на основе кинетической модели. Electronic Scientific Journal of Oil and Gas Business. 2018;(6):78–97.
9. Brasseur G.P., Jacob D.J. Modeling of Atmospheric Chemistry. Cambridge: Cambridge University Press; 2017. 606 p. https://doi.org/10.1017/9781316544754
10. Gubaydullin I., Koledina K., Sayfullina L. Mathematical Modeling of Induction Period of the Olefins Hydroalumination Reaction by Diisobutylaluminiumchloride Catalyzed with Cp2ZrCl2. Engineering Journal. 2014;18(1):13 – 24. https://doi.org/10.4186/ej.2014.18.1.13
11. Meshalkin V.P., Dovi V.G., Soboleva I.V. Method and Algorithm for Bayesian Estimation of Kinetic Parameters of Chemical Processes with Fluctuating Independent Variables. Theoretical Foundations of Chemical Engineering. 2009;43(6):861 – 868. http://doi.org/10.1134/S0040579509060037
12. Сафиуллина Л.Ф., Коледина К.Ф., Губайдуллин И.М., Зайнуллин Р.З. Исследование математической модели каталитического риформинга бензина методами анализа чувствительности. Вычислительные методы и программирование. 2020;21(4):440–451. https://doi.org/10.26089/NumMet.v21r435
13. Murphy J.A. Physical Organic Chemistry. Beilstein Journal of Organic Chemistry. 2010;(6):1025. https://doi.org/10.3762/bjoc.6.116
14. Zaynullin R.Z., Koledina K.F., Gubaydullin I.M., Akhmetov A.F., Koledin S.N. Kinetic Model of Catalytic Gasoline Reforming with Consideration for Changes in the Reaction Volume and Thermodynamic Parameters. Kinetics and Catalysis. 2020;61:613–622. https://doi.org/10.1134/S002315842004014X
15. Safiullina L.F., Gubaydullin I.M., Uzyanbaev R.M., Musina A.E. Computational Aspects of Simplification of Mathematical Models of Chemical Reaction Systems. Journal of Physics: Conference Series. 2019;1368:042022. http://doi.org/10.1088/1742-6596/1368/4/042022
Об авторах
Н. А. ЛысенкоРоссия
Никита Андреевич Лысенко, магистрант кафедры информационные технологии и прикладная математика, ResearcherID
450064, г. Уфа, ул. Космонавтов, 1
К. Ф. Коледина
Россия
Камила Феликсовна Коледина, доктор физико-математических наук, профессор кафедры информационные технологии и прикладная математика; старший научный сотрудник лаборатории математической химии, ResearcherID, ScopusID
450064, г. Уфа, ул. Космонавтов, 1
450075, г. Уфа, проспект Октября, 141
Рецензия
Для цитирования:
Лысенко Н.А., Коледина К.Ф. Автоматизация формирования математического описания кинетики для многостадийных химических реакций и численное решение прямой задачи. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):398-409. https://doi.org/10.23947/2687-1653-2023-23-4-398-409. EDN: PDPGGO
For citation:
Lysenko N.A., Koledina K.F. Automation of the Formation of a Mathematical Formulation of Kinetics for Multistage Chemical Reactions and Numerical Solution to a Direct Problem. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):398-409. https://doi.org/10.23947/2687-1653-2023-23-4-398-409. EDN: PDPGGO