Перейти к:
Оптимальная 2D-расстановка виртуальных объектов в физическом пространстве для приложений дополненной реальности
https://doi.org/10.23947/2687-1653-2023-23-4-410-421
EDN: QPFEMG
Аннотация
Введение. Научные и прикладные работы о размещении виртуальных объектов в реальном пространстве чаще всего фокусируются на вопросах интерактивности, интеграции реальности и виртуальности, физических свойствах виртуальных элементов. Однако недостаточно проработана задача одновременно свободного и оптимального размещения объектов с учетом их размеров и окружающей зоны комфортности вокруг них. В литературе можно найти описание схожей задачи — об упаковке в прямоугольный контейнер. В нашем случае цель не ограничивается максимально плотным размещением. Следует учесть два условия: жесткие размеры объектов (их запрещено нарушать) и дополнительные области — зоны комфортности (их нежелательно занимать). Цель работы — создание и реализация такого 2D-алгоритма размещения объектов в физическом пространстве, который будет учитывать обозначенные выше ограничения.
Материалы и методы. Используя аппарат численных методов, авторы задействовали созданный ранее 1D-алгоритм размещения объектов. Расчеты основываются на системе линейных уравнений. В одномерном случае оптимальное размещение виртуальных объектов сводится к задаче, не зависящей от вида функции комфортности. Элементы такой системы — размеры объектов, дистанции между ними, а также расстояния до края области встраивания, зоны комфортности. Предлагаемый 2D-алгоритм оптимальной расстановки виртуальных объектов реализовали в виде программного кода на языке C# с использованием известного игрового движка Unity. Решение тестировали на гаджетах в режиме пиковой нагрузки для 5, 10, 15, 20, 25, 35, 40, 45 и 50 объектов. Для опытов задействовали 1,8 тыс. устройств. Проанализировали около 77 тыс. событий. Чтобы исключить нерепрезентативные значения, каждый расчет повторяли 10 раз, и для каждого значения провели z-оценку. Аномальные (больше 3 и меньше –3) исключили.
Результаты исследования. В работе создан алгоритм 2D-расстановки, который реализует заполнение прямоугольной области виртуальными объектами. У каждого из них есть размер и еще одна характеристика — зона комфортности. Авторы составили блок-схему реализации данного алгоритма в заданной двумерной левосторонней системе координат. Показано, в частности, на каком этапе объекты сортируются по длине, когда формируются их партии и выполняются расстановки по двум осям. Первая — горизонтальная, вторая направлена вперед от пользователя (это вектор глубины, или фронтальное измерение). Алгоритм 1D-размещения для сформированного ряда позволяет оптимально расположить объекты вдоль оси X на основе рассчитанного коэффициента комфортности К. Выполнены расчеты и составлены схемы с целью достичь определенных показателей комфортности. Для каждого объекта первой линии смещение по оси Z от края плоскости определяется так, чтобы комфортность спереди равнялась комфортности по X. Начиная со 2-го ряда для вычисления отступа проверяется наличие потенциальных соседей, которые находятся на ряд выше и имеют общие участки по X с обрабатываемым объектом. Каждый элемент строки устанавливается по оси Z так, чтобы его комфортность сверху была максимальной из односторонних горизонтальных комфортностей в данной и предыдущей строках. Принцип расчета координаты Z для объекта строки представлен в виде блок-схемы.
Исходными данными для реализации этого алгоритма были 7 объектов с 14 разными размерами и 28 зонами комфортности. После программной реализации работу описанного 2D-алгоритма проверили на практике — в мобильном приложении дополненной реальности. Записали аналитические данные пользовательских сессий. Рассчитали среднее время выполнения. Возникшую в ходе работы гипотезу о квадратичной зависимости проверили на персональном компьютере. С этой целью провели аналогичный эксперимент для диапазона [10–10000] объектов. Гипотеза подтвердилась. Алгоритму можно присвоить сложность O(n2). Для сравнения скорости вычисления задействовали 10 самых популярных моделей пользовательских устройств. Результаты представили в виде диаграммы. Минимальное зарегистрированное время выполнения — 0,093 мс, максимальное — 0,146 мс. Расчеты показали высокую эффективность двумерного алгоритма. Дополнительно визуализировали схемы расстановки для разного количества и параметров объектов.
Обсуждение и заключение. Предлагаемый алгоритм двумерного размещения позволяет работать с набором виртуальных объектов с разными размерами и зонами комфортности. Показаны достаточно высокие производительность и стабильность. В среднем алгоритм реализуется за доли миллисекунды даже при больших партиях объектов. Возможные будущие направления работы:
- расширение подхода для построения 3D моделей и алгоритмов;
- включение в алгоритм вращения объектов для большей гибкости их расположения и лучшего использования пространства.
Итоги работы могут представлять интерес для инженеров и дизайнеров интерфейсов. В перспективе следует изучить пользовательский опыт и возможности включения дополнительных ограничений на позиционирование.
Ключевые слова
Для цитирования:
Алпатова М.В., Рудяк Ю.В. Оптимальная 2D-расстановка виртуальных объектов в физическом пространстве для приложений дополненной реальности. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):410-421. https://doi.org/10.23947/2687-1653-2023-23-4-410-421. EDN: QPFEMG
For citation:
Alpatova M.V., Rudyak Yu.V. Optimal 2D Placement of Virtual Objects in Physical Space for Augmented Reality Applications. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):410-421. https://doi.org/10.23947/2687-1653-2023-23-4-410-421. EDN: QPFEMG
Введение. Известная задача приложений дополненной реальности (augmented reality, AR) — размещение виртуальных объектов в реальном физическом пространстве. Ряд исследований [1–3] фокусируются на интерактивности, слиянии реальной и виртуальной сфер. Изучаются также вопросы физических свойств виртуальных объектов.
Недостаточно проработана задача такого размещения объектов, которое одновременно было бы свободным и оптимальным, учитывало не только геометрические размеры объектов, но и зоны комфортности вокруг них. В [6] отмечена внешняя схожесть этой задачи с известной задачей об упаковке в прямоугольный контейнер [5]. Однако есть существенная разница. В исследуемом случае недостаточно обеспечить максимально плотную упаковку. При размещении виртуальных объектов нужно учесть не только их жесткие размеры, которые нельзя нарушать, но и дополнительные области — зоны комфортности. Их занимать нежелательно. Эти дополнительные области позволяют приблизиться к объекту и выполнить с ним какие-то действия.
Целями представленной работы являются создание, реализация и оценка 2D-алгоритма оптимального размещения виртуальных объектов в физическом пространстве.
Материалы и методы. Ранее [4] авторы определили, что такое комфортное размещение виртуальных объектов, ввели понятие функции комфортности k(x). Она монотонно возрастает от 0 до 1 при 0≤x≤1 и равна 1 при х>1, где x = X/D, X — расстояние от края объекта до ближайшего препятствия, D — размер зоны комфортности. Для каждого измерения у объекта есть две односторонние зоны комфортности D– и D+. Комфортность с каждой стороны вычисляется отдельно.
В [6] показано, что задача одномерного размещения n виртуальных объектов в свободной области пространства протяженностью L сводится к системе линейных уравнений, не зависящих от вида функции комфортности k(x):
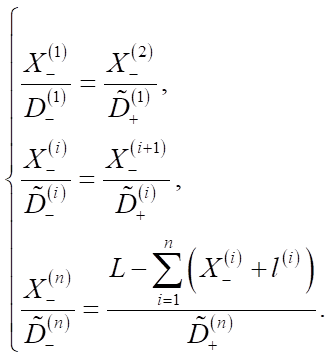
Здесь
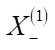 — расстояние первого объекта от левого края области встраивания;
— расстояние первого объекта от левого края области встраивания;
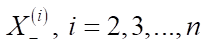 — расстояние между объектами с номерами i и (i – 1);
— расстояние между объектами с номерами i и (i – 1);
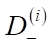 и
и 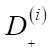 — левая и правая зоны комфортности соответственно;
— левая и правая зоны комфортности соответственно;
l(i) — размер объекта;
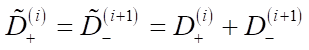 ,
,
i = 1,2,…, (n – 1).
Матрица системы (1) сильно разрежена, поэтому можно избежать использования не самых быстрых универсальных методов и достаточно просто найти решение. Например, в первых (n – 1) равенствах можно в каждом i-м уравнении выразить 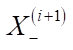 через
через 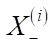 , затем подставить это в последнее уравнение и получить линейное уравнение относительно
, затем подставить это в последнее уравнение и получить линейное уравнение относительно 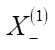 . После этого от первого уравнения к (n – 1)-му последовательно определяются значения
. После этого от первого уравнения к (n – 1)-му последовательно определяются значения 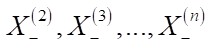 . Авторы реализовали данный 1D-алгоритм размещения объектов с помощью численных методов. Он показал высокую скорость и эффективность. Этот 1D-алгоритм стал основой для научных изысканий, описанных в представленной работе. Авторы предложили 2D-алгоритм оптимальной расстановки виртуальных объектов. Его реализовали в виде программного кода на языке C# с использованием игрового движка Unity, который широко используется для создания мобильных приложений дополненной реальности [8]. В ходе эксперимента на устройстве пользователя, работающего в режиме пиковой нагрузки, запускался алгоритм для 5, 10, 15, 20, 25, 35, 40, 45 и 50 объектов. Замеряли время, затраченное на вычисления (в миллисекундах). Каждый расчет повторяли 10 раз во избежание аномальных значений. Всего в эксперименте участвовали 1,8 тыс. устройств, с них собрали и проанализировали около 77 тыс. событий с результатами.
. Авторы реализовали данный 1D-алгоритм размещения объектов с помощью численных методов. Он показал высокую скорость и эффективность. Этот 1D-алгоритм стал основой для научных изысканий, описанных в представленной работе. Авторы предложили 2D-алгоритм оптимальной расстановки виртуальных объектов. Его реализовали в виде программного кода на языке C# с использованием игрового движка Unity, который широко используется для создания мобильных приложений дополненной реальности [8]. В ходе эксперимента на устройстве пользователя, работающего в режиме пиковой нагрузки, запускался алгоритм для 5, 10, 15, 20, 25, 35, 40, 45 и 50 объектов. Замеряли время, затраченное на вычисления (в миллисекундах). Каждый расчет повторяли 10 раз во избежание аномальных значений. Всего в эксперименте участвовали 1,8 тыс. устройств, с них собрали и проанализировали около 77 тыс. событий с результатами.
Фильтрация аномалий с помощью z-оценки позволила выявить значения, которые можно определить как выбросы [9]. Авторы стандартизировали данные и вычислили z-оценку для каждого значения. Аномальными сочли те, у которых z-оценка оказалась больше 3 или меньше –3. Их исключили и сосредоточились на типичных и репрезентативных данных.
Результаты исследования. Итак, на плоскости X, Z есть прямоугольная область с шириной 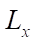 и длиной
и длиной 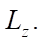 Ее следует заполнить некоторым количеством виртуальных объектов. Каждый объект помимо своих размеров
Ее следует заполнить некоторым количеством виртуальных объектов. Каждый объект помимо своих размеров 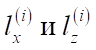 (где i — номер объекта) характеризуется еще зонами комфортности
(где i — номер объекта) характеризуется еще зонами комфортности 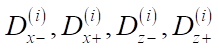 . На рис. 1 представлена блок-схема описываемого алгоритма.
. На рис. 1 представлена блок-схема описываемого алгоритма.
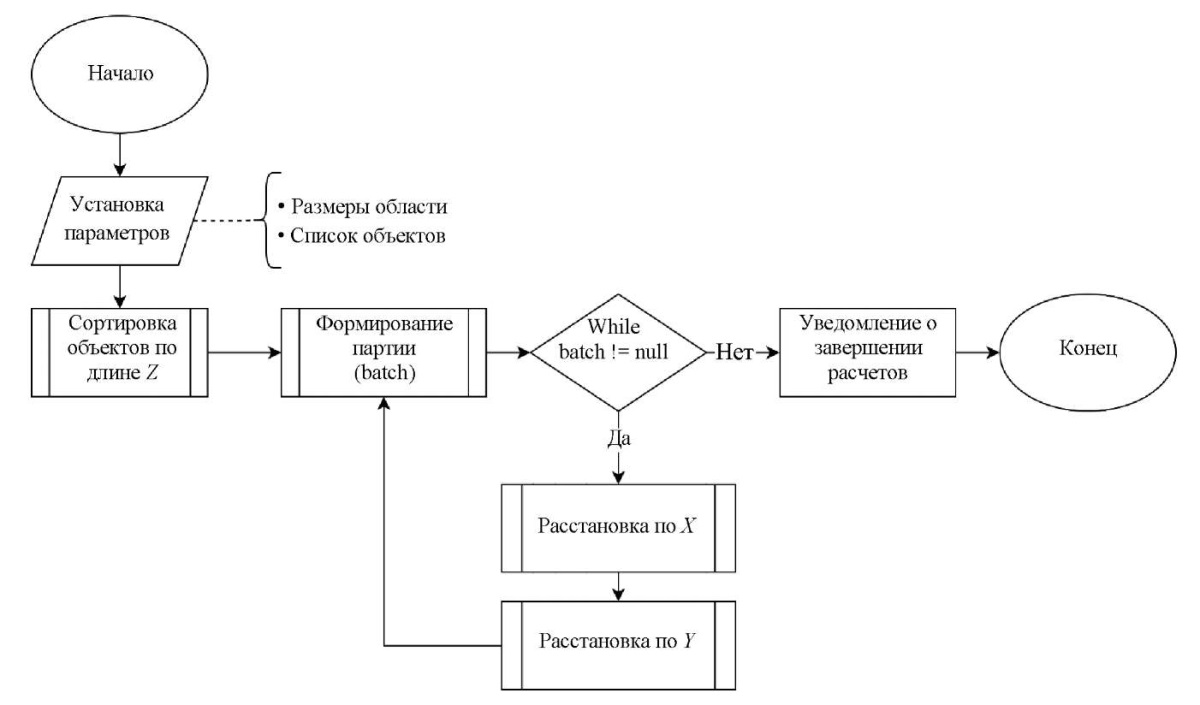
Рис. 1. Верхнеуровневый алгоритм 2D-расстановки
В данной работе используется левосторонняя система координат: ось X обозначает горизонтальный вектор размещения, ось Z направлена вперед от пользователя и является вектором глубины или фронтальным измерением [7]. Объекты размещаются в горизонтальной плоскости (например, на полу, столешнице и пр.), поэтому вертикальная ось Y не рассматривается, а все иллюстрации предполагают вид сверху на получившуюся композицию.
В левом нижнем углу каждого виртуального объекта обозначим опорную точку (pivot). Она будет определять конечные координаты размещения объекта. Далее набор объектов сортируется в порядке убывания по 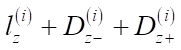 — габаритной длине объектов с учетом зон комфортности, расположенных спереди и сзади в соответствии с рассматриваемой осью координат. После сортировки объекты, занимающие больше пространства по глубине, располагаются дальше от пользователя (или выше для схемы, представленной в горизонтальной проекции). Блок-схема формирования партии из объектов представлена на рис. 2.
— габаритной длине объектов с учетом зон комфортности, расположенных спереди и сзади в соответствии с рассматриваемой осью координат. После сортировки объекты, занимающие больше пространства по глубине, располагаются дальше от пользователя (или выше для схемы, представленной в горизонтальной проекции). Блок-схема формирования партии из объектов представлена на рис. 2.
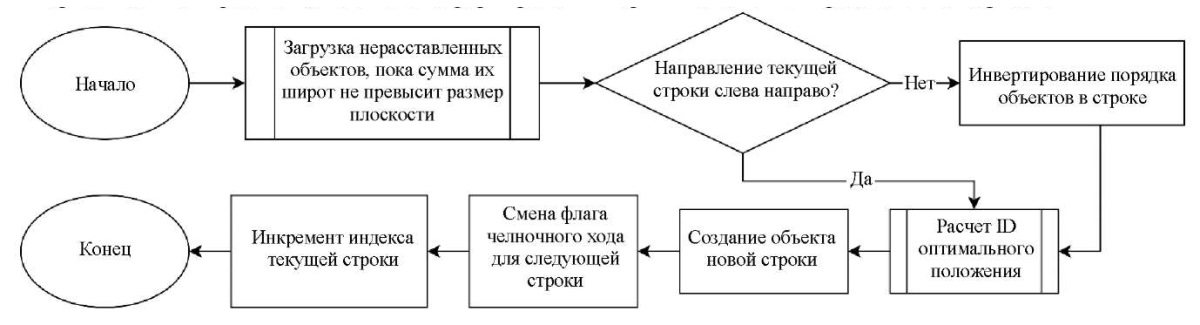
Рис. 2. Алгоритм формирования ряда из объектов
Затем из упорядоченного множества объектов формируются отдельные строки или партии (batch). В каждую строку включается минимальное количество объектов, сумма ширины которых вместе с зонами комфортности превосходит ширину заполняемой области 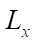 . Если при добавлении следующего объекта вычисленная занимаемая ширина превысит горизонтальный размер доступного пространства внутри прямоугольника, партия считается завершенной. Таким образом, каждая партия может быть размещена в виде линии в пределах области. Ряды чередуются слева направо и справа налево для смешивания крупных и мелких объектов. Это можно назвать «челночным ходом» (рис. 3).
. Если при добавлении следующего объекта вычисленная занимаемая ширина превысит горизонтальный размер доступного пространства внутри прямоугольника, партия считается завершенной. Таким образом, каждая партия может быть размещена в виде линии в пределах области. Ряды чередуются слева направо и справа налево для смешивания крупных и мелких объектов. Это можно назвать «челночным ходом» (рис. 3).

Рис. 3. Схема «челночного хода» на координатной плоскости
Для сформированного ряда применяется алгоритм 1D-размещения, который позволяет оптимально расположить ряд объектов вдоль оси X на основе рассчитанного коэффициента комфортности К, одинакового для всех объектов ряда. Для каждого объекта первой линии смещение по оси Z от края плоскости определяется таким образом, чтобы комфортность спереди равнялась комфортности по X:
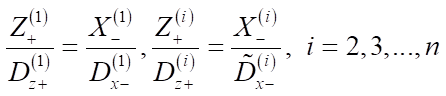 .
.
Начиная со 2-го ряда для вычисления отступа Z+ проверяется наличие потенциальных соседей сверху из вышележащего ряда, имеющих с текущим обрабатываемым объектом общие участки по координате X. При этом каждый объект размещаемой строки устанавливается по оси Z таким образом, чтобы его комфортность сверху была максимальной из односторонних горизонтальных комфортностей в данной и предыдущей строках. Алгоритм расчета координат Z представлен на рис. 4.
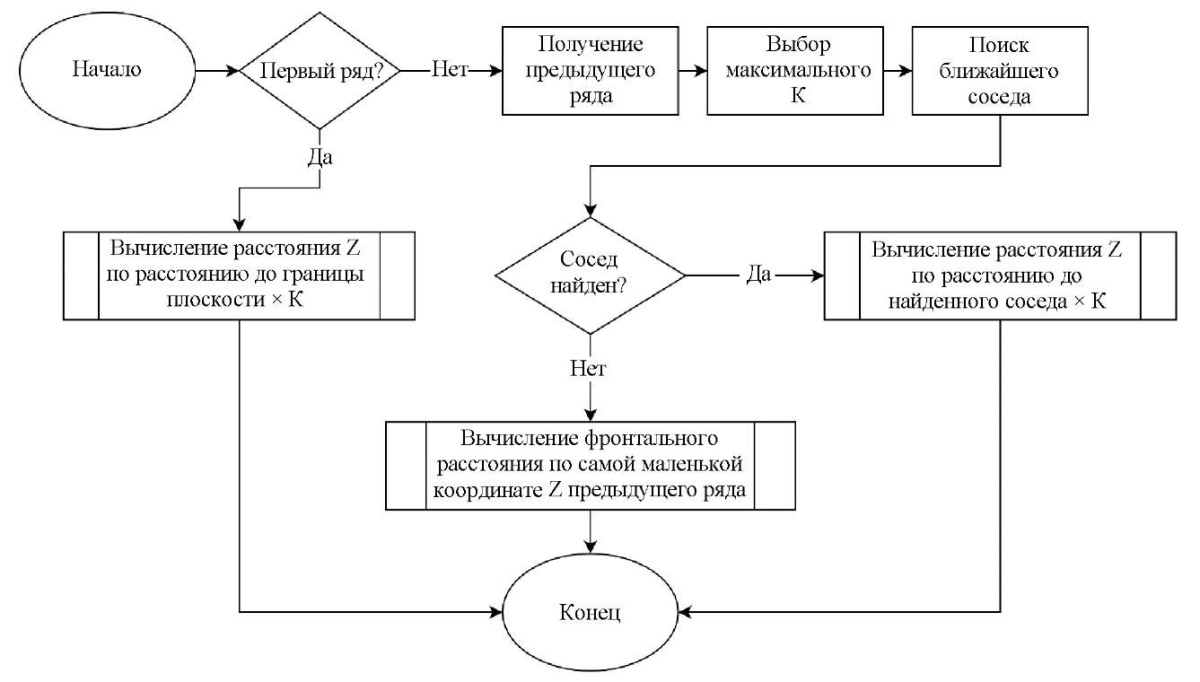
Рис. 4. Принцип расчета координаты Z для объекта строки
Из блок-схемы видно, что отступ вычисляется аналогично для всех трех возможных сценариев:
- отступ от края плоскости для установки объекта;
- отступ от соседа сверху;
- при отсутствии соседа в предыдущей строке берется самый близкий по Z объект из всех предыдущих строк.
Новые партии формируются до тех пор, пока всем объектам не присвоят ряд или пока не закончится физическое пространство.
Исходные данные к описанному алгоритму систематизированы в таблице 1. Объекты рассортированы по их вертикальным размерам.
Таблица 1
Исходные данные к примеру работы описанного алгоритма
|
Номер объекта |
Размер |
Зона комфортности |
|
1 |
(7; 4) |
(4; 3; 3; 5) |
|
2 |
(10; 4) |
(4; 3; 5; 3) |
|
3 |
(5; 4) |
(2; 3; 5,25; 2,25) |
|
4 |
(12; 4) |
(2,8; 3,3; 3,8; 4,65) |
|
5 |
(5; 4) |
(2,5; 4; 1,75; 5,8) |
|
6 |
(18; 4) |
(3,2; 2,4; 5; 2,25) |
|
7 |
(11; 4) |
(2,1; 2,45; 2; 14,2) |
Таблица 1 соответствует рис. 5, демонстрирующему размещение объектов.
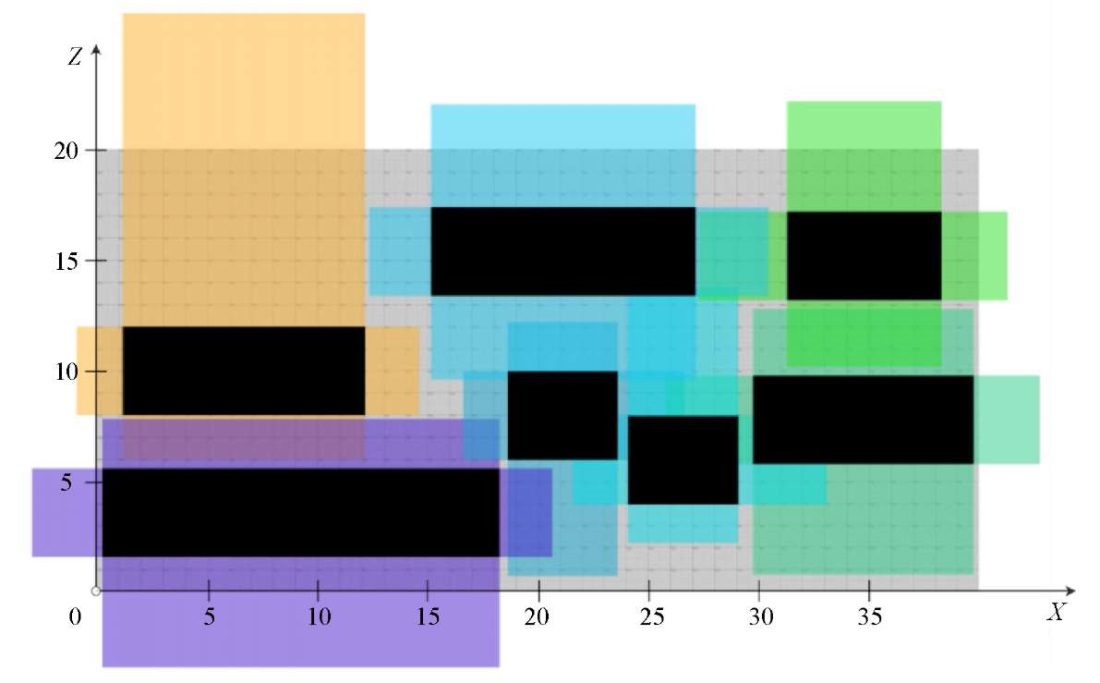
Рис. 5. Схема расположения объектов для рассматриваемого примера. Вид сверху
Серый прямоугольник — это свободная площадь, на которой расставляются объекты. Черные области — объекты в их габаритных размерах. Цветные, с наложениями, — предустановленные зоны комфортности для каждого объекта. Как отмечалось выше, зоны комфортности объектов могут частично перекрываться и выходить за пределы свободного пространства, но применяемый подход позволяет обеспечить баланс, чтобы в равной мере уменьшались комфортности различных объектов.
Напомним, что в данную модель входит понятие функции комфортности k(x). От нее не зависит полученная система уравнений (1), а значит и оптимальное размещение объектов. А вот значения односторонних комфортностей объектов определяются и их размещением, и видом функции k(x). Приведем два примера:
- в случае линейной функции k(x) односторонние комфортности объектов верхнего ряда рис. 5 оказываются равными 0,6;
- для зависимости
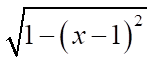 — значение 0,9.
— значение 0,9.
После программной реализации описанного 2D-алгоритма его внедрили в мобильное приложение с дополненной реальностью и записали аналитические данные пользовательских сессий. Сгруппировали информацию по каждой уникальной модели устройства, по каждому количеству расставляемых объектов в диапазоне [10–50]. Рассчитали среднее время выполнения (рис. 6).
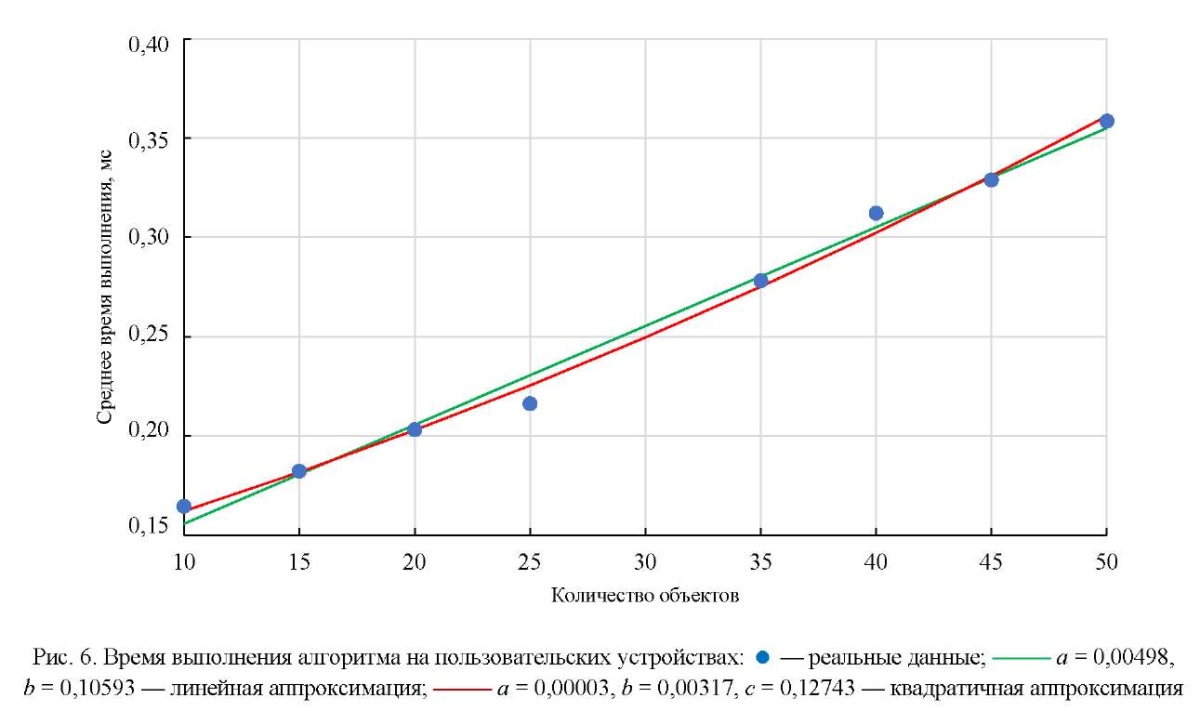
На указанном диапазоне невозможно сразу определить точную сложность вычисления алгоритма. Как видно из рис. 6, данные близки к линейной и квадратичной аппроксимации. С помощью метода остаточной суммы квадратов рассчитана количественная оценка обеих аппроксимаций и получены значения 0,00035 и 0,00021 соответственно [10].
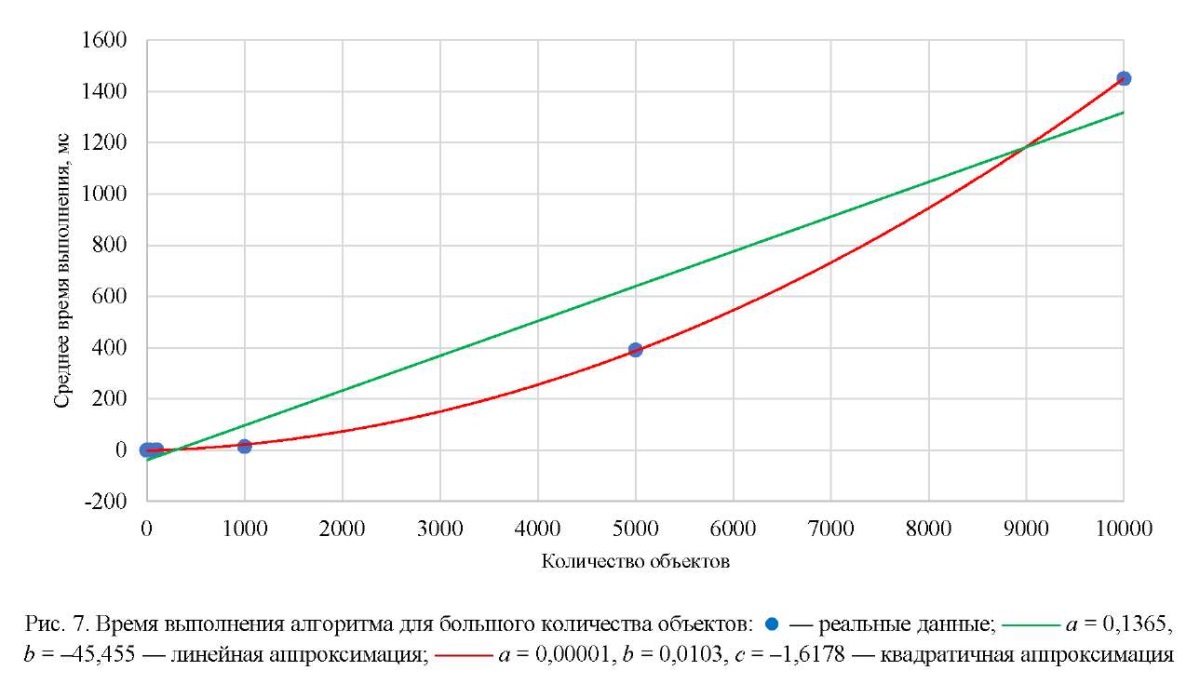
Для подтверждения гипотезы о квадратичной зависимости на персональном компьютере запустили аналогичный эксперимент для диапазона [ 10–10000] объектов. Рис. 7 подтверждает гипотезу, значит алгоритму можно присвоить сложность O(n2). Впрочем, ситуация с 10000 объектами, скорее, теоретическая, и на практике в дополненной реальности пользователь вряд ли будет работать более чем с 1–2 десятками объектов.
Сопоставили время выполнения на разных пользовательских устройствах. Отобрали 10 самых популярных моделей и по результатам вычислений построили диаграмму (рис. 8).
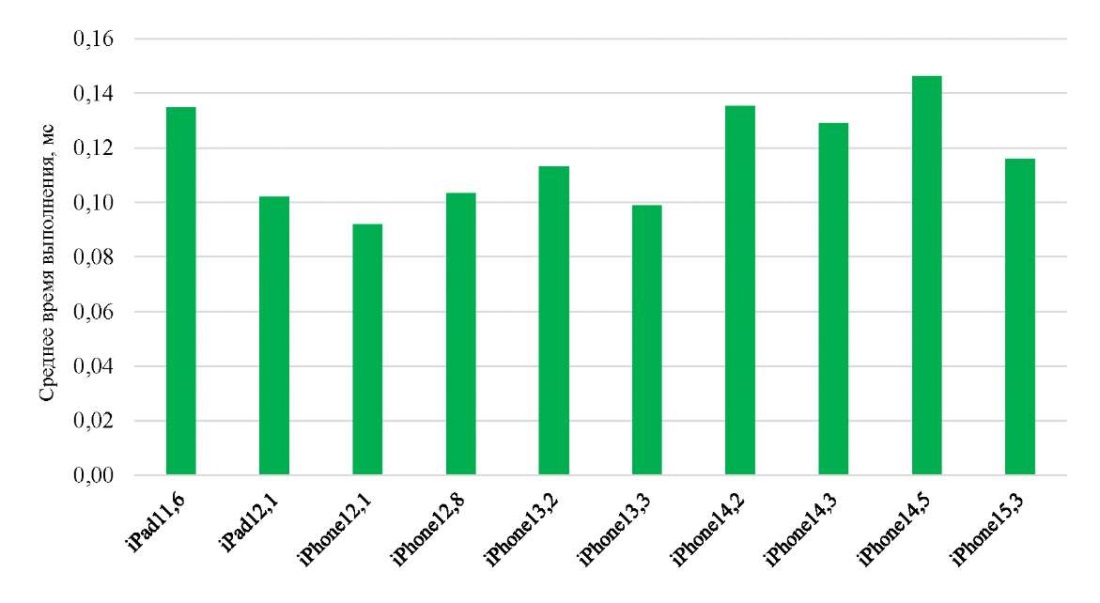
Рис. 8. Сравнение скорости вычисления на разных устройствах для 10 объектов
Минимальное зарегистрированное время выполнения — 0,093 мс, максимальное — 0,146 мс. Для данной выборки корреляция между моделью устройства и временем выполнения — всего 0,177. Это довольно низкое значение.
Расчеты показали высокую эффективность двумерного алгоритма. Это обусловлено разбиением всей совокупности объектов на отдельные строки и использованием в каждой строке быстрого одномерного алгоритма, описанного в начале статьи. Этот алгоритм позволяет решить задачу с меньшими затратами ресурсов и времени.
На рис. 9 представлены дополнительные визуализации схем расстановки для разного количества объектов и их параметров.
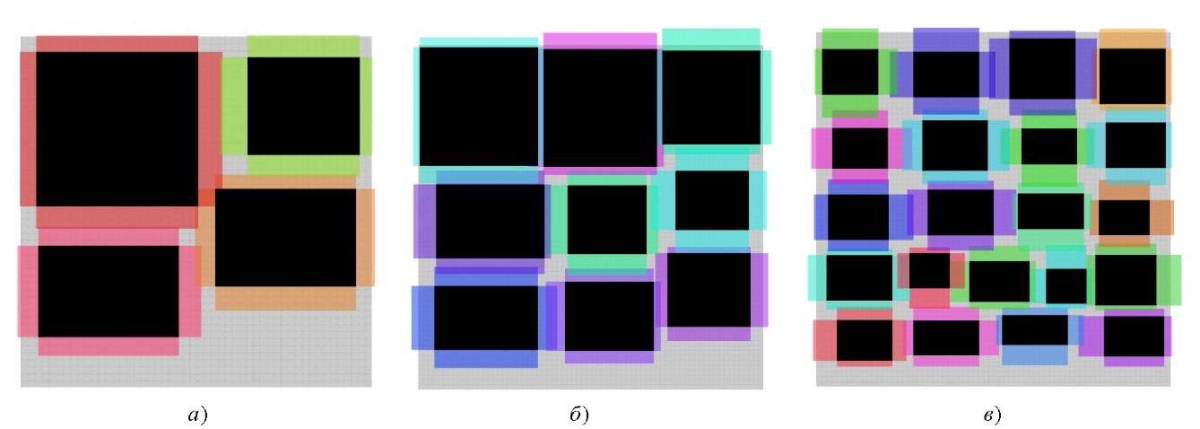
Рис. 9. Примеры расстановки разного количества объектов:
а — 4 объекта; б — 9 объектов; в — 21 объект
Итак, предлагаемый алгоритм двумерного размещения позволяет работать с набором виртуальных объектов. Каждый из них характеризуется определенными размерами и зонами комфортности. Алгоритм предназначен для оптимального расположения таких объектов в прямоугольном физическом пространстве, которое воссоздает окружение пользователя.
Обсуждение и заключение. Для ранее описанной одномерной задачи предложен и реализован в программном коде эффективный алгоритм оптимального размещения виртуальных объектов. Для двумерного случая построена модель оптимального размещения. На ее основе разработан эффективный алгоритм, реализованный в программном коде.
Проанализирована производительность алгоритма, которая измеряется временем выполнения. Установлено, что нет значимой корреляции между временем выполнения и моделью устройства. Среднее время — доли миллисекунды даже для больших партий объектов. Это говорит об относительно стабильной производительности алгоритма в различных условиях. Однако нельзя исключить возможное влияние других непроверенных факторов. Для полной характеристики зависимостей производительности нужны дальнейшие исследования.
Обозначим несколько направлений будущей работы для повышения производительности и адаптивности алгоритма. Это, во-первых, совершенствование решения, которое позволит использовать полные размеры объектов, по возможности без пересечений комфортных зон. Их размеры будут уменьшаться только в случае крайней необходимости. Это должно обеспечить оптимальное использование пространства и дальнейшее улучшение интерактивного опыта пользователя.
Во-вторых, включение вращения элементов в алгоритм повысит гибкость в их расположении и даст возможность лучше использовать пространство. К тому же это позволит алгоритму учитывать больше разных объектов, тем самым расширяя его практическое применение.
Заметим, что в приложении с дополненной реальностью расстановка пользователем трех и более объектов — достаточно трудоемкая задача. Она требует значительного времени и существенно затрудняет работу.
Предложенная технология размещения объектов в 2D позволяет оптимально позиционировать виртуальный контент для улучшения пользовательского опыта в дополненной реальности. Автоматизированный расчет расположения сокращает ручную работу и дает возможность сосредоточиться на полноценном взаимодействии с AR.
Научные изыскания в данном направлении ведут к бесшовной интеграции виртуального и физического пространств. Результаты могут применить на практике разработчики очков дополненной реальности, которые сталкиваются с проблемой быстрого интеллектуального позиционирования объектов в зависимости от пользовательских предпочтений и контекста. Кроме того, итоги работы могут представлять интерес для:
- инженеров, работающих над умными домашними системами;
- дизайнеров интерфейсов, для которых важно эффективно и гармонично сочетать элементы управления и информацию на экране.
Введение нечеткой логики позволяет разработчикам адаптировать решение под конкретные задачи и сценарии использования. В будущих исследованиях целесообразно изучить и задействовать пользовательский опыт, включать дополнительные ограничения на позиционирование объектов.
Список литературы
1. Yahya Ghazwani, Shamus Smith. Interaction in Augmented Reality. In: Proc. 4th Int. Conf. on Virtual and Augmented Reality Simulations. New York, NY: Association for Computing Machinery; 2020. P. 39–44. https://doi.org/10.1145/3385378.3385384
2. Müller J., Butscher S., Feyer S.P., Reiterer H. Studying Collaborative Object Positioning in Distributed Augmented Realities. In: Proc. 16th Int. Conf. on Mobile and Ubiquitous Multimedia. New York, NY: Association for Computing Machinery; 2017. P. 123–132. https://doi.org/10.1145/3152832.3152856
3. Regenbrecht H.T, Wagner M.T. Interaction in a Collaborative Augmented Reality Environment. In: CHI '02 Extended Abstracts on Human Factors in Computing Systems. New York, NY: Association for Computing Machinery; 2002. P. 504–505. https://doi.org/10.1145/506443.506451
4. Alpatova M.V., Glazkov A.V., Rudyak Yu.V. Mathematical Model of Rational Location of Augmented Reality Objects in User's Environment. In: Proc Int. Sci. Conf. “Smart Nations: Global Trends In The Digital Economy”. Cham: Springer; 2022. P. 248–254. https://doi.org/10.1007/978-3-030-94873-3_30
5. Гимади Э.Х, Залюбовский В.В. Задача упаковки в контейнеры: асимптотический подход. Известия высших учебных заведений. 1997;(12(427)):25–33. URL: https://kpfu.ru/portal/docs/F1486686603/03_12.PDF (дата обращения: 20.09.2023).
6. Алпатова М.В., Рудяк Ю.В. Размещение нескольких виртуальных объектов в физическом пространстве в дополненной реальности. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):203–211. https://doi.org/10.23947/2687-1653-2023-23-2-203-211
7. Karev G.B. Directionality in Right, Mixed and Left Handers. Cortex. 1999;35(3):423–431. https://doi.org/10.1016/S0010-9452%2808%2970810-4
8. Sung Lae Kim, Hae Jung Suk, Jeong Hwa Kang, Jun Mo Jung, Laine T.H., Westlin J. Using Unity 3D to Facilitate Mobile Augmented Reality Game Development. In: Proc. IEEE World Forum on Internet of Things (WF-IoT). New York City: IEEE; 2014. P. 21–26. https://doi.org/10.1109/WF-IoT.2014.6803110
9. Warner R.A. Using Z Scores for the Display and Analysis of Data. In book: Optimizing the Display and Interpretation of Data. Amsterdam: Elsevier; 2016. P. 7–51. https://doi.org/10.1016/B978-0-12-804513-8.00002-X
10. Wolfe D.A. Ranked Set Sampling: Its Relevance and Impact on Statistical Inference. ISRN Probability and Statistics. 2012;2012:568385. https://doi.org/10.5402/2012/568385
Об авторах
М. В. АлпатоваРоссия
Марианна Валерьевна Алпатова, старший преподаватель кафедры информатики и информационных технологий, ScopusID
107023, г. Москва, ул. Большая Семеновская, 38
Ю. В. Рудяк
Россия
Юрий Владимирович Рудяк, доктор физико-математических наук, профессор кафедры информатики и информационных технологий, ScopusID
107023, г. Москва, ул. Большая Семеновская, 38
Рецензия
Для цитирования:
Алпатова М.В., Рудяк Ю.В. Оптимальная 2D-расстановка виртуальных объектов в физическом пространстве для приложений дополненной реальности. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):410-421. https://doi.org/10.23947/2687-1653-2023-23-4-410-421. EDN: QPFEMG
For citation:
Alpatova M.V., Rudyak Yu.V. Optimal 2D Placement of Virtual Objects in Physical Space for Augmented Reality Applications. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):410-421. https://doi.org/10.23947/2687-1653-2023-23-4-410-421. EDN: QPFEMG












































