Перейти к:
Web-приложение для математического моделирования нестационарного течения нефти в пористой среде
https://doi.org/10.23947/2687-1653-2023-23-4-422-432
EDN: RBUFLG
Аннотация
Введение. Основу для анализа и интерпретации данных гидродинамических исследований составляют теоретические модели и вычислительные алгоритмы. Но, несмотря на востребованность данной тематики, многие вопросы, связанные с нестационарными течениями жидкостей в нефтяных пластах, все еще требуют решений. Поэтому математические постановки задач, связанных с учетом нестационарного течения жидкости, разработка эффективных численных методов и алгоритмов, их решение с применением современных web-технологий являются актуальными. Цель данной работы — разработка web-приложения для математического моделирования процесса фильтрации жидкости в однопоровых коллекторах при проведении гидродинамического исследования на добывающей скважине.
Материалы и методы. Для решения поставленной задачи применены методы механики сплошной среды и вычислительной математики. Представлена модель течения нефти в однопоровом коллекторе. При разработке приложения использованы языки программирования Python и JavaScript. Результаты расчетов хранятся в реляционной базе данных, реализованной средствами PostgreSQL.
Результаты исследования. Разработано новое web-приложение для моделирования процесса фильтрации нефти в однопоровых коллекторах, которое применимо для изучения флюидодинамических процессов и может быть использовано для прогноза дебитов, добычи и расчета оптимальных режимов работы скважин.
Обсуждение и заключение. Разработанное web-приложение позволяет строить поля давления и температуры в пласте около работающей и остановленной добывающей скважины и на различных расстояниях от нее. Данная информация дает возможность оперативно оценивать длительность гидродинамических исследований, а также регулировать работу скважин. Приложение может быть развернуто в существующей сетевой инфраструктуре, пользоваться всем функционалом, подключаясь к удаленному серверу. Оно оптимизировано для использования на различных платформах и имеет широкие перспективы дальнейшего развития.
Ключевые слова
Для цитирования:
Мазитов А.А. Web-приложение для математического моделирования нестационарного течения нефти в пористой среде. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):422-432. https://doi.org/10.23947/2687-1653-2023-23-4-422-432. EDN: RBUFLG
For citation:
Mazitov A.A. Web Application for Mathematical Modeling of Unsteady Oil Flow in Porous Medium. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):422-432. https://doi.org/10.23947/2687-1653-2023-23-4-422-432. EDN: RBUFLG
Введение. Российская Федерация является одной из ведущих стран мира по объемам производства нефти. Каждый год на месторождениях страны добывается свыше 500 миллионов тонн нефти, подавляющая часть которой в сыром виде экспортируется в страны азиатско-тихоокеанского региона, Европы и ближнего зарубежья. Развитие нефтяной промышленности в нашей стране оказывает влияние на другие отрасли и сферы деятельности, поэтому решение задач по эффективному освоению и разработке нефтяных месторождений было и остается перспективным. Основой современных научных технологий нефтяной разработки является комплексное изучение свойств продуктивных коллекторов, содержащихся в них веществ и происходящих сложных процессов при течении флюида.
Главная цель при добыче нефти — увеличение темпа отбора флюида из продуктивного пласта и поддержание пластового давления. Планирование работ по эффективному освоению и оптимальной эксплуатации нефтяной скважины носит комплексный характер, связанный с гидродинамическими процессами, происходящими при течении жидкости в системе «скважина — пласт» [1]. Для изучения продуктивных свойств пластов и жидкостей применяются гидродинамические исследования скважин (ГДИС). Средствами ГДИС проводятся замер совокупности данных коллектора с использованием глубинных или устьевых приборов, а также последующая обработка замеров и интерпретация полученных данных (продуктивность, фильтрационные свойства жидкостей, тип коллектора и т. д.) [2].
При исследовании коллекторов с использованием ГДИС применяются теоретические модели, основанные на классических уравнениях и законах, а также вычислительные алгоритмы для моделирования процессов фильтрации флюидов. Однако, несмотря на востребованность данной тематики, многие вопросы, связанные с математическими и вычислительными аспектами моделирования нестационарных потоков в коллекторах, требуют дальнейшей разработки и развития [3][4].
Для анализа и интерпретации результатов ГДИС существует ряд отечественных («Автон», «Гидрозонд») и зарубежных (OLGA, LedaFlow, FlowVision, MAST, Saphir NL) программ [5–7]. При всех имеющихся преимуществах они обладают некоторыми недостатками, такими как невозможность проведения полного спектра расчетов, просмотра и изменения параметров исходных моделей. Все представленные программные продукты являются настольными, коммерческими, сложными в эксплуатации, многие обладают перегруженным интерфейсом. В условиях, когда необходимо оперативно или в режиме реального времени провести расчет, большие коммерческие симуляторы оказываются малоэффективными. Поэтому для выполнения схожих работ предлагается использовать web-приложение, обладающее множеством преимуществ.
В отличие от настольных, web-приложения независимы от операционной системы и вычислительных мощностей персональных компьютеров. Программный код web-приложения пишется единожды для конкретной платформы, где оно будет развернуто. Web-приложения выделяются простой реализацией, легкостью применения, высокой производительностью. Их основными характеристиками являются доступность, надежность, безопасность, масштабируемость, гибкость, кросс-платформенность. Для работы с web-приложением от персонального компьютера пользователя необходимо находиться в одной сети с сервером, на котором оно развернуто. Такой сетью может быть локальная сеть предприятия или глобальная сеть Интернет, если речь идет о веб-сайтах. По сравнению с настольными, у web-приложений можно выделить один недостаток — время отклика, зависящее от удаленности персонального компьютера от сервера.
Логика работы web-приложения отличается от настольного, которое запускается и выполняет код на компьютере пользователя. Поэтому настольные приложения отличаются более расширенным и отзывчивым пользовательским интерфейсом и позволяют реализовывать более сложную бизнес-логику работы. Однако с развитием web-технологий это достоинство с каждым годом нивелируется, и web-приложения все чаще бывают способны реализовывать сложные пользовательские сценарии. Таким образом, в части реализации производственных задач web-приложения становятся более конкурентными.
В связи с этим математические постановки задач с учетом нестационарного течения жидкости во всех его элементах (пласт, стволовые трубы, проточные каналы), разработка эффективных численных методов и алгоритмов, последующие их решения с применением современных технологий web-разработки являются актуальными. Использование полученных численных алгоритмов позволяет количественно описывать поведение давления и температуры в нефтяных скважинах. Алгоритм и web-приложение предоставят пользователям, специалистам в области анализа и интерпретации гидродинамических исследований, удобный и легко адаптируемый к их практическим потребностям инструмент для расчета сложных процессов, происходящих при разработке пористых коллекторов.
Материалы и методы. Рассматривается добывающая скважина, на которой проводится гидродинамическое исследование методом кривой восстановления давления. Скважина эксплуатирует терригенный коллектор, который относится к однопоровым. Пласт является неограниченным, воздействие соседних скважин отсутствует. Течение флюида в пласте — горизонтальное, перетоки между пропластками отсутствуют. Скважина работает в установившемся режиме с постоянным забойным давлением. На границе контура поддерживаются постоянные давление и температура. Для проведения исследования измерительный прибор опускается на глубину верхних дыр перфорации. Расчет динамики давления и температуры проводится в пространственно-одномерном случае.
При численном моделировании важно учитывать все параметры пласта и флюида, чтобы достичь наиболее качественного описания процесса массопереноса нефти в однопоровом коллекторе. Рассмотрим математическую модель, описывающую процесс фильтрации нефти в однопоровом коллекторе. Основой для модели служат уравнения пьезопроводности и теплопроводности. Математическая модель в радиальных координатах представляет собой систему дифференциальных уравнений в частных производных:
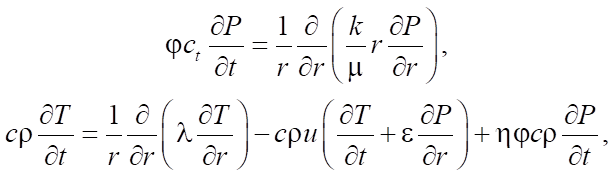 (1)
(1)
где
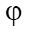 — пористость пласта;
— пористость пласта;
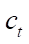 — сжимаемость породы (1/Па);
— сжимаемость породы (1/Па);
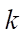 — проницаемость пласта (м²);
— проницаемость пласта (м²);
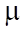 — вязкость жидкости (Па с);
— вязкость жидкости (Па с);
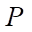 — пластовое давление (Па);
— пластовое давление (Па);
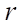 — расстояние до стенки скважины (м);
— расстояние до стенки скважины (м);
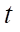 — время (с);
— время (с);
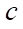 — теплоемкость нефти (Дж/кг К);
— теплоемкость нефти (Дж/кг К);
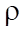 — плотность нефти (кг/м³);
— плотность нефти (кг/м³);
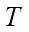 — пластовая температура (К);
— пластовая температура (К);
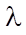 — теплопроводность пористой среды (Вт/м³∙К);
— теплопроводность пористой среды (Вт/м³∙К);
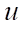 — скорость конвективного переноса тепла в пористой среде (м/с);
— скорость конвективного переноса тепла в пористой среде (м/с);
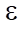 — коэффициент Джоуля-Томсона (К/Па);
— коэффициент Джоуля-Томсона (К/Па);
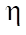 — коэффициент адиабатического расширения (К/Па).
— коэффициент адиабатического расширения (К/Па).
Первое уравнение описывает процесс изменения давления в пласте, второе — процесс теплопереноса жидкости.
Скорость конвективного переноса тепла в пористой среде определяется выражением
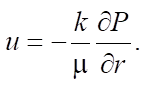 (2)
(2)
Система уравнений (1) задается в пространственно-временном интервале:
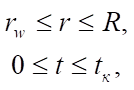 (3)
(3)
где
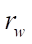 — радиус скважины;
— радиус скважины;
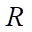 — расстояние до границы контура исследования (м);
— расстояние до границы контура исследования (м);
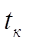 — время исследования (с).
— время исследования (с).
Исходя из поставленных выше условий для скважины и рассматриваемой области для системы (1) начальные и граничные условия задаются следующим образом:
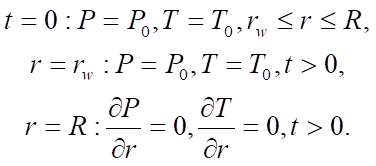 (4)
(4)
После определения начальных и граничных условий получена модель процесса фильтрации нефти в однопоровом коллекторе (1)–(4), характеризующая перераспределение давления и температуры в пласте.
Первоначальным этапом решения системы является приведение его к дискретному виду. Для этого используется метод конечных разностей [8]. Строится равномерная пространственно-временная сетка:
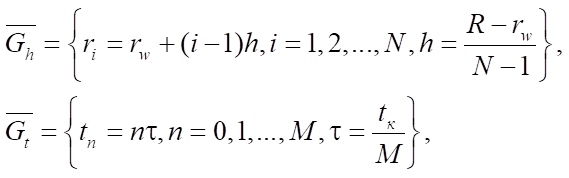 (5)
(5)
где
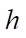 — шаг сетки по пространству;
— шаг сетки по пространству;
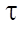 — шаг сетки по времени;
— шаг сетки по времени;
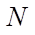 — число узлов по пространству;
— число узлов по пространству;
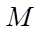 — число узлов по времени.
— число узлов по времени.
После замены дифференциальных выражений разностными аналогами получается система уравнений:
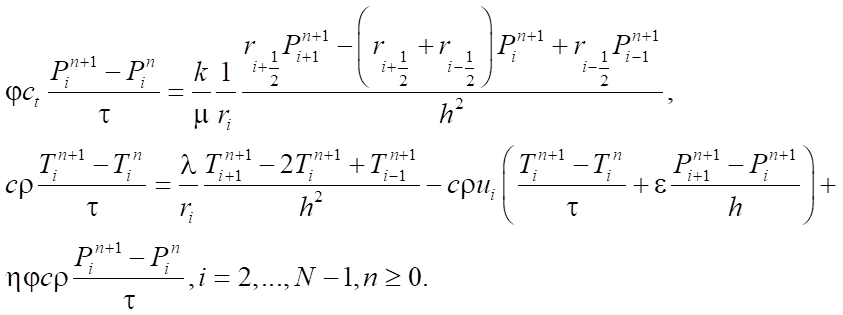 (6)
(6)
Система (6) представляет собой систему линейных алгебраических уравнений (СЛАУ), которая сводится к трехточечному уравнению общего вида:
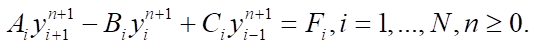 (7)
(7)
Коэффициенты равны:
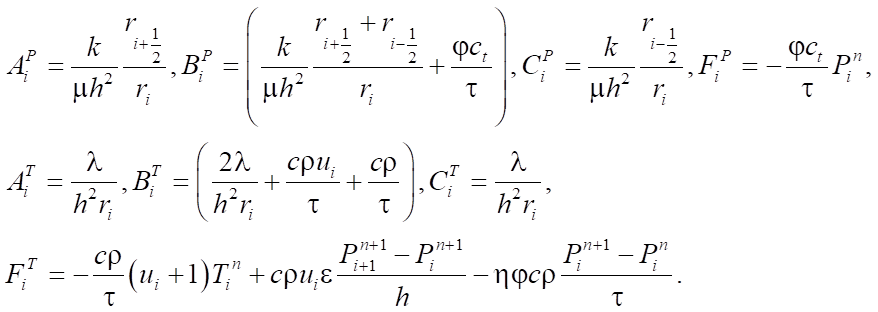 (8)
(8)
Система (7) решается методом скалярной прогонки [9][10]. Задача является нестационарной, поэтому метод применяется для определения пространственного распределения давления и температуры пласта на каждом временном слое [11][12]. Задача решается последовательно, на первом этапе решается уравнение для давления, на втором — для температуры.
Для автоматизации решения задачи разработано web-приложение. В общем виде его структура представлена на рис. 1. В ней выделяются пять основных компонентов: входные информационные потоки, выходные информационные потоки, методы обработки информации, технические средства обработки информации, база данных [13][14].
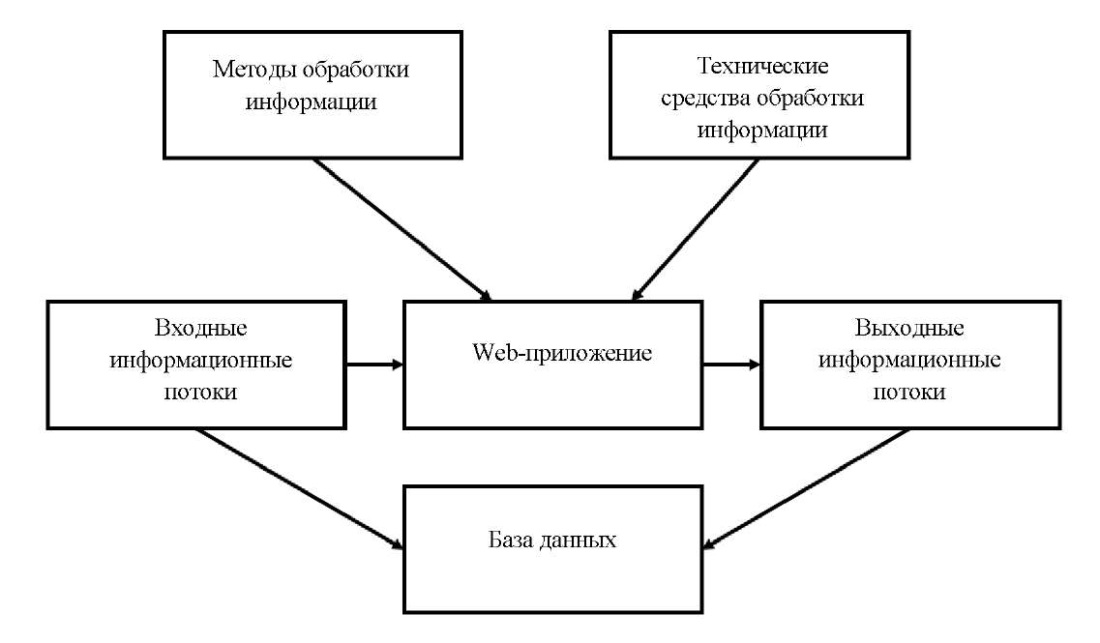
Рис. 1. Структура приложения в общем виде
Входными информационными потоками являются данные о параметрах модели, а выходными — графики, отражающие временные или пространственные зависимости забойного давления и температуры. Под методами обработки информации понимаются численные методы и методы интерпретации гидродинамических исследований. Техническими средствами обработки информации являются сервер, на котором размещено приложение, и персональный компьютер пользователя. Для хранения входных параметров и результатов расчетов используется база данных.
Конечный вид программного обеспечения зависит от средств, выбранных для его разработки. Средствами разработки являются парадигмы и языки программирования, среды и технологии для разработки. Выбор инструментария влияет на способ реализации задачи, критерии качества программного обеспечения, представление данных и тип графического интерфейса пользователя. Для разработки приложения в качестве языка программирования для серверной части выбран Python c использованием микрофреймворка Flask, для клиентской части — JavaScript c Vue.js [15][16]. В качестве СУБД для проектирования и разработки базы данных используется PostgreSQL [17].
Результаты исследования. Разработанное программное обеспечение представляет собой кросс-платформенное клиент-серверное web-приложение. Хранение данных и вычисления происходят на web-сервере, с которым пользователь взаимодействует через браузер (поддерживаются все современные интернет-браузеры). Клиентская часть может использоваться на широком спектре платформ (ПК, ноутбуки, смартфоны) и операционных систем (Windows, MacOS, Android, iOS).
Большую часть главного окна web-приложения занимает средство построения графиков температуры и давления. Графики строятся после произведения расчета путем выбора соответствующего пункта меню. Также имеется возможность построения графиков по ранее произведенным расчетам, для этого выбирается необходимый расчет в левой части окна. Графики строятся по пространственным и временным координатам. Для изменения вида графика выбираются соответственные пункты в верхней части окна.
Все произведенные расчеты хранятся в разработанной реляционной базе данных flowcalcdb, структура которой представлена на рис. 2.
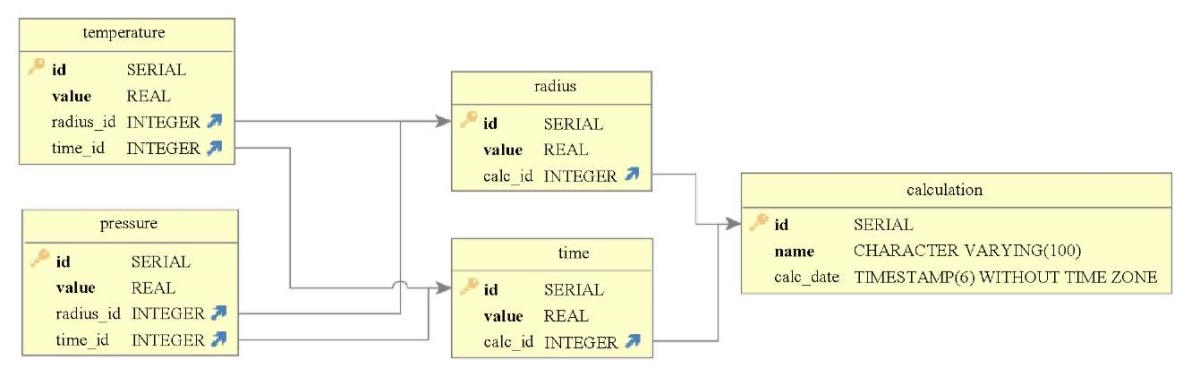
Рис. 2. Структура базы данных flowcalcdb
В общей сложности база данных содержит пять таблиц, которые находятся в третьей нормальной форме [18]. Все таблицы имеют первичные ключи. Главная таблица, calculation, хранит название расчета и дату его произведения. Две зависимые от нее таблицы, radius и time, хранят информацию о пространственно-временных координатах. Таблицы temperature и pressure хранят значения температуры и давления соответственно.
В разработанном приложении проведен ряд вычислительных экспериментов, позволяющих оценить результат его работы. Для проведения моделирования использованы значения из таблицы 1.
Таблица 1
Начальные и граничные условия, параметры расчета
|
Параметр |
Значение |
Единица измерения |
|
Радиус скважины, rw |
0,102 |
м |
|
Радиус исследования, R |
100 |
м |
|
Время исследования, t |
24 |
ч |
|
Начальное давление, P0 |
25 |
МПа |
|
Конечное давление, Pк |
30 |
МПа |
|
Проницаемость, k |
1e-14 |
м² |
|
Пористость |
0,2 |
|
|
Вязкость нефти, μ |
1,10e-3 |
Па∙с |
|
Сжимаемость нефти |
1,58e-9 |
1/Па |
|
Теплоемкость, cρ |
1,4 |
МДж/ м³∙К |
|
Теплопроводность, λ |
0,6 |
Вт/м∙К |
|
Коэффициент Джоуля-Томсона, ε |
3,94e-7 |
К/Па |
|
Коэффициент адиабатического расширения, η |
3,15e-7 |
К/Па |
|
Начальная температура, T0 |
363,15 |
К |
|
Количество точек по времени, N |
1000 |
|
|
Количество точек по пространству, M |
1000 |
С использованием данных из таблицы 1 построены графики распределения давления и температуры по пространству, представленные соответственно на рис. 3 и 4.
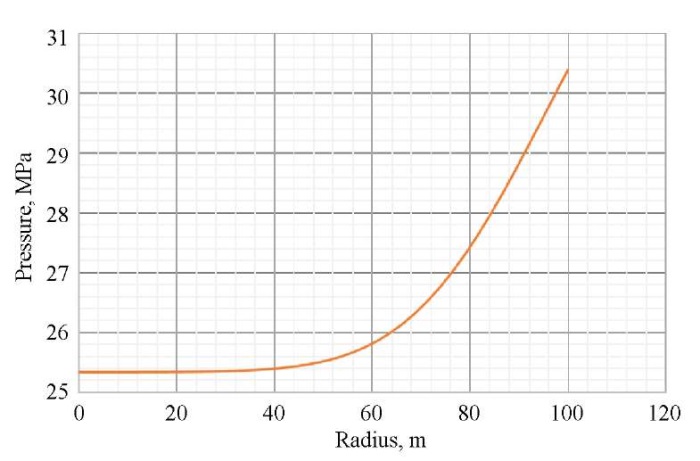
Рис. 3. Распределение давления по пространству в конечный момент времени
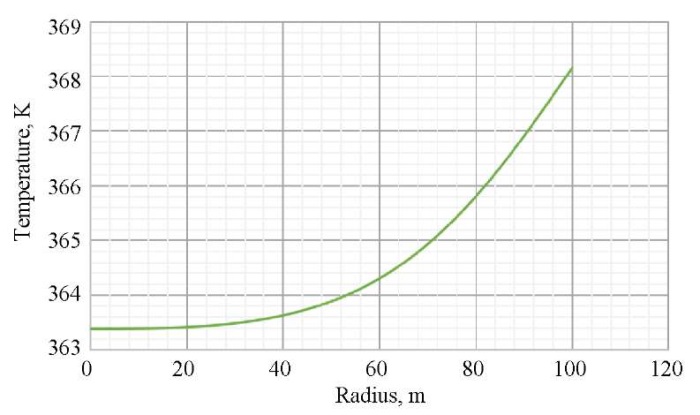
Рис. 4. Распределение температуры по пространству в конечный момент времени
Как следует из данных на рис. 3 и 4, после остановки скважины на гидродинамическое исследование наблюдается восстановление давления и температуры, причем чем дальше от стенок скважины, тем больше величина восстановления. На рис. 5 и 6 показано, как именно распределены давление и температура в различные моменты времени (6, 12, 24 ч.) после остановки скважины. Эта информация полезна специалистам по анализу и интерпретации гидродинамических исследований, поскольку позволяет оценить динамику давления и температуры и принять решение о продолжении или остановке исследования, а также проведении дополнительных мероприятий.
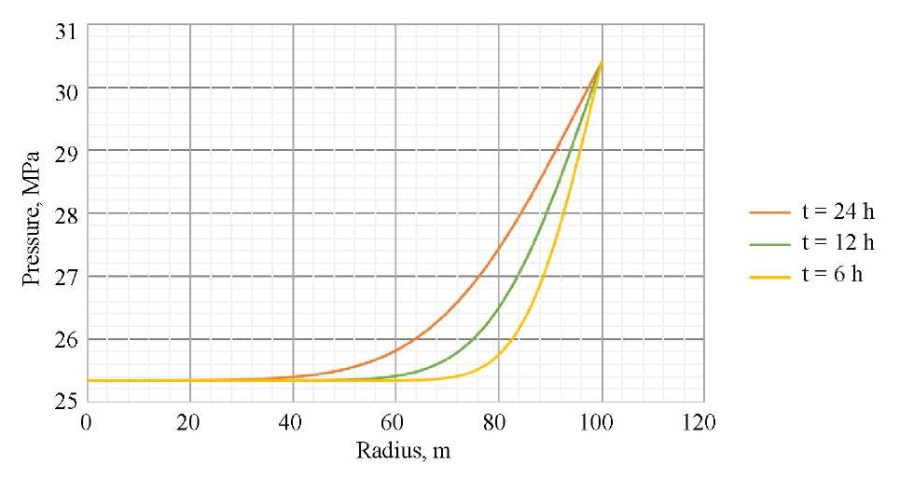
Рис. 5. Распределение давления по пространству в различные моменты времени
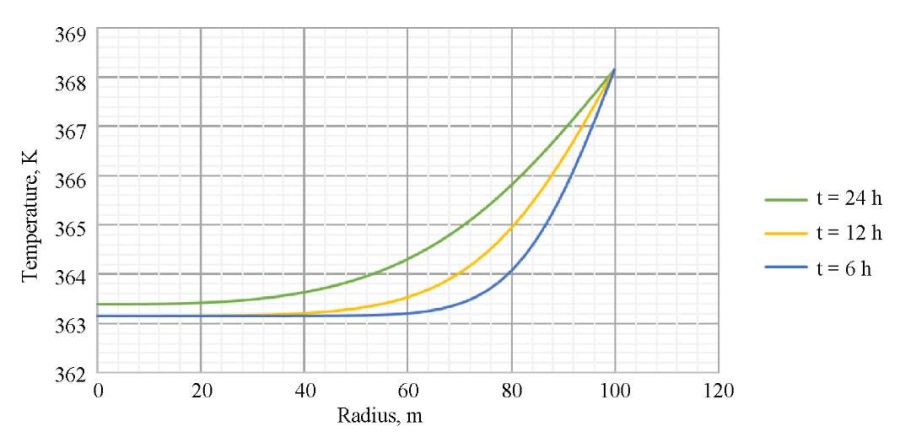
Рис. 6. Распределение температуры по пространству в различные моменты времени
На основе произведенных расчетов установлено, что наибольшее влияние на поведение давления и температуры оказывает проницаемость пласта. На рис. 7 и 8 изображены графики динамики давления и температуры в зависимости от различных значений проницаемости вблизи от стенок скважины (низкопроницаемый коллектор — 1 мД, среднепроницаемый — 10 мД, высокопроницаемый — 100 мД (1Д = 10-12м²)). Как видно на графиках, при увеличении проницаемости коллектора скорость восстановления давления и температуры увеличивается. На рис. 7 изображен график для реальных промысловых данных (проницаемость коллектора — 80 мД).
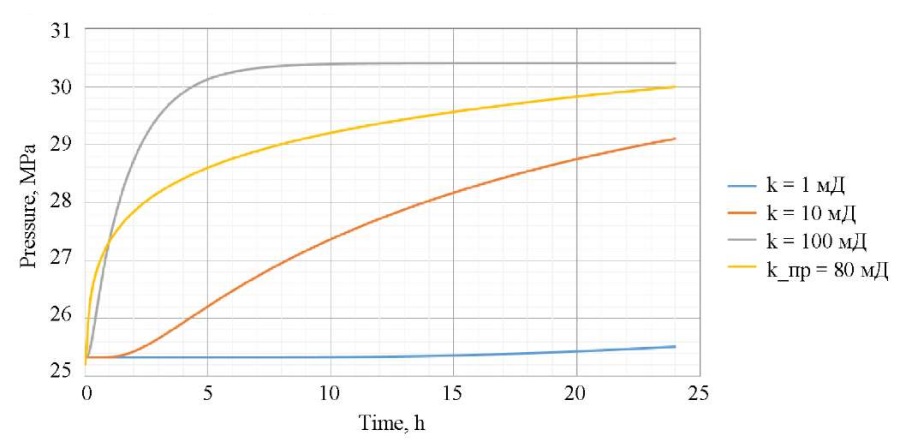
Рис. 7. Динамика давления при разных проницаемостях
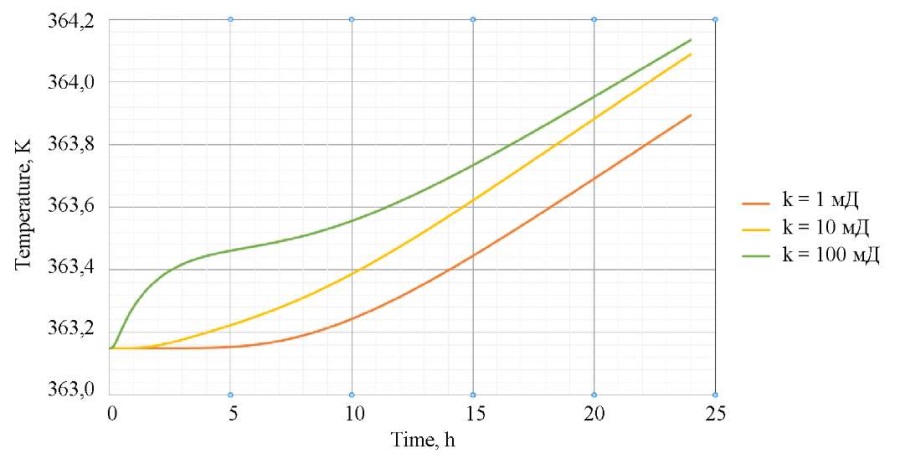
Рис. 8. Динамика температуры для разных проницаемостей
На основе динамики давления можно определить время проведения исследования (рис. 7). Например, для высокопроницаемого коллектора не имеет смысла проводить исследование более чем ~6 часов, поскольку после этого времени давление практически не меняется, а простой скважины является неэффективным, поскольку идут потери добычи.
Обсуждение и заключение. Разработанное web-приложение может быть использовано для анализа и интерпретации данных гидродинамических исследований. Web-приложение обеспечивает удобный пользовательский интерфейс и снижает затраты на поддержку. Оно может быть развернуто в существующей сетевой инфраструктуре или подключено к удаленному серверу для обеспечения полной функциональности. Применение приложения позволяет качественно и количественно оценивать поведение давления и температуры в однопоровых коллекторах. А хранение результатов расчетов в базе данных дает возможность проводить анализ с использованием результатов множества исследований, на основе которого можно составлять сводный отчет и формировать рекомендации по дальнейшему использованию скважины или месторождения в целом. Используемые модели являются устойчивыми и сходящимися. Графики строятся с помощью написанного web-приложения, и поэтому оно может использоваться на производстве.
Приложение имеет широкие перспективы развития, например, можно реализовать другие модели течения жидкости или предусмотреть наличие нескольких фаз. Также на момент написания данной работы остро встал вопрос об отказе от зарубежных коммерческих продуктов в пользу отечественных симуляторов. Поэтому разработка подобных продуктов является перспективной.
Список литературы
1. Hussein A. Essentials of Flow Assurance Solids in Oil and Gas Operations: Understanding Fundamentals, Characterization, Prediction, Environmental Safety, and Management, 1st ed. Houston, TX: Gulf Professional Publishing; 2022. 1122 p.
2. Камартдинов М.Р., Кулагина Т.Е., Мангазеев П.В., Панков М.В. Гидродинамические исследования скважин. Москва: ЮКОС; 2003. 810 с.
3. Bobreneva Yu.O., Mazitov A.A., Gubaydullin I.M. Researching the Mechanisms of Fluid Flow in the Fracture-Porous Reservoir Based on Mathematical Modeling. Computational Mathematics and Information Technologies. 2018;2(2):133–143.
4. Bobreneva Yu.O, Mazitov A.A., Gubaydullin I.M. Mathematical Modelling of Fluid Flow Processes in the Fracture-Porous Reservoir. Journal of Physics: Conference Series. 2019;1096:012187. https://doi.org/10.1088/1742-6596/1096/1/012187
5. Лисаков С.А., Сыпин Е.В., Зырянова М.Н., Павлов А.Н., Галенко Ю.А. Моделирование процесса нестационарного горения метано-воздушной смеси в угольных шахтах. Вестник научного центра по безопасности работ в угольной промышленности. 2018;(1):40–52. URL: https://tesis.com.ru/infocenter/downloads/flowvision/fv_bti-secna.pdf (дата обращения: 18.09.2023).
6. Жлуктов С.В., Аксенов А.А., Харченко С.А., Москалев И.В., Сушко Г.Б., Шишаева А.С. Моделирование отрывных течений в программном комплексе FlowVision-HPC. Вычислительные методы и программирование. 2010;11(3):234–245. URL: https://num-meth.ru/index.php/journal/article/view/395/402 (дата обращения: 18.09.2023).
7. Коновалов Д.А., Шматов Д.П., Дроздов И.Г., Дахин С.В. Моделирование нестационарного теплообмена в пористых элементах систем тепловой защиты с использованием программного комплекса FlowVision. Вестник Воронежского государственного технического университета. 2011;7(4):143–147. URL: https://cyberleninka.ru/article/n/modelirovanie-nestatsionarnogo-teploobmena-v-poristyh-elementah-sistem-teplovoy-zaschity-s-ispolzovaniem-programmnogo-kompleksa/viewer (дата обращения: 18.09.2023).
8. Мазитов А.А., Бобренёва Ю.О., Губайдуллин И.М., Повещенко Ю.А. Математическое моделирование многофазного потока в однопоровом коллекторе. Препринты ИПМ им. М.В. Келдыша. 2022;62:1–14. https://doi.org/10.20948/prepr-2022-62
9. Федоров А.А., Быков А.Н. Метод двухуровневого распараллеливания прогонки для решения систем алгебраических трехточечных уравнений на гибридных ЭВМ с многоядерными сопроцессорами. В: Труды международной научной конференции «Параллельные вычислительные технологии». Челябинск: Издательский центр ЮУрГУ; 2016. С. 334–346. URL: https://ceur-ws.org/Vol-1576/009.pdf (дата обращения: 18.09.2023).
10. Быков А.Н., Ерофеев А.М., Сизов Е.А. Федоров А.А. Метод распараллеливания прогонки на гибридных ЭВМ. Вычислительные методы и программирование. 2013;14(2):43–47. URL: https://num-meth.ru/index.php/journal/article/view/732 (дата обращения: 18.09.2023).
11. Bobreneva Yu.O., Rahimly P.I., Poveshchenko Yu.A., Podryga V.O., Enikeeva L.V. On One Method of Numerical Modeling of Piezoconductive Processes of a Two-Phase Fluid System in a Fractured-Porous Reservoir. Journal of Physics: Conference Series. 2021;2131:022001. https://doi.org/10.1088/1742-6596/2131/2/022001
12. Бобренёва Ю.О., Мазитов А.А., Губайдуллин И.М. Математическое моделирование процесса массопереноса в коллекторе трещиновато-порового типа. В: Труды V международной конференции и молодёжной школы «Информационные технологии и нанотехнологии». Самара: Новая техника; 2018. С. 1775–1780. URL: http://repo.ssau.ru/handle/Informacionnye-tehnologii-i-nanotehnologii/Matematicheskoe-modelirovanie-processa-massoperenosa-v-kollektore-treshinovatoporovogo-tipa-69518 (дата обращения: 18.09.2023).
13. Губайдуллин И.М., Коледина К.Ф., Сафин Р.Р. Автоматизированная система структурной и параметрической идентификации кинетических моделей химических реакций с участием металлоорганических соединений на основе базы данных кинетических исследований. Системы управления и информационные технологии. 2014;4(58):10–16.
14. Губайдуллин И.М., Коледина К.Ф., Спивак С.И. Структурная и параметрическая идентификация кинетических моделей химических реакций с участием металлоорганических соединений на основе информационно-вычислительной аналитической системы. Химическая промышленность сегодня. 2014;(11):18–27.
15. Grinberg M. Flask Web Development, 2nd ed. Sebastopol, CA: O'Reilly Media, Inc.; 2018. 312 p.
16. Au-Yeung J. Vue.js 3 By Example: Blueprints to Learn Vue Web Development, Full-Stack Development, and Cross-Platform Development Quickly. Birmingham, UK: Packt Publishing; 2021. 320 p.
17. Riggs S., Ciolli G. PostgreSQL 14 Administration Cookbook. Birmingham, UK: Packt Publishing; 2022. 608 p.
18. DeBarros A. Practical SQL, 2nd Edition: A Beginner's Guide to Storytelling with Data. San Francisco, CA: No Starch Press; 2022. 464 p.
Об авторе
А. А. МазитовРоссия
Айнур Асгатович Мазитов, стажер-исследователь лаборатории математической химии
450075, Уфа, пр. Октября, 141
Рецензия
Для цитирования:
Мазитов А.А. Web-приложение для математического моделирования нестационарного течения нефти в пористой среде. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):422-432. https://doi.org/10.23947/2687-1653-2023-23-4-422-432. EDN: RBUFLG
For citation:
Mazitov A.A. Web Application for Mathematical Modeling of Unsteady Oil Flow in Porous Medium. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):422-432. https://doi.org/10.23947/2687-1653-2023-23-4-422-432. EDN: RBUFLG












































