Scroll to:
Modeling of Ultrasonic Flaw Detection Processes in the Task of Searching and Visualizing Internal Defects in Assemblies and Structures
https://doi.org/10.23947/2687-1653-2023-23-4-433-450
EDN: RKAOTZ
Abstract
Introduction. Inverse problems are a specific type of tasks where the consequences of phenomena are studied to identify their causes. They are widely used in scientific studies, specifically, those dealing with large amounts of experimental data. In the presented paper, inverse problems in mechanical engineering and structural diagnostics are considered. These areas require precise methods to identify internal defects in various materials, which can be critical to ensure the safety and efficiency of technical structures. Despite the many flaw detection methods available, there is a need for innovative developments that can provide higher accuracy and efficiency. This study integrates different scientific methods and technologies. It opens up new perspectives in nondestructive testing for the detection of internal defects in various materials and structures. Its objective is to develop and implement nondestructive testing methods based on a neural network device to improve the accuracy of defect identification, as well as to build a neural network model and evaluate its effectiveness for the refinement of ultrasonic visualization of internal defects in solid materials. In this regard, the task to be solved is to create a reliable tool for accurate visualization of sizes, shapes, location and orientation of internal defects in various materials.
Materials and Methods. The technique of determining the geometric parameters of defects in materials through nondestructive testing is used. The approach combining modeling of ultrasonic wave propagation in acoustic medium and artificial neural network technologies is applied. This approach identifies nonlinear relationships between the geometry of defects and the amplitude-frequency and amplitude-time data obtained during signal analysis. Artificial neural networks are a model that can be trained on examples, which provides for an effective solution to problems that are difficult to express in traditional forms. The study uses the finite difference method in the time domain. It is applied to identify and visualize internal defects in materials using ultrasonic nondestructive testing and convolutional generative neural networks.
Results. A convolutional neural network has been developed to visualize internal defects using ultrasonic nondestructive testing techniques. This neural network successfully determines the size of defects, their location, shape and orientation with high accuracy and reliability.
Discussion and Conclusion. The authors highlight the key influence of defect size on the accuracy of ultrasonic imaging in various scenarios. The validation of the model for three different cases of defects with different mechanical parameters has shown that for successful visualization of defects, the wavelength of the ultrasonic pulse must be ten times smaller than the size of the defect. When analyzing the impact of defect size on the accuracy of the neural network, it is found that the visualization error increases for defects of smaller size. It has also been found that the relative speed of sound in materials has a greater effect on the accuracy of the method than the relative density of the material. Based on the results obtained by the authors, it can be argued that the developed methods and technical solutions are of great importance for future research in the field of flaw detection. They have significant potential for scientific and practical applications.
Keywords
For citations:
Sobol B.V., Soloviev A.N., Vasiliev P.V., Lyapin A.A. Modeling of Ultrasonic Flaw Detection Processes in the Task of Searching and Visualizing Internal Defects in Assemblies and Structures. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):433-450. https://doi.org/10.23947/2687-1653-2023-23-4-433-450. EDN: RKAOTZ
Introduction. Inverse problems in the framework of research are those tasks in which the consequences of certain phenomena or processes are analyzed to formulate hypotheses and conclusions about their causality. Inverse problems are found in various areas of research, especially, in cases where there are large amounts of experimental data that allow for identifying the characteristics and features of the process that have given rise to these data. Thus, inverse problems provide scientists with the opportunity to determine the parameters of processes that are not available for direct observation.
Currently, there is a standard technique for solving inverse problems, which is based on the analysis of the system's response to certain input actions. Modern approaches to solving inverse problems divide them into different categories, which facilitates their formalization and adaptation depending on the specific situation.
The technique of solving inverse problems for the diagnosis of mechanical systems is widely used in mechanical engineering. The study of the dynamic response of such systems, including the analysis of transient characteristics, provides for obtaining detailed and accurate information about the state of the system, which, in turn, makes it possible to determine its performance and quality.
In the field of diagnostics of structures and products, there is a growing need to assess the current state of technical systems to identify and eliminate potential hazards that can cause production losses or accidents. Such assessments can only be given by highly qualified experts in reengineering.
Taking into account these aspects, the task was set to develop and further evaluate the possibilities of using a neural network model to solve applied problems of ultrasonic imaging of internal defects in solids for various materials.
There are a large number of scientific papers on this topic. Thus, in [1], the authors focused their attention on the analysis of composite materials containing defects. The presence of defects in such composites can significantly affect their performance characteristics; therefore, it is of particular interest to researchers. To search for defects, each of the studied objects is subjected to ultrasonic scanning, during which vibrations are recorded and their characteristics are determined. The next stage of the analysis is the classification of the obtained characteristics using artificial neural networks. This method provides obtaining an image of the defect area with high accuracy. Such visualization reflects both the nature and extent of the defect in the material under study. It is important to note that this technique provides a clear identification of the damage zone, and the resulting image corresponds to visual observations.
Paper [2] presents the acoustic emission method in the context of the assessment of composite materials, which is a promising area of research. Special attention is paid to the identification of acoustic signals associated with the microstructure of fibers under conditions of high noise levels and using film sensors. Multilayer composites based on reinforced glass fiber, made by various methods, were prepared for research. The experiments included loading composite samples under static conditions, while a PVDF film was installed on their surface. The acoustic signals were carefully recorded and then classified using an artificial neural network. The results of this study indicate the possibility of successfully classifying various destruction mechanisms in composite materials using neural networks.
Study [3] analyzed the collapse incidents that occurred during excavations in rock layers at the Wudongde hydroelectric power plant in China. Its authors presented an improved artificial neural network (ANN) model for predicting the probability and depth of such collapses. However, it should be said that a single parameter is not capable of providing absolute accuracy in predicting the depth of collapses. In this study, an integrated method of intelligent forecasting based on the use of artificial neural networks was proposed. Analytical and statistical studies were carried out for its development, which allowed for determining six key input parameters: coating depth, ratio of main and minor stresses, geological strength index, excavation method, support strength, and rock orientation.
The ANN model was trained using data collected during excavations at the Wudongde hydroelectric power plant, among them there were 45 samples for training and 6 test samples for verification. A genetic algorithm was used to optimize the parameters of the ANN, such as structural characteristics and initial weights. After completing the learning stage, the trained neural network was successfully applied to predict the depth of collapses at several excavation sites. The results of the forecasts showed high compliance with the data obtained during observations at these sites.
Article [4] presents an innovative method for detecting defects in frame structures. It differs significantly from the others and consists of two stages. The first stage focuses on the exact localization of the defect in the bar. To do this, an analysis of the frequencies and waveforms associated with the object under study is used. The results of the analysis of oscillation patterns play a crucial role in solving the problem of the first stage. At the second stage, after successful localization of the defect, an analytical or finite element model of the structure is created, taking into account the identified defects. Using this model, the degree of damage to the frame structure is assessed. The application of this method is illustrated by the example of calculating the defect parameters in an elastic cantilever bar. This calculation is based on experimental observations obtained in a finite element complex. The presented algorithm provides a new tool for more accurate and effective identification of defects in frame structures, which is of great importance for research activities and engineering practice. The results of the modeling carried out within the framework of this study indicate a decrease in the precipitation prediction error. This indicates an improvement in functional approximation and, consequently, excellent learning characteristics of this method, compared to traditional neural networks with sigmoid or other activation functions.
Study [5] proposes an innovative method for diagnosing defects in a manual transmission based on the analysis of vibration signals obtained during experimental tests. The main focus is on the early detection of anomalies in the operation of gears. For effective analysis of vibration signals, data processing focused on the time-frequency domain is used. One of the key methods is the use of continuous wavelet transform, which makes it possible to extract statistically significant characteristics from the signals. To optimize the signal processing, a method of distinguishing features is being introduced, which helps to determine the most important parameters, which, in turn, reduces the computational load and speeds up the analysis process. Genetic algorithms are used to select optimal input features and further reduce the computational complexity of the study. This intelligent approach contributes to improving the efficiency of the data analysis process. The next important step in the research is to evaluate the effectiveness of the proposed method. Advanced technologies of neural back propagation networks were used for this purpose. The attained results and the performance of the classifiers were carefully evaluated on a variety of vibration signals obtained through experimental tests under various operating conditions of mechanical gearboxes.
Studies on nondestructive testing systems and the search for defects in solids often affect the field of modeling the corresponding processes [6]. The primary focus is on solving inverse geometric problems closely related to the theory of elasticity, for their further application in the analysis of a flat rectangular area. The task is to restore the characteristics of circular cavities and cracks.
To effectively solve inverse problems, researchers rely on the obtained information about the first four natural resonant frequencies. These parameters represent an additional dataset that significantly enriches information about the system. The technique used to solve inverse problems is based on minimizing the residual functional. The principle of this technique is to minimize the discrepancy between the measured input data and the values obtained as a result of numerical solution to direct problems. In this case, the parameters of defects in the solid are preset.
Thus, research in the field of nondestructive testing of defects in solids is focused on the development and application of mathematical methods and modeling, which makes it possible to accurately identify and analyze defects hidden inside the material. These studies are applied in the field of safety and quality control of technical systems. The authors explore the possibilities of using neural network technologies in solving inverse problems of mechanics, including the problem of two-dimensional visualization of internal defects. These methods are widely used in medicine, civil engineering, nondestructive testing and other fields.
In [7], a system was proposed for detecting cracks in metal structures and determining their depth based on the analysis of two-dimensional images. The major objective of this work was to create an affordable and convenient control system, a more cost-effective alternative to expensive measuring devices. Within the framework of this study, a specific learning strategy was developed, and several neural network architectures were considered, contributing to a more accurate detection of cracks and assessment of their depth.
The neural network training process included providing the network with characteristics of two-dimensional crack profiles, as well as data on the maximum depth of the crack measured using a laser microscope. This made it possible to create a model that was able to accurately determine the depth of defects in the material. It should be noted that the average error in the operation of this neural network was only about 18% on test samples. This result exceeded critically the results of previous studies, which were based on a variety of learning strategies and analysis techniques. Thus, this study has significantly improved the quality of determining the depth of cracks in metal structures. Its value resides in the development of new learning strategies and a tool for more accurate assessment of the depth of cracks.
Study [8] emphasizes the importance of labeled data containing images with defects. One of the latest proposals in this field is the presented deep transfer learning model designed to extract the characteristic signs of internal defects in X-ray images obtained as a result of inspection of aviation composite materials. This model is a tool for automatic analysis of such images. This tool provides optimizing the defect detection process and increasing the efficiency of nondestructive testing.
In the course of the study, the proposed model efficiency was checked on the problem of detecting defects-inclusions in X-ray images. An analysis of the experimental results has shown that this model is capable of achieving high accuracy (96% according to F1 metric). Such encouraging results indicate the potential of this approach and its ability to produce satisfactory results in defect identification tasks. This opens up new horizons in the field of nondestructive testing and makes it possible to more effectively provide the safety and reliability of composite materials in the aviation industry.
Paper [9] shows a method that offers reconstruction and visualization of internal anomalies in the form of three-dimensional representations. This approach uses an economically and temporarily advantageous technique known as pulsed thermography. In this context, an innovative method is presented that is able to quickly and accurately assess both the depth and thickness of internal anomalies using a one-way inspection. The practicability and efficiency of this method have been successfully demonstrated through studying composite and steel samples containing semi-closed air gaps. The study results confirmed that with the proposed method, the error in estimating the total volume of three-dimensional anomalies is only 10% for composite samples. Thus, this innovative method provides new opportunities for nondestructive testing and visualization of internal defects in various materials and samples, while providing high accuracy and cost-effectiveness.
In [10], the fundamental factors causing failures in the operation of solid rocket engines are considered. One of the key aspects that have a critical impact on the integrity of the engines is the peeling phenomenon at the interface between propellant, insulation and protective layer. Modern methods of diagnostics and assessment of the structural integrity of rocket engines, as a rule, are limited to visual inspection and analysis of their components. This approach has its limitations and requires improvement. In this context, an innovative algorithm is presented, designed to identify surface skin defects that can disrupt the connection between solid fuel and rocket engine insulation. To optimize the operation of the neural network, a number of tests were conducted in which various network parameters were changed. These studies allow for achieving the classification accuracy of 99.08% for the class of serviceable elements, 90.66% — for the class of foreign objects, and 99.48% — for the class associated with defects. The results obtained indicate the high efficiency of the proposed method and its potential for use for the diagnostics of solid-fuel rocket engines.
The research conducted and published by the author in article [11] was aimed at exploring the potential of deep learning methods in the context of electromagnetic inversion. The principle of this approach is to use deep neural networks based on a convolutional architecture to analyze and process data obtained within the framework of this task. An important aspect of this research is learning using extensive sets of synthetic data obtained through three-dimensional modeling. Deep neural networks here are trained on a variety of synthetic data representing information about the distribution of electromagnetic fields inside objects and environments. These data provide valuable information about their properties and compositions, which makes the electromagnetic inversion method more accurate and effective. The efficiency of the proposed method has been successfully demonstrated on various models that are of high practical importance. As an example, when monitoring the electromagnetic field in the area of carbon dioxide accumulation located underground, the inversion method allows for analyzing and controlling this field using a source on the surface.
Previously, the authors of the presented study have already considered tasks combining modern methods of deep machine learning and well-established classical approaches to defect identification [12–14]. In the current work, the emphasis is on a neural network model that effectively performs two-dimensional acoustic visualization of internal anomalies. This project takes the field of nondestructive ultrasonic testing to a new level providing an opportunity to conduct system analysis using numerical experiments.
The objective of the presented research is to develop and evaluate the efficiency of a neural network model for improving ultrasonic visualization of internal defects in solid materials. To identify nonlinear relationships between geometry of defects and ultrasonic control signals, the authors propose to use a technique based on solving the inverse problem of solid mechanics and using artificial neural networks. The basic task in this case is to create a reliable tool for accurate visualization of the sizes, shapes, location and orientation of internal defects in various materials. Numerical experiments approximate the process of ultrasonic probing of samples in which internal defects with various geometric shapes and mechanical characteristics are present. These experiments serve as the initial data for training a neural network and then checking it for proper functioning and accuracy. Thus, it can be argued that this study covers a wide range of scientific methods and technologies, including the development of neural networks, modeling of ultrasonic waves, and analysis of acoustic data.
Materials and Methods. In this work, feed-forward neural networks (FFNN) and convolutional neural networks (CNN) are used. Analytical software is used to determine the most rational network architecture. ANN are trained by the algorithm RProp (stable back propagation) and Adam (adaptive moment estimation method).
RProp algorithm is based on the gradient descent method. In contrast to the standard error back-propagation algorithm, RProp uses only the signs of partial productions to adjust the weight coefficients. The algorithm uses epoch-based learning, and the correction of weights occurs after processing the entire volume of the training sample. The weight values are updated as follows:
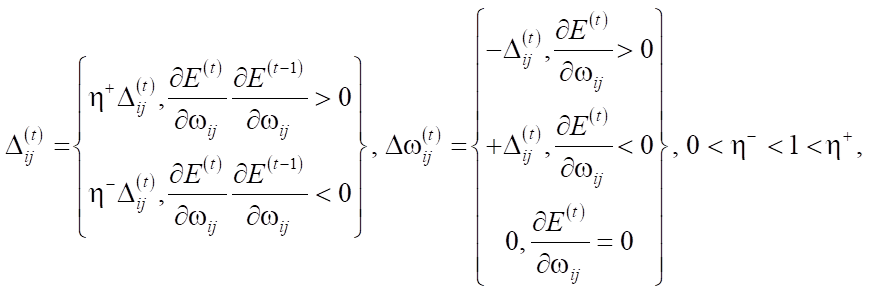
after which the weights are adjusted:
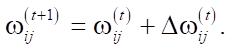
Adam uses grouped averages of both gradients and second moments of gradients. If parameters w(t) are set, and loss function ℒ(t), where t reflects the index of the current iteration, the recalculation of the parameter by the algorithm is specified as follows:
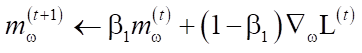
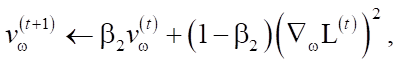
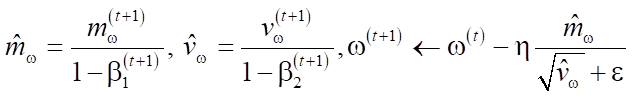
where ε is a small additive used to prevent division by 0, and β1 and β2 are the forgetting factors for gradients and second moments of gradients, respectively, η —basic learning rate. Squaring and square root are calculated elementwise.
Images processed by a convolutional ANN can be represented as a size tensor:
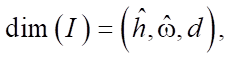
where hˆ and wˆ — dimensions of a 2D image, d — number of image channels. Convolution core K has the following dimensions:
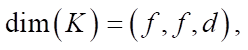
where f — square convolution filter side.
The convolution operation can be defined as follows. The object of the convolution is two-dimensional image I. Convolution core K has dimensions h × w. The result of the convolution is:
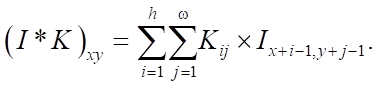
A convolutional layer is built on this operator, which consists of a certain set of kernels 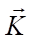 , their corresponding displacements
, their corresponding displacements 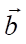 :
:
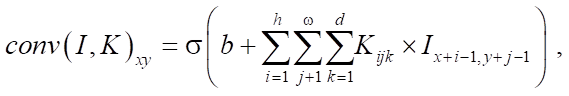
where d — index of the image channel; b — displacement component; σ — activation function of the convolutional layer.
The trained parameters of this layer are filter K and displacement b.
There are several regularization techniques in machine learning. To prevent over-training of complex ANN models with a large number of parameters, Tikhonov regularization method (ridge regression, or L2), also called weight decay in machine learning, is used. Regularization coefficient is λ, which controls the minimization of the norm relative to the minimization of losses on the training dataset. Thus, for each weight w, the summand is added to objective function:
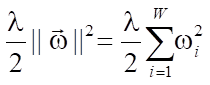 .
.
Within the applied Keras framework, regularization is used for each convolutional layer of the ANN model.
The initial initialization of the weights is carried out by Xavier method. During the initial setting of the weight values, a probability distribution is applied, both uniform and normal with variance
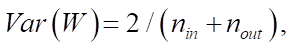
where 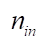 and
and 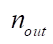 — numbers of neurons in the previous and subsequent layers, respectively.
— numbers of neurons in the previous and subsequent layers, respectively.
The variance of the output values of a linear neuron (without displacements) has the form:
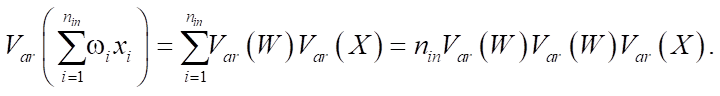
It is assumed that the weights and input values are uncorrelated and have zero expectation. From this, the variance of the probability distribution is obtained, on whose basis the primary initialization of the weights takes place, and which ensures that the variance of the input data is preserved after passing through the layer.
In this paper, the batch normalization layers (Ioffe and Szegedy) are actively applied in most of the developed ANN models using Keras framework. The method normalizes the input data in such a way that their expectation is zero, and the variance is one. In this case, normalization is performed on each layer for each data batch β:
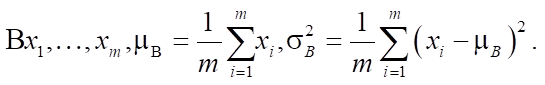
Based on these characteristics, the activation function is transformed:
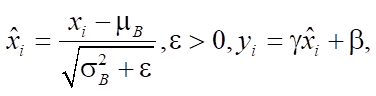
where 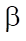 and
and 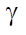 — parameters that can be optimized using the gradient descent method based on the training set.
— parameters that can be optimized using the gradient descent method based on the training set.
Dropout layers are used in ANN models in the task of identifying defects on the road surface, which serve to prevent over-training. When using this regularization tool, the mutual adaptation of neurons at the learning stage of the ANN is prevented. This method blocks (disables) neurons during learning with probability p. Given that
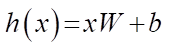 — linear projection of input di-dimensional vector x на dh-dimensional vector x onto a(h) — an activation function, the application of Dropout to this projection at the training stage can be represented as modified activation function
— linear projection of input di-dimensional vector x на dh-dimensional vector x onto a(h) — an activation function, the application of Dropout to this projection at the training stage can be represented as modified activation function
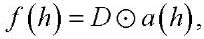
where 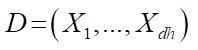 — dh-dimensional vector of random variables
— dh-dimensional vector of random variables 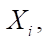 distributed according to Bernoulli's law.
distributed according to Bernoulli's law. 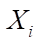 has the following probability distribution:
has the following probability distribution:
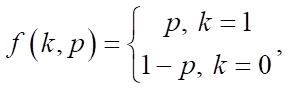
where k — all possible output values.
The application of Dropout to the i-th neuron looks like this:
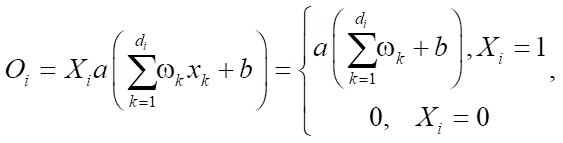
where
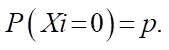
The neural networks described in this paper belong to direct propagation networks. The input information is compiled from data of numerical experiments and, passing through the network, generates output values that are estimated by the metric. Based on these data, the internal values of the weights of the neural network are adjusted. An iterative approach is used, which ensures that a satisfactory level of accuracy of the neural network is obtained.
Defect identification technique. In this paper, we consider a technique for determining the geometric parameters of defects based on data obtained during influencing the object under study. This task is included in the nondestructive testing of properties and parameters of objects oriented to the inverse problem of solid mechanics. To solve this problem, a systematic approach is used with the key role of artificial neural networks. The principle of this approach is to identify nonlinear relationships between various geometric characteristics of defects, such as their size, depth, angle of rotation and type, and the data obtained during the analysis.
Such data can be the amplitude-frequency and amplitude-time characteristics of the signals received in response to the action. This method makes it possible to effectively identify and evaluate the parameters of defects and provides accurate and reliable monitoring of the condition of objects. Artificial neural networks are a computational model used in machine learning, computer science, and other research disciplines. It is based on a large set of connected simple units called artificial neurons, similar to axons in the biological brain. Connections between neurons transmit an activation signal of varying magnitude. If the combined incoming signals are strong enough, the neuron is activated, and the signal travels to other neurons associated with it. Such systems can be trained using pre-prepared examples, rather than explicitly programmed. This method provides a significant advantage in areas where solutions and functions are difficult to express in traditional forms. Neural networks, as well as other machine learning methods, are used to solve various problems that are difficult to resolve through traditional programming based on such rules as computer vision and speech recognition. ANN are most commonly used to model complex connections between inputs and outputs to find patterns in experimental or other data (data mining) [15][16].
A systematic approach to the identification problem under consideration involves dividing the technical task into a number of subtasks, which are solved using existing tools and approaches. The combination of these tasks forms a whole system that addresses production problems comprehensively.
An innovative method for identifying and visualizing internal defects using ultrasonic nondestructive testing (UNDT) and convolutional generative neural network architecture is proposed. The UNDT signal registered on the surface of the control object is passed through a trained neural network. As a result of processing by the network, a high-quality image is generated, which is a heatmap showing the internal defect of the object. To illustrate the efficiency of the proposed method and its prospects in industrial applications, a metal steel strip is selected as the object of research. Defects are assumed to be present inside this strip, which can simulate both cavities and rigid inclusions. The possibility of absence of defects is also taken into account. It should be noted that the characteristics of defects, such as shape, size and orientation, can vary significantly, which presents additional complexity for the visualization task. The procedure of this approach consists in conducting a series of numerical experiments on whose results a deep neural network is trained. To form a training dataset, a systematic change of mechanical parameters, geometric characteristics, as well as the position of internal defects is performed. Special attention is paid to modeling the process of propagation of an acoustic ultrasonic wave inside a material.
This innovative approach to the identification and visualization of internal defects provides an opportunity for more accurate and effective quality control of materials and products in various industries. Its application can contribute to improving the reliability and safety of end products, which is an important aspect in the modern industry. Based on the collected data, the optimal structure of the neural network model is built and trained. As a result, the neural network model can reconstruct the shape, size and position of the defect from the raw ultrasonic signal captured on the surface of the strip. Figure 1 shows a block diagram of the study.
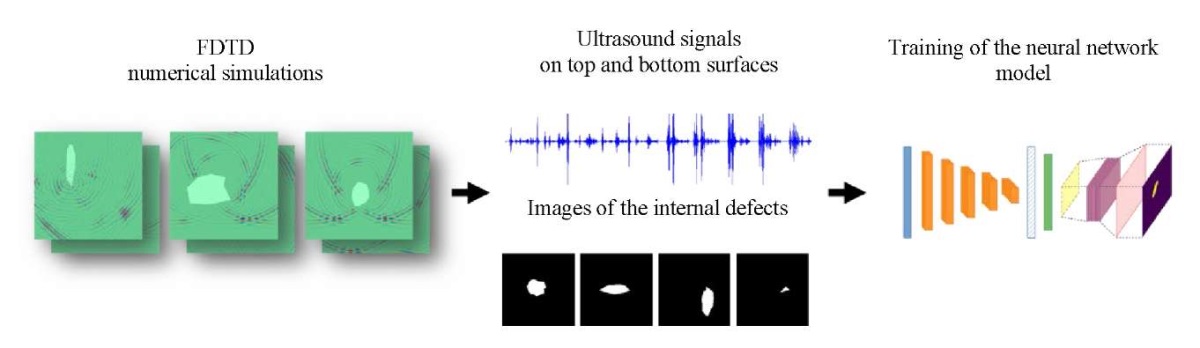
Fig. 1. Scheme for conducting a series of numerical experiments
using the finite difference method (FDTD) in the time domain.
A fragment of a strip in the defect area
and the propagation of an ultrasonic wave (on the left).
Construction of a dataset consisting of ultrasonic signals
and corresponding binary images of the defect (in the center).
Architecture building and neural model training (on the right).
Method of finite differences in the time domain. It was proposed by Kane Yee [17]. Solving differential equations in the context of modeling media with dispersed and nonlinear properties identifies a unique class of methods — grid methods. These methods have found wide application in a variety of fields, ranging from geophysical tasks to tasks in the optical range.
One of the efficient techniques of studying physical phenomena in various media is the finite difference method in the time domain. It is a valuable tool in solving acoustic problems. It can also be successfully applied in elastic media.
The basic equation of this acoustic model in a flat formulation is:
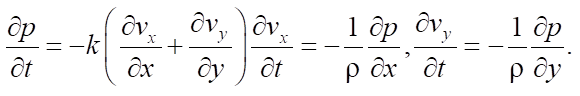
The speed and acoustic pressure of the particles of the simulated object are sampled in the spatial grid. It is possible to analyze the propagation of the sound field over a certain time interval by sequential calculating the values of these parameters. This method offers an opportunity to study various physical processes and phenomena, providing valuable data on the behavior of an environment with diverse characteristics.
Although the finite difference method in the time domain was originally developed to solve acoustic problems, it has a wide range of applications in other fields of physics. In particular, it finds its application in modeling the propagation of sound in various media, such as air or liquid. This versatility of the method makes it an integral part of scientific and engineering research in the field of physics and acoustics.
To verify the efficiency of the selected technique, a reference model was developed in the COMSOL calculation package designed to analyze the propagation of an acoustic ultrasonic wave. Two main numerical methods were used in this study: the finite element method (FEM) and the finite difference method (FDTD). The model is a square-shaped structure made of steel, with an inner hole.
Significant distinctions in the shape of the received signals are explained by different methods of specifying the source of ultrasonic vibrations. In the case of the finite element method, the source points are located on the circumference of the inner hole, while in the finite difference method in the time domain, the source is represented by a point located at the node of the grid.
However, it should be noted that the limited dimensions of the computational grid do not allow modeling the propagation of acoustic waves outside this area. To account for this fact, special boundary conditions are applied, such as absorbing Moore layers or PML (Perfectly Matched Layers). These boundary conditions significantly reduce the reflection of acoustic waves from the boundary of the computational domain, which makes it possible to simulate the passage of an ultrasonic wave into the structure with a high degree of accuracy.
Nondestructive testing model. A steel strip containing a defect is used as a model of nondestructive testing. Its size is 100x15 mm. The absorbing layers are installed on the left and right borders of the strip. The upper and lower parts of the bar are connected to the areas to which the mechanical parameters of the air are set. The defects are represented as convex polygons. The variety of internal defects is specified by changing the number of sides of the polygon, their length, and the distance between the vertices and the center of the defect. The physical parameters of defects vary relative to the thickness of the strip. The position of the defect varies from 0.3 to 0.7, the length of the sides is from 0.1 to 0.5. The input area of the sensor pulse is located on the upper surface of the strip. Vibrations are read on both the upper and lower surfaces. Thus, echo and shadow methods of nondestructive ultrasonic testing are modeled.
In this study, the input signal represented as a fixed set of discrete values depending on the time of the experiment is analyzed. The experimental time is strictly determined taking into account the requirement that the probing pulse, released on the initiating side and directed to the opposite surface of the tested beam, had sufficient time for the traveled distance and return to the source point.
It should be noted that the frequency of the probing pulse used is 10 MHz, which provides high resolution of the experimental system. This makes it possible to study the properties of the bar and its structural characteristics more precisely, based on the analysis of the reflected signal.
Figure 2 shows the scheme of the conducted numerical experiment. The defect is located inside the steel strip. The source of the ultrasonic signal is indicated in red; the signal reading points are indicated in green. The signal is also read at the points of its emission.
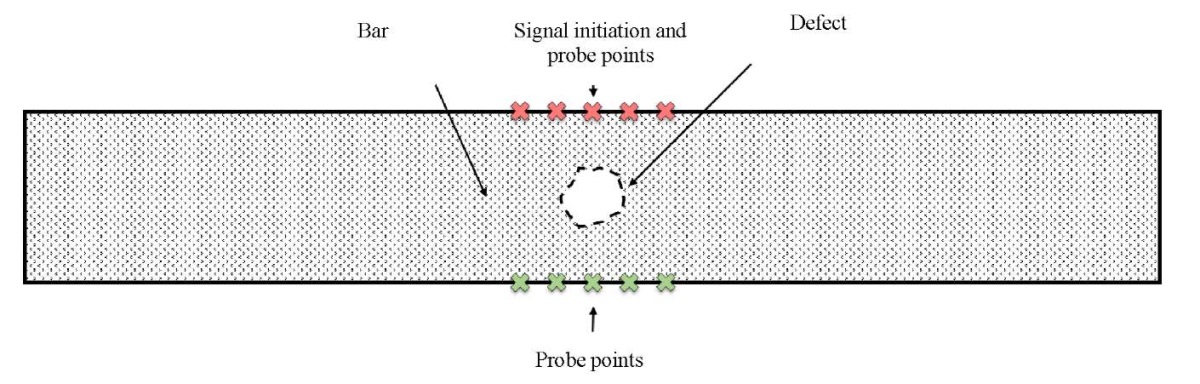
Fig. 2. Numerical experiment scheme
Figure 3 shows the vibrations of ultrasonic signals received at the specified points on the upper surface of the strip (right) and on the lower surface of the strip (left). This simulates the location of sensors on opposite surfaces of the control object. The given model assumes that sensors can move along the strip in search of a defect synchronously.
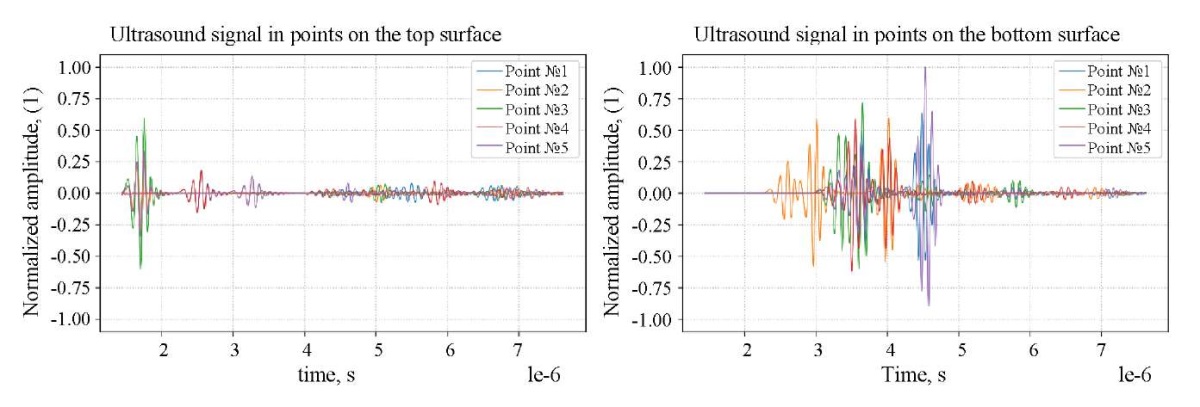
Fig. 3. Ultrasonic signals on the upper and lower surfaces of the strip
obtained as a result of numerical simulation
Neural network model. Convolutional neural networks (CNN) are a special neural network tool for processing discrete data (two-dimensional images, one-dimensional signals) [18]. Currently, it is one of the fastest growing and most promising deep learning tools [19–21].
Convolutional neural networks are effectively used in various fields, including video analysis and time series processing. They provide processing time series as one-dimensional arrays of data and highlighting important features in them using the convolution operation.
To visualize defects in control objects, the model architecture is used, including layers of one-dimensional convolution (Conv1D) and down-sampling layers (MaxPooling), to extract features from ultrasonic signals. The data is then transferred to a fully connected layer for analysis in the context of the defect visualization task. The second part of the network generates images showing the characteristics of defects.
To create the final image of the defect, data from a fully connected layer is processed and fed to a two-dimensional layer. Then, using the trained convolutional layers (Conv2D Transpose), the final image is formed.
Figure 4 shows the architecture of a convolutional neural network with an indication of the size of the input data and the number of convolutional filters for each layer.
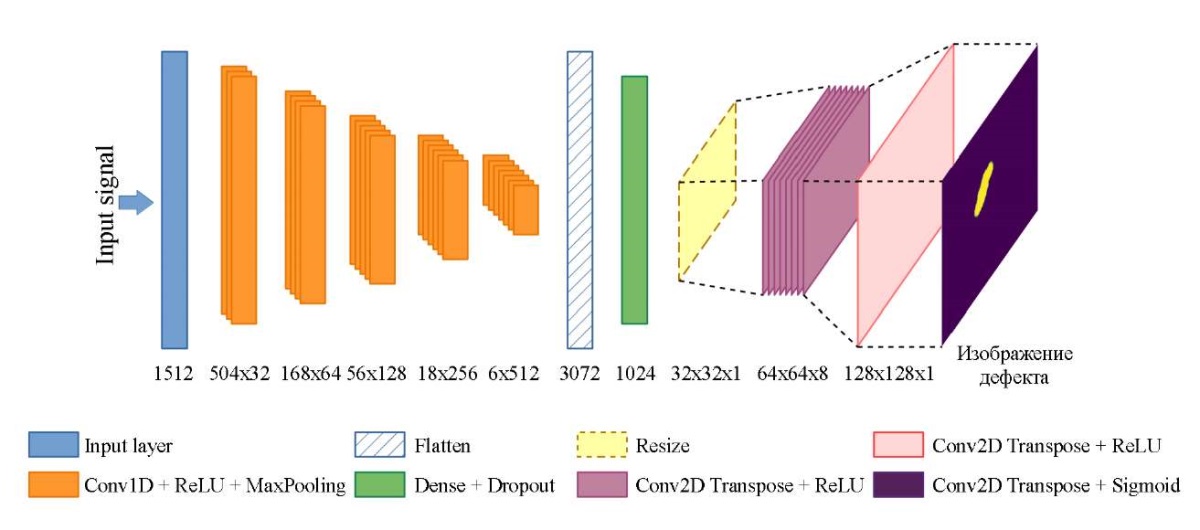
Fig. 4. Convolutional neural network model structure
Model training and validation. Three cases were considered within the framework of a set of numerical experiments. In case A, the defect modeled the cavity, and the parameters of the defect material corresponded to the parameters of the air. In case B, the defect simulated a rigid inclusion, and the defect parameters had the parameters of a material that was more rigid than steel. In this case, it was tungsten carbide. In case C, the mechanical parameters of defects varied, which corresponded to the parameters of gases, liquids, and solid materials.
For cases A and B, a total of 50,000 problems were solved for various geometric parameters of the defect. Of these, 35,000 copies were used for training, 10,000 — for testing, and 5,000 — for certification. In case C, 60,000 tasks were solved with the same percentage of test and validation samples.
In the process of evaluating the performance of the model, the key metrics are the minimum learning error and the reduction of the gap between learning and testing error. The efficiency of the machine learning model is analyzed using various regularization methods, such as Tikhonov regularization, also known as L2 regularization. The initialization of weights, carried out, e.g., by the Xavier method, is a significant stage in the training of neural networks.
One of the tools used to reduce the internal covariance shift and stabilize neural network learning is the batch normalization method. To increase the stability and generalization ability of the model, various regularization techniques are used, such as early stop and Dropout.
It should be noted that data augmentation is not used in this research work due to the extensive amount of training information. There is also no balancing of the dataset, which, however, has its advantages due to the normal distribution of defects in size.
It should be emphasized that neural network training is an optimization task, where selection of the appropriate loss function plays a crucial role. As an example, in computer vision and semantic segmentation tasks, the Jaccard similarity coefficient may turn out to be of great relevance. In this paper, the application of the Jaccard similarity coefficient in the context of the problem of object detection and segmentation is considered, which provides obtaining more accurate and stable results in image analysis:
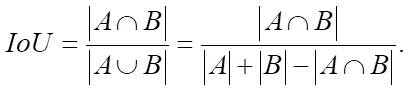
In this context, the loss function is expressed as the inverse of the Jaccard similarity coefficient (1–IoU) and is a metric that evaluates the difference between two instances. The Jaccard metric is known in the data analysis and machine learning as an indicator of the intersection and similarity of sets.
To evaluate the efficiency of a neural network model in the validation process, this metric is used as one of the criteria. It allows for determining the degree of correspondence between the output of the model and the reference data, which is important for analyzing and improving the operation of neural networks in information processing tasks:
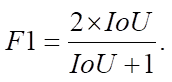
In this study, one of the most common optimization algorithms, called Adam, is applied. Some of the most recognized and widely used libraries, TensorFlow and Keras, are utilized to solve the tasks of machine learning and neural network training. These software products currently act as standard tools for creating and training neural models and include advanced technologies in this field.
To achieve high accuracy of the models, training was conducted over 30 epochs in each of the three cases considered: A, B and C.
The neural network approach for solving inverse problems has already shown itself to good advantage [22–24]. With the deepening in the field of machine learning and the subsequent development of new techniques, cutting-edge tools for data analysis and solving traditional problems in mechanics and flaw detection are opening up. One of the significant scientific achievements in this field is a convolutional neural network created specifically to solve the problem of visualization of internal defects using ultrasonic nondestructive testing methods. A notable feature of this model is its relatively small volume, amounting to 37.2 mln parameters. This fact characterizes high efficiency of the learning process and expands the scope of its application in a variety of related fields. To simulate the propagation of ultrasonic waves more effectively, the finite difference method in the time domain is selected in this study. This choice of method has critically increased the speed of calculations compared to previous approaches used in earlier studies.
Research Results. In this paper, three states of the internal defect were considered. In case A, the defect simulated a cavity, while the parameters of the medium in the defect area corresponded to the parameters of the air. In case B, the defect modeled a rigid inclusion, while the medium parameters had parameters of a more rigid material than the strip material. In this case, it was tungsten carbide. In case C, the mechanical parameters of the defect were varied, which corresponded to the parameters of gases, liquids, and solids.
The results of this study, presented in Figure 5, demonstrate the efficiency of neural networks in analyzing and restoring information about defects. The visualized fragments of the strip in the defect area are displayed on the graph. The real defect is indicated by a solid black line, whereas the shape and position of the defect, predicted by the neural network, are represented by a dotted red line. The analysis of the drawing allows us to argue that the neural network model is able to restore the size of the defect, accurately determine its location, partially reproduce its shape, and even establish orientation. These results validate the potential of neural networks in solving image processing and analysis problems using high accuracy and reliability.
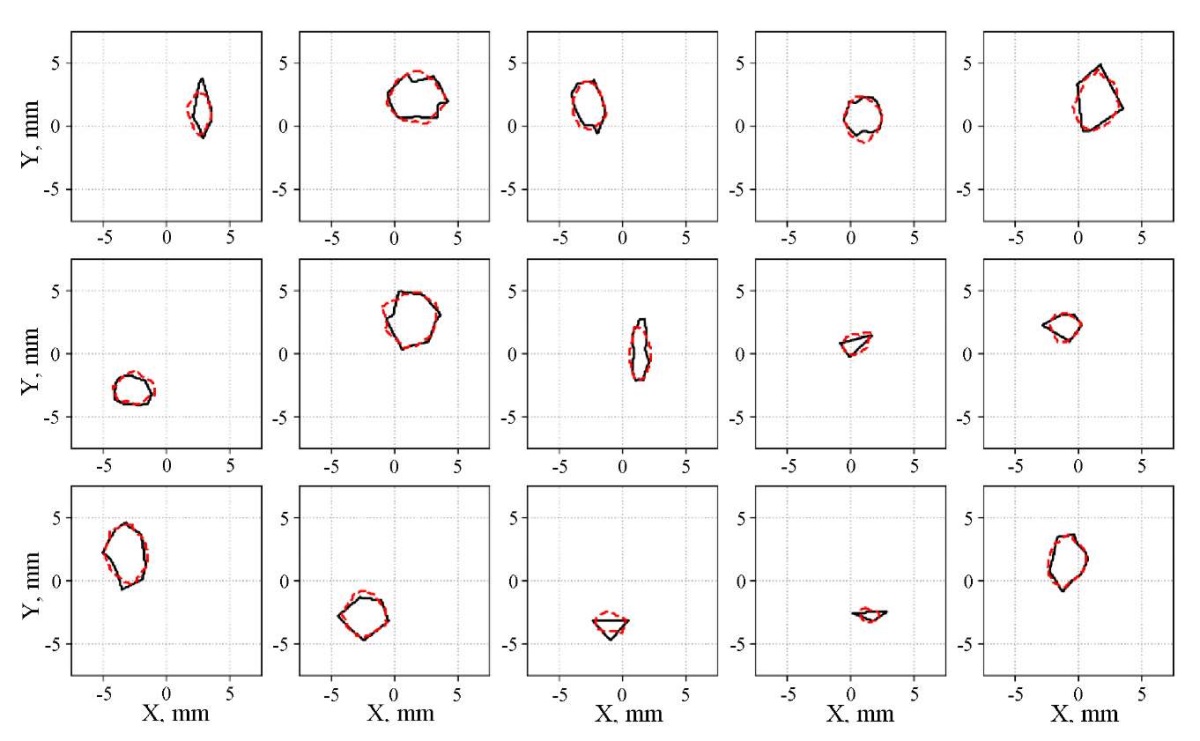
Fig. 5. Defect visualization results.
Real defect is highlighted in black.
Neural network prediction is highlighted in red.
Validation was performed for each of the cases. Metric F1 was used to evaluate the overall efficiency of the model. In general, the accuracy of the proposed method was at a high level. Average value F1 for the entire validation set was 92% for case A, 90% — for case B, and 85% — for case C.
Figure 6 shows the dependence of visualization accuracy of the defect on its size. The defect size is the maximum distance between the vertices of the polygon simulating the defect. The data obtained show that for successful visualization of defects, the wavelength of the ultrasonic pulse must be ten times smaller than the size of the defect. The figure also shows the effect of an unbalanced data set on the neural network accuracy. For defects of the largest size, the visualization error increases.
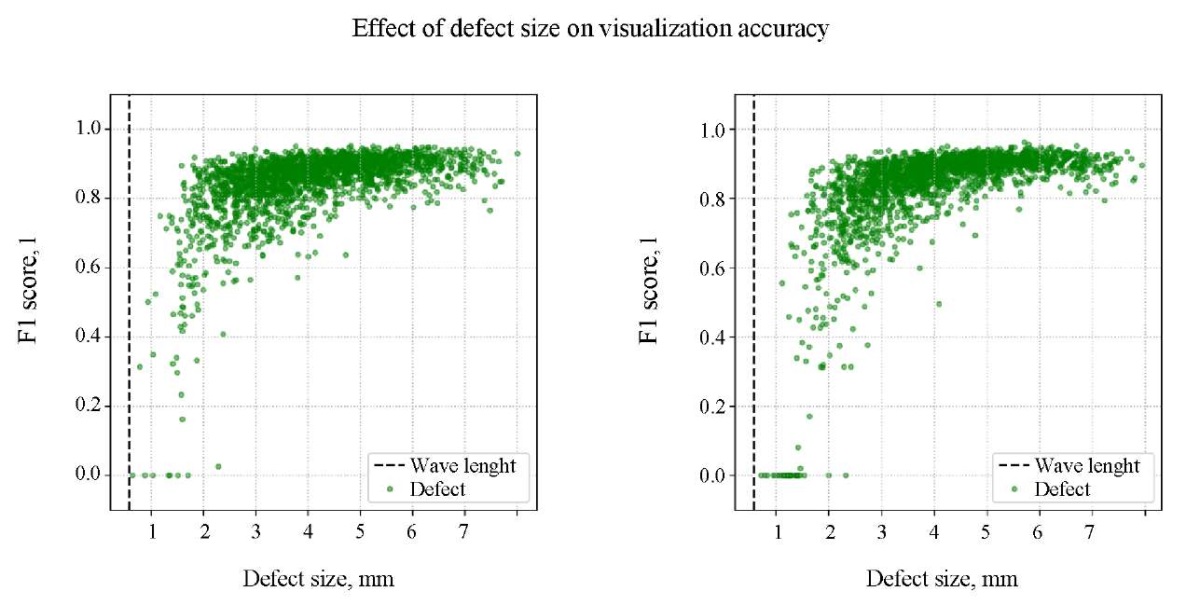
Fig. 6. Dependence of visualization accuracy of defects
on their size for cases A (left) and B (right).
Black dashed line shows the wavelength of the probing ultrasonic pulse
The authors also analyzed the effect of the mechanical parameters of the defect on their visualization accuracy. For each neural network from cases A, B, and C, validation was performed on a dataset with different mechanical parameters of defects. This study shows how well-trained neural network models are able to visualize various types of defects, including defects that are absent in the training sets. For ease of perception, the parameters of the material density and the speed of sound in the materials are presented as relative:
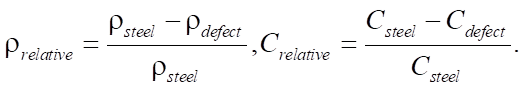
Figure 7 shows how accurately neural network models A, B, and C visualize defects for a wide range of parameters. In the case where the neural network is trained only on dataset A, when the defect models a cavity, acceptable accuracy is achieved only for defects with 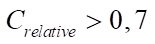 . In case B, when the defect simulates a hard inclusion, the accuracy of the neural network operation deteriorates significantly when value
. In case B, when the defect simulates a hard inclusion, the accuracy of the neural network operation deteriorates significantly when value 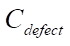 от заданного в эксперименте. deviates from the one specified in the experiment. In case C, when the neural network is trained on a dataset with different defect parameters, the results of the work are stable over the entire range of parameter changes. The exception is defects with value
от заданного в эксперименте. deviates from the one specified in the experiment. In case C, when the neural network is trained on a dataset with different defect parameters, the results of the work are stable over the entire range of parameter changes. The exception is defects with value 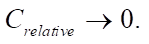 In these cases, the sound speeds in the strip material and the defect material are very close to each other. It can also be concluded that the accuracy of the proposed method is more influenced by a change in parameter C, than
In these cases, the sound speeds in the strip material and the defect material are very close to each other. It can also be concluded that the accuracy of the proposed method is more influenced by a change in parameter C, than 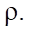 Thus, the limits of the application of various neural network models for the identification of defects with different mechanical parameters are demonstrated.
Thus, the limits of the application of various neural network models for the identification of defects with different mechanical parameters are demonstrated.
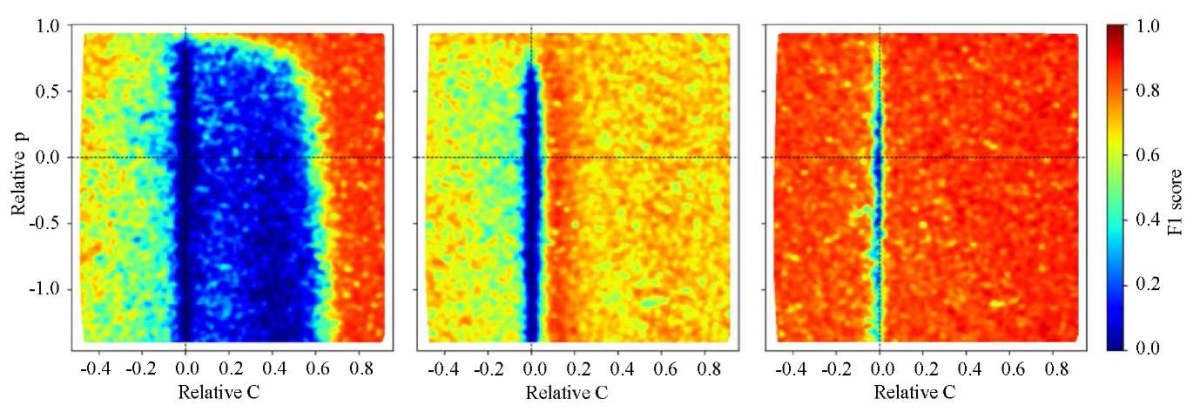
Fig. 7. Effect of defect parameters on the accuracy of neural networks.
Neural network A on the left,
neural network B in the center,
neural network C on the right.
Thus, it can be concluded that the neural network model developed by the authors represents a breakthrough in the field of nondestructive control, providing effective tools for the visualization of internal defects and creating new prospects for application in industry and scientific research [24–25].
Discussion and Conclusion. The results obtained present a new perspective on the field of nondestructive testing and its potential in detecting internal defects in various materials and structures. In the presented study, an innovative method based on the use of convolutional neural networks is proposed for the express diagnosis of defects in the structure of materials. A key aspect of this research is the demonstrated potential efficiency of the use of convolutional neural networks to improve the quality of ultrasound imaging. The authors have developed a model designed for nondestructive testing, and generated appropriate datasets used to train artificial neural networks. This convolutional neural network model is able to accurately determine not only the shape, but also the position and orientation of internal defects in a solid material. The experimental data obtained demonstrate the informative value of the ultrasonic signal, as well as its ability to accurately convey real characteristics of internal defects.
The authors analyzed several types of defects, each of which was given special attention. In the first case, the defect was classified as A and modeled as a cavity, in the second case — as B and represented a rigid inclusion, in the third — as C, with different mechanical parameters of the defect. In all scenarios of the study, a critical effect of the defect size on the ultrasound imaging accuracy was identified. In addition, the results obtained clearly confirm that the selection of the frequency of the probing signal is of crucial importance and should be optimized so that the wavelength is significantly smaller than the size of internal defects.
After conducting a system validation of convolutional neural networks in the context of each of the above-mentioned types of defects (A, B, and C), a range of values of the mechanical parameters of the defect was established for different mechanical characteristics of the defects, within which the proposed method did not provide sufficiently high-quality visualization.
In conclusion, it should be noted that the methods and technical solutions developed in the course of this study are of great importance for further research in the field of flaw detection and solving inverse problems in a wide context of scientific and practical applications.
References
1. Samanta S, Mandal A, Thingujam JS. Application of ANN in Identifying Defects in Impacted Composite. Procedia Materials Science. 2014;6:926–930. https://doi.org/10.1016/j.mspro.2014.07.162
2. Bar HN, Bhat MR, Murthy CRL. Identification of Failure Modes in GFRP Using PVDF Sensors: ANN Approach. Composite Structures. 2004;65(2):231–237. https://doi.org/10.1016/j.compstruct.2003.10.019
3. Dong-Fang Chen, Xia-Ting Feng, Ding-Ping Xu, Quan Jiang, Cheng-Xiang Yang, Pin-Pin Yao. Use of an Improved ANN Model to Predict Collapse Depth of Thin and Extremely Thin Layered Rock Strata during Tunneling. Tunnelling and Underground Space Technology. 2016;51:372–386. https://doi.org/10.1016/j.tust.2015.09.010.
4. Cherpakov AV, Akopyan VA, Soloviev AN. Algorithm for Multi-parameter Identification of Defects in Frame Structures. Technical Acoustics. 2013;13:1–11. (In Russ.)
5. Rajeswari C, Sathiyabhama B, Devendiran S, Manivannan K. A Gear Fault Identification Using Wavelet Transform, Rough Set Based GA, ANN and C4.5 Algorithm. Procedia Engineering. 2014;97:1831–1841. https://doi.org/10.1016/j.proeng.2014.12.337
6. Solovyev AN, Shevtsov MYu. Reconstruction of Defects in Elastic Bodies by Combination of Genetic Algorithm and Finite Element Method. Vestnik of DSTU. 2016;16(2):5–12. https://doi.org/10.12737/19686 (In Russ.)
7. Yasser S Mohamed, Hesham M Shehata, Mohamed Abdellatif, Taher H Awad. Steel Crack Depth Estimation Based on 2D Images Using Artificial Neural Networks. Alexandria Engineering Journal. 2019;58(4):1167-1174. https://doi.org/10.1016/j.aej.2019.10.001
8. Yanfeng Gong, Hongliang Shao, Jun Luo, Zhixue Li. A Deep Transfer Learning Model for Inclusion Defect Detection of Aeronautics Composite Materials. Composite Structures. 2020;252:112681. https://doi.org/10.1016/j.compstruct.2020.112681
9. Adisorn Sirikham, Yifan Zhao, Haochen Liu, Yigeng Xu, Stewart Williams, Jörn Mehnen. Three-Dimensional Subsurface Defect Shape Reconstruction and Visualisation by Pulsed Thermography. Infrared Physics & Technology. 2020;104:103151. https://doi.org/10.1016/j.infrared.2019.103151
10. Luiz Felipe Simões Hoffmann, Francisco Carlos Parquet Bizarria, José Walter Parquet Bizarria. Detection of Liner Surface Defects in Solid Rocket Motors Using Multilayer Perceptron Neural Networks. Polymer Testing. 2020;88:106559. https://doi.org/10.1016/j.polymertesting.2020.10655
11. Vladimir Puzyrev. Deep Learning Electromagnetic Inversion with Convolutional Neural Networks. Geophysical Journal International. 2019;218(2):817–832. https://doi.org/10.1093/gji/ggz204
12. Soloviev AN, Sobol BV, Vasiliev PV. Ultrasonic and Magnetic Flow Inspection Methods of Identification of Cracks in the Pipe Coupled with Artificial Neural Networks. In book: Parinov I, Chang SH, Jani M. (eds). Advanced Materials. Springer Proceedings in Physics. Cham: Springer; 2017. P. 381–395. https://doi.org/10.1007/978-3-319-56062-5_32
13. Soloviev A, Sobol B, Vasiliev P, Senichev A. Generative Artificial Neural Network Model for Visualization of Internal Defects of Structural Elements. In book: Parinov I, Chang SH, Long B. (eds). Advanced Materials. Springer Proceedings in Materials. Cham: Springer; 2020. P. 587–595. https://doi.org/10.1007/978-3-030-45120-2_48
14. Sobol BV, Soloviev AN, Rashidova EV, Vasiliev PV. Identification of Crack-like Defect and Investigation of Stress Concentration in Coated Bar. PNRPU Mechanics Bulletin. 2019;(4):165–174. https://doi.org/10.15593/perm.mech/2019.4.16
15. Fang X, Luo X, Jiong Tang. Structural Damage Detection Using Neural Network with Learning Rate Improvement. Computers and Structures. 2005;83(25–26):2150–2160. https://doi.org/10.1016/j.compstruc.2005.02.029
16. Soloviev A, Sobol B, Vasiliev P. Identification of Defects in Pavement Images Using Deep Convolutional Neural Networks. In book: Parinov I, Chang SH, Kim YH. (eds). Advanced Materials. Springer Proceedings in Physics. Cham: Springer; 2019. P. 615–626. https://doi.org/10.1007/978-3-030-19894-7_46
17. Kane Yee. Numerical Solution of Initial Boundary Value Problems Involving Maxwell's Equations in Isotropic Media. IEEE Transactions on Antennas and Propagation. 1966;14(3):302–307. https://doi.org/10.1109/TAP.1966.1138693
18. LeCun Y, Boser B, Denker JS, Henderson D, Howard RE, Hubbard W, et al. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Computation. 1989;1(4):541–551. https://doi.org/10.1162/neco.1989.1.4.541
19. Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge, MA: MIT Press; 2016. 777 p.
20. Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks. Communications of the ACM. 2017;60(6):1097–1105. http://dx.doi.org/10.1145/3065386
21. Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. Deep Residual Learning for Image Recognition. In: Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). New York City, UA: IEEE; 2016. P. 770–778 https://doi.org/10.1109/CVPR.2016.90
22. De Angelo M, Spagnuolo M, D’Annibale F, Pfaff A, Hosche K, Misra A, et al. The Macroscopic Behavior of Pantographic Sheets Depends Mainly on Their Microstructure: Experimental Evidence and Qualitative Analysis of Damage in Metallic Specimens. Continuum Mechanics and Thermodynamics. 2019;31:1181–1203. https://doi.org/10.1007/s00161-019-00757-3
23. Nagatani Y, Okumura S, Wu S, Matsuda T. Two-dimensional Ultrasound Imaging Technique Based on Neural Network Using Acoustic Simulation. arXiv preprint. arXiv:2004.08775. 2020. https://doi.org/10.48550/arXiv.2004.08775
24. Solov’ev AN, Sobol’ BV, Vasil’ev PV. Ultrasonic Location of Inner Crack Defects in a Compound Elastic Cylinder Using an Artificial Neural-Network Apparatus. Russian Journal of Nondestructive Testing. 2016;52(3):119–124. https://doi.org/10.1134/S1061830916030098
25. Soloviev AN, Sobol BV, Vasiliev PV, Senichev AV, Novikova AI. Identification of Defects in a Coating Wedge Based on Ultrasonic Non-destructive Testing Methods and Convolutional Neural Networks. PNRPU Mechanics Bulletin. 2023;(1):111–124. https://doi.org/10.15593/perm.mech/2023.1.11
About the Authors
B. V. SobolRussian Federation
Boris V. Sobol, Dr.Sci. (Eng.), Professor, Head of the Information Technologies Department, Scopus ID
1, Gagarin sq., Rostov-on-Don, 344003
A. N. Soloviev
Russian Federation
Arkadiy N. Soloviev, Dr.Sci. (Phys.-Math.), Professor, ResearcherID, ScopusID
8, Uchebnyy Ln, Simferopol, 295015
P. V. Vasiliev
Russian Federation
Pavel V. Vasiliev, Senior Lecturer of the Information Technologies Department, Scopus ID
1, Gagarin sq., Rostov-on-Don, 344003
A. A. Lyapin
Russian Federation
Alexandr A. Lyapin, Dr.Sci. (Phys.-Math.), Professor, Head of the Information Systems in Civil Engineering Department, ScopusID
1, Gagarin sq., Rostov-on-Don, 344003
Review
For citations:
Sobol B.V., Soloviev A.N., Vasiliev P.V., Lyapin A.A. Modeling of Ultrasonic Flaw Detection Processes in the Task of Searching and Visualizing Internal Defects in Assemblies and Structures. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):433-450. https://doi.org/10.23947/2687-1653-2023-23-4-433-450. EDN: RKAOTZ












































