Scroll to:
Coupled Axisymmetric Thermoelectroelasticity Problem for a Round Rigidly Fixed Plate
https://doi.org/10.23947/2687-1653-2024-24-1-23-35
EDN: DUOERK
Abstract
Introduction. To describe the operation of temperature piezoceramic structures, the theory of thermoelectroelasticity is used, in which the mathematical model is formulated as a system of nonself-adjoint differential equations. The complexity of its integration in general leads to the study of problems in an unrelated formulation. This does not allow us to evaluate the effect of electroelastic fields on temperature. The literature does not present studies on these problems in a three-dimensional coupled formulation in which closed solutions would be constructed. At the same time, conducting such studies allows us to understand the interaction picture of mechanical, thermal and electric fields in a structure. To solve this problem, a new closed solution of a coupled problem for a piezoceramic round rigidly fixed plate has been constructed in this research. It provides for qualitative assessment of the cross impact of thermoelectroelastic fields in this electroelastic system.
Materials and Methods. The object of the study is a piezoceramic plate. The case of unsteady temperature change on its upper front surface is considered, taking into account the convection heat exchange of the lower plane with the environment (boundary conditions of the 1st and 3rd kind). The electric field induced as a result of the thermal strain generation is fixed by connecting the electrodated surfaces to the measuring device. The thermoelectroelasticity problem includes the equations of equilibrium, electrostatics, and the unsteady hyperbolic heat equation. It is solved by the generalized method of finite biorthogonal transformation, which makes it possible to construct a closed solution of a nonself-adjoint system of equations.
Results. A new closed solution of the coupled axisymmetric thermoelectroelasticity problem for a round plate made of piezoceramic material was constructed.
Discussion and Conclusion. The obtained solution to the initial boundary value problem made it possible to determine the temperature, electric and elastic fields induced in a piezoceramic element under arbitrary temperature axisymmetric external action. The calculations performed provided determining the dimensions of solid electrodes, which made it possible to increase the functionality of piezoceramic transducers. Numerical analysis of the results enabled us to identify new connections between the nature of external temperature action, the deformation process, and the value of the electric field in a piezoceramic structure. This can validate a proper program of experiments under their designing and significantly reduce the volume of field studies.
Keywords
For citations:
Shlyakhin D.A., Savinova E.V. Coupled Axisymmetric Thermoelectroelasticity Problem for a Round Rigidly Fixed Plate. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):23-35. https://doi.org/10.23947/2687-1653-2024-24-1-23-35. EDN: DUOERK
Introduction. Various mathematical models are used to improve the functionality of piezoceramic sensors [1–3] based on the interdependence of thermoelectroelastic fields. To more accurately account for the effect of coupling of these fields, it is needed to construct closed solutions. Some simplifications are used to solve systems of initial nonself-adjoint differential equations. Thus, the problems can be considered in an uncoupled formulation, or the problems consider and analyze elements that have a degenerate geometry. An uncoupled stationary problem for a long electroelastic cylinder is considered in [4][5], and article [6] is devoted to the analysis of thermal stresses in a hollow sphere. Papers [7][8] are related to the determination of the temperature field in a piezoceramic shell and a round plate in solving uncoupled problems. Coupled dynamic problems for a homogeneous piezoceramic layer, as well as dynamic problems in a coupled formulation for a gradient–inhomogeneous piezoceramic layer, were considered in [9][10]. In [11][12], fields in an unbounded medium were analyzed. In [13][14], a long hollow cylinder was considered, and thermoelectroelastic fields were analyzed.
Currently, the literature does not describe the results of constructing closed solutions to the mentioned non-stationary problems in a three-dimensional coupled formulation. Therefore, in this paper, we consider a round plate made of piezoceramic composition and having a rigid fixation, for which a new closed solution to the problem of thermoelectroelasticity is obtained. The use of a limit on the rate of temperature change on its front surface [10] makes it possible not to include the inertial characteristics of the system under study and apply the equilibrium equations in the calculated ratios.
Materials and Methods. In the process of solving, a generalized finite biorthogonal transformation was used, which provided the reduction of the dimension of a nonself-adjoint system of equations and the construction of a closed solution through significant simplifying research in the image space.
Mathematical model. Consider certain area  which is occupied by a piezoceramic solid circular plate in the cylindrical coordinate system
which is occupied by a piezoceramic solid circular plate in the cylindrical coordinate system  Arbitrary temperature boundary conditions can be used for the problem under study. However, for the certainty of the solution, on the upper
Arbitrary temperature boundary conditions can be used for the problem under study. However, for the certainty of the solution, on the upper  front surface, the temperature change
front surface, the temperature change  at a given ambient temperature
at a given ambient temperature  on the lower
on the lower  plane (
plane ( — time) is considered. The cylindrical thermally insulated surface is rigidly fixed: there is no radial component of the displacement vector and the angle of rotation, and its lower part is fixed in the vertical plane. The lower plane of the round plate in question is grounded. The front electrodated planes of the plate are connected to the measuring device. The design scheme of the plate is shown in Figure 1.
— time) is considered. The cylindrical thermally insulated surface is rigidly fixed: there is no radial component of the displacement vector and the angle of rotation, and its lower part is fixed in the vertical plane. The lower plane of the round plate in question is grounded. The front electrodated planes of the plate are connected to the measuring device. The design scheme of the plate is shown in Figure 1.

Fig. 1. Plate design diagram
The mathematical formulation of the problem under consideration in a dimensionless form for an axially polarized piezoceramic material with a hexagonal crystal lattice of 6 mm composition has the form:


where

 — temperature increment in dimensional form;
— temperature increment in dimensional form; 
 — components of the displacement vector, electric field potential; σzz (r, z, t), σrz (r, z, t) — components of the mechanical stress tensor; Dr (r, z, t) — radial component of the electric field induction vector; Λ, k, αt — coefficients of thermal conductivity, volumetric heat capacity, and linear thermal expansion;
— components of the displacement vector, electric field potential; σzz (r, z, t), σrz (r, z, t) — components of the mechanical stress tensor; Dr (r, z, t) — radial component of the electric field induction vector; Λ, k, αt — coefficients of thermal conductivity, volumetric heat capacity, and linear thermal expansion;  — electric potential induced on the upper front surface; γii, gii — components of the tensor of temperature stresses and pyroelectric coefficients (i = 1,3, γii = Сiiαt); e15, e31, e33, ε11, ε33 — piezoelectric modules and permittivity coefficients; Θ* = T – T; T, T0 — current temperature and temperature of the original state of the body; βrel — relaxation time; α — heat transfer coefficient,
— electric potential induced on the upper front surface; γii, gii — components of the tensor of temperature stresses and pyroelectric coefficients (i = 1,3, γii = Сiiαt); e15, e31, e33, ε11, ε33 — piezoelectric modules and permittivity coefficients; Θ* = T – T; T, T0 — current temperature and temperature of the original state of the body; βrel — relaxation time; α — heat transfer coefficient,  — known rate of temperature change
— known rate of temperature change  ;
;
To determine the potential of the electric field induced under deformation on the upper front surface  in the case of connecting electrodes to a measuring device with a large input resistance, an additional boundary condition is used:
in the case of connecting electrodes to a measuring device with a large input resistance, an additional boundary condition is used:
 (5)
(5)
where Dz (r, z, t) — axial component of the induction vector; S — surface area.
Construction of a general solution. To fulfill the condition of fixing the cylindrical surface of the plate in the vertical plane, new functions w (r, z, t), W1(t) are introduced:
 (6)
(6)
this makes it possible to form a boundary value problem with respect to functions U, w, ϕ, Θ, which is investigated by the method of finite Fourier-Bessel transformations:

where jn — positive zeros of the function  — Bessel functions.
— Bessel functions.
It should be noted here that to satisfy the last boundary condition (2), it is necessary to assume that the original temperature of plate T0 is equal to the ambient temperature , and the temperature increment function on the upper front surface ω1(1, t) = 0. These assumptions, without much error, allow assuming that on the cylindrical surface of the plate, Θ(1, z, t) = 0.
As a result of using the transformation algorithm in the image area, the following initial boundary value problem is obtained:

where 
At the next stage of the solution, the introduction of functions UH(n, z, t), WH(n, z, t), φH(n, z, t), QH(n, z, t) using the following relations:
 (12)
(12)
allows the reduction of conditions (9) to homogeneous.
Here, 
 — twice differentiable functions.
— twice differentiable functions.
Substitution (12) in (9) – (11) when the conditions are satisfied:
 (13)
(13)
provides the formulation of the following task:
 (14)
(14)

where

Using the biorthogonal finite transformation (CMD) [15], we obtain a solution to problem (14) – (16). CMD with unknown components of vector functions of transformations is introduced on the segment [0, h] K1(λin, z)…K4(λin, z), N1(μin, z)…N1(μin, z):
 (17)
(17)
where λin, μin — the eigenvalues of the corresponding problems with respect to the components of the vector functions of the CMD (k = 1…4).
In the course of transformations, we obtain a task for determining transformants G(n, λin, t):

whose solution has the following form:
 (20)
(20)
in addition, two homogeneous problems with respect to components K1(λin, z)…K4(λin, z),
 (21)
(21)
 (22)
(22)
and N1(μin, z)…N4(μin, z):

where

m1in, m2in — roots of the characteristic equation: 
Constructed homogeneous problem (23), (24) with respect to functions N1(μin, z)…N4(μin, z) is invariant to the initial calculated relations (14), (15).
Systems (21), (23) are reduced to the following equations with respect to K2(λin, z), N2(μin, z):
 (25)
(25)
In the paper, coefficients are not given due to the limitation of its volume.
In equation (25), the left part is decomposed into commutative factors, presented below:
 (26)
(26)
where  — real positive roots of the following characteristic equations:
— real positive roots of the following characteristic equations:

When examining a round rigidly fixed piezoceramic plate, the general integral of equations (26) has the following form:
 (27)
(27)
where 
It should be noted here that the condition of the actual positive values of coefficients B1in, S1in, A1in…A4in is fulfilled for most structures made of piezoceramic material. Otherwise, the formula structure (26), (27) simply changes.
Considering that the connections were previously obtained as a result of reducing (21), (23) to (25), we get expressions for functions K1(λin, z), K3(λin, z), K4(λin, z), N1(λin, z), N3(λin, z), N4(λin, z).
Substituting K1(λin, z)…K4(λin, z), N1(μin, z)…N1(μin, z) in conditions (22), (24) provides determining constants D1in…D8in, E1in …E8in and eigenvalues λin, μin.
The final expressions of functions U (n, z, t), W (n, z, t), ϕ (n, z, t), Θ (n, z, t) are obtained by applying the inversion formulas (17), (8). Then, taking into account (6), (12), we have:
 (28)
(28)
Functions f1(z)… f12(z) are calculated from the simplification condition F1… F4 when conditions (13) are satisfied:

Function W1(t) is determined from condition W(1, h, t) = 0:

For a qualitative assessment of the induced electric pulse on its upper front surface, it is required to form two electrodes with a radius of separation R and connect them to a measuring device. In this case, potential ϕ0(r, t), induced on two equipotential surfaces is represented as:
 (29)
(29)
where H(…) — the Heaviside step function.
Substituting (29) into (5) makes it possible to define expressions for determining potentials ϕ0(t), ϕ02(t):
 (30)
(30)
As a result of solution (30), functions ϕ0(t), ϕ02(t) are defined as follows:

where

In this case, the potential difference V(t) is determined by the equality:
 (31)
(31)
Research Results. Numerical results are presented for a plate made of piezoceramics of the composition
PZT–4 [4][11][16]:
{C11, C12, C13, C33, C55} = {13.9, 7.78, 7.3, 11.5, 2.26}×1010 Pa, {ε11, ε33} = {6.46, 5.62} × 10–9 F/m,
{e15, e31, e33} = {12.7, –5.2, 15.1} C/m2, Λ = 1,6 W/(m∙K), αt = 0.4×10–5 K–1,
k = 3×106 J/ (m3∙K), g11 = g33 = –0.6×10–4 C/(m2∙K), βrel = 10–4 s, α = 5.6 W/(m2∙K).
The following case of temperature change  is investigated:
is investigated:

where  — maximum temperature value and the corresponding time
— maximum temperature value and the corresponding time 
Figure 2 shows graphs reflecting at various points in time  the change in temperature Θ*(0, z, t) in the thickness of the plate (b = 14×10–3 m, h* = 1×10–3 m).
the change in temperature Θ*(0, z, t) in the thickness of the plate (b = 14×10–3 m, h* = 1×10–3 m).
According to the calculation result, it is observed that due to the high coefficient of thermal conductivity and the small thickness of the piezoceramic plate, the steady-state temperature regime is formed quite quickly when it reaches Θ*(0, z, t) on the lower front surface (z = h) 78°C (Fig. 2).
Figure 3 shows the change  in time
in time  taking into account (represented by a solid line) and without account for (represented by dotted line, β = 0) the relaxation of the heat flux (b = 14×10–5 m, h* = 1×10–5 m). It should be emphasized that the application of the hyperbolic Lord-Shulman heat conduction equation is needed only in the study of a piezoceramic micro-dimensional structure with a very rapid change
taking into account (represented by a solid line) and without account for (represented by dotted line, β = 0) the relaxation of the heat flux (b = 14×10–5 m, h* = 1×10–5 m). It should be emphasized that the application of the hyperbolic Lord-Shulman heat conduction equation is needed only in the study of a piezoceramic micro-dimensional structure with a very rapid change 
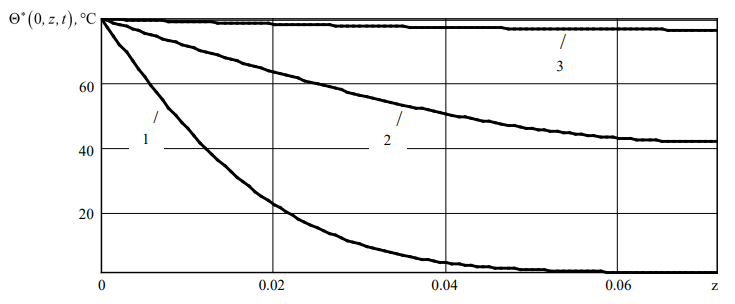
Fig. 2. Diagrams 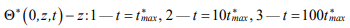
The numerical results of determining function Θ*(r, z, t) show that when conducting a study of a structure made of piezoceramic material, it is possible to neglect the impact of the rate of change of body volume and tension on the temperature field, i.e., to use only the equation of thermal conductivity in calculations.
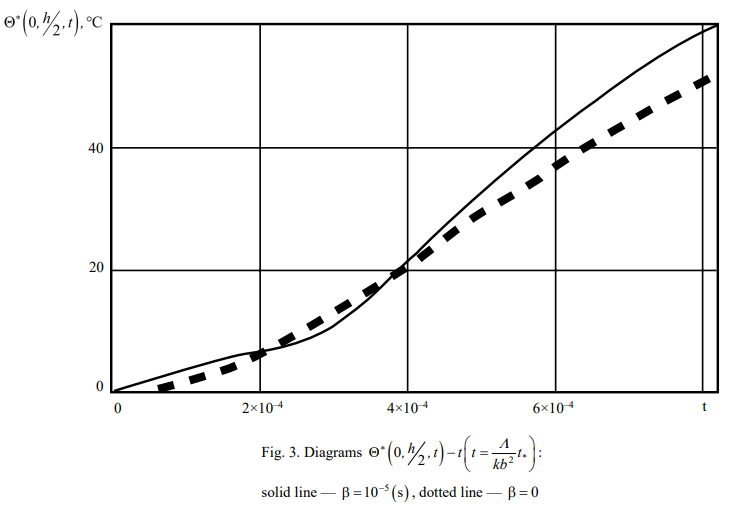
Figure 4 shows a diagram of movements W*(0, z, t) over time t, and Figure 5 shows the dependence of the change in the radial component of normal stresses σrr(r, z, t) along coordinate at different points in time: solid line — z = 0, dotted line — z = h.
Fig. 4. Diagrams W*(0, z, t) – t
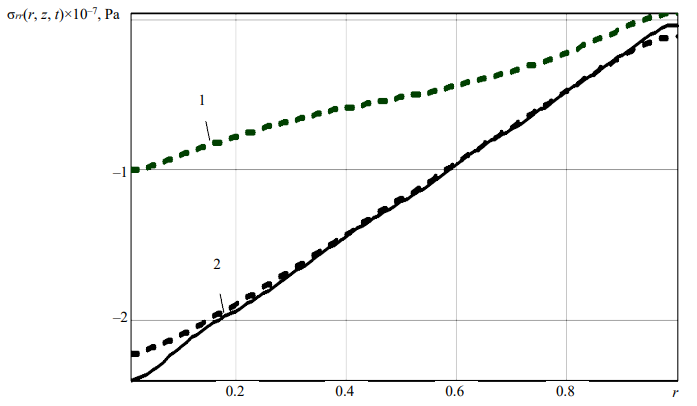
Fig. 5. Diagrams σrr(r, z, t) – r: 1 — t = tmax, 2 — t = 10tmax
It should be noted that under heating, the plate bends with increasing thickness; due to fixation, compressive normal stresses σrr(r, z, t) are formed at all points. In the case of complete heating of the structure (t = 10tmax), the value of normal stresses σrr(r, z, 10tmax) in the height of the section practically coincide (Fig. 5, Diagram 2, solid and dotted lines). At this, σrr(r, 0, t) remains constant over the entire time interval t ≥ tmax (Fig. 5, solid line), and on the lower plane at the initial moment of time σrr(r, h, t), it is significantly less (Fig. 5, Diagram 1, dotted line).
For a qualitative assessment of the induced electric pulse in the form of a potential difference V(t) (31), two electrodes with a radius of separation R = 0.7 and connected to a measuring device (Fig. 6, solid line) must be formed on the upper front surface of the element in question. At this, determination of V(t) by connecting the upper and lower (grounded) solid electrodated surfaces of the plate to the voltmeter (Fig. 6, dotted line) is ineffective.
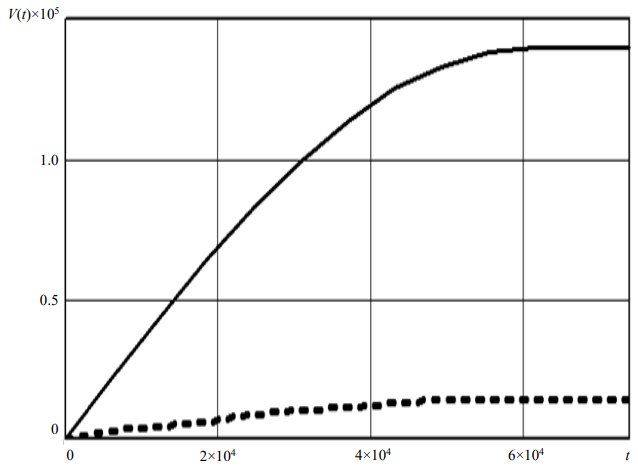
Fig. 6. Diagrams V(t) – t
Discussion and Conclusion. The developed closed solution of the coupled axisymmetric thermoelectroelasticity problem for a round plate made of piezoceramic material is more accurate than the solution that was developed when solving problems in an uncoupled formulation. This is due to the fact that the calculated ratios obtained make it possible to determine how the non-stationary temperature field affects the stress-strain state and the electric field of the element in question, which makes it possible to describe the behavior of a round piezoceramic plate under the influence of thermal and electrical loads with greater accuracy. In addition, it becomes possible to scientifically establish the dimensions of two uncoupled electrodes, which provides measuring the induced electric pulse most effectively.
References
1. Ionov BP, Ionov AB. Statistic-Spectral Approach to Noncontact Temperature Measurement. Sensors & Systems. 2009;117(2):9–12. URL: https://rucont.ru/efd/600855 (accessed: 30.11.2023).
2. Kazaryan AA. Fine-Film Captive Pressure and Temperature. Sensors & Systems. 2016;(3):50–56. URL: https://rucont.ru/efd/579511 (accessed: 30.11.2023).
3. Pan’kov AA. Resonant Diagnostics of Temperature Distribution by the Piezo-Electro-Luminescent Fiber-Optical Sensor according to the Solution of the Fredholm Integral Equation. PNPRU Mechanics Bulletin. 2018;(2):72–82. https://doi.org/10.15593/perm.mech/2018.2.07
4. Saadatfar M, Razavi AS. Piezoelectric Hollow Cylinder with Thermal Gradient. Journal of Mechanical Science and Technology. 2009;23:45–53. https://doi.org/10.1007/s12206-008-1002-8
5. Weiqiu Chen, Tadashi Shioya. Piezothermoelastic Behavior of a Pyroelectric Spherical Shell. Journal Thermal Stresses. 2001;24:105–120. http://doi.org/10.1080/01495730150500424
6. Podil'chuk YuN. Exact Analytical Solutions of Static Electroelastic and Thermoelectroelastic Problems for a Transversely Isotropic Body in Curvilinear Coordinate Systems. International Applied Mechanics. 2003;39(2):132–170. https://doi.org/10.1023/A:1023953313612
7. Shlyakhin DA, Kalmova MA. Uncoupled Problem of Thermoelectroelasticity for a Cylindrical Shell. In: P Akimov, N Vatin (eds). XXX Russian-Polish-Slovak Seminar Theoretical Foundation of Civil Engineering (RSP 2021). Cham: Springer. 2022;189:263–271. https://doi.org/10.1007/978-3-030-86001-1_31
8. Shlyakhin DA, Savinova EV, Yurin VA. Dynamic Problem of Thermoelectricity for Round Rigidly Fixed Plate. FEFU: School of Engineering Bulletin. 2022;50(1):3–16. https://doi.org/10.24866/2227-6858/2022-1/3-16
9. Vatulyan AO. Heat Stroke on a Thermoelectroelastic Layer. Vestnik of DSTU. 2001;1(1):82–89. (In Russ.).
10. Vatulyan AO, Nesterov SA. The Dynamic Problem of Thermoelectroelasticity for Functionally Graded Layer. Computational Continuum Mechanics. 2017;10(2):117–126. https://doi.org/10.7242/1999-6691/2017.10.2.10
11. Shang F, Kuna M, Kitamura T. Theoretical Investigation of an Elliptical Crack in Thermopiezoelectric Material. Part 1: Analytical Development. Theoretical and Applied Fracture Mechanics. 2003;40(3):237–246. https://doi.org/10.1016/J.TAFMEC.2003.08.003
12. Kirilyuk VS. Thermostressed State of a Piezoelectric Body with a Plate Crack under Symmetric Thermal Load. International Applied Mechanics. 2008;44(3):320–330. http://doi.org/10.1007/s10778-008-0048-8
13. Shlyakhin DA, Kal’mova MA. The Coupled Non-Stationary Thermo-Electro-Elasticity Problem for a Long Hollow Cylinder. Journal of Samara State Technical University, Ser. Physical and Mathematical Sciences. 2020;24(4):677–691. https://doi.org/10.14498/vsgtu1781
14. Shlyakhin DA., Kalmova MA. The Nonstationary Thermoelectric Elasticity Problem for a Long Piezoceramic Cylinder. PNPRU Mechanics Bulletin. 2021;(2):181–190. https://doi.org/10.15593/perm.mech/2021.2.16
15. Senitsky YuE. Finite Integral Transformations Method – Generalization of Classic Procedure for Eigenvector Decomposition. Izvestiya of Saratov University. Mathematics. Mechanics. Informatics. 2011;11(3-1):61–89. https://doi.org/10.18500/1816-9791-2011-11-3-1-61-89
16. Selvamani R. Influence of Thermo-Piezoelectric Field in a Circular Bar Subjected to Thermal Loading due to Laser Pulse. Materials Physics and Mechanics. 2016;27(1):1–8. URL: https://www.ipme.ru/e-journals/MPM/no_12716/MPM127_01_selvamani.pdf (accessed: 30.11.2023).
About the Authors
D. A. ShlyakhinRussian Federation
Dmitriy A. Shlyakhin, Dr.Sci. (Eng.), Associate Professor, Head of the Structural Mechanics, Engineering Geology, Foundation Engineering Department
244, Molodogvardeyskaya St., Samara, 443100
E. V. Savinova
Russian Federation
Elena V. Savinova, postgraduate student, senior lecturer of the Structural Mechanics, Engineering Geology, Foundation Engineering Department
244, Molodogvardeyskaya St., Samara, 443100
Review
For citations:
Shlyakhin D.A., Savinova E.V. Coupled Axisymmetric Thermoelectroelasticity Problem for a Round Rigidly Fixed Plate. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):23-35. https://doi.org/10.23947/2687-1653-2024-24-1-23-35. EDN: DUOERK













































