Перейти к:
Прогнозирование реологических параметров полимеров методами машинного обучения
https://doi.org/10.23947/2687-1653-2024-24-1-36-47
EDN: HTOURY
Аннотация
Введение. Для всех полимерных материалов и композитов на их основе характерны явно выраженные реологические свойства, прогнозирование которых является одной из важнейших задач механики полимеров. Большие возможности для прогнозирования реологических параметров полимеров открывают методы машинного обучения. Ранее проводились исследования на предмет построения прогнозных моделей с использованием искусственных нейронных сетей и алгоритма CatBoost. Наряду с этими методами, благодаря возможности обрабатывать данные с сильно нелинейными зависимостями между признаками, широкое применение в смежных областях находят методы машинного обучения — метод k-ближайших соседей и метод опорных векторов (SVM). Однако ранее к проблеме, рассмотренной в данной статье, эти методы не применялись. Целью работы явилась разработка прогнозной модели для оценки реологических параметров полимеров методами искусственного интеллекта на примере поливинилхлорида.
Материалы и методы. В работе применены метод k-ближайших соседей и метод опорных векторов для определения реологических параметров полимеров на основе кривых релаксации напряжений. Обучение моделей выполнялось на синтетических данных, сгенерированных на основе теоретических кривых релаксации, построенных с использованием нелинейного уравнения Максвелла-Гуревича. Входными параметрами моделей выступали величина деформации, при которой производился эксперимент, начальное напряжение, напряжение в конце процесса релаксации, время релаксации и условное время окончания процесса. Выходные параметры: модуль скорости и коэффициент начальной релаксационной вязкости. Модели разработаны в среде Jupyter Notebook на языке Python.
Результаты исследования. Построены новые прогнозные модели для определения реологических параметров полимеров на основе методов искусственного интеллекта. Предложенные модели обеспечивают высокое качество прогнозирования. Метрики качества модели в алгоритме SVR составляют: MAE — 1,67 и 0,72; MSE — 5,75 и 1,21; RMSE — 1,67 и 1,1; MAPE — 8,92 и 7,3 для параметров начальной релаксационной вязкости и модуля скорости соответственно с коэффициентом детерминации R2 — 0,98. Разработанные модели показали среднюю абсолютную процентную ошибку в диапазоне 5,9–8,9 %. Помимо синтетических данных, разработанные модели также апробировалась на реальных экспериментальных данных для поливинилхлорида в диапазоне температур от 20° до 60 °C.
Обсуждение и заключение. Апробация разработанных моделей на реальных экспериментальных кривых показала высокое качество их аппроксимации, сопоставимое с другими методами. Таким образом, алгоритмы
k-ближайших соседей и SVM могут использоваться для прогнозирования реологических параметров полимеров как альтернатива искусственным нейронным сетям и алгоритму CatBoost, требующая меньших усилий по предварительной настройке. При этом в данном исследовании наиболее предпочтительным методом машинного обучения оказался метод SVM, так как он более эффективен в обработке большого числа признаков.
Ключевые слова
Для цитирования:
Кондратьева Т.Н., Чепурненко А.С. Прогнозирование реологических параметров полимеров методами машинного обучения. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):36-47. https://doi.org/10.23947/2687-1653-2024-24-1-36-47. EDN: HTOURY
For citation:
Kondratieva T.N., Chepurnenko A.S. Prediction of Rheological Parameters of Polymers by Machine Learning Methods. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):36-47. https://doi.org/10.23947/2687-1653-2024-24-1-36-47. EDN: HTOURY
Введение. Полимеры применяются в различных областях промышленности, включая производство пластика, текстиля, упаковочных материалов и многих других. Точное прогнозирование реологических параметров полимеров является сложной задачей, имеющей важное значение для оптимизации производственных процессов и создания продуктов с желаемыми свойствами.
На сегодняшний день методы машинного обучения приобрели большую популярность в различных областях, включая химию и материаловедение, благодаря своей способности эффективно обрабатывать и анализировать большие объемы данных. Данные методы позволяют прогнозировать свойства материалов. В работе [1] описана платформа, основанная на машинном обучении, предложена интеграция метрологического обеспечения в условиях цифровой трансформации. В [2] прогнозируется локальное распределение деформации, развитие пластической анизотропии и разрушения в аддитивно изготовленных сплавах. Проблемы разработки регуляторов измерительного контроля на цифровых платформах сформулированы в работе [3]. Интеллектуальная модель управления параметрами сварки соединений внахлестку построена в [4]. Однако вопросы применения методов машинного обучения для прогнозирования реологических свойств полимеров остаются недостаточно исследованными. Это вызвано как техническими, так и методологическими сложностями, такими как неоднородность структуры полимеров, их чувствительность к внешним условиям и сложные взаимодействия между молекулами в процессе деформации.
Исследования в области реологических свойств полимеров и композитов методами машинного обучения несут большие перспективы в строительной индустрии [5]. Для многих полимеров экспериментальные данные хорошо описывает обобщенное нелинейное уравнение Максвелла-Гуревича [6], для одноосного напряженного состояния имеющее вид [7]:
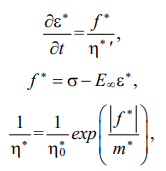 (1)
(1)
где ε* — деформация ползучести; f* — функция напряжений; σ — напряжение; E∞ — модуль высокоэластичности; 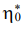 — начальная релаксационная вязкость; m* — модуль скорости.
— начальная релаксационная вязкость; m* — модуль скорости.
Для определения реологических параметров полимеров, таких как начальная релаксационная вязкость (далее просто «вязкость») и модуль скорости, можно использовать различные интеллектуальные модели машинного обучения [8, 9]. Например, одной из таких моделей является нейронная сеть, которая может обучаться на сгенерированных наборах данных для определения оптимальных параметров полимеров [10].
Прогнозирование на синтезированных данных достаточно распространённая практика, в том числе для методов нелинейной оптимизации [11, 12]. Одним из способов генерации данных выступает применение функций Розенброка, Химмельблау, Бута [13], которые эффективно используются для тестирования методов оптимизации, таких как методы градиентного спуска, генетические алгоритмы и метод Ньютона. Такой подход применен в работе [14], где для проверки эффективности различных методов оптимизации сгенерирован набор данных на основе теоретических кривых релаксации напряжений с использованием нелинейного уравнения Максвелла-Гуревича.
В работе [15] для прогнозирования долговечности железобетонной балки приведено несколько подходов машинного обучения, такие как нейронная сеть обратного распространения, линейная и гребневая регрессия, дерево решений, случайный лес. Входными параметрами исследования явились как различные характеристики материала, так и их свойства, в зависимости от окружающей среды (температура, влажность). В итоге по результатам исследования модель обратного распространения определила более точный прогноз (85 %), средние значения (MAE) и MAPE составили 1,13 % и 14,5 % соответственно.
Другой подход к решению обратных задач теории ползучести методом нейронных сетей основан на обучении модели на больших объемах экспериментальных данных. В работе [16] была разработана нейросетевая модель, которая обучалась на данных, полученных в результате многолетних экспериментов над полимерными материалами, и успешно прогнозировала вязкоупругое поведение этих материалов. Для исследования были использованы данные, полученные в результате экспериментов над образцами различных материалов.
В отличие от вышеперечисленных работ, представленная работа призвана содействовать развитию более точных и надежных методов прогнозирования свойств полимеров, таких как метод k-ближайших соседей и метод опорных векторов, что имеет важное значение для различных отраслей промышленности и науки.
Цель исследования заключалась в разработке прогностической модели на основе методов искусственного интеллекта для анализа реологических свойств полимеров. Ранее авторы в своих работах уже применяли алгоритм машинного обучения на основе градиентного бустинга CatBoost для обработки кривых релаксации напряжений [17, 18]. CatBoost является одним из наиболее мощных алгоритмов машинного обучения, применимым для решения не только задач регрессии, но и задач классификации и ранжирования [19].
Метод CatBoost может быть полезным для решения некоторых задач, но он также имеет свои ограничения и недостатки. В связи с этим появился интерес к использованию и других, упомянутых ранее [20], алгоритмов для решения поставленной задачи.
Материалы и методы. Сгенерированный массив данных частично представлен в таблице 1. Данный массив был сформирован на основе теоретических кривых релаксации напряжений, описываемых уравнением Максвелла-Гуревича, по методике, представленной в работе [14]. Диапазоны изменения модуля скорости и начальной релаксационной вязкости в сгенерированном массиве соответствуют реальным диапазонам для поливинилхлорида в интервале температур от 20° до 60 °С. Общее количество численных экспериментов (n) составляло 30 000.
Таблица 1
Таблица исходных данных для обучения модели
№ | Деформация, % | Напряжение | Напряжение | Время релаксации tn, ч | Условное время окончания процесса t95, ч | Модуль скорости m*, МПа | Вязкость 106 МПа∙с |
1 | 1,000 | 10,000 | 0,909 | 0,277 | 1,484 | 6,000 | 3,000 |
2 | 2,000 | 20,000 | 1,818 | 0,109 | 1,003 | 6,000 | 3,000 |
3 | 3,000 | 30,000 | 2,727 | 0,046 | 0,820 | 6,000 | 3,000 |
4 | 1,000 | 10,000 | 0,909 | 0,861 | 4,615 | 6,000 | 9,333 |
5 | 2,000 | 20,000 | 1,818 | 0,339 | 3,122 | 6,000 | 9,333 |
6 | 3,000 | 30,000 | 2,727 | 0,142 | 2,552 | 6,000 | 9,333 |
7 | 1,000 | 10,000 | 0,909 | 1,445 | 7,747 | 6,000 | 15,667 |
… | |||||||
29997 | 3 | 45 | 37,5 | 0,285 | 2,476 | 15 | 53,666 |
29998 | 1 | 15 | 12,5 | 1,003 | 4,255 | 15 | 60 |
29999 | 2 | 30 | 25,0 | 0,558 | 3,371 | 15 | 60 |
30000 | 3 | 45 | 37,5 | 0,319 | 2,769 | 15 | 60 |
Набор данных составил пять входных переменных и две выходных переменных. Входные переменные (единица измерения): деформация — ε (%); напряжение в начале процесса — σ0 (МПа); напряжение в конце процесса — σ∞ (МПа); время релаксации — tn (ч); условное время окончания процесса — t95 (ч). Выходные переменные (единица измерения): модуль скорости — m* (МПа); начальная релаксационная вязкость — 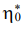
(в таблице 1 и далее просто «вязкость») (106 МПа∙с). Величины σ0, σ∞, tn и t95 схематически показаны на типовой кривой релаксации напряжений, представленной на рис. 1.
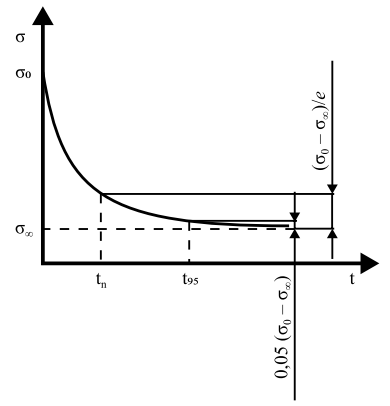
Рис. 1. Типовая кривая релаксации напряжений
Алгоритм k-ближайших соседей (k-NN) основан на анализе сходства ближайших объектов. Метод k-NN пользуется большим спросом при решении различных типов задач машинного обучения.
Формула (2) представляет общий вид алгоритма, где w(i, x) — весовая функция, оценивающая степень важности i-го соседа.
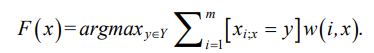 (2)
(2)
Максимально суммарный вес может достигаться для нескольких объектов одновременно. Энтропию этого процесса можно регулировать с помощью нелинейной последовательности w(i, x) = [i ≤ k]qi (метод экспоненциально взвешенных k-ближайших соседей) при условии, что 0 ≤ q ≤ 0,5.
Представляя собой достаточно простой алгоритм машинного обучения, k-NN хорошо применим при решении задач классификации и регрессии. Преимущества данного метода: простота реализации, отсутствие необходимости в предварительном обучении модели. Он используется для любых типов данных, включая категориальные и числовые. Недостатки: склонность к переобучению (при условии, если k слишком мало), низкая производительность при больших объемах данных, нет возможности учитывать взаимосвязь между признаками.
Алгоритм опорных векторов (SVR) — регрессия опорных векторов, решает задачи минимизации суммы средней абсолютной ошибки. SVR является более устойчивым к выбросам, в отличии от метода наименьших квадратов, за счёт коэффициента регуляризации (С) и «эпсилон-нечувствительной трубки» (ε). При этом ε определяет ширину трубки, в которой ошибки игнорируются. Для нахождения минимума функции используется стохастический градиентный спуск.
Алгоритм обучения по методу опорных векторов представляет собой функцию F(x) аппроксимации и регуляризации эмпирического риска, преобразующую обучающую и тестовую выборки в выходные данные для каждого объекта соответствующей выборки. Формула (3) представляет общий вид алгоритма; (4) — линейно разделимая выборка; (5) — линейно неразделимая выборка, где C — коэффициент регуляризации;
Mi(w, w0) — скалярное произведение векторов (признака и опорного вектора); — весовые коэффициенты.
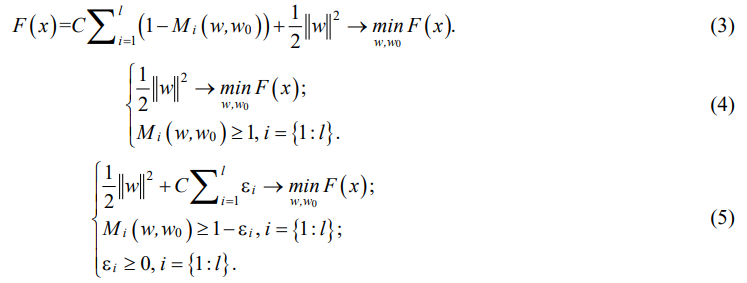
Функция 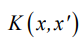 есть функция от пары объектов
есть функция от пары объектов 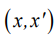 представима в виде скалярного произведения в некотором пространстве H, для которого имеет место преобразование
представима в виде скалярного произведения в некотором пространстве H, для которого имеет место преобразование 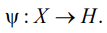 Функция
Функция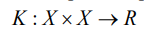 — ядро, если
— ядро, если 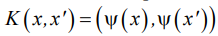 при условии, что K симметричная:
при условии, что K симметричная: 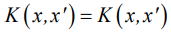 и неотрицательно определённая:
и неотрицательно определённая: 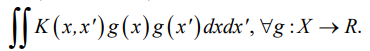 Коэффициент регуляризации определяется методом скользящего контроля.
Коэффициент регуляризации определяется методом скользящего контроля.
Преимущества метода SVM: высокая точность в задачах классификации в нелинейных пространствах; способность работать с большим количеством признаков (включая категориальные и числовые), обобщать данные (что позволяет применять модель для новых данных), работать с данными, которые не являются линейно разделимыми благодаря использованию ядерных функций.
Недостатки метода SVM: неэффективность работы с большими объемами данных; низкая интерпретируемость модели; требование настройки множества параметров, таких как тип ядра (его параметры, параметры регуляризации) и т.д.
В данном исследовании алгоритмы разрабатываются в интеллектуальной вычислительной среде
Jupyter Notebook методами машинного обучения.

Подбор такого параметра, как количество соседей, влияет на обобщающую способность разработанной модели и является важным для её корректной работы. Наиболее подходящий алгоритм расчёта расстояния на основе данных является Distance, при котором веса объектов обратно пропорциональны их расстоянию. Соответственно, в случае более близких соседей объекта запроса, они имеют большее влияние, нежели их соседи, находящиеся на большем расстоянии от объекта.
Набор данных разбит на обучающую и тестовую выборки в соотношении 75/25. В свою очередь, 20 % обучающей выборки становится валидационной. Размерность выборок составила: обучающая — xtrain = 20 400; тестовая — xtest = 6 000; валидационная — xeval = 3 600. Для переменных ytrain, ytest, yeval данные распределены аналогичным образом.
Для построения модели k-ближайших соседей были выбраны следующие параметры: количество соседей, размер листа, интервал, функция веса. Диапазон и функционал значений для настраиваемых параметров представлен в таблице 2.
Таблица 2
Таблица параметров для модели k-NN
№ | Параметр | Значение | Функционал |
1 | Количество соседей (k) | 3, 5, 7, 9 | Определяет оптимальное количество соседей |
2 | Размер листа (n) | 15, 20, 30 | Определяет скорость построения запроса |
3 | Интервал (p) | 1 (l1), 2 (l2) | Определяет параметр мощности (метрика Минковского) |
4 | Функция веса (w) | 'uniform', 'distance' | Прогнозирование весов |
Для построения модели SVR были выбраны следующие параметры: тип ядра, порядок ядра, коэффициент регуляризации (квадратичный регуляризатор), ε. Диапазон и функционал значений для настраиваемых параметров представлены в таблице 3.
Таблица 3
Таблица параметров для модели SVR
№ | Параметр | Значение | Функционал |
1 | Тип ядра | 'linear'; 'poly'; 'rbf'; 'sigmoid' | Определяет тип гиперплоскости (линейная/нелинейная) |
2 | Порядок ядра | 1, 2, 3, 4, 5, 7 | Определяет степень полиномиальной функции ядра |
3 | Квадратичный регуляризатор (C) | 2; 3; 4; 5; 7; 10 | Решает проблемы мультиколлинеальности вектор |
4 | ε | 0,1; 0,2; 0,5; 1; 1,5; 2; 3 | Определяет отклонение объекта (мера близости) |
Результаты исследования
На рис. 2 представлены корреляционные связи между переменными.
Можно отметить следующие виды линейных корреляционных связей между отдельными входными и выходными переменными модели:
- достаточно сильные — между переменными «Деформация» и «Напряжение в начале»
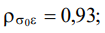 «Время релаксации» и «Время окончания процесса»
«Время релаксации» и «Время окончания процесса» 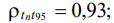
- средние — между переменными «Деформация» и «Напряжение в конце»
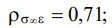 «Напряжение в начале» и «Напряжение в конце»
«Напряжение в начале» и «Напряжение в конце» 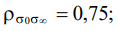
- слабые — между переменными «Время окончания процесса» и «Вязкость»
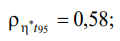 «Вязкость» и «Время релаксации»
«Вязкость» и «Время релаксации» 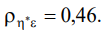
Наличие умеренной корреляционной связи между переменными или её отсутствие говорит лишь об отсутствии линейной связи, следовательно, возможно наличие нелинейной связи между переменными.
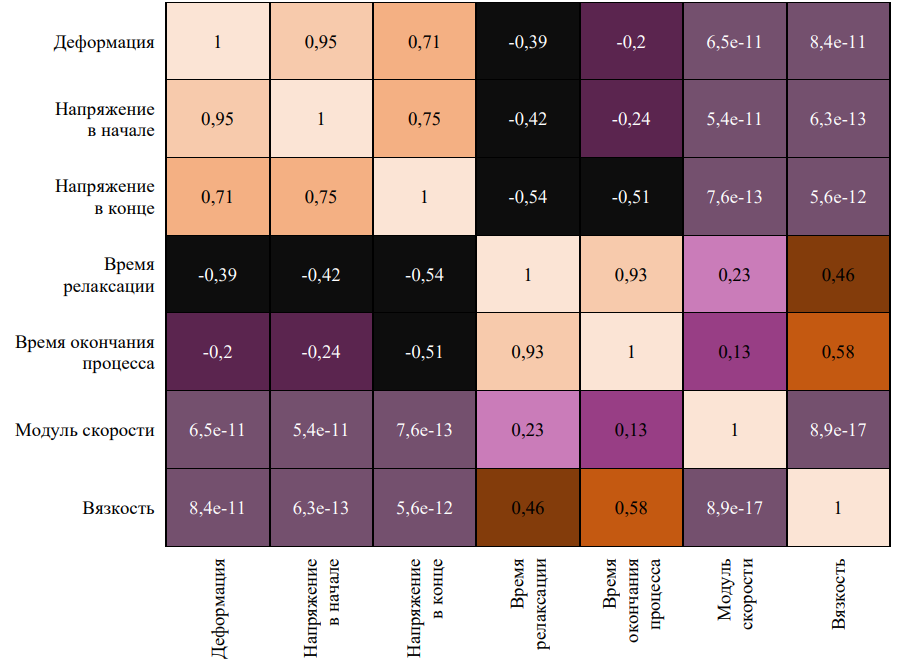
Рис. 2. Корреляционная матрица
В таблице 4 предоставлены статистические характеристики исходного набора данных.
Таблица 4
Статистические характеристики исходного набора данных
Параметр | ε | σ0 | σ∞ | tn | t95 | m* | |
Ед. измерения | % | МПа | МПа | ч | ч | МПа | 106 МПа с |
count | 30 000,00 | 30 000,00 | 30 000,00 | 30 000,00 | 30 000,00 | 30 000,00 | 30 000,00 |
mean | 2,00 | 25,00 | 15,78 | 0,75 | 4,41 | 10,50 | 31,50 |
std | 0,82 | 10,77 | 9,10 | 0,94 | 4,40 | 2,87 | 18,19 |
min | 1,00 | 10,00 | 0,91 | 0,00 | 0,07 | 6,00 | 3,00 |
max | 3,00 | 45,00 | 37,50 | 10,04 | 38,02 | 15,00 | 60,00 |
Наиболее лучшие параметры для модели k-ближайших соседей были определены в результате работы 5-ти блочной кросс-валидации (таблица 5).
Таблица 5
Наилучшие параметры модели k-NN
Параметр | Количество соседей (k) | Размер листа (n) | Интервал (p) | Функция веса (w) |
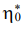 | 3 | 15 | 2 | 'distance' |
m* | 5 | 15 | 2 | 'distance' |
Наилучшие параметры модели SVR для параметров вязкости (в начале релаксационного процесса) и модуля скорости были получены эмпирическим путём (таблица 6).
Таблица 6
Наилучшие параметры модели SVR
Параметр | Тип ядра | Порядок ядра | Квадратичный регуляризатор | ε |
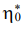 | 'rbf' | 2 | 5 | 0,3 |
m* | 'rbf' | 3 | 6 | 0,3 |
Соотношение между реальными и предсказанными значениями для модели k-NN по параметрам «Вязкость» и «Модуль скорости» показаны на рис. 3, 4.
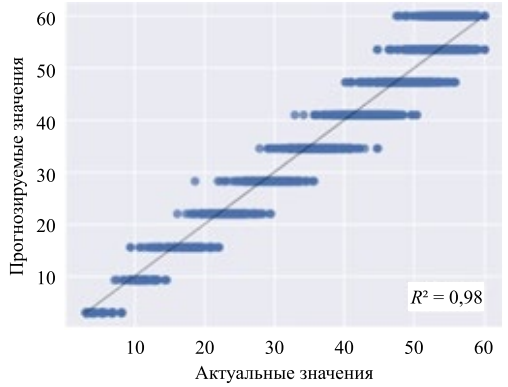
Рис. 3. Графики ошибок прогноза k-NN, «Вязкость»
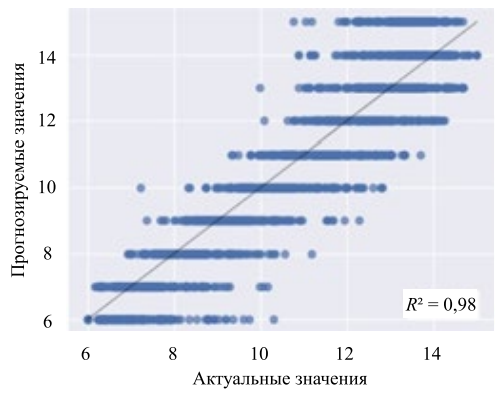
Рис. 4. Графики ошибок прогноза k-NN, «Модуль скорости»
Соотношение между реальными и предсказанными значениями для модели SVR по параметрам «Вязкость» и «Модуль скорости» показаны на рис. 5, 6.
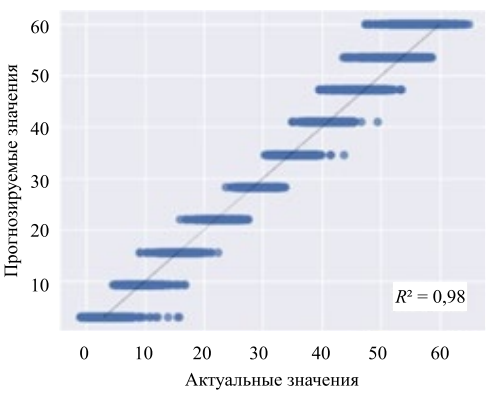
Рис. 5. Графики ошибок прогноза SVR, «Вязкость»
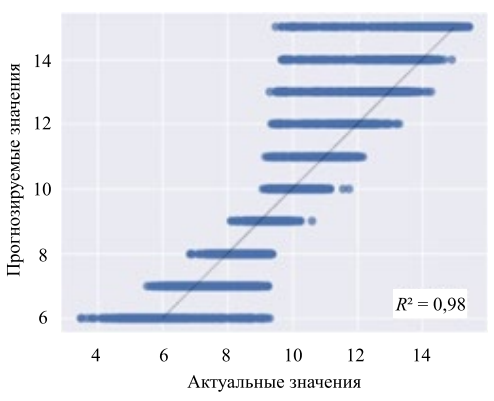
Рис. 6. Графики ошибок прогноза SVR, «Модуль скорости»
Метрики разработанных моделей k-ближайших соседей и опорных векторов представлены в таблицах 7 и 8 соответственно.
Таблица 7
Метрики разработанных моделей k-NN
Параметр | MAE | MSE | RMSE | MAPE, % | R2 train | R2 test |
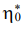 | 1,8 | 6,8 | 2,6 | 5,9 | 1,00 | 0,98 |
m* | 0,7 | 0,8 | 0,9 | 6,9 | 0,99 | 0,98 |
Таблица 8
Метрики разработанных моделей SVR
Параметр | MAE | MSE | RMSE | MAPE, % | R2 train | R2 test |
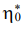 | 1,67 | 5,75 | 1,67 | 8,92 | 0,98 | 0,97 |
m* | 0,72 | 1,21 | 1,1 | 7,3 | 0,89 | 0,87 |
Помимо синтетических данных, разработанные модели также апробировалась на реальных экспериментальных данных, представленных в работе [13]. Использовались экспериментальные кривые релаксации поливинилхлорида для различных температур в интервале от 20° до 60 °С. На рис. 7 маркерами отмечены экспериментальные значения напряжений при различных температурах в различные моменты времени, а сплошными линиями показаны кривые релаксации напряжений, построенные на основе спрогнозированных моделями величин m* и 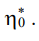
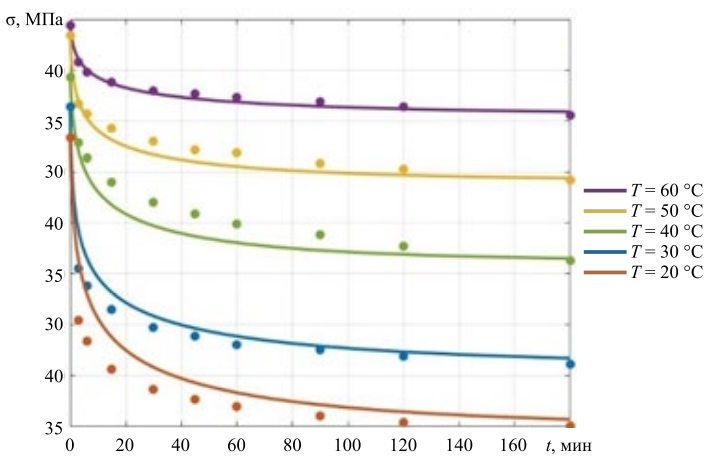
Рис. 7. Результаты апробации модели на экспериментальных данных
Обсуждение и заключение. Из рис. 5 видно, что качество прогнозирования по экспериментальным данным достаточно высокое, особенно для температур 30 °С, 50 °С и 60 °С. Для других температур качество прогнозирования несколько ниже, что связано с качеством самих экспериментальных кривых. Следовало продлить время эксперимента и дождаться выхода кривых на горизонтальную асимптоту.
В данном исследовании наиболее предпочтительным выступает метод опорных векторов (SVM). Это связано с тем, что SVM может обрабатывать данные с большим количеством признаков, что является важным для анализа реологических параметров материалов. Кроме того, SVM работает с нелинейными зависимостями между признаками, применим для решения задачи регрессии, которая является необходимой для определения реологических параметров материалов.
Однако метод CatBoost также может быть эффективным в этой задаче, особенно если в данных есть категориальные признаки. Кроме того, CatBoost может обрабатывать пропущенные данные, что может быть важно для анализа реологических параметров материалов.
Метод k-ближайших соседей является менее предпочтительным в данной задаче по причине невысокой эффективности в обработке большого числа признаков, а также наличия проблем с высокой размерностью данных.
В ходе исследования было показано, что применение методов машинного обучения позволяет эффективно анализировать и обрабатывать большие объемы данных, включающие информацию о характеристиках полимеров и их реологических свойствах. Модель, разработанная на основе такого анализа, демонстрирует высокую точность прогнозирования реологических параметров поливинилхлорида, что подтверждается результатами кросс-валидации и сравнением с экспериментальными данными.
Одним из ключевых преимуществ данного подхода является возможность автоматизации процесса прогнозирования реологических параметров полимеров, что позволяет сократить время и затраты на исследование и разработку новых материалов. Кроме этого, модель может быть легко адаптирована для анализа других типов полимеров и предсказания их свойств.
В результате выполнения данной работы была разработана прогнозная модель для оценки реологических параметров поливинилхлорида методами искусственного интеллекта на основе данных о его характеристиках и реологических свойствах. Модель демонстрирует высокую точность прогнозирования и может быть использована для оптимизации процессов производства и разработки новых материалов на основе полимеров.
Список литературы
1. Dudukalov EV, Munister VD, Zolkin AL, Losev AN, Knishov AV. The Use of Artificial Intelligence and Information Technology for Measurements in Mechanical Engineering and in Process Automation Systems in Industry 4.0. Journal of Physics: Conference Series. IOP Publishing. 2021;1889(5):052011. https://doi.org/10.1088/1742-6596/1889/5/052011
2. Waqas Muhammad, Abhijit P Brahme, Olga Ibragimova, Jidong Kang, Kaan Inal. A Machine Learning Framework to Predict Local Strain Distribution and the Evolution of Plastic Anisotropy & Fracture in Additively Manufactured Alloys. International Journal of Plasticity. 2021;136:102867. https://doi.org/10.1016/j.ijplas.2020.102867
3. Won-Bin Oha, Tae-Jong Yuna, Bo-Ram Leea, Chang-Gon Kima, Zong-Liang Lianga, Ill-Soo Kim. A Study on Intelligent Algorithm to Control Welding Parameters for Lap-joint. Procedia Manufacturing. 2019;30:48–55. http://doi.org/10.1016/j.promfg.2019.02.008
4. Amit R Patel, Kashyap K Ramaiya, Chandrakant V Bhatia, Hetalkumar N Shah, Sanket N Bhavsar. Artificial Intelligence: Prospect in Mechanical Engineering Field—A Review. In book: Data Science and Intelligent Applications. Singapore: Springer; 2021. P. 267–282. https://doi.org/10.1007/978-981-15-4474-3_31
5. Amjadi M, Fatemi A. Creep and Fatigue Behaviors of High-Density Polyethylene (HDPE): Effects of Temperature, Mean Stress, Frequency, and Processing Technique. International Journal of Fatigue. 2020;141:105871. http://doi.org/10.1016/j.ijfatigue.2020.105871
6. Chepurnenko V, Yazyev B, Xuanzhen Song. Creep Calculation for a Three-Layer Beam with a Lightweight Filler. MATEC Web of Conferences. 2017;129:05009. https://doi.org/10.1051/matecconf/201712905009
7. Litvinov SV, Yazyev BM, Turko MS. Effecting of Modified HDPE Composition on the Stress-Strain State of Constructions. IOP Conference Series: Materials Science and Engineering. 2018;463(4):042063. https://doi.org/10.1088/1757-899X/463/4/042063
8. Guangjian Xiang, Deshun Yin, Ruifan Meng, Siyu Lu. Creep Model for Natural Fiber Polymer Composites (NFPCs) Based on Variable Order Fractional Derivatives: Simulation and Parameter Study. Journal of Applied Polymer Science. 2020;137(24):48796. http://doi.org/10.1002/app.48796
9. Tugce Tezel, Volkan Kovan, Eyup Sabri Topal. Effects of the Printing Parameters on Short‐Term Creep Behaviors of Three‐Dimensional Printed Polymers. Journal of Applied Polymer Science. 2019;136(21):47564. http://doi.org/10.1002/app.47564
10. Litvinov SV, Trush LI, Yazyev SB. Flat Axisymmetrical Problem of Thermal Creepage for Thick-Walled Cylinder Made of Recyclable PVC. Procedia Engineering. 2016;150:1686–1693. https://doi.org/10.1016/j.proeng.2016.07.156
11. Dudnik AE, Chepurnenko AS, Litvinov SV. Determining the Rheological Parameters of Polyvinyl Chloride, with Change in Temperature Taken into Account. International Polymer Science and Technology. 2017;44(1):43–48. https://doi.org/10.1177/0307174X1704400109
12. Litvinov S, Yazyev S, Chepurnenko A, Yazyev B. Determination of Rheological Parameters of Polymer Materials Using Nonlinear Optimization Methods. In book: A. Mottaeva (ed). Proceedings of the XIII International Scientific Conference on Architecture and Construction. Singapore: Springer; 2020. P. 587–594. https://doi.org/10.1007/978-981-33-6208-6_58
13. Соловьева Е.В., Аскадский А.А., Попова М.Н. Исследование релаксационных свойств первичного и вторичного поливинилхлорида. Пластические массы. 2013;2:54–62.
14. Chepurnenko A. Determining the Rheological Parameters of Polymers Using Artificial Neural Networks. Polymers. 2022;14(19):3977. https://doi.org/10.3390/polym14193977
15. Yu Xuan Rui. Developing an Artificial Neural Network Model to Predict the Durability of the RC Beam by Machine Learning Approaches. Case Studies in Construction Materials. 2022;17:e01382. http://doi.org/10.1016/j.cscm.2022.e01382
16. Nagababu Andraju, Greg W Curtzwiler, Yun Ji, Kozliak Evguenii, Prakash Ranganathan. Machine-Learning-Based Predictions of Polymer and Postconsumer Recycled Polymer Properties. A Comprehensive Review. ACS Applied Materials & Interfaces. 2022;14(38):42771–42790. http://doi.org/10.1021/acsami.2c08301
17. Чепурненко А.С., Кондратьева Т.Н., Дебердеев Т.Р., Акопян В.Ф., Аваков А.А., Чепурненко В.С. Прогнозирование реологических параметров полимеров с помощью алгоритма градиентного бустинга CatBoost. Все материалы: Энциклопедический справочник. 2023;(6):21–29.
18. Kondratieva T, Prianishnikova L, Razveeva I. Machine Learning for Algorithmic Trading. E3S Web of Conferences. 2020;224:01019. https://doi.org/10.1051/e3sconf/202022401019
19. Stelmakh SA, Shcherban EM, Beskopylny AN, Mailyan LR, Meskhi B, Razveeva I, et al. Prediction of Mechanical Properties of Highly Functional Lightweight Fiber-Reinforced Concrete Based on Deep Neural Network and Ensemble Regression Trees Methods. Materials. 2022;15(19):6740. https://doi.org/10.3390/ma15196740
20. Beskopylny AN, Stelmakh SA, Shcherban EM, Mailyan LR, Meskhi B, Razveeva I, et al. Concrete Strength Prediction Using Machine Learning Methods CatBoost, k-Nearest Neighbors, Support Vector Regression. Applied Sciences. 2022;12(21):10864. https://doi.org/10.3390/app122110864
Об авторах
Т. Н. КондратьеваРоссия
Татьяна Николаевна Кондратьева, кандидат технических наук, доцент кафедры математики и информатики
344003, г. Ростов-на-Дону, пл. Гагарина, 1
А. С. Чепурненко
Россия
Антон Сергеевич Чепурненко, доктор технических наук, доцент, профессор кафедры сопротивление материалов
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Кондратьева Т.Н., Чепурненко А.С. Прогнозирование реологических параметров полимеров методами машинного обучения. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):36-47. https://doi.org/10.23947/2687-1653-2024-24-1-36-47. EDN: HTOURY
For citation:
Kondratieva T.N., Chepurnenko A.S. Prediction of Rheological Parameters of Polymers by Machine Learning Methods. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):36-47. https://doi.org/10.23947/2687-1653-2024-24-1-36-47. EDN: HTOURY













































