Scroll to:
Optimal Temperature Calculation for Multicriteria Optimization of the Hydrogenation of Polycyclic Aromatic Hydrocarbons by NSGA-II Method
https://doi.org/10.23947/2687-1653-2024-24-1-109-118
EDN: VNTDAG
Abstract
Introduction. Multicriteria optimization, taking into account contradicting criteria, is used to improve production efficiency, reduce costs, improve product quality and environmental safety of processes. The literature describes the application of multicriteria optimization for production purposes, including the selection of reaction conditions and improvement of technological processes. In the presented paper, the object of research is the process of hydrogenation of polycyclic aromatic hydrocarbons (PAH) in the production of high-density fuels. To determine the optimal conditions of the process, the problem of multicriteria optimization based on the kinetic model is solved. The criteria include maximizing the yield of targeted naphthenes and conversion of feedstock. The research objective is to create a program implementing the multicriteria optimization non-dominated sorting genetic algorithm-II (NSGA-II). Due to this, it is possible to calculate the optimal temperature for the PAH hydrogenation process on the basis of the kinetic model.
Materials and Methods. The NSGA-II genetic algorithm was used to solve the multicriteria optimization problem. Modified parental and survival selection within the Pareto front was also used. If it was necessary to divide the front, solutions based on the Manhattan distance between them were selected. The program was implemented in Python.
Results. In the system of ordinary nonlinear differential equations of chemical kinetics, the concentration was designated yi, the conditional contact time of the reaction mixture with the catalyst — τ. The system was solved for the hydrogenation reaction of polycyclic aromatic hydrocarbons. The calculations showed that at τ = 0 y1(0) = 0.025; y2(0) = 0.9; y6(0) = 0.067; y9(0) = 0.008; yi(0) = 0, i = 3–5, 7, 8, 10–20; Q(0) = 1. The process temperature was considered as a control parameter according to two optimality criteria: maximizing the yield of target naphthenes (f1) at the end of the reaction, and maximizing the conversion of feedstock (f2). Values f1 were in the range of 0.43–0.79; conversion — 0.01–0.03; temperature — 200–300 K. The growth of temperature was accompanied by an increase in the yield of target naphthenes and a decrease in the conversion of feedstock. Each solution obtained was not an unimprovable one. When modeling the process of hydrogenation of PAH, an algorithm was launched with a population size of 100 and a number of generations of 100. A program implementing the NSGA-II algorithm was developed. The optimal set of values of the PAH hydrogenation reaction temperature was calculated, which made it possible to obtain unimprovable values of the optimality criteria — maximizing the yield of target naphthenes and conversion of feedstock.
Discussion and Conclusion. The NSGA-II algorithm is effective for solving the problem of non-dominance, and deriving the optimal solution for all criteria. Future research should be devoted to the selection of optimal algorithm parameters to increase the speed of the solution. Based on the obtained theoretical optimal conditions of the PAH hydrogenation reaction, it is possible to implement the process in industry
Keywords
For citations:
Alexandrova A.A., Koledin S.N. Optimal Temperature Calculation for Multicriteria Optimization of the Hydrogenation of Polycyclic Aromatic Hydrocarbons by NSGA-II Method. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):109-118. https://doi.org/10.23947/2687-1653-2024-24-1-109-118. EDN: VNTDAG
Introduction. Optimization of multistage reactions is used in chemical, oil and gas, food, and other industries. In practice, optimization tasks are multicriteria, and the criteria are often contradictory and have an optimum at different points. Multicriteria optimization remains urgent, as it provides taking into account several parameters and selecting the best solution from a variety of options.
Within the framework of this study, the object of research is the catalytic hydrogenation reaction of polycyclic aromatic hydrocarbons (PAH). They are a class of organic compounds whose molecules contain at least two benzene rings [1]. PAH are common in the interstellar medium. They are part of heavy oil fractions, and are formed by laser irradiation of carbon materials. The study of these compounds is of interest from the point of view of establishing the dependences between their chemical structure and physico-chemical properties. In addition, the data obtained as a result of such scientific research can be used to create new organic and hybrid compounds with a strong carbon frame, which are applicable in nanoarchitectonics.
Applied science correlates the presence of PAH with the production purposes. As an example, the presence of PAH in raw materials is desirable if it is used to produce coke with a given structure [2]. However, in the production of fuel, PAH can negatively affect the performance characteristics of the product, specifically, the density [3].
Extremely strict requirements are imposed on the production of high-density jet fuel. At high density, it should have a boiling point no higher than the upper limit of the boiling point of the kerosene fraction. Another mandatory criterion is the low content of aromatic hydrocarbons. We also note the high cost of well-known technologies for producing high-density fuels.
Considering the above, the problem must be solved according to the Pareto dominance principle to determine the set of unimprovable options using a genetic algorithm of non-dominated sorting [4].
The research objective is to develop a program that implements NSGA-II (Non-dominated sorting genetic algorithm II) multicriteria optimization algorithm and provides calculating the optimal temperature for the PAH hydrogenation process based on a kinetic model.
Materials and Methods
Mathematical Model. We describe the changes in the concentrations of the components depending on the reaction time. To do this, the equations of chemical kinetics are used, which are a system of ordinary nonlinear differential equations (SONDE):
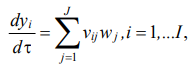 (1)
(1)
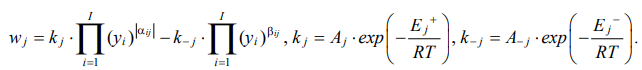 (2)
(2)
Here are the initial conditions: yi(0) = yi0 at τ = 0; τ ∊ [0, τ*]; yi — reagent concentrations, mole fractions;
τ — conditional contact time of the reaction mixture with the catalyst, kg∙min/mol; J — number of stages; I — number of substances; νij — stoichiometric matrix; wj — speed of the j-th stage, 1/min or mol/(kg∙min); kj, k–j — speed constants of the stages (given), 1/min; aij — negative elements of matrix νij; bij — positive elements νij; Aj, A–j — pre-exponential multipliers, 1/min; Ej+, Ej– — activation energies of direct and reverse reactions, kcal/mol; R — gas constant,
2 cal/(mol∙K); T — temperature, K; τ* — reaction duration, kg∙min/mol.
The model of catalytic hydrogenation of PAH takes into account the dynamics of the molar composition and volume of the reaction mixture. Therefore, changes in the concentration of components at each point in time are considered [3]:
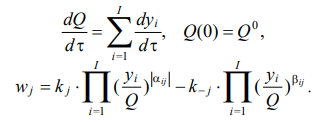 (3)
(3)
To describe a nonstationary reaction that occurs with a change in the volume of the reaction mixture, it is necessary to solve a system of nonlinear differential equations at each moment of time. The direct kinetic problem is the solution to SONDE (1)–(3).
In the process of hydrogenation of PAH, naphthenes are obtained from the source aromatic hydrocarbons, which have a higher density and can be used as rocket fuel. For this purpose, nickel catalysts are used, and the control or variable parameter is the process temperature, which should be within 200–500 K. Optimality criteria — maximizing the output of target naphthenes at the end of the reaction and maximizing the conversion of feedstock.
Research Algorithm. Multicriteria optimization is the selection of the best solution from a variety of alternatives, taking into account several criteria. The importance of each of them is determined by the weight (priority).
Suppose, f(x) — an objective function, and the constraints given in the form of equalities h1(x)…hm(x) and inequalities gm+1(x)…gp(x) are represented by a column vector of components x = [x1,…, xn]T in n-dimensional Euclidean space.
We formulate the problem of nonlinear programming [5].
Optimize
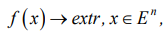 (4)
(4)
with m linear or nonlinear constraints in the form of equalities
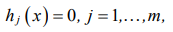 (5)
(5)
and with (p – m) linear or nonlinear constraints in the form of inequalities
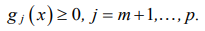 (6)
(6)
Decomposition (4)–(6) is the formulation and solution of a linear and quadratic programming problem. Each of them is determined by the type of equations (4)–(6). Thus, in the case of quadratic function (4) and linear equations (5), (6) — the quadratic programming problem described below.
We define the extremum of function
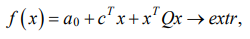 (7)
(7)
with constraints:
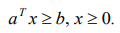 (8)
(8)
In equations (7), (8) Q — nonnegatively defined quadratic symmetric matrix; a, b, c — coefficient matrices.
When setting multicriteria Pareto optimization problem, (4)–(6) will have the form:
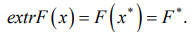 (9)
(9)
In equation (9), 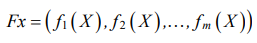 — vector-function of optimality criteria f1 and f2. Set x* — desired solution to the problem in the region of variation parameters. Set represents the desired solution to the problem in the region of optimality criteria, which is unimprovable in terms of Pareto approximation. Then, x* defines the Pareto set,
— vector-function of optimality criteria f1 and f2. Set x* — desired solution to the problem in the region of variation parameters. Set represents the desired solution to the problem in the region of optimality criteria, which is unimprovable in terms of Pareto approximation. Then, x* defines the Pareto set,
F* — Pareto front.
Priori and posteriori Pareto approximation algorithms were used to solve (9). One of them is the ideal point method, which represents the best solution according to all criteria [6]. To find it, we must first determine the minimum and maximum values of each criterion of all the solutions under consideration. Then, for each criterion, the maximum value of all the minimum and the minimum of all the maximum values are selected.
However, this approach has some drawbacks. Firstly, it may be ineffective if the ideal point is outside the range of acceptable criteria values. In this case, other methods of solving multicriteria optimization problems are used. In addition, the ideal point method does not take into account the relationship between the criteria and may cause the selection of a compromise solution that is not optimal for all criteria. Therefore, when using this method, it is needed to additionally analyze and verify the optimality of the solutions obtained [7].
The lexicographic ordering method is also used in solving multicriteria optimization problems. In this case, the criteria are ordered by priority and considered sequentially. If the solutions cannot be sorted by the first criterion, then they are sorted by the next criterion, etc. [7]. The advantages of lexicographic ordering are simplicity and transparency. Using this method, it is possible to obtain a single optimal solution that is easily interpreted. As for the disadvantages, we note, firstly, the inability to take into account compromise solutions that may turn out to be optimal by all criteria. Secondly, there is a risk of selecting an unfavorable solution if the first criterion has a lot of weight, but is not the most important for this task [8].
The presented work provides a solution to the problem of multicriteria optimization of the hydrogenation process of polycyclic aromatic hydrocarbons through the well-known NSGA-II method. It is based on a genetic algorithm and uses several techniques to solve the problem of non-dominance [9]. The main steps of the algorithm are described below [10].
- Initialization of the population. The initial population is randomly generated.
- Population assessment. Each element of the population is evaluated according to several criteria.
- Sorting the population. The elements of the population are sorted by non-dominance level. Dominant and non-dominant elements are placed in the first level. Elements dominated only by elements of the first level are placed in the second level, etc.
- Selecting parent elements. To create a new population, parent elements are selected from the first few levels.
- Crossover and mutation. Parent elements undergo crossing-over and mutation to create new elements of the population.
- Assessment of the new population. New elements are evaluated according to the criteria.
- Sorting the new population. New items are sorted by non-dominance level.
- Selection of a new population. Elements for the next generation are selected from the new population.
- Repeat steps 4–8 until the stop criterion is reached.
NSGA-II allows working accurately and efficiently with multicriteria optimization tasks. It effectively solves the problem of non-dominance, which provides getting optimal solutions for all criteria.
NSGA-II is based on a genetic algorithm with parental selection and survival. Individuals are selected along the fronts, while the front is divided if not all individuals can survive. Solutions in the split front are selected on the basis of the distance between them, which is the Manhattan distance in the criteria space [9]. The endpoints are saved at each generation and are assigned a conditionally infinite distance for use in subsequent iterations [11] (Fig. 1).
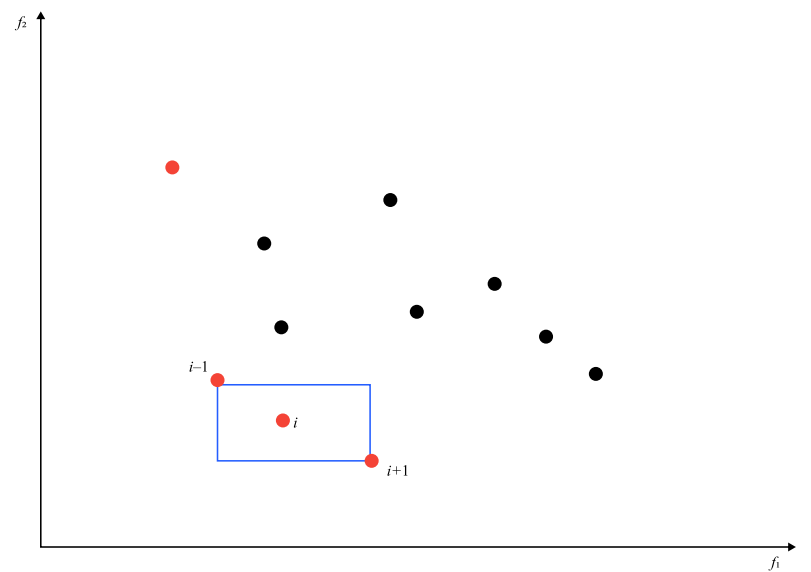
Fig. 1. Visualization of the Pareto front and selection of solutions based on distances
Figure 1 shows an example of a set of solutions for a multicriteria optimization problem using criteria f1 and f2. The red dots represent the Pareto front. The calculation of the cluster distance for solution i is shown — this is the average length of the side of the cuboid in which solution i is located (marked with a blue frame).
To enhance the impact on the selection of parents, NSGA-II uses binary tournament selection [9]. Each individual is first compared by rank, and then — by the distance between them.
Research Results. The program implementing the algorithm for solving the multicriteria optimization problem is written in Python.
In the course of the study, a system of differential equations (1–3) was solved. For the hydrogenation reaction of polycyclic aromatic hydrocarbons, it has the form [12]:

At τ=0, y1(0)=0.025; y2(0)=0.9; y6(0)=0.067; y9(0)=0.008; yi(0)=0, i=3–5,7,8,10–20; Q(0)=1.
Figure 2 shows the calculated set of solutions satisfying the constraints of the system and the Pareto front, where f1 — output of the target naphthenes, and f2 — conversion of the feedstock.
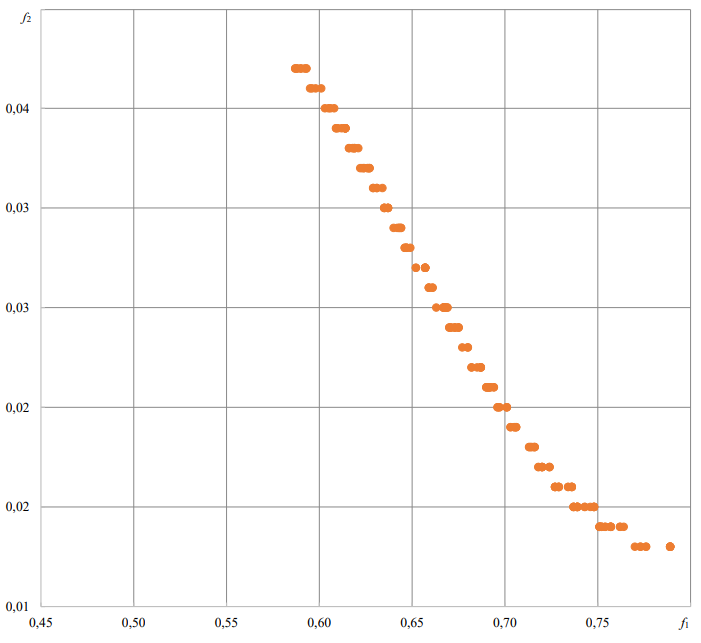
Fig. 2. Pareto front of the hydrogenation process of polycyclic aromatic hydrocarbons
The controlled parameter is the process temperature [13]. The optimality criteria are maximizing the output of target naphthenes at the end of the reaction and maximizing the conversion of feedstock [14]. Calculations using the proposed algorithm gave the results of matching the optimality criteria and the values of the temperature parameter, which are summarized in Table 1.
Table 1
Compliance of optimality criteria and temperature parameter value of the hydrogenation of polycyclic aromatic hydrocarbons
|
Output of targeted naphthenes f1 |
Feedstock conversion f2 |
Temperature T, K |
|
0.43 |
0.03 |
200.00 |
|
0.59 |
0.03 |
221.20 |
|
0.71 |
0.01 |
250.00 |
|
0.76 |
0.01 |
271.10 |
|
0.79 |
0.01 |
300.00 |
Thus, as the temperature grows, the output of the target naphthenes increases, and the conversion of the feedstock decreases. Each of these solutions is unimprovable, and the selection of specific values depends on the decision maker.
For NSGA-II to work successfully, it is required to select the algorithm parameters correctly. Specifically, the criteria of population size, number of generations, probability of crossover and mutation, should be optimized. When launching the algorithm on the model of the hydrogenation process of polycyclic aromatic hydrocarbons, the following parameters were used: population size — 100, number of generations — 100. An insufficiently large population may cause premature convergence of the algorithm to the local optimum. Too large population can slow down the optimization process [15]. An excessive number of generations potentially leads to retraining the algorithm, whereas with an insufficient number of generations there may not be enough time to achieve optimal solutions.
Discussion and Solution. A program has been created that implements the NSGA-II multicriteria optimization algorithm. Working with the corresponding problem within the framework of this method includes solving a system of differential equations, visualizing a set of solutions satisfying the constraints of the system, and constructing a Pareto front. In addition, the values of the variable parameters were found to achieve optimization goals. For the PAH hydrogenation process, based on the kinetic model, a set of temperature values has been calculated that are optimal for obtaining the unimprovable values of two optimality criteria: naphthene output and feedstock conversion. With increasing temperature, the reaction rate and the output of naphthenes increases. However, the conversion of raw materials is decreasing. In addition, too high temperatures can cause adverse reactions and decomposition of products.
The data obtained in the framework of the presented research can be useful for optimizing the process of hydrogenation of PAH under industrial conditions. It is important to take into account the impact of temperature on the output of naphthenes and the conversion of raw materials when developing a production strategy. In addition, other parameters, on which the kinetics of the reaction depends, should be considered. These are, e.g., pressure, flow rate of reagents, and the role of catalysts.
Thus, the developed program and the proposed algorithm make it possible to simultaneously analyze several criteria for the optimality of the process based on a kinetic model, and generate a set of unimprovable values of variable parameters.
References
1. Akhmetov AF, Akhmetov AV, Zagidullin ShG, Shayzhanov NS. Hydrofinery Processing Heavy Fraction of Aromatic Hydrocarbons C10+ on Catalyzer Nickel on Kizelgur. Bashkir Chemical Journal. 2018;25(1):96–98. https://doi.org/10.17122/bcj-2018-1-96-98
2. Akhmetov AF, Akhmetov AV, Shayzhanov NS, Zagidullin ShG. Hydrogenolysis of Residual Fractions Obtained by Pyrolysis Process. Bashkir Chemical Journal. 2017;24(2):29–32. URL: https://bcj.rusoil.net/files/slider/BCJ-2-2017.pdf (accessed: 07.11.2023).
3. Shayzhanov NS, Zagidullin ShG, Akhmetov AV. Activity Analysis of Hydrogenation Catalysts in the Process of High-Density Jet Fuels Production. Bashkir Chemical Journal. 2014;21(2):94–98. URL: https://cyberleninka.ru/article/n/analiz-aktivnosti-katalizatorov-gidrirovaniya-v-protsesse-polucheniya-vysokoplotnyh-reaktivnyh-topliv/viewer (accessed: 07.11.2023).
4. Koledina KF, Koledin SN, Karpenko AP, Gubaydullin IM, Vovdenko MK. Multi-Objective Optimization of Chemical Reaction Conditions Based on a Kinetic Model. Journal of Mathematical Chemistry. 2019;57(2):484–493. https://doi.org/10.1007/s10910-018-0960-z
5. Emmerich M, Deutz A. Multicriteria Optimization and Decision Making: Master Course. Leiden: Leiden University Publishing; 2014. 102 p. URL: https://liacs.leidenuniv.nl/~emmerichmtm/modapage/MCOReaderEmmeirchDeutz2017.pdf (accessed: 17.11.2023).
6. Deb K, Mohan M, Mishra S. Towards a Quick Computation of Well-Spread Pareto-Optimal Solutions. In book: CM Fonseca, PJ Fleming, E Zitzler, L Thiele, K Deb (eds). Evolutionary Multi-Criterion Optimization. Berlin, Heidelberg: Springer; 2003. P. 222–236. https://doi.org/10.1007/3-540-36970-8_16
7. Koledina KF. Multi-Criteria Interval Optimization of Conditions for Complex Chemical Reactions on the Basis of a Kinetic Model. Mathematical Models and Computer Simulations. 2022;34(8):97–109. https://doi.org/10.20948/mm-2022-08-06
8. Miernik K, Węglińska E, Danek T, Leśniak A. An Application of the NSGA-II Algorithm in Pareto Joint Inversion of 2D Magnetic and Gravity Data. Geology Geophysics & Environment. 2021;47(2):59–70. https://doi.org/10.7494/geol.2021.47.2.59
9. Martínez S, Perez E, Eguia P, Erkoreka A, Granada E. Model Calibration and Exergoeconomic Optimization with NSGA-II Applied to a Residential Cogeneration. Applied Thermal Engineering. 2020;169:114916. https://doi.org/10.1016/j.applthermaleng.2020.114916
10. Kamshilova YuA, Semenkin ES. Comparative Analysis of Multiobjective Evolutionary Algorithms’ SPEA2 and NSGA-II Efficiency. In: Proc. XVI Int. Sci. Conf. dedicated to the memory of the General Designer of rocket and space systems Academician MF Reshetnev “Reshetnev Readings”. Part 2. Krasnoyarsk: Siberian State Aerospace University named after academician MF Reshetnev; 2012. P. 484. URL: https://disk.sibsau.ru/website/reshetnevsite/materials/2012_2.pdf (accessed: 17.11.2023).
11. Cîrciu MS, Leon F. Comparative Study of Multiobjective Genetic Algorithms. Bulletin of the Polytechnic Institute of Iasi. 2010;56(60):1-13. URL: https://www.researchgate.net/publication/228845090 (accessed: 02.03.2024).
12. Koledina KF, Gubaidullin IM, Zagidullin ShG, Koledin SN, Sabirov DSh. Kinetic Regularities of Hydrogenation of Polycyclic Aromatic Hydrocarbons on Nickel Catalysts. Russian Journal of Physical Chemistry A. 2023;97(10):2104–2110. https://doi.org/10.1134/s003602442309008x
13. Zagidullin ShG, Koledina KF. Mathematical Modeling of the Kinetics of Hydration of Polycyclic Aromatic Hydrocarbons. Bulletin of BSU. 2021;26(3):664–669. https://doi.org/10.33184/bulletin-bsu-2021.3.23
14. Bukhtoyarov SE, Emelichev VA. Stability Aspects of Multicriteria Integer Linear Programming Problems. Journal of Applied and Industrial Mathematics. 2019;13:22–29. https://doi.org/10.1134/S1990478919010034
15. Tan Liguo, Novikova SV. Application of the Step Learning Method for the Evolutionary Algorithm in Problems of Multi-Criteria Optimization. Vestnik KGEU. 2022;14(3):114–124.a
About the Authors
A. A. AlexandrovaRussian Federation
Anastasiya A. Alexandrova, graduate student of the Information Technologies and Applied Mathematics Department
1, Kosmonavtov St., Ufa, 450064
S. N. Koledin
Russian Federation
Sergey N. Koledin, Cand.Sci. (Phys.-Math.), Associate Professor of the Information Technologies and Applied Mathematics Department
1, Kosmonavtov St., Ufa, 450064
Review
For citations:
Alexandrova A.A., Koledin S.N. Optimal Temperature Calculation for Multicriteria Optimization of the Hydrogenation of Polycyclic Aromatic Hydrocarbons by NSGA-II Method. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):109-118. https://doi.org/10.23947/2687-1653-2024-24-1-109-118. EDN: VNTDAG












































