Scroll to:
Assessment of Dynamic States of Railway Vehicles: Structural Mathematical Modeling
https://doi.org/10.23947/2687-1653-2024-24-2-125-134
EDN: PEUPEC
Abstract
Introduction. The speed rise of railway transport and an increase in the loads on the axles of wheelsets necessitate the modernization of the existing fleet. Scientific studies in the field of rolling stock dynamics are aimed at taking into account the oscillatory processes that occur during the movement of railway vehicles in a traditional design. The attachment of supplementary elements was considered at the coupling level of two cars and the attachment of a third trolley in the center of gravity of the railway platform. The scientific literature has not paid enough attention to the construction of mathematical models that make it possible to assess the dynamic states of such constructive solutions. The objective of this study is to create a method for evaluating the dynamic conditions of a car. The situation is considered when an additional set of mass-inertial and elastic elements is introduced into its structure, and the general dynamic condition of the vehicle depends on the adjustment of their parameters.
Materials and Methods. The basic research tool is the structural mathematical modeling, which is based on an approach where the source design scheme is a mechanical oscillatory system in the form of a solid body on elastic supports with supplementary typical elements introduced into its structure. The dynamic analogue of the calculation scheme used is the block diagram of the automatic control system, the use of which provides detailing the connections between typical elastic and mass-inertia elements.
Results. A method for estimating the dynamic states of railway vehicles is proposed. It is based on the construction of mathematical models, taking into account the introduction of an additional structure of mass-inertia and elastic elements. The impact of additional parameters on the dynamic condition of the vehicle is investigated. Analytical relations have been obtained that provide reducing the dynamic loads on the major structural elastic elements when changing the corresponding parameters of a technical object. The transfer function of interpartial relations is given, which provides controlling the interaction between the coordinates of the vehicle movement under the action of two kinematic disturbances of the in-phase type.
Discussion and Conclusion. The generated mathematical model provides for assessment, monitoring and control of the dynamic state of the vehicle under conditions of kinematic disturbances. The research results can be used to modernize existing vehicles and create new ones with improved dynamics.
For citations:
Bolshakov R.S., Gozbenko V.E., Vuong Q.T. Assessment of Dynamic States of Railway Vehicles: Structural Mathematical Modeling. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):125-134. https://doi.org/10.23947/2687-1653-2024-24-2-125-134. EDN: PEUPEC
Introduction. The expansion of technical-and-economic ties at the interregional level, providing the growth of the country's industrial engineering potential, and maintaining the growing system of international trade and commercial relations largely depends and relies on rail transport [1]. The rail traffic volume is constantly increasing. This drives the need to take into account the perverse effects of increased dynamic loads [2], which directly affect the reliability of operation of both rolling stock and the track structure. Despite such negative factors, it is necessary to fulfill the planned indicators, which include an increase in the service speed, compliance with weight and length standards for trains, increasing axle load to 30 tons or more. This reflects the real demands of the development of the Russian economy and stimulates the creation of new more powerful locomotives, the renewal of the fleet of rolling stock, and the modernization of track facilities [3]. At the same time, the possibility of negative consequences of the intensification of transportation processes should also be considered. One of the major issues is the increase in the rate of wear of the track structure with the corresponding resulting difficulties [4].
Currently, particular attention is being paid to the development of a methodology for assessing the dynamic condition of rolling stock, the interaction of technical means and rail tracks, energy savings, and improving the reliability and safety of transportation processes. The mathematical modeling methodology is described, e.g., in [5]. At the same time, there are other possibilities for finding rational solutions [6]. It is important to pay attention to the modernization of the existing fleet of freight wagons, whose operation is no longer effective under increased loads [7]. One of the approaches that could be adopted for the development is the concept of installing an additional two-axle bogie for freight 4ax wagons [8]. In this case, we can expect a more uniform distribution of the load on the track structure, as well as the possibility of increasing the weight of the transported goods while maintaining the regulations for axial load values within 22 tons [9]. The unevenness of the wheel-rail contact parameters initiates the oscillatory movements of the car, which in turn forms the oscillatory movements of the car body. The oscillation process is also formed by the conditions of interaction of wagons inside the train [10]. In this case, dynamic restraint forces occur, superimposing on the static components of the overall reaction, which can significantly increase the level of dynamic interactions in the wheel-rail contact [11][12]. However, the possibilities of structural mathematical modeling in assessing the dynamic states of railway vehicles with the introduction of additional links have not yet been given enough attention. Therefore, the objective of this study is to form a method for evaluating the dynamic states of a railway vehicle when introducing an additional set of mass-inertial and elastic elements into its structure, the correction of the parameters of which would affect the overall dynamic state of the vehicle.
Materials and Methods. The methodological basis of the research is the structural theory of vibration isolation systems, which provides for the accurate assessment of the dynamic properties of a railway vehicle in a linear formulation, taking into account concentrated parameters and small oscillations relative to the position of static equilibrium or a steady-state process. The design scheme is a mechanical vibratory system with dynamic equivalent in the form of a block diagram of an automatic control system. This makes it possible to detail the connections between the elements of the vehicle, as well as to use methods characteristic of the theory of automatic control (transfer functions, transformations of structural circuits, convolution and simplification, frequency characteristics) [13].
Standard design schemes of freight railway vehicles are described by well-known calculation schemes, and their dynamic features can be estimated using linear calculation schemes. The article considers a railway vehicle in the form of a four-axle freight wagon designed for the transportation of heavy goods such as coal, ore, sand, rolled metal, small-sized metal structures, etc. (Fig. 1).
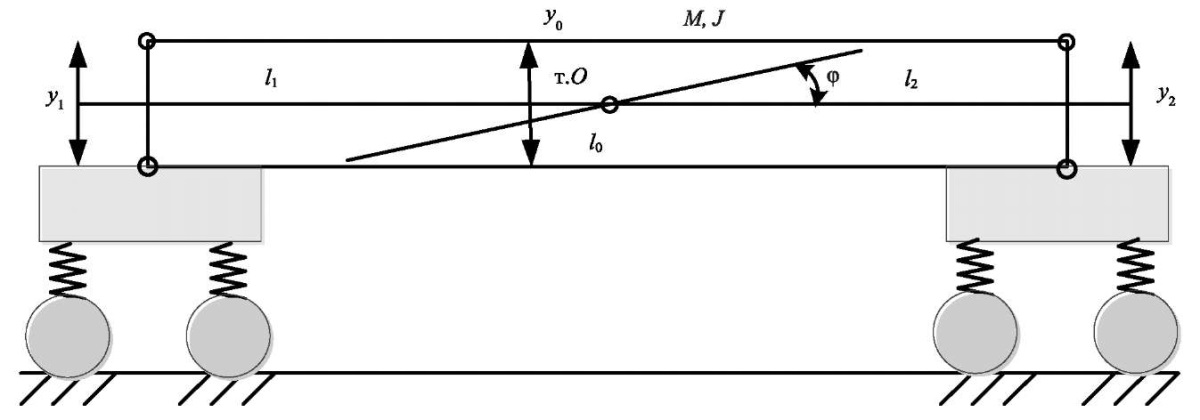
Fig. 1. Schematic diagram of a four-axle freight wagon
The structure of the presented railway vehicle contains a body with mass M and moment of inertia J. It is based on two four-wheel bogies, conventionally represented as a set of mass-inertial and elastic elements. The dynamic features of the system under consideration show the excessive impact on the structural elements of the bogies of the railway vehicle. In this regard, to improve its dynamic properties, a third two-axle truck is additionally introduced into the suspension structure, which is located in the center of the wagon (Fig. 2).
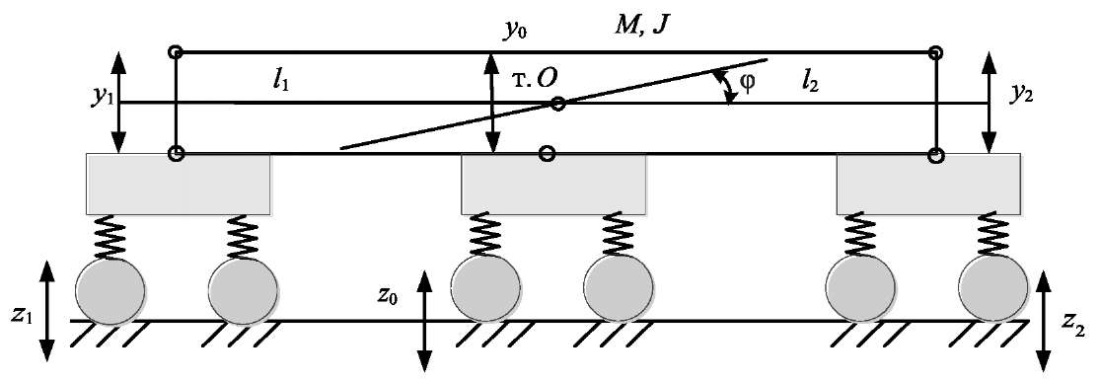
Fig. 2. Schematic diagram of a six-axle freight car
With a car's own weight of about 23 tons, and an axial load of 22 tons, this can provide an increase in the weight of transported goods by approximately 20 tons, i.e., significantly increase the efficiency of transportation processes without creating excessive dynamic loads on the track structure (TS). The practical implementation of the proposed approach requires the modernization of the design of a standard wagon. The modernization consists in creating an additional bogie attachment unit to reduce the load on the axle of a freight wagon by introducing an additional two-axle track. The upgrading of the attachment unit is carried out in the same structural and technical forms as the fastening using pins in two “standard” two-axle bogies, i.e., through the installation of over- and underpin bolsters with the corresponding standard-type pin assembly.
The proposed method of increasing the efficiency of using four-axle freight cars under conditions of additional loads is aimed at solving the problem of increasing the load on the axle of the wheelset to 30 tons, and speeding up the trains. This is achieved through upgrading a typical freight car by installing an additional two-axle bogie with an appropriate device that provides conditions for its dynamic interaction with the frame structure of the freight car.
The installation of an additional two-axle bogie by redistributing the load between a common set of wheelsets provides the possibility of transporting heavy loads while reducing the load on the axle. This maintains better operating conditions for the track and the superstructure while maintaining an acceptable length of the train.
It is assumed that the pin assembly has an elastic rubber gasket that provides cushioning for the interaction of the bogie and the frame of the wagon body. At the same time, it is not supposed to upgrade the wheels of the wheelsets. Only the form of wiring of the elements of the “regular” pneumatic braking system and the configuration of the supply of pneumatic pipelines are changed.
Research Results. The design scheme of the considered railway vehicle in the first approximation can be represented as a mechanical oscillatory system consisting of a solid body with mass m and moment of inertia J, based on three elastic elements with stiffness k1, k0, k2. Kinematic effects are represented by in-phase harmonic functions of the same frequency (Fig. 3).
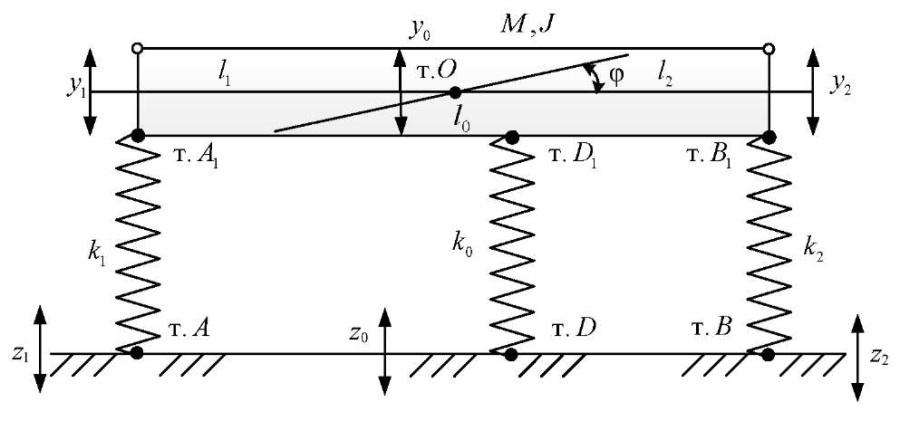
Fig. 3. Design scheme of a railway vehicleunder kinematic disturbance (z1, z2, z0)
The center of mass of the system — point О is located at distances l1 and l2 from the ends of the solid (points А1, В1). The element with stiffness k0 is fixed at points D and D1; distance ОD1 is indicated as l0. The movement of the system is considered in coordinates y1, y2 and y0, φ, associated with a fixed basis. The calculations use the following ratios:
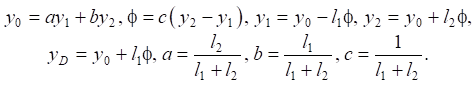 (1)
(1)
Lagrange formalism is used to derive differential equations of motion [14], which requires the construction of expressions for kinetic and potential energies. In this case, we have:
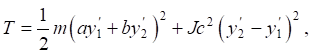 (2)
(2)
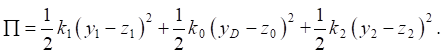 (3)
(3)
Note that potential energy (3) can also be written as:
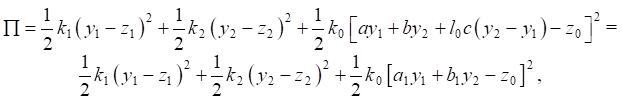 (4)
(4)
where a1 = a – l0c, b1 = b + l0c.
The system of equations of motion in coordinates y1, y2 in the time domain takes the form:
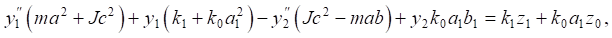 (5)
(5)
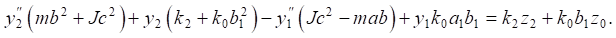 (6)
(6)
After applying the Laplace integral transformations under zero initial conditions [15], the system of equations (5), (6) can be represented in the operator form:
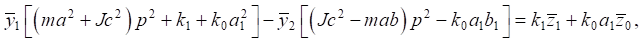 (7)
(7)
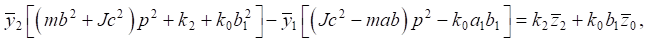 (8)
(8)
where p = jω — complex variable (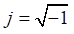 ), indicator <–> above the variable means its Laplace image [5].
), indicator <–> above the variable means its Laplace image [5].
On the basis of (7), (8), in accordance with the provisions of the method of structural mathematical modeling [5], a structural mathematical model in the form of a block diagram is constructed, which is dynamically equivalent to an automatic control system (Fig. 4).
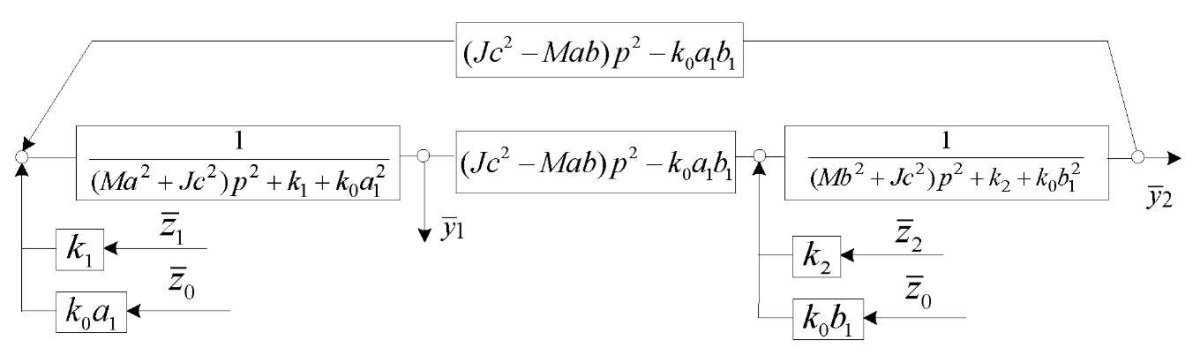
Fig. 4. Structural mathematical model of a railway vehicle
Discussion and Conclusion. The feature of the system is that it has two partial blocks, each of which determines the corresponding partial frequencies:
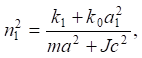 (9)
(9)
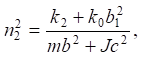 (10)
(10)
which, in turn, determine the boundaries of the location of the natural oscillation frequencies of the system as a whole:
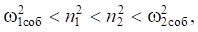 (11)
(11)
where ω1соб, ω2соб — natural oscillation frequencies of the system. When operating on them, resonant modes may occur.
Among the features of the system there are several simultaneously acting external disturbances. Assuming, for the sake of simplification, that 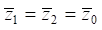 (quite acceptable at the stages of preliminary dynamic estimates), we consider that force factors act on the input of the first and second partial blocks:
(quite acceptable at the stages of preliminary dynamic estimates), we consider that force factors act on the input of the first and second partial blocks:
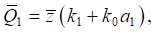 (12)
(12)
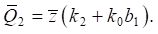 (13)
(13)
Using the block diagram in Figure 4, we write down the expressions for the transfer functions, assuming that there is a relationship between the external perturbation factors formed by the ratio:
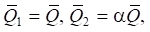 (14)
(14)
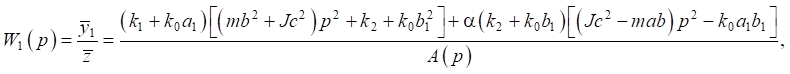 (15)
(15)
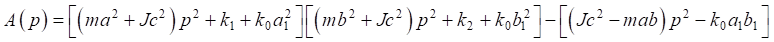 (16)
(16)
where
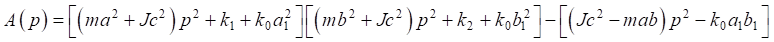 (17)
(17)
is the frequency characteristic equation of the system.
The numerator of the transfer functions in expressions (15), (16) determines the modes of dynamic vibration damping, which can be detailed from the equations obtained by “zeroing” numerators (15), (16):
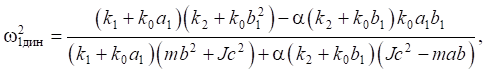 (18)
(18)
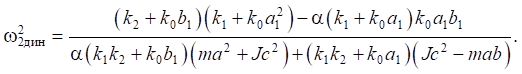 (19)
(19)
It follows from expressions (18), (19) that in a system with two degrees of freedom, in the presence of two interconnected disturbing factors, dynamic vibration damping modes at two frequencies may occur, whose parameters depend on the values of connectivity coefficient α. This coefficient can take negative, positive and zero values.
The analysis of the structural mathematical model (Fig. 4) also implies the possibility of a special dynamic mode at the frequency:
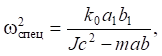 (20)
(20)
when the partial blocks get the possibility of disconnection. In this case, the system (Fig. 3) splits into two autonomous blocks, which do not create situations of interaction of partial structures.
The implementation of this mode can cause a significant difference in the values of deviations at points А1 and В1, and a “spread” of values of the dynamic reactions at points А1, В1 and D1. The determination of dynamic reactions at points А, В and D can be implemented according to the methodology described in [14], in which the dynamic reaction is defined as the product of a dynamic displacement (e.g., points А1, В1 and D1) by the value of the reduced dynamic stiffness.
For coordinate 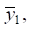 the dynamic offset is determined from the expression for transfer function (15), and for coordinate
the dynamic offset is determined from the expression for transfer function (15), and for coordinate 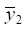 — from expression (16). The frequency characteristic equation is used to determine the reduced dynamic stiffness (17):
— from expression (16). The frequency characteristic equation is used to determine the reduced dynamic stiffness (17):
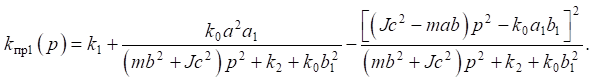 (21)
(21)
Similarly, the value of the reduced dynamic stiffness in coordinate 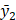 can be found:
can be found:
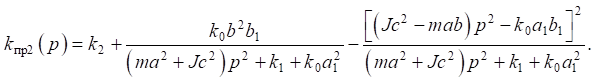 (22)
(22)
To determine the specific values 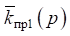 and
and 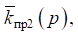 it is necessary to find the value of frequency ω2, which is determined from the condition that
it is necessary to find the value of frequency ω2, which is determined from the condition that 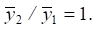 More generally, it is assumed that:
More generally, it is assumed that:
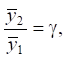 (23)
(23)
where γ — coefficient of connectivity of the movement of elements by coordinates ![]() and
and 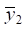 . Thus, this coefficient (for the case γ=1) can be written as:
. Thus, this coefficient (for the case γ=1) can be written as:
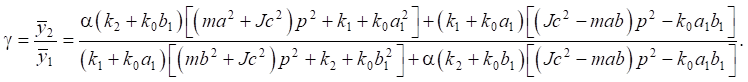 (24)
(24)
Taking specific values γ, it is possible to find the oscillation frequencies for the motion of the object in question in coordinates 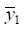 and
and 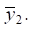 Specifically, at γ = 1, the frequency of translational vertical vibrations of a solid is determined from the expression:
Specifically, at γ = 1, the frequency of translational vertical vibrations of a solid is determined from the expression:
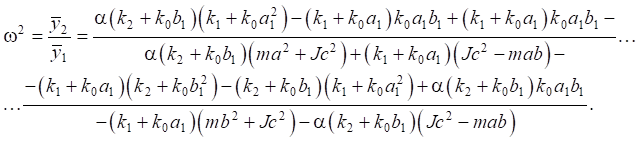 (25)
(25)
Frequency ω of in-phase harmonic disturbances z1(t), z2(t) and z0(t) provides the motion of a solid body at φ = 0, i.e., 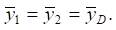 For other values γ (γ ≠ 1),
For other values γ (γ ≠ 1), 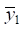 and
and 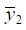 are determined, and on their basis, for geometric reasons, value
are determined, and on their basis, for geometric reasons, value 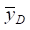 is determined. For a solid body with known
is determined. For a solid body with known 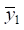 and
and 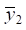 , the position of the center of rotation (or oscillations) can be easily found [12].
, the position of the center of rotation (or oscillations) can be easily found [12].
The dynamic constraint reactions 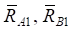 and
and 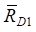 can be found in the first approximation by the formulas:
can be found in the first approximation by the formulas:
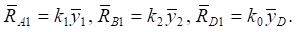
In general, dynamic reactions are determined using dynamic displacements 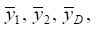 that are defined by expressions (15), (16). As for the dynamic displacement at point D, expression
that are defined by expressions (15), (16). As for the dynamic displacement at point D, expression 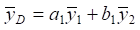 is used, whose parameters are determined by the above values. In expressions (15), (16), data on the connectivity of force factors of influence (parameter α) can be entered. To obtain specific data on the values of dynamic reactions, frequency parameters are introduced at which the ratio of oscillation amplitudes
is used, whose parameters are determined by the above values. In expressions (15), (16), data on the connectivity of force factors of influence (parameter α) can be entered. To obtain specific data on the values of dynamic reactions, frequency parameters are introduced at which the ratio of oscillation amplitudes 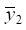 and
and 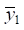 is implemented through the coefficient of coupling of oscillation amplitudes γ.
is implemented through the coefficient of coupling of oscillation amplitudes γ.
The overall restraint force at points А, В and D is determined by the sum of two components: static and dynamic. The static component can be found from the expression for the transfer functions of dynamic reactions at p = 0 and setting the parameters of the static load (weight of the wagon and the cargo being transported). With the intensive development of oscillatory processes, when fluctuations in coordinates 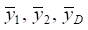 increase, the overall reaction can vary significantly and differ from the static restraint force. In the presence of a dynamic component, the overall reaction can take on various values, in particular, zero or negative.
increase, the overall reaction can vary significantly and differ from the static restraint force. In the presence of a dynamic component, the overall reaction can take on various values, in particular, zero or negative.
The mathematical model formed within the framework of the proposed method is indicated by expression (25). It provides assessing the dynamic state of railway vehicles when additional connections are introduced into their structure to form a set of recommendations for obtaining stable modes of operation. The investigation of the features of the system using approaches typical of structural mathematical modeling allows us to consider in detail the connections between the elements. With regard to the technical object in question, this makes it possible to adjust the dynamic state of the technical object, based on varying the parameters of the set of additionally introduced elements, to reduce the load on the main parts of the suspension, as well as to establish the presence of natural frequencies and frequencies of dynamic vibration damping in the system.
In the future, it is planned to conduct research on the introduction of dampers and motion conversion devices into the structure of the vehicle to assess the possibilities of structural mathematical modeling. Another interesting area is the assessment of the possibilities of changing dynamic reactions depending on external actions, which will allow us to assess the efforts exerted on various elements of the vehicle suspension.
References
1. Kossov VS, Knyazev DA, Krasyukov NF, Makhutov NA, Gadenin MM. Regulatory Framework for Ensuring the Safe Operation of Railway Equipment Based on the Service Life of Load-Bearing Structures. World of Transport and Transportation. 2023;21(3):254–262. https://doi.org/10.30932/1992-3252-2023-21-3-10
2. Makhutov NA, Lapidus BM, Gadenin MM, Titov EYu. Tasks and Prospects for the Development of Scientific Research within the Framework of Cooperation between JSC “Russian Railways” and the Russian Academy of Sciences. Zheleznodorozhnyi transport. 2023;(7):6–11. (In Russ.).
3. Lapidus BM. Tasks of Advanced Development of Russian Railways. Zheleznodorozhnyi transport. 2023;(2):4–14. (In Russ.).
4. Kolesnikov VI, Migal YuF, Kolesnikov IV, Sitrev AP, Voropaev AP. Increasing the Wear Resistance of Heavily Loaded Tribosystems by Forming the Structure and Properties of Their Contact Surfaces. Nauka Yuga Rossii (Science in the South Russia). 2022;18(4):59–65. https://www.doi.org/10.7868/S25000640220407 (In Russ.).
5. Eliseev SV, Eliseev AV, Bolshakov RS, Khomenko AP. Methodology of System Analysis in Problems of Assessment, Formation and Control of the Dynamic State of Technological and Transport Machines. Moscow: “Nauka”; 2021. 679 p. (In Russ.).
6. Romen YuS, Belgorodtseva TM, Dediaev MV. Condition of Wagon Wheels and Axles and Interaction Forces in the “Crew – Track” System. Transport of Russian Federation. 2021;95(4):36–40. https://rostransport.elpub.ru/
7. jour/article/view/127/127 (accessed: 19.02.2024).
8. Savoskin AN, Romen YuS, Akashev MG. A Useful Random Process of Acting Lateral Forces between a Wheel and Rail and Its Probabilistic Characteristics. Vestnik Mashinostroeniya. 2022;(4):14–19. URL: https://www.mashin.ru/eshop/journals/vestnik_mashinostroeniya/2031/19/ (accessed: 19.02.2024).
9. Ermolenko IYu, Morozov DV, Astashkov NP. Influence of Longitudinal Loads on Traffic Safety When Operating on Mountain Passway Sections. Vestnik RGUPS, Rostov State Transport University. 2021;82(2):104–111. https://doi.org/10.46973/0201-727X_2021_2_104
10. Buldaev AS, Khishektueva IKhD, Anakhin VD, Dambaev ZhG. On One Method for Solving the Problem of Identifying Dynamic Systems. Bulletin of Buryat State University. Mathematics, Informatics. 2020;(4):14–25. https://doi.org/10.18101/2304-5728-2020-4-14-25
11. Buldaev AS. Projection Perturbation Methods in Optimization Problems of Controlled Systems. Bulletin of Irkutsk State University. Series: Mathematics. 2014;8:29–43. URL: https://mathizv.isu.ru/en/journal?id=7 (accessed: 19.02.2024).
12. Mizhidon AD, Khamkhanov AK. A Hybrid System of Differential Equations Describing a Rigid Body Attached to Two Elastic Rods. Bulletin of Buryat State University. Mathematics, Informatics. 2022;(4):38–47. https://doi.org/10.18101/2304-5728-2022-4-38-47
13. Eliseev AV, Mironov AS, Eliseev SV. Formation of Mathematical Models of Vibration Interactions of Elements of Technical Means of Transport and Technological Purposes. Proceedings of Voronezh State University. Series: Systems Analysis and Information Technologies. 2022;(1):32–42. https://doi.org/10.17308/sait.2022.1/9199
14. Eliseev AV, Kuznetsov NK, Eliseev SV. New Approaches to the Estimation of Dynamic Properties of Vibrational Structures: Frequency Functions and Connectivity of Movements. Trudy MAI. 2021;(120):08. https://doi.org/10.34759/trd-2021-120-08
15. Eliseev AV, Kuznetsov NK. The Concept of a Generalized Lever in Assessing the Dynamic States of Mechanical Oscillatory Systems under Conditions of Connected Vibration Loads. Systems. Methods. Technologies. 2023;59(3):7–12. https://doi.org/10.18324/2077-5415-2023-3-7-12
16. Kashuba VB, Bolshakov RS, Mozalevskaya AK, Nguyen Huynh Duc. Identification of Ties Responses between Vibroprotection Systems Elements on Base of Structural Transformation Method. In: Proc. XV All-Russian Sci.-Tech. Conference with International Participation “Mechanical Engineers to XXI Century”. Bratsk: BrSU; 2016. P. 295–300.
About the Authors
R. S. BolshakovRussian Federation
Roman S. Bolshakov, Cand.Sci. (Eng.), Associate Professor of the Operational Work Management Department
15, Chernyshevskogo Str., Irkutsk, 664074
V. E. Gozbenko
Russian Federation
Valery E. Gozbenko, Dr.Sci. (Eng.), Professor of the Mathematics Department
15, Chernyshevskogo Str., Irkutsk, 664074
Quang Truc Vuong
Russian Federation
Vuong Quang Truc, postgraduate of the Department of Physics, Mechanics and Instrumentation
15, Chernyshevskogo Str., Irkutsk, 664074
Review
For citations:
Bolshakov R.S., Gozbenko V.E., Vuong Q.T. Assessment of Dynamic States of Railway Vehicles: Structural Mathematical Modeling. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):125-134. https://doi.org/10.23947/2687-1653-2024-24-2-125-134. EDN: PEUPEC
JATS XML














































