Перейти к:
Возможности оценки динамических состояний железнодорожных транспортных средств: структурное математическое моделирование
https://doi.org/10.23947/2687-1653-2024-24-2-125-134
EDN: PEUPEC
Аннотация
Введение. Увеличение скоростей движения железнодорожного транспорта и повышение нагрузок на оси колесных пар обуславливают необходимость модернизации существующего парка. Научные исследования в области динамики подвижного состава направлены на учёт колебательных процессов, возникающих при движении железнодорожных транспортных средств в традиционном конструктивном исполнении. Присоединение дополнительных элементов рассматривалось на уровне сцепки двух вагонов и присоединении третьей тележки в центре тяжести железнодорожной платформы. Построению математических моделей, позволяющих оценить динамические состояния таких конструктивных решений, в научной литературе не уделено достаточно внимания. Цель данного исследования — создать метод оценки динамических состояний вагона. Рассматривается ситуация, когда в его структуру вводится дополнительная совокупность масс-инерционных и упругих элементов, причем от корректировки их параметров зависит общее динамическое состояние транспортного средства.
Материалы и методы. Базовым инструментом проведения исследований является структурное математическое моделирование, в основе которого лежит подход, когда исходная расчетная схема представляет собой механическую колебательную систему в виде твердого тела на упругих опорах с дополнительной введёнными в её структуру типовыми элементами. Динамическим аналогом используемой расчетной схемы является структурная схема системы автоматического управления, применение которой позволяет детализировать связи между типовыми упругими и масс-инерционными элементами.
Результаты исследования. Предложен метод оценки динамических состояний железнодорожных транспортных средств, основанный на построении математических моделей, с учетом введения дополнительной структуры масс-инерционных и упругих элементов. Исследовано влияние дополнительных параметров на динамическое состояние транспортного средства. Получены аналитические соотношения, позволяющие при изменении соответствующих параметров технического объекта снизить динамические нагрузки на основные конструктивные упругие элементы. Приведена передаточная функция межпарциальных связей, позволяющая контролировать взаимодействие между координатами движения транспортного средства при действии двух кинематических возмущений синфазного типа.
Обсуждение и заключение. Сформированная математическая модель позволяет оценить динамическое состояние железнодорожного транспортного средства в условиях действия кинематических возмущений. Результаты исследований могут быть применены при модернизации существующих и создании новых транспортных средств с улучшенной динамикой.
Ключевые слова
Для цитирования:
Большаков Р.С., Гозбенко В.Е., Выонг К.Ч. Возможности оценки динамических состояний железнодорожных транспортных средств: структурное математическое моделирование. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):125-134. https://doi.org/10.23947/2687-1653-2024-24-2-125-134. EDN: PEUPEC
For citation:
Bolshakov R.S., Gozbenko V.E., Vuong Q.T. Assessment of Dynamic States of Railway Vehicles: Structural Mathematical Modeling. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):125-134. https://doi.org/10.23947/2687-1653-2024-24-2-125-134. EDN: PEUPEC
Введение. Расширение технико-экономических связей межрегионального уровня, обеспечение роста производственно-технического потенциала страны и поддержание разрастающейся системы международных торгово-коммерческих отношений во многом зависит и опирается на железнодорожный транспорт [1]. Объёмы перевозок, выполняемых железнодорожным транспортом, постоянно возрастают, что обусловливает необходимость учета нежелательных эффектов от повышения динамических нагрузок [2], напрямую влияющих на надежность эксплуатации как подвижного состава, так и верхнего строения пути. Несмотря на наличие таких негативных факторов, необходимо выполнять плановые показатели, к которым можно отнести повышение участковой скорости, соблюдение норм веса и длины составов, увеличение осевой нагрузки до 30 тонн и более. Это отражает реальные запросы развития российской экономики и стимулирует создание новых более мощных локомотивов, обновление парка подвижных средств, модернизацию путевого хозяйства [3]. Вместе с тем нельзя не рассматривать и возможности проявления негативных последствий интенсификации перевозочных процессов. Одним из важных вопросов является возрастание или увеличение темпов износа верхнего строения пути с соответствующими вытекающими сложностями [4].
В текущий момент времени повышенное внимание уделяется развитию методологии оценки динамического состояния подвижного состава, взаимодействию технических средств с рельсовыми путями, экономии электроэнергии, повышению надёжности и безопасности перевозочных процессов. Методология математического моделирования описана, например, в [5]. Вместе с тем, существуют и другие возможности для поиска рациональных решений [6]. Важно уделить внимание вопросам модернизации существующего парка грузовых вагонов, эксплуатация которых при повышенных нагрузках уже не является эффективной [7]. Одним из подходов, который мог бы быть принят к разработке, является концепция установки для грузовых 4-осных вагонов дополнительной двухосной тележки [8]. В этом случае можно ожидать более равномерного распределения нагрузки на верхнее строение пути, а также возможность увеличения веса перевозимых грузов при сохранении регламента на значения осевой нагрузки в пределах 22 т [9]. Неравномерность параметров контакта колесо-рельс инициирует колебательные движения вагона, что формирует в свою очередь колебательные движения корпуса вагона. Процесс колебаний формируется также условиями взаимодействия вагонов внутри состава [10]. В этом случае возникают динамические реакции связей, накладывающиеся на статические составляющие полной реакции, что может существенно увеличить уровень динамических взаимодействий в контакте колесо-рельс [11][12]. Однако возможностям структурного математического моделирования при оценке динамических состояний железнодорожных транспортных средств при введении дополнительных связей пока не уделялось достаточно внимания. Поэтому целью данного исследования явилось формирование метода оценки динамических состояний железнодорожного транспортного средства при введении в его структуру дополнительной совокупности масс-инерционных и упругих элементов, корректировка параметров которых будет влиять на общее динамическое состояние транспортного средства.
Материалы и методы. Методологической основой исследований выбрана структурная теория виброзащитных систем, позволяющая в линейной постановке с учетом сосредоточенных параметров и малых колебаний относительно положения статического равновесия или установившегося процесса, достаточно точно оценить динамические свойства железнодорожного транспортного средства. Расчётной схемой является механическая колебательная система c динамическим эквивалентом в виде структурной схемы системы автоматического управления. Это позволяет детализировать связи между элементами транспортного средства, а также использовать методы, характерные для теории автоматического управления (передаточные функции, преобразования структурных схем, свертки и упрощения, частотные характеристики) [13].
Стандартные конструктивные схемы грузовых железнодорожных транспортных средств описываются известными расчётными схемами, а их динамические особенности можно оценить с использованием линейных расчётных схем. Рассматривается железнодорожное транспортное средство в виде грузового четырехосного вагона, предназначенного для перевозки тяжёлых грузов, таких как каменный уголь, руда, песок, металлопрокат, малогабаритные металлические конструкции и др. (рис. 1).
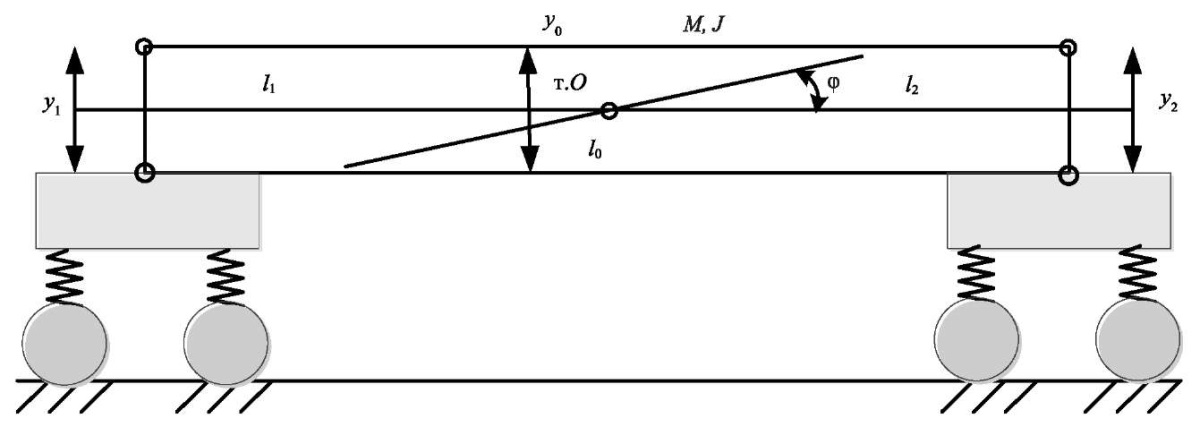
Рис. 1. Принципиальная схема грузового четырехосного вагона
Структура представленного железнодорожного транспортного средства содержит кузов, обладающий массой M, моментом инерции J и опирающийся на две двухосные тележки, условно представленные как совокупности масс-инерционных и упругих элементов. Динамические особенности рассматриваемой системы показывают наличие избыточного влияния на конструктивные элементы тележек железнодорожного транспортного средства. В этой связи для улучшения его динамических свойств в структуру подвески дополнительно вводится третья двухосная тележка, которая размещается в центре вагона (рис. 2).
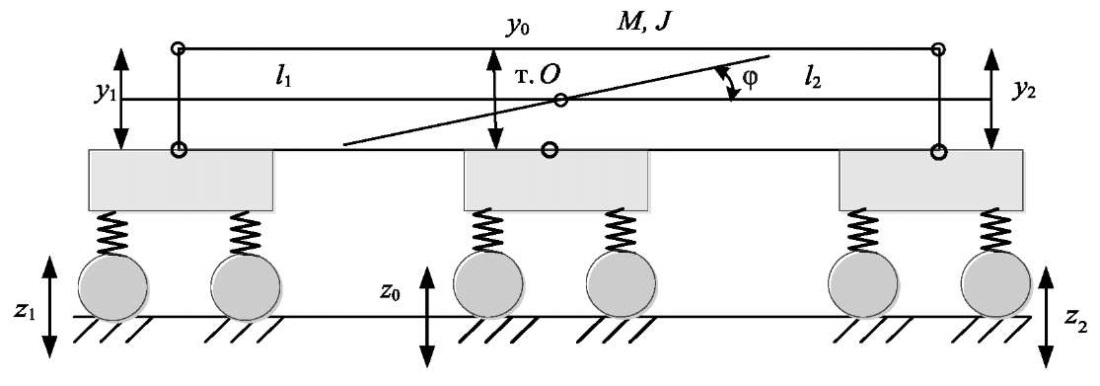
Рис. 2. Принципиальная схема грузового шестиосного вагона
При собственном весе вагона около 23 тонн и осевой нагрузке в 22 тонны, это может обеспечить увеличение веса перевозимых грузов ориентировочно на 20 тонн, то есть существенно повысить эффективность перевозочных процессов, не создавая излишних динамических нагрузок на верхнее строение пути (ВСП). Практическая реализация предлагаемого подхода требует модернизации конструкции типового вагона, которая заключается в создании узла крепления дополнительной тележки для уменьшения нагрузки на ось грузового вагона за счёт введения дополнительной двухосной тележки. Модернизация узла крепления осуществляется в тех же конструктивно-технических формах, что и крепления с использованием шкворней в двух «штатных» двухосных тележках, то есть через установку надшкворневой и подшкворневой балок с соответствующим шкворневым узлом стандартного типа.
Предлагаемая методика повышения эффективности использования четырехосных грузовых вагонов в условиях дополнительных нагружений ориентирована на решение проблемы повышения нагрузки на ось колёсной пары до 30 тонн и увеличении скорости движения поездов. Это достигается модернизацией типового грузового вагона путём установки дополнительной двухосной тележки соответствующим устройством, обеспечивающим условия её динамического взаимодействия с конструкцией рамы грузового вагона.
Установка дополнительной двухосной тележки за счёт перераспределения нагрузки между общим набором колёсных пар обеспечивает возможности перевозки грузов больших по весу при одновременном снижении нагрузки на ось. Это обеспечивает более рациональные условия эксплуатации рельсового пути и верхнего строения железнодорожного полотна при сохранении приемлемой длины состава.
Предполагается, что шкворневый узел будет иметь упругую резиновую прокладку, обеспечивающую амортизацию взаимодействия тележки и рамы корпуса вагона. При этом не предполагается модернизация дисков колесных пар. Изменяются лишь форма проводки элементов «штатной» пневматической системы торможения состава и конфигурация проводки пневмопроводов.
Результаты исследования. Расчётная схема рассматриваемого железнодорожного транспортного средства в первом приближении может быть представлена в виде механической колебательной системы, состоящей из твёрдого тела, обладающего массой m, и моментом инерции J, опирающемся на три упругих элемента с жесткостями k1, k0, k2. Кинематические воздействия представлены синфазными гармоническими функциями одной частоты (рис. 3).
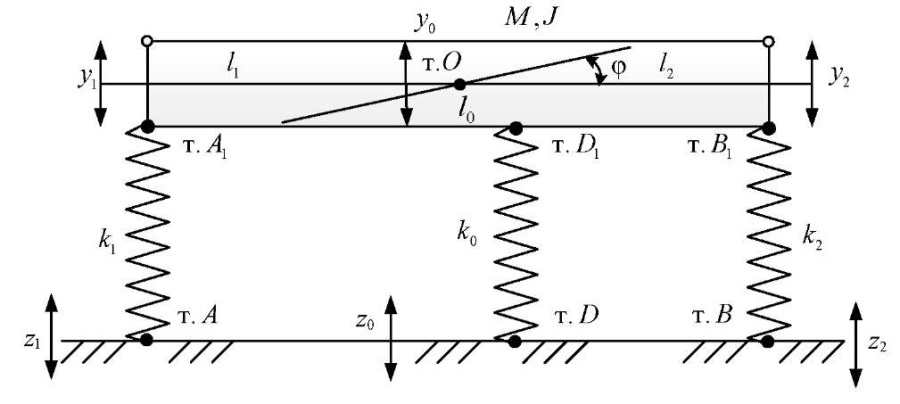
Рис. 3. Расчётная схема железнодорожного транспортного средства
при кинематическом возмущении (z1, z2, z0)
Центр масс системы — точка О находится на расстояниях l1 и l2 от концов твёрдого тела (точек А1, В1). Элемент с жесткостью k0 закреплён в точках D и D1; расстояние ОD1 обозначено как l0. Движение системы рассматривается в координатах y1, y2 и y0, φ, связанных с неподвижным базисом. В расчётах используются соотношения:
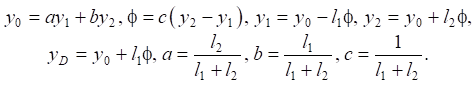 (1)
(1)
Для вывода дифференциальных уравнений движения используется формализм Лагранжа [14], что требует построения выражений для кинетической и потенциальной энергий. В данном случае имеем:
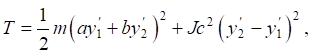 (2)
(2)
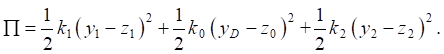 (3)
(3)
Учтём, что потенциальная энергия (3) может быть записана также в виде:
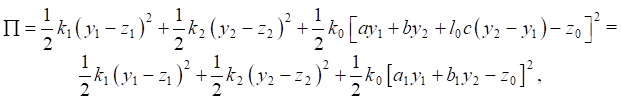 (4)
(4)
где a1 = a – l0c, b1 = b + l0c.
Система уравнений движения в координатах y1, y2 во временной области примет вид:
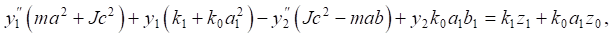 (5)
(5)
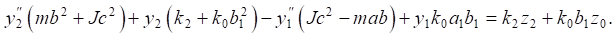 (6)
(6)
После применения интегральных преобразований Лапласа при нулевых начальных условиях [15] система уравнений (5), (6) может быть представлена в операторной форме:
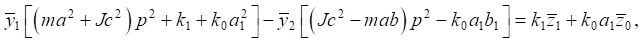 (7)
(7)
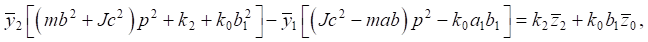 (8)
(8)
где p = jω — комплексная переменная (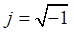 ), значок <–> над переменной означает её изображение по Лапласу [5].
), значок <–> над переменной означает её изображение по Лапласу [5].
На основе (7), (8) построена, в соответствии с положениями метода структурного математического моделирования [5], структурная математическая модель в виде структурной схемы эквивалентной в динамическом отношении системе автоматического управления (рис. 4).
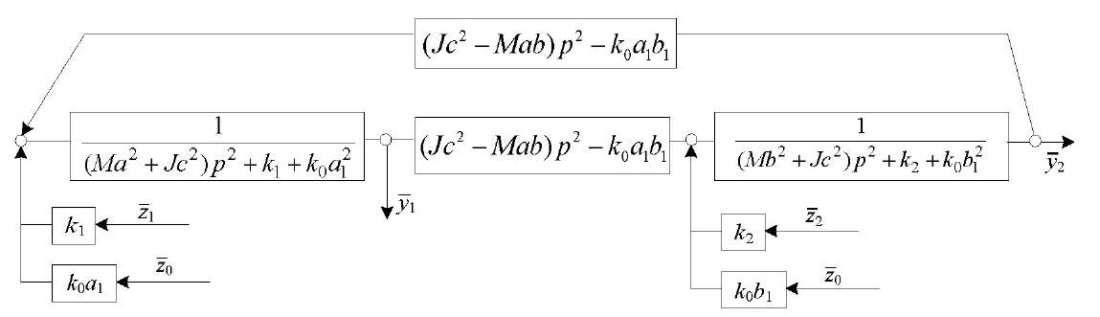
Рис. 4. Структурная математическая модель железнодорожного транспортного средства
Обсуждение и заключение. Особенности системы заключаются в том, что она имеет два парциальных блока, каждый из которых определяет соответствующие парциальные частоты:
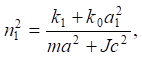 (9)
(9)
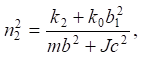 (10)
(10)
которые, в свою очередь, определяют границы расположения частот собственных колебаний системы в целом:
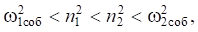 (11)
(11)
где ω1соб, ω2соб — частоты собственных колебаний системы, при работе на которых возможно возникновение резонансных режимов.
К числу особенностей системы относится наличие нескольких одновременно действующих внешних возмущений. Полагая в целях упрощения, что 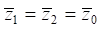 (вполне допустимо на стадиях предварительных динамических оценок) примем, что на вход первого и второго парциальных блоков действуют силовые факторы:
(вполне допустимо на стадиях предварительных динамических оценок) примем, что на вход первого и второго парциальных блоков действуют силовые факторы:
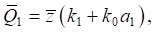 (12)
(12)
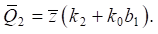 (13)
(13)
Используя структурную схему на рис. 4, запишем выражения для передаточных функций, полагая, что между внешними факторами возмущения имеется связь, формируемая соотношением:
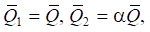 (14)
(14)
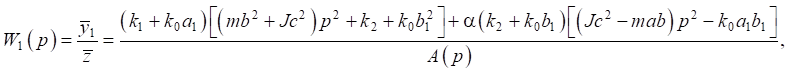 (15)
(15)
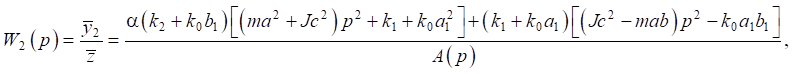 (16)
(16)
где
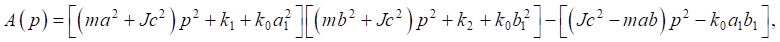 (17)
(17)
является частотным характеристическим уравнением системы.
Числителем передаточных функций в выражениях (15), (16) определяют режимы динамического гашения колебаний, что может быть детализировано из уравнений, получаемых при «обнулении» числителей (15), (16):
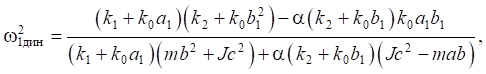 (18)
(18)
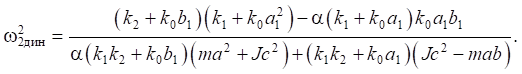 (19)
(19)
Из выражений (18), (19) следует, что в системе с двумя степенями свободы при наличии двух связанных между собой возмущающих факторов возможно возникновение режимов динамического гашения колебаний на двух частотах, параметры которых зависят от значений коэффициента связности α. Этот коэффициент может принимать отрицательные, положительные и нулевые значения.
Из анализа структурной математической модели (рис. 4) следует также и возможность возникновения особого динамического режима на частоте:
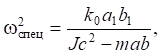 (20)
(20)
когда парциальные блоки получают возможность разъединения. В этом случае система (рис. 3) распадается на два автономных блока, которые не будут создавать ситуаций взаимодействия парциальных структур.
Реализация такого режима может привести к существенной разнице в значениях отклонений в точках А1 и В1 и «разбросу» значений динамических реакций в точках А1, В1 и D1. Определение динамических реакций в точках А, В и D может быть реализовано по методике, изложенной в работе [14], в которой динамическая реакция определяется как произведение динамического смещения (например, точках А1, В1 и D1) на значение приведённой динамической жёсткости.
Для координаты 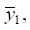 динамическое смещение определяется из выражения для передаточной функции (15), а для координаты
динамическое смещение определяется из выражения для передаточной функции (15), а для координаты 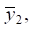 из выражения (16). Для определения приведённой динамической жёсткости используется частотное характеристическое уравнение (17):
из выражения (16). Для определения приведённой динамической жёсткости используется частотное характеристическое уравнение (17):
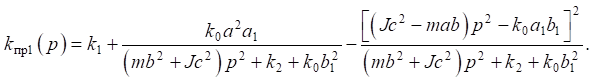 (21)
(21)
Аналогично может быть найдено значение приведённой динамической жёсткости по координате 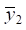
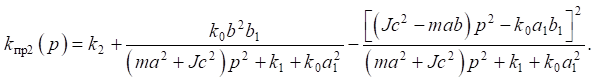 (22)
(22)
Для определения конкретных значений 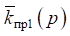
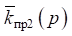 необходимо найти значение частоты ω2, которая определяется из условия, что
необходимо найти значение частоты ω2, которая определяется из условия, что 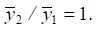 В более общем случае предполагается, что:
В более общем случае предполагается, что:
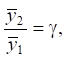 (23)
(23)
где γ — коэффициент связности движения элементов по координатам 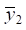 и
и 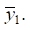 Таким образом этот коэффициент (для случая γ = 1) может быть записан в виде:
Таким образом этот коэффициент (для случая γ = 1) может быть записан в виде:
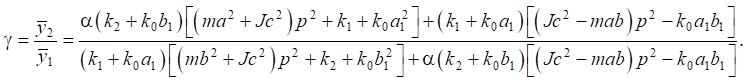 (24)
(24)
Принимая конкретные значения γ, можно найти частоты колебаний для движения рассматриваемого объекта в координатах 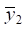 и
и 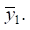 Например, при γ = 1 частота поступательных вертикальных колебаний твёрдого тела определится выражением:
Например, при γ = 1 частота поступательных вертикальных колебаний твёрдого тела определится выражением:
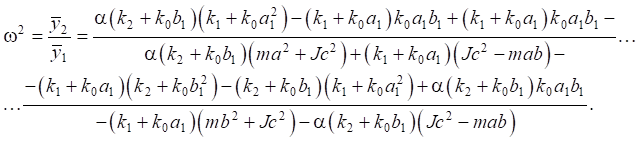 (25)
(25)
Частота ω синфазных гармонических возмущений z1(t), z2(t) и z0(t) обеспечивает движение твёрдого тела при φ = 0, то есть 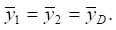 При других значениях γ (γ ≠ 1) определяются
При других значениях γ (γ ≠ 1) определяются 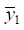 и
и 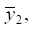 а на их основе из геометрических соображений определяется значение
а на их основе из геометрических соображений определяется значение 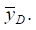 Для твёрдого тела при известных
Для твёрдого тела при известных 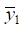 и
и 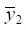 легко может быть найдено положение центра вращения (или колебаний) [12].
легко может быть найдено положение центра вращения (или колебаний) [12].
Динамические реакции связей 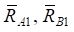 и
и 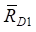 могут быть в первом приближении найдены по формулам:
могут быть в первом приближении найдены по формулам:
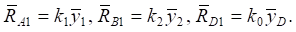
В общем случае динамические реакции определяются с использованием динамических смещений 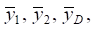 определяемых выражениями (15), (16). Что касается динамического смещения в точке D, то используется выражение
определяемых выражениями (15), (16). Что касается динамического смещения в точке D, то используется выражение 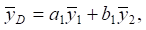 параметры которого определяются вышеприведёнными значениями. В выражения (15), (16) могут быть введены данные о связности силовых факторов воздействия (параметр α). Для получения конкретных данных о значениях динамических реакций вводятся параметры частоты, при которой реализуется соотношение амплитуд колебаний
параметры которого определяются вышеприведёнными значениями. В выражения (15), (16) могут быть введены данные о связности силовых факторов воздействия (параметр α). Для получения конкретных данных о значениях динамических реакций вводятся параметры частоты, при которой реализуется соотношение амплитуд колебаний 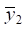 и
и 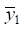 через коэффициент связности амплитуд колебаний γ.
через коэффициент связности амплитуд колебаний γ.
Полная реакция связей в точках А, В и D определяется суммой двух компонент: статической и динамической. Статическая компонента может быть найдена из выражения для передаточных функций динамических реакций при p = 0 и задании параметров статической нагрузки (вес вагона и перевозимого груза). При интенсивном развитии колебательных процессов, когда возрастают колебания по координатам 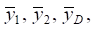 полная реакция может изменяться в значительных пределах и отличаться от статической реакции связей. При наличии динамической компоненты полная реакция может принимать различные значения, в частности, нулевые или отрицательные.
полная реакция может изменяться в значительных пределах и отличаться от статической реакции связей. При наличии динамической компоненты полная реакция может принимать различные значения, в частности, нулевые или отрицательные.
Сформированная в рамках предложенного метода математическая модель, обозначенная выражением (25), позволяет оценивать динамическое состояние железнодорожных транспортных средств при введении дополнительных связей в их структуру для формирования комплекса рекомендаций по получению устойчивых режимов их эксплуатации. Изучение особенностей системы при помощи подходов, характерных для структурного математического моделирования, позволяет детализировано рассмотреть связи между элементами. Применительно к рассматриваемому техническому объекту это даёт возможность корректировки динамического состояния технического объекта на основе варьирования параметров совокупности дополнительно введённых элементов и позволяет уменьшить нагрузку на основные части подвески, а также установить наличие в системе собственных частот и частот динамического гашения колебаний.
В дальнейшем планируется проведение исследований при введении в структуру транспортного средства демпферов и устройств преобразования движения для оценки возможностей структурного математического моделирования. Также интересным направлением является оценка возможностей изменения динамических реакций в зависимости от внешнего воздействия, что позволит оценить усилия, прилагаемые к различным элементами подвески транспортного средства.
Список литературы
1. Коссов В.С., Князев Д.А., Красюков Н.Ф., Махутов Н.А., Гаденин М.М. Нормативная база обеспечения безопасной эксплуатации железнодорожной техники по ресурсу несущих конструкций. Мир транспорта. 2023;21(3):106–114. https://doi.org/10.30932/1992-3252-2023-21-3-10
2. Махутов Н.А., Лапидус Б.М., Гаденин М.М., Титов Е.Ю. Задачи и перспективы развития научных исследований в рамках сотрудничества между ОАО «РЖД» и Российской академией наук. Железнодорожный транспорт. 2023;(7):6.
3. Лапидус Б.М. Задачи опережающего развития российских железных дорог. Железнодорожный транспорт. 2023;(2):4–14.
4. Колесников В.И., Мигаль Ю.Ф., Колесников И.В., Сычев А.П., Воропаев А.И. Повышение износостойкости тяжелонагруженных трибосистем путем формирования структуры и свойств их контактных поверхностей. Наука Юга России. 2022;18(4):59–65. https://www.doi.org/10.7868/S25000640220407
5. Елисеев С.В., Елисеев А.В., Большаков Р.С., Хоменко А.П. Методология системного анализа в задачах оценки, формирования и управления динамическим состоянием технологических и транспортных машин. Москва: «Наука»»; 2021. 679 с.
6. Ромен Ю.С, Белгородцева Т.М, Дедяев М.В. Состояние ходовых частей вагона и силы взаимодействия в системе «экипаж – путь». Транспорт Российской Федерации. 2021;95(4):36–40. URL: https://rostransport.elpub.ru/jour/article/view/127/127 (дата обращения: 19.02.2024).
7. Савоськин А.Н., Ромен Ю.С., Акашев М.Г. Определение вероятностных характеристик боковых сил между колесом и рельсом как полезного случайного процесса на фоне помех. Вестник машиностроения. 2022;(4):14–19. URL: https://www.mashin.ru/eshop/journals/vestnik_mashinostroeniya/2031/19/ (дата обращения: 19.02.2024).
8. Ермоленко И.Ю., Морозов Д.В., Асташков Н.П. Влияние продольных нагрузок на безопасность движения при эксплуатации на горно-перевальных участках пути. Вестник Ростовского государственного университета путей сообщения. 2021;82(2):104–111. https://doi.org/10.46973/0201-727X_2021_2_104
9. Булдаев А.С., Хишектуева И.Х.Д., Анахин В.Д., Дамбаев Ж.Г. Об одном методе решения задачи идентификации динамических систем. Вестник Бурятского государственного университета. Математика, информатика. 2020;(4):14–25. https://doi.org/10.18101/2304-5728-2020-4-14-25
10. Булдаев А.С. Проекционные методы возмущений в задачах оптимизации управляемых систем. Известия Иркутского государственного университета. Серия: Математика. 2014;8:29–43. URL: https://mathizv.isu.ru/ru/journal?id=7 (дата обращения: 19.02.2024).
11. Мижидон А.Д., Хамханов А.К. Гибридная система дифференциальных уравнений, описывающая твердое тело, прикрепленное к двум упругим стержням. Вестник Бурятского государственного университета. Математика, информатика. 2022;(4):38–47. https://doi.org/10.18101/2304-5728-2022-4-38-47
12. Елисеев А.В., Миронов А.С., Елисеев С.В. Формирование математических моделей вибрационных взаимодействий элементов технических средств транспортного и технологического назначения. Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. 2022;(1):32–42. https://doi.org/10.17308/sait.2022.1/9199
13. Елисеев А.В., Кузнецов Н.К., Елисеев С.В. Новые подходы в оценке динамических свойств колебательных структур: частотные функции и связность движений. Труды МАИ. 2021;(120):08. https://doi.org/10.34759/trd-2021-120-08
14. Елисеев А.В., Кузнецов Н.К. Концепция обобщенного рычага в оценке динамических состояний механических колебательных систем в условиях связных вибрационных нагружений. Системы. Методы. Технологии. 2023;59(3):7–12. https://doi.org/10.18324/2077-5415-2023-3-7-12
15. Кашуба В.Б., Большаков Р.С., Мозалевская А.К., Нгуен Д.Х. Определение реакций связей между элементами виброзащитных систем на основе метода структурных преобразований. В: Материалы XV Всероссийской научно-технической конференции с международным участием «Механики XXI веку». Братск: Братский государственный университет; 2016. С. 295–300.
Об авторах
Р. С. БольшаковRussian Federation
Роман Сергеевич Большаков, кандидат технических наук, доцент кафедры управления эксплуатационной работой
664074, г. Иркутск, ул. Чернышевского, 15
В. Е. Гозбенко
Russian Federation
Валерий Ерофеевич Гозбенко, доктор технических наук, профессор кафедры математики
664074, г. Иркутск, ул. Чернышевского, 15
К. Ч. Выонг
Russian Federation
Выонг Куанг Чык, соискатель кафедры физики, механики и приборостроения
664074, г. Иркутск, ул. Чернышевского, 15
Рецензия
Для цитирования:
Большаков Р.С., Гозбенко В.Е., Выонг К.Ч. Возможности оценки динамических состояний железнодорожных транспортных средств: структурное математическое моделирование. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):125-134. https://doi.org/10.23947/2687-1653-2024-24-2-125-134. EDN: PEUPEC
For citation:
Bolshakov R.S., Gozbenko V.E., Vuong Q.T. Assessment of Dynamic States of Railway Vehicles: Structural Mathematical Modeling. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):125-134. https://doi.org/10.23947/2687-1653-2024-24-2-125-134. EDN: PEUPEC
JATS XML














































