Scroll to:
On the Method for Solving the Problem of Ice Cover Deformation under an Arbitrary Moving Load
https://doi.org/10.23947/2687-1653-2024-24-2-170-177
EDN: ZASIUO
Abstract
Introduction. The development of the polar areas of the World Ocean and the need to solve various problems associated with a large number of freezing inland water bodies issue new challenges for science. These challenges include the problem of studying the behavior of ice cover when exposed to various types of loads. Of great interest is the consideration of problems about the action of a moving load on the ice cover. A moving load simulates the effect of moving vehicles on ice. However, in papers devoted to the above problems, cases of load movement along a straight-line trajectory are considered. The objective of this research is to develop a method for studying the behavior of ice cover under the action of a load moving arbitrarily.
Materials and Methods. The article proposes a method for solving the problem of the action of a force moving along an arbitrary trajectory on the ice cover of a reservoir of finite depth. The problem amounts to solving a system of two differential equations. The first of them models the behavior of the ice cover, and it is the equation of vibrations of a viscoelastic plate. The second equation simulates the behavior of fluid in a state of potential flow, and it is Laplace's equation. To solve the system of differential equations, integral transformations in time, space and variables were used. The resulting solution was expressed through an iterated integral, which was calculated using numerical methods.
Results. The development and implementation of the method resulted in solving the problem of the movement of a concentrated force along an ice cover according to an arbitrary law. At the same time, studies were carried out on the behavior of displacements and stresses in the ice cover depending on the speed and acceleration of the movement of the vertical load, on the depth of the reservoir, and on the viscoelastic properties of ice. In addition, the distribution of the velocity vector of fluid particles along the depth of the reservoir was calculated.
Discussion and Conclusion. The proposed method is very effective for solving problems of moving loads acting on the ice cover of a reservoir of finite depth. It provides solving problems about the action of a load moving along an ice cover along a complex trajectory. The results obtained can be used to calculate the stress and displacement of the ice cover during the laying of ice roads or the construction of airfields on the ice.
For citations:
Galaburdin A.V. On the Method for Solving the Problem of Ice Cover Deformation under an Arbitrary Moving Load. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):170-177. https://doi.org/10.23947/2687-1653-2024-24-2-170-177. EDN: ZASIUO
Introduction. The development of the polar areas of the World Ocean and a large number of freezing inland reservoirs drive the need to study the fields of displacement and stresses of the ice cover caused by the action of various types of loads. Numerous papers by domestic and foreign scientists are devoted to solving these problems. Previously, it has been found that the mechanical properties of ice depend on its temperature and water salinity. Much attention was paid to the development of numerical ice models that accurately reflected the interaction of ice and ideal incompressible fluid. In [1][2], the smoothed particle hydrodynamics was used for this purpose, in [3][4] — the method of discrete elements. In [5], ice was modeled by an elastic plate lying on the surface of a stratified fluid. Models that allow cracks were considered in [6][7]. Models of ice strengthened with reinforcing elements were presented in [8][9].
At this, in some papers, an ice cover is considered as an elastic plate lying on the surface of a reservoir [10][11]. At the same time, in [12], on the basis of the conducted research, it is concluded that in some cases, the properties of ice are best described by the Kelvin-Voigt rheological model with one parameter (damping time). Therefore, numerous researchers use a viscoelastic plate when modeling the ice cover [13]. In [14], nonlinear models were used to describe the properties of ice.
In some articles, the effect of a moving load on the ice cover was considered. In [15], the impact of a mobile load on the ice cover in a frozen channel was studied. In [16], the action of a load with an impulsive movement on the ice cover was described. Paper [17] is devoted to the study of the load moving along a frozen riverbed. Here, the rectilinear motion of the load was investigated [18]. However, in real conditions, it is often needed to deal with a load moving in a more complex way. Therefore, the objective of this work is to develop a method for solving problems about the action of a load moving over an ice cover along a complex trajectory. This will provide for a more accurate investigation of the effect of vehicles moving in a complex way on ice.
This work is a continuation of research related to the problems about the effect of a moving load on various objects, whose results are presented in papers [19][20].
Materials and Methods. Setting the task. A reservoir of finite depth with an infinite ice cover (an infinite plate), which is subject to the action of a vertical force moving in an arbitrary way — impulsively, is considered. It is assumed that the reservoir fluid is incompressible and executes irrotational motion.
The problem is reduced to a system of differential equations [15]:
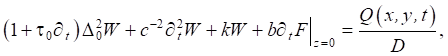

where W(x,y,t) — ice cover deflection; Е and μ — Young's modulus and Poisson's ratio of ice, respectively; D = Eh3/12(1–μ2) — cylindrical bending stiffness; h — ice cover thickness; τo — strain relaxation time; ∆o2 = (∂x2+∂y2)2; ∆ = ∂x2+ ∂y2+∂z2; ρл and ρв — density of ice and water, respectively; с-2 = ρлh/D; k = ρвg/D; b = ρв/D; Q(x,y,t) — load acting on the ice surface; F(x,y,z,t) — speed potential.
Under boundary conditions at z = 0 (ice-water boundary):
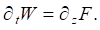
At the bottom of the reservoir at z = –H:
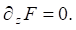
In addition, it was assumed that the ice cover and the fluid in the reservoir were resting at the start time. The load was a concentrated unit force (one Newton) Q (x, y, t), which moved arbitrarily along open free-form curve γ. It was assumed that the displacement of the force was given in the form Q = Q(s(t)), where s — arc coordinate measured from some fixed point of trajectory γ. The trajectory of movement was set parametrically in the form
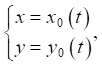
where t — time.
The moving load was approximated by the expression:
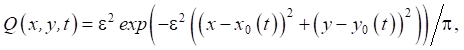
where ε — numeric parameter.
After applying the integral Fourier transform with respect to variables x and y, the integral Laplace transform with respect to t, formulas for calculating unknown functions W and F were obtained:
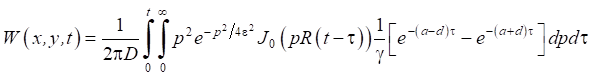 ,
,
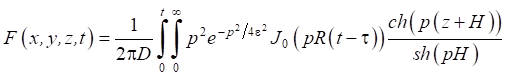 ,
,
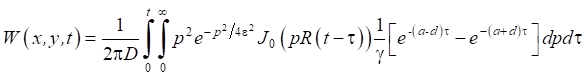 ,
,
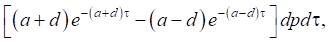
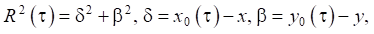
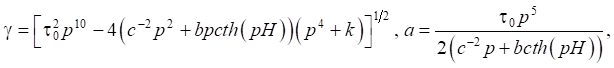
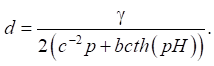
Using the known relations from the theory of thin plates and the theory of the potential ideal flow, it is possible to obtain relations for calculating displacements and stresses in the ice cover, as well as the velocity vector component of fluid particles.
When calculating the improper integral through numerical methods, the approximate relationship
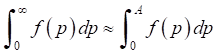
was used, in which value А was chosen so large, that the error estimate
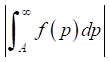
did not exceed the set value.
Thus, for the amount of ice deflection
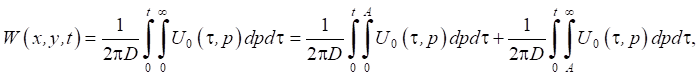
this estimate has the form:
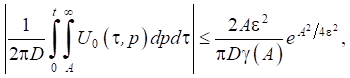
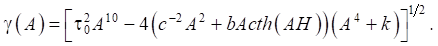
Similar estimates can be obtained for other calculated quantities. These estimates were used to determine value А.
In the calculations carried out, value А was chosen such, that the estimate
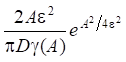
did not exceed
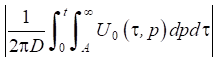 0.001.
0.001.
When calculating the repeated integral, Simpson's quadrature formula (for variable τ) and Chebyshev quadrature formula with equal weights for two nodes (for variable p) were used. The other values were calculated in the same way.
Research Results. A method has been developed for solving problems on the action of a load moving along the ice cover of a reservoir filled with ideal fluid along a complex trajectory with variable speed. Using this method, calculations were carried out that showed the degree of impact of various parameters on the deformation of the ice cover.
The described method does not impose restrictions on the shape of the trajectory of the concentrated force. In the calculations, a special case of a trajectory consisting of arcs of circles was considered (Fig. 1). The red dot indicates the position of the concentrated force at the time under consideration and the direction of movement of the force.
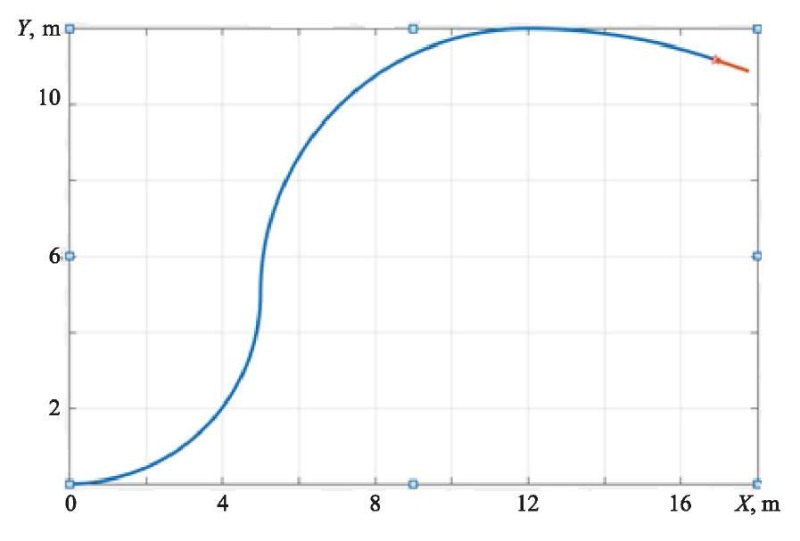
Fig. 1. Trajectory of concentrated force
The following parameter values were taken into account in the calculations: ice cover thickness h = 0.25 m, Young's modulus E = 500,000,000 H/m2, Poisson's ratio of ice μ = 1/3, ice density ρ = 900 kg/m3, fluid density ρ = 1,000 kg/m3, ε = 5. The calculation results are presented below.
Figure 2 shows the change in the deflection of the ice cover at speed of force v = 2.5 m/s, tangential acceleration wt = 1 m/s2, reservoir depth H = 25 m, and relaxation time τo = 1s.
The law of force motion along the trajectory was taken as:
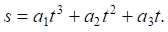
Coefficients a1, a2, a3 were selected in such a way that the force, being at the same point of the trajectory, had the required speed and tangential acceleration.
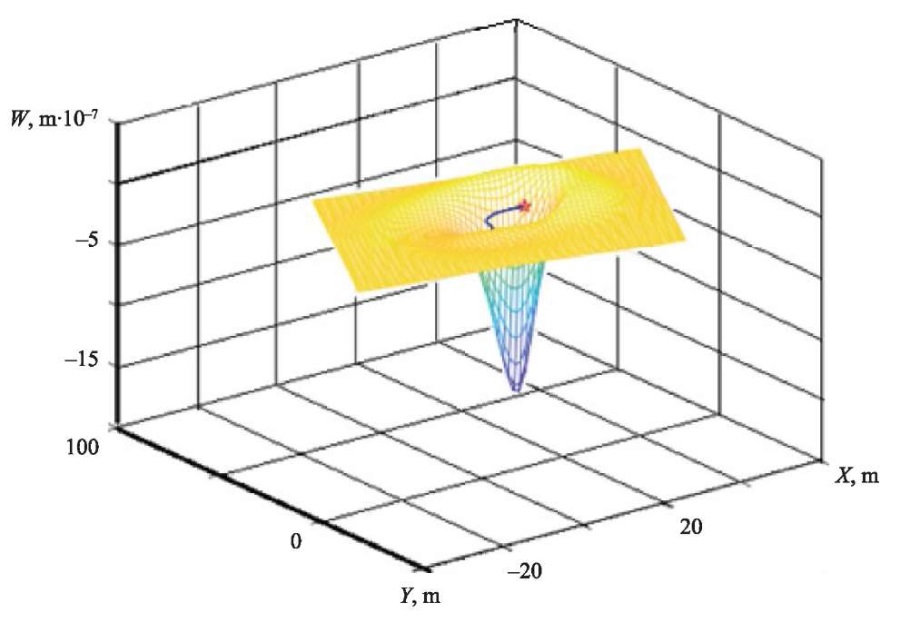
Fig. 2. Change in ice cover deflection
At other values of these parameters, the qualitative nature of the distribution of ice cover deflections remained almost unchanged.
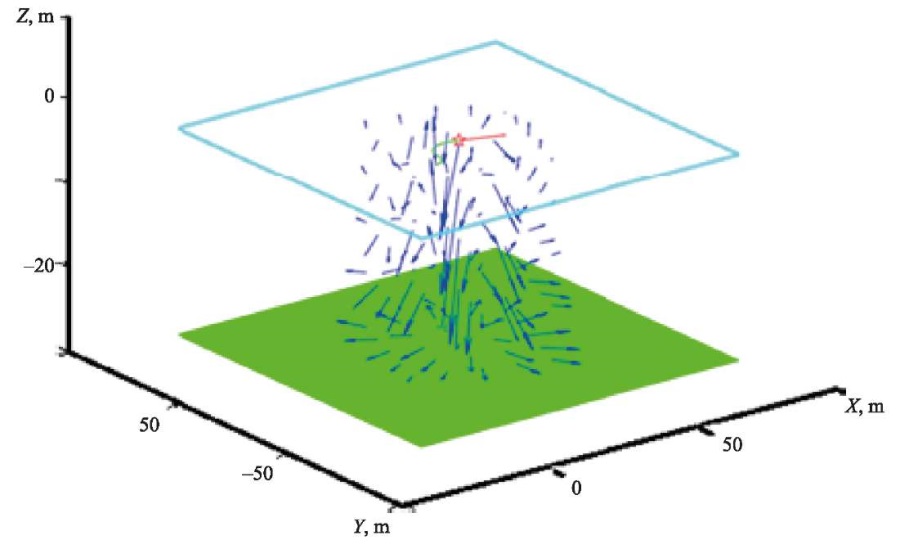
Fig. 3. Fluid motion caused by action of moving load on the ice cover
The fluid motion caused by the action of a moving load at the same values of velocity, tangential acceleration of the load movement, relaxation time, and depth of the reservoir is shown in Figure 3 (the distribution of the velocity vector of fluid particles is shown).
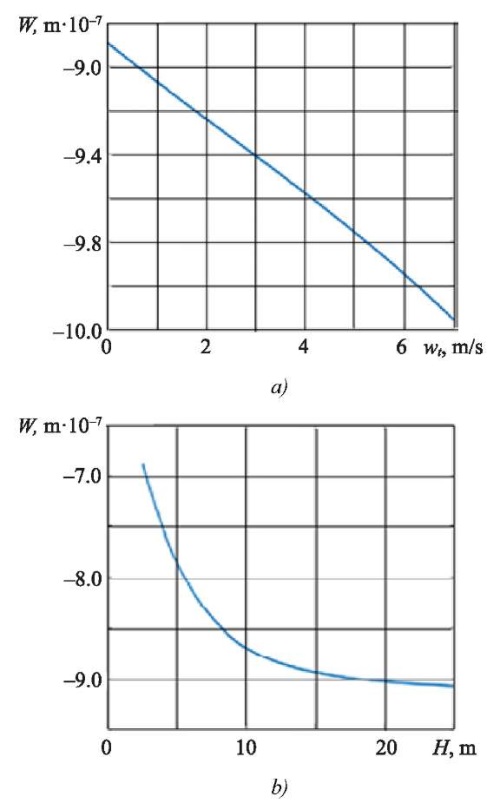
Fig. 4. Change in amount of maximum deflection of ice cover depending on:
a — tangential acceleration rate; b — depth of reservoir
The effect of the tangential acceleration of the force movement on the maximum deflection of the ice cover is shown in Figure 4 a. In this case, the force speed was equal to v = 17.5 m/s, and the relaxation time τo = 1 s.
Figure 4 b shows a graph of the dependence of the maximum deflection of the ice cover W on the reservoir depth H. Here, the speed of the load movement was v = 17.5 m/s, tangential acceleration wt = 1 m/s2, and relaxation time τo = 1s.
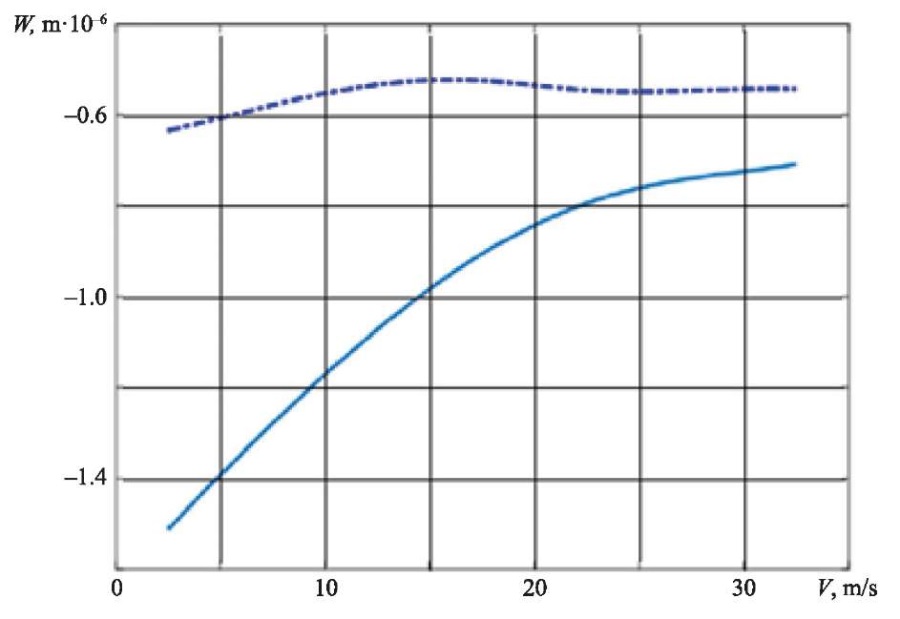
Fig. 5. Change in maximum deflection of ice cover depending on force speed
The dependence of the maximum deflection of the ice cover on the force speed is graphically shown in Figure 5. The depth of the reservoir was assumed to be 25 m, and the tangential acceleration — wt = 1 m/s2. The solid line shows the dependence corresponding to the relaxation time τo = 1 s, the dotted line corresponds to the relaxation time τo = 10 s.
Discussion and Conclusion. The influence of the reservoir depth on the maximum deflection of the ice was studied. A picture of the deflection of the ice cover was obtained due to the action of a concentrated force moving along a complex trajectory with variable speed. Calculations showed that with increasing depth of the reservoir, the maximum deflection of the ice cover decreased (Fig. 2). At the same time, a noticeable dependence of the deflection of the ice cover on the depth of the reservoir H occurred only for H≤25 m. At great depths, the amount of the maximum deflections stabilized near a certain constant value and practically did not change. Thus, if H>25 m, then the depth of reservoirs can be considered infinite when calculating.
An increase in tangential acceleration caused an increase in the deflection of the ice cover. Moreover, the dependence of deflection on tangential acceleration was very close to the linear dependence (Fig. 4).
At low relaxation times τo, the speed of the load movement affected significantly the amount of ice deflection. At large times, the impact of the load movement speed on the deflection of the ice cover was noticeably reduced (Fig. 5).
To study the state of the reservoir fluid, the distribution of the velocity vector of the fluid particles due to the action of the moving force on the ice was determined (Fig. 3).
The developed method of solving problems and the results obtained with its help can be used in the construction of ice roads, design and construction of runways on ice.
References
1. Ningbo Zhang, Xing Zheng, Qingwei Ma, Zhenhong Hu. A Numerical Study on Ice Failure Process and Ice-Ship Interactions by Smoothed Particle Hydrodynamics. International Journal of Naval Architecture and Ocean Engineering. 2019;11(2):796–808. https://doi.org/10.1016/j.ijnaoe.2019.02.008
2. Wenxiao Pan, Tartakovsky AM, Monaghan JJ. A Smoothed-Particle Hydrodynamics Model for Ice-Sheet and Ice-Shelf Dynamics. Journal of Glaciology. 2012;58(208):216–222. https://doi.org/10.3189/2012JoG11J084
3. Shunying Ji. Discrete Element Modeling of Ice Loads on Ship and Offshore Structures. In: Proceedings of the 7th International Conference on Discrete Element Methods. Singapore: Springer; 2017. Р. 45–54. http://doi.org/10.1007/978-981-10-1926-5_6
4. Hisette Q, Alekseev A, Seidel J. Discrete Element Simulation of Ship Breaking Through Ice Ridges. In: Proceedings of the 27th International Ocean and Polar Engineering Conference. International Society of Offshore and Polar Engineers. Cupertino, CA: ISOPE; 2017. P. 1–15.
5. Tsvetkov DO. Small Motions of an Ideal Stratified Fluid Partially Covered with Elastic Ice. Bulletin of Udmurt University. Mathematics. Mechanics. Computer Science. 2018;28(3):328–347. https://doi.org/10.20537/vm180305
6. Wenjun Lu, Raed Lubbad, Sveinung Løset. Out-of-Plane Failure of an Ice Floe: Radial-Crack-Initiation-Controlled Fracture. Cold Regions Science and Technology. 2015;119:183−203. https://doi.org/10.1016%2Fj.coldregions.2015.08.009
7. Renshaw CE, Schulson EM, Sigward SJG. Experimental Observation of the Onset of Fracture Percolation in Columnar Ice. Geophysical Research Letters. 2017;44(4):1795−1802. https://doi.org/10.1002/2016GL071919
8. Yakimenko OV, Sirotyuk VV. Reinforcement of Ice Crossings. Earth's Cryosphere. 2014;18(1):88−91.
9. Kozin VM, Vasilyev AS, Zemlyak VL, Ipatov KI. Research of the Limiting State of Ice Cover under Conditions of Pure Bending with Reinforcement by Reinforcing Elements. Tomsk State University Journal of Mathematics and Mechanics. 2019;(61):61–69. https://doi.org/10.17223/19988621/61/6
10. Bukatov AE, Bukatov AA, Zharkov VV, Zav’yalov DD. Propagation of Surface Waves in Ice Conditions. Monograph. Sevastopol: Marine Hydrophysical Institute; 2019. 204 p. (In Russ.)
11. Tkacheva LA. Behavior of Semi-Infinite Ice Cover under Periodic Dynamic Impact. Journal of Applied Mechanics and Technical Physics. 2017;58(4):82-94.
12. Tabata T. Studies on Visco-Elastic Properties of Sea Ice. In: Arctic Sea Ice: Proceedings of the Conference. Washington, DC: US National Academy of Sciences; 1958. P. 139–147.
13. Zemlyak VI, Vasilyev AS, Zhukov DS. Determination of the Stress-Strain State of the Ice Cover with Surface Reinforcement under the Influence of Static and Dynamic Loads. The Eurasian Scientific Journal. 2022;14(2):51–60.
14. Guyenne P, Părău EI. Computations of Fully Nonlinear Hydroelastic Solitary Waves on Deep Water. Journal of Fluid Mechanics. 2012;713:307–329. https://doi.org/10.1017/jfm.2012.458
15. Shishmarev KA, Khabakhpasheva TI. Unsteady Deflection of Ice Cover in a Frozen Channel under a Moving Load. Computational Technologies. 2019;24(2);111–128. https://doi.org/10.25743/ICT.2019.24.2.010
16. Wang K, Hosking RJ, Milinazzo F. Time-Dependent Response of a Floating Viscoelastic Plate to an Impulsively Started Moving Load. Journal of Fluid Mechanics.2004;521:295–317. https://doi.org/10.1017/S002211200400179X
17. Shishmarev K, Khabakhpasheva T, Korobkin A. The Response of Ice Cover to a Load Moving along a Frozen Channel. Applied Ocean Research. 2016;59:313–326. http://doi.org/10.1016/j.apor.2016.06.008
18. Sturova IV. Motion of an External Load over a Semi-Infinite Ice Sheet in the Subcritical Regime. Fluid Dynamics. 2018;53(1):51–60. https://doi.org/10.7868/S056852811801005X
19. Galaburdin AV. Infinite Plate Loaded with Normal Force Moving along a Complex Path. Advanced Engineering Research (Rostov-on-Don). 2020;20(4):370–381. https://doi.org/10.23947/2687-1653-2020-20-4-370-381
20. Galaburdin AV. Method for Solving the Problem of Load Movement over the Ice Cover of a Reservoir along a Complex Trajectory. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):34–40. https://doi.org/10.23947/2687-1653-2023-23-1-34-40
About the Author
A. V. GalaburdinRussian Federation
Alexander V. Galaburdin, Cand.Sci. (Phys.-Math.), Associate Professor of the Mathematics and Informatics Department
1, Gagarin Sq., Rostov-on-Don, 344003
Review
For citations:
Galaburdin A.V. On the Method for Solving the Problem of Ice Cover Deformation under an Arbitrary Moving Load. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):170-177. https://doi.org/10.23947/2687-1653-2024-24-2-170-177. EDN: ZASIUO
JATS XML














































