Перейти к:
Разработка метода решения задачи деформации ледяного покрова под действием произвольно движущейся нагрузки
https://doi.org/10.23947/2687-1653-2024-24-2-170-177
EDN: ZASIUO
Аннотация
Введение. Освоение полярных районов Мирового океана, необходимость решения различных задач, связанных с наличием большого числа замерзающих внутренних водоемов, ставят перед наукой новые проблемы. К их числу относится проблема изучения поведения ледяного покрова под воздействием на него различного вида нагрузок. Большой интерес представляет рассмотрение задач о действии на ледяной покров подвижной нагрузки. Подвижная нагрузка моделирует действие на лед движущихся транспортных средств. Однако в работах, посвященных вышеуказанным задачам, рассматриваются случаи движения нагрузки по прямолинейной траектории. Целью данной работы является разработка метода исследования поведения ледяного покрова под действием нагрузки, перемещающейся произвольным образом.
Материалы и методы. В статье предложен метод решения задачи о действии на ледяной покров водоема конечной глубины движущейся по произвольной траектории силы. Задача сводится к решению системы двух дифференциальных уравнений. Первое из них моделирует поведение ледяного покрова и является уравнением колебаний вязкоупругой пластины. Второе — моделирует поведение жидкости, находящейся в состоянии потенциального течения, и является уравнением Лапласа. Для решения системы дифференциальных уравнений применялись интегральные преобразования по временной и пространственным переменным. Полученное в результате решение выражалось через повторный интеграл, для вычисления которого применялись численные методы.
Результаты исследования. В результате реализации предложенного метода получено решение задачи о движении сосредоточенной силы по ледяному покрову по произвольному закону. При этом произведены исследования характера поведения перемещений и напряжений в ледяном покрове в зависимости от скорости и ускорения движения вертикальной нагрузки, глубины водоема и вязкоупругих свойств льда. Кроме того, рассчитано распределение вектора скорости частиц жидкости по глубине водоема.
Обсуждение и заключение. Предложенный метод является весьма эффективным для решения задач о подвижных нагрузках, действующих на ледяной покров водоема конечной глубины. Он позволяет решать задачи о действии нагрузки, движущейся по ледяному покрову по сложной траектории. Полученные результаты могут быть использованы для расчета напряжения и перемещений ледового покрова при прокладке ледовых дорог или строительстве аэродромов на льду.
Ключевые слова
Для цитирования:
Галабурдин А.В. Разработка метода решения задачи деформации ледяного покрова под действием произвольно движущейся нагрузки. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):170-177. https://doi.org/10.23947/2687-1653-2024-24-2-170-177. EDN: ZASIUO
For citation:
Galaburdin A.V. On the Method for Solving the Problem of Ice Cover Deformation under an Arbitrary Moving Load. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):170-177. https://doi.org/10.23947/2687-1653-2024-24-2-170-177. EDN: ZASIUO
Введение. Освоение полярных районов Мирового океана и наличие большого количества замерзающих внутренних водоемов приводят к необходимости изучения полей перемещений и напряжений ледяного покрова, обусловленных действием различного вида нагрузок. Решению этих проблем посвящено большое количество работ отечественных и зарубежных ученых. Ранее было установлено, что механические свойства льда зависят от солености воды и его температуры. Большое внимание уделялось разработке численных моделей льда, которые достаточно точно отражали взаимодействие льда и идеальной несжимаемой жидкости. В работах [1][2] для этого применялся метод гидродинамики сглаженных частиц, в [3][4] — метод дискретных элементов. В статье [5] лед моделируется упругой пластиной, лежащей на поверхности стратифицированной жидкости. Модели, допускающие наличие трещин, рассматривались в работах [6][7]. Модели льда, усиленного армирующими элементами, представлены в работах [8][9].
При этом в некоторых работах ледяной покров рассматривается как упругая пластина, лежащая на поверхности водоема [10][11]. В то же время в [12] на основе приведенных исследований делается вывод о том, что в некоторых случаях свойства льда лучше всего описывает реологическая модель Кельвина-Фойгта с одним параметром (временем затухания). Поэтому многие исследователи при моделировании ледового покрова применяют вязкоупругую пластину [13]. В [14] для описания свойств льда применялись нелинейные модели.
В некоторых работах рассматривалось действие на ледяной покров подвижной нагрузки. В [15] исследовалось действие подвижной нагрузки на ледяной покров в замороженном канале, в [16] рассматривалось действие на ледяной покров нагрузки с импульсивным характером движения. Работа [17] посвящена изучению нагрузки, движущейся по замерзшему руслу. При этом исследовалось прямолинейное движение нагрузки [18]. Однако в реальных условиях часто приходится иметь дело с нагрузкой, перемещающейся более сложным образом. Поэтому целью данной работы явилась разработка метода решения задач о действии нагрузки, движущейся по ледяному покрову по сложной траектории. Это позволит более точно исследовать действие на лед транспортных средств, движущихся сложным образом.
Данная работа является продолжением исследований, связанных с рассмотрением задач о действии подвижной нагрузки на различные объекты, результаты которых представлены в работах [19][20].
Материалы и методы. Постановка задачи. Рассматривается водоем конечной глубины с бесконечным ледяным покровом (бесконечная пластина), который подвержен действию вертикальной силы, движущейся произвольным образом — импульсивно. Предполагается, что жидкость водоема несжимаема и совершает потенциальное движение.
Задача сводится к системе дифференциальных уравнений [15]:
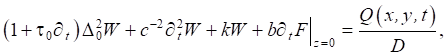
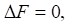
где W(x, y, t) — прогиб ледяного покрова; Е и μ — соответственно модуль Юнга и коэффициент Пуассона льда; D = E h3/12(1 – μ2) — цилиндрическая жесткость на изгиб; h — толщина ледяного покрова; τo — время релаксации деформаций; ∆o2 = (∂x2 + ∂y2)2; ∆ = ∂x2 + ∂y2 + ∂z2; ρл и ρв — соответственно плотность льда и воды; с–2 = ρл h/D; k = ρв g/D; b = ρв/D; Q(x, y ,t) — действующая на поверхности льда нагрузка; F(x, y, z, t) — потенциал скорости.
При краевых условиях при z=0 (граница лед-вода):
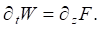
На дне водоема при z = –H:
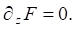
Кроме того, предполагалось, что ледяной покров и жидкость в водоеме в начальный момент времени находились в состоянии покоя. Нагрузка представляла собой сосредоточенную единичную силу (величиной в один
Ньютон) Q(x, y, t), которая перемещалась произвольно по незамкнутой кривой γ произвольной формы. Полагалось, что перемещение силы задавалось в виде Q = Q(s(t)), где s — дуговая координата, отсчитываемая от некоторой фиксированной точки траектории γ. Траектория движения задавалась параметрически в виде
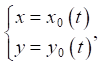
где t — время.
Подвижная нагрузка аппроксимировалась выражением
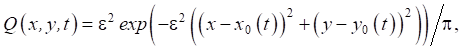
где ε — числовой параметр.
После применения интегрального преобразования Фурье по переменным x и y, интегрального преобразования Лапласа по t, были получены формулы для вычисления неизвестных функций W и F:
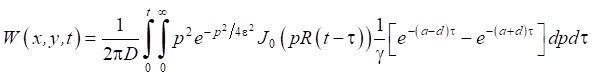 ,
,
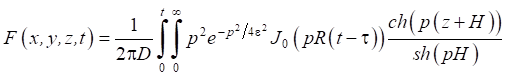 ,
,
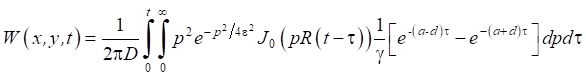 ,
,
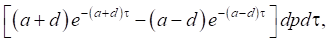
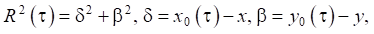
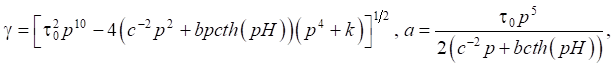
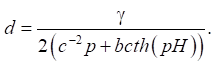
Используя известные соотношения из теории тонких пластин и теории потенциального течения идеальной жидкости, можно получить соотношения для вычисления перемещений и напряжений в ледовом покрове, а также компонент вектора скорости частиц жидкости.
При вычислении несобственного интеграла с помощью численных методов использовалось приближенное соотношение
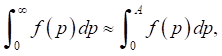
в котором величина А выбиралась настолько большой, чтобы оценка ошибки
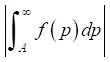
не превышала установленного значения.
Так, для величины прогиба льда
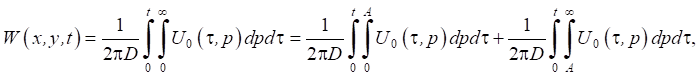
данная оценка имеет вид:
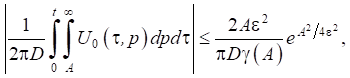
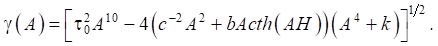
Подобные оценки можно получить и для остальных вычисляемых величин. Эти оценки использовались при определении величины А.
В проведенных расчетах величина А выбиралась такой, чтобы оценка
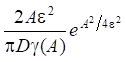
не превышала
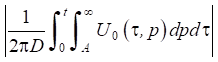 0,001.
0,001.
При вычислении повторного интеграла использовались квадратурная формула Симпсона (по переменной τ) и квадратурная формула Чебышева с равными весами для двух узлов (по переменной p). Аналогичным образом вычислялись и остальные величины.
Результаты исследования. Разработан метод решения задач о действии нагрузки, движущейся по ледяному покрову водоема, наполненного идеальной жидкостью, по сложной траектории с переменной скоростью. Применяя данный метод, проведены расчеты, которые показали степень влияния различных параметров на деформацию ледяного покрова.
Изложенный метод не накладывает ограничений на форму траектории движения сосредоточенной силы. При расчетах рассматривался частный случай траектории, состоящей из дуг окружностей (рис. 1). Красной точкой указано положение сосредоточенной силы в рассматриваемый момент времени и направление движения силы.
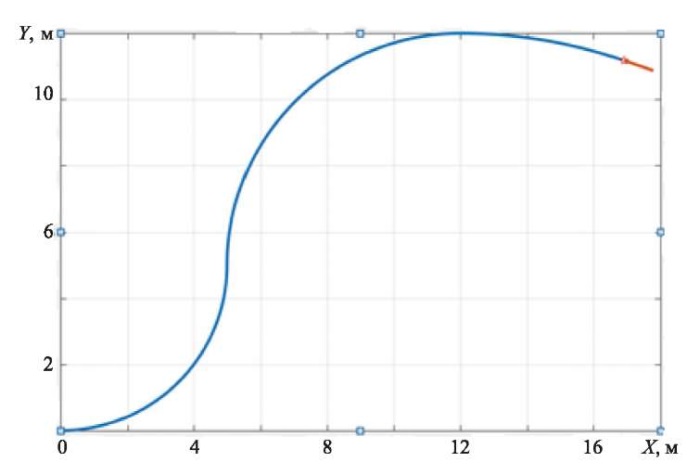
Рис. 1. Траектория движения сосредоточенной силы
При расчетах принимались следующие значения используемых параметров: толщина ледяного покрова h = 0,25 м, модуль Юнга E = 500 000 000 H/м2, коэффициент Пуассона льда μ = 1/3, плотность льда ρ = 900 кг/м3, плотность воды ρ = 1 000 кг/м3, ε = 5. Ниже представлены результаты проведенных расчетов.
На рис. 2 приведено изменение прогиба ледяного покрова при скорости движения силы v = 2,5 м/c, касательном ускорении wt = 1 м/c2, глубине водоема H = 25 м и времени релаксации τo = 1 с.
Закон движения силы по траектории принимался в виде:
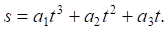
Коэффициенты a1, a2, a3 подбирались таким образом, чтобы сила, находясь в одной и той же точке траектории, имела необходимые скорость и касательное ускорение.
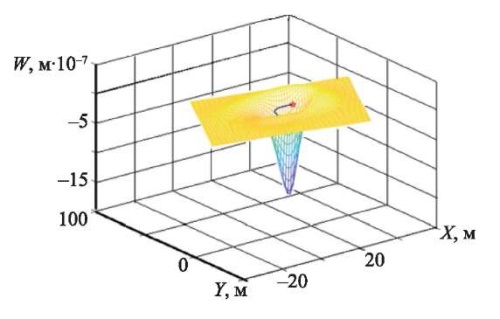
Рис. 2. Изменение прогиба ледяного покрова
При других значениях указанных параметров качественный характер распределения прогиба ледяного покрова оставался практически неизменным.
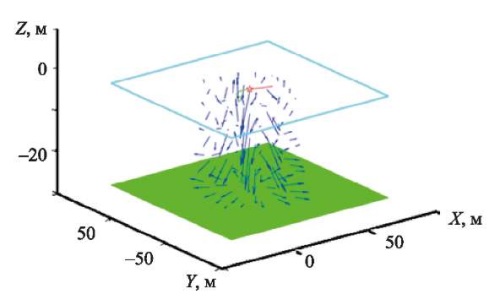
Рис. 3. Движение жидкости, обусловленное действием подвижной нагрузки на ледяной покров
Движение жидкости, обусловленное действием подвижной нагрузки при тех же значениях скорости, касательного ускорения движения нагрузки, времени релаксации и глубины водоема, представлено на рис. 3 (изображено распределение вектора скоростей частиц жидкости).
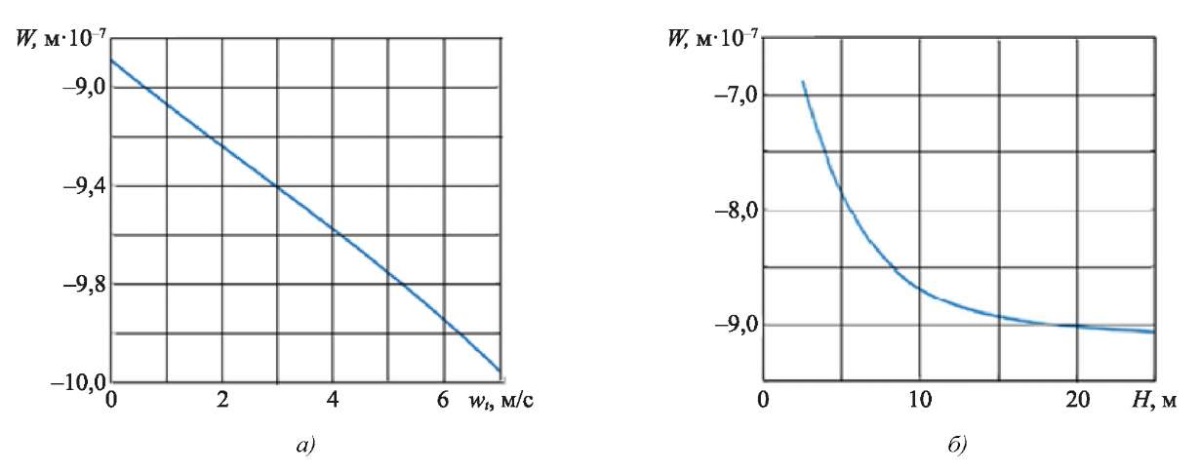
Рис. 4. Изменение величины максимального прогиба ледяного покрова в зависимости:
а — от величины касательного ускорения; б — от глубины водоема
Влияние на максимальный прогиб ледяного покрова касательного ускорения движения силы представлено на рис. 4 а. В этом случае скорость движения силы была равной v = 17,5 м/c, а время релаксации τo = 1 с.
На рис. 4 б изображен график зависимости величины максимального прогиба ледяного покрова W от глубины водоема H. Скорость движения нагрузки при этом равнялась v = 17,5 м/c, касательное ускорение wt = 1 м/c2 и время релаксации τo = 1 с.
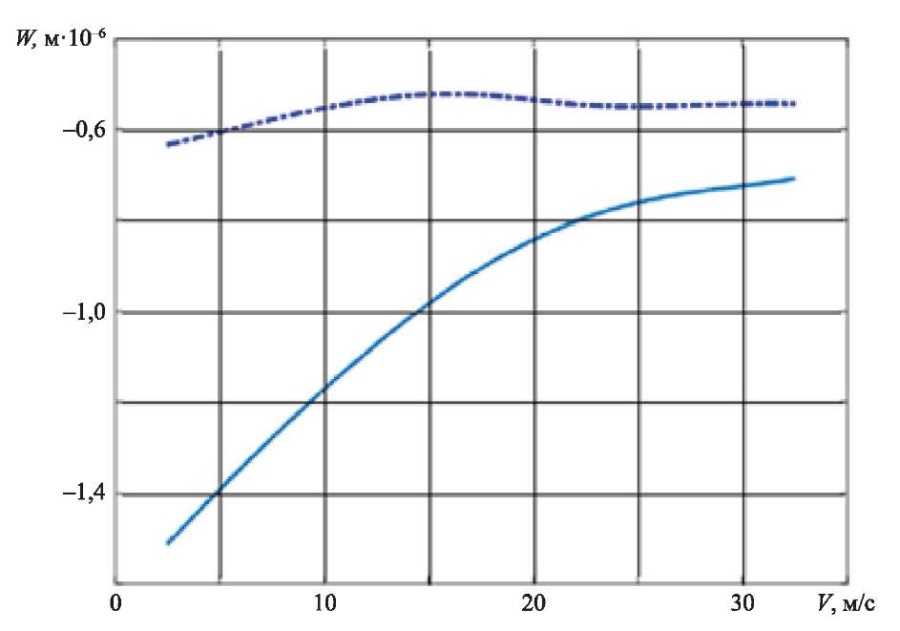
Рис. 5. Изменение максимального прогиба ледяного покрова
в зависимости от скорости движения силы
Зависимость максимального прогиба ледяного покрова от скорости движения силы представлена графически на рис. 5. Глубина водоема при этом принималась равной 25 м, а величина касательного ускорения — wt = 1 м/c2. Сплошной линией изображена зависимость, соответствующая времени релаксации τo = 1 с, пунктирная линия соответствует времени релаксации τo = 10 с.
Обсуждение и заключение. Исследовано влияние глубины водоема на максимальный прогиб льда. Получена картина прогиба ледового покрова, обусловленная действием сосредоточенной силы, движущейся по сложной траектории с переменной скоростью. Расчеты показали, что с увеличением глубины водоема максимальный прогиб ледяного покрова уменьшается (рис. 2). При этом заметная зависимость прогиба ледяного покрова от глубины водоема H имеет место лишь для H ≤ 25 м. При больших глубинах величина максимальных прогибов стабилизируется около некоторого постоянного значения и практически не изменяется. Таким образом, если H > 25 м, то при расчетах глубину водоемов можно считать бесконечной.
Увеличение касательного ускорения приводит к увеличению прогиба ледяного покрова. Причем зависимость прогиба от касательного ускорения очень близка к линейной зависимости (рис. 4).
При малых временах релаксации τo скорость движения нагрузки заметно влияет на величину прогиба льда. При больших временах влияние скорости движения нагрузки на прогиб ледяного покрова заметно уменьшается (рис. 5).
Для изучения состояния жидкости водоема определено распределение вектора скорости движения частиц жидкости, обусловленное действием подвижной силы по льду (рис. 3).
Разработанный метод решения задач и результаты, полученные с его помощью, могут быть использованы при строительстве ледовых дорог, проектировании и строительстве взлетно-посадочных полос на льду.
Список литературы
1. Ningbo Zhang, Xing Zheng, Qingwei Ma, Zhenhong Hu. A Numerical Study on Ice Failure Process and Ice-Ship Interactions by Smoothed Particle Hydrodynamics. International Journal of Naval Architecture and Ocean Engineering. 2019;11(2):796–808. https://doi.org/10.1016/j.ijnaoe.2019.02.008
2. Wenxiao Pan, Tartakovsky AM, Monaghan JJ. A Smoothed-Particle Hydrodynamics Model for Ice-Sheet and Ice-Shelf Dynamics. Journal of Glaciology. 2012;58(208):216–222. https://doi.org/10.3189/2012JoG11J084
3. Shunying Ji. Discrete Element Modeling of Ice Loads on Ship and Offshore Structures. In: Proceedings of the 7th International Conference on Discrete Element Methods. Singapore: Springer; 2017. Р. 45–54. http://doi.org/10.1007/978-981-10-1926-5_6
4. Hisette Q, Alekseev A, Seidel J. Discrete Element Simulation of Ship Breaking Through Ice Ridges. In: Proceedings of the 27th International Ocean and Polar Engineering Conference. International Society of Offshore and Polar Engineers. Cupertino, CA: ISOPE; 2017. P. 1–15.
5. Цветков Д.О. Малые движения идеальной стратифицированной жидкости, частично покрытой упругим льдом. Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. 2018;28(3):328–347. https://doi.org/10.20537/vm180305
6. Wenjun Lu, Raed Lubbad, Sveinung Løset. Out-of-Plane Failure of an Ice Floe: Radial-Crack-Initiation-Controlled Fracture. Cold Regions Science and Technology. 2015;119:183−203. https://doi.org/10.1016%2Fj.coldregions.2015.08.009
7. Renshaw CE, Schulson EM, Sigward SJG. Experimental Observation of the Onset of Fracture Percolation in Columnar Ice. Geophysical Research Letters. 2017;44(4):1795−1802. https://doi.org/10.1002/2016GL071919
8. Якименко О.В., Сиротюк В.В. Армирование ледовых переправ. Криосфера Земли. 2014;18(1):88−91.
9. Козин В.М., Васильев А.С., Земляк В.Л., Ипатов К.И. Исследование предельного состояния ледяного покрова в условиях чистого изгиба при усилении армирующими элементами. Вестник Томского государственного университета. 2019;(61):61–69. https://doi.org/10.17223/19988621/61/6
10. Букатов А.Е., Букатов А.А., Жарков В.В., Завьялов Д.Д. Распространение поверхностных волн в ледовых условиях. Монография. Севастополь: Морской гидрофизический институт РАН; 2019. 204 с.
11. Ткачева Л.А. Поведение полубесконечного ледяного покрова при периодическом динамическом воздействии. Прикладная механика и техническая физика. 2017;58(4):82–94.
12. Tabata T. Studies on Visco-Elastic Properties of Sea Ice. In: Arctic Sea Ice: Proceedings of the Conference. Washington, DC: US National Academy of Sciences; 1958. P. 139–147.
13. Земляк В.Л., Васильев А.С., Жуков Д.С. Определения напряжённо-деформированного состояния ледяного покрова при поверхностном армировании под воздействием статических и динамических нагрузок. Вестник евразийской науки. 2022;14(2):51–60.
14. Guyenne P, Părău EI. Computations of Fully Nonlinear Hydroelastic Solitary Waves on Deep Water. Journal of Fluid Mechanics. 2012;713:307–329. https://doi.org/10.1017/jfm.2012.458
15. Шишмарев К.А., Хабахпашева Т.И. Нестационарные колебания ледового покрова в замороженном канале под действием движущегося внешнего давления. Вычислительные технологии. 2019;24(2);111–128. https://doi.org/10.25743/ICT.2019.24.2.010
16. Wang K, Hosking RJ, Milinazzo F. Time-Dependent Response of a Floating Viscoelastic Plate to an Impulsively Started Moving Load. Journal of Fluid Mechanics.2004;521:295–317. https://doi.org/10.1017/S002211200400179X
17. Shishmarev K, Khabakhpasheva T, Korobkin A. The Response of Ice Cover to a Load Moving along a Frozen Channel. Applied Ocean Research. 2016;59:313–326. http://doi.org/10.1016/j.apor.2016.06.008
18. Стурова И.В. Движение внешней нагрузки по полубесконечному ледяному покрову в докритическом режиме. Известия Российской академии наук. Механика жидкости и газа. 2018;53(1):51–60. https://doi.org/10.7868/S056852811801005X
19. Галабурдин А.В. Бесконечная пластина, нагруженная нормальной силой, движущейся по сложной траектории. Advanced Engineering Research (Rostov-on-Don). 2020;20(4):370–381. https://doi.org/10.23947/2687-1653-2020-20-4-370-381
20. Галабурдин А.В. Метод решения задачи о движении нагрузки по ледяному покрову водоема по сложной траектории. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):34–40. https://doi.org/10.23947/2687-1653-2023-23-1-34-40
Об авторе
А. В. ГалабурдинRussian Federation
Александр Васильевич Галабурдин, кандидат физико-математических наук, доцент кафедры математики и информатики
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Галабурдин А.В. Разработка метода решения задачи деформации ледяного покрова под действием произвольно движущейся нагрузки. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):170-177. https://doi.org/10.23947/2687-1653-2024-24-2-170-177. EDN: ZASIUO
For citation:
Galaburdin A.V. On the Method for Solving the Problem of Ice Cover Deformation under an Arbitrary Moving Load. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):170-177. https://doi.org/10.23947/2687-1653-2024-24-2-170-177. EDN: ZASIUO
JATS XML














































