Перейти к:
Особенности определения пеленга на подводный объект с использованием фазовой информации дифференциального стереодатчика
https://doi.org/10.23947/2687-1653-2024-24-2-198-206
EDN: FPQRSJ
Аннотация
Введение. Безопасность судоходства и разработок подводных месторождений полезных ископаемых требуют точного обнаружения различных подводных объектов. В литературе рассматриваются вопросы отслеживания их перемещений и траектории движения. Предлагаются методы гидролокации, обеспечивающие высокую точность позиционирования подводных объектов. Отмечена высокая точность пеленга стереодатчиков с ультракороткой базой. Однако такое оборудование чувствительно к частоте дискретизации сигналов, что вызывает «шум дискретизации». В открытом доступе нет публикаций, посвященных решению этой проблемы. Представленное исследование призвано восполнить данный пробел. Цель работы — изучение возможности получения данных, уточняющих информацию о пеленге подводных объектов за счет использования фазовой информации отраженных зондирующих сигналов и дополнительной процедуры передискретизации исходных данных.
Материалы и методы. Местоположение объекта определяли с помощью экспериментального комплекса для исследования гидроакустических датчиков, созданного В.А. Широковым и В.Н. Милич в Удмуртском федеральном исследовательском центре Уральского отделения Российской академии наук. Использовали стереодатчик с малой базой (30 мм) по сравнению с расстоянием до объекта (≈800–900 мм). Для обработки данных применяли методы цифровой фильтрации и математический аппарат корреляционного анализа отраженных гидроакустических сигналов, полученных фазовым методом.
Результаты исследования. Представлены итоги сопоставления двух способов определения пеленга на объект: по разности времени прихода передних фронтов импульсов и по максимуму кросс-корреляционной функции (ККФ). Графически показано изменение пеленга при движении объекта. Использование переднего фронта сигнала обусловило небольшие выбросы значений вдоль всей кривой пеленга (менее 0,12 рад). При максимуме ККФ выбросы фиксировались лишь в некоторых областях, но были довольно значительными (около 0,17 рад). Показано, как выбрать точки, соответствующие более гладкой и валидной траектории объекта, и как работать с ошибочными точками. Представленный метод устранения ошибки можно реализовать программно. При квазигармоничном сигнале редкие измерения исходного сигнала интерполируются частыми вычисленными значениями. Благодаря такому виртуальному увеличению частоты дискретизации (передискретизации) можно фиксировать промежуточные показатели в оцифрованных исходных данных. Интерполяция значений сигнала кубическим сплайном позволила получить 20 точек на 1 период сигнала вместо 5 точек в исходном варианте. В этом случае более корректна траектория, сформированная с максимумом ККФ.
Обсуждение и заключение. Задачу пеленгации можно решить с точностью, необходимой для практического применения. Учет фактора гладкости и непрерывности траектории движения объекта позволяет качественно корректировать выбор максимума кросс-корреляционной функции сигналов стереодатчика. Предложенные методы обладают большим потенциалом для разработки систем подводного видения.
Ключевые слова
Для цитирования:
Широков В.А., Баженова А.И., Милич В.Н. Особенности определения пеленга на подводный объект с использованием фазовой информации дифференциального стереодатчика. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):198-206. https://doi.org/10.23947/2687-1653-2024-24-2-198-206. EDN: FPQRSJ
For citation:
Shirokov V.A., Bazhenova A.I., Milich V.N. Features of Bearing on Underwater Object Using Phase Information of a Differential Stereo Sensor. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):198-206. https://doi.org/10.23947/2687-1653-2024-24-2-198-206. EDN: FPQRSJ
Введение. Обеспечение безопасности судоходства и работы на подводных месторождениях полезных ископаемых требуют качественного обнаружения подводных объектов и отслеживания их перемещений [1]. В системах подводного наблюдения применяются гидроакустические датчики. Они улавливают сигнал, отраженный от объекта, и позволяют вычислить его местоположение методом трилатерации [2]. В этом процессе каждый датчик предоставляет информацию об интервале времени прохождения зондирующего сигнала, отраженного от объекта. В случае использования нескольких датчиков [3] возникает возможность решения задачи обратной пространственной засечки и определения координат наблюдаемого объекта [4]. Для повышения точности измерений представляется перспективным использование в качестве приемника стереодатчиков с ультракороткой базой [5], позволяющих получать фазовую информацию [6] и определять пеленг на объект [7]. Изучены возможности использовании гидролокационных данных об удаленных подводных целях, а также о пеленге подводных объектов [8] за счет использования фазовой [9] или частотной [10] информации отраженных зондирующих сигналов.
При этом известно, что процедура дискретизации сигнала обусловливает ошибки при определении параметров траектории движения подводных объектов [11]. Это относится как к дальномерным измерениям, так и к процедурам определения пеленга. Оцифровка аналогового сигнала датчика, необходимая для дальнейшей цифровой обработки, вносит так называемую «погрешность дискретизации». Погрешность, вызванная квантованием амплитуды сигнала, оценивается количеством уровней квантования аналого-цифрового преобразователя. Погрешность, вызванная дискретизацией по времени, пропорциональна величине интервала времени квантования и скорости изменения напряжения. Поэтому частоту дискретизации сигнала стремятся сделать как можно выше верхней частоты самого сигнала. Однако увеличение частоты дискретизации во многих случаях ограничивается возможностями регистрирующей аппаратуры: процессора, аналого-цифрового преобразователя, каналов передачи данных, устройствами хранения данных. Ограниченность возможностей дискретизации во времени при выполнении траекторных измерений не позволяет точно фиксировать экстремальные значения траектории (дальность и пеленг). Как следствие, снижается точность результатов измерений, появляются выбросы на фиксируемых траекториях. Для устранения этого недостатка необходимо изучить потенциал передискретизации оцифрованного гидроакустического сигнала. В открытом доступе нет публикаций, посвященных решению данной проблемы. Имеющийся пробел восполняют материалы этой статьи.
Цель представленного исследования состоит в оценке возможностей определения пеленга на объект с использованием фазовой информации и в отработке фазового метода пеленгования с применением передискретизации оцифрованного гидроакустического сигнала.
Материалы и методы. Рассматривается алгоритм определения координат с применением пеленгации фазовым методом. Приводятся результаты его тестирования для объекта, движущегося по круговой траектории в экспериментальном бассейне.
Постановка эксперимента. При проведении опытов для определения местоположения объекта в гидросреде при пеленгации фазовым методом задействовали экспериментальную установку, созданную В.А. Широковым и В.Н. Милич в Удмуртском федеральном исследовательском центре Уральского отделения Российской академии наук [12]. Это лабораторный измерительный комплекс с линейной аквасредой в виде протяженного цилиндрического резервуара (гидроволновода) и бассейном, оснащенным системой генерации испытательных гидроакустических сигналов. Ниже детально описаны элементы установки, которые использовались в опытах.
1. Излучатель гидроакустического сигнала с известными координатами S (рис. 1). В работе используется амплитудно-модулированный сигнал [13].
2. Отражающий объект. В эксперименте в качестве тестового используется протяженный цилиндрический объект — медный провод, диаметр которого (0,15 мм) значительно меньше длины акустической волны (1,5 мм). В представленной работе задача решается на плоскости, поэтому для составления вычислительных процедур расчета координат данный объект можно считать точечным.
3. Стереодатчик, преобразующий гидроакустический сигнал в электрический. Известны координаты каждого из двух приемников стереодатчика (st1, st2 на рис. 1).
4. Аппаратно-программный комплекс, выполняющий усиление, оцифровку и обработку сигналов датчиков.
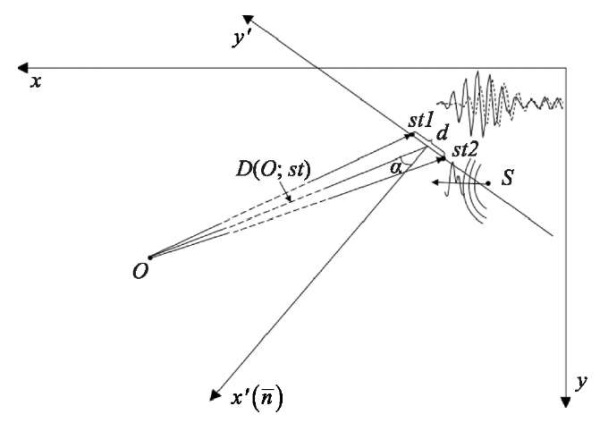
Рис. 1. Расположение принимающих датчиков (стереодатчик с двумя приемниками st1 и st2) и излучателя (S) в плоскости экспериментального бассейна (xy). Здесь d — база стереодатчика; D(O; st) — расстояние между стереодатчиком и объектом; α — пеленг на объект; плоскость (x’y’) образована плоскостью стереодатчика и нормалью n к ней
Результатом измерений является файл регистрации принимаемого двухканального сигнала.
Алгоритм обработки результатов измерений. Использование стереодатчика с малой базой (30 мм) по сравнению с расстоянием до объекта (≈ 800–900 мм) позволяет применить упрощенные формулы.
Итак, рассчитаем координаты исследуемого объекта в системе x'y', образованной плоскостью стереодатчика и нормалью к ней. Для этого задействуем алгоритм, включающий пять этапов.
1. Предварительная обработка:
- удаление слепой зоны (первые N отсчетов);
- фильтрация сигнала.
В работе применяется высокочастотная фильтрация.
2. Выделение из всего сигнала информативных фрагментов imp1, imp2 (в двух каналах), содержащих импульсы, отраженные от исследуемого объекта. Для этого выполняется пороговая обработка по амплитуде А сигнала. Порог принимается равным p×max(A) (p = 0,5).
Такая обработка позволяет определить передний фронт импульса (BeginIndex), отраженного от объекта. Из двух каналов сигнала вырезаются участки [BeginIndex–0,5×LenSignal; BeginIndex+LenSignal]. Здесь LenSignal — длина сигнала, подаваемого на вход. В результате получаем два сигнала imp1 и imp2 длиной 1,5×LenSignal. В каждом из них содержится импульс, отраженный от объекта.
3. Расчет расстояния D(O; st) между объектом и стереодатчиком.
- Определение расстояния, пройденного импульсом от излучателя до объекта и от объекта до датчика приема, по формуле D(S,O,st)=BeginIndex×dt×C. Здесь C=1475 м/c — скорость распространения акустической волны, dt = 0,2×10–6 с — интервал дисктретизации.
- Расчет значения:
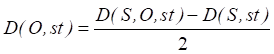 . (1)
. (1)
4. Определение пеленга α на объект [14]:
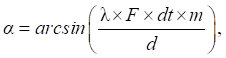 (2)
(2)
где λ — длина волны; F — частота сигнала; dt — интервал дискретизации; m — разница прихода отраженного импульса на два стереодатчика (в отсчетах); d — база стереодатчика (в представленном исследовании λ = 1,5 мм, F = 1 МГц, dt = 0,2 мкс, d = 30 мм).
5. Вычисление координат анализируемого объекта в системе, образованной плоскостью стереодатчика и его нормалью (рис. 1), по формулам: x’=D(O, st) ×cos(α); y’=D(O, st) ×sin(α).
Определение пеленга на объект. Примем условие малости стереобазы по сравнению с расстоянием от датчика до объекта. В этом случае стереодатчик позволяет определить пеленг на объект с помощью информации о разности фаз принятых импульсов, ранее отраженных от объекта, а также по разности времени прихода передних фронтов импульсов, поступивших на стереодатчик (рис. 2).
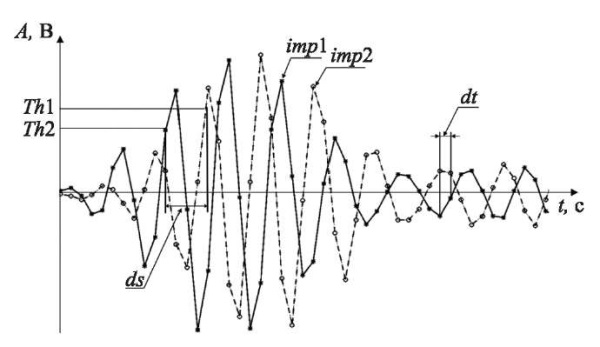
Рис. 2. Определение разности моментов прихода ds стереосигналов, которые обозначены сплошной imp1(t) и пунктирной imp2(t) линиями. Th1, Th2 — пороги для первого и второго сигнала стереопары соответственно; dt — интервал дискретизации; А — значение сигнала в вольтах; t — время
Для реализации такого подхода выполняются описанные ниже процедуры.
1. Идентификация моментов прихода передних фронтов стереосигналов с помощью пороговой обработки [15] с порогом p×max(A). В данной работе коэффициент p принят равным 0,5 [16].
2. Вычисление разности ds (количество интервалов dt) между передними фронтами импульсов, зарегистрированных в двух приемниках стереодатчика.
3. Вычисление пеленга α по формуле (1). За m принимаем значение ds.
При таком способе вычисления сдвига фазы передний фронт сигнала будет главным индикатором импульса, отраженного от объекта. Не учитывается внутренняя структура сигнала, которая может иметь решающее значение для корректного определения пеленга на объект. Учтем схожесть принимаемых сигналов и рассмотрим в работе другой подход к вычислению пеленга — на основе кросс-корреляционной функции (ККФ) стереосигналов. Логично определять сдвиг фазы по максимуму ККФ. Ниже описаны элементы алгоритма вычисления пеленга с помощью ККФ.
1. Расчет ККФ импульсов, поступивших на два приемника одного стереодатчика: r = xcorr(imp1, imp2). Значение функции xcorr при смещении m второго сигнала относительно первого вычисляется следующим образом:
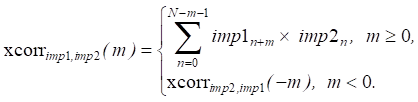
Здесь N — длина imp1 и imp2, –N<m<N.
2. Определение максимума ККФ и соответствующего ему сдвига dc (в отсчетах).
3. Вычисление пеленга α по формуле (1) с учетом, что за m принимается величина dc.
Результаты исследования
Тестирование методов определения пеленга. Представленные способы определения пеленга на объект (по разности времени прихода передних фронтов импульсов и по максимуму ККФ) протестировали для объекта, движущегося по круговой траектории в экспериментальном бассейне. Использовался гармонический сигнал длительностью 7 периодов и частотой 1 МГц. Оцифрованные стереосигналы регистрировались в 256 точках траектории движения объекта. Частота оцифровки — 5 МГц.
На рис. 3 показано изменение значений пеленга по мере движения объекта по окружности для двух предложенных подходов (разница передних фронтов, максимум ККФ).
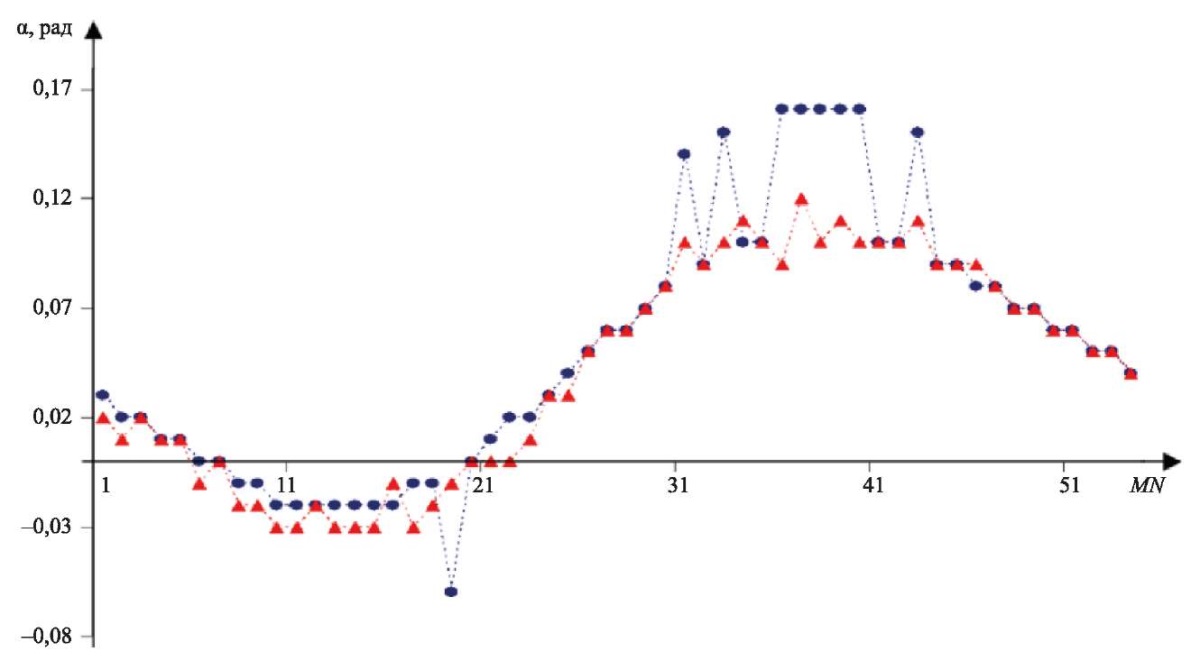
Рис. 3. Изменение пеленга α на объект, совершающий круговое движение. Показатели получены при использовании двух подходов (красный маркер — разница времени прихода передних фронтов стереосигналов, синий маркер — максимум ККФ). MN — номер измерения, α — пеленг на объект
При использовании переднего фронта сигнала (рис. 3, красный маркер) почти вдоль всей кривой изменения пеленга на объект наблюдаются небольшие выбросы значений. При использовании максимума ККФ (рис. 3, синий маркер) только в некоторых областях присутствуют выбросы значений пеленга, но они достаточно большие. Возможно, это объясняется особенностями движения объекта в области, где зондирующий и отраженный сигналы пересекают зону турбулентности, вызванной движением объекта. При нахождении фазового сдвига стереосигналов с помощью максимума ККФ возникают дополнительные ошибки, что затем отражается в вычисленной траектории объекта. Также выбросы в вычисленных значениях пеленга могут быть обусловлены недостаточно высокой частотой дискретизации. Значения этих ошибок существенно выше показателей выбросов, наблюдаемых для метода с использованием переднего фронта импульса.
На рис. 4 а представлены траектории движения объекта, вычисленные с использованием глобального максимума ККФ и его соседних локальных максимумов.
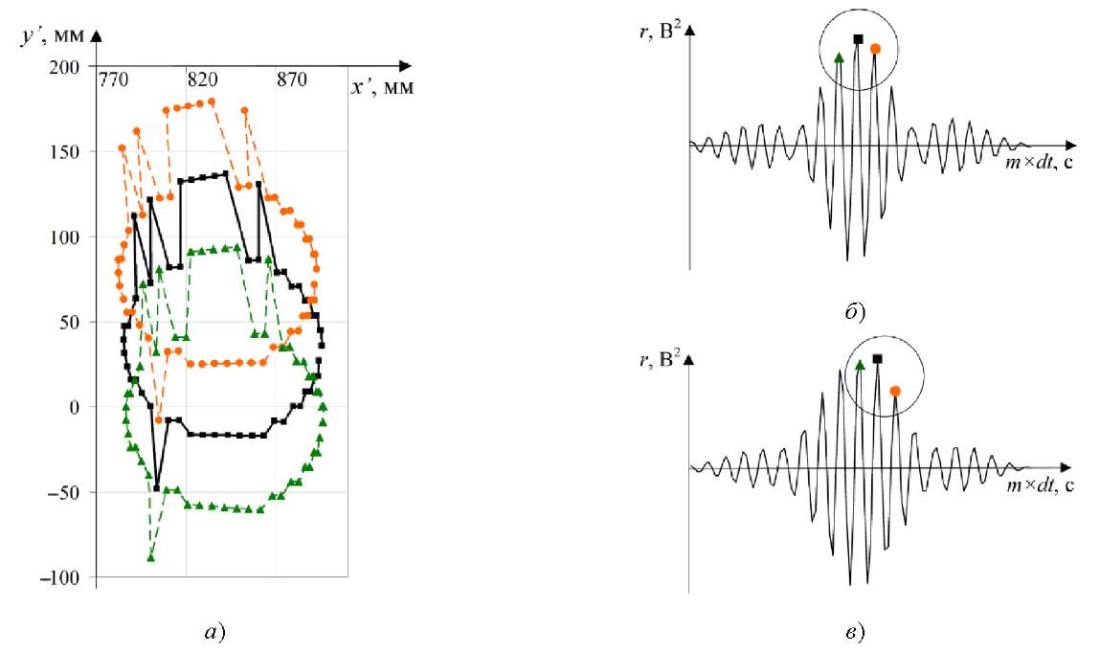
Рис. 4. Анализ траекторий кругового движения объекта: а — траектории, вычисленные с использованием глобального максимума ККФ (черный маркер), локального ближайшего правого максимума ККФ (оранжевый маркер), локального ближайшего левого максимума ККФ (зеленый маркер); б — пример ККФ, глобальный максимум которой соответствует корректному значению координат объекта; в — пример ККФ, в которой корректному значению координат объекта соответствует левый локальный максимум ККФ
Используя априорную информацию о плавности перемещения экспериментального объекта, можно выбрать точки, которые соответствуют более гладкой и валидной траектории. Такой подход применяется в других работах [17]. На рис. 4 а при x’ϵ[ 800;870], y’>0 корректные значения находятся на кривой для траектории, рассчитанной по левому локальному максимуму ККФ. Есть также ошибочные точки. Если их заменить точками траектории, полученной в результате использования правого локального максимума ККФ, можно вычислить корректное значение точки траектории (x’≈800, y’<0 на рис. 4 а). Данный графический метод устранения ошибки может быть реализован программно.
Таким образом, в некоторых точках траектории корректный сдвиг фазы стереосигналов, необходимый для вычисления пеленга, может соответствовать не глобальному максимуму ККФ, а одному из соседних локальных экстремумов (рис. 4 б, в). Такое смещение максимумов ККФ может быть обусловлено недостаточно высокой частотой дискретизации сигналов. Этим же объясняется ступенчатый характер результирующей траектории.
С учетом квазигармоничности сигнала предлагается использовать интерполяцию редких измерений исходного сигнала частыми вычисленными значениями. Такое виртуальное увеличение частоты дискретизации (передискретизации) дает возможность зафиксировать промежуточные значения в оцифрованных исходных данных. Интерполяция значений сигнала кубическим сплайном позволила получить 20 точек на 1 период сигнала вместо 5 точек в исходном варианте. На рис. 5 приведены расчетные траектории движения объекта, сформированные с предварительной передискретизацией сигналов.
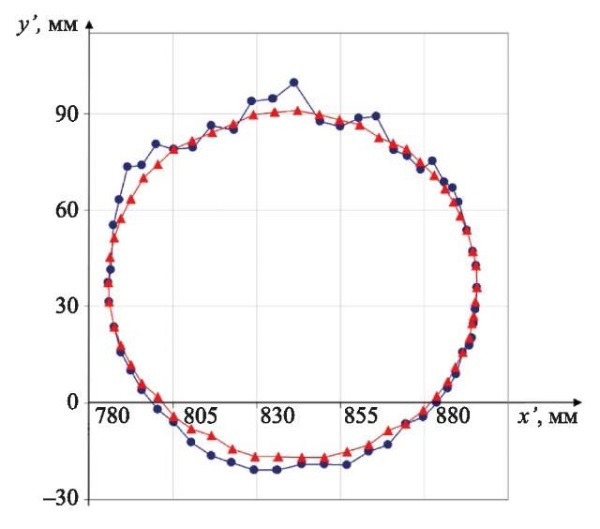
Рис. 5. Расчетные траектории движения объекта, полученные для стереосигналов с виртуально повышенной частотой дискретизации: синий маркер — используется разница времени прихода передних фронтов сигналов; красный маркер — используется максимум ККФ)
Красная линия — это траектория движения объекта, полученная с использованием максимума ККФ для расчета пеленга по предварительно интерполированным данным. Она представляется более корректной по сравнению с аналогичной траекторией, полученной с использованием разницы передних фронтов отраженных импульсов (синяя линия).
Обсуждение и заключение. Анализ особенностей определения пеленга на подводный объект с использованием взаимной фазовой информации сигналов дифференциального стереодатчика дает возможность сделать следующие выводы:
- разность времени прихода передних фронтов импульсов, зарегистрированных стереодатчиком, позволяет получать значения пеленга, показывающие направление на объект. Качество результата зависит от принятой величины порога (используемого при определении переднего фронта импульса) и изменчивости амплитуд принимаемых сигналов;
- применение подхода с использованием максимума кросс-корреляционной функции при недостаточной частоте дискретизации исходных сигналов приводит к существенным выбросам в расчетной траектории (рис. 3);
- передискретизация сигналов с помощью интерполяции исходных квазигармонических сигналов с использованием максимума ККФ для расчета пеленга и координат объекта позволяет получить гладкую траекторию (рис. 5), соответствующую плавному перемещению объекта по кругу. Такой подход требует значительно больших вычислительных затрат в сравнении с другими, рассмотренными в этой статье. Это может повлиять на скорость обработки сигналов в режиме реального времени.
Таким образом, исследованные возможности уточнения фазового метода пеленгации (передискретизация оцифрованных сигналов и использование максимума ККФ) позволяют эффективно оценивать траекторию движения подводного объекта.
Описаны условия получения гладкой корректной траектории движения отслеживаемого объекта. Этой цели служит передискретизация оцифрованных с недостаточной частотой дискретизации интерполированных квазигармонических стереосигналов. Вместе с этим задействуется метод расчета пеленга, использующий максимум кросс-корреляционной функции сигналов стереодатчика.
Данные на рис. 5 подтверждают, что задачу пеленгации можно решить с точностью, необходимой для практического применения. Учет фактора гладкости и непрерывности траектории движения объекта позволяет однозначно корректировать выбор максимума кросс-корреляционной функции сигналов стереодатчика (рис. 4).
Предложенные методы имеют большое значение для разработки систем подводного видения.
Список литературы
1. Meng Joo Er, Jie Chen, Yani Zhang, Wenxiao Gao. Research Challenges, Recent Advances, and Popular Datasets in Deep Learning-Based Underwater Marine Object Detection: A Review. Sensors. 2023;23(4):1990. https://doi.org/10.3390/s23041990
2. Андреев М.Я., Охрименко С.Н., Паршуков В.Н., Рубанов И.Л., Козловский С.В., Илларионов А.А. Бистатическая система обнаружения подводной цели (бистатический гидролокатор). Датчики и системы. 2019;233(2):50–56.
3. Матвеева И.В., Шейнман Е.Л. Определение текущих координат цели в бистатическом режиме гидролокации при неопределенности оценки пеленга на цель. Гидроакустика. 2017;31(3):9–12.
4. Matveeva IV, Sheinman EL, Shkol’nikov IS. Efficiency of Determination of Coordinates and Motion of Sea Objects at Bistatic Location of Moving Observing Systems. Hydroacoustics. 2016;26(2):28–32.
5. Арсентьев В.Г., Криволапов Г.И. Позиционирование объектов в гидроакустической навигационной системе с ультракороткой базой. Вестник Сибирского государственного университета телекоммуникаций и информатики. 2018;(4):66–75.
6. Матвиенко Ю.В., Хворостов Ю.А., Кулешов В.П. Особенности применения скалярно-векторных приемников звука в системах контроля подводной обстановки локальных районов. Подводные исследования и робототехника. 2022;42(4):4–15. https://doi.org/10.37102/1992-4429_2022_42_04_01
7. Terrachiano DS, Costanzi R, Manzari V, Stifani M, Caiti A. Passive Bearing Estimation Using a 2-D Acoustic Vector Sensor Mounted on a Hybrid Autonomous Underwater Vehicle. IEEE Journal of Oceanic Engineering. 2022;47(3):799–814. https://doi.org/10.1109/JOE.2021.3132647
8. Yanhou Zhang, Chao Wang, Qi Zhang, Lianglong Da, Zhaozhen Jiang. Bearing-only Motion Analysis of Target Based on Low-Quality Bearing-Time Recordings Map. IET Radar, Sonar & Navigation. 2024;18(5):765–781. https://doi.org/10.1049/rsn2.12519
9. Профатилова Г.А., Соловьев Г.Н. Измерение малых углов места фазовым методом в условиях интерференции. Вестник МГТУ им. Н.Э. Баумана. Серия «Приборостроение». 2013;90(1):3–12.
10. Каевицер В.И., Кривцов А.П., Смольянинов И.В., Элбакидзе А.В. Частотный метод измерения угловых координат подводного аппарата гидроакустической системой локального позиционирования. Журнал радиоэлектроники. 2021;3:11. https://doi.org/10.30898/1684-1719.2021.3.1
11. Арсентьев В.Г., Криволапов В.И. О характеристиках фазового пеленгатора гидроакустической системы приведения автономного необитаемого подводного аппарата. Вестник Сибирского государственного университета телекоммуникаций и информатики. 2021;53(1):23–35. https://doi.org/10.55648/1998-6920-2021-15-1-23-35
12. Широков В.А., Милич В.Н. Экспериментальный комплекс для исследования возможностей использования гидроакустических датчиков в системах подводного видения. Вестник ИжГТУ им. М.Т. Калашникова. 2021;24(4):54–64. https://doi.org/10.22213/2413-1172-2021-4-54-64
13. Арсентьев В.Г., Криволапов Г.И. Гидроакустический фазовый пеленгатор с амплитудно-модулированным навигационным сигналом. Вестник Сибирского государственного университета телекоммуникаций и информатики. 2021;54(2):14–26. https://doi.org/10.55648/1998-6920-2021-15-2-14-26
14. Матвиенко Ю.В. Оценка практически достижимой точности современных гидроакустических навигационных систем с ультракороткой измерительной базой для подводных роботов. Гироскопия и навигация. 2023;31(2):106–120.
15. Егоров С.Б., Горбачев Р.И. Определение порогов селекции по уровню и длительности в обнаружителях с нормализованным индикаторным процессом. Морские интеллектуальные технологии. 2020;2(2):144–147. https://doi.org/10.37220/MIT.2020.48.2.056
16. Abraham DA. Underwater Acoustic Signal Processing. Modeling, Detection, and Estimation. Cham: Springer; 2019. P. 457–619. https://doi.org/10.1007/978-3-319-92983-5
17. Денисов В.П., Дубинин Д.В., Крутиков М.В., Мещеряков А.А. Алгоритм отбраковки аномально больших ошибок пеленгования фазовым пеленгатором. Доклады ТУСУР. 2012;26(2):36–42.
Об авторах
В. А. ШироковРоссия
Владимир Анатольевич Широков, кандидат технических наук, старший научный сотрудник
426067, г. Ижевск, ул. им. Татьяны Барамзиной, 34
А. И. Баженова
Россия
Айгуль Илсуровна Баженова, кандидат технических наук, научный сотрудник
426067, г. Ижевск, ул. им. Татьяны Барамзиной, 34
В. Н. Милич
Россия
Владимир Николаевич Милич, кандидат технических наук, ведущий научный сотрудник
426067, г. Ижевск, ул. им. Татьяны Барамзиной, 34
Рецензия
Для цитирования:
Широков В.А., Баженова А.И., Милич В.Н. Особенности определения пеленга на подводный объект с использованием фазовой информации дифференциального стереодатчика. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):198-206. https://doi.org/10.23947/2687-1653-2024-24-2-198-206. EDN: FPQRSJ
For citation:
Shirokov V.A., Bazhenova A.I., Milich V.N. Features of Bearing on Underwater Object Using Phase Information of a Differential Stereo Sensor. Advanced Engineering Research (Rostov-on-Don). 2024;24(2):198-206. https://doi.org/10.23947/2687-1653-2024-24-2-198-206. EDN: FPQRSJ












































