Перейти к:
Определение динамических напряжений и перемещений при действии ударной нагрузки на двухслойную конструкцию в процессе индентирования
https://doi.org/10.23947/2687-1653-2024-24-3-264-273
EDN: VVRPYB
Аннотация
Введение. Многие исследователи надежности строительных конструкций уделяют внимание твердости — важной характеристике конструкционного материала. Ее определяют индентированием — вдавливанием наконечника инструмента в поверхность. Исследуются преимущества методов динамического индентирования, распределение интенсивности напряжений на поверхности и внутри образца. Однако мало изучено состояние слоистых материалов при ударе. Цели представленной работы — рассмотреть индентирование для двухслойного образца и определить чувствительность верхнего слоя к прочности подложки. Это позволит выявить значимые характеристики прочностных свойств однородных и неоднородных конструкций.
Материалы и методы. Использовали упруго-пластическую модель поведения материала и схему ударного индентирования, которая учитывает массы индентора и ударника, сцепленных линейными пружинами. Поверхность индентора — коническая, угол раскрытия — 120°. Удар моделировали в системе Matlab. Конечноэлементную модель в Ansys APDL применили для верификации данных и анализа результатов эксперимента. Для расчетов взяли традиционные модели теории упругости. Поведение материала в области пластического деформирования описали с помощью опций мультилинейного изотропного упрочнения и критерия пластичности Мизеса.
Результаты исследования. Приводятся итоги сопоставления трех вариантов варьирования уровня предела текучести в нижнем слое: когда предел текучести в нижнем слое вдвое меньше верхнего, равен ему и вдвое больше. Проанализированы перемещения в разных точках наблюдения для образцов с верхним слоем 2 мм и 1 мм. В первом случае при горизонтальном сдвиге не меняются показатели перемещений внутри образца, если уровень предела текучести вдвое ниже или выше, чем в верхнем. При равенстве этих показателей разница становится заметной. Во втором случае (слой 1 мм) разница перемещений видна во всех точках наблюдения. Так можно обоснованно заключить, что конструкция с меньшим верхним слоем более чувствительна к ударному воздействию. В ходе изысканий стало известно, что в зоне 2 мм совершаются колебания, связанные с переходом в зону пластичности, ниже этой зоны — упругие затухающие колебания. Решили задачу классификации для верхнего слоя материала с меняющимися характеристиками основания. Показатель для сравнения — твердость по Бринеллю (НВ) в диапазоне 200–600. Результаты визуализировали в виде графиков и обработали с помощью нейросети. Точность ее вычислений составила 98 %.
Обсуждение и заключение. Для определения прочностных свойств однородных конструкций достаточно характеристики скорости перемещения внутри образца. Для неоднородной структуры необходимо вводить дополнительные параметры — перемещения на поверхности и внутри образца в фиксированных точках наблюдений. Комплексный подход к определению прочностных свойств неоднородной конструкции повышает точность расчетов, а использование нейросетей — их скорость.
Ключевые слова
Для цитирования:
Бабушкина Н.Е., Ляпин А.А. Определение динамических напряжений и перемещений при действии ударной нагрузки на двухслойную конструкцию в процессе индентирования. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):264-273. https://doi.org/10.23947/2687-1653-2024-24-3-264-273. EDN: VVRPYB
For citation:
Babushkina N.E., Lyapin A.A. Determination of Dynamic Stresses and Displacements under the Action of an Impact Load on a Two-Layer Structure during the Indentation Process. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):264-273. https://doi.org/10.23947/2687-1653-2024-24-3-264-273. EDN: VVRPYB
Введение. При проектировании и эксплуатации строительных конструкций предъявляются высокие требования к их прочности и надежности [1]. В литературе рассматриваются вопросы безотказности работы конструкции [2], а также сохранения ее эксплуатационных свойств на протяжении всего срока службы [3].
С инженерной точки зрения твердость — одна из важных характеристик материала. Она связана с такими механическими свойствами, как предел текучести, предел прочности, предел выносливости и пр. Твердость материала определяют вдавливанием наконечника инструмента в поверхность. Различают статическое и динамическое вдавливание. Испытание на статическое вдавливание включает вдавливание твердого индентора в плоскую и гладкую поверхность мягкого материала (мишени), механические свойства которого определяются по измеренной зависимости приложенной нагрузки от глубины внедрения. Статические методы не позволяют оценить физико-математические характеристики материала в условиях динамического нагружения [4]. Для этого используют методы динамического индентирования [4].
ГОСТ Р 56474–20151представляет динамическое индентирование как внедрение индентора в материал под действием однократного ударного импульса, создаваемого специальным разгонным устройством или силой тяжести. Такой подход относится к методам неразрушающего контроля. Их основной принцип — безопасное обследование, определение целостности и основных рабочих свойств объекта [5]. Главное преимущество — простота применения.
Испытание на вдавливание — это сложный процесс, который включает механику контакта, нелинейность материала и механику разрушения. Для общих случаев очень трудно получить аналитические решения. Поэтому понимание рассматриваемых процессов основано главным образом на экспериментах и моделировании методом конечных элементов.
Упругий контакт впервые изучил Г. Герц [6] в конце XIX века. Он пытался найти точное определение твердости, используя эластичный процесс. Позже Ж.В. Буссинеск разработал основанный на теории потенциала метод расчета напряжений и перемещений в упругом теле, нагруженном любым жестким осесимметричным индентором. Что касается углублений, связанных с пластической деформацией, то ранние исследования были сосредоточены на пределе текучести и прочности при растяжении.
В публикациях уделяется внимание методам динамического индентирования с целью определения прочностных свойств конструкций. Так, Н.Н. Автономов и А.В. Тололо рассмотрели задачу вдавливания шарового индентора в упругопластический материал [7]. Авторы проанализировали распределение интенсивности напряжений на поверхности и внутри образца. Так стало известно, что зоны максимальной интенсивности располагаются на небольшом расстоянии от зоны контакта индентора и образца, а при увеличении нагрузки расширяются.
Зарубежные авторы [8] разработали метод динамического вдавливания, заключающийся в измерении глубины и реакции на нагрузку образца в процессе вдавливания. Для определения углубления использовался метод измерения смещений, основанный на муаровой интерферометрии. Нагрузку измеряли кварцевым датчиком. Результаты численного моделирования методом конечных элементов свидетельствуют о том, что такой подход достаточно хорошо согласуется со значениями, полученными при традиционных методах определения скорости деформации.
Ученые рассматривали прочностные свойства материалов в процессе индентирования. Этому посвящено немало работ, например [9]. Изучение поведения «мишени» под воздействием механических нагрузок играет ключевую роль в разработке новых материалов, конструкций и изделий [10]. Комплексные исследования позволяют решать задачи оптимизации технологических процессов, обеспечения надежности конструкций и предотвращения отказов в их работе.
Полученные решения открывают возможность создавать более эффективные и устойчивые структуры [11], что обусловливает актуальность изысканий в данном направлении. При этом все еще недостаточно изучен вопрос состояния слоистых конструкций при ударном воздействии.
Цели работы — анализ напряжений и перемещений в двухслойной конструкции и выявление уровня чувствительности верхнего слоя образца к прочности подложки. Исследование позволит установить значимые характеристики для определения прочностных свойств однородных и неоднородных конструкций.
Материалы и методы. Схема прибора ударного индентирования представлена на рис. 1.
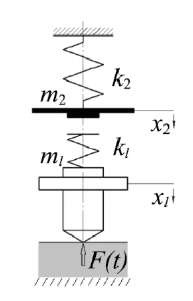
Рис. 1. Схема прибора ударного индентирования
Система дифференциальных уравнений, соответствующая динамике механических элементов прибора ударного индентирования, имеет вид:
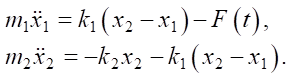 (1)
(1)
Так описывается колебательный процесс динамической системы с двумя массами: m1 — масса индентора;
m2 — масса ударника. Массы сцеплены линейными пружинами с жесткостью k1 и k2 соответственно [12]. Величины вертикальных перемещений x1(t), x2(t) как степени свободы массивных элементов неизвестны во времени. Ударник взвели на высоту h. После спуска в момент контакта с индентором он достиг скорости
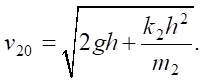
Таким образом, к системе (1) следует добавить начальные условия:
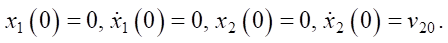 (2)
(2)
Неизвестна величина F(t) силы сопротивления со стороны индентируемого материала.
Считаем, что поверхность индентора — коническая с углом раскрытия α = 120 град. Значит, необходимо использовать упруго-пластическую модель поведения испытуемого материала. В вершине конуса совпадает начало ударного воздействия и пластической деформации.
Ударный процесс моделировали в системе «Матлаб» (Matlab). Это позволило подобрать механические параметры установки. Для верификации данных и анализа результатов эксперимента использовали конечноэлементную модель в среде Ansys APDL. Рассматривалась двухслойная конструкция. Анализировались ее перемещения и напряжения, возникающие в двухслойном образце при действии динамической нагрузки. В расчетах применялись традиционные модели теории упругости. Для описания поведения материала в области пластического деформирования задействовали опции мультилинейного изотропного упрочнения и критерий пластичности Мизеса:
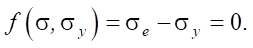 (3)
(3)
где σe — эквивалентное напряжение фон Мизеса,
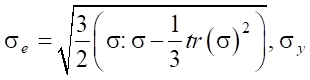 — предел текучести при одноосной нагрузке.
— предел текучести при одноосной нагрузке.
Для контроля точности сходимости предварительно подобрали сетку конечных элементов. При исследовании параметров двуслойной конструкции рассмотрели три варианта варьирования уровня предела текучести в нижнем слое в трех случаях — когда предел текучести в нижнем слое вдвое меньше верхнего, равен ему и вдвое больше (таблица 1).
Таблица 1
Структура и параметры исследуемых конструкций
|
№ п/п |
Уровень предела текучести в нижнем слое |
Слой, мм |
|
|
верхний |
нижний |
||
|
1 |
1/2 |
1 |
9 |
|
2 |
1 |
||
|
3 |
2 |
||
|
4 |
1/2 |
2 |
8 |
|
5 |
1 |
||
|
6 |
2 |
||
Детальный анализ перемещений в различных точках наблюдения наглядно показывает отличие характера перемещений в области пластических деформаций. Для изучения перемещений выбрали следующую схему (рис. 2). Верхний слой конструкции для наглядности выделили более темным серым цветом.

Рис. 2. Определение точек для измерений вертикальных и горизонтальных перемещений:
а — конструкция с верхним слоем 1 мм;
б — конструкция с верхним слоем 2 мм.
Цифры 1, 3 и 5 обозначают уровень предела текучести в нижнем слое
по отношению к верхнему в соответствии с таблицей 1
Результаты исследования. На рис. 3 представлена сравнительная характеристика уровня перемещений на поверхности образца с горизонтальным сдвигом точки наблюдения от точки ударного воздействия.
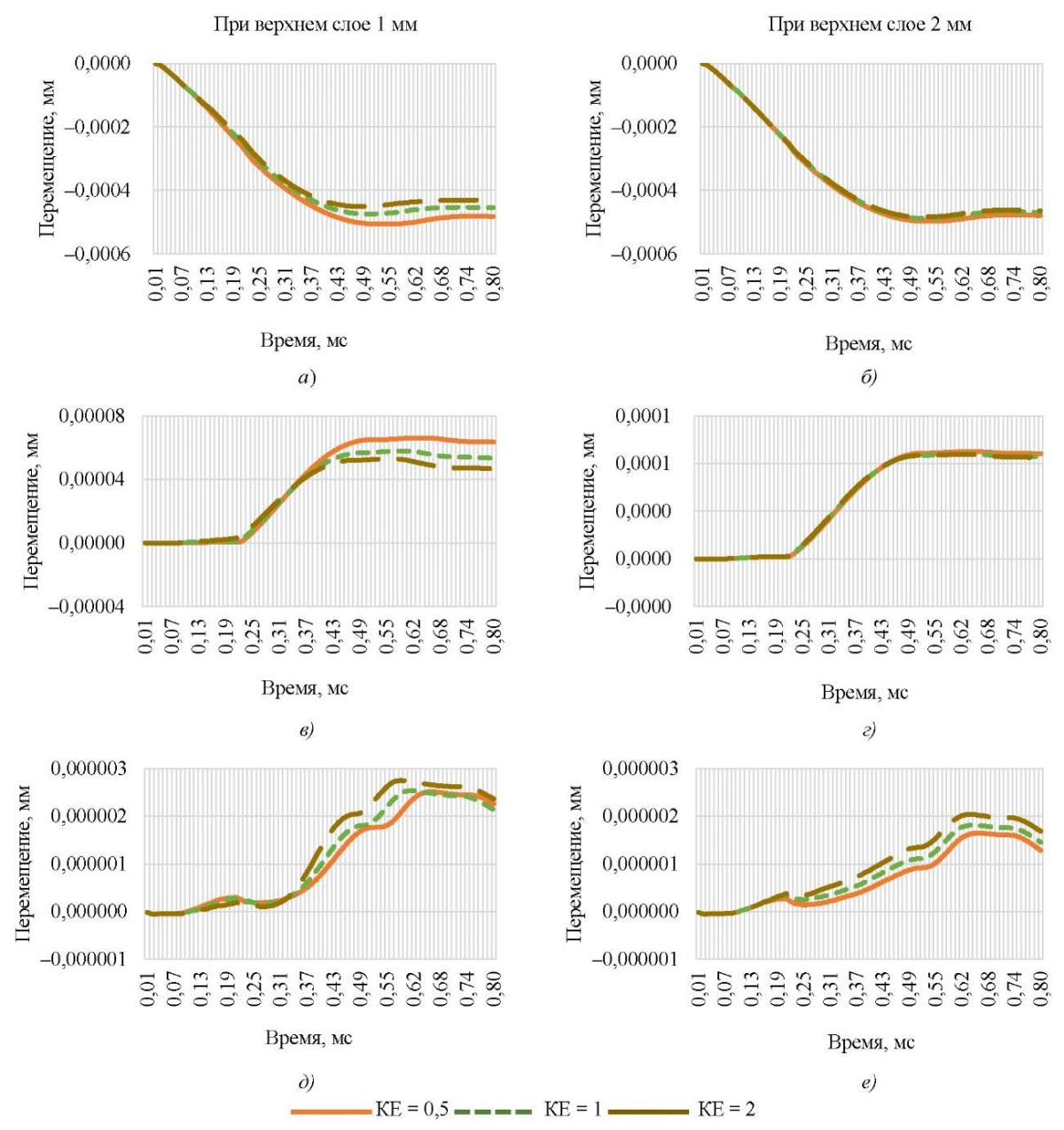
Рис. 3. Перемещения на поверхности образца в различных точках контакта:
а, б — в 1-й точке контакта;
в, г — в 3-й точке на поверхности;
д, е, — в 5-й точке на поверхности
Как видим, для двухслойной конструкции с верхним слоем 2 мм изменение уровня текучести в 1-й и 3-й точках контакта при горизонтальном сдвиге не влияет на показатели перемещений внутри образца. В 5-й точке разница становится заметной. Для конструкции с верхним слоем 1 мм разница уровня перемещений заметна во всех точках наблюдения. Можно сделать вывод, что конструкция с меньшим верхним слоем более чувствительна к ударному воздействию.
На рис. 4 показаны распределения интенсивности напряжения при различном уровне верхнего покрытия. Приведенные данные позволяют утверждать, что в зоне 2 мм происходят колебания, связанные с переходом в зону пластичности, ниже этой зоны — упругие колебания, затухающие со временем.
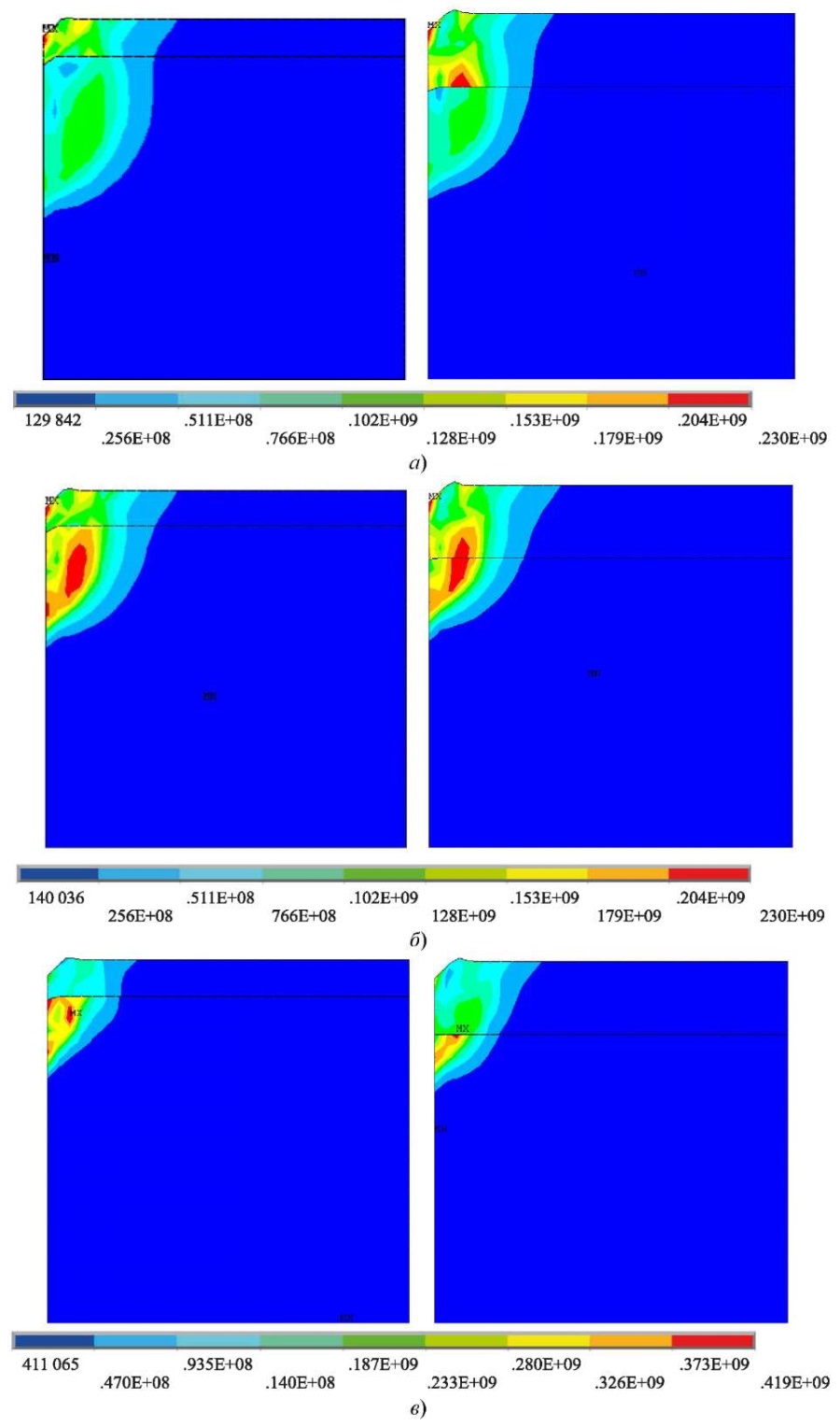
Рис. 4. Интенсивность напряжений при различных значениях КЕ, МПа:
а — КЕ = 0,5; б — КЕ = 1; в — КЕ = 2
На рис. 5 построены графики напряжений на поверхности в различных точках наблюдений.
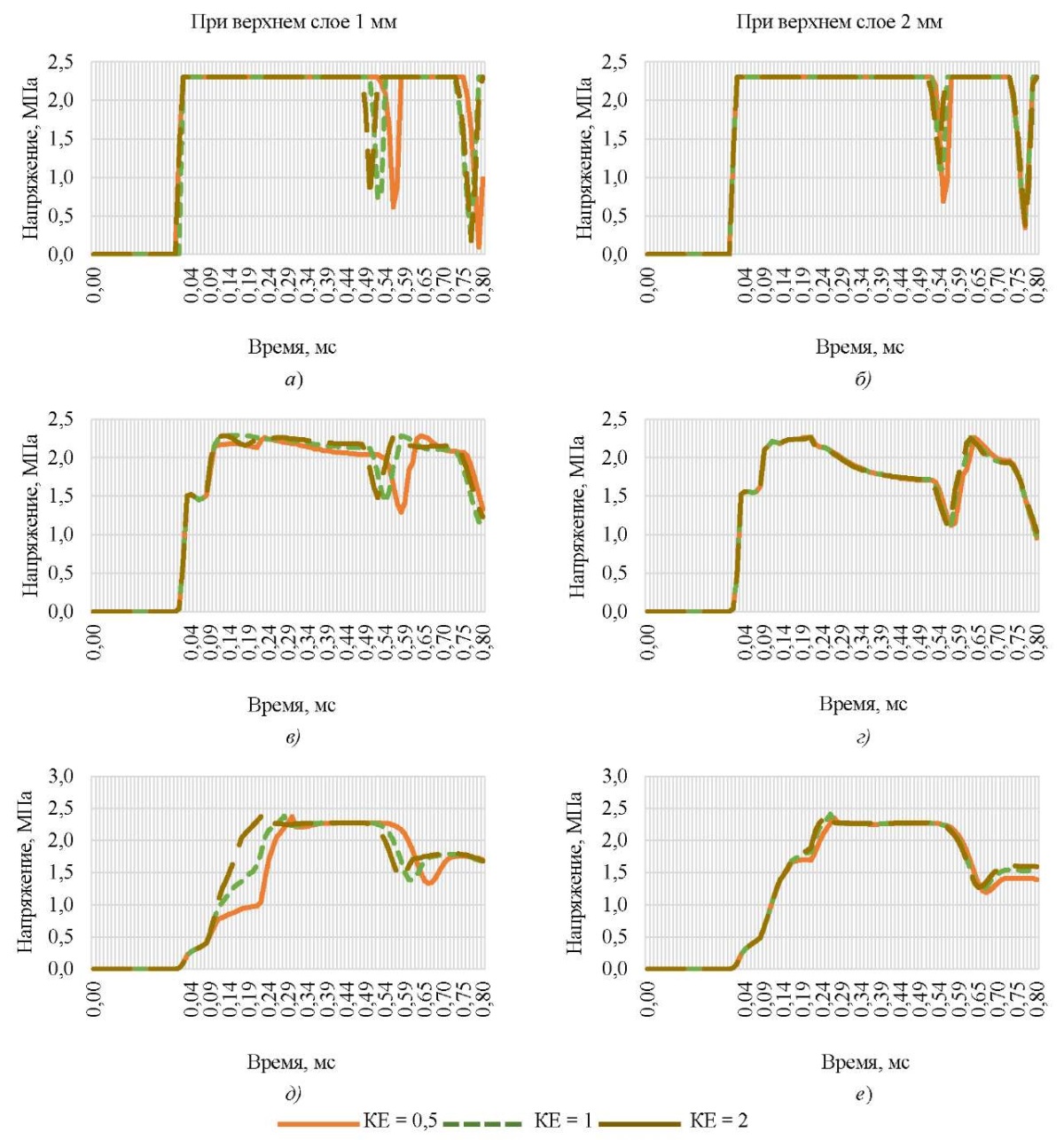
Рис. 5. Напряжения на поверхности образца в различных точках контакта:
а, б — в точке контакта;
в, г — в 3-й точке на поверхности;
д, е, — в 5-й точке на поверхности
Для анализа влияния основания на прочностные свойства образца решили задачу классификации [12] по значению Бринеллевой твердости (НВ) верхнего слоя материала с изменяющимися характеристиками основания. В рамках исследования выделили пять классификационных групп (таблица 2).
Таблица 2
Классификационные группы
|
№ п/п |
Группа |
Значение НВ |
|
1 |
I |
200 |
|
2 |
II |
300 |
|
3 |
III |
400 |
|
4 |
IV |
500 |
|
5 |
V |
600 |
Расчетные значения, полученные с помощью математической модели, подавались на вход нейронной сети. На рис. 6 представлены значения скоростей и перемещений для выделенных групп твердости.
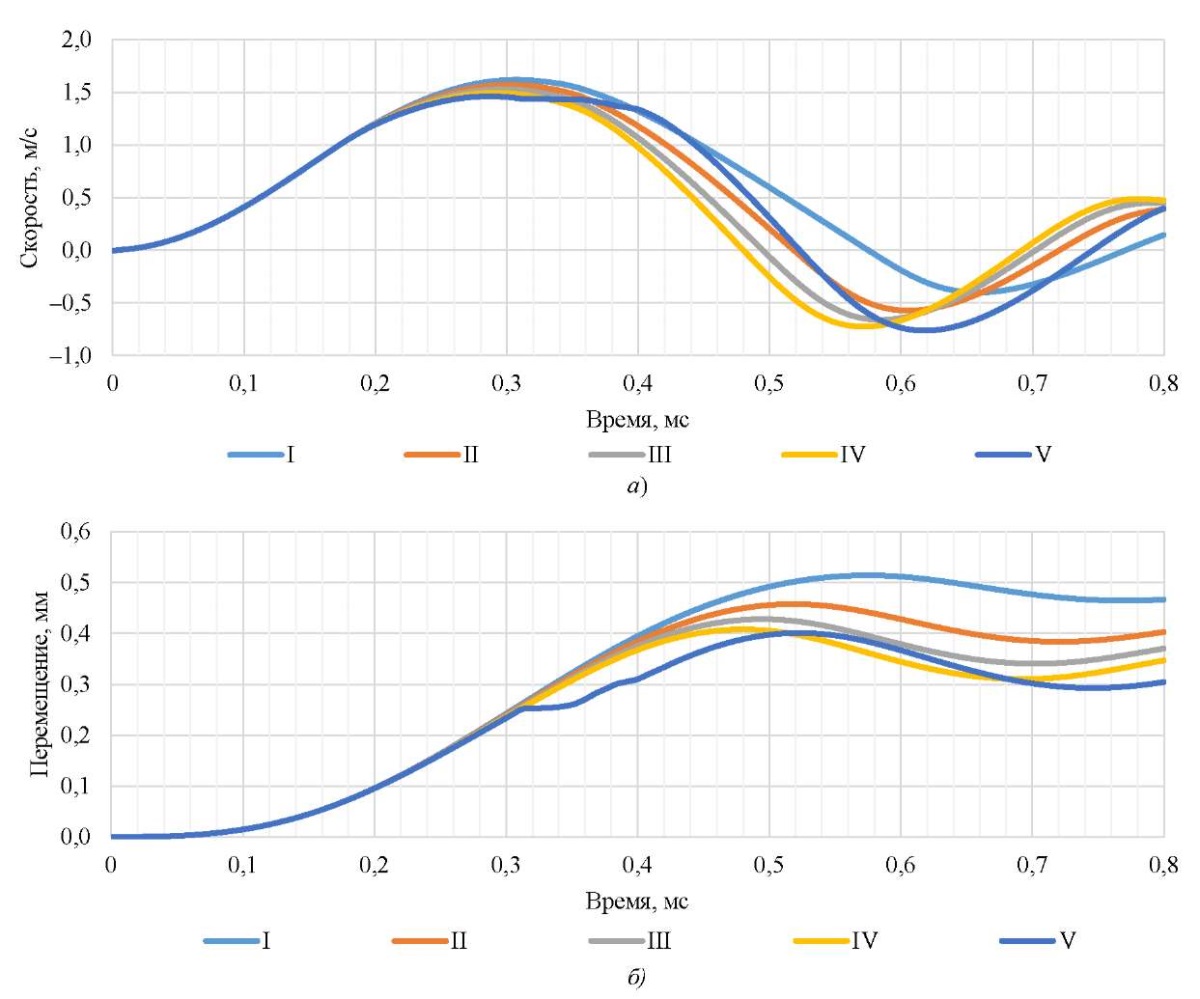
Рис. 6. Расчетные значения по классификационным группам:
а — скорость внедрения индентора; б — перемещения
Для дальнейшей обработки данных использовали созданную и обученную нейронную сеть с полносвязной структурой [13]. Стоит отметить, что нейронные сети обладают широкими возможностями в решении такого типа задач [14], в частности в области строительства [15]. Нейронные сети часто используются для качественной оценки, прогнозирования и мониторинга состояния строительных конструкций [16], а также для параметрической идентификации объектов [17]. Увеличение вычислительных мощностей нейронных сетей напрямую влияет на развитие их функционала [18].
Точность вычислений нейросети составила 98 %. Следовательно, нейросеть верно анализирует экспериментальные данные и способна адекватно учесть поведение материала при ударном нагружении.
Обсуждение и заключение. Таким образом, анализ распределения перемещений и напряжений в образце позволяет сделать ряд заключений.
- Уровень вертикальных перемещений в волновом процессе значительно выше, чем в горизонтальном.
- Уровень жесткости подложки влияет на распределение перемещений и напряжений.
- В более прочном нижнем слое перемещения заметно меньше, чем в мягком.
- Верхний слой чувствителен к прочности подложки, если его высота не превышает 1 мм.
- С удалением от места индентирования деформации становятся упругими, напряжение не выходит в область пластических деформаций.
По итогам работы можно утверждать, что для определения прочностных свойств однородных конструкций достаточно одной величины, характеризующей скорость перемещения внутри образца. Для неоднородной структуры необходимо вводить такие дополнительные параметры, как перемещения на поверхности и внутри образца в фиксированных точках наблюдений. Комплексный подход к определению прочностных свойств неоднородной конструкции позволит повысить точность расчетов. А использование нейросетевых технологий для решения такого типа задач открывает возможность более быстрых вычислений.
1. ГОСТ Р 56474–2015. Системы космические. Контроль неразрушающий физико-механических свойств материалов и покрытий космической техники методом динамического индентирования. Электронный фонд правовых и нормативно-технических документов. URL: https://docs.cntd.ru/document/1200122009 (дата обращения: 14.05.2024).
Список литературы
1. Lyapin A, Beskopylny A, Meskhi B. Structural Monitoring of Underground Structures in Multi-Layer Media by Dynamic Methods. Sensors. 2020;20(18):5241. https://doi.org/10.3390/s20185241
2. Чесноков А.В., Михайлов В.В., Долматов И.В. Выявление повреждений мягкой оболочки тентовой строительной конструкции покрытия при помощи искусственной нейронной сети. Строительная механика и конструкции. 2022;33(2):98–109.
3. Куклина М.В., Лебер А.И., Махакова А.М. Использование технологии нейронных сетей в строительной организации. Вестник Алтайской академии экономики и права. 2022;(5–3):362–368. https://doi.org/10.17513/vaael.2219
4. Кузьмичев М.В., Егоров Р.А. Моделирование и алгоритмическое обеспечение процесса динамического индентирования. Научно-технический вестник информационных технологий, механики и оптики. 2018;18(5):794–800. https://doi.org/10.17586/2226-1494-2018-18-5-794-800
5. Матлин М.М., Казанкин В.А., Казанкина Е.Н. Прогнозирование технического состояния деталей индентированием в различных условиях нагружения. Вестник Тверского государственного технического университета. Технические науки. 2022;13(1):22–27.
6. Рудницкий В.А., Крень А.П., Ланцман Г.А. Оценка пластичности металлических материалов методом динамического индентирования. Литье и металлургия. 2017;(2):81–87. https://doi.org/10.21122/1683-6065-2017-2-81-87
7. Oliver WC, Pharr GM. An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. Journal of Materials Research. 1992;7:1564–1583. http://doi.org/10.1557/JMR.1992.1564
8. Автономов Н.Н., Тололо А.В. Исследование распределения напряжения в образце при вдавливании шарового индентора. Актуальные проблемы авиации и космонавтики. 2018;14(1):245–247.
9. Jun Lu, Subra Suresh, Guruswami Ravichandran. Dynamic Indentation for Determining the Strain Rate Sensitivity of Metals. Journal of the Mechanics and Physics of Solids. 2003;51(11–12):1923–1938. https://doi.org/10.1016/j.jmps.2003.09.007
10. Matyunin VM, Nuha Abusaif, Marchenkov AYu. Analysis of the Indentation Size Effect on the Hardness Measurements of Materials. Journal of Physics: Conference Series. 2019;1399(4):044016. https://doi.org/10.1088/17426596/1399/4/044016
11. Varghese J, Radig GF, Herkommer D, Dasgupta A. Hybrid Experimental and Computational Approach for Rate Dependent Mechanical Properties Using Indentation Techniques. In: EuroSimE 2005. Proc. 6th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Micro-Electronics and Micro-Systems. New York City: IEEE; 2005. P. 510–514. https://doi.org/510-514.10.1109/ESIME.2005.1502858
12. Kubenko V. Nonstationary Displacements in an Axisymmetric Problem for an Elastic Half-Space Under Mixed Boundary Conditions. International Applied Mechanics. 2021;57:148–159. https://doi.org/10.1007/s10778-021-01069-3
13. Бескопыльный А.Н., Веремеенко А.А., Копылов Ф.С., Крымский В.С. Задача о статическом внедрении конического индентора в область с поверхностным упрочнением. Инженерный вестник Дона. 2018;49(2):214–218.
14. Zesheng Lin, Hongxia Ye, Bin Zhan, Xiaofeng Huang. An Efficient Network for Surface Defect Detection. Applied Sciences. 2020;10(17):6085. https://doi.org/10.3390/app10176085
15. Babushkina N, Lyapin A, Kovaleva A. Analysis of Neural Network Results Based on Experimental Data during Indentation. In: Topical Problems of Agriculture, Civil and Environmental Engineering. E3S Web of Conferences (TPACEE). 2020;224:01018. https://doi.org/10.1051/e3sconf/202022401018
16. Elfaki AO, Alatawi S, Abushandi E. Using Intelligent Techniques in Construction Project Cost Estimation: 10-Year Survey. Advances in Civil Engineering. 2014;2014:107926. https://doi.org/10.1155/2014/107926
17. Patel DA, Jha KN. Evaluation of Construction Projects Based on the Safe Work Behavior of Co-employees through a Neural Network Model. Safety Science. 2016;89:240–248. https://doi.org/10.1016/J.SSCI.2016.06.020
18. Порошин И.Е., Титов М.А. Использование искусственных нейронных сетей для параметрической идентификации объектов. Молодой ученый. 2020;316(26):39–42.
19. Алферьев Д.А. Использование искусственных нейронных сетей в современном обществе. Социальная сфера. 2020;6(3):6. https://doi.org/10.15838/sa.2020.3.25.6
Об авторах
Н. Е. БабушкинаRussian Federation
Наталья Евгеньевна Бабушкина, ассистент кафедры вычислительной техники и программирования
344003, г. Ростов-на-Дону, пл. Гагарина, 1
А. А. Ляпин
Russian Federation
Александр Александрович Ляпин, доктор физико-математических наук, профессор, заведующий кафедрой информационных систем в строительстве
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Бабушкина Н.Е., Ляпин А.А. Определение динамических напряжений и перемещений при действии ударной нагрузки на двухслойную конструкцию в процессе индентирования. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):264-273. https://doi.org/10.23947/2687-1653-2024-24-3-264-273. EDN: VVRPYB
For citation:
Babushkina N.E., Lyapin A.A. Determination of Dynamic Stresses and Displacements under the Action of an Impact Load on a Two-Layer Structure during the Indentation Process. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):264-273. https://doi.org/10.23947/2687-1653-2024-24-3-264-273. EDN: VVRPYB
JATS XML














































