Перейти к:
Оценка напряжений в пластине с концентратором посредством ультразвуковых измерений акустической анизотропии
https://doi.org/10.23947/2687-1653-2024-24-4-307-315
EDN: RMBTZU
Аннотация
Введение. Акустическая анизотропия измеряется при ультразвуковом неразрушающем контроле и позволяет оценить величину напряжений методом акустоупругости. В литературе подробно описано применение такого подхода в случае двухосного напряженного состояния протяженных конструкций: магистральных трубопроводов, рельсовых плетей, парогенераторов и других. Для них предполагается наличие однородного поля с нулевыми либо слабыми градиентами напряжений и деформаций. Однако не решена проблема своевременного обнаружения и оценки критических напряжений, вызванных локальными концентраторами, посредством ультразвукового контроля. Представленный материал призван восполнить этот пробел. Цель работы — определить возможности применения метода акустоупругости для оценки разности главных двухосных напряжений вокруг концентратора — кругового выреза в прямоугольной пластине.
Материалы и методы. Из листа технически чистого алюминия марки АМц поперек направления проката вырезали пластину 510×120×15 мм с центральным отверстием диаметром 40 мм и подвергли ее одноосному ступенчатому нагружению в испытательной машине Instron-8850. Для ультразвуковых измерений задействовали акустический датчик с несущей частотой 5 МГц. Напряжения рассчитывались путем решения задачи о растяжении изотропной линейно-упругой пластины в пакете конечно-элементного моделирования «Ансис» (Ansys) и по соотношениям плоской задачи Кирша, полученным в полярной системе координат.
Результаты исследования. Итоги работы позволяют утверждать, что результаты аналитических и численных расчетов во многом совпадут только для точек, расположенных рядом с зоной наибольшей концентрации напряжений. Во всех остальных случаях показатели отличаются в несколько раз по знаку, и по модулю. Разница объясняется тем, что подход Кирша предполагает действие сжимающих напряжений в области расположения некоторых точек, однако этот фактор отсутствует, если речь идет о реальной пластине. Установлено, что в области материала с преобладающими растягивающими напряжениями метод акустоупругости позволяет количественно оценить их разность с погрешностью, не превышающей инженерную. Расчеты по соотношениям Кирша коррелируют с остальными только в точках с максимальной концентрацией растягивающих напряжений.
Обсуждение и заключение. Результаты исследования позволяют применять метод акустоупругости для оценки величины растягивающих двухосных напряжений в области вокруг технологических отверстий. Они согласуются с известными научными результатами и дают возможность рационально выбрать точки измерения акустической анизотропии. Итоги данной научной работы можно применить при ультразвуковом неразрушающем контроле методом акустоупругости.
Ключевые слова
Для цитирования:
Третьяков Д.А., Осовик Д.С. Оценка напряжений в пластине с концентратором посредством ультразвуковых измерений акустической анизотропии. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):307-315. https://doi.org/10.23947/2687-1653-2024-24-4-307-315. EDN: RMBTZU
For citation:
Tretyakov D.A., Osovik D.S. Estimation of Stresses in a Plate with a Concentrator through Ultrasonic Measurements of Acoustic Anisotropy. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):307-315. https://doi.org/10.23947/2687-1653-2024-24-4-307-315. EDN: RMBTZU
Введение. В последние десятилетия разрабатываются отечественные технологии неразрушающего контроля для определения напряженно-деформированного состояния элементов энергетических систем, железнодорожного и трубопроводного транспорта [1]. Эти подходы предполагают решение обратных задач в случае неоднородного напряженного состояния [2], бесконтактную электромагнитно-акустическую тензометрию [3], учет деградации упругих свойств при комбинированном неразрушающем контроле [4], а также прецизионное измерение временных задержек при распространении упругих волн в материале [5]. Технологии прошли верификацию в ходе промышленных измерений1 [6], их применение сопровождается работой современного диагностического оборудования [7]. Однако остается актуальной задача апробации существующих подходов при диагностике анизотропных конструкционных материалов, к числу которых относится промышленный прокат [8].
Данная работа посвящена исследованию акустической анизотропии [9] начально неоднородного материала. В данном случае это технически чистый алюминий марки АМц. Образцы, вырезанные из катаного листа, не проходили подготовку по снятию начальных внутренних напряжений, вызванных пластической деформацией в процессе прокатки [10]. Задача — установить возможность оценки разности величины двухосных напряжений в металле с неоднородной начальной акустической анизотропией [11].
Материалы и методы. В экспериментах использовали ультразвуковой анализатор акустической анизотропии ИН-5101А2. Это сертифицированный прибор для измерения механических напряжений методом акустоупругости [12]. Напряжения рассчитывались по формуле:
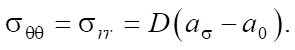 (1)
(1)
Здесь σθθ и σrr — главные компоненты тензора напряжений в полярных координатах; D — коэффициент упругоакустической связи материала; a0 — начальная акустическая анизотропия в точке измерений; aσ — значение параметра акустической анизотропии при текущей величине одноосной растягивающей нагрузки σ. Для алюминиевого сплава АМц коэффициент D = –2,0 ± 0,3 ∙ 10–4 МПа [13].
Текущее значение параметра акустической анизотропии a0 [14] определялось по формуле (2) как относительная разность времен распространения поперечных ультразвуковых волн взаимно ортогональной поляризации [15]:
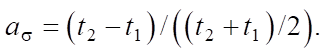 (2)
(2)
Здесь t1, t2 — текущие значения временных задержек при прохождении пакетов поперечных волн по толщине материала после их многократного отражения, скорости которых направлены вдоль и поперек линии одноосного нагружения.
Измерения проводились с помощью акустических датчиков с частотой излучения импульсов 5 МГц. Точность измерений временных задержек t1, t2 составляла 3 нс.
Исследовался малолегированный коррозионно-стойкий алюминиево-марганцевый сплав марки АМц, близкий по своим свойствам к технически чистому алюминию (97/99 % Al по составу). Алюминий — это модельный материал для ультразвуковых исследований. Именно с ним получены основные результаты в области акустоупругости [1].
Механические испытания проводились на прямоугольной пластине размером 510×120×15 мм, вырезанной из катаного алюминиевого листа поперек направления проката. Образец имел концентратор напряжений в виде центрального кругового отверстия диаметром 40 мм (рис. 1).

Рис. 1. Схема образца из листа алюминиевого проката марки АМц
Направление проката влияет на знак начальной акустической анизотропии a0 [16]:
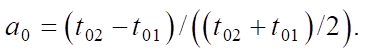 (3)
(3)
Здесь t01, t02 — начальные временные задержки поперечных волн. В случае образцов, вырезанных поперек проката, безразмерный параметр начальной акустической анизотропии a0, вычисленный по формуле (3), будет отрицательным: a0 < 0.
Для жесткого ступенчатого нагружения пластины применили одноосное растяжение в гидравлической машине Instron-8850 (рис. 3). Рассматривалось напряженно-деформированное состояние на трех этапах нагружения при значениях растягивающей нагрузки F1 = 30 кН, F2 = 50 кН и F3 = 70 кН. Для исследования выбрали n = 8 участков (точек) образца. Схема их расположения представлена на рис. 2.
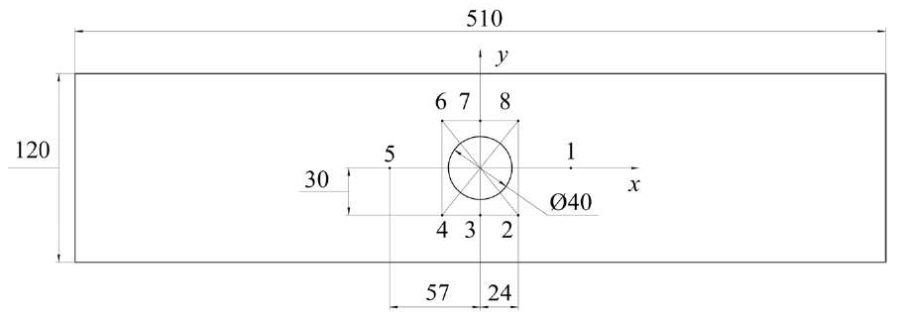
Рис. 2. Схема расположения исследуемых точек образца
Ультразвуковой контроль проводили вдоль трех рядов точек: 1–5, 2–4 и 6–8, симметрично расположенных друг относительно друга вокруг концентратора напряжений (рис. 2). Характерный размер пластин пьезоэлектрических элементов акустического датчика — 12×12 мм. Это означает, что с каждой точкой был связан свой локальный представительный объем материала. Точки выбрали так, чтобы представительные объемы существенно различались по напряженно-деформированному состоянию [17].
Механические испытания на растяжение в машине типа Instron предполагают разные граничные условия для образца. Нижняя его часть (точки 4, 5, 6 на рис. 2) жестко зафиксирована в неподвижном захвате испытательной машины (рис. 3). В верхней части (точки 1, 2 и 8 на рис. 2), закрепленной в подвижном захвате, образец растягивался с малой постоянной скоростью деформации (рис. 3). Точки 3 и 7 располагались на центральной поперечной оси образца (рис. 2).

Рис. 3. Образец под нагрузкой в испытательной машине
Асимметрия условий задачи учитывалась при численном моделировании методом конечных элементов. Использовались реальные размеры образца, его упругие и механические свойства, полученные в ходе испытаний образцов из той же партии (модуль Юнга E, предел текучести σy, модуль упругости H), а также известные данные для технически чистого алюминия (плотность ρ, коэффициент Пуассона ν). Учитывалось, что образец закрепляется в испытательной машине по широкой поверхности и касательная растягивающая нагрузка прикладывается к ней, а не к торцу образца, как в случае двумерных моделей.
Напряженно-деформированное состояние рассчитывали в пакете конечно-элементного моделирования Ansys. С учетом площади приложения нагрузок F1, F2, F3 определены значения растягивающих напряжений: σ1 = 16,67 МПа, σ2 = 27,78 МПа и σ3 = 38,89 МПа. Их использовали при численном решении. На рис. 4 представлена модель образца с отображением конечно-элементной сетки и граничных условий. Она состоит из 936 152 элементов и 3 981 073 узлов.
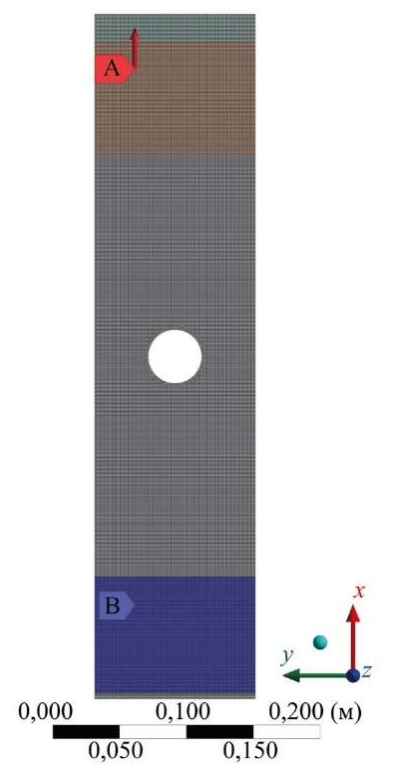
Рис. 4. Конечно-элементная модель образца с учетом граничных условий
Аналитическое решение основывалось на использовании формул (4) и (5), являющихся решением задачи Кирша в полярных координатах [18]:
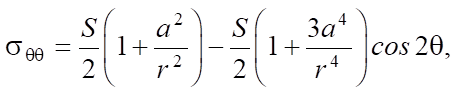 (4)
(4)
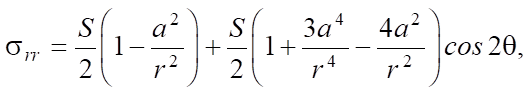 (5)
(5)
где S — нагрузка, прикладываемая к пластине; a — радиус отверстия пластины; r — расстояние от центра отверстия до точки расчета напряжений; θ — угол, соответствующий рассчитываемой точке.
Постановка задачи в данной работе предполагает наличие только упругих деформаций образца. Ее дальнейшее развитие, учитывающее влияние неупругих деформаций, связано с рассмотрением решения плоской упругопластической задачи о растяжении пластинки с круговым отверстием (идеального пластического тела), полученного Л.А. Галиным в 1946 году [19].
Рассчитаны главные напряжения, сонаправленные с продольной осью x (σθθ) и поперечной осью y образца (σrr) для всех n = 8 исследуемых точек. Компоненты σθθ, σrr — функции от радиального расстояния до центра отверстия r и от угла θ, измеренного относительно исходной оси. Соотношения (4) и (5) получены в предположении, что круглое отверстие находится в центре бесконечной изотропной линейно-упругой пластины, подверженной равномерному плоскому нагружению. Ранее они использовались в работе [20] для определения напряжений в двух областях на границе отверстия, расположенных вдоль (θ = 0°) и поперек (θ = 90°) линии действия нагрузки.
Ультразвуковые измерения проводились в точках 1, 2 и 3 (рис. 2) в образце до нагружения (F0 = 0 кН), а также при достижении уровней упругой деформации, соответствующих нагрузкам F1, F2, F3. Исследовалось влияние конечных размеров пластины (в основном, в ее поперечном сечении) на расхождение между значениями напряжений, полученных экспериментально, численно и аналитически. Значения акустической анизотропии a0, % и aσ, % рассчитали по формулам (2) и (3). Для учета эффектов, связанных с релаксацией напряжений, проводили контрольные измерения в начале и конце каждого этапа. Всего измерили 198 временных задержек (t01, t02) и (t1, t2) при распространении поперечных волн вдоль и поперек образца.
Результаты исследования. В таблице 1 приводятся значения внутренних напряжений σxx (аналог σθθ в полярной системе координат) и σyy (аналог σrr) для n = 8 точек вокруг отверстия пластины (рис. 2). Их получили в результате конечно-элементного моделирования и расчетов по формулам (4) и (5) при внешних растягивающих напряжениях σ1, σ2, σ3 (соответствуют нагрузкам F1, F2, F3).
Таблица 1
Расчетные значения напряжений вокруг отверстия пластины, МПа
|
Нагрузка |
F1 = 30 кН (σ1 = 16,67 МПа) |
F2 = 50 кН (σ2 = 27,78 МПа) |
F3 = 70 кН (σ3 = 38,89 МПа) |
|||
|
N |
σxx, σyy, |
σθθ, σrr, |
σxx, σyy, |
σθθ, σrr, |
σxx, σyy, |
σθθ, σrr, |
|
1,0 |
12,120 1,270 |
0,647 11,920 |
20,210 2,110 |
1,078 19,860 |
28,280 2,960 |
1,510 27,800 |
|
2,8 |
22,090 –3,380 |
13,060 5,800 |
38,160 –5,640 |
21,760 9,666 |
53,420 –7,890 |
30,460 13,530 |
|
3,7 |
27,690 6,390 |
25,310 6,174 |
46,157 10,650 |
42,180 10,290 |
64,610 14,910 |
59,060 14,400 |
|
4,6 |
22,890 –3,390 |
13,060 5,800 |
38,170 –5,650 |
21,760 9,666 |
53,430 –7,920 |
30,460 13,530 |
|
5,0 |
12,180 1,230 |
0,647 11,920 |
20,310 2,500 |
1,078 19,860 |
28,430 2,870 |
1,510 27,800 |
Условия закрепления образца различны: левая часть зафиксирована, правая подвижна. Отсюда асимметрия в паттерне поля деформаций образца, которая сохраняется при всех значениях нагрузок в упругой области (пример для F1 = 30 кН представлен на рис. 5).
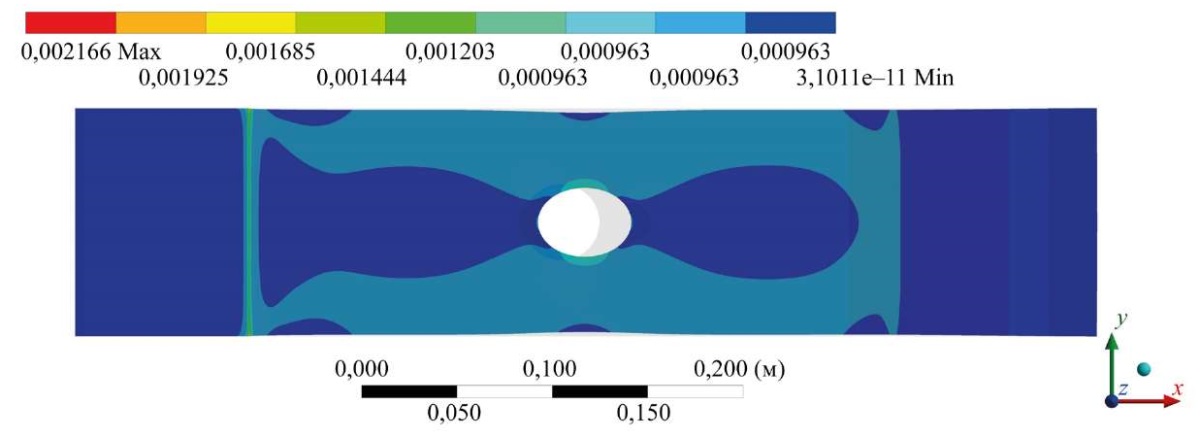
Рис. 5. Расчетное поле деформаций при растягивающей нагрузке F = 30 кН
Из-за отмеченной выше асимметрии при решении задачи методом конечных элементов значения напряжений в парах точек:
- совпадают, если они получены зеркальным отражением относительно центральной продольной оси образца;
- отличаются, если они получены отражением относительно поперечной оси образца.
В первом случае примером могут служить пары 2 и 8; 3 и 7; 4 и 6, во втором — 1 и 5; 2 и 4; другие. Отметим, что даже если разница напряжений есть, она не превышает 1 МПа. Это соответствует уровню инженерной погрешности ±5 % (таблица 1). Совпадают значения напряжений, рассчитанные для указанных пар точек по формулам (4) и (5).
В итоге близкие значения между результатами аналитических и численных расчетов наблюдаются только для точек 3 и 7, расположенных вблизи области с наибольшей концентрацией напряжений (таблица 1). В остальных точках имеет место их кратное отличие не только по модулю (2 и 8; 4 и 6), но и по знаку (1 и 5). Это связано с тем, что вычисления по формулам (4) и (5) для пластины равных (бесконечных) размеров предполагают наличие зоны сжимающих напряжений в области расположения точек 1 и 5. Иная ситуация — с реальной пластиной (рис. 1 и 2), размеры которой ограничены и отличаются между собой по соотношению длины и ширины в 4,25 раза. В этом случае нет зоны сжимающих напряжений (таблица 1 и рис. 5).
Сравнение результатов говорит в пользу того, что влияние конечных размеров пластины не позволяет использовать соотношения (4) и (5) для оценки напряжений в данной задаче. Это противоречит выводам работы [20]. Отметим, что наличие корреляции для точек с максимальным значением коэффициента концентрации напряжений подтверждается результатами для пары точек 3 и 7.
В таблице 2 представлены начальные a0 и текущие aσ значения акустической анизотропии в области расположения точек 1, 2 и 3, вычисленные по формулам (2) и (3) в ненагруженном состоянии (F0) и при трех значениях нагрузок F1, F2, F3.
Таблица 2
Акустическая анизотропия и средние значения временных задержек на разных этапах нагружения
|
Нагрузка |
F0 = 0 кН σ0 = 0 МПа |
F1 = 30 кН σ1 = 16,67 МПа |
F2 = 50 кН σ2 = 27,78 МПа |
F3 = 70 кН σ3 = 38,89 МПа |
||||
|
N |
a0 |
<t01>, <t02>, мкс |
aσ1 |
<t1>, <t2>, мкс |
aσ2 |
<t1>, <t2>, мкс |
aσ3 |
<t1>, <t2>, мкс |
|
1 |
–0,005886 |
9,4805 9,4248 |
–0,006198 |
9,4765 9,4180 |
–0,006379 |
9,4802 9,4200 |
–0,006445 |
9,4783 9,4174 |
|
2 |
–0,004508 |
9,4602 9,4177 |
–0,005947 |
9,5057 9,4494 |
–0,006650 |
9,5107 9,4476 |
–0,007636 |
9,5147 9,4423 |
|
3 |
–0,005433 |
9,4730 9,4217 |
–0,006461 |
9,5113 9,4500 |
–0,007142 |
9,5161 9,4484 |
–0,007055 |
9,5158 9,4489 |
Из таблицы 2 следует, что различие значений параметра начальной акустической анизотропии a0 в точках 1, 2 и 3 во многом определяется начальной неоднородностью материала. Это видно по вариации параметра до нагружения. К тому же с приложением внешней нагрузки растет расхождение между значениями параметра акустической анизотропии aσ в исследуемых точках.
На основании данных ультразвуковых измерений (таблица 3) рассчитаны значения (σθθ – σrr) разности главных напряжений в полярных координатах по соотношениям акустоупругости (1) [21]. Они приведены в таблице 3 в сравнении с результатами конечно-элементного моделирования и расчетов по формулам (4) и (5). В круглых скобках указаны значения напряжений, отличающиеся для пар симметрично расположенных точек, полученных отражением относительно поперечной оси образца.
Таблица 3
Сравнение результатов ультразвуковых измерений, аналитических и численных конечно-элементных расчетов, МПа
|
Нагрузка |
F1 = 30 кН (σ1 = 16,67 МПа) |
F2 = 50 кН (σ2 = 27,78 МПа) |
F3 = 70 кН (σ3 = 38,89 МПа) |
|
N |
(σxx – σyy), Ansys (σθθ – σrr), Кирш D(aσ1 – a0) |
(σxx – σyy), Ansys (σθθ – σrr), Кирш D(aσ2 – a0) |
(σxx – σyy), Ansys (σθθ – σrr), Кирш D(aσ3 – a0) |
|
1 (5) |
10,85 (10,95) –11,273 6,24 |
18,1 (17,81) –18,782 9,85 |
25,32 (25,56) –26,29 11,18 |
|
2,8 (4,6) |
25,47 (26,28) 7,26 28,78 |
43,8 (43,82) 12,094 42,84 |
61,31 (61,35) 16,93 62,56 |
|
3, 7 |
21,3 19,136 20,55 |
35,507 31,89 34,17 |
49,7 44,66 44,80 |
Из таблицы 3 видно, что данные измерений методом акустоупругости и решения методом конечных элементов качественно и количественно коррелируют друг с другом. Следовательно, можно говорить о взаимной верификации результатов натурных и численных экспериментов. Наибольшая корреляция наблюдается для точек 2, 8; 4, 6; 3, 7, находящихся вблизи области максимальных растягивающих напряжений.
Иные результаты получены для точек 1 и 5, где по формулам (4) и (5) предполагалось наличие сжимающих напряжений. Здесь разности главных значений (σθθ – σrr), полученные по данным ультразвуковых измерений, оказываются в среднем в два раза меньше прогнозируемых численных значений. Таким образом, расчеты по значениям акустической анизотропии дают нижнюю оценку напряжений для исследуемых участков образца.
Обсуждение и заключение. Исследованы главные двухосные напряжения в алюминиевой пластине вокруг концентратора — центрального кругового отверстия. Сопоставляются значения, полученные в результате натурных ультразвуковых измерений, численных экспериментов методом конечных элементов и аналитических расчетов по соотношениям Кирша. Учтено влияние асимметрии полей напряжений и деформаций, возникающей из-за различных условий закрепления образца и отражающей процесс одноосной упругой деформации при растяжении в испытательной машине.
Отмечено, что схожие результаты аналитических и численных расчетов наблюдаются только для точек, расположенных рядом с областью наибольшей концентрации напряжений. Во всех других случаях значения различаются в несколько раз и по модулю, и по знаку. Это объясняется наличием или отсутствием сжимающих напряжений. Аналитический подход предполагает, что они есть. В реальной пластине их нет. Таким образом, соотношения Кирша для напряжений одноосно растягиваемой бесконечной изотропной линейно-упругой пластины невозможно корректно применить в рассматриваемом случае.
Методом акустоупругости установлена корреляция между результатами численного моделирования и ультразвуковых измерений двухосных напряжений. Это особенно заметно в отношении точек, расположенных рядом с зоной максимальных растягивающих напряжений.
Результаты исследования могут быть использованы в промышленном неразрушающем контроле при диагностике напряжений в объектах из металлического проката.
1. ГОСТ Р 52731–2007. Контроль неразрушающий. Акустический метод контроля механических напряжений. Общие требования. Электронный фонд правовых и нормативно-технических документов. URL: https://docs.cntd.ru/document/1200051032 (дата обращения: 25.05.2024).
2. Приборы для измерения механических напряжений ИН-5101А. Руководство по эксплуатации. ИНКО.468160.008 РЭ. URL: https://encotes.ru/system/files/RE-IN-5101A_0.pdf?ysclid=m00rujbqr0495004447 (дата обращения: 25.05.2024).
Список литературы
1. Беляев А.К., Полянский В.А., Третьяков Д.А. Оценка механических напряжений, пластических деформаций и поврежденности посредством акустической анизотропии. Вестник Пермского национального исследовательского политехнического университета. Механика. 2020;(4):130–151. https://doi.org/10.15593/perm.mech/2020.4.12
2. Vatul’yan AO. The Theory of Inverse Problems in the Linear Mechanics of a Deformable Solid. Journal of Applied Mathematics and Mechanics. 2010;74(6):648–653. https://doi.org/10.1016/j.jappmathmech.2011.01.004
3. Муравьев В.В., Стрижак В.А., Пряхин А.В. Исследование внутренних напряжений в металлоконструкциях методом акустоупругости. Заводская лаборатория. Диагностика материалов. 2016;82(12):52–57. URL: https://www.zldm.ru/jour/article/view/349/350 (дата обращения: 25.05.2024).
4. Kurashkin KV, Gonchar AV, Klyushnikov VA, Mishakin VV. Use of Texture-Dependent Ultrasonic Parameter as Indicator of Degradation of Hot-Rolled Thin-Sheet Steel Under Uniaxial Tension. Journal of Nondestructive Evaluation. 2022;41(2):46. https://doi.org/10.1007/s10921-022-00879-w
5. Uglov AL, Khlybov AA. On the Inspection of the Stressed State of Anisotropic Steel Pipelines Using the Acoustoelasticity Method. Russian Journal of Nondestructive Testing. 2015;51:210–216. https://doi.org/10.1134/S1061830915040087
6. Степанова Л.Н., Бехер С.А., Курбатов А.Н., Тенитилов Е.С. Исследование напряженного состояния рельса с использованием акустоупругости и тензометрии. Известия высших учебных заведений. Строительство. 2013;65(7):103–109.
7. Ivanova Y, Partalin T, Pashkuleva D. Acoustic Investigations of the Steel Samples Deformation during the Tensile. Russian Journal of Nondestructive Testing. 2017;53(1):39–50. https://doi.org/10.1134/S1061830917010077
8. Volkova LV, Murav’eva OV, Murav’ev VV. Nonuniformity of Acoustic Anisotropy of Thick-Sheet Steel. Steel in Translation. 2021;51:335–341. https://doi.org/10.3103/S0967091221050120
9. Belyaev AK, Lobachev AM, Modestov VS, Pivkov AV, Polyanskii VA, Semenov AS, et al. Estimating the Plastic Strain with the Use of Acoustic Anisotropy. Mechanics of Solids. 2016;51:606–611. https://doi.org/10.3103/S0025654416050149
10. Murav’ev VV, Murav’eva OV, Volkova LV. Influence of the Mechanical Anisotropy of Thin Steel Sheets on the Parameters of Lamb Waves. Steel in Translation. 2016;46:752–756. https://doi.org/10.3103/S0967091216100077
11. Khlybov AA, Uglov AL. On an Acoustic Testing Method for Monitoring the Spatial Inhomogeneity of Plastic Deformation in Weakly Anisotropic Orthotropic Materials. Russian Journal of Nondestructive Testing. 2023;59(1):22–32. https://doi.org/10.1134/S1061830923700183
12. Nikitina NYe, Kamyshev AV, Kazachek SV. Application of the Acoustoelasticity Phenomenon in Studying Stress States in Technological Pipelines. Russian Journal of Nondestructive Testing. 2009;45:861–866. https://doi.org/10.1134/S1061830909120043
13. Никитина Н.Е. Акустоупругость. Опыт практического применения. Нижний Новгород: ТАЛАМ; 2005. 208 с. Nikitina NYe. Acoustoelasticity. Application Experience. Nizhny Novgorod: TALAM; 2005. 208 p. (In Russ.)
14. Erofeev VI, Ilyakhinsky AV, Nikitina EA, Pakhomov PA, Rodyushkin VM. Ultrasonic Sensing Method for Evaluating the Limit State of Metal Structures Associated with the Onset of Plastic Deformation. Physical Mesomechanics. 2020;23:241–245. https://doi.org/10.1134/S102995992003008X
15. Murav’eva O, Murav’ev V, Volkova L, Kazantseva N, Nichipuruk A, Stashkov A. Acoustic Properties of Low-Carbon 2% Mn-Doped Steel Manufactured by Laser Powder Bed Fusion Technology. Additive Manufacturing. 2022;51:102635. https://doi.org/10.1016/j.addma.2022.102635
16. Kurashkin KV. Study of the Acoustoelastic Effect in an Anisotropic Plastically Deformed Material. Acoustical Physics. 2019;65(3):316–321. https://doi.org/10.1134/S1063771019030047
17. Grishchenko AI, Modestov VS, Polyanskiy VA, Tretyakov DA, Shtukin LV. Experimental Investigation of the Acoustic Anisotropy Field in the Sample with a Stress Concentrator. St. Petersburg Polytechnical University Journal: Physics and Mathematics. 2017;3(1):77–82. https://doi.org/10.1016/j.spjpm.2017.02.005
18. Kirsch G. Die Theorie der Elastizitat und die Bedurfnisse der Festigkeitslehre. Zeitshrift des Vereines deutscher Ingenieure. 1898;42:797–807.
19. Галин Л.А. Плоская упругопластическая задача. Прикладная математика и механика. 1946;10(3):367–386. URL: https://pmm.ipmnet.ru/ru/get/1946/10-3/367-386 (дата обращения: 25.05.2024).
20. Nikitina NE, Kazachek SV. Theoretical and Experimental Study of Stress Concentration during Stretching of a Plate with a Cut. Journal of Machinery Manufacture and Reliability. 2008;37(1):38–41. URL: https://link.springer.com/article/10.1007/s12001-008-1009-9 (accessed: 25.05.2024).
21. Nikitina NYe, Kamyshev AV, Kazachek SV. The Application of the Acoustoelasticity Method for the Determination of Stresses in Anisotropic Pipe Steels. Russian Journal of Nondestructive Testing. 2015;51:171–178. https://doi.org/10.1134/S1061830915030079
Об авторах
Д. А. ТретьяковРоссия
Дмитрий Алексеевич Третьяков, кандидат технических наук, доцент Высшей школы автоматизации и робототехники института машиностроения, материалов и транспорта
195251, г. Санкт-Петербург, ул. Политехническая, 29 б
Д. С. Осовик
Россия
Дмитрий Сергеевич Осовик, студент Высшей школы автоматизации и робототехники института машиностроения, материалов и транспорта
195251, г. Санкт-Петербург, ул. Политехническая, 29 б
Рецензия
Для цитирования:
Третьяков Д.А., Осовик Д.С. Оценка напряжений в пластине с концентратором посредством ультразвуковых измерений акустической анизотропии. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):307-315. https://doi.org/10.23947/2687-1653-2024-24-4-307-315. EDN: RMBTZU
For citation:
Tretyakov D.A., Osovik D.S. Estimation of Stresses in a Plate with a Concentrator through Ultrasonic Measurements of Acoustic Anisotropy. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):307-315. https://doi.org/10.23947/2687-1653-2024-24-4-307-315. EDN: RMBTZU






































