Scroll to:
Finite Element Modeling of a Flat Cell of Highly Porous Piezocomposite with Inclined Edges Taking into Account Nonuniform Polarization
https://doi.org/10.23947/2687-1653-2024-24-4-339-346
EDN: BNDEOI
Abstract
Introduction. Highly porous composites — metal foams — are widely used due to their mechanical properties. The literature presents various methods for their mathematical modeling, including those based on periodic Gibson-Ashby cells. Piezoactive composites have a number of properties, such as high sensor sensitivity and a large bandwidth. This is the reason for the interest in their modeling. However, when constructing such models from piezoceramic materials, a certain difficulty, associated with the selection of the distribution of preliminary polarization, arises. It should be noted that this issue, specifically for highly porous piezoceramics, has not been sufficiently studied in the literature. Therefore, the objective of this work was to establish the effect of the polarization model on the characteristics of the piezoactive composite.
Materials and Methods. The design material is PZT-4 piezoceramics, whose polarization depends significantly on the conditions of its guidance (model geometry, electrode arrangement). The study was divided into two steps: in the first, the residual polarization was calculated based on the theory known in the literature, the implementation of which was performed in the ACELAN package; in the second, a number of problems for a composite cell were solved, and the dependence of its properties on the polarization model was found. The finite element method implemented in the ACELAN package was used as a method for solving the corresponding boundary value problems of electroelasticity for piecewise inhomogeneous bodies.
Results. The problem of determining nonuniform polarization for two types of flat cell designs of highly porous piezoceramics was solved. Some features of the obtained polarization distribution were noted, in particular, its nonuniformity and the presence of counter polarization in some edges. The problems of determining natural frequencies and vibration modes “intra cell” and their dependence on the polarization model (homogeneous and nonhomogeneous) were solved. It was noted that some frequencies differed by 10%, while the vibration modes qualitatively coincided. The dependence of the stress-strain state and output characteristics on polarization, whose difference in some values reached 15%, was analyzed.
Discussion and Conclusion. The process of polarization of highly porous piezoceramics has a number of features that must be taken into account to obtain reliable information about its mechanical and electrical behavior. Auxetic properties, the difference in the mechanical and electrical response of the cell in question are directly related to these features. Thus, the polarization model has a significant impact on the characteristics of the piezoactive composite, which determines the importance of its correct selection. The results obtained should be taken into account when modeling representative volumes of highly porous piezoelectric composites to determine their effective properties, on the basis of which models of piezoelectric devices are constructed, and their output characteristics are calculated.
For citations:
Soloviev A.N., Germanchuk M.S. Finite Element Modeling of a Flat Cell of Highly Porous Piezocomposite with Inclined Edges Taking into Account Nonuniform Polarization. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):339-346. https://doi.org/10.23947/2687-1653-2024-24-4-339-346. EDN: BNDEOI
Introduction. One type of highly porous composite is a material constructed on the basis of Gibson-Ashby cells [1]. In [2], an assessment of the effective Young's modulus of porous titanium with open pores was performed on the basis of a three-dimensional array of such cells. A comparison of the mechanical behavior of foam models composed of regular and irregular arrays of open Gibson-Ashby cells is carried out in [3]. Figure 1 a shows an open cell, Figures 1 b and 1 c show modified Gibson-Ashby models with inclined edges for functionally graded lattice structures [4].
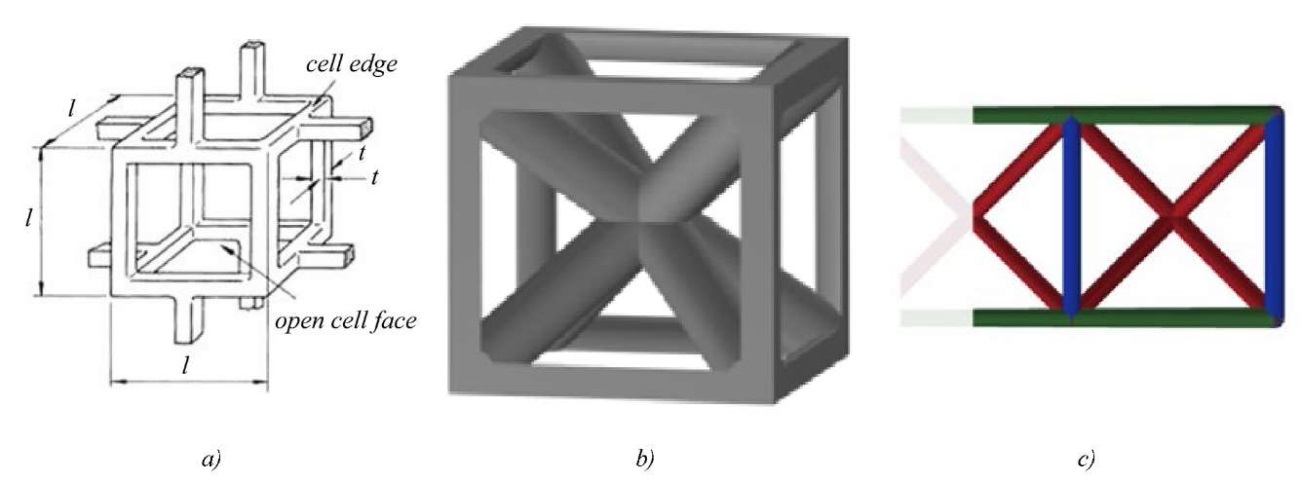
Fig. 1. Schemes of cells of highly porous composite: a — Gibson-Ashby cell; b — cell with inclined edges; c — flat cell with inclined edges [4]
Homogenization methods used in modeling the effective properties of composites are considered in monographs [5][6]. Studies on highly porous structures, such as foamy, cellular, honeycomb and cell structures are presented in monographs [7][8], in reviews [9–12], etc. In [13], the polarization of porous piezoceramics is considered experimentally and theoretically and, based on a model example, features of some of its effective properties are theoretically explained, as mentioned above. The issue of the effective properties of highly porous piezoelectric composites has not been sufficiently studied in the scientific literature. This is primarily due to the fact that the process of describing the polarization of such structures is a certain difficulty. This research is aimed at studying the influence of the polarization model on the stress-strain state of the cell and on the effective properties of such composites. Two models are considered: the first model assumes uniform polarization; in the second, the polarization distribution is calculated using methods and software known from the literature, among the developers of which is one of the authors of this work. The work shows that the selection of the polarization model affects significantly the mechanical properties of highly porous piezoelectric composites.
Materials and Methods
Mathematical Formulation of the Problem. We consider flat cells, which are elements of the structures shown in Figure 1. The cell material is PZT-4 piezoelectric ceramics, described within the framework of the linear theory of electroelasticity [14]. In the homogeneous case, it is polarized along the vertical axis, in the inhomogeneous case — the polarization distribution is found according to the theory proposed in [15] and implemented in the finite element package ACELAN [16].
Materials. Figure 2 a shows the geometry of a flat cell corresponding to the diagram in Figure 1 a with inclined edges, the edge thickness is 1 mm, the external size is 10×10 mm. Figure 2 b shows a diagram of nonuniform polarization for such a design, when the electrodes are located on the outer ends of the upper and lower vertical edges. The characteristic feature of this polarization is its nonuniformity on inclined edges and the presence of its opposite directions on the upper and lower horizontal edges. Figure 2 c shows the polarization scheme for a composite element, whose periodicity is realized through vertical and horizontal edges. The characteristic feature of the polarization of this element is the practically unpolarized horizontal edges.
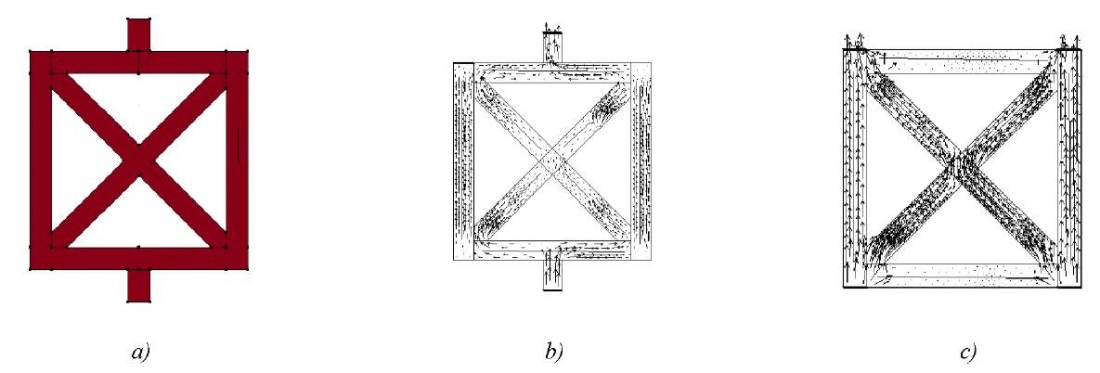
Fig. 2. Schemes of cells and polarization of highly porous composite: a — uniform polarization; b — nonuniform with electrodes on the lower and upper edges; c — nonuniform with electrodes at the bottom and top on vertical edges
Methods. The finite element method (FEM) implemented in the ACELAN package is used as a method for calculating the stress-strain state of cells [16].
Research Results. First, the natural frequencies and modes of vibrations “inside” the cell shown in Figures 1 c and 2 c are investigated. In this case, the cell is fixed in the corners along the normal to the thickness of the horizontal and vertical edges, which corresponds to the periodicity of the composite structure. Table 1 shows the natural resonance frequencies for uniform and nonuniform polarization (Fig. 2 c), and Figures 3–5 show eigenvibrations at these frequencies.
Table 1
Eigenvibrations for Uniform and Nonuniform Polarization
|
Frequency number \ Polarization |
Eigenvibrations in Hz |
|
|
Uniform |
Nonuniform |
|
|
1 |
0.43455 × 10⁵ |
0.41271 × 10⁵ |
|
2 |
0.47277 × 10⁵ |
0.47249 × 10⁵ |
|
3 |
0.54538 × 10⁵ |
0.49562 × 10⁵ |
|
4 |
0.61497 × 10⁵ |
0.58611 × 10⁵ |
|
5 |
0.67255 × 10⁵ |
0.67607 × 10⁵ |
For nonuniform polarization 1, 3 and 4, the natural frequencies are lower than for uniform polarization, but the vibration modes 1–5 are qualitatively the same. Therefore, Figures 3–5 show the natural modes for a cell with uniform polarization. Figures 3 a, b show the distribution of horizontal displacements and vertical displacements for the first vibration mode. In Figures 4 a, b the distributions for the second mode of vibrations of horizontal displacements and for the third mode of vibrations of vertical displacements are presented, respectively. In Figures 5 a, b the distribution of the displacement modulus is presented for the fourth and fifth modes, respectively.
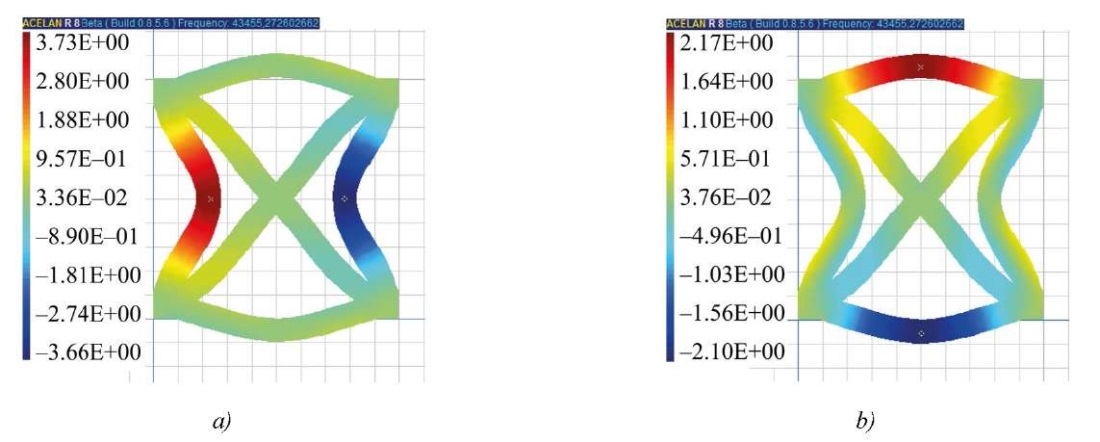
Fig. 3. The first form of vibrations is uniform polarization: a — distribution of horizontal displacements; b — distribution of vertical displacements
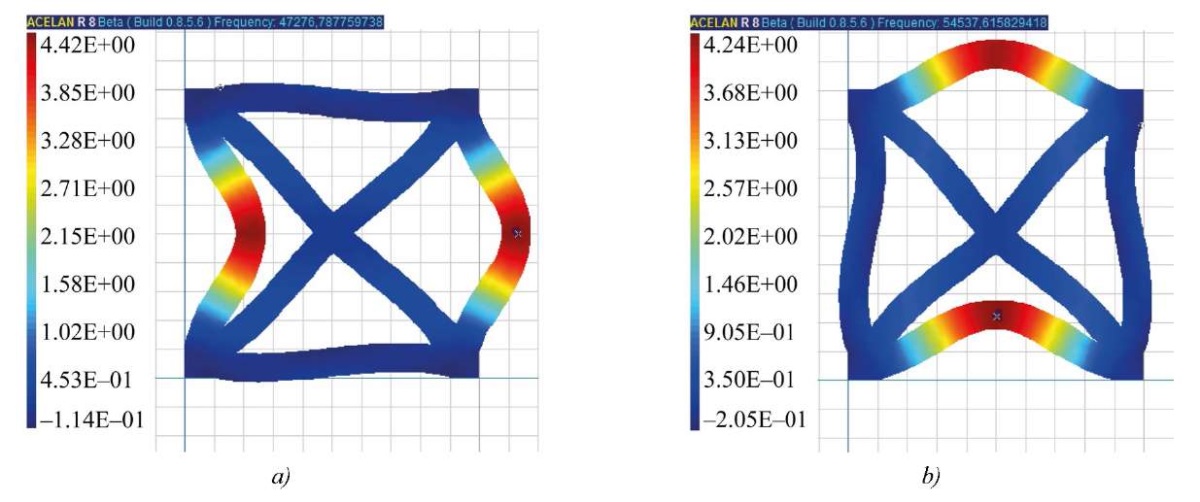
Fig. 4. Forms of vibrations of uniform polarization: a — the second, distribution of horizontal displacements; b — the third, distribution of vertical displacements
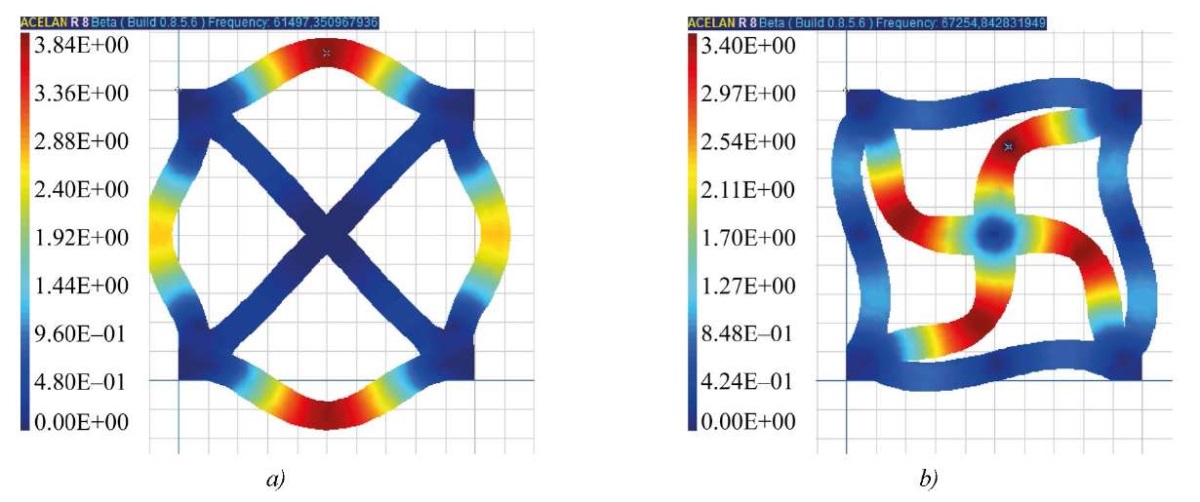
Fig. 5. Forms of vibrations with the distribution of the displacement modulus for uniform polarization: a — the fourth mode; b — the fifth mode
With longitudinal tension-compression of this cell in the vertical direction in the composite structure (modeled by the free entire upper surface and the application of uniform pressure to the upper end of the vertical edges), the displacement in the case of uniform polarization is 15% greater (Fig. 6 a). The potential on free electrodes is 3% higher in the case of nonuniform polarization. It should be noted that the shear stresses (Fig. 6 b) are 10% higher in the case of nonuniform polarization. The electromechanical coupling coefficient for the 7th oscillation mode (Fig. 6 c) is 14% higher for uniform polarization of the cell.
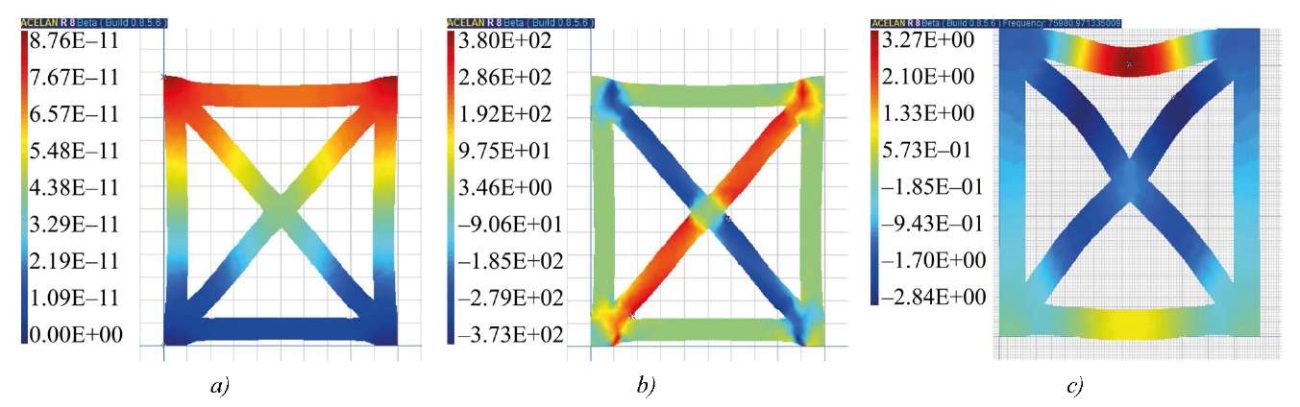
Fig. 6. Under the action of vertical pressure, the distribution of: a — vertical displacement; b — shear stresses; c — distribution of vertical displacement on the 7th oscillation mode
Calculations for the cell presented in Figures 2 a and b show that the vertical displacement (Fig. 7 a) under the action of pressure on the end of the upper rod in the case of nonuniform polarization is 11% greater. In statics, under the action of the potential difference at the lower and upper ends, the cell exhibits auxetic properties, which is associated with the opposite polarization (Fig. 2 b) of the horizontal edges. Figures 7 b and c show the distributions of vertical and horizontal displacements. It is evident that when stretched vertically, the cell also expands horizontally.
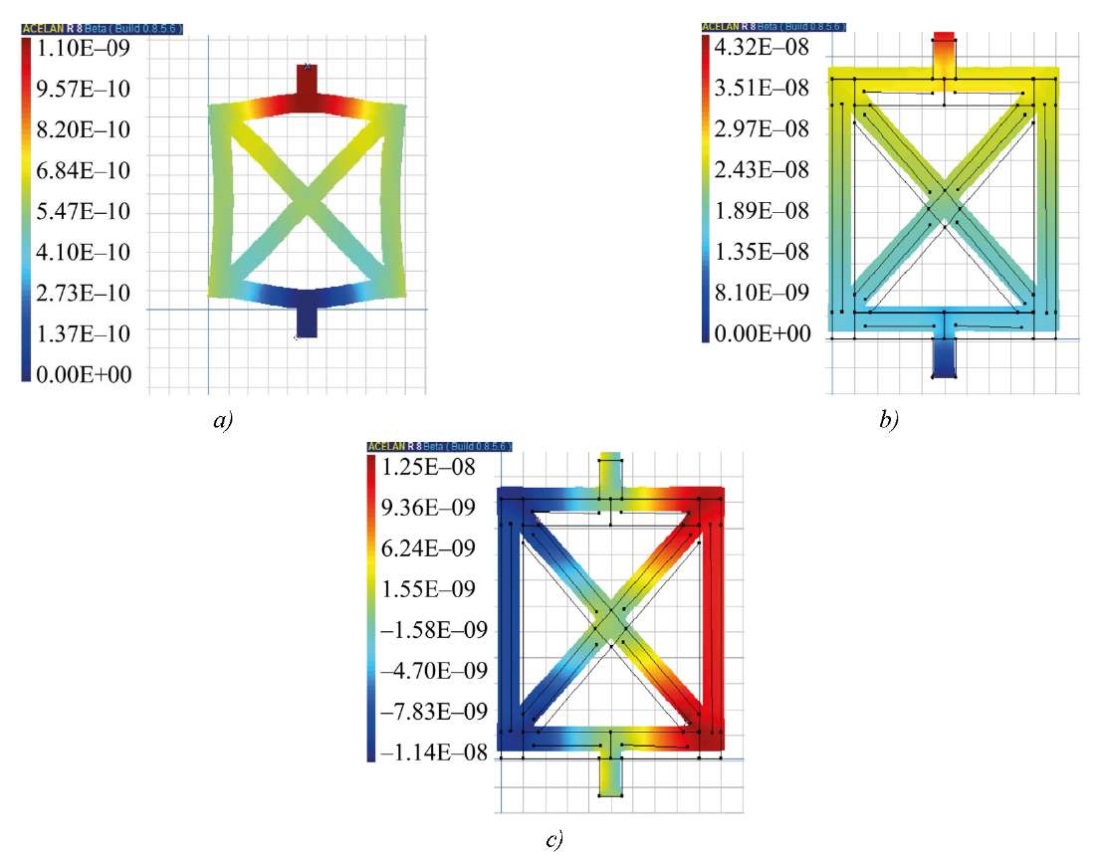
Fig. 7. Distribution: a — vertical displacement under the action of vertical pressure; b — vertical displacement under the action of potential difference; c — horizontal displacement under the action of potential difference
Discussion and Conclusion. Thus, on the basis of this stress-strain state (SSS), the effective properties of composites, which are used in modeling piezoelectric devices, are found. Therefore, the study of the influence of the type of polarization on the SSS of a highly porous piezoactive material is urgent.
The calculation of the preliminary polarization field in a cell of a highly porous material has shown that it depends significantly on its geometry and the arrangement of the electrodes. These features include the fact that some edges are practically not polarized, others are polarized in one direction, but nonuniformly, and, finally, edges with opposite polarization may appear. The calculation of the mechanical and electrical response of the cell and its natural resonance frequencies have proven that taking into account the nonuniformity of polarization leads to the fact that the magnitude of the discrepancy between these results and the results for the model with uniform polarization reaches 15% and 10%, respectively. And the cell with edges on which there is counter polarization exhibits auxetic properties. The paper shows that in problems of determining the effective properties of highly porous piezoelectric composites based on the construction of representative volumes from its cells, it is essential to take into account the inhomogeneous polarization corresponding to their structure.
The practical relevance of the results obtained is due to the fact that the effective properties of composites allow for modeling, calculation and optimization of various piezoelectric devices (sensors, emitters and receivers of acoustic waves, piezoelectric generators, etc.) at the design stage.
References
1. Gibson LJ, Ashby MF. The Mechanics of Three-Dimensional Cellular Materials. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 1982;382:43–59. https://doi.org/10.1098/rspa.1982.0088
2. Nikitin AV, Mikhasev FI. Estimation of the Effective Young’s Modulus for Open Cell Porous Titanium Based on 3D Gibson-Ashby Cell Array. Journal of the Belarusian State University. Mathematics and Informatics. 2022;(1):75–82. https://doi.org/10.33581/2520-6508-2022-1-75-82
3. Kornievsky AS, Nasedkin AV. Comparison of Foam Models from Regular and Irregular Arrays of Gibson-Ashby Open-Cells. PNPRU Mechanics Bulletin. 2021;(3):70–83. https://doi.org/10.15593/perm.mech/2021.3.07
4. Seyed Kamal Jalali, Mohammad Javad Beigrezaee, Diego Misseroni, Nicola Maria Pugno. A Modified GibsonAshby Model for Functionally Graded Lattice Structures. Mechanics of Materials. 2024;188:104822. https://doi.org/10.1016/j.mechmat.2023.104822
5. Kachanov M, Sevostianov I. Micromechanics of Materials, with Applications. Cham: Springer; 2018. 712 p. https://doi.org/10.1007/978-3-319-76204-3
6. Milton GW. The Theory of Composites. Cambridge: Cambridge University Press; 2002. 568 p. https://doi.org/10.1017/CBO9780511613357
7. Scheffler M, Colombo P. (eds) Cellular Ceramics: Structure, Manufacturing, Properties and Applications. Hoboken, NJ: John Wiley & Sons; 2005. 645 p. http://doi.org/10.1002/3527606696
8. Gibson LJ, Ashby MF. Cellular Solids: Structure and Properties. 2nd ed. Cambridge: Cambridge University Press; 1997. 510 p. https://doi.org/10.1017/CBO9781139878326
9. Hössinger-Kalteis A, Reiter M, Jerabek M, Major Z. Overview and Comparison of Modelling Methods for Foams. Journal of Cellular Plastics. 2021;57(6):951–1001. https://doi.org/10.1177/0021955X20966329
10. Chen Pan, Yafeng Han, Jiping Lu. Design and Optimization of Lattice Structures: A Review. Applied Sciences. 2020;10(18):6374. https://doi.org/10.3390/app10186374
11. Srivastava V, Srivastava R. On the Polymeric Foams: Modeling and Properties. Journal of Materials Science. 2014;49:2681–2692. https://doi.org/10.1007/s10853-013-7974-5
12. Firooz S, Steinmann P, Javili A. Homogenization of Composites with Extended General Interfaces: Comprehensive Review and Unified Modeling. Applied Mechanics Reviews. 2021;73(4):040802. https://doi.org/10.1115/1.4051481
13. Vernigora GD, Lupeiko TG, Skaliukh AS, Solovyev AN. On Polarization and Identification of Porous Piezoceramics Effective Characteristics. Vestnik of Don State Technical University. 2011;11(4):462–469. URL: https://www.vestnikdonstu.ru/jour/article/view/746/745 (accessed: 28.08.2024).
14. Belokon’ AV, Eremeyev VA, Nasedkin AV, Solovyev AN. Partitioned Schemes of the Finite-Element Method for the Dynamic Problems of Acoustoelectroelasticity. Journal of Applied Mathematics and Mechanics. 2000;64(3):381–393.
15. Belokon AV, Skaliukh AS. Mathematical Modeling of Irreversible Polarization Processes. Moscow: Fizmatlit; 2010. 328 p. (In Russ.)
16. Skaliukh AS, Oganesyan PA, Soloviev AN. Modeling of Piezoelectric Elements with Inhomogeneous Polarization in ACELAN. Ferroelectrics. 2015;483(1):95–101. https://doi.org/10.1080/00150193.2015.1059138
About the Authors
A. N. SolovievRussian Federation
Arkadiy N. Soloviev, Dr.Sci. (Phys.-Math.), Professor of the Mathematics and Physics Department;
Chief Researcher
8, Uchebnyi Lane, Simferopol, 295015;
105/42, Bolshaya Sadovaya Str., Rostov-on-Don, 344006
M. S. Germanchuk
Russian Federation
Maria S. Germanchuk, Cand.Sci. (Phys.-Math.), Associate Professor of the Informatics Department;
Associate Professor of the Mathematics and Physics Department
4, Prospect Vernadskogo, Simferopol, 295007;
8, Uchebnyi Lane, Simferopol, 295015
Review
For citations:
Soloviev A.N., Germanchuk M.S. Finite Element Modeling of a Flat Cell of Highly Porous Piezocomposite with Inclined Edges Taking into Account Nonuniform Polarization. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):339-346. https://doi.org/10.23947/2687-1653-2024-24-4-339-346. EDN: BNDEOI












































