Перейти к:
Алгоритм построения функции риска расширенной модели Кокса и его применение на базе данных больных раком предстательной железы
https://doi.org/10.23947/2687-1653-2024-24-4-413-423
EDN: LNZDKF
Аннотация
Введение. В медицине и связанных с нею отраслях для анализа выживаемости используются биоинспирированные подходы, среди которых особое место занимает регрессионная модель Кокса. Практика ее применения описана в теоретической и прикладной литературе. Однако требует тщательной проработки существенный недостаток данного метода. Дело в том, что признаки коррелируют с функцией риска линейно, и модель не задействует более сложные зависимости. Это создает трудности при исследовании анализа выживаемости. Представленная работа нацелена на решение данной проблемы. Объект изучения — расширенная модель Кокса, в которой функция риска включает нелинейную комбинацию признаков.
Материалы и методы. Использовалась база данных больных раком предстательной железы, так как в мировой онкологии это широко распространенный диагноз. Определен класс расширенных моделей Кокса с аддитивно-мультипликативной функцией риска. Для решения задачи методом оптимизации построена функция приспособленности, которая оценивает результаты прогнозов, количество признаков, а также степень переобучения модели — сложность и нагруженность составленной функции риска. Для оптимизации функции приспособленности разработан алгоритм муравьев-опылителей. Он имитирует размножение цветковых растений с помощью насекомых-опылителей и состоит из трех частей: муравьиный алгоритм, генетический алгоритм и алгоритм опыления. Качество обучения модели Кокса оценивали по С-индексу.
Результаты исследования. Предложен метаэвристический алгоритм оптимизации муравьев-опылителей, позволяющий строить функции риска расширенной модели Кокса. Набор параметров для обучения стандартной модели Кокса — весь используемый комплекс признаков: распространенность опухолевого процесса, время удвоения простатспецифического антигена (ПСА), сумма баллов по шкале Глисона, сывороточная концентрация ПСА на момент постановки диагноза, возраст и образование пациента, резус-фактор. Значение c-индекса обученной модели — 0,853691. Расширенная модель Кокса с найденной аддитивно-мультипликативной функцией риска имеет более высокий показатель С-индекса — 0,856241 с меньшим количеством используемых признаков (распространенность опухолевого процесса, время удвоения ПСА и сумма баллов по Глисону). По качеству этот подход не уступает классической модели Кокса или превосходит ее. Сокращение числа задействованных признаков должно повысить оперативность врачебного решения и ускорить начало лечения.
Обсуждение и заключение. Представленный алгоритм построения моделей анализа выживаемости повысил точность предсказания наступления терминального события и уменьшил количество используемых для этой цели признаков. Разница в точности для исследуемого набора данных представляется несущественной — С-индекс возрос с 0,853691 до 0,856241 (на 0,3 %). При этом количество принимаемых во внимание признаков сократилось с 7 до 3 (на 57,1 %). Следовательно, предложенный метод эффективно решает задачу выбора признаков и может быть применен для повышения качества прогнозирования.
Ключевые слова
Для цитирования:
Микулик И.И., Жаринов Г.М., Кнеев А.Ю. Алгоритм построения функции риска расширенной модели Кокса и его применение на базе данных больных раком предстательной железы. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):413-423. https://doi.org/10.23947/2687-1653-2024-24-4-413-423. EDN: LNZDKF
For citation:
Mikulik I.I., Zharinov G.M., Kneev A.Yu. Algorithm for Constructing the Hazard Function of the Extended Cox Model and its Application to the Prostate Cancer Patient Database. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):413-423. https://doi.org/10.23947/2687-1653-2024-24-4-413-423. EDN: LNZDKF
Введение. Анализ выживаемости представляет собой совокупность статистических методов, позволяющих оценить вероятность наступления терминального события, после которого объект выходит из-под наблюдения. Методы предполагают работу с данными, имеющими временную характеристику. Это время от начала наблюдения до наступления терминального события или выхода объекта из-под наблюдения. Возможность работы с объектами, вышедшими из-под наблюдения, представляет интерес для прикладных областей науки, в том числе для медицины [1].
Одна из классических моделей анализа выживаемости — регрессионная модель Кокса [2]. Ее функция риска использует линейную комбинацию признаков, что в общем случае может быть не вполне корректно, так как влияние признаков на значение функции риска может быть выражено нелинейной корреляцией. Для каждой задачи вклад признаков и функция риска могут коррелировать по-разному. Это определяется используемыми данными и требует особых подходов к поиску форм зависимостей. Разные способы определения зависимостей признаков в функции риска рассмотрены в [3]. В настоящей работе предлагается использовать расширенную модель Кокса, функция риска которой устанавливает не только аддитивную, но и мультипликативную комбинацию признаков. Кроме того, описан метод построения таких моделей в зависимости от используемых данных и набора признаков.
Построение модели предполагает решение задачи отбора признаков, одной из ключевых в анализе данных [4]. Она заключается в поиске оптимального набора признаков, достаточного для построения прогноза. Решение дает представление о том, какие признаки имеют бо́льшую прогностическую значимость. Задачу можно сформулировать в терминах оптимизации и решить методами оптимизации. Предложенный для ее решения алгоритм муравьев-опылителей относится к метаэвристическим гибридным методам оптимизации. Он задействует муравьиный и генетический алгоритмы оптимизации, а также впервые разработанную модель скрещивания цветов.
Алгоритм реализован на базе данных больных раком предстательной железы. В мировой медицинской практике это одно из наиболее распространенных злокачественных новообразований у мужчин [5]. Внедрение скрининга на основе оценки сывороточной концентрации простатспецифического антигена (ПСА) существенно изменило структуру впервые выявленных случаев рака предстательной железы. Если ранее большинство из них приходилось на местно-распространенную и метастатическую формы опухоли, то в настоящее время доминирует локализованная. Благодаря этому увеличилась частота радикальных вмешательств и приблизились к 100 % показатели десятилетней выживаемости отдельных групп пациентов, перенесших радикальную простатэктомию или комбинированную гормонолучевую терапию.
Несмотря на очевидные успехи в диагностике и лечении рака предстательной железы, остаются нерешенными несколько важных вопросов, требующих исследования.
Современные методы прогнозирования выживаемости при раке предстательной железы основаны на совокупности факторов: возраст, распространенность и гистологическая дифференцировка опухоли, сывороточная концентрация ПСА, время его удвоения [6] и плотность [7]. Модель Кокса и другие модели анализа выживаемости дают о ней общее представление, но их точность в прогнозировании исходов для отдельных пациентов может варьироваться. Более того, прогноз, составленный по совокупности признаков, не дает представления о значимости каждого из них. Данное обстоятельство ограничивает возможности клиницистов адаптировать рекомендации по лечению к потребностям конкретного пациента.
Улучшение подходов к оценке выживаемости онкологического пациента — ключевой аспект научного поиска в области онкологии. Все больше внимания уделяется точности прогнозирования, которая критически важна для выбора терапевтической стратегии. Качественная прогностическая модель более точно определяет риск для больного и позволяет адаптировать подходы к лечению в зависимости от ожидаемого исхода. Это может улучшить и результаты лечения, и качество жизни пациента.
В условиях высокой нагрузки на медицинский персонал сокращение количества признаков в модели прогноза представляет значительную практическую ценность, так как сокращает временны́е затраты на принятие врачебных решений. Упрощение модели позволяет сделать акцент на ключевых аспектах клинической картины, что снижает вероятность некорректных интерпретаций данных. Кроме того, использование ограниченного набора признаков повышает воспроизводимость и стабильность результатов прогноза, то есть его надежность.
Цель настоящего исследования — разработка алгоритма построения моделей анализа выживаемости с отбором ключевых признаков. Точность нового подхода должна быть не ниже, чем у модели Кокса. Отметим, что различные способы построения функций риска модели Кокса задают не одну расширенную модель Кокса, а целый класс алгоритмов с различными функциями риска. Этот подход к адаптации функции риска под набор имеющихся данных и признаков выбран в качестве способа достижения поставленной цели.
Ниже перечислены задачи, решенные в данной работе.
- Определен класс расширенных моделей Кокса с аддитивно-мультипликативной функцией риска.
- Построена функция приспособленности, оценивающая результаты прогнозов расширенной модели Кокса.
- Создан метод оптимизации, решающий поставленную задачу.
- Разработана программа, реализующая предложенный алгоритм.
- Получен результат работы программы на базе данных пациентов, больных раком предстательной железы, и показана эффективность разработанного алгоритма.
Материалы и методы. В анализе выживаемости для оценки риска наступления рассматриваемого события используются функции выживаемости и риска. Первая — это стохастическая характеристика, определяющая вероятность выживания (отсутствие терминального события) на протяжении заданного времени. Другими словами, функция выживаемости S(t) определяется как вероятность того, что терминальное событие не наступит до момента времени t:
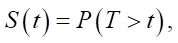
где T — время наступления терминального события.
Модели анализа выживаемости строят кривые выживаемости для каждого образца данных по его признакам. Модели часто задают с помощью функции риска, которая определяет вероятность наступления терминального события в бесконечно малый промежуток времени между t и Δt при условии, что оно не наступило до момента t:
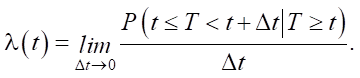
Модель пропорциональных рисков Кокса вычисляет функцию риска для одного экземпляра как линейную комбинацию его признаков, устанавливая взаимосвязь между признаками экземпляра и функцией риска.
С одной стороны, явное задание функции риска делает модель прозрачной и удобной для интерпретации прогнозов. С другой стороны, предположение о линейной взаимосвязи признаков и прогноза является ограничением и не может выполняться для всех практических задач.
Результаты исследования. Пусть S — набор данных для обучения. Функция риска в классической модели Кокса:
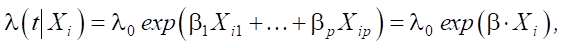
где β — вектор влияния признаков; Xi ∊ S — экземпляр данных.
В [3] функция риска модели Кокса рассматривается в обобщенном виде λ(t|Xi) = λ0exp(g(β⋅Xi)), где g(β⋅Xi) — функция, устанавливающая зависимость между признаками экземпляров. В данной работе функция g является полиномом специального вида.
Пусть F = {f1, f2, …, fn} — множество всех признаков. |F| = p. Ft — подмножество признаков: Ft ⊂ F. Pq(Ft) — полином, составленный из признаков f ∊ Ft:
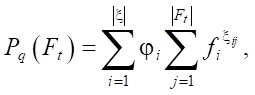
где 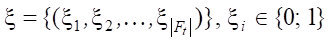 — множество индикаторов вхождения i-го признака в слагаемое полинома; φi ∊ {0, 1} — маркер, указывающий на вхождение i-го монома в Pq.
— множество индикаторов вхождения i-го признака в слагаемое полинома; φi ∊ {0, 1} — маркер, указывающий на вхождение i-го монома в Pq.
Таким образом, полином Pq(Ft) — это сумма одночленов, каждый из которых является произведением признаков. При этом степень признака в одночлене не более единицы. Функцию риска λ(t|Xi) = λ0exp(g(β⋅Xi)), где g(β⋅Xi) = Pq(Ft, β⋅Xi), назовем аддитивно-мультипликативной, так как значение каждого признака в ней может входить либо в состав суммы, либо в состав произведения.
Для получения и обработки результатов необходимо оценить качество построенной модели. В работе [8] качество модели оценивается с помощью функции потерь, и это общий подход для любой обучающейся модели. В качестве оценивающего показателя чаще других используется индекс соответствия (С-индекс). Его же выбрали для оценки расширенной модели Кокса. C-индекс учитывает как наблюдаемые события, так и цензурированные случаи [9]. При этом количественно определяется ранговая корреляция между фактическим временем выживания и прогнозами модели. С-индекс показывает соотношение правильно упорядоченных (согласованных) и сопоставимых пар [10].
В работе рассматривается гипотеза о расширенной модели Кокса с точностью предсказаний не ниже, чем у классической модели Кокса.
Пусть c(S, Pq(Ft)) — С-индекс расширенной модели Кокса, обученной на данных S, с аддитивно-мультипликативной функцией риска, построенной с помощью полинома Pq(Ft), а c(S, P∑(F)) — С-индекс классической модели Кокса, обученной на тех же данных S. Гипотезу можно сформулировать в виде:
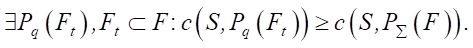 (1)
(1)
Для поиска нетривиальных примеров гипотезы поставили задачу и разработали алгоритм. Задачу можно сформулировать в терминах теории оптимизации. Необходимо построить полином Pq(Ft) на подмножестве F с наибольшим значением c(S, Pq(Ft)) при минимальном наборе признаков Ft. Таким образом, вводятся два условия оптимизации c(S, Pq(Ft)) → max и |Ft| → min. Следует учитывать еще одну проблему построения полинома. С увеличением числа возможных признаков экспоненциально растет количество возможных многочленов, в том числе сконструированных из-за переобучения. Как правило, такие многочлены состоят из суммы сравнительно большого количества мономов, а сами мономы — из большого количества множителей. Такие полиномы увеличивают точность модели лишь на обученных данных и слабо поддаются анализу.
Чтобы избавиться от проблемы переобучения, в работе предложена оптимизация по двум дополнительным критериям: количеству мономов в составе Pq(Ft) и нагруженности полинома Pq(Ft), которая отражает количество мультипликативных связей в полиноме.
Количество мономов определяется как 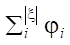 . Однако для построения корректного условия необходимо учитывать нелинейность вклада количества признаков в целевую функцию. При малом количестве входящих признаков ожидается более существенное изменение показателя, чем при большом. Поэтому в работе предложен показатель:
. Однако для построения корректного условия необходимо учитывать нелинейность вклада количества признаков в целевую функцию. При малом количестве входящих признаков ожидается более существенное изменение показателя, чем при большом. Поэтому в работе предложен показатель:
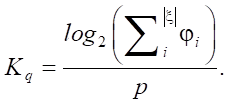
Отметим, что значение Kq не превышает 1.
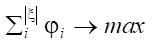 при Ɐφi = 1, следовательно:
при Ɐφi = 1, следовательно:
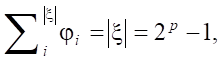
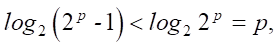
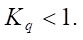
Не совсем корректно определять нагруженность полинома как количество мультипликативных связей. В этом случае не отражается реальная оценка сложности полинома при разном количестве входящих в него мономов. Показатель должен демонстрировать нагруженность каждого входящего монома, поэтому в работе введена следующая величина, не превышающая 1:
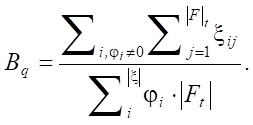
С учетом введенных характеристик задача оптимизации заключается в поиске Pq(Ft) при условиях:
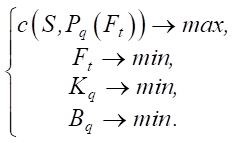 (2)
(2)
Перейдем к одномерной оптимизации с помощью введения балансировочных коэффициентов ω:
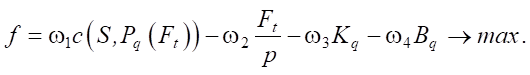
Или представим в виде суммы:
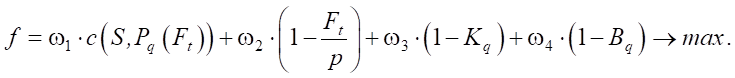 (3)
(3)
Последняя форма записи при необходимости позволяет зафиксировать значение целевой функции f, введя явную зависимость между балансировочными коэффициентами:
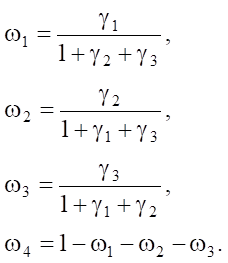
При любых γ1, γ2, γ3 ∊ (0; 1). Так, выбирая нужные γi или напрямую ωi, можно усиливать или ослаблять соответствующие условия системы (2). Задача заключается в поиске максимума целевой функции f (3) при определенных ωi.
Для решения задачи оптимизации в статье представлен разработанный алгоритм муравьев-опылителей. Он основан на модели муравьиной колонии, адаптированной под поставленную задачу. Алгоритм преобразовывает в модель набор вершин графа, представляющих признаки или их произведение. Имитируется процесс опыления и размножения цветковых растений с помощью насекомых-опылителей. Решение включает три алгоритма:
- муравьиный используется для построения модели;
- генетический улучшает работу муравьиного алгоритма;
- алгоритм опыления позволяет выбрать признаки или их произведения.
Результат работы алгоритма — полином Pq(Ft), максимизирующий функцию f (3). Каждый моном, входящий в сумму полинома, представлен цветком. Множество цветков образует граф. По нему строят путь муравьи-опылители. Каждый муравей определяет множество цветов, и сумма соответствующих им мономов образует полином Pq(Ft). Оценка построенного муравьем пути — это значение функции f (3) для расширенной модели Кокса с g = Pq(Ft).
Муравьиный этап алгоритма представляет собой адаптированный к задаче простой муравьиный алгоритм [11]. Каждый муравей k имеет разный набор параметров αk, βk, Qk. Чувствительность муравьев к феромонам αk определяет степень эксплуатации муравьями найденных решений. Эвристическая чувствительность βk устанавливает уровень эксплуатации эвристической информации. Интенсивность феромона Qk определяет количество феромона, которое отложит муравей на цветок в процессе поиска решения. Статические параметры алгоритма: количество муравьев n, скорость испарения ρ, первоначальный уровень феромонов τ0.
Каждый муравей выбирает вершину стохастически по правилу:
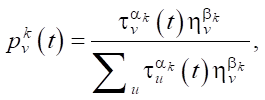 (4)
(4)
где 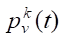 — вероятность выбора цветка v муравьем k на итерации t; τv(t) — количество отложенного феромона на цветке v на итерации t; ηv — эвристическая информация, которая вычисляется как ηv = c(S, Pi ≡ v). Во второй части этого равенства — c-индекс расширенной модели Кокса, обученной на одном мономе цветка v.
— вероятность выбора цветка v муравьем k на итерации t; τv(t) — количество отложенного феромона на цветке v на итерации t; ηv — эвристическая информация, которая вычисляется как ηv = c(S, Pi ≡ v). Во второй части этого равенства — c-индекс расширенной модели Кокса, обученной на одном мономе цветка v.
Каждый муравей откладывает феромон в соответствии с правилом:
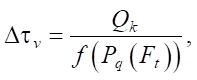 (5)
(5)
где Pq(Ft) — полином, построенный муравьем k; f — целевая функция.
Второй этап — приложение генетического алгоритма. Он модифицирует параметры муравьиного алгоритма с учетом эффективности найденных решений [12]. Алгоритм последовательно применяет к популяции муравьев (к их параметрам) три оператора: выбора, кроссинговера, мутации. В качестве оператора выбора используется метод рулетки. Муравей попадает в новую популяцию с вероятностью:
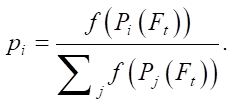 (5)
(5)
Оператор скрещивания — побитовая сумма битовых представлений параметров выбранных особей. Оператор мутации — инверсия случайного бита у битового представления параметра особи.
Феромоны, оставленные на вершинах-цветах, также применяются на этапе опыления. Данный этап использует популяционную идею. К популяции цветов прилагаются четыре оператора: селекции, кроссбридинга, лайнбридинга и старения. Каждый цветок кроме хранимого значения вершины-монома имеет параметр — возраст. Оператор селекции выбирает цветы с наибольшей концентрацией феромонов. Оператор кроссбридинга с некоторой вероятностью вводит новые цветы, моном которых представляет произведение объединения признаков из мономов цветов-родителей:
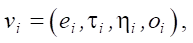
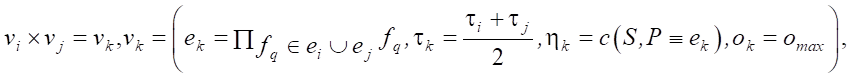
где e — моном нового цветка; τ — случайное количество феромона, не превосходящее τ0, отложенного на цветок; η — эвристическая составляющая; o — возраст цветка; omax — установленная продолжительность жизни цветка.
Если в результате преобразования появились цветы, уже находящиеся в популяции, то новые цветы не создаются, а обновляется возраст у имеющихся. Оператор лайнбридинга с небольшой вероятностью добавляет в популяцию новый цветок с единственным признаком. Этот оператор используется, чтобы оставить возможность вытесненным признакам участвовать в работе алгоритма. Оператор старения понижает индикатор возраста у каждого цветка. Если индикатор старения стал равен нулю, цветок выбывает из популяции.
Таким образом, конфигурируемые параметры алгоритма: n, τ0, ρ, omax, α0, β0, Q0, pkross, pmut. Выбор их значений зависит от текущей прикладной задачи и влияет на скорость сходимости алгоритма. Отметим, что параметры α0, β0, Q0 адаптируются в ходе работы генетического алгоритма, поэтому их первоначальные значения не имеют большого влияния на скорость сходимости алгоритма, особенно при значительном количестве итераций представленного ниже алгоритма.
Начало
1. Определить параметры n, τ0, ρ, omax, α0, β0, Q0, pkross, pmut
2. Положить c = 0, P = ∅
3. Положить множество цветов V = {vi = (ei = fi, τi = rand(0, τ0), ηi = c(S, Pi ≡ fi), oi = omax) | Ɐfi ∈ F}
4. Положить множество муравьев A = {αk = (αk = α0, βk = β0, Qk = Q0)}
5. До достижения критерия остановки
5.1. Для каждого муравья αk ∈ A
5.1.1 Ek(t) = {vrandom}
5.1.2. ck(t – 1)
5.1.3. ck(t) = ηi
5.1.4. Пока ck(t) > ck(t – 1)
5.1.4.1. Выбрать v в соответствии с правилом (4)
5.1.4.2. Ek(t) = ∪ {v}
5.1.4.3. ck(t – 1) = ck(t)
5.1.4.4. 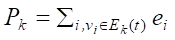
5.1.4.5 ck(t) = f(S, Pk)
5.1.5. Если ck(t) > c
5.1.5.1. c = ck(t)
5.1.5.2. P = Pk
5.1.6. Для каждого vi ∈ Ek(t) вычислить Δτv в соответствии с правилом (5)
5.2. Применить оператор выбора A = Sselection(A)
5.3. Применить оператор кроссинговера A = Scrossover(A)
5.4. Применить оператор мутации A = Smutation(A)
5.5. Применить оператор селекции цветов V = Sselection(V)
5.6. Применить оператор кроссбридинга V = Scrossbreeding(V)
5.7. Применить оператор лайнбридинга V = Slinebreeding(V)
5.8. Применить оператор старения V = Saging(V)
6. Вернуть значения c, P
Критерием остановки алгоритма может быть количество итераций или сходимость решений к одному значению. Таким образом, представленный метод оптимизации муравьев-опылителей решает задачу построения функции риска и отбора признаков для расширенной модели Кокса. Если для гипотезы (1) есть нетривиальные примеры, их можно найти описанным методом.
Алгоритм протестировали на базе данных больных раком предстательной железы. Они лечились или наблюдались с января 1996 по декабрь 2016 года в Российском научном центре радиологии и хирургических технологий имени академика А. М. Гранова Минздрава России [13]. В исследование включены обезличенные данные о распространенности опухолевого процесса у 5073 пациентов.
Перечень признаков, используемых в работе, с их описанием и количеством ненулевых записей представлен в таблице 1.
Таблица 1
Признаки набора данных
|
Название признака |
Описание |
Значение |
Количество заполненных записей |
|
|
краткое |
полное |
|||
|
‘ТР’ |
Тип распространения опухолевого процесса |
Поражение соседних органов и структур, наличие регионарных и отдаленных метастазов |
1 — локализованный 2 — местно-распространенный 3 — метастатический |
5073 |
|
‘ВУ’ |
Время удвоения ПСА |
Удвоение сывороточной концентрации ПСА, указывающее на возможное удвоение числа опухолевых клеток |
Число с плавающей точкой |
2423 |
|
‘ПГ’ |
Сумма баллов по шкале Глисона |
Порядковая переменная. Отражает гистологическую дифференцировку опухоли |
1 — ПГ < 7 2 — ПГ = 7 3 — ПГ > 7 |
3968 |
|
‘ПСА’ |
Сывороточная концентрация ПСА, послужившая основанием для биопсии |
Простат-специфический антиген. Гликопротеин, сериновая протеаза в норме вырабатывается секреторным эпителием предстательной железы. Разжижает эякулят, улучшает подвижность сперматозоидов. Концентрация выше 4 нг/мл может быть основанием для биопсии |
Число с плавающей точкой |
4760 |
|
‘образование’ |
Уровень образования пациента |
Завершенное образование пациента на момент постановки диагноза |
0 — среднее общее 1 — среднее специальное 2 — высшее 3 — ученая степень |
4622 |
|
‘возраст’ |
Возраст пациента |
Возраст пациента на момент постановки диагноза |
Целое число |
5073 |
|
‘резус’ |
Резус-фактор |
Наличие или отсутствие белка, отвечающего за резус-фактор |
1 — положительный 2 — отрицательный |
399 |
Не все признаки, представленные в таблице 1, существенны для исследования выживаемости. Есть и малозначимые (например, ‘образование’, ‘резус’). Они нужны для демонстрации корректной работы алгоритма, решающего задачу отбора признаков. Наличие коррелируемых и не очень важных признаков показывает практическую возможность использования алгоритма в условиях, когда заранее не известны ни зависимость признаков, ни их значимость.
Алгоритм реализован на языке программирования Python в пакете CoxPHFitter из библиотеки Lifelines. Для хранения и обработки данных использовалась программная библиотека Pandas.
Перед запуском алгоритма данные предварительно обработали. Это обусловлено тем, что в базе данных больных раком предстательной железы есть пропуски по ряду значений у некоторых пациентов. Для устранения проблемы использовали два способа обработки базы данных — удаление наблюдений и замена с учетом других значений в столбце [14]. Признаки ‘ТР’, ‘ВУ’ и ‘возраст’ являются важными и играют роль индикатора консистентности данных, поэтому удалялись наблюдения без этих признаков. Показатель Глисона ранжировали. Каждому наблюдению присвоили одно из трех значений: 1 — ПГ < 7 (1281 наблюдений); 2 — ПГ = 7 (1479 наблюдений); 3 — ПГ > 7 (1208 наблюдений).
Для остальных признаков отсутствующие значения заполняли методом k-взвешенных ближайших соседей. Такое восстановление пропущенных значений основывается на предположении, что близость экземпляров по измеренным признакам указывает на их близость по неизмеренным признакам [15]. Метод k-взвешенных ближайших соседей предпочтителен ввиду небольших временных затрат на восстановление пропущенных значений [16], хотя есть более эффективные подходы [17].
Алгоритм реализован со следующим набором параметров: n = 12; τ0 = 0,01; ρ = 0,8; omax = 3; α0 = 0,5; β0 = 2; Q0 = 25; pkross = 0,9; pmut = 0,2. Приведенный список значений параметров рекомендуется для первоначальной конфигурации алгоритма. Однако его можно изменить для решения конкретной задачи. В таблице 2 представлены результаты предложенного алгоритма.
Таблица 2
Значения С-индекса и функции приспособленности 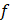 в зависимости от полинома функции риска расширенной модели Кокса, найденного при заданных балансировочных коэффициентах
в зависимости от полинома функции риска расширенной модели Кокса, найденного при заданных балансировочных коэффициентах
|
Полином аддитивно-мультипликативной функции риска расширенной модели Кокса |
C-индекс |
Функция приспособленности |
Балансировочные коэффициенты ω1; ω2; ω3; ω4 |
|
‘ТР’+‘ВУ’ |
0,836789 |
0,782894 |
0,91;0,05;0,05;0,05 |
|
‘ТР’×‘ПГ’+‘ВУ’ |
0,840516 |
0,842814 |
0,99;0,05;0,05;0,05 |
|
‘ТР’+‘ВУ’+‘ПГ’ |
0,849790 |
0,746328 |
0,9;0,0;0,05;0,05 |
|
‘ТР’+‘ВУ’+‘ПГ’+‘ТР’×‘ВУ’ |
0,849828 |
0,827410 |
0,94;0,05;0,0;0,0 |
|
‘ТР’+‘ПГ’+‘ТР’×‘ВУ’×‘ПГ’ |
0,849830 |
0,841567 |
0,97;0,05;0,05;0,0 |
|
‘ТР’+‘ПГ’+‘ВУ’×‘ПГ’ |
0,850000 |
0,787661 |
0,94; 0,0;0,05;0,0 |
|
‘ТР’+‘ВУ’+‘ПГ’+‘ПСА’+‘образование’+ |
0,853691 |
0,838012 |
0,99; 0,0;0,0;0,05 |
|
‘ТР’+‘ВУ’+‘ПГ’+‘ТР’×‘ПГ’ |
0,855292 |
0,809308 |
0,94;0,05;0,0;0,05 |
|
‘ТР’+‘ТР’×‘ПГ’+‘ПГ’+‘ТР’×‘ВУ’ |
0,856241 |
0,764870 |
0,91;0,0;0,05;0,0 |
|
‘ТР’+‘ТР’×‘ПГ’×‘ПСА’+‘ПГ’+‘ПСА’+ |
0,861085 |
0,839459 |
0,95;0,05;0,0;0,0 |
|
‘ТР’+‘ВУ’+‘ПГ’+‘ПСА’+‘образование’+ |
0,861643 |
0,826508 |
0,97;0,0;0,0;0,05 |
|
‘ТР’+‘ВУ’+‘ПГ’+‘ПСА’+‘образование’+ |
0,862345 |
0,845098 |
0,98;0,0;0,0;0,0 |
В таблице 2 вариации вхождения признаков в функцию риска ранжированы по возрастанию С-индекса. Здесь также указаны значения балансировочных коэффициентов фитнесс-функции (3), при которых найдено представленное решение и значение самой функции. Последние строки таблицы содержат функции риска с наиболее высоким индексом согласованности. Они достаточно сложны для анализа из-за нагруженности, связанной с низкими значениями соответствующих балансировочных коэффициентов.
Обсуждение и заключение. Лучший набор признаков для обучения стандартной (нерасширенной) модели Кокса — это весь представленный набор признаков, то есть функция ‘ТР’ + ‘ВУ’ + ‘ПГ’ + ‘ПСА’ + ‘образование’ + ‘возраст’ + ‘резус’ со значением c-индекса 0,853691. В то же время расширенная модель Кокса с найденной функцией риска ‘ТР’ + ‘ТР’ × ‘ПГ’ + ‘ПГ’ + ‘ТР’ × ‘ВУ’ имеет более высокий показатель c-индекса — 0,856241 с меньшим количеством используемых признаков.
Итоги данной научной работы позволяют сделать определенные выводы. Если иметь в виду представленную базу данных, то параметров ‘ТР’, ‘ВУ’, ‘ПГ’ достаточно для построения качественной модели анализа выживаемости. Таким образом, результат исследования — это возможность построения модели выживаемости с меньшим количеством используемых признаков. Причем предложенное решение не уступает или превосходит результативность классической модели Кокса, для обучения которой задействуют много признаков.
Алгоритм, созданный в рамках данной работы, способен решать задачу нахождения лучшей комбинации признаков за приемлемое число итераций (30). Набор регуляризующих коэффициентов позволяет задать алгоритму определенную конфигурацию. Благодаря этому специалист прикладной области может сделать выбор в пользу улучшения качества предсказания, сокращения количества признаков или исключения проблемы переобучения.
Итак, класс метаэвристических алгоритмов приемлем для решения поставленной задачи. На этапе опыления строятся мономы в полиноме, то есть проводится поиск мультипликативных зависимостей признаков. На этапе муравьиного алгоритма строится полином из мономов, то есть идет поиск аддитивных зависимостей признаков. Генетический этап необходим, чтобы улучшить сходимость и стабильность работы муравьиного алгоритма.
Для рассмотренного набора данных предложенный алгоритм повысил точность предсказания. Правда, незначительно. С-индекс увеличился всего на 0,3 %, с 0,853691 до 0,856241. Однако количество рассматриваемых признаков сократилось на 57,1 %, с 7 до 3. Меньшее число признаков в прогностической модели облегчает работу врачей, позволяет выиграть время при принятии решений и может снизить вероятность ошибок при интерпретации данных.
Список литературы
1. Archetti A, Lomurno E, Lattari F, Martin A, Matteucci M. Heterogeneous Datasets for Federated Survival Analysis Simulation. In: Proc. Companion of the 2023 ACM/SPEC International Conference on Performance Engineering. New York: Association for Computing Machinery; 2023. P. 173–180. http://doi.org/10.1145/3578245.3584935
2. Atlam M, Torkey H, El-Fishawy N, Salem H. Coronavirus Disease 2019 (COVID-19): Survival Analysis Using Deep Learning and Cox Regression Model. Pattern Analysis and Applications. 2021;24:993–1005. http://doi.org/10.1007/s10044-021-00958-0
3. Govindarajulu US, Malloy EJ, Ganguli B, Spiegelman D, Eisen EA. The Comparison of Alternative Smoothing Methods for Fitting Non-Linear Exposure-Response Relationships with Cox Models in a Simulation Study. The International Journal of Biostatistics. 2009;5(1):2. http://doi.org/10.2202/1557-4679.1104
4. Miren Hayet-Otero, Fernando García-García, Dae-Jin Lee, Joaquín Martínez-Minaya, Pedro Pablo España Yandiola, Isabel Urrutia Landa, et al. Extracting Relevant Predictive Variables for COVID-19 Severity Prognosis: An Exhaustive Comparison of Feature Selection Techniques. PLoS One. 2023;18(4):e0284150. https://doi.org/10.1371/journal.pone.0284150
5. Berenguer CV, Pereira F, Câmara JS, Pereira JA. Underlying Features of Prostate Cancer — Statistics, Risk Factors, and Emerging Methods for Its Diagnosis. Current Oncology. 2023;30(2):2300–2321. https://doi.org/10.3390/curroncol30020178
6. Жаринов, Г.М., Богомолов О.А. Исходное время удвоения простатспецифического антигена: клиническое и прогностическое значение у больных раком предстательной железы. Онкоурология. 2014;(1):44–48.
7. Kneev AY, Shkol’nik MI, Bogomolov OA, Zharinov GM. Prostate Specific Antigen Density as a Prognostic Factor in Patients with Prostate Cancer Treated with Combined Hormonal Radiation Therapy. Siberian Journal of Oncology. 2022;21(3):12–23. https://doi.org/10.21294/1814-4861-2022-21-3-12-23
8. Ewees AA, Al-qaness MA Abualigah L, Oliva D, Algamal ZY, Anter AM, et al. Boosting Arithmetic Optimization Algorithm with Genetic Algorithm Operators for Feature Selection: Case Study on Cox Proportional Hazards Model. Mathematics. 2021;9(18):2321. https://doi.org/10.3390/math9182321
9. Alabdallah A, Ohlsson M, Pashami S, Rögnvaldsson Th. The Concordance Index Decomposition: A Measure for a Deeper Understanding of Survival Prediction Models. Artificial Intelligence in Medicine. 2024;148:102781. https://doi.org/10.48550/ARXIV.2203.00144
10. Cavalcante Th, Ospina R, Leiva V, Cabezas X, Martin-Barreiro C. Weibull Regression and Machine Learning Survival Models: Methodology, Comparison, and Application to Biomedical Data Related to Cardiac Surgery. Biology. 2023;12(3):442. https://doi.org/10.3390/biology12030442
11. Guangyu Liu, Yuwei Bai, Ling Zhu, Qingyun Wang, Wei Zhang. A Sequential Excitation and Simplified Ant Colony Optimization Based Global Extreme Seeking Control Method for Performance Improvement. Swarm and Evolutionary Computation. 2024;86:101522. https://doi.org/10.1016/j.swevo.2024.101522
12. Blagoveshchenskaya EA, Mikulik II, Strüngmann LH. Ant Colony Optimization with Parameter Update Using a Genetic Algorithm for Travelling Salesman Problem. In: Proc. Workshop “Models and Methods for Researching Information Systems in Transport”. 2020;2803:20–25. URL: https://ceur-ws.org/Vol-2803/paper3.pdf (accessed: 17.09.24).
13. Жаринов Г.М. База данных больных раком предстательной железы. База данных РФ. № 2016620331. 2016. 1 с. URL: https://www1.fips.ru/fips_servl/fips_servlet?DB=DB&DocNumber=2016620331&TypeFile=html (дата обращения: 17.09.2024).
14. Ghannad-Rezaie M, Soltanian-Zadeh H, Hao Ying, Ming Dong. Selection-Fusion Approach for Classification of Datasets with Missing Values. Pattern Recognition. 2010;43(6):2340–2350. https://doi.org/10.1016/j.patcog.2009.12.003
15. Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, et al. Missing Value Estimation Methods for DNA Microarrays. Bioinformatics. 2001;17(6):520–525. https://doi.org/10.1093/bioinformatics/17.6.520
16. Koshechkin AA, Andryushchenko VS, Zamyatin AV. A New Method to Missing Value Imputation for Immunosignature Data. CTM (Sovremennye tehnologii v medicine). 2019;11(2):19–24. https://doi.org/10.17691/stm2019.11.2.03
17. Eunseo Oh, Hyunsoo Lee. Quantum Mechanics-Based Missing Value Estimation Framework for Industrial Data. Expert Systems with Applications. 2024;236:121385. https://doi.org/10.1016/j.eswa.2023.121385
Об авторах
И. И. МикуликРоссия
Илья Игоревич Микулик, аспирант кафедры высшей математики
190031, г. Санкт-Петербург, Московский пр., 9
Г. М. Жаринов
Россия
Геннадий Михайлович Жаринов, доктор медицинских наук, профессор, главный научный сотрудник отдела лучевых и комбинированных методов лечения
197758, г. Санкт-Петербург, пос. Песочный, ул. Ленинградская, 70
А. Ю. Кнеев
Россия
Алексей Юрьевич Кнеев, кандидат медицинских наук, старший преподаватель кафедры радиологии, хирургии и онкологии, врач-онколог отделения онкоурологии
197758, г. Санкт-Петербург, пос. Песочный, ул. Ленинградская, 70
Рецензия
Для цитирования:
Микулик И.И., Жаринов Г.М., Кнеев А.Ю. Алгоритм построения функции риска расширенной модели Кокса и его применение на базе данных больных раком предстательной железы. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):413-423. https://doi.org/10.23947/2687-1653-2024-24-4-413-423. EDN: LNZDKF
For citation:
Mikulik I.I., Zharinov G.M., Kneev A.Yu. Algorithm for Constructing the Hazard Function of the Extended Cox Model and its Application to the Prostate Cancer Patient Database. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):413-423. https://doi.org/10.23947/2687-1653-2024-24-4-413-423. EDN: LNZDKF












































